Тесты по теме «Операции над множествами» онлайн
-
Множества и операции над ними
19.12.2022 859 0
Тест для проверки знаний учащихся 8 класса по теории вероятности по теме «Множества. Операции над множествами». Тест содержит 20 вопросов с выбором ответа
-
Множества. Операции над множествами.
21.09.2021 1049 0
Данный тест можно использовать на этапе контроля усвоения материала по теме «Множества и операции над ними» Возраст учеников 6-9 классы.
-
Комбинаторика 6 класс проверочная работа.

20.04.2020 1144 0
Проверочный тест по теме «Решение комбинаторных задач» для 6 класса
-
Множества в математике
15.03.2023 4 0
Данный тест предназначен для учеников школ и студентов как итоговый по теме «Множества».
-
Операции над множествами
10.10.2019 2125 0
Тест по теме «Операции над множествами». Информатика 7 класс
-
Множества и операции над ними — Вариант № 8
04.
 11.2021
6
0
11.2021
6
0
Перед Вами тест, проверяющий усвоение темы «Множества и операции над ними». Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по вашей специальности. Планируется, что на выполнение этого теста Вы потратите не более 20 минут.
-
Множества и операции над ними — Вариант № 9
04.11.2021 5 0
Перед Вами тест, проверяющий усвоение темы «Множества и операции над ними». Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по вашей специальности. Планируется, что на выполнение этого теста Вы потратите не более 20 минут.

-
Множества и операции над ними
19.03.2023 4 0
Данный тест составлен специально для учебника по дисциплине » Способы математической обработки данных», включает в себя 15 разнообразных вопросов по теме «Множества»
-
Некоторые сведения из теории множеств
14.02.2020 1520 0
Человеческое мышление устроено так, что мир представляется состоящим из отдельных «объектов». Философам давно ясно, что мир – единое неразрывное целое и выделение в нем объектов – это не более чем произвольный акт нашего мышления, позволяющий сформировать доступную для рационального анализа картину.
 Но как бы там ни было, выделение объектов и их совокупностей – естественный способ организации нашего мышления, поэтому неудивительно, что он лежит в основе главного инструмента описания точного знания – математики. Понятие множества принадлежит к числу фундаментальных неопределяемых понятий математики.
Но как бы там ни было, выделение объектов и их совокупностей – естественный способ организации нашего мышления, поэтому неудивительно, что он лежит в основе главного инструмента описания точного знания – математики. Понятие множества принадлежит к числу фундаментальных неопределяемых понятий математики. Основы дискретной математики
14.06.2020 351 0
Тест предназначен для проверки знания понятия множества, операций над множествами, логических операции, таблиц истинности.
-
Множества для начальной школы
22.12.2020 2 0
Необходимо пройти тест для закрепления изученоой темы по множествам для начальных классов
-
Множества и операции над ними — Вариант № 1
04.
 11.2021
12
0
11.2021
12
0
Перед Вами тест, проверяющий усвоение темы «Множества и операции над ними». Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по вашей специальности. Планируется, что на выполнение этого теста Вы потратите не более 20 минут.
-
Множества и операции над ними — Вариант № 2
04.11.2021 34 0
Перед Вами тест, проверяющий усвоение темы «Множества и операции над ними». Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по вашей специальности. Планируется, что на выполнение этого теста Вы потратите не более 20 минут.

-
Множества и операции над ними — Вариант № 4
04.11.2021 5 0
Перед Вами тест, проверяющий усвоение темы «Множества и операции над ними». Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по вашей специальности. Планируется, что на выполнение этого теста Вы потратите не более 20 минут.
-
Множества и операции над ними — Вариант № 7
04.11.2021 5 0
Перед Вами тест, проверяющий усвоение темы «Множества и операции над ними».
 Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по вашей специальности. Планируется, что на выполнение этого теста Вы потратите не более 20 минут.
Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по вашей специальности. Планируется, что на выполнение этого теста Вы потратите не более 20 минут. -
Множества и операции над множествами
11.03.2023 2 0
Данный тест позволит Вам проверить свои знания по теме «Множества». Время на прохождение теста не ограничено.
-
Операция над множествами
12.03.2023 2 0
Тесты помогут определить как усвоены понятия множество, подмножество, равные множества, а также пересечение и объединение множеств.
 При выполнении каждого теста отмечается правильный ответ и указывается правильность выполнения задания
При выполнении каждого теста отмечается правильный ответ и указывается правильность выполнения задания -
Множества и их основные элементы
26.03.2023 2 0
Для закрепления результата вам необходимо пройти тест. Все вопросы взяты из ранее изученного материала, все вопросы решаемы, желаем вам удачи.
-
Множества и операции над ними
04.11.2021 141 0
Перед Вами тест, проверяющий усвоение темы «Множества и операции над ними». Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по вашей специальности.
 Планируется, что на выполнение этого теста Вы потратите не более 60 минут.
Планируется, что на выполнение этого теста Вы потратите не более 60 минут. -
Множества и операции над ними — Вариант № 3
04.11.2021 5 0
Перед Вами тест, проверяющий усвоение темы «Множества и операции над ними». Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по вашей специальности. Планируется, что на выполнение этого теста Вы потратите не более 20 минут.
-
Множества и операции над ними — Вариант № 6
04.11.2021 6 0
Перед Вами тест, проверяющий усвоение темы «Множества и операции над ними».
 Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по вашей специальности. Планируется, что на выполнение этого теста Вы потратите не более 20 минут.
Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по вашей специальности. Планируется, что на выполнение этого теста Вы потратите не более 20 минут. -
Множества и операции над ними — Вариант № 10
04.11.2021 6 0
Перед Вами тест, проверяющий усвоение темы «Множества и операции над ними». Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по вашей специальности. Планируется, что на выполнение этого теста Вы потратите не более 20 минут.
-
Теоретико-множественные основы математической обработки информации.

12.03.2023 1 0
Вам предлагается тест по теме «Элементы теории множеств. Теоретико-множественные основы математической обработки информации». Данный тест состоит из 15 вопросов. На выполнение теста отводится 40 минут. Задания необходимо выполнять последовательно. После прохождения теста, система выдаст вашу оценку. Желаем удачи!
-
Операции над множествами
12.03.2023 1 0
Данный тест предназначен для проверки знаний пор разделу «Множества».
-
Тест по теме «Множества и операции над ними»
15.
 03.2023
5
0
03.2023
5
0
Уважаемые обучающиеся! Вам необходимо пройти образовательный тест по теме «Множества и их операции», в котором присутствуют элементы теории множеств, теоретико-множественные основы математической обработки информации.
-
Теоретико-множественные основы математической обработки информации
18.03.2023 3 0
Уважаемые обучающиеся! Вам необходимо пройти образовательный тест по теме «Множества и их операции», в котором присутствуют элементы теории множеств, теоретико-множественные основы математической обработки информации.
-
Тест «Множества»
19.
 03.2023
1
0
03.2023
1
0
Данный тест предназначен для проверки знаний по разделу «Множества».
-
Теоретико-множественные основы математической обработки информации.
19.03.2023 1 0
Вам предлагается тест по теме «Элементы теории множеств.Теоретико-множественные основы математической обработки информации». Данный тест состоит из 15 вопросов разных типов. Внимательно читайте задание. Он отлично подойдет тем, кто изучил множества, и хочет проверить свои знания. Желаем успехов!
-
Что Вы знаете о множествах?
26.03.2023 1 0
Проверьте, как хорошо вы владеете понятием «множество» и насколько хорошо разбираетесь в диаграммах Эйлера-Венна.

-
Множества и операции над ними
15.03.2023 1 0
После пройденной темы вам представлен тест, в котором включены как проверка теоретических знаний, так и практическая часть.
-
Теоретико-множественные основы математической обработки данных
15.03.2023 1 0
Тест для проверки знаний по теме «Множества», «Операции над множествами» и «Декартово произведение»
Множества. Операции над множествами — презентация онлайн
Множества.
Операции над
множествами
1
23
0011 0010 1010 1101 0001 0100 1011
45
1
2
4
Множество – совокупность объектов,
объединенных по какому – нибудь признаку.
0011 0010 1010 1101 0001 0100 1011
Множества обозначают большими буквами
латинского алфавита: А, В, С, D и т. д.
Объекты, составляющие множество,
называются элементами множества.
1
2
4
0011 0010 1010 1101 0001 0100 1011
Объекты, из которых образовано множество,
называются элементами.
Элементы множества принято обозначать строчными
буквами латинского алфавита: a, b, c… z.
Если элемент х принадлежит множеству М, то
записывают х М, если не принадлежит – x M
1
2
4
4. Виды множеств:
Дискретные множества(прерывные)- имеют отдельные элементы. Путёмсчёта распознаются.
Непрерывные множества- нет отдельных элементов. Распознаются путём
измерения.
Конечные множества- состоят из конечного числа элементов, когда можно
пересчитать все элементы множества.
Бесконечные множества- когда невозможно пересчитать все элементы
множества.
Упорядочные множества. Элемент из множества предшествует или следует
за другим.
 Множество натуральных чисел, расположенных в виде
Множество натуральных чисел, расположенных в виденатурального ряда.
Неупорядочные множества. Любое неупорядочное множество можно
упорядочить.
множество
Множество
0011 0010
1010 1101 0001 0100 1011
четырехугольников
Пространственные тела
Натуральные числа
элемент
Трапеция, параллелограмм, ромб,
квадрат, прямоугольник
Шар, прямоугольный
параллелепипед, призма,
пирамида, октаэдр
1
2
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11…
4
Квадраты чисел
1, 4, 9, 16, 25, 36, 49, 64, 81, 100 ..
Цифры десятичной системы
счисления
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Двузначные четные числа
10, 12, 14, 16 … 96, 98
множество людей на Солнце
0011 0010 1010 1101 0001 0100 1011
множество прямых углов равностороннего
треугольника
множество точек пересечения двух
параллельных прямых
1
2
4
Пустое множество- множество, не
содержащее ни одного элемента.
Обозначения некоторых
числовых множеств:
0011 0010 1010 1101 0001 0100 1011
N – множество натуральных чисел;
Z – множество целых чисел;
Q – множество рациональных чисел;
I — множество иррациональных чисел;
R – множество действительных чисел.
1
2
4
8. Способы задания множеств
Перечислением элементов (подходит для конечных множеств).Указать характеристическое свойство множества, т.е. то свойство,
которым обладают все элементы данного множества.
С помощью изображения :
— На луче
— В виде графика
С помощью кругов Эйлера. В основном используется при выполнении
действий с множествами или демонстрации их отношений.
0011 0010 1010 1101 0001 0100 1011
Характеристическое свойство – это такое
свойство, которым обладает каждый элемент,
принадлежащий множеству, и не обладает ни один
элемент, который ему не принадлежит.
1
2
Этот способ задания множеств является общим и
для конечных множеств, и для бесконечных.
4
«Множество А натуральных чисел,
меньших 7»: А = {x | x N и x<7}
0011 0010 1010 1101 0001 0100 1011
Множество В является подмножеством множества А (В А),
если каждый элемент множества В является также элементом
множества А.
 Пустое множество считают подмножеством
Пустое множество считают подмножествомлюбого множества. Любое множество является
подмножеством самого себя.
1
2
4
Отношения между множествами наглядно
представляют при помощи кругов Эйлера
0011 0010 1010 1101 0001 0100 1011
Круги Эйлера – это особые чертежи, при помощи
которых наглядно представляют отношения между
множествами.
А
В
А
В
Множества А и В
имеют общие
элементы, но ни
одно из них не
является
подмножеством
другого
В А
В
А
А В
1
А
А=В
2
4
А=В
В
Множества А и В
не пересекаются
произвольного
0011конечного
0010 1010 1101или
0001 0100
1011
бесконечного
множества
множеств называется множество, состоящее
из тех и только тех элементов, которые
принадлежат хотя бы одному из множеств А
или В.
Объединение множеств обозначается
1
П р и м е р : {1,2,3}
2
4
{2,3,4} = {1,2,3,4}.
13.
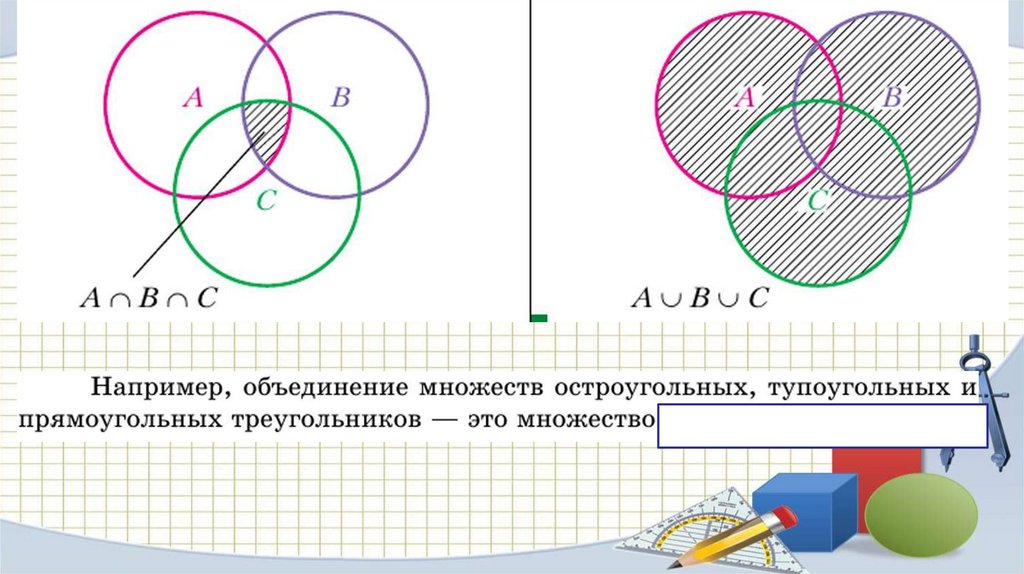
 ОБЪЕДИНЕНИЕ МНОЖЕСТВ0011 0010 1010 1101 0001 0100 1011
ОБЪЕДИНЕНИЕ МНОЖЕСТВ0011 0010 1010 1101 0001 0100 10111
2
4
любого конечного или
бесконечного множества множеств
множество,
состоящее из тех и
0011называется
0010 1010 1101 0001
0100 1011
только тех элементов, которые принадлежат
множествам А и В одновременно.
Пересечение множеств обозначается
Пример:
1
{2,3,4} = {2,3}
{1,2,3}
2
4
15. ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ
0011 0010 1010 1101 0001 0100 10111
2
4
0011
0010 1010
1101 0001
1011
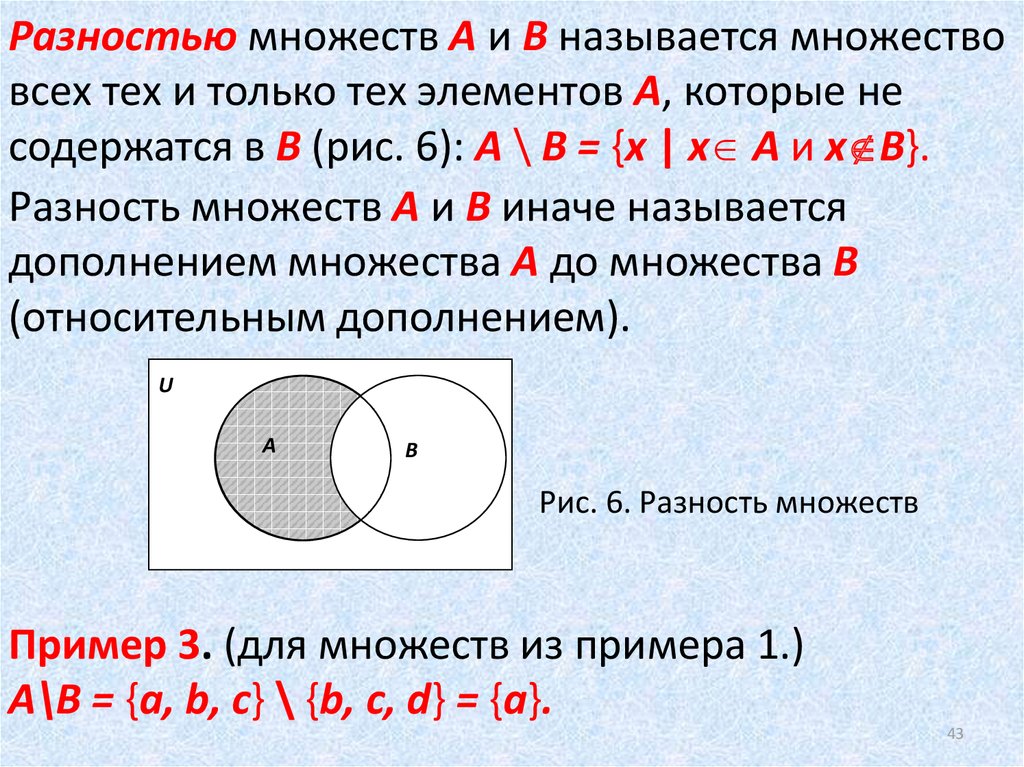
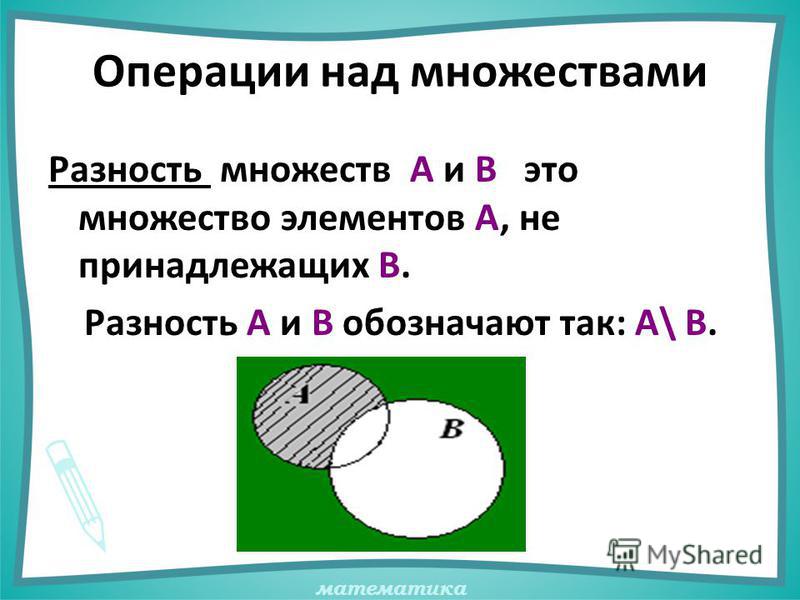
Разностью
множеств
А и 0100
В называется
множество, содержащее те и только те
элементы, которые принадлежат множеству А и не принадлежат множеству В.
Разность А и В Разность множеств А и В обозначают А \ В.
А
В
А\В
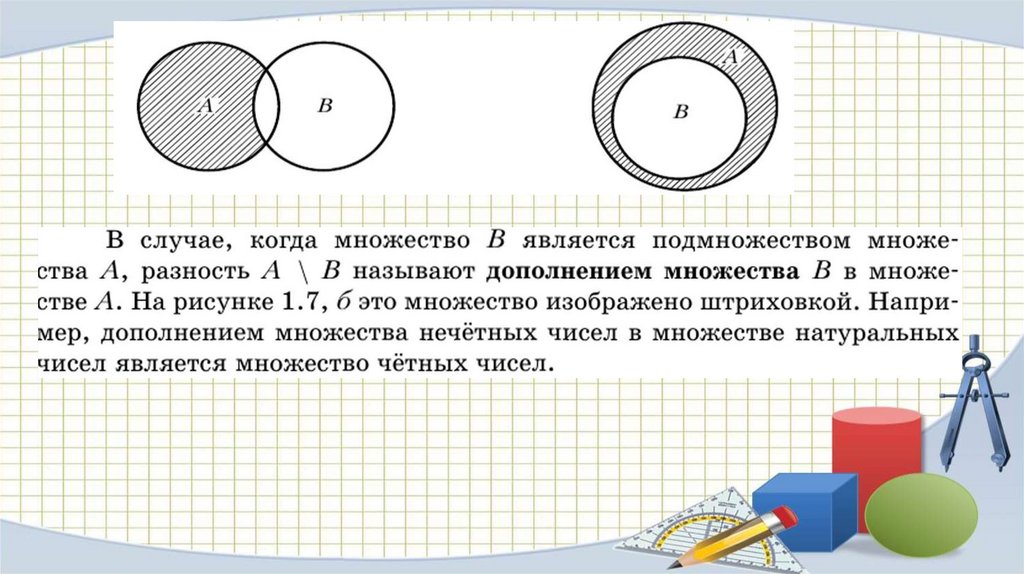
Пусть В А. Дополнением
множества В до множества А
называется множество,
содержащее те и только те
элементы множества А, которые
не принадлежат множеству В.
Дополнение множества В до
множества А обозначают В’
А
В’А
В
1
2
4
Общий вид
характеристического
свойства: «x А и x
В»
0011 0010 1010 1101 0001 0100 1011
Декартовым произведением
множеств А и В называется
множество всех пар, первая
компонента которых
принадлежит множеству А, а
вторая компонента
принадлежит множеству В.

Декартово произведение
обозначают А X В.
Операцию
нахождения
декартова
произведения
множеств
называют
декартовым умножением.
Если множества А и В
конечны и содержат
небольшое
число
элементов,
можно
изобразить декартово
произведение
этих
множеств при помощи
графа или таблицы.
Декартово
произведение
двух
числовых
множеств
(конечных
и
бесконечных)
можно
изображать
на
координатной
плоскости.
1
2
4
0011 0010 1010 1101 0001 0100 1011
А = {1, 2, 3}
В = {3, 5}
А
1
2
3
.
.
.
В
.
.
3
5
граф
1
2
4
таблица
0011 0010 1010 1101 0001 0100 1011
А = {1, 2, 3}
В = {3, 5}
1
2
4
Множества и операции с множествами
Операции с множествами — это концепция, аналогичная фундаментальным операциям над числами. Множества в математике имеют дело с конечным набором объектов, будь то числа, алфавиты или любые объекты реального мира.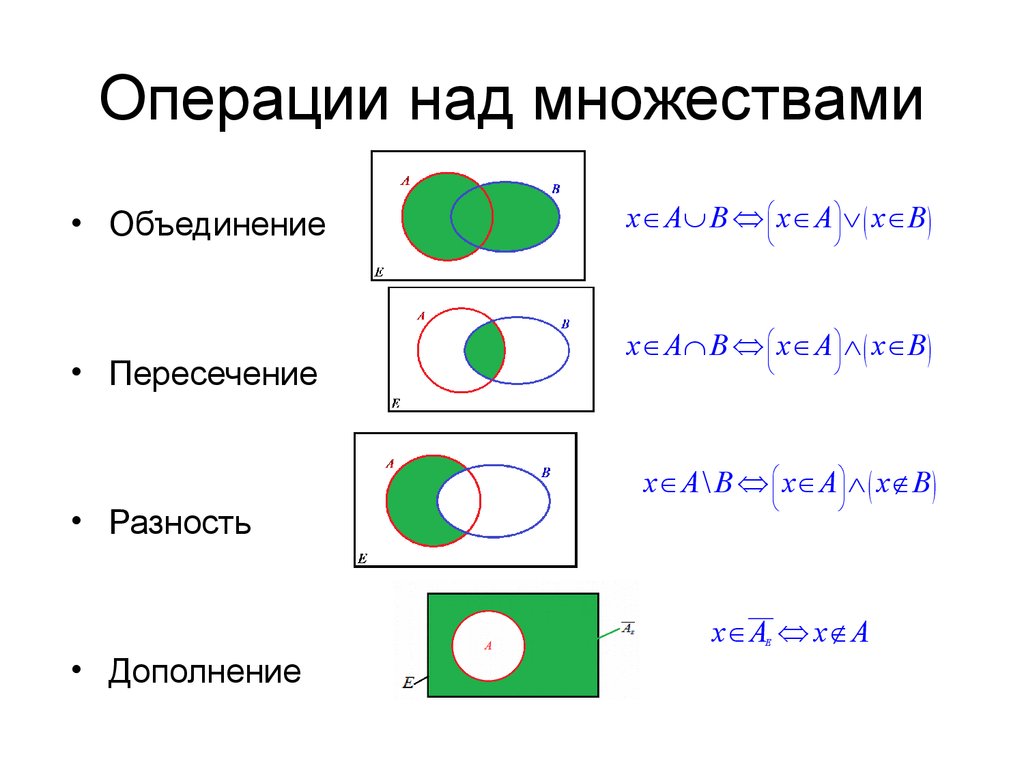 Иногда возникает необходимость установить связь между двумя или более множествами. Возникает понятие операций над множествами.
Иногда возникает необходимость установить связь между двумя или более множествами. Возникает понятие операций над множествами.
Существует четыре основных операции над множествами, включая объединение множеств, пересечение множеств, дополнение множеств и разность множеств . На этот раз мы изучим различные операции с множествами, обозначения представления множеств, способы работы с множествами и их использование в реальной жизни.
Что такое набор операций?
Набор определяется как набор объектов. Каждый объект внутри набора называется «Элемент». Множество может быть представлено в трех формах. Это форма заявления, форма списка и форма построителя наборов. Операции над множествами — это операции, которые применяются к двум другим множествам для установления связи между ними. Существует четыре основных вида операций над множествами:
- Объединение комплектов
- Пересечение наборов
- Дополнение к набору
- Разница между наборами/относительное дополнение
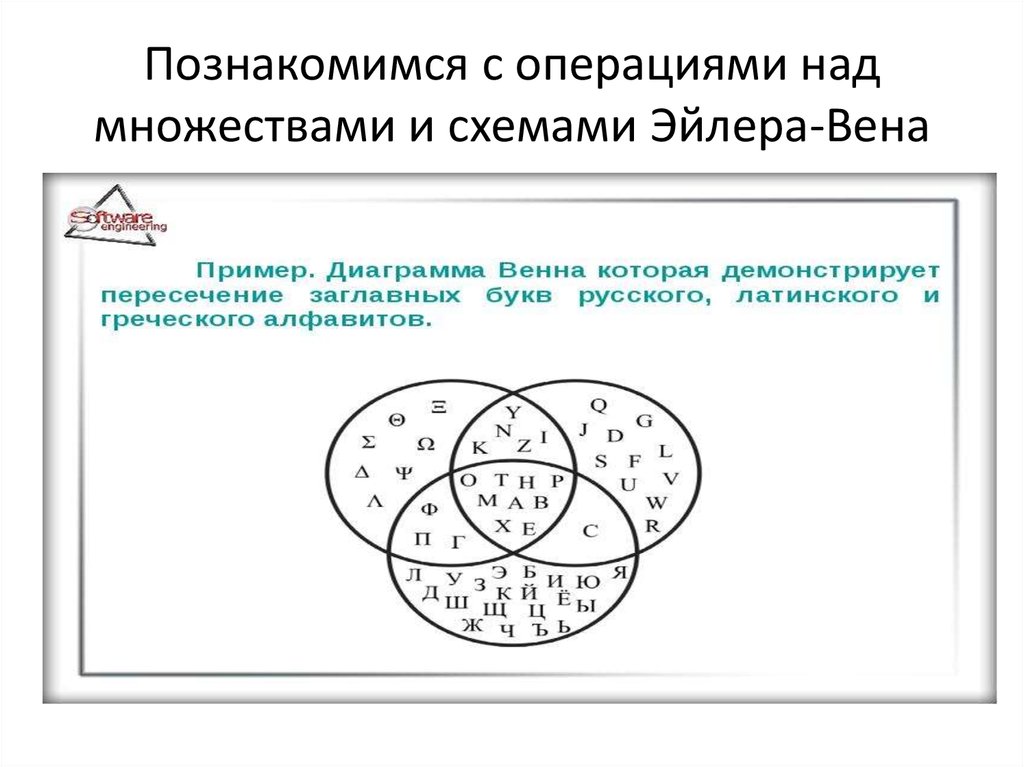
Прежде чем мы перейдем к обсуждению различных операций над множествами, давайте вспомним концепцию диаграмм Венна, поскольку она важна для понимания операций над множествами. Диаграмма Венна – это логическая диаграмма, показывающая возможную связь между различными конечными множествами. Это выглядит так, как показано ниже.
Диаграмма Венна – это логическая диаграмма, показывающая возможную связь между различными конечными множествами. Это выглядит так, как показано ниже.
Базовые операции над множествами
Теперь, когда мы знаем концепцию множества и диаграмму Венна, давайте подробно обсудим каждую операцию над множеством. Различные операции над множествами:
Объединение множеств
Для двух заданных множеств A и B, A∪B (читается как объединение B) — это множество различных элементов, которые принадлежат множествам A и B или обоим. Количество элементов в A ∪ B определяется выражением n(A∪B) = n(A) + n(B) − n(A∩B), где n(X) — количество элементов в множестве X. Чтобы Чтобы лучше понять эту операцию объединения множеств, давайте рассмотрим пример: если A = {1, 2, 3, 4} и B = {4, 5, 6, 7}, то объединение A и B равно определяется как A ∪ B = {1, 2, 3, 4, 5, 6, 7}.
Пример :
Дано U = {1, 2, 3, 4, 5, 6, 7, 8, 10}
X = {1, 2, 6, 7} и Y = {1, 3 , 4, 5, 8}
Найдите X ∪ Y и нарисуйте диаграмму Венна, иллюстрирующую X ∪ Y.
Решение:
X ∪ Y = {1, 2, 3, 4, 5, 6, 7, 8 } ← 1 записывается только один раз.
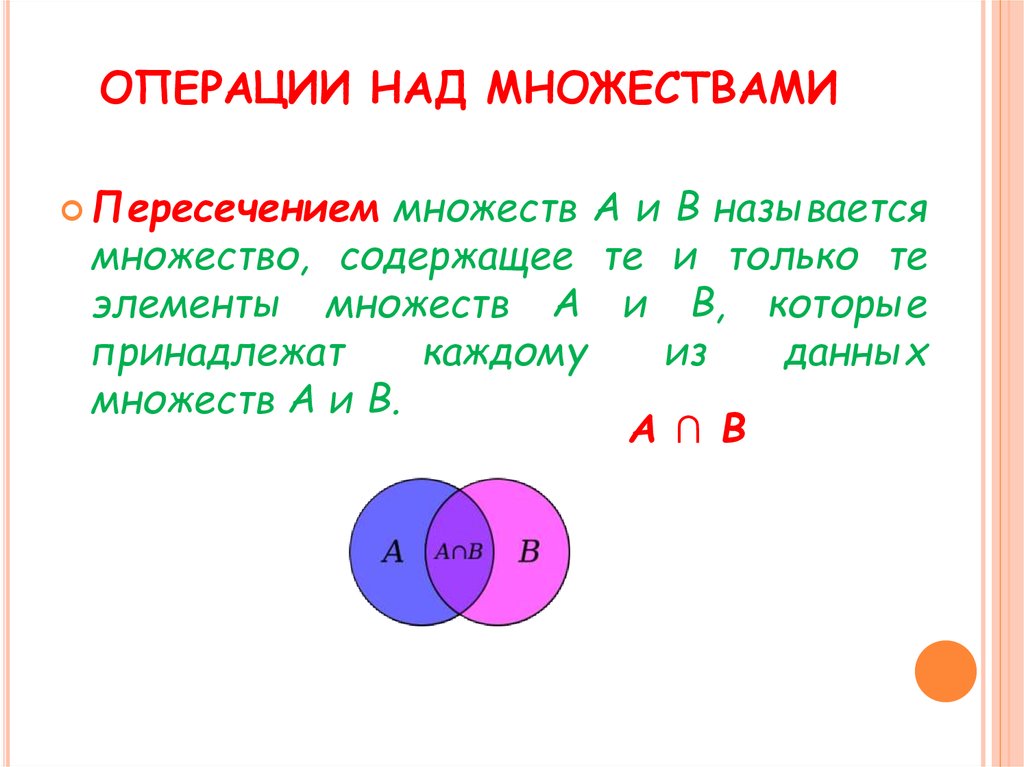
Пересечение множеств
Для двух заданных множеств A и B, A ∩ B (читается как пересечение A B) — это множество общих элементов, принадлежащих множествам A и B. Количество элементов в A ∩ B равно задается формулой n(A∩B) = n(A)+n(B)−n(A∪B), где n(X) — количество элементов в множестве X. Чтобы понять эту множественную операцию пересечения множеств лучше рассмотрим пример: если A = {1, 2, 3, 4} и B = {3, 4, 5, 7}, то пересечение A и B задается A ∩ B = {3, 4}.
Пример
Рассмотрим набор A = {3, 6, 9, 12} и набор B = {0, 3, 5, 8, 12}. Покажите пересечение между A и B через диаграмму Венна. Пусть множество U = {множество целых чисел до 20}.
Решение:
Пересечение между двумя множествами A и B можно определить как: 12}
Пересечение:
A ∩ B = {3, 12}
Представление диаграммы Венна для пересечения между множествами A и B:
Разность множеств
Разность операций над множествами подразумевает вычитание элементов из множества, что аналогично понятию разности между числами. Разность между множествами A и B, обозначенная как A − B, перечисляет все элементы, которые находятся в множестве A, но не в множестве B. Чтобы лучше понять эту операцию множества разности множеств, давайте рассмотрим пример: если A = {1, 2 , 3, 4} и B = {3, 4, 5, 7}, то разница между множествами A и B определяется соотношением A — B = {1, 2}.
Разность между множествами A и B, обозначенная как A − B, перечисляет все элементы, которые находятся в множестве A, но не в множестве B. Чтобы лучше понять эту операцию множества разности множеств, давайте рассмотрим пример: если A = {1, 2 , 3, 4} и B = {3, 4, 5, 7}, то разница между множествами A и B определяется соотношением A — B = {1, 2}.
Пример:
1. Если A = {2, 3, 4, 5, 6, 7} и B = {3, 5, 7, 9, 11, 13}, то найдите ( i) A – B и (ii) B – A.
Решение:
Согласно данному заявлению; A = {2, 3, 4, 5, 6, 7} и B = {3, 5, 7, 9, 11, 13}
(i) A – B
= {2 , 4, 6}
(ii) B – A
= {9, 11, 13}
Дополнение множеств
Дополнение множества A, обозначаемое как A′ или Ac (читается как дополнение), определяется как множество всех элементов данного универсального множества (U), которые не присутствуют в множестве A. Чтобы лучше понять эту операцию дополнения множеств, давайте рассмотрим пример: если U = {1, 2, 3, 4, 5, 6, 7, 8, 9} и A = {1, 2, 3, 4 }, то дополнение множества A задается формулой A’ = {5, 6, 7, 8, 9}.
Чтобы лучше понять эту операцию дополнения множеств, давайте рассмотрим пример: если U = {1, 2, 3, 4, 5, 6, 7, 8, 9} и A = {1, 2, 3, 4 }, то дополнение множества A задается формулой A’ = {5, 6, 7, 8, 9}.
Пример:
Учитывая = {0,1,2,3,4,5,6,7,8,9} и B = {0, 1, 4, 5, 6, 7, 8}, найдите дополнение B .
Ответ: B ‘ = {2, 3, 9}, таким образом, B ‘ — это множество всех чисел из 9. 903 B 9, которые не входят в 903 B 903.
Важные примечания по работе с наборамиФормула операции над множеством для объединения множеств: n(A∪B) = n(A) + n(B) − n(A∩B), а формула операции над множеством для пересечения множеств: n(A∩B) = n( А)+n(B)−n(A∪B).
Объединение любого множества с универсальным множеством дает универсальное множество, а пересечение любого множества А с универсальным множеством дает множество А
Объединение, пересечение, разность и дополнение — это различные операции над множествами.

Дополнением универсального множества является пустое множество U′ = ϕ. Дополнением пустого множества является универсальное множество ϕ′ = U.
Примеры операций установки
Пример 1: В школе каждый ученик играет либо в футбол, либо в футбол. Было установлено, что 200 студентов играли в футбол, 150 студентов играли в футбол и 100 студентов играли в оба. Найдите, сколько учеников было в школе, используя формулу операции над множествами.
Решение: Представим количество студентов, игравших в футбол, как n(F), а количество студентов, игравших в футбол, как n(S). Имеем n(F) = 200, n(S) = 150 и n(F ∩ S) = 100.
 Мы знаем, что
Мы знаем, чтоn(F∪S) = n(F) + n(S) − n(F∩S)
Следовательно, n(F∪S)=(200+150)−100
n(F∪S) = 350 — 100 = 250
Ответ: Всего в школе 250 учеников.
Пример 2: Если A = {a, b, c, d, e}, B = {a, e, i, o, u}, U = {a, b, c, d, e, f, г, з, и, к, к, л, о, и}. Найти
а) А ∪ В
б) А ∩ В
в) А’
г) А — ВРешение:
a) A ∪ B = {a, b, c, d, e, i, o, u}
b) A ∩ B = {a, e}
c) A’ = {f, g, h, i, j, k, l, o, u}d) A — B = {b, c, d}
Практические задачи
Задача 1 :
При опросе студентов университета 64 человека изучали курс математики, 94 — курс химии, 58 — курс физики, 28 — курс математики и физики, 26 изучали математику и химию, 22 — курс химии и физики, а 14 — все три курса. Найдите, сколько человек прошли только один курс.
Решение:
Шаг 1:
Пусть M, C, P представляют наборы студентов, изучавших математику, химию и физику соответственно
Шаг 2:
900 Из данной информации мыn(M) = 64, n(C) = 94, n(P) = 58,
n(MnP) = 28, n(MnC) = 26, n(CnP) = 22
n(MnCnP ) = 14
Шаг 3 :
Из основного материала у нас есть
Количество учеников, которые сдавали только математику
= n(M) — [n(MnP) + n(MnC) — n(MnCnP)]
= 64 — [28 + 26 — 14]
= 64 — 40
= 24
2 Шаг 4:
Количество студентов, которые прошли только химию:
= N (C) — [N (MNC) + N (CNP) — N (MNCNP)]
= 94 — [26 + 22-14 ].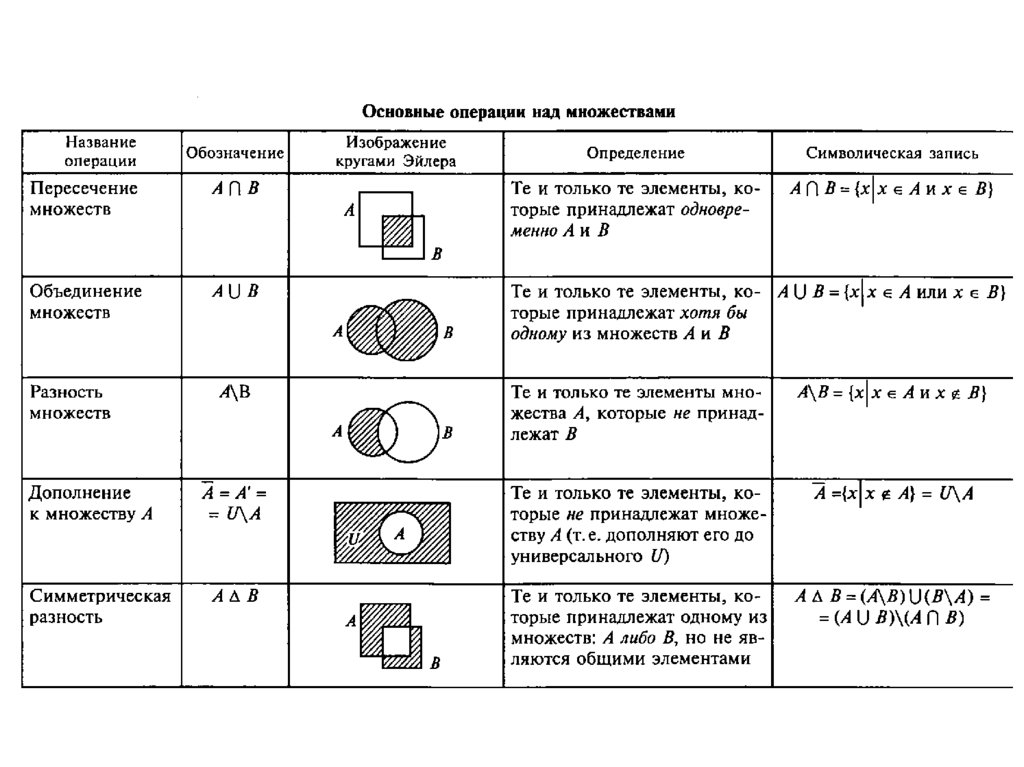 0006
0006
Число студентов, изучавших только физику:
= n(P) — [n(MnP) + n(CnP) — n(MnCnP)]
= 58 — [28 + 22 — 14]
= 58 — 36
= 22
Шаг 6:
Всего № студентов, которые прошли только один курс:
= 24 + 60 + 22
= 106
Следовательно, общее количество студентов, которые прошли только один курс, составляет 106.
Альтернативный метод (с использованием диаграммы Венна):
Шаг 1:
Диаграмма Венна, связанная с информацией, приведенной в вопросе:
Шаг 2:
Из диаграммы Венна выше, мы, мы have
Кол-во студентов, изучавших только математику = 24
Кол-во студентов, изучавших только химию = 60
Кол-во студентов, изучавших только физику = 22
Шаг 3:
Общее количество
= 24 + 60 + 22
= 106
Таким образом, общее количество студентов, прошедших только один курс, равно 106.
группа студентов, 65 играют в футбол, 45 играют в хоккей, 42 играют в крикет, 20 играют в футбол и хоккей, 25 играют в футбол и крикет, 15 играют в хоккей и крикет и 8 играют во все три игры. Найдите общее количество учащихся в группе (предположим, что каждый учащийся в группе играет хотя бы в одну игру).
Решение :
Шаг 1 :
Пусть F, H и C представляют набор студентов, которые играют в футбол, хоккей и крикет соответственно.
Шаг 2 :
Из предоставленной информации имеем
n(F) = 65 , n(H) = 45, n(C) = 42,
n(FnH) = 20, n( FnC) = 25, n(HnC) = 15
n(FnHnC) = 8
Шаг 3:
Из основного материала имеем
Общее количество учеников в группе равно n(FuHuC).
n(FuHuC) равно
= n(F) + n(H) + n(C) — n(FnH) — n(FnC) — n(HnC) + n(FnHnC)
Тогда, имеем
n(FuHuC) = 65 + 45 + 42 -20 — 25 — 15 + 8
n(FuHuC) = 100
Следовательно, общее количество студентов в группе равно 100.
Альтернативный метод (Используя диаграмму Венна) :
Шаг 1 :
Диаграмма Венна, относящаяся к информации, указанной в вопросе:
Шаг 2:
Общее количество студентов в группе:
= 28 + 12 + 18 + 7 + 10 + 17 + 8
= 100
Таким образом, общее количество студентов в группе равно 100.
Для дальнейшего понимания вы можете прочитать некоторые связанные темы о наборе и его работе:
- Надмножество
- Блок питания
- Конечные и бесконечные наборы
Набор операций с диаграммами Венна (видео)
Когда дело доходит до теории множеств и проблем работы с ними, часто бывает полезно визуализировать проблему с помощью изображения. Диаграммы Венна являются полезными инструментами для того, чтобы сделать именно это.
Диаграмма Венна обычно рисуется с двумя перекрывающимися кругами. Каждый круг представляет набор, а средняя область, где они перекрываются, представляет элементы, принадлежащие обоим наборам. Например, мы можем построить диаграмму Венна, которая показывает, что набор круглых фруктов и набор красных фруктов различны, но имеют некоторое перекрытие:
Каждый круг представляет набор, а средняя область, где они перекрываются, представляет элементы, принадлежащие обоим наборам. Например, мы можем построить диаграмму Венна, которая показывает, что набор круглых фруктов и набор красных фруктов различны, но имеют некоторое перекрытие:
Здесь мы видим, что апельсины, грейпфруты, киви, яблоки и гранаты являются круглыми фруктами, потому что они принадлежат левому кругу. Но поскольку яблоки и гранаты находятся в перекрывающейся области, они также принадлежат к набору красных фруктов, наряду с клубникой и красным перцем чили.
Давайте посмотрим на другой пример диаграммы Венна. У этого есть два набора, называемых A и B, каждый из которых содержит набор чисел. Некоторые из этих чисел принадлежат как к \(A\), так и к \(B\), в то время как некоторые другие числа не принадлежат ни к одному из наборов.
Основываясь на этой диаграмме, мы можем определить, какие числа принадлежат объединению, пересечению и дополнению \(A\) и \(B\).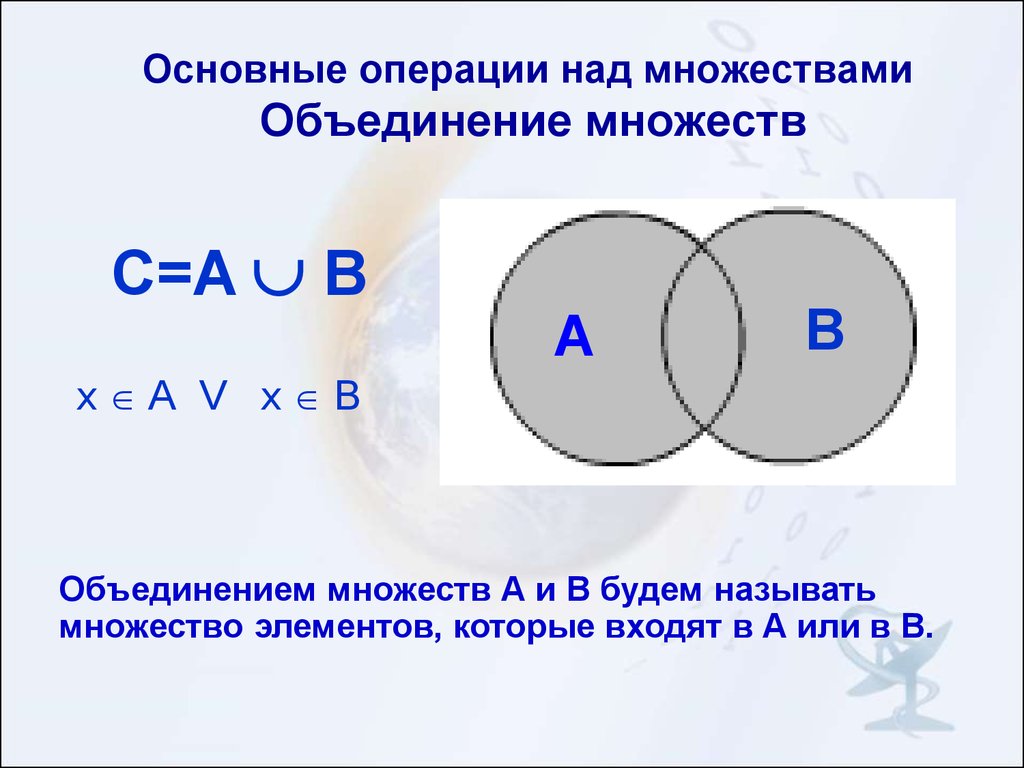 Давайте попробуем некоторые из них сейчас.
Давайте попробуем некоторые из них сейчас.
Что находится в \(A\стакане B\)? \(A\) объединение \(B\) означает объединение множеств. Чтобы найти это, нам нужно собрать всех элементов \(A\) и всех элементов \(B\). Это означает, что \(A\cup B\) будет содержать 9, 10, 7, 3, 16, 2, 15 и 12.
\(A\cup B = {9, 10, 7, 3, 16, 2, 15,12}\)
Как насчет \(A\cap B\)? \(A\) пересечь \(B\) означает найти то, что общего у множеств. Чтобы найти это пересечение, мы должны собрать только те числа, которые находятся в \(A\) и \(B\) одновременно. Это средняя часть. Остаются 3, 7 и 16.
\(A\cap B={3, 7, 16}\)
Теперь найдем дополнения. Что находится в \(A’\)? Это будут все числа, которые не входят в \(A\). Таким образом, у нас будут 2, 15 и 12 из B, а также 8 и 14, которые не находятся ни в \(A\), ни в \(B\).
\(A’={2,15,12,8,14}\)
Аналогично, \(B’\) будет иметь все числа, которых нет в \(B\). Это будет включать 9 и 10 из \(A\) и 8 и 14 извне \(A\) и \(B\).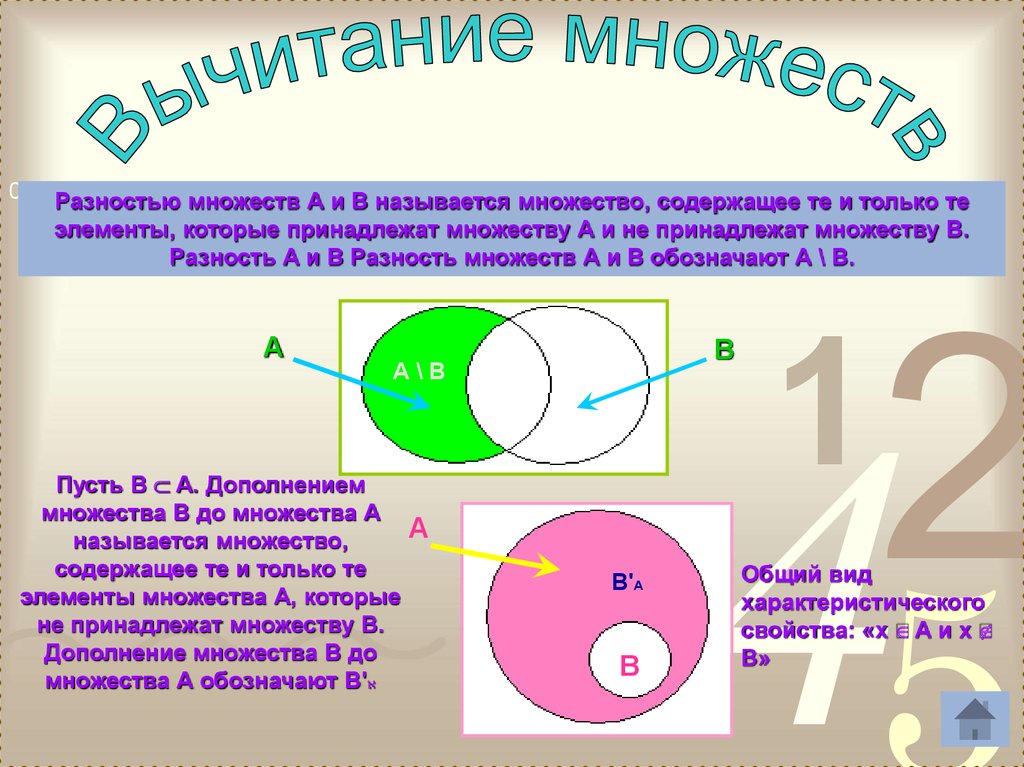
\(B’={9,10,8,14}\)
Интересно отметить, что если мы возьмем пересечение \(A’\) и \(B’\), мы получим \(A’\cap B’={8,14}\). Это все числа, которые не входят ни в \(A\), ни в \(B\). Итак, \(A’\cap B’\) эквивалентно дополнению \(A\cup B\).
\(A’\cap B’=(A\cup B)’\)
Еще пара вещей, которые мы можем легко найти из этой диаграммы Венна, — это разности множеств. Например, \(A\) минус \(B\) — это все в \(A\), чего нет в \(B\). Таким образом, мы не будем включать 7, 3 или 16.
\(A∖B={9,10}\)
И \(B\) минус \(A\) будет все в \(B \), которого нет в \(A\).
\(B∖A={2, 15, 12}\)
Эти различия между наборами игнорируют элементы, принадлежащие пересечению \(A\) и \(B\).
Хорошо, теперь, когда мы немного попрактиковались в использовании диаграммы Венна для определения объединений, пересечений, дополнений и различий между множествами, давайте теперь применим эти знания к текстовой задаче!
Ученые в аптечной лаборатории проводят эксперименты с различными растворами, чтобы определить, какой из них лучше всего использовать в новом антибиотике. Было протестировано десять растворов, которые были пронумерованы от одного до десяти. Согласно этим наборам, одни были определены как эффективные в борьбе с инфекцией, в то время как другие были настроены на быстрое распространение в организме пациента.
Было протестировано десять растворов, которые были пронумерованы от одного до десяти. Согласно этим наборам, одни были определены как эффективные в борьбе с инфекцией, в то время как другие были настроены на быстрое распространение в организме пациента.
Эффективные решения: {3, 4, 6, 7, 8, 9}
Быстрые решения: {1, 3, 5, 8, 10}
Создайте диаграмму Венна, чтобы определить, какие решения были одновременно эффективными и быстрые, которые были эффективными или быстрыми, и которые были эффективными, но не быстрыми.
Давайте начнем с рисования диаграммы Венна. Пометьте левый круг буквой «\(E\)» для «эффективного», а правый круг буквой «\(Q\)» для «быстрого». Отсюда мы можем просто написать, куда должно идти каждое из решений. Обратите внимание, что решения 3 и 8 находятся как в \(E\), так и в \(Q\), поэтому 3 и 8 будут записаны в перекрытии двух кругов. 2 не находится ни в \(E\), ни в \(Q\), поэтому 2 будет написано вне кружков.
Итак, первый вопрос, на который мы хотим ответить, таков: какие решения являются одновременно быстрыми и эффективными? Попробуем перефразировать это в терминах множественной записи. Всякий раз, когда вы слышите слово и, вы должны думать о «пересечении».
Всякий раз, когда вы слышите слово и, вы должны думать о «пересечении».
«и» подразумевает пересечение
Если решение считается быстрым и эффективным, оно должно быть и тем, и другим одновременно. В диаграмме Венна это означает, что она должна лежать в секции перекрытия и принадлежать пересечению двух множеств. Итак, какие решения находятся в \(E\cap Q\)? Бегло взглянув на нашу диаграмму, мы видим, что решения 3 и 8 единственные в \(E\cap Q\).
\(E\cap Q={3, 8}\)
Второй вопрос, который мы рассматриваем: «Какие решения были эффективными или быстрыми?» Этот вопрос обманчиво похож на предыдущий, но с одним существенным отличием. Теперь вместо того, чтобы искать, какие решения принадлежат обоим множествам одновременно, мы хотим найти, какие решения принадлежат множеству \(E\) или множеству \(Q\). Когда вы слышите слово или, вы должны думать «союз».
«или» подразумевает объединение
В задачах теории множеств математики считают, что слово «или» указывает на то, что элемент может принадлежать одному или другому множеству, или обоим, если элемент принадлежит хотя бы одному множеству.


 11.2021
6
0
11.2021
6
0

 Но как бы там ни было, выделение объектов и их совокупностей – естественный способ организации нашего мышления, поэтому неудивительно, что он лежит в основе главного инструмента описания точного знания – математики. Понятие множества принадлежит к числу фундаментальных неопределяемых понятий математики.
Но как бы там ни было, выделение объектов и их совокупностей – естественный способ организации нашего мышления, поэтому неудивительно, что он лежит в основе главного инструмента описания точного знания – математики. Понятие множества принадлежит к числу фундаментальных неопределяемых понятий математики.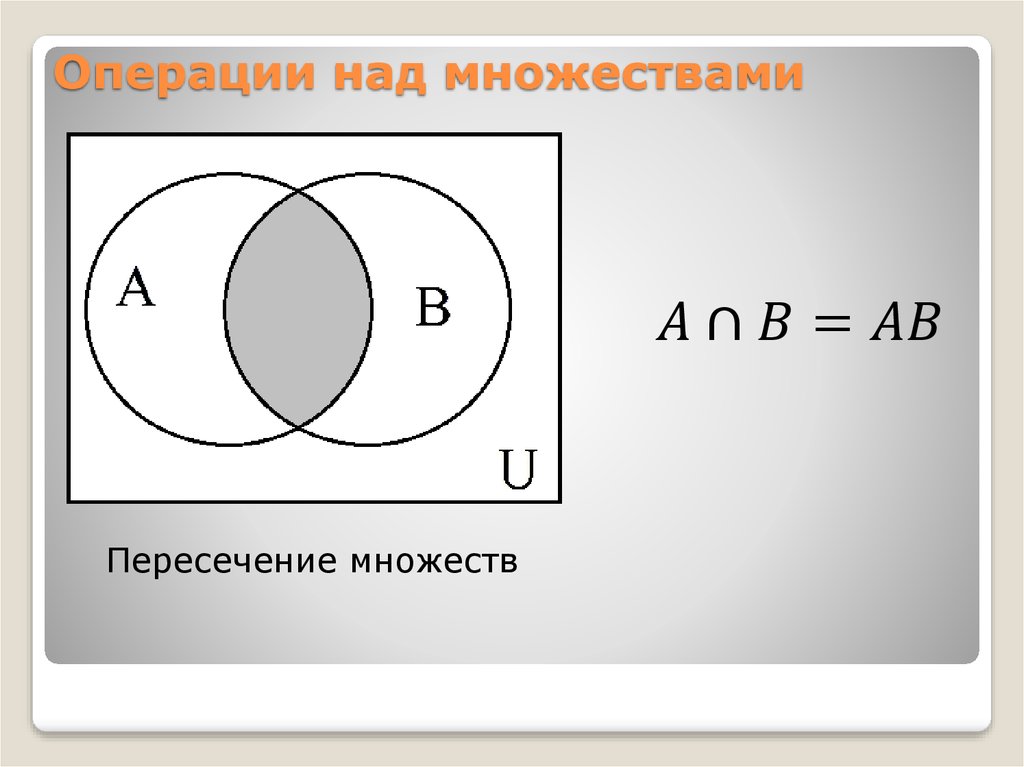 11.2021
12
0
11.2021
12
0
 Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по вашей специальности. Планируется, что на выполнение этого теста Вы потратите не более 20 минут.
Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по вашей специальности. Планируется, что на выполнение этого теста Вы потратите не более 20 минут. При выполнении каждого теста отмечается правильный ответ и указывается правильность выполнения задания
При выполнении каждого теста отмечается правильный ответ и указывается правильность выполнения задания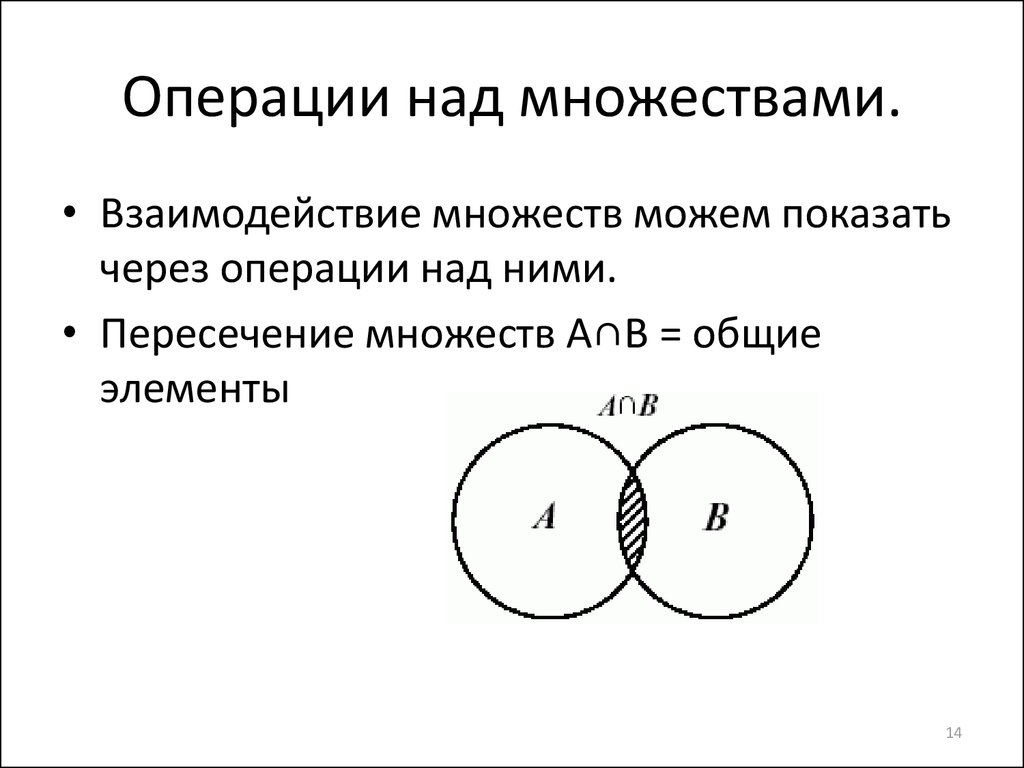 Планируется, что на выполнение этого теста Вы потратите не более 60 минут.
Планируется, что на выполнение этого теста Вы потратите не более 60 минут. Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по вашей специальности. Планируется, что на выполнение этого теста Вы потратите не более 20 минут.
Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по вашей специальности. Планируется, что на выполнение этого теста Вы потратите не более 20 минут.
 03.2023
5
0
03.2023
5
0
 03.2023
1
0
03.2023
1
0


 Мы знаем, что
Мы знаем, что