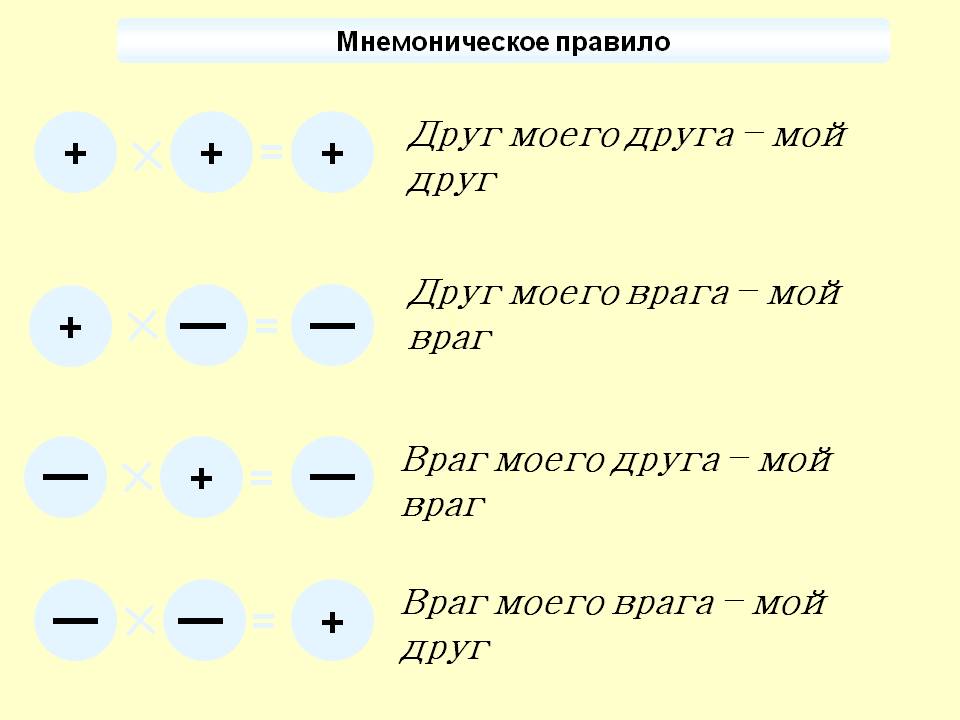
Деление чисел с разными знаками: правило и примеры
В этой статье мы рассмотрим деление положительных чисел на отрицательные и наоборот. Дадим подробный разбор правила деления чисел с разными знаками, а также приведем примеры.
Правило деления чисел с разными знаками
Правило для целых чисел с разными знаками, полученное в статье о делении целых чисел, справедливо также для рациональных и действительных чисел. Приведем более общую формулировку этого правила.
Правило деления чисел с разными знакамиПри делении положительного числа на отрицательное и наоборот нужно модуль делимого разделить на модуль делителя, а результат записать со знаком минус.
В буквенном виде это выглядит так:
a÷-b=-a÷b
-a÷b=-a÷b.
Результатом деления чисел с разными знаками всегда является отрицательное число. Рассмотренное правило, по сути, сводит деление чисел с разными знаками к делению положительных чисел, так как модули делимого и делителя являются положительными.
Еще одна эквивалентная математическая формулировка данного правила имеет вид:
a÷b=a·b-1
Чтобы разделить числа a и b, имеющие разные знаки, нужно число a умножить на число, обратное числу b, то есть b-1. Данная формулировка применима на множестве рациональных и действительных чисел, она позволяет перейти от деления к умножению.
Рассмотрим теперь, как применять описанную выше теорию на практике.
Как делить числа с разными знаками? Примеры
Ниже мы рассмотрим несколько характерных примеров.
Пример 1. Как делить числа с разными знаками?Разделим -35 на 7.
Сначала запишем модули делимого и делителя:
-35=35, 7=7.
Теперь разделим модули:
-357=357=5.
Допишем перед результатом знак минус и получим ответ:
-357=-5.
Теперь воспользуемся другой формулировкой правила и вычислим число, обратное 7.
7-1=17.
Теперь проведем умножение:
-35·17=—35·17=-357=-5.
Пример 2. Как делить числа с разными знаками?Вычислим значение 8÷-60.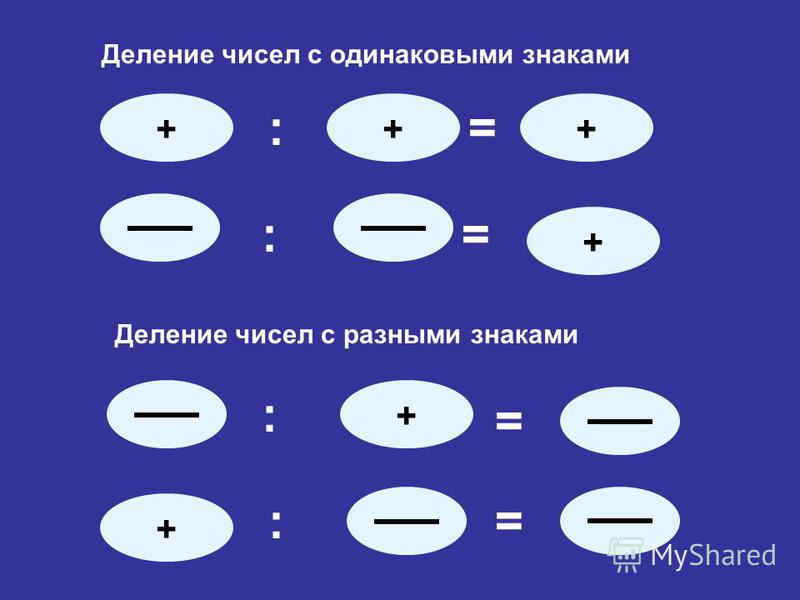
По правилу, имеем:
8÷-60=-8÷-60=-8÷60=-860.
Мы получили дробь, которую можно сократить на 4. После сокращения получаем:
8÷-60=-860=-215.
Это и есть окончательный ответ.
Если мы делим дробные числа с рациональными знаками, делимое и делитель нужно представить в виде обыкновенных дробей.
Пример 3. Как делить числа с разными знаками?Разделим смешанное число -3322 на десятичную дробь 0,(23).
Модули делимого и делителя соответственно равны 3322 и 0,(23). Переводя 3322 в обыкновенную дробь, получаем:
3322=3·22+322=6922.
Делитель также представим в виде обыкновенной дроби:
0,(23)=0,23+0,0023+0,000023=0,231-0,01=0,230,99=2399.
Теперь делим обыкновенные дроби, выполняем сокращения и получаем результат:
-6922÷2399=-6922·9923=-32·91=-272=-1312.
В заключение рассмотрим случай, когда делимое и делитель являются иррациональными числами и записываются в виде корней, логарифмов, степеней и т.д.
В такой ситуации частное записывается в виде числового выражения, которое по возможности упрощается.
Разделим числа 57 и -23.
По правилу деления чисел с разными знаками, запишем равенство:
57÷-23=-57÷-23=-57÷23=-57·23.
Избавимся от иррациональности в знаменателе и получим окончательный ответ:
-57·23=-5·4314.
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Отрицательные дроби. Действия с отрицательными дробями
- Сложение и вычитание
- Умножение и деление
Отрицательные дроби — это дроби, числитель или знаменатель которых является отрицательным числом.
Отрицательные дроби могут быть записаны по-разному. Например, рассмотрим два частных:
-2 : 7 и 2 : (-7),
каждое из них равно отрицательному числу
Каждое из данных частных можно записать в виде дроби, в которой дробная черта заменит знак деления:
| -2 : 7 | = | -2 | и | 2 : (-7) | = | 2 | . |
| 7 | -7 |
Следовательно, при записи отрицательных дробей знак минус
можно ставить перед дробью, перед числителем или перед знаменателем:
| — | 2 | = | -2 | = | 2 | . |
| 7 | 7 | -7 |
Сложение и вычитание
Чтобы сложить две отрицательные дроби, надо сначала привести их к общему знаменателю, а затем сложить числители по правилам сложения рациональных чисел.
Пример.
| — | 2 | + (- | 1 | ) | . |
| 5 | 4 |
Приведём дроби к общему знаменателю:
| — | 2 | + (- | 1 | ) = | -8 | + | -5 | . |
| 5 | 4 | 20 | 20 |
Теперь сложим числители дробей по правилам сложения рациональных чисел:
| -8 | + | -5 | = | -8 + (-5) | = | -13 | = | — | 13 | . |
| 20 | 20 | 20 | 20 | 20 |
Таким образом:
| — | 2 | + (- | 1 | ) = | -8 | + | -5 | = |
| 5 | 4 | 20 | 20 |
| = | -8 + (-5) | = | -13 | = | — | 13 | . |
| 20 | 20 | 20 |
Для вычисления разности двух отрицательных дробей можно вычитание заменить сложением, взяв уменьшаемое со свои знаком, а вычитаемое с противоположным.
Пример.
| — | 5 | — (- | 11 | ) = | — | 5 | + (+ | 11 | ) = |
| 12 | 12 | 12 | 12 |
| = | — | 5 | + | 11 | = | -5 + 11 | = | 6 | . |
| 12 | 12 | 12 | 12 |
Сложение и вычитание отрицательных дробей производится по правилам сложения обыкновенных дробей, то есть сначала идёт приведение к общему знаменателю, если это нужно, а затем производятся вычисления.
Умножение и деление
Чтобы найти произведение двух отрицательных дробей, надо знаки минус перенести или в числители, или в знаменатели, а затем перемножить дроби по правилу умножения дробей.
Пример.
| — | 2 | · (- | 4 | ) = | -2 | · | -4 | = | -2 · (-4) | = | 8 | . |
| 3 | 5 | 3 | 5 | 3 · 5 | 15 |
Так как при умножении двух отрицательных чисел результат будет положительным, то данный пример можно решить сразу, отбросив оба минуса:
| — | 2 | · (- | 4 | ) = | 2 | · | 4 | = | 2 · 4 | = | 8 | . |
| 3 | 5 | 3 | 5 | 3 · 5 | 15 |
При умножении отрицательной дроби на положительную результат будет отрицательным.
Пример.
| — | 2 | · | 4 | = | — | 2 · 4 | = | — | 8 | . |
| 3 | 5 | 3 · 5 | 15 |
К отрицательным дробям можно применять любые законы умножения. Поэтому предыдущий пример можно переписать так:
| 4 | · (- | 2 | ) = | — | 4 · 2 | = | — | 8 | . |
| 5 | 3 | 5 · 3 | 15 |
То есть при умножении положительной дроби на отрицательную результат будет отрицательным.
Чтобы найти частное двух отрицательных дробей, надо знаки минус перенести или в числители, или в знаменатели, а затем произвести вычисления.
Пример.
| — | 2 | : (- | 4 | ) = | -2 | : | -4 | = |
| 3 | 5 | 3 | 5 |
| = | -2 · 5 | = | -10 | = | 10 | . |
| 3 · (-4) | -12 | 12 |
Знак результата умножения или деления отрицательных дробей можно узнать по правилам знаков целых чисел.
Как делить отрицательные числа
- Войти
- Биографии репетитора
- Подготовка к тесту
СРЕДНЯЯ ШКОЛА
- ACT Репетиторство
- SAT Репетиторство
- Репетиторство PSAT
- ASPIRE Репетиторство
- ШСАТ Репетиторство
- Репетиторство STAAR
ВЫСШАЯ ШКОЛА
- Репетиторство MCAT
- Репетиторство GRE
- Репетиторство по LSAT
- Репетиторство по GMAT
К-8
- Репетиторство AIMS
- Репетиторство по HSPT
- Репетиторство ISEE
- Репетиторство ISAT
- Репетиторство по SSAT
- Репетиторство STAAR
Поиск 50+ тестов
- Академическое обучение
репетиторство по математике
- Алгебра
- Исчисление
- Элементарная математика
- Геометрия
- Предварительный расчет
- Статистика
- Тригонометрия
репетиторство по естественным наукам
- Анатомия
- Биология
- Химия
- Физика
- Физиология
иностранные языки
- французский
- немецкий
- Латинский
- Китайский мандарин
- Испанский
начальное обучение
- Чтение
- Акустика
- Элементарная математика
прочие
- Бухгалтерия
- Информатика
- Экономика
- Английский
- Финансы
- История
- Письмо
- Лето
Поиск по 350+ темам
- О
- Обзор видео
- Процесс выбора наставника
- Онлайн-репетиторство
- Мобильное обучение
- Мгновенное обучение
- Как мы работаем
- Наша гарантия
- Влияние репетиторства
- Обзоры и отзывы
- Освещение в СМИ
- О преподавателях университета
Звоните прямо сейчас, чтобы записаться на обучение:
(888) 888-0446
Все математические ресурсы ACT
14 диагностических тестов 767 практических тестов Вопрос дня Карточки Learn by Concept
ACT Math Help » Арифметика » Целые числа » Отрицательные числа » Как делить отрицательные числа
Что такое ?
Возможные ответы:
Правильный ответ:
Объяснение:
Отрицательное число, деленное на отрицательное число, всегда дает положительное число.
разделить на равно . Поскольку ответ положительный, ответ не может быть или любым другим отрицательным числом.
Сообщить об ошибке
Решить для :
Возможные ответы:
Правильный ответ:
Объяснение:
Начните с выделения вашей переменной.
Вычтите из обеих частей:
или
Затем вычтите из обеих частей:
или
Затем разделите обе части на:
Помните, что деление отрицательного числа на , поэтому:
или
Сообщить об ошибке
Решите следующее уравнение:
Возможные ответы:
Правильный ответ:
Объяснение:
Правило деления отрицательных чисел такое же, как и для умножения отрицательных чисел.
Если оба числа отрицательные, вы получите положительный ответ.
Если одно число положительное, а другое отрицательное, вы получите отрицательный ответ.
Следовательно:
Сообщить об ошибке
Выберите ответ, который наилучшим образом решает следующее уравнение:
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить, сначала запишите уравнение в терминах :
Сначала умножьте x на обе части.
Теперь разделите на 12, чтобы найти x.
Здесь, поскольку одно из чисел в уравнении положительное, а другое отрицательное, ответ должен быть отрицательным числом:
Сообщить об ошибке
Уведомление об авторских правах
Посмотреть ACT Math Tutors
Sekou
Сертифицированный репетитор
Университет Нью-Хейвена, бакалавр искусств, математика.
Просмотр ACT Репетиторы по математике
Беверли
Сертифицированный репетитор
Уэслианский университет, бакалавриат, математика. Техасский университет в Арлингтоне, магистр, лингвистика.
Просмотр ACT Репетиторы по математике
Кэтрин
Сертифицированный репетитор
Юго-Западный университет, бакалавриат, химия и математика. Техасский университет-колледж A&M, доктор наук, синтетические органические…
Все математические ресурсы ACT
14 диагностических тестов 767 практических тестов Вопрос дня Карточки Learn by Concept
Умножение и деление отрицательных чисел — GCSE Maths
Здесь мы узнаем о умножении и делении отрицательных чисел , в том числе о том, что такое отрицательные числа и как их умножать и делить.
В рабочих листах также есть рабочие листы с отрицательными числами и экзаменационные вопросы, основанные на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные указания о том, что делать дальше, если вы все еще застряли.
Что такое отрицательные числа?
Отрицательные числа — это любые числа меньше нуля, перед которыми стоит знак минус (-).
Числа больше нуля называются положительными числами . Если перед числом нет знака, то число положительное.
В числовой строке ниже мы можем видеть некоторые положительные и отрицательные целые числа (целые числа):
Числа оранжевого цвета отрицательные, а числа синего цвета положительные.
Так же, как вы можете умножать и делить положительные числа, вы можете делать то же самое с отрицательными числами.
Чтобы умножать или делить отрицательные числа, нужно помнить:
Если знаки совпадают, то ответ положительный.
Если знаки разные, ответ отрицательный.
При умножении отрицательных чисел:
Те же правила применяются и при делении отрицательных чисел:
Щелкните здесь, чтобы узнать о сложении и вычитании отрицательных чисел.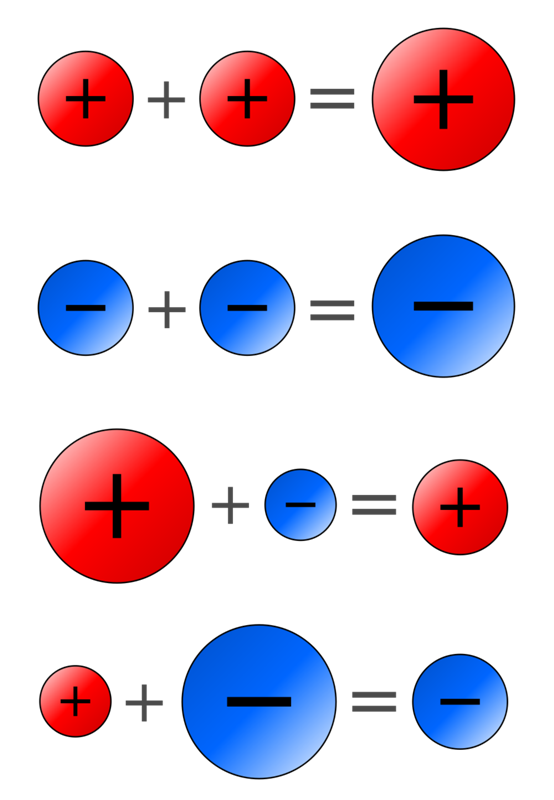
Что нужно помнить при умножении и делении отрицательных чисел?
Как умножать и делить отрицательные числа
Чтобы умножать и делить отрицательные числа:
- Умножать или делить числа как обычно.
- При необходимости измените знак, используя правила умножения и деления отрицательных чисел:
Если знаки совпадают, ответ положительный.
Если знаки разные, ответ отрицательный.
Объясните, как умножать и делить отрицательные числа в 2 шага
Рабочий лист по умножению и делению отрицательных чисел
Получите бесплатный рабочий лист по умножению и делению отрицательных чисел, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
ИксУмножение и деление отрицательных чисел лист
Получите бесплатную таблицу умножения и деления отрицательных чисел, содержащую более 20 вопросов и ответов.
Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
Примеры умножения и деления отрицательных чисел
Пример 1: умножение отрицательных чисел
Умножение:
\[ -3\times5\]
- Обычное умножение или деление чисел.
\[ 3\times5 = 15\]
2 Измените знак, используя правила умножения и деления отрицательных чисел:
Если знаки совпадают, ответ положительный.
Если знаки разные, ответ отрицательный.
\[-3\times5\]
В этом случае мы имеем положительное число, умноженное на отрицательное число (минус, умноженный на положительное, дает минус).
Знаки разные, поэтому ответ должен быть отрицательным:
\[= -15\]
Пример 2: деление отрицательных чисел
Разделить:
\[ -24\div-6 \]
Обычное умножение или деление чисел.
\[ 24\div6 = 4\]
Измените знак, используя правила умножения и деления отрицательных чисел:
Если знаки совпадают, то ответ положительный.
Если знаки разные, ответ отрицательный.
\[-24\div-6\]
В этом случае у нас есть отрицательное число, деленное на отрицательное число.
Знаки одинаковые, поэтому мы должны получить положительный ответ:
\[= 4\]
Пример 3: порядок операций
Решить:
\[ -12\div(-6) +4\times(-2)\]
Умножить или разделить числа обычным способом .
В данном случае мы имеем дело с тремя разными операциями (+, x и ÷). Нам нужно использовать BIDMAS, чтобы определить порядок расчета.
Давайте временно проигнорируем отрицательные знаки.
Если мы начнем с деления:
\[12\div6 = 2\]
Следующее умножение:
\[4\times2 = 8\]
Между ними есть знак добавления, поэтому мы должны сложить два числа после того, как разобрались с отрицательными значениями.
Измените знак, используя правила умножения и деления отрицательных чисел:
Если знаки совпадают, ответ положительный.
Если знаки разные, ответ отрицательный.
Для первой части, −12 ÷ (−6), знаки те же.
Значит, ответ положительный 2.
Для второй части 4 x (−2) знаки другие. 93\]
Нормальное умножение или деление чисел.
2 3 = 2 × 2 × 2 = 8
Измените знак, используя правила умножения и деления отрицательных чисел:
Если знаки совпадают, то ответ положительный.
Если знаки разные, ответ отрицательный.
Помните, что (−2) 3 совпадает с (−2) × (−2) × (−2).
Если мы начнем только с (−2) × (−2), результирующий ответ = 4. Он положительный, потому что знаки одинаковы.
Если принять, что 4 и умножить на конечное (−2), 4 × (−2) равно −8, поскольку отрицательное число, умноженное на положительное, дает отрицательный ответ.
\[= -8\]
Пример 5: сформулированная задача
В таблице ниже показаны температуры, зарегистрированные в Манчестере в разное время суток. Чему равно произведение самой высокой и самой низкой температуры?
| Время суток | Температура (℃) |
| 2 часа ночи | −6 |
| 7:00 | −4 |
| 13:00 | 2 |
| 18:00 | −2 8 |
Самая высокая температура была 2℃ в 13:00.
Самая низкая температура была в 2 часа ночи -6℃.
\[2\times6 = 12\]
Измените знак, используя правила умножения и деления отрицательных чисел:
Если знаки совпадают, то ответ положительный.
Если знаки разные, ответ отрицательный.
\[2\times-6\]
В этом случае мы имеем положительное число, умноженное на отрицательное.
Знаки одинаковые, поэтому наш ответ должен быть отрицательным.
\[= -12\]
Распространенные заблуждения
- Большее отрицательное число не означает большее число
Распространенной ошибкой является предположение, что чем больше отрицательное число, тем больше число.
Напр.
−3 меньше 2
- Возведение отрицательного числа в степень больше единицы
Помните, что при возведении отрицательного числа в степень больше 1 результирующий ответ может быть положительным или отрицательным.
Когда вы возводите отрицательное число в нечетную степень, в результате получается отрицательный ответ.
Когда вы возводите отрицательное число в четную степень, в результате получается положительный ответ.
Умножение и деление отрицательных чисел является частью нашей серии уроков, направленных на повторение отрицательных чисел.
Возможно, вам будет полезно начать с основного урока по отрицательным числам, чтобы получить краткое изложение того, чего ожидать, или использовать пошаговые руководства ниже для получения дополнительной информации по отдельным темам. Другие уроки в этой серии включают в себя:
- Отрицательные числа
- Сложение и вычитание отрицательных чисел
Практика умножения и деления отрицательных чисел вопросы
12 х 6=72
Знаки одинаковые, поэтому ответ положительный:
-12\раз (-6)=72
60 \дел 12 = 5
Знаки разные, поэтому ответ отрицательный:
60 \div (-12)=-5
Не забудьте применить БИДМАС здесь.
4 \div 2=2
Знаки разные, поэтому -2
7 \times 8=56
Здесь нужно быть очень осторожным со знаками. Мы вычитаем
7 \times (-8)
Знаки разные, поэтому получается -56 .
Расчет становится равным -2 – – 56 .
Есть – – вместе, поэтому мы меняем это на +
\begin{выровнено} -2 – – 56 &= – 2 + 56\\ &=54 \end{выровнено} 9{\circ}\text{C}
Расчет, который нам нужно сделать, это 3 \times -8
3 \times 8 = 24
Знаки разные, поэтому ответ отрицательный.
3 х -8=-24
Умножение и деление отрицательных чисел Вопросы GCSE
В таблице показана температура в разных городах Канады.
| Город | Температура |
| Торонто | −3 |
| Калгари | −12 |
| Оттава | 2 |
| Квебек Сити | −6 |
(a) В каком городе самая низкая температура?
(b) Найдите произведение между самым теплым и самым холодным городами.
(3 балла)
Показать ответ
a)
Калгари
(1)
Определение самых теплых и самых низких температур (Оттава и Калгари).
(1)
Правильное умножение 2 и -12 дает -24
(1)
собирается выбрать 2 карты и умножить их.
(а) Какое максимально возможное число она может составить?
(b) Какое наименьшее число она может составить?
(4 балла)
Показать ответ
а)
Для определения − 9 или − 8.
(1)
Правильное умножение − 9 и − 8 или видно.
(1)
b)
Для определения -9 или 7.
(1)
3. Температура в Лондоне в среду была -6℃. В тот же день температура на северном полюсе была в 4 раза ниже, чем в Лондоне.
Какая была температура на Северном полюсе?
(2 балла)
Показать ответ
(−6) x 4 видно.