Формула для арифметической прогрессии: Арифметическая прогрессия — урок. Алгебра, 9 класс.

Элементарная математика

Сканави М.И. Элементарная математика. 2-е изд., перераб. и доп., М.: 1974г. — 592с. Книга представляет собой повторительный курс элементарной математики и рассчитана на тех, кто хочет пополнить, укрепить и систематизировать свои знания. Как и в первом издании, содержание ориентировано на программы вступительных экзаменов в технические вузы и, в особенности, на программы подготовительных отделений при высших учебных заведениях, для учащихся которых, как мы надеемся, книга окажется полезной. (Книга включает в себя Ч1 — Арифметика, алгебра и элементарные функции и Ч2 — Геометрия. Каждый раздел включает в себя теоретическую часть и большое количество задач с решениями.) Оглавление ВВЕДЕНИЕ Часть первая. АРИФМЕТИКА, АЛГЕБРА И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ Глава I. ДЕЙСТВИТЕЛЬНЫЕ И КОМПЛЕКСНЫЕ ЧИСЛА 2. Простые и составные числа. Признаки делимости. 3. Наибольший общий делитель и наименьшее общее кратное. 4. Целые числа. Рациональные числа. 5. Десятичные дроби. Представление рациональных чисел десятичными дробями. 6. Иррациональные числа. Действительные числа. 7. Действия с приближенными числами. 8. Числовая ось. Координаты точки на плоскости. § 2. Степени и корни 9. Степени с натуральными показателями. 10. Степени с целыми показателями. 11. Корни. 12. Степени с рациональными показателями. Степени с действительными показателями. 13. Алгоритм извлечения квадратного корня. § 3. Комплексные числа 14. Основные понятия и определения. 15. Рациональные действия с комплексными числами. 16. Геометрическое изображение комплексных чисел. Тригонометрическая форма комплексного числа. 17. Действия с комплексными числами, заданными в тригонометрической форме. Формула Муавра. 18. Извлечение корня из комплексного числа. Глава II. ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ 19. Алгебраические выражения. Одночлены и многочлены. 20. Формулы сокращенного умножения. 21. Бином Ньютона. 22. Разложение многочлена на множители. 23. Дробные алгебраические выражения. § 2. Иррациональные алгебраические выражения 24. Радикалы из алгебраических выражений. 25. Освобождение от иррациональности в знаменателе дроби. Глава III. ЛОГАРИФМЫ 26. Определение и свойства логарифмов. 27. Логарифмы по различным основаниям. Модуль перехода. § 2. Десятичные логарифмы 28. Характеристика и мантисса десятичного логарифма. 29. Применение десятичных логарифмов к вычислениям. Глава IV. ФУНКЦИИ И ГРАФИКИ 30. Величина. Числовые множества. 31. Определение функции. 32. График функции. Способы задания функций. 33. Элементарное исследование поведения функции. 34. Сложная функция. 35. Обратная функция. 36. 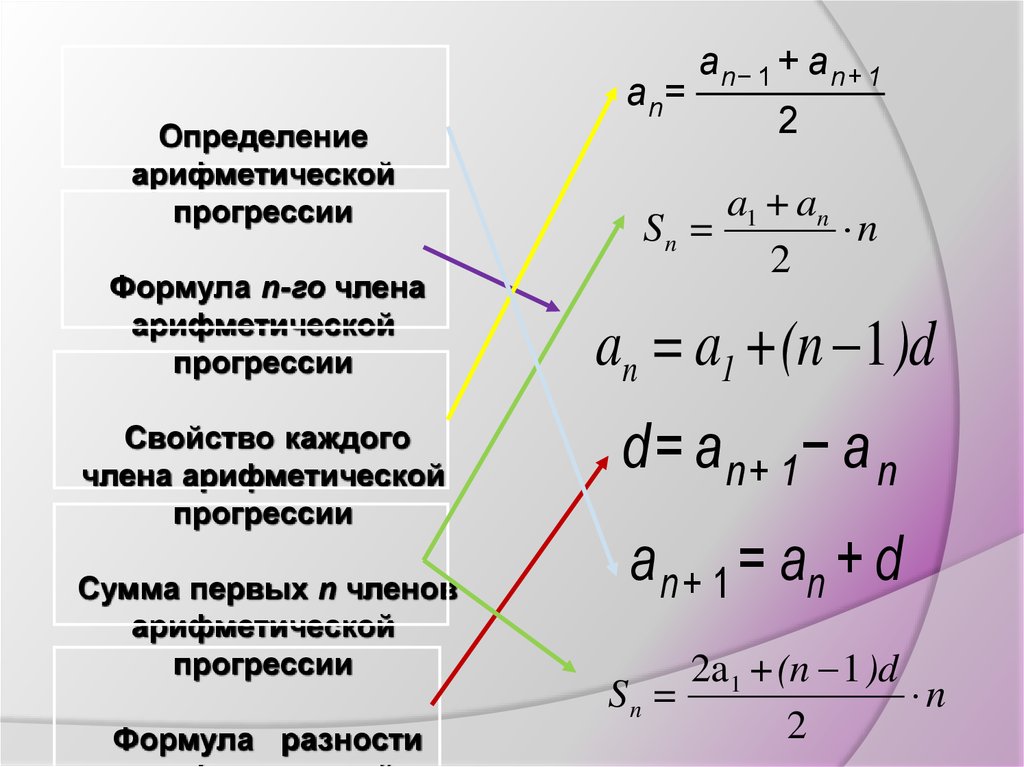n. 41. Обратная пропорциональная зависимость. Степенная функция с рациональным показателем степени. 42. Показательная функция. 43. Логарифмическая функция. § 3. Преобразование графиков 44. Параллельный сдвиг графика. 45. График квадратного трех члена. 46. График дробно-линейной функции. 47. Преобразование симметрии. Сжатие и растяжение графика. 48. Построение графиков функций. 49. Сложение графиков. § 4. Некоторые сведения о рациональных функциях 50. Целые и дробные рациональные функции. Деление многочленов. 51. Схема Горнера. Теорема Безу. 52. Нули многочлена. Разложение многочлена на множители. Глава V. УРАВНЕНИЯ 53. Уравнение. Корни уравнения. 54. Равносильные уравнения. 55. Системы уравнений. 56. Графическое решение уравнений. §. 2. Алгебраические уравнения с одной неизвестной 57. Число и кратность корней. 58. Уравнения первой степени (линейные уравнения). 59. Уравнения второй степени (квадратные уравнения). 60. Формулы Виета. Разложение квадратного трехчлена на множители. 61. Исследование квадратного уравнения. 62. Уравнения высших степеней. Целые корни. 63. Двучленные уравнения. 64. Уравнения, сводящиеся к квадратным. 65. Возвратные уравнения. § 3. Системы алгебраических уравнений 66. Линейные системы. 67. Определители второго порядка. Исследование линейных систем двух уравнений с двумя неизвестными. 68. Системы, состоящие из уравнения второй степени и линейного уравнения. 69. Примеры систем двух уравнений второй степени. Системы уравнений высших степеней. § 4. Иррациональные, показательные и логарифмические уравнения 70. Иррациональные уравнения. 71. Показательные уравнения. 72. Логарифмические уравнения. 73. Разные уравнения. Системы уравнений. Глава VI. НЕРАВЕНСТВА 74. Свойства неравенств. Действия над неравенствами. 75. Алгебраические неравенства. § 2. Решение неравенств 76. Множество решений неравенства. Равносильные неравенства. 77. Графическое решение неравенств. 79. Квадратные неравенства. 80. Неравенства высших степеней. Неравенства, содержащие дробные рациональные функции от х. 81. Иррациональные, показательные и логарифмические неравенства. 82. Неравенства с двумя неизвестными. Глава VII. ПОСЛЕДОВАТЕЛЬНОСТИ 83. Числовая последовательность. 84. Предел числовой последовательности. 85. Бесконечно малые. Правила предельного перехода. § 2. Арифметическая прогрессия 86. Арифметическая прогрессия. Формула общего члена. 87. Свойства арифметической прогрессии. 88. Формула для суммы n членов арифметической прогрессии. § 3. Геометрическая прогрессия 89. Геометрическая прогрессия. Формула общего члена. 90. Свойства геометрической прогрессии. 91. Формулы для суммы n членов геометрической прогрессии. 92. Бесконечно убывающая геометрическая прогрессия. Глава VIII. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА (ДУГИ) 93. Вектор, проекция вектора. 94. Положительные углы и дуги, меньшие 360°. 95. Углы и дуги, большие 360°. 96. Отрицательные углы. Сложение и вычитание углов. § 2. Тригонометрические функции произвольного угла 97. Определение основных тригонометрических функций. 98. Изменение основных тригонометрических функций при изменении угла от 0 до 2pi. § 3. Соотношения между тригонометрическими функциями одного и того же угла 99. Основные тригонометрические тождества. 100. Вычисление значений тригонометрических функций по значению одной из них. 101. Значения тригонометрических функций некоторых углов. § 4. Четность, нечетность и периодичность тригонометрических функций 102. Четность и нечетность. 103. Понятие периодической функции. 104. Периодичность тригонометрических функций. § 5. Формулы приведения 105. Зависимость между тригонометрическими функциями дополнительных углов. 106. Формулы приведения. Глава IX. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЧИСЛОВОГО АРГУМЕНТА И ИХ ГРАФИКИ § 1. Тригонометрические функции числового аргумента 108. Области определения и области изменения значений тригонометрических функций. 109. Некоторые неравенства и их следствия. § 2. Графики тригонометрических функций 110. Первоначальные сведения о таблицах тригонометрических функций. 111. Основные графики. 112. Примеры построения графиков некоторых других тригонометрических функций. 113. Дальнейшие примеры построения графиков функций. Глава X. ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ 114. Расстояние между двумя точками на плоскости. 115. Косинус суммы и разности двух аргументов. 116. Синус суммы и разности двух аргументов. 117. Тангенс суммы и разности двух аргументов. 118. О формулах сложения для нескольких аргументов. § 2. Формулы для двойного и половинного аргумента. Выражение sin na и cos na через степени sin a и cos a 119. Тригонометрические функции двойного аргумента. 120. Выражение sin na и cos na через степени sin a и cos a при натуральном числе n. 121. Тригонометрические функции половинного аргумента. 122. Выражение основных тригонометрических функций аргумента а через tg(a/2). § 3. Преобразование в сумму выражений вида sina•cosb, cosa•cosb и sinа•sinb § 4. Преобразование в произведение сумм вида § 5. Преобразование некоторых выражений в произведения с помощью введения вспомогательного аргумента 127. Преобразование в произведение выражения a•sina + b•cosa. 128. Преобразование в произведение выражений a•sina+b и a•cosa+b 129. Преобразование в произведение выражения a•tga+b. Глава XI. ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ И ИХ ГРАФИКИ 130. Функция у = arcsin x (арксинус). 131. Функция y = arccos x (арккосинус). 132. Функция y = arctg x (арктангенс). 133. Функция y = arcctg x (арккотангенс). 134. Пример. § 2. Операции над обратными тригонометрическими функциями 135. Тригонометрические операции. 136. Операции сложения (вычитания). § 3. Обратные тригонометрические операции над тригонометрическими функциями 137. Функция у = arcsin (sin x). 138. Функция y = arctg (tg x). Глава XII. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА 139. Уравнение sin х = а. 140. Уравнение cos х = a. 141. Уравнение tg x = a. 142. Уравнение ctg x = a. 143. Некоторые дополнения. § 2. Способ приведения к одной функции одного и того же аргумента 145. Некоторые типы уравнений, приводящихся к уравнениям относительно функции одного аргумента. 146. Способ разложения на множители. 147. Решение рациональных тригонометрических уравнений с помощью универсальной тригонометрической подстановки tg(x/2) = t. § 3. Некоторые частные приемы решения тригонометрических уравнений и систем 148. Введение вспомогательного аргумента. 149. Преобразование произведения в сумму или разность. 150. Переход к функциям удвоенного аргумента. 151. Решение уравнения типа… 152. Применение подстановок sinx ± соsx = y. § 4. Решение тригонометрических неравенств 154. Простейшие тригонометрические неравенства. 155. Примеры тригонометрических неравенств, сводящихся к простейшим. Часть вторая. ГЕОМЕТРИЯ 156. Точка. Прямая. Луч. Отрезок. 157. Плоскость. Фигуры и тела. 160. Равенство фигур. Движение. 161. Равенство тел. § 2. Измерение геометрических величин 162. Сложение отрезков. Длина отрезка. 163. Общая мера двух отрезков. 164. Сравнительная длина отрезков и ломаных. 165. Измерение углов. 166. Радианная мера угла. 167. Измерение площадей. 168. Площадь прямоугольника. Объем прямоугольного параллелепипеда. Глава XIV. ПЕРПЕНДИКУЛЯРНЫЕ И ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ. ЗАДАЧИ НА ПОСТРОЕНИЕ 169. Перпендикуляр и наклонные. 170. Свойство перпендикуляра, проведенного к отрезку в его середине. 171. Параллельные прямые. 172. Углы, образованные двумя параллельными прямыми и секущей. 173. Углы с параллельными или перпендикулярными сторонами. § 2. Геометрические места точек. Окружность 174. Геометрическое место точек. 175. Свойство биссектрисы угла. 176. Окружность. 177. Взаимное расположение прямой и окружности. Касательная и секущая. 178. Хорда и диаметр. Сектор и сегмент. 179. Взаимное расположение двух окружностей. § 3. Основные задачи на построение 181. Деление отрезка пополам. Построение перпендикуляров. 182. Построение углов. 183. Другие задачи на построение. Глава XV. ТРЕУГОЛЬНИКИ, ЧЕТЫРЕХУГОЛЬНИКИ 184. Стороны и углы треугольника. 185. Биссектрисы треугольника. Вписанная окружность. 186. Оси симметрии сторон треугольника. Описанная окружность. 187. Медианы и выcоты треугольника. 188. Равенство треугольников. 189. Построение треугольников. 190. Равнобедренные треугольники. 191. Прямоугольные треугольники. § 2. Параллелограммы 192. Четырехугольники. 193. Параллелограмм и его свойства. 194. Прямоугольник. § 3. Трапеция 196. Трапеция. 197. Средняя линия треугольника. 198. Средняя линия трапеции. 199. Деление отрезка на равные части. 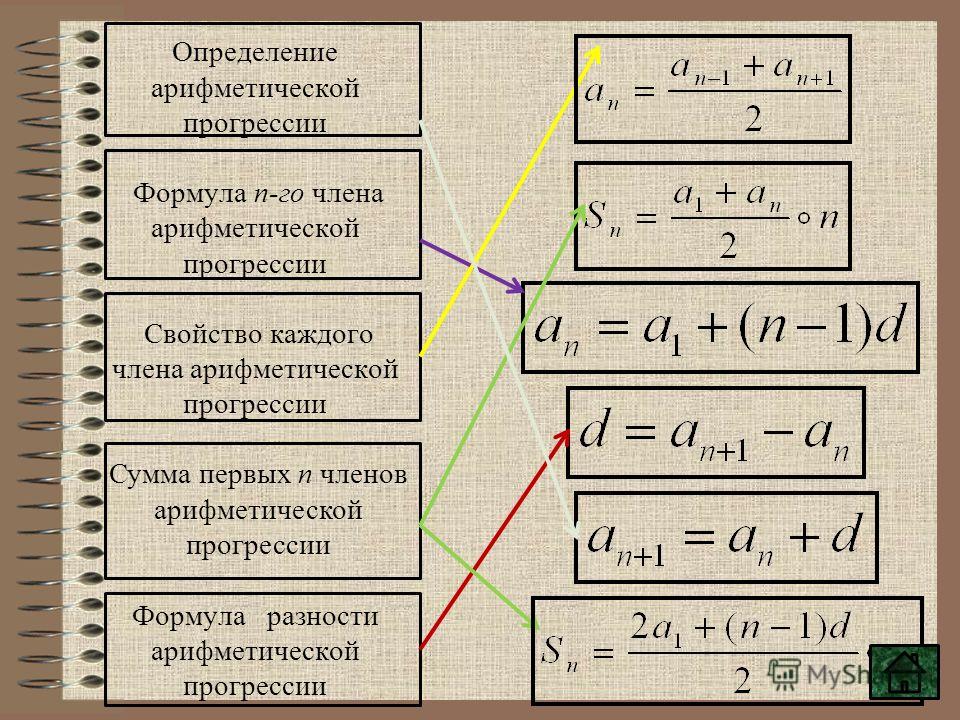§ 4. Площади треугольников и четырехугольников 200. Площадь параллелограмма. 201. Площадь треугольника. 202. Площадь трапеции. Глава XVI. ПОДОБИЕ ГЕОМЕТРИЧЕСКИХ ФИГУР 203. Пропорциональные отрезки. 204. Свойства биссектрис внутреннего и внешнего углов треугольника. § 2. Подобное преобразование фигур (гомотетия) 205. Определение гомотетичных фигур. 206. Свойства преобразования подобия. § 3. Общее подобное соответствие фигур 207. Подобные фигуры. 208. Периметры и площади подобных треугольников. 209. Применение подобия к решению задач на построение. Глава XVII. МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В ТРЕУГОЛЬНИКЕ И КРУГЕ 210. Углы с вершиной на окружности. 211. Углы с вершиной внутри и вне круга. 212. Угол, под которым виден данный отрезок. 213. Четырехугольники, вписанные в окружность. 214. Пропорциональные отрезки в круге. 215. Задачи на построение. § 2. Метрические соотношения в треугольнике 216. Пропорциональные отрезки в прямоугольном треугольнике. Теорема Пифагора. 218. Теорема синусов. Формула Герона. 217. Квадрат стороны, лежащей против острого или тупого утла и треугольнике. Теорема косинусов. 218. Теорема синусов. Формула Герона. 219. Радиусы вписанной и описанной окружностей. § 3. Решение треугольников 220. Таблицы функций. 221. Решение треугольников. Сводка основных формул. 222. Решение прямоугольных треугольников. 223. Решение косоугольных треугольников. Глава XVIII. ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ. ДЛИНА окружности И ПЛОЩАДЬ КРУГА 224. Выпуклые многоугольники. 225. Правильные многоугольники. 226. Соотношения между стороной, радиусом и апофемой. 227. Периметр и площадь правильного n-угольника. 228. Удвоение числа сторон правильного многоугольника. § 2. Длина окружности. Площадь круга и его частей 229. Длина окружности. 230. Площадь круга и его частей. Глава XIX. ПРЯМЫЕ И ПЛОСКОСТИ В ПРОСТРАНСТВЕ 231. Взаимное расположение двух прямых в пространстве. 232. Взаимное расположение прямой линии и плоскости. 233. Взаимное расположение двух плоскостей. 234. Свойства параллельных прямых и плоскостей. 235. Построения в стереометрии. § 2. Перпендикулярность прямых и плоскостей 236. Перпендикуляр к плоскости. 237. Перпендикуляр и наклонные. 238. Угол между прямой и плоскостью. 239. Связь между перпендикулярностью и параллельностью прямых и плоскостей. 240. Общий перпендикуляр двух скрещивающихся прямых. § 3. Двугранные и многогранные углы 241. Двугранный угол. 242. Взаимно перпендикулярные плоскости. 243. Трехгранные углы. 244. Многогранные углы. § 4. Многогранники 245. Многогранники. 246. Правильные многогранники. Глава XX. МНОГОГРАННИКИ И КРУГЛЫЕ ТЕЛА 247. Цилиндры и призмы. 248. Параллелепипеды. 249. Объемы призм и цилиндров. 250. Площадь боковой поверхности призмы. 251. Площадь поверхности цилиндра. § 2. Пирамида. Конус 252. Свойства пирамиды и конуса. 253. Объем пирамиды и конуса. 254. Площадь боковой поверхности правильной пирамиды и конуса. 255. Усеченный конус и усеченная пирамида. § 3. Шаровая поверхность. Шар 256. Шар и шаровая поверхность. 257. Объем шара и его частей. 258. Площадь поверхности шара и ее частей. 259. Понятие телесного угла. Ответы к упражнениям Приложения

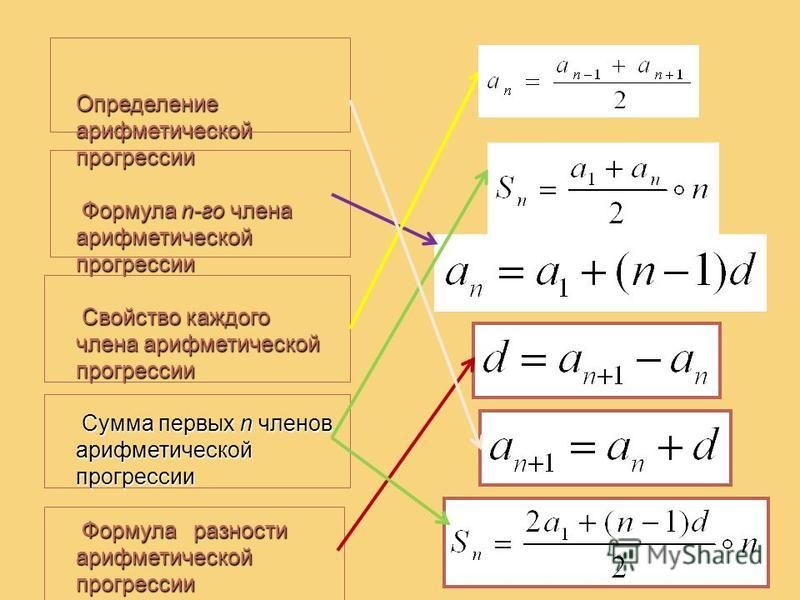
Определение арифметической прогрессии. Формула n-го члена арифметической прогрессии.

Муниципальное бюджетное общеобразовательное учреждение «Гимназия №1 имени Ризы Фахретдина» г. Альметьевск Республики Татарстан

Учитель математики: Закирова Миннур Анваровна

Тема: «Определение арифметической прогрессии. Формула n-го члена арифметической прогрессии»

Учебник : Алгебра 9 класс , Ю.Н.Макарычев, Н.Г. Миндюк, М «Просвещение» 2012г.

Тип урока: ОНЗ( открытие новых знаний)

Основные цели урока:

— формировать понятие арифметической прогрессии;

— способствовать выводу формулы n-го члена арифметической прогрессии;

— повторить понятие последовательности;

— тренировать умения применять изученную формулу.

Мыслительные операции, необходимые на этапе проектирования: анализ, синтез, обобщение, сравнение, выявление закономерностей.

Оборудование: демонстрационные и раздаточные материалы, учебник.

Демонстрационный материал.

Карточки с формулами:

an+1= an+d — условие для арифметической прогрессии для любого натурального числа n.

an+1- an=d — разность арифметической прогрессии.

3.an = а1+d(n- 1) — формула n-го члена арифметической прогрессии

4. Карточки с последовательностями

5. Карточки с формулами последовательностей

6. Карточки с заданной последовательностью

7. Таблица с эталоном решения

8. План проекта.

а) установим зависимость между членами прогрессии;

б) определим, как находится второй, третий, четвертый члены прогрессии;

в) установим взаимосвязь между этими действиями;

г) выведем формулу для нахождения n-го члена арифметической прогрессии.

Раздаточный материал.

Карточки с последовательностями.

А) 2 ; 4 ; 6 ; 8;…

Б) 1 ;3 ; 5 ; 7 ;…

В) -10 ; 10 ; -10;…

Г) 3 ; 3 ; 3 ; …

2. Карточки с формулами последовательностей.

an= 2n an= 2n+1 an=(-1) n ·10 an=3 an=n2 — 3n

Карточки с последовательностью.

1 ; 4 ; 7 ; 10 ;…

Таблицы с эталонами решения задач.

№ 344 (bn) – арифметическая прогрессия

b1 – первый член арифметической прогрессии, d – разность арифметической прогрессии.

Выразить: а) b7 ; г)bk ; д)bk+1.

bn= b1 +d(n- 1)

а) b7 = b1 +6d.

г) bk =b1 +d(k- 1).

д) bk+5 =b1 +d(k+ 4).

№ 345 а) (сn) – арифметическая прогрессия

с1= 20, d = 3 , с5 -?

сn= с1 +d(n- 1) с5=20 + 3(5 – 1)= 32

Ответ: 32

Ход урока

Самоопределение к учебной деятельности.

Цель:

Включить учащихся в учебную деятельность;

Определить содержательные рамки урока: расширить знания о применении понятия последовательности к решению задач в практической деятельности.

Организация учебной деятельности на этапе 1.

Здравствуйте ребята! Я рада вас видеть в хорошем настроении и добрым здравии.

В качестве настроя « То, что вы были вынуждены открыть сами, оставляет в вашем уме дорожку, которой вы можете снова воспользоваться, когда в этом возникает необходимость»

Г.Лихтенберг.

2. Актуализация и фиксирование индивидуального затруднения в пробном действии.

Цель:

1) актуализировать знания последовательности;

актуализировать мыслительные операции для нахождения членов последовательности;

зафиксировать затруднения в нахождении n-го члена последовательности.

Организация учебного процесса на этапе 2.

Индивидуальная работа

— у вас на партах даны карточки со следующими записями:

2 ; 4 ; 6 ; 8 ;…,

1 ; 3 ; 5 ; 7 ;…,

-10 ; 10 ; -10 ; …,

3 ; 3 ; 3 ; … .

Что представляют собой эти записи? ( последовательности).

— Выполните сопоставление последовательностей и формул n-го члена их задающих.

an= 2n an= 2n+1 an=(-1) n ·10 an=3 an=n2 — 3n

Индивидуальная работа

— Возьмите карточки с последовательностями:

2 ; 4 ; 6 ; 8;… 1 ; 4 ; 7 ; 10 ;…

— Найдите первый, пятый и седьмой члены последовательности.

— Для нахождения членов последовательности, чем вы пользовались?

(обсуждение).

— В какой последовательности, легче было находить члены последовательности? Почему?

— В последовательности 1 ; 4 ; 7 ; 10 ;… на сколько каждый следующий член больше предыдущего?

— Откройте учебник алгебры на стр. 84. Прочитайте, как называются последовательность у которой каждый член начиная со второго , равен предыдущему, сложенному с одним и тем же числом. (арифметическая прогрессия).

— На доске табличка с формулой an+1= an+d — условие для арифметической прогрессии для любого натурального числа n.

— Какие из последовательностей , у вас на столе, являются арифметическими прогрессиями? ( а,б,г).

— На доске табличка с формулой an+1- an=d — разность арифметической прогрессии.

3. Постановка проблемы.

Цель:

1) зафиксировать, где возникло затруднение при нахождении членов последовательности;

2) соотнести свои действия с используемым способом действия по нахождению n-го члена последовательности.

Организация учебного процесса на этапе 3.

— Для первой последовательности имеется формула нахождения n-го члена.

— Что нужно сделать, чтобы найти n-ый член, арифметической прогрессии? (…)

4. Построение проекта выхода из затруднения.

Цель: построить проект для нахождения n-го члена, арифметической прогрессии.

Организация учебного процесса на этапе 4.

— Какую цель урока вы бы себе поставили? (…)

— Составьте план по достижению цели.

— Сравните свой план с эталоном.

План проекта.

а) установим зависимость между членами прогрессии;

б) определим, как находится второй, третий, четвертый члены прогрессии;

в) установим взаимосвязь между этими действиями;

г) выведем формулу для нахождения n-го члена арифметической прогрессии.

5. Реализация построенного проекта.

Цель:

1) реализовать построенный проект в соответствии с планом;

2)формулу n-го члена, арифметической прогрессии;

3)уточнить общий характер полученной формулы;

4)зафиксировать преодоление в затруднении.

Организация учебного процесса на этапе 5

— Запишите последовательность а1 ; а2 ; а3 ; …. Данная последовательность является арифметической прогрессией (аn ), где d- разность арифметической прогрессии.

— Как найти а2? (а2= а1 + d)

— Как найти а3? (а3= а2 + d = а1 + 2d)

— Как найти а4? (а4= а3 + d=а1 + 3d)

— Как найти а7? (а7= а6 + d= а1 + 6d)

— Как найти аn? (аn= аn-1 + d= а1 + d (n-1)). Сравните последнюю запись с карточкой эталоном. an= а1+d(n- 1)

— Выделите формулу в тетради.

Используя эту формулу, мы можем найти любой член арифметической прогрессии.

Первичное закрепление с проговариванием во внешней речи.

Цели:

организовать усвоение детьми нахождение членов арифметической прогрессии, с их проговариванием во внешней речи.

Организация учебного процесса на этапе 6

Работа в группах.

— В последовательности – арифметической прогрессии- 1 ; 4 ; 7 ; 10 ;… вы нашли первый, второй, члены прогрессии.

— Найдите разность арифметической прогрессии.

— Найдите по формуле an= а1+d(n- 1), а7, а20.

Запишите результат в тетради и сравните получившиеся ответы: а7 =19,, а20=58.

— Проговорите друг другу, что нужно для того чтобы найти n-ый член, арифметической прогрессии.

— № 343(а,б) устно.

Самостоятельная работа с проверкой по эталону.

Цель:

1) проверить на основе сопоставления с эталоном свое умение применять формулу n-го члена, арифметической прогрессии ;

2) организовать рефлексию усвоения изученной формулы для решения задач.

Организация учебного процесса на этапе 7.

— № 344 (а, г, д) – решение в тетради с последующей проверкой по эталону.

— №345- решение в тетради с последующей проверкой по эталону.

— После проверки по эталону , определить ошибки, найти причину, найти выход для их исправления.

— № 349 (для сильных).

Включение в систему знаний и повторение.

Цель:

1) выявить границы применимости формулы n-го члена, арифметической прогрессии ;

2) повторить учебное содержание изученного материала.

Организация учебного процесса на этапе 8.

— Что называется арифметической прогрессией?

— Что можно найти используя формулу n-го члена, арифметической прогрессии ;

— Запишите последовательность (аn), являющейся арифметической прогрессией, если

а1= -7 и d= 2 и все члены которой являются отрицательными числами.

Рефлексия учебной деятельности на уроке.

Цель:

зафиксировать новое содержание, изученное на уроке;

провести рефлексивный анализ учебной деятельности с точки зрения выполнения требований, известных учащимся4

оценить собственную деятельность на уроке;

зафиксировать неразрешенные затруднения как направления будущей учебной деятельности;

обсудить и записать домашнее задание.

Организация учебного процесса на этапе 9.

— Что помогло нам сегодня на уроке?

— Что нового вы узнали?

— Где можно использовать изученную формулу?

— Оцените свою работу на уроке.

Домашнее задание . п.16 стр. 84-86, пример 1- рассмотреть. №346, № 350, № 348 решать всем, № 368 повторение № 438(а) дополнительно.

Арифметические последовательности: определение и формула

Процентная часть ежемесячных платежей, сделанных для погашения автомобильного или жилищного кредита, и список максимальных дневных температур в одном районе в течение месяца — все это последовательности.

Последовательность — это набор элементов, расположенных последовательно. В математике у нас есть арифметическая прогрессия, геометрическая прогрессия, квадратичная прогрессия и другие.

В этой статье мы узнаем больше о арифметических последовательностях .

Определение арифметической последовательности

Арифметическая последовательность представляет собой набор упорядоченных чисел, которые имеют общую разность между любыми двумя последовательными элементами.

Каждое число в наборе последовательности называется термином.

Арифметическая последовательность также известна как арифметическая прогрессия .

Возьмем следующую арифметическую последовательность. Обратите внимание, что при добавлении 2 к любому термину мы получим следующий термин. Таким образом, общая разность между каждыми двумя последовательными членами равна 2,9.0003

Другой пример: Разница между любыми двумя последовательными элементами в этой последовательности равна 3.

Члены арифметической последовательности

Первый член

Первый член арифметической последовательности является первым элементом в последовательности.

В последовательности первый член равен 5, потому что это первое число последовательности. Первый термин обычно обозначается .

Общая разность

Общая разность последовательности — это разница между двумя последовательными членами арифметической последовательности.

Это константа, которая получается путем вычитания двух последовательных членов.

Добавление общей разницы к одному из терминов даст вам следующий термин. Общая разница обычно обозначается .

Не всякая последовательность является арифметической. Вы должны сначала определить тип последовательности, прежде чем пытаться решить ее. И способ сделать это — узнать общее различие. Если общая разность постоянна на протяжении всей последовательности, то это арифметическая последовательность.

Для всей последовательности общая разница равна 2, потому что

.

Это арифметическая последовательность.

Для последовательности общая разность непостоянна, потому что

Это не арифметическая последовательность.

Энный член

Энный член арифметической последовательности относится к любому члену последовательности.

Задается как

, где обозначает индекс термина.

Чтобы вычислить , подставим n на 1 в выражение , то же самое касается остальных членов последовательности.

Другая форма выражения арифметической последовательности:

, где первый член

общая разность.

Это означает, что если мы знаем первый член арифметической прогрессии и знаем, какова должна быть общая разность, то мы сможем получить все члены этой последовательности.

Если первый член арифметической прогрессии равен 6, а общая разность равна 3, то последовательность будет

Формула арифметической прогрессии

Формула арифметической прогрессии задается формулой для n-го члена арифметической прогрессии . Формула ниже.

где энный член,

первый член,

позиция члена,

обычная разность

Эта формула является общей формулой, используемой для нахождения членов арифметической прогрессии.

Примеры арифметической последовательности

Найдите следующие три члена арифметической последовательности ниже.

Решение

Сначала мы определяем первый член, который равен 4.

Затем мы находим общую разность, вычитая из последовательности два последовательных члена.

Итак, общая разность равна 3.

Теперь, когда мы знаем первый член и общую разность, мы можем найти следующие три члена последовательности, добавив общую разность к последнему члену последовательности.

Последний известный член в последовательности равен 16. Итак, мы прибавим 3 к 16, чтобы получить

Нам нужно искать следующие три члена, поэтому мы проделаем это еще два раза. Последний член больше не 16, а 19. Таким образом, мы должны добавить 3 к 19, чтобы получить,

Теперь мы добавим 3 к 22, чтобы получить,

Итак, следующие три члена 19, 22 и 25.

Арифметическая последовательность будет,….

Возьмем другой пример.

Найдите следующие три члена арифметической прогрессии

Решение

Чтобы решить это, мы должны знать первый член и общую разность. Первый член равен 5, а общая разность равна -2.

Мы получаем общую разность, вычитая два последовательных числа в последовательности, чтобы получить разницу,

.

Следовательно,

.

Чтобы получить следующие три члена, мы добавим общую разность к последнему члену.

Последний известный член -3. Итак, следующий член будет

.

Нам нужно получить три термина, поэтому повторим этот шаг еще дважды.

Последнее слагаемое теперь равно -5. Итак, следующий член будет

.

Следующим термином будет

.

Таким образом, следующие три члена арифметической последовательности равны .

Следовательно, арифметическая последовательность: ,….

Мы рассмотрели примеры, в которых вас просят найти последовательные члены арифметической последовательности. Будут ситуации, когда вас попросят найти определенный термин в последовательности.

Вас могут попросить найти термин 9 ^th или 5 ^th или 100 ^th член последовательности.

Для этого вам нужно будет использовать приведенную ниже формулу:

Давайте рассмотрим несколько примеров.

Найдите третий член приведенной ниже арифметической прогрессии

.

Решение

Нас просят найти третий член последовательности. Мы будем использовать приведенную ниже формулу.

Определим все параметры формулы,

Теперь подставим в формулу,

Следовательно, третий член равен 21.

Найдите недостающие члены в приведенной ниже арифметической последовательности.

.

Решение

Нас просят найти недостающие элементы в последовательности, и обычно для этого мы используем первый член в последовательности. В этом случае первое слагаемое является одним из пропущенных слагаемых. Итак, как бы мы это сделали?

Сначала мы найдем общее различие и подумаем, как использовать его для поиска пропущенных терминов.

Чтобы получить общую разность, мы вычтем два последовательных слагаемых.

.

Мы не можем использовать формулу, использованную в предыдущих примерах, из-за отсутствия первого члена.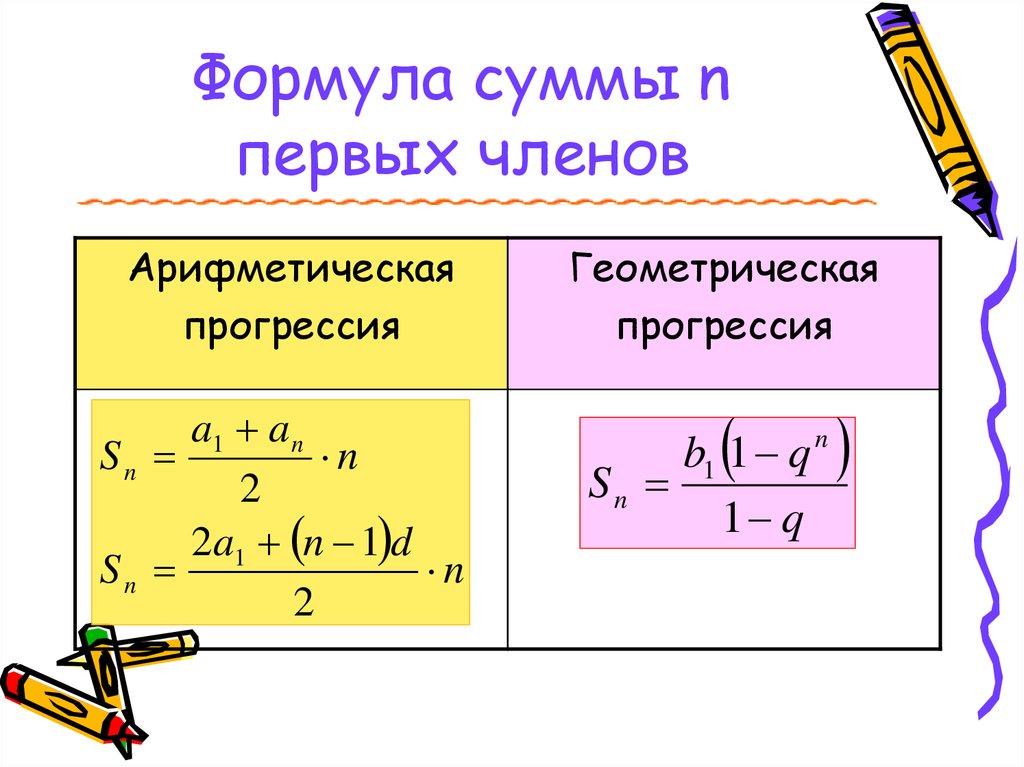 Итак, давайте искать закономерность, которой мы можем следовать. Обозначим первое слагаемое как , а второе как .

Таким образом, последовательность будет

Связь между каждым термином является общей разницей. Если вы найдете разницу между любыми двумя последовательными терминами, вы получите одно и то же число.

Таким образом, если

.Затем,

Возьмем первое уравнение,

Мы найдем у, собрав подобные члены и сделав их предметом формулы.

Это означает, что второй член равен .

Напомним, теперь мы знаем значение as , таким образом,

Это означает, что первый член равен .

Итак, последовательность .

Возьмем другой пример.

Найдите 17-й ^-й -й член арифметической прогрессии ниже,

.

Решение

Чтобы найти 17-й ^-й -й член последовательности, мы должны будем использовать приведенную ниже формулу.

Найдем общую разность d.

Теперь найдем 17 ^й член,

17 ^й член равен 98.

Сумма арифметической последовательности будет обозначена формулой арифметической последовательности

.

Сумма первых n слагаемых будет равна сложению каждого слагаемого следующим образом:

.

Если количество членов в последовательности так велико, что вы не можете их сложить или вы не знаете значение всех членов, вам понадобится формула, чтобы получить сумму.

Для нахождения суммы среднего арифметического используются две формулы. Первая формула имеет вид

, где сумма арифметической последовательности,

— количество членов в последовательности,

_{— первый член,}

— общая разность.

Эта формула используется, когда последний член последовательности неизвестен.

Другая формула имеет вид

, где — сумма последовательности,

— количество элементов в последовательности,

— первый член,

— последний член,

Эта формула используется, когда известен последний член. Давайте рассмотрим несколько примеров.

Найдите сумму арифметической прогрессии до 10 членов.

Решение

Из вопроса нам дан первый член, который равен 5, но мы не знаем последний член. Но мы знаем, что количество терминов равно 10. Формула, которую следует использовать, когда последний термин неизвестен, такова.

Общая разница:

Теперь подставим значения в формулу:

Сумма слагаемых равна 230.

Возьмем другой пример.

Найдите сумму арифметической прогрессии из 4 членов, первый член которой равен 4, а последний член равен 19.

Решение

Здесь мы знаем, что такое первый и последний член. Формула для использования в этом случае:

Теперь мы подставим значения в формулу,

Сумма 4 слагаемых равна 46. последовательность — это набор чисел, где разница между каждым членом одинакова, то есть постоянна.

Обычная разница арифметической последовательности — это разница между членами арифметической последовательности. Это константа, и она получается путем вычитания двух последовательных членов. Добавление общей разности к одному из членов даст нам следующий член. Общая разница обозначается .

арифметическая прогрессия | My Spreadsheet Lab

Давайте взглянем на то, что сегодня НАСТОЛЬКО легко рассчитать с помощью простой электронной таблицы, но было очень сложно рассчитать в прошлом.

(пост, вдохновленный статьей Евгении Чен на wsj)

«Последовательность, в которой числа увеличиваются на одинаковую величину на каждом шаге» (источник).

Попробуйте посчитать в уме:

Начните с 2. Прибавьте к нему 4 10 раз.

Что такое СУММА? Что такое МЕДИАНА?

Вот значения: 2, 6, 10, 14, 18, 22, 26, 30, 34, 38, 42. СУММА равна 242, а МЕДИАНА равна 22. компьютеры.

В Excel легко создавать последовательности. (Файл Excel: сохраните на компьютер, а затем откройте).

Это входы.

Ниже приведено решение для нединамического массива, обратно совместимое.

And finally the calculations:

My solution above contains several steps . Давайте создадим значения последовательности из одной формулы!

Вариант A

=ПОСЛЕДОВАТЕЛЬНОСТЬ(C2,A2,B2)

=TEXTJOIN(“, “,ИСТИНА,ПОСЛЕДОВАТЕЛЬНОСТЬ(C2,A2,B2))

ПОСЛЕДОВАТЕЛЬНОСТЬ — это динамический массив. Требуется версия Office 365 Excel. TEXTJOIN предотвращает его расплескивание.

Вариант B

=TEXTJOIN(“, “,TRUE,B2*ROW(INDIRECT(“1:”&C2))-A2)

Формула выше представляет собой массив и требует Control Shift Enter (только не Enter) .

Опция C

=B2*СТРОКА(ДВССЫЛ(«1:»&C2))-A2

Формула выше не требует Control Shift Enter (просто Enter). Он стекает в ячейки внизу.

(скачать мой файл PBIX.)

Генерирует 42, интервалы 4. GENERATESERIES создает таблицу с 1 столбцом.

Ниже я использую переменные, но это делает то же самое, что и выше. Так действительно ли это необходимо?

SequenceV2 =

var seqcount = 11

var seqinterval = 4

var seqstart = 2

var final = Generateseries (seqstart, seqcount*seqinterval-seqstart, seqinterval)

return

. Версии DAX выше содержат только внутренние входные данные. Могу ли я подключиться к входу извне?

После экспериментов я создал меру, на которую ссылался при создании новой таблицы.

Вот мера:

DistinctProductKeys = DISTINCTCCOUNT(FactTable[Product Key])

Вот новая таблица, которая ссылается на указанную выше меру:

DynamicSequenceTBL = GENERATESERIES(1,[DistinctProductKeys],1)

Если количество различных объектов изменяется, это значение также обновляется. Табличной функции GENERATESERIES требуется 3 одиночных значения (начало, конец, приращение). Это нормально, когда мера является конечным значением. Мы могли бы также использовать меры для начальных и приращенных значений.

Мой папа был хорош в математике. Мы задавали ему вопросы на умножение и деление. Казалось, он мог вычислить что угодно. Хм… может быть, он также подделывал некоторые ответы, зная, что мы не заметим разницы.

Не думаю, что даже он смог бы вычислить простую сумму для длинной последовательности в уме.