Предприятие выпускает 2 вида изделий используя для этого сырье трех видов
Высшая математика, Решение задач
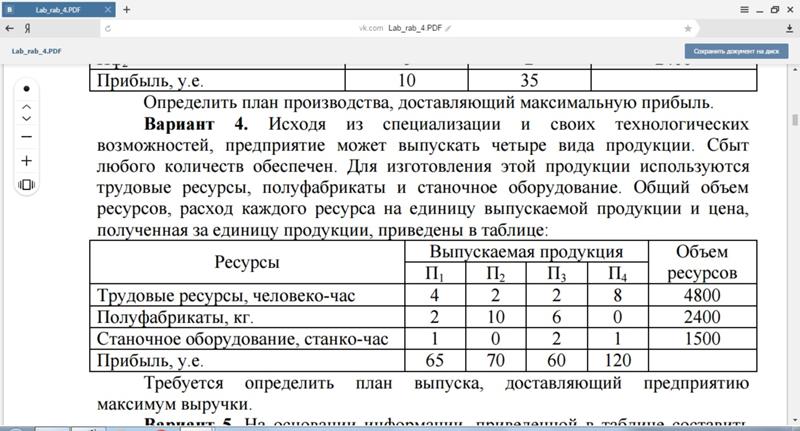
Предприятие выпускает 2 вида изделий, используя для этого сырье трех видов. Норма расхода сырья на изготовление единицы каждого вида изделий, а также запасы сырья и прибыль от реализации изделий каждого вида даны в таблице.
Сырье Норма расхода сырья на единицу изделия (кг) Запасы сырья (кг)
1 2
1 2 5 120
2 1 4 100
3 5 3 150
прибыль от реализации единицы изделия в у.е. 30 40
Найти план выпуска изделий, дающий наибольшую прибыль.
Составить математическую модель задачи, решить ее графически. Составить двойственную задачу, решить ее с помощью теорем двойственности. Дать экономическую интерпретацию двойственных задач.
Решение:
Неизвестными являются количества изделий: x1 и x2
Целью является максимизация прибыли от производства:
F=30×1+40×2
Ограничения на ресурсы:
2×1+5×2<=120
x1+4×2<=100
5×1+3×2<=150
Ограничение на переменные:
x1,x2>=0, целые
Необходимо найти максимум функции F=30×1+40×2 при ограничениях:
2×1+5×2≤120×1+4×2≤1005×1+3×2≤150
x1,x2>=0, целые
Решим задачу графически:
Необходимо найти максимальное значение целевой функции F = 30×1+40×2 → max, при системе ограничений:2×1+5×2≤120, (1)x1+4×2≤100, (2)5×1+3×2≤150, (3)x1 ≥ 0, (4)x2 ≥ 0, (5)где x1, x2 – целые числа.
 Построим область допустимых решений и определим полуплоскости, заданные неравенствами. Обозначим границы области многоугольника решений.
Построим область допустимых решений и определим полуплоскости, заданные неравенствами. Обозначим границы области многоугольника решений.Рассмотрим целевую функцию задачи F = 30×1+40×2 → max. Построим прямую, отвечающую значению функции F = 30×1+40×2 = 0. Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации F(X). Начало вектора – точка (0; 0), конец – точка (30;40). Будем двигать эту прямую до последнего касания обозначенной области. На графике эта прямая обозначена пунктирной линией.
Прямая F(x) = const пересекает область в точке C. Так как точка C получена в результате пересечения прямых (1) и (3), то ее координаты удовлетворяют уравнениям этих прямых:
Перемещение линии уровня целевой функции F(X) в направлении, задаваемом ее градиентом, показывает, что наибольшее значение F(X)=1240 она примет в точке (20, 16).
Составим двойственную задачу к прямой задаче.2y1+y2+5y3≥305y1+4y2+3y3≥40120y1+100y2+150y3 → miny1 ≥ 0y2 ≥ 0y3 ≥ 0Решение двойственной задачи дает оптимальную систему оценок ресурсов.Для решения двойственной задачи используем вторую теорему двойственности.Подставим оптимальный план прямой задачи в систему ограниченной математической модели:2*20 + 5*16 = 120 = 1201-ое ограничение прямой задачи выполняется как равенство. Это означает, что 1-й ресурс полностью используется в оптимальном плане, является дефицитным и его оценка согласно второй теореме двойственности отлична от нуля (y1 > 0).
5*20 + 3*16 = 148 < 1503-ое ограничение выполняется как строгое неравенство, т.е. ресурс 3-го вида израсходован не полностью. Значит, этот ресурс не является дефицитным и его оценка в оптимальном плане y3 = 0
Тогда подставим в целевую функцию
120y1+100y2+150y3 =1240
120y1+0+0=1240
получим
y1= 10.
 33
33Линейная алгебра — презентация онлайн
Похожие презентации:
Матрицы, определители. Обратная матрица. Ранг матрицы. Системы линейных уравнений элементы векторной алгебры
Элементы линейной алгебры
Линейная алгебра
Линейная алгебра. Матрицы
Линейная алгебра
Линейная алгебра
Элементы линейной алгебры
Линейная алгебра и аналитическая геометрия
Линейная алгебра
Линейная алгебра
1. Краткий курс лекций по математике
В настоящее время в условиях рыночныхпреобразований в экономике возрастает роль
экономико-математических методов.
Математический инструментарий становится
неотъемлемой частью экономической науки.
Автор
данного
курса
лекций
руководствовался
принципом
повышения
уровня
фундаментальной
математической
подготовки
студентов
с
усилением
ее
прикладной экономической направленности.
Раздел 1.

Линейная алгебра.
Линейна
алгебра
является
необходимым
инструментарием для компактного и эффективного
описания
и
анализа
экономико-математических
моделей и методов.
Тема 1. Матрицы.
Понятие матрицы и основанный на нем раздел
математики – матричная алгебра – имеет важное значение
для экономистов, так как значительная часть математических
моделей экономических объектов может быть записана в
компактной матричной форме.
Матрицей размера m n или mn — матрицей называется
прямоугольная таблица чисел.
Матрица содержит m строк и n столбцов.
Матрицы
обозначаются
прописными
латинскими
буквами.
Матрица записывается следующим образом:
a11
a21
A
…
am1
или
Am n (aij )
am 2
… a1n
… a2 n
… …
… amn
где
aij
a12
a22
…
— элемент матрицы.
j Первый индексi — это номер строки, второй
индекс номер столбца, где расположен элемент.

Виды матриц.
1. Если в матрице число строк не равно числу столбцов, то
матрица называется прямоугольной матрицей.
2. Если в матрице число строк равно числу столбцов, то
матрица называется квадратной матрицей.
3. Матрица строка
A (a1 a2 … an )
4.Матрица столбец
a1
a2
A
…
an
5. Матрица, все элементы которой равны нулю называется
нулевой матрицей.
0
0
0
…
0
0 … 0
0 … 0
… … …
0 … 0
6. Квадратная матрица называется диагональной, если все
элементы, не принадлежащие главной диагонали, равны
нулю.
a11 0 … 0
0
a
…
0
22
A
… … … …
0 … ann
0
7.
Диагональная матрица, у которой все элементы
главной диагонали равны единице, называется единичной
матрицей и обозначается символом Е.
1
0
E
…
0
0 … 0
1 … 0
… … …
0 … 1
9. Операции над матрицами.
 1. Суммой двух матриц А и В одинакового размера
1. Суммой двух матриц А и В одинакового размераназывается матрица той же размерности, элементы которой
равны сумме соответствующих элементов матриц.
a11 a12 a13 b11 b12 b13
A B
a21 a21 a23 b21 b22 b23
a11 b11 a12 b12 a13 b13
a21 b21 a22 b22 a23 b23
2 ( 4) 4 1 5 6 5
3 2 4 2 4 1 3 2
3 ( 4) 5 0 4 1 5
C A B 1 3 5 5 4 0 1 5
1 7 5 2 3 1 1 ( 2) 7 ( 3) 5 1 1 4 4
2. Произведением матрицы А и числа называется матрица
той же размерности, все элементы которой умножаются на
это число:
a11 a12 a13
A
a
a
a
21 21 23
1 0 2 3 1 0 3 3 2 3 0 6
A 3 2 1 0 3 2 3 1 3 0 6 3 0
3. Произведением матрицы размерности m n и матрицы
размерности n k называется матрица размером m k ,
элементы которой равны сумме произведений элементов строки матрицы, стоящей на первом месте
на
соответствующие элементы столбца матрицы, стоящей на
втором месте.
a11 a12
A B
a21 a22
b11 b12
a13
b
b
21 22
a23
b
b
31 32
a11 b11 a12 b21 a13 b31 a11 b12 a12 b22 a13 b32
a21 b11 a22 b21 a23 b32 a21 b12 a22 b22 a23 b32
Произведение существует в том случае, если число столбцов первой
матрицы равно числу строк второй матрицы.

Размер матрицы произведения равен m k
Например, даны две матрицы
1 2
A
3
1
2 1
B 0 3
1 1
Произведение матрицы А на матрицу В неопределено, так как число
столбцов первой матрицы не равно числу строк второй матрицы, однако,
произведение матрицы В на матрицу А определено
2 2 1 1 5 5
2 1
2 1 1 3
1 2
B A 0 3
0
1
3
3
0
2
3
1
9
3
3
1
1 1
1 1 ( 1) 3 1 2 ( 1) 1 2 1
Рассмотрим произведение двух матриц А и В
2 1
1 2 1
A
B 1 3
3 1 2
0 1
2 1
1 2 1
1 2 2 1 1 0 1 ( 1) 2 3 1 1 4 6
A B
1
3
3
1
2
3
2
1
1
2
0
3
(
1)
1
3
2
1
7
2
0
1
2 1
2 1 ( 1) 3 2 2 ( 1) 1 2 1 ( 1) 2 1 3 0
1 2 1
B A 1 3
1
1
3
3
1
2
3
1
1
1
3
2
10
5
7
3
1
2
0 1
0 1 1 3
0 2 1 1
0 1 1 2 3 1 2
При
умножении
матриц
(переместительный) закон не выполняется
коммутативный
A B B A
4.
Целой положительной степенью Am (m 1) квадратной
матрицы А называется произведение m равных матриц
Am A A A…. A
Операция возведение в степень определена только для
квадратных матриц.
Пример. Возвести матрицу А в вторую степень
1 2
A
3
4
1 2 1 2 7 10
A
3
4
3
4
15
22
2
5. Транспонирование матрицы.
Под этой операцией понимается переход от матрицы А к
матрице АТ , в которой строки и столбцы поменялись
местами с сохранением порядка.
Матрица АТ называется транспонированной относительно
матрицы А:
a11 a12 a13
a11 a21 a31
A a21 a22 a23
AT a12 a22 a31
a
a
31 a32 a33
13 a23 a33
Свойства операции транспонирования
( AT )T A ( A)T AT
( A B)T AT BT
( AB)T BT AT
Задачи с экономическим содержанием
Понятие матрицы часто используется в практической
деятельности.
Например, данные о выпуске продукции нескольких
видов, нормы затрат нескольких ресурсов на производство
продукции нескольких типов, цены реализации единицы
продукции, нормы затрат ресурсов на производство единиц
продукции и т.
 д удобно записывать в виде матриц.
д удобно записывать в виде матриц.Задача.
Предприятие выпускает продукцию трех видов и
использует сырье двух типов. Определить затраты сырья,
необходимые для планового выпуска продукции, и общую
стоимость сырья.
Обозначим P1 , P2 , P3 видыпродукции S1 , S2 видысырья
Считая известными нормы расхода каждого вида сырья на
изготовление каждого вида продукции составим матрицу норм
расхода сырья
2 3
A 5 2 нормы расхода сырья
1 4
Каждый элемент этой матрицы показывает, сколько
единиц сырья каждого типа расходуется на производство
единицы продукции.
С 100 80 130 план выпуска продукции
Стоимость единицы каждого типа сырья задана матрицейстолбцом
30
B стоимость единицы каждого типа сырья
50
Решение. 1 способ.
1. Вычисляют матрицу затрат сырья
2 3
100 2 80 5 130 1
S C A 100 80 130 5 2
100 3 80 2 130 4
1 4
730 980 матрица затрат сырья
2.
 Вычисляют общую стоимость сырья
Вычисляют общую стоимость сырья30
Q S B 730 980
50
(730 30 980 50) (70900)
2 способ.
1.Вычисляют матрицу стоимости затрат сырья на единицу
продукции
2 3
210
30
R A B 5 2 250 матрица стоимости затрат
50
1 4
230
на единицу продукции
2. Вычисляют общую стоимость сырья
210
Q C R 100 80 130 250 (70900) общая стоимость сырья
230
Задача.
В некоторой отрасли m заводов выпускают n видов
продукции.
Матрица Am n — задает объемы продукции на каждом заводе
в первом квартале, Bm n матрица — во втором; aij , bij — объемы
продукции j — го типа на i — м заводе в первом и втором
кварталах соответственно:
3 0 2
2 3 7
2 4 1
1 2 2
B
A
4 3 2
4 1 5
5 2 4
2 1 3
В данном случае m=4 и n=3
Замечание. Число строк в матрице соответствует числу
предприятий, а число столбцов – количеству видов
выпускаемой продукции.
Найти:
1. объем продукции за полугодие, за год:
5
3
C A B
8
7
3 9
6 3
4 7
3 7
10 6 18
6 12 6
D 2( A B)
16 8 14
14 6 14
2.
 Прирост объемов производства во втором квартале по
Прирост объемов производства во втором квартале посравнению с первым по видам продукции и заводам:
Прирост во втором квартале по сравнению с первым
определяется разностью матриц
1
1
0
3
3 5
2 1
2 3
1 1
Отрицательные элементы матрицы показывают, что на
данном заводе объем производства j-го продукта
уменьшился; положительные — увеличился; нулевые — не
изменился.
3. Стоимостное выражение выпущенной продукции за
полгода (в долларах), если — курс доллара по отношению к
рублю.
C A B
Задача.
Предприятие производит n типов продукции, объемы
выпуска заданы матрицей A1 n . Цена реализации единицы –
i-го типа продукции в j-м регионе задана матрицей Bn k , где
k- число регионов, в которых реализуется продукции
Найти матрицу выручки C по регионам.
Выручка определяется матрицей
Пусть
C1 k A1 n Bn k
2 3 1 5
A1 3 (100 200 100)
B3 4 1 3 2 2
2 4 2 4
Замечание.
 Число столбцов матрицы А и число строк
Число столбцов матрицы А и число строкматрицы В равно количеству видов выпускаемой продукции,
число столбцов матрицы В равно числу регионов, где
реализуется продукция.
2 3 1 5
C 100 200 1 3 2 2 600 1300 700 1300 .
2 4 2 4
Задача.
Предприятие производит n типов продукции, используя
m видов ресурсов. Нормы затрат ресурса i- го вида на
производство единицы продукции j-го типа заданы матрицей
затрат A. Пусть за определенный отрезок времени
предприятие выпустило определенное количество продукции
каждого типа, записанное матрицей X .
Определить S — матрицу полных затрат ресурсов каждого
вида на производство всей продукции за данный период
времени.
2 5 3
100
0 1 8
80
X
A4 3
3 1
1
3
1
110
2 2 3
Матрица полных затрат ресурсов S определяется как
произведение матриц A и X , т.е.
S
2
5
0
1
1
3
2
2
3
930
100
8
960
80
450
14
110
3
690
Если известна стоимость каждого вида ресурса в расчете
на единицу продукции, то можно определить полную
стоимость всех затраченных ресурсов по формуле C PS
P (10 20 10 10)
В данном случае
930
960
39900
C (10 20 10 10)
450
690
English Русский Правила
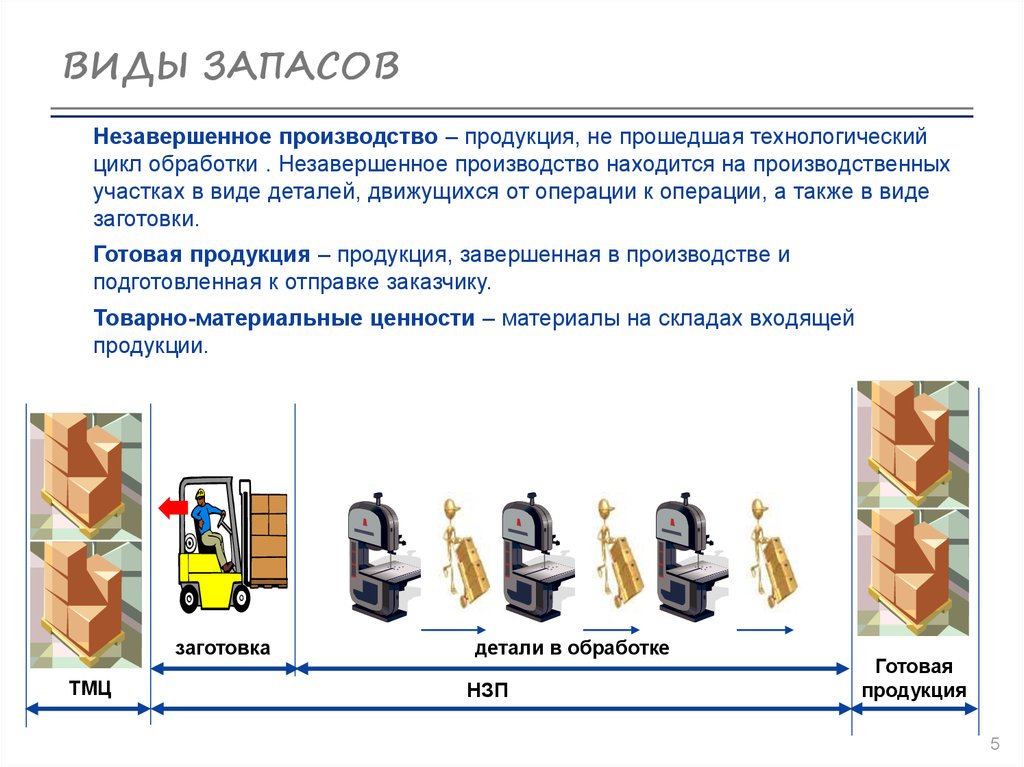
3 типа инвентаря | Сырье | WIP
3 основных типа запасов
Три типа запасов: запасы прямых материалов, запасы незавершенного производства и запасы готовой продукции, где запасы прямых материалов включают запасы сырья, которое компания приобрела для использования в производство; Запасы незавершенного производства — это стоимость, накопленная для товаров, которые частично завершены, а запасы готовой продукции — это запасы, которые завершили все этапы производства и теперь доступны для продажи.
Товарно-материальные запасы означают те оборотные активы, которые были или будут преобразованы в конечную продукцию компании для продажи в ближайшее время. Другими словами, товарно-материальные запасы представляют собой готовые товары или товары на разных стадиях производства, которые компания хранит в своих помещениях или у третьих лиц, при этом доля собственности сохраняется до тех пор, пока товары не будут проданы. Тремя наиболее важными типами запасов являются сырье, запасы незавершенного производства (НЗП) и готовая продукция.
Взгляните на разбивку товарно-материальных запасов Colgate за 2016 и 2015 годы. Здесь перечислены три типа запасов: сырье и материалы, незавершенное производство и готовая продукция. Также обратите внимание, что большая часть запасов Colgate — это запасы готовой продукции.
Содержание
- 3 основных типа запасов
- №1 – Запас сырья:
- №2 – Запас незавершенного производства (НЗП)
- №3 – Запас готовой продукции:
- : Прочие запасы
- Рекомендуемые статьи
- 3 типа инвентаризации Видео
- Заключение
Ниже приведены различные типы инвентаря:
Вы можете использовать это изображение на своем веб-сайте, шаблонах и т. д. нас со ссылкой на авторствоКак указать авторство?Ссылка на статью должна быть гиперссылкой
д. нас со ссылкой на авторствоКак указать авторство?Ссылка на статью должна быть гиперссылкой
Например:
Источник: Types of Inventory (wallstreetmojo.com)
#1 — Инвентаризация сырья:
Сырье — это основные материалы, которые производственная компания покупает у своих поставщиков. Первый использует их для преобразования в конечные продукты путем применения производственных процессов. Например, алюминиевый лом является сырьем для компании, производящей алюминиевые слитки. Мука является сырьем для компании, производящей хлеб или пиццу. Точно так же металлические детали и слитки являются сырьем, покупаемым компанией, производящей автомобили, а сырая нефть является сырьем для нефтеперерабатывающего завода.
Широко распространено и легко заметить, что конечные продукты одной компании покупаются в качестве сырья для какой-то другой компании. Например, многие компании, занимающиеся бурением нефтяных скважин, производят сырую нефть в качестве конечного продукта.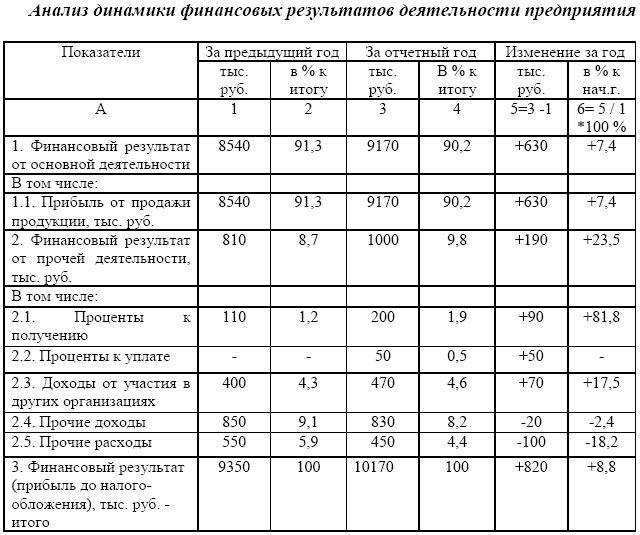 Но, с другой стороны, ту же сырую нефть покупают нефтеперерабатывающие компании в качестве сырья для производства своей конечной продукции, т. е. бензина, керосина, парафина и т. д.
Но, с другой стороны, ту же сырую нефть покупают нефтеперерабатывающие компании в качестве сырья для производства своей конечной продукции, т. е. бензина, керосина, парафина и т. д.
источник: годовые отчеты ВР
отчетГодовой отчетГодовой отчет — это документ, который корпорация публикует для своих внутренних и внешних заинтересованных сторон, чтобы описать производительность компании, финансовую информацию и раскрытие информации, связанной с ее деятельностью. Со временем эти отчеты стали законодательными и нормативными требованиями. Подробнее: Сырая нефть и природный газ являются запасами сырья, включенными в Классификацию типов запасов.
Очень важно оптимизировать запасы сырья. Если компания хранит слишком много сырья, запасыСырьевые запасыСырьевые запасы — это стоимость продукции в запасах компании, которая не использовалась для готовой продукции и запасов незавершенного производства. Запасы сырья являются частью себестоимости запасов, которая отражается в составе оборотных средств в балансовом отчете. Более того, запасы на складе влекут за собой более высокие расходы на хранение, а также существует нежелательная возможность устаревания запасов. Например, сырье может быть скоропортящимся в фармацевтической или пищевой промышленности. Если их не использовать в течение установленного срока, они могут истечь, и их нельзя будет использовать в производстве. С другой стороны, компания должна иметь определенный минимальный уровень запасов, чтобы удовлетворить объемы производства, которые в основном соответствуют тенденции рыночного спроса. Таким образом, оптимизация запасов сырья имеет важное значение.
Более того, запасы на складе влекут за собой более высокие расходы на хранение, а также существует нежелательная возможность устаревания запасов. Например, сырье может быть скоропортящимся в фармацевтической или пищевой промышленности. Если их не использовать в течение установленного срока, они могут истечь, и их нельзя будет использовать в производстве. С другой стороны, компания должна иметь определенный минимальный уровень запасов, чтобы удовлетворить объемы производства, которые в основном соответствуют тенденции рыночного спроса. Таким образом, оптимизация запасов сырья имеет важное значение.
#2 — Запасы незавершенного производства (НЗП)
Запасы незавершенного производства также можно назвать полуфабрикатами. Это сырье, которое было взято со склада сырья и сейчас проходит процесс превращения в конечные продукты. Итак, это частично переработанное сырье, лежащее на производственном участке. И они также не достигли стадии превращения в конечный продукт.
Объем запасов, заблокированных в процессе незавершенного производства, чем меньше, тем лучше. Это понятно, так как запасы в процессе производства бесполезны, пока они не будут преобразованы в конечный продукт. Его можно продать по какой-то цене, но его нельзя продать, чтобы получить какой-либо доход для основного бизнеса компании. Фактически, в системах бережливого производства запасы незавершенного производства считаются отходами.
Это понятно, так как запасы в процессе производства бесполезны, пока они не будут преобразованы в конечный продукт. Его можно продать по какой-то цене, но его нельзя продать, чтобы получить какой-либо доход для основного бизнеса компании. Фактически, в системах бережливого производства запасы незавершенного производства считаются отходами.
Таким образом, желательно, чтобы объем запасов, лежащих в форме незавершенного производства, был сведен к минимуму. Время, необходимое для преобразования его в окончательное, также сведено к минимуму, поэтому заблокированное значение может быть освобождено как можно быстрее. Идея состоит в том, что этот капитал, который заблокирован в виде запасов незавершенного производства, в противном случае может быть вложен в другое место для получения гораздо большей прибыли.
#3 – Инвентаризация готовой продукции:
Готовая продукция – это конечная продукция, полученная после применения производственных процессов к сырью и полуфабрикатам, описанным выше в статье. Их можно продать, и их продажа полностью пополняет доходы от основной деятельности компании.
Их можно продать, и их продажа полностью пополняет доходы от основной деятельности компании.
Что касается уровня запасов готовой продукции, нам нужно рассмотреть два типа отраслей. Во-первых, мы возьмем отрасли, в которых готовая продукция производится массово, а продажа происходит после производства. Примерами таких отраслей являются FMCGFMCGFast-Moving Consumer Goods (FMCG) — это потребительские товары недлительного пользования, которые раскупаются как горячие пирожки, поскольку они обычно имеют низкую цену и высокое удобство использования. Их примеры включают зубную пасту, готовую еду, мыло, печенье, блокноты, шоколад и т. д. Читать далее промышленность и нефтяная промышленность. Для компании в такой отрасли правильный подход состоит в том, чтобы поддерживать запасы готовой продукции так же, как запасы сырья, т. е. на уровне, оптимизированном в соответствии с спросом на рынке.
Источник: Autonews.com
Ford сокращает запасы готовой продукцииЗапасы готовой продукцииЗапасы готовой продукции относятся к конечным продуктам, полученным в процессе производства или через товары. Это конечный продукт компании, готовый к продаже на рынке. подробнее по обрезке продукции. Как мы отмечали выше, в феврале у Ford было всего 78 дней запаса по сравнению с 97 днями запаса в январе.
Это конечный продукт компании, готовый к продаже на рынке. подробнее по обрезке продукции. Как мы отмечали выше, в феврале у Ford было всего 78 дней запаса по сравнению с 97 днями запаса в январе.
Другим видом промышленности является производство товаров по требованию, т. е. сначала поступает заказ, а затем начинается производство. Примерами таких отраслей являются капитальные товары. Капитальные товары. Основные товары — это искусственные активы, используемые в процессе производства продукта. Они используются для производства конечных товаров, которые люди потребляют ежедневно. Они являются одним из четырех факторов производства, остальные три — это природные ресурсы, рабочая сила и предпринимательство. Читать далее промышленность и производство товаров на заказ. Для компании в такой отрасли нет необходимости и целесообразности вести какие-либо запасы готовой продукции, потому что ее готовая продукция, хранящаяся на складе, может никогда не быть продана, даже если она имеет малейшее отклонение от спецификаций новых заказов, поступающих от поставщика. клиенты. Таким образом, они могут никогда не получить отдачу от своих инвестиций в подготовку готовой продукции.
клиенты. Таким образом, они могут никогда не получить отдачу от своих инвестиций в подготовку готовой продукции.
Другие типы инвентаря:
Существует два других важных типа инвентаря, а именно инвентарь упаковочных материалов и ТОиР (техническое обслуживание, ремонт и эксплуатация) запасы расходных материалов .
Как следует из названия, инвентарь для упаковки — это запас материалов компании для упаковки товаров. В этой категории есть то, что называется первичным упаковочным инвентарем и вторичным упаковочным инвентарем. Первичная упаковка – это то, без чего товар не может быть использован. Например, туба мази является ее первичной упаковкой.
Вторичная упаковка используется для упаковки товаров таким образом, чтобы они не повреждались при обработке, транспортировке и т. д., или чтобы товары выглядели более привлекательными для покупателей. Например, картонная упаковка, используемая для упаковки тубы с мазью, является ее вторичной упаковкой.
Расходные материалы для ТОиР или просто запасы или расходные материалы – это материалы, потребляемые в производственных процессах, но не составляющие часть готовой продукции или не составляющие крошечную часть готовой продукции. Вместо этого они являются вспомогательными материалами для производственного процесса. К расходным материалам для технического обслуживания и ремонта относятся смазочное масло, охлаждающая жидкость, болты, гайки и т. д., которые используются при производстве различных машин и компонентов машин. Текущие поставки включают в себя канцелярские и офисные принадлежности, используемые компанией.
Рекомендуемые товары
- Конечный запас Конечный запас Формула конечного запаса вычисляет общую стоимость готовой продукции, оставшейся на складе на конец отчетного периода для продажи. Он оценивается путем вычитания стоимости проданных товаров из общей суммы начальных запасов и покупок. Подробнее
- Коэффициент покрытия процентов
- Дебиторская задолженностьСчета к получениюСчета к получению — это деньги, которые должны бизнесу клиенты, для которых бизнес оказал услуги или поставил продукт, но еще не получил оплату.
 Они классифицируются как оборотные активы в балансе как платежи, ожидаемые в течение года.
читать дальше
Они классифицируются как оборотные активы в балансе как платежи, ожидаемые в течение года.
читать дальше - Отчет об акционерном капитале Отчет об акционерном капитале Акционерный капитал представляет собой остаточную долю акционеров в компании и рассчитывается как разница между активами и обязательствами. Отчет об акционерном капитале в балансовом отчете подробно описывает изменение стоимости акционерного капитала с начала до конца отчетного периода.Подробнее предметы, указанные в книге учета, чем в настоящее время физ. Как и в случае оценки запасов, потеря определяется как разница между стоимостью запасов, указанной в бухгалтерской книге, и стоимостью запасов, существующих физически.Подробнее
3 Типы запасов Видео
Заключение
Запасы — это активы, которые будут преобразованы 9 в конечную продукцию компании. Они бывают трех основных типов: сырье, незавершенное производство и готовая продукция. Управление запасами требует оптимального уровня запасов, который можно поддерживать, создавая план закупок запасов в соответствии со стратегией, принятой компанией.
Что такое инвентарь? Типы, примеры и анализ
Управление запасами является важнейшим активом для предприятий, поскольку позволяет минимизировать стоимость запасов на балансе компании при получении этих товаров. Запасы можно классифицировать тремя способами, включая материалы, незавершенное производство и готовую продукцию.
Что такое инвентарь?
Инвентаризация – это учет предметов, комплектующих и сырья, которые компания либо использует в производстве, либо продает. Как бизнес-лидер, вы практикуете управление запасами, чтобы убедиться, что у вас достаточно запасов и определить, когда есть дефицит.
Глагол «инвентаризация» относится к акту подсчета или перечисления предметов. С точки зрения бухгалтерского учета запасы являются текущими активами и относятся ко всем запасам на различных этапах производства. Сохраняя запасы, как розничные продавцы, так и производители могут продолжать продавать или производить товары. Запасы являются основным балансовым активом для большинства компаний, однако слишком большой запас может стать практическим недостатком.
Видео: Что такое инвентарь?
Ключевые выводы
- Товарно-материальные запасы, описывающие любые товары, готовые к покупке, напрямую влияют на финансовое благополучие и процветание организации.
- Хотя существует много типов запасов, четыре основных из них — это сырье и компоненты, незавершенное производство, готовая продукция и материалы для технического обслуживания, ремонта и эксплуатации.
- Хотя существует множество способов подсчета и оценки вашего инвентаря, важно точно отслеживать, анализировать и управлять им. Информация, полученная в результате оценки запасов, необходима для успеха, поскольку она помогает компаниям принимать более разумные и экономически эффективные бизнес-решения.

Инвентаризация Объяснение
Инвентаризация организации, которую часто описывают как этап между производством и выполнением заказа, занимает центральное место во всех ее бизнес-операциях, поскольку часто служит основным источником получения дохода. Хотя запасы можно описывать и классифицировать по-разному, в конечном итоге именно управление ими напрямую влияет на возможности организации по выполнению заказов.
Например, при отслеживании сырья, страхового запаса, готовой продукции или даже упаковочных материалов предприятия собирают важные данные, которые влияют на их будущие операции по закупкам и выполнению заказов. Понимание тенденций закупок и скорости продажи товаров определяет, как часто компаниям необходимо пополнять запасы и какие товары являются приоритетными для повторной покупки. Наличие этой информации под рукой может улучшить отношения с клиентами, поток денежных средств и прибыльность, а также уменьшить количество денег, потерянных из-за неиспользованных запасов, дефицита и задержек с пополнением запасов.
13 видов запасов
Сырье: Сырье — это материалы, которые компания использует для создания и отделки продукции. Когда продукт готов, сырье обычно невозможно отличить от его первоначальной формы, например, масло, используемое для создания шампуня.
Компоненты: Компоненты похожи на сырье в том смысле, что это материалы, которые компания использует для создания и отделки продуктов, за исключением того, что они остаются узнаваемыми, когда продукт готов, например, винт.
Незавершенное производство (НЗП): Запасы незавершенного производства относятся к предметам, находящимся в производстве, и включают сырье или компоненты, рабочую силу, накладные расходы и даже упаковочные материалы.

Готовая продукция: Готовая продукция – это товары, готовые к продаже.
Техническое обслуживание, ремонт и эксплуатация (ТОиР) Товары: MRO — это инвентарь — часто в виде расходных материалов — который поддерживает производство продукта или поддержание бизнеса.
Упаковка и упаковочные материалы: Существует три типа упаковочных материалов. Первичная упаковка защищает продукт и делает его пригодным для использования. Вторичная упаковка — это упаковка готового товара, которая может включать этикетки или информацию о SKU.
 Третичная упаковка – это оптовая упаковка для транспортировки.
Третичная упаковка – это оптовая упаковка для транспортировки.Страховой запас и ожидаемый запас: Страховой запас — это дополнительные запасы, которые компания покупает и хранит на случай непредвиденных обстоятельств. Страховой запас имеет расходы на содержание, но он поддерживает удовлетворенность клиентов. Точно так же ожидаемый запас состоит из сырья или готовых изделий, которые бизнес покупает на основе тенденций продаж и производства. Если цена на сырье растет или приближается время пиковых продаж, предприятие может приобрести страховой запас.
Развязка Инвентарь: Разделение запасов — это термин, используемый для обозначения дополнительных элементов или WIP, хранящихся на каждой станции производственной линии для предотвращения простоев в работе.
 В то время как все компании могут иметь страховой запас, разделение запасов полезно, если части линии работают с разной скоростью, и применимо только к компаниям, производящим товары.
В то время как все компании могут иметь страховой запас, разделение запасов полезно, если части линии работают с разной скоростью, и применимо только к компаниям, производящим товары.Инвентаризация циклов: Компании заказывают циклические запасы партиями, чтобы получить нужное количество запасов с наименьшими затратами на хранение. Узнайте больше о формулах циклической инвентаризации в «Основном руководстве по планированию инвентаризации».
Сервисный инвентарь: Инвентаризация услуг — это концепция управленческого учета, которая относится к тому, сколько услуг бизнес может предоставить за определенный период. Например, гостиница с 10 номерами имеет запас услуг на 70 ночей в неделю.

Транзитный инвентарь: Транзитные запасы, также известные как конвейерные запасы, — это запасы, которые перемещаются между производителем, складами и распределительными центрами. Транзитный инвентарь может занять недели, чтобы перемещаться между объектами.
Теоретическая инвентаризация: Теоретические запасы, также называемые бухгалтерскими запасами, представляют собой наименьшее количество запасов, которое необходимо компании для завершения процесса без ожидания. Теоретическая инвентаризация используется в основном в производстве и пищевой промышленности. Он измеряется с использованием фактической и теоретической формулы.
Избыточный запас: Излишние запасы, также известные как устаревшие запасы, представляют собой непроданные или неиспользованные товары или сырье, которые компания не планирует использовать или продавать, но которые все равно должны платить за хранение.

Запасы известны как товары и продукты компании, которые могут быть проданы. Он помечен как оборотный актив на балансе компании. Посредник между производством и выполнением заказа.
Примеры инвентаризации
Реальные примеры облегчают понимание моделей инвентаризации. Следующие примеры демонстрируют, как различные типы запасов работают в розничной торговле и на производстве.
Сырье/Компоненты: Компания, производящая футболки, имеет такие компоненты, как ткань, нитки, красители и принты.
Готовая продукция: Производитель ювелирных изделий производит ожерелья с подвесками. Персонал прикрепляет ожерелье к предварительно напечатанной открытке и вкладывает ее в целлофановые конверты, чтобы создать готовый товар, готовый к продаже.
 Себестоимость проданных товаров (COGS) готового товара включает как его упаковку, так и труд, затраченный на его изготовление.
Себестоимость проданных товаров (COGS) готового товара включает как его упаковку, так и труд, затраченный на его изготовление.В работе: Сотовый телефон состоит из корпуса, печатной платы и компонентов. Процесс сборки деталей на выделенной рабочей станции называется WIP.
MRO Товары: Расходные материалы для обслуживания, ремонта и эксплуатации многоквартирного дома включают копировальную бумагу, папки, тонер для принтера, перчатки, средство для мытья стекол и метлы для подметания территории.
Упаковочные материалы: В семеноводческой компании основным упаковочным материалом является запечатанный пакет, содержащий, например, семена льна.
 Помещение мешков с семенами льна в ящик для транспортировки и хранения является вторичной упаковкой. Третичная упаковка — это термоусадочная пленка, необходимая для транспортировки поддонов с товарными ящиками.
Помещение мешков с семенами льна в ящик для транспортировки и хранения является вторичной упаковкой. Третичная упаковка — это термоусадочная пленка, необходимая для транспортировки поддонов с товарными ящиками.Страховой запас: Ветеринар в изолированном сообществе запасается дезинфицирующим средством и лакомствами для собак и кошек, чтобы удовлетворить потребности клиентов на случай наводнения на шоссе во время весенней распутицы и задержки грузовиков.
Ожидаемый/сглаживающий инвентарь: Организатор мероприятий покупает со скидкой катушки с лентами и цветочные скатерти в преддверии июньского свадебного сезона.
Decoupled Инвентарь: В пекарне декораторы хранят запас сахарных роз, которыми можно украсить свадебные торты, поэтому, даже если команда декораторов задержит поставку глазури, декораторы могут продолжать работу.
 Поскольку цветы являются частью дизайна торта, если они закончатся у пекаря, он не сможет доставить готовый торт.
Поскольку цветы являются частью дизайна торта, если они закончатся у пекаря, он не сможет доставить готовый торт.Циклический инвентарь: Поскольку ресторан использует последние 500 бумажных салфеток, поступает новый заказ на пополнение. Салфетки легко помещаются в специальное место для хранения.
Сервис Инвентарь: Кафе открыто 12 часов в день, с 10 столиками, за которыми посетители проводят в среднем один час за едой. Таким образом, его сервисный инвентарь составляет 120 приемов пищи в день.
Теоретическая инвентарная стоимость: Ресторан намеревается потратить 30% своего бюджета на еду, но обнаруживает, что на самом деле тратит 34%.
 «Теоретический запас» — это 4% продуктов, которые были потеряны или выброшены впустую.
«Теоретический запас» — это 4% продуктов, которые были потеряны или выброшены впустую.Инвентаризация книги: Теоретическая инвентаризация запасов в инвентарной записи или системе, которая может отличаться от фактической инвентаризации при выполнении подсчета.
Транзит Инвентарь: Художественный магазин заказывает и оплачивает 40 банок популярного набора карандашей. Банки находятся в пути от поставщика и, следовательно, в пути.
Лишние запасы: Компания по производству шампуней производит 50 000 специальных бутылочек с шампунем, предназначенных для летних Олимпийских игр, но продает только 45 000, а Олимпийские игры закончились — никто не хочет их покупать, поэтому они вынуждены делать скидки или выбрасывать их.
 .
.
Что такое производственные запасы?
В производстве запасы состоят из имеющихся на складе предметов, сырья и компонентов, используемых для изготовления товаров. Производители внимательно следят за уровнем запасов, чтобы убедиться в отсутствии дефицита, который может остановить работу.
Бухгалтерский учет делит производственные запасы на сырье, незавершенное производство и готовую продукцию, поскольку каждый тип запасов имеет разную стоимость. Сырье обычно стоимость за единицу меньше, чем у готовых изделий.
Что означает инвентаризация в сфере услуг?
У каждой компании есть акции, которые поддерживают ее регулярную деятельность. Для сервисных компаний этот инвентарь нематериален. Инвентаризация юридической фирмы, например, включает ее файлы, а бумага, на которой печатаются юридические документы, — это MRO фирмы.
Важность управления запасами
Управление запасами помогает компаниям покупать нужное количество запасов в нужное время.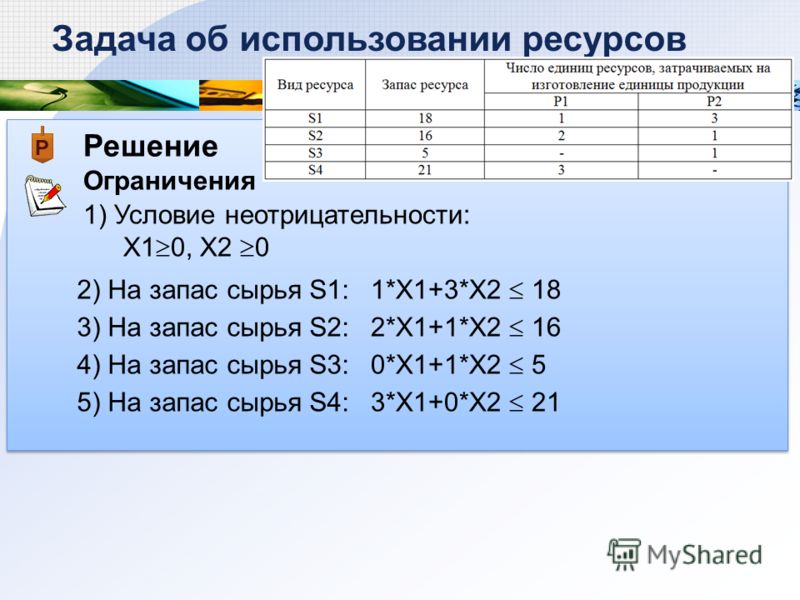 Этот процесс, также известный как контроль запасов, помогает оптимизировать уровни запасов, снизить затраты на хранение и предотвратить дефицит.
Этот процесс, также известный как контроль запасов, помогает оптимизировать уровни запасов, снизить затраты на хранение и предотвратить дефицит.
Инвентаризация позволяет компаниям получать максимальную прибыль. Это позволяет им минимизировать инвестиции в акции, позволяя компаниям лучше всего оценивать свои текущие активы, остатки на счетах и финансовые отчеты. Это важно, потому что предотвращает чрезмерные расходы из-за покупки слишком большого или ненужного инвентаря, вместо этого отдавая приоритет обязательным инвентарям.
Благодаря соответствующему внутреннему и производственному контролю эта практика гарантирует, что компания может удовлетворить спрос клиентов и обеспечить финансовую эластичность. Управление запасами позволяет получить максимальную прибыль при наименьших инвестициях в запасы, не влияя на удовлетворенность клиентов. Если все сделано правильно, это позволяет компаниям оценивать свое текущее состояние в отношении активов, остатков на счетах и финансовых отчетов.
Узнайте больше в «Основном руководстве по управлению запасами».
Передовой опыт инвентаризации
Деловая поговорка «если вы не можете что-то измерить, вы не можете этим управлять» применима к управлению запасами и передовым методам. В то время как первая лучшая практика — отслеживать ваш инвентарь, другие включают:
Carry Safety Stock:
Эти продукты, также известные как буферный запас, помогают компаниям избежать нехватки материалов или предметов повышенного спроса. Как только компании истощают свои расчетные запасы, страховой запас служит резервной копией на случай неожиданного увеличения уровня спроса.Инвестиции в облачную программу управления запасами:
Облачные системы управления запасами позволяют компаниям в режиме реального времени знать, где находится каждый продукт и SKU по всему миру. Эти данные помогают организации быть более оперативной, актуальной и гибкой.
Эти данные помогают организации быть более оперативной, актуальной и гибкой.Запустить программу циклической инвентаризации:
Преимущества циклической инвентаризации распространяются далеко за пределы склада, обеспечивая согласованность запасов и удовлетворение клиентов, а также экономя время и деньги предприятий.Использование отслеживания партии/партии :
Запись информации, связанной с каждой партией или партией продукта. В то время как некоторые предприятия регистрируют точные данные, такие как даты истечения срока годности, которые предоставляют информацию о сроках продажи их продуктов, компании, у которых нет скоропортящихся товаров, используют отслеживание партий / партий, чтобы понять стоимость доставки своих продуктов или срок годности.
Управление запасами имеет решающее значение для укрепления цепочки поставок компаний, поскольку оно помогает стабилизировать динамику между потребительским спросом, складскими площадями и ограничениями наличности.
Что такое процесс инвентаризации?
Процесс инвентаризации отслеживает запасы, поскольку компании получают, хранят, управляют и изымают или потребляют их в процессе производства. По сути, процесс инвентаризации — это жизненный цикл товаров и сырья.
Посмотрите схему процесса инвентаризации и узнайте больше, прочитав «Основное руководство по планированию инвентаризации».
Что такое инвентаризация?
Инвентаризация — это физический акт подсчета и проверки состояния предметов на складе или на складе. Инвентаризация также проверяет состояние предметов. Для целей бухгалтерского учета инвентаризация помогает оценить активы и долги.
Инвентаризация также проверяет состояние предметов. Для целей бухгалтерского учета инвентаризация помогает оценить активы и долги.
Подсчет запасов помогает понять, какие запасы хорошо продаются, и менеджеры по запасам часто используют эту информацию для прогнозирования потребности в запасах и управления бюджетом. Чтобы узнать больше о инвентаризации, прочитайте статьи «Проведение физической инвентаризации» и «Циклическая инвентаризация 101».
Методы инвентаризации
Существуют два метода инвентаризации: периодический и непрерывный. При периодической инвентаризации вы подсчитываете запасы в определенное время и добавляете итоги в главную книгу. В бессрочном методе вы записываете изменения запасов по мере их возникновения.
Хотя периодические инвентаризации можно использовать в любом виде бизнеса, небольшие организации часто используют их, особенно когда нет планов по масштабированию бизнеса. Периодический метод не требует специального программного обеспечения или оборудования. Организации, которые используют постоянные методы инвентаризации и требуют подсчета в реальном времени, часто используют сканеры и точки продаж (POS).
Организации, которые используют постоянные методы инвентаризации и требуют подсчета в реальном времени, часто используют сканеры и точки продаж (POS).
Что такое оборачиваемость запасов?
Оборачиваемость запасов — это количество раз, когда компания продает или использует товар в определенный период времени, что может показать, не слишком ли много запасов в наличии у компании. Чтобы определить оборачиваемость запасов, используйте следующие уравнения:
Средний запас = ( Начальный запас + Конечный запас ) / 2
Оборачиваемость запасов = Продажи Средний запас 0006 Чтобы узнать больше об оборачиваемости запасов, прочтите «Оборачиваемость запасов: расчеты, показатели и анализ». Инвентаризационный анализ — это исследование того, как спрос на продукцию меняется с течением времени, и он помогает предприятиям хранить нужное количество товаров и прогнозировать, сколько клиентов потребуют в будущем. Хорошо известным методом проведения инвентаризационного анализа является ABC-анализ. Для проведения АВС-анализа сгруппируйте товары по трем категориям: Инвентаризация: Инвентаризация включает наиболее продаваемые товары, для хранения которых требуется минимум места и средств. Многие эксперты говорят, что это составляет около 20% вашего инвентаря. Запасы B: предметов B перемещаются с той же скоростью, что и предметы A, но их хранение стоит дороже. Как правило, это составляет около 40% вашего инвентаря. C инвентарь: Хранение остатка ваших запасов обходится дороже всего и приносит наименьшую прибыль. Инвентарь C представляет остальные 40% вашего инвентаря. ABC-анализ использует принцип Парето, или принцип 80/20, и должен выявить 20% ваших запасов, которые приносят 80% вашей прибыли. Компания захочет сосредоточиться на этих элементах, чтобы увеличить продажи и чистую прибыль. Анализ запасов может повлиять на выбор методов управления запасами, будь то «точно вовремя» или «на всякий случай». Анализ запасов повышает прибыль за счет снижения затрат и поддержки товарооборота. Также: Улучшает денежный поток: Инвентаризационный анализ помогает вам находить товары, которые вы часто продаете, и переупорядочивать их, поэтому вы не тратите деньги на инвентарь, который движется медленно. Сокращение дефицита: Когда вы понимаете, какие товары больше всего нужны покупателям, вы можете лучше прогнозировать спрос и предотвращать дефицит. Повышает удовлетворенность клиентов: Анализ запасов дает представление о том, что и как клиенты покупают товары. Сокращает запасы впустую: Понимание того, что, когда и сколько люди покупают, сводит к минимуму необходимость хранения устаревших продуктов, а также сроков годности продуктов, чтобы вы могли разработать стратегию их использования. Сокращение задержек проекта: Информация о сроках выполнения заказов поставщиками поможет вам понять, когда следует повторно заказывать и как избежать поздних поставок. Улучшает ценообразование у поставщиков и продавцов: Анализ запасов может привести к тому, что вы будете регулярно заказывать большие объемы продукции, а не небольшие объемы по менее надежному графику. Эта регулярность может поставить вас в более выгодное положение при ведении переговоров о скидках с поставщиками. Расширяет ваше понимание бизнеса: Просмотр запасов дает представление о ваших запасах, клиентах и бизнесе. Прогнозирование спроса — это практика прогнозирования потребительского спроса на основе анализа прошлых покупательских тенденций, таких как рекламные акции и сезонность. Точное прогнозирование спроса позволяет лучше понять, какой объем запасов вам потребуется, и снижает потребность в хранении избыточных запасов. Прогнозирование запасов опирается на данные для обоснования решений, применяя информацию и логику, чтобы гарантировать, что у вас есть достаточное количество продукции для удовлетворения спроса, и при этом не тратить деньги на ненужные запасы. Используется ряд расширенных симуляций, но обычно они представлены в форме прогнозирования тенденций, графического прогнозирования, качественного прогнозирования или количественного прогнозирования. Хорошая стратегия управления запасами и точный учет запасов могут помочь сэкономить деньги компаний, поскольку они будут предоставлять только товары, которые покупают клиенты, и, следовательно, упрощают их операции. Учет запасов — это система, которая подсчитывает и регистрирует изменения стоимости запасов, таких как сырье, незавершенное производство и готовая продукция, которые считаются активами. Финансовый учет запасов обеспечивает точную оценку этих складских активов. Учет запасов определяет стоимость запасов и правильное количество предметов. Эти цифры определяют стоимость проданных товаров и конечную стоимость запасов, которые влияют на общую стоимость компании. Средняя стоимость запасов — это метод расчета себестоимости единицы проданных товаров. Чтобы рассчитать среднюю стоимость, получите сумму стоимости всех товаров, выставленных на продажу, и разделите ее на количество проданных товаров. Этот метод также называется средневзвешенной стоимостью и является ценным способом определения стоимости ваших текущих запасов. Однако управление запасами и ведение финансовой отчетности — это гораздо больше, чем просто отслеживание стоимости запасов. Узнайте больше о средней стоимости запасов в статье «Ключ к использованию методов учета стоимости запасов в вашем бизнесе». Правильное управление запасами может создать или разрушить бизнес. Наличие информации о ваших акциях в любой момент имеет решающее значение для успеха. Лица, принимающие решения, знают, что им нужны правильные инструменты, чтобы иметь возможность эффективно управлять своими запасами. NetSuite предлагает набор собственных инструментов для отслеживания запасов в нескольких местах, определения точек повторного заказа и управления резервным запасом и подсчетом циклов. NetSuite предоставляет решения для управления запасами в облаке, которые идеально подходят для начинающих компаний, малых предприятий и компаний из списка Fortune 100. Узнайте больше о том, как вы можете использовать NetSuite для планирования запасов и управления ими, снижения затрат на обработку и увеличения денежного потока. Существует четыре основных типа запасов: сырье/компоненты, незавершенное производство, готовая продукция и ТОиР. Однако некоторые люди признают только три типа инвентаря, исключая MRO. Понимание различных типов запасов необходимо для принятия обоснованных решений в области финансового и производственного планирования. Инвентаризация — или управление запасами — позволяет убедиться, что ваш бизнес имеет необходимые запасы для удовлетворения потребительского спроса. Что такое инвентаризационный анализ?

На этой круговой диаграмме показан пример того, как ABC-анализ может помочь в расшифровке стоимости каждой единицы запасов исключительно на основе той ценности, которую они представляют для компании. 
Преимущества анализа запасов
На этом графике показаны преимущества управления запасами и показано, как оно может увеличить продажи и доход компании за счет постоянного обеспечения нужного количества продуктов, необходимого для выполнения заказов клиентов.


Что такое прогнозирование спроса?
Преимущества управления запасами и точной инвентаризации
 О других преимуществах читайте в статье «Основные преимущества управления запасами».
О других преимуществах читайте в статье «Основные преимущества управления запасами». Учет запасов
Что такое средняя стоимость запасов?
 Это лучше всего работает для брендов, которые имеют большие объемы запасов и одинаковые по стоимости артикулы. Одним из его преимуществ по сравнению с другими методами является то, что он упрощает отслеживание и непротиворечивый расчет стоимости запасов с помощью смешанного среднего значения.
Это лучше всего работает для брендов, которые имеют большие объемы запасов и одинаковые по стоимости артикулы. Одним из его преимуществ по сравнению с другими методами является то, что он упрощает отслеживание и непротиворечивый расчет стоимости запасов с помощью смешанного среднего значения. Программное обеспечение NetSuite для управления всеми вашими запасами
 Найдите правильный баланс между спросом и предложением во всей организации с помощью функций планирования спроса и планирования требований к распределению.
Найдите правильный баланс между спросом и предложением во всей организации с помощью функций планирования спроса и планирования требований к распределению. Часто задаваемые вопросы по инвентаризации
Какие существуют четыре различных типа инвентаря?
Как осуществляется управление запасами?


 Они классифицируются как оборотные активы в балансе как платежи, ожидаемые в течение года.
читать дальше
Они классифицируются как оборотные активы в балансе как платежи, ожидаемые в течение года.
читать дальше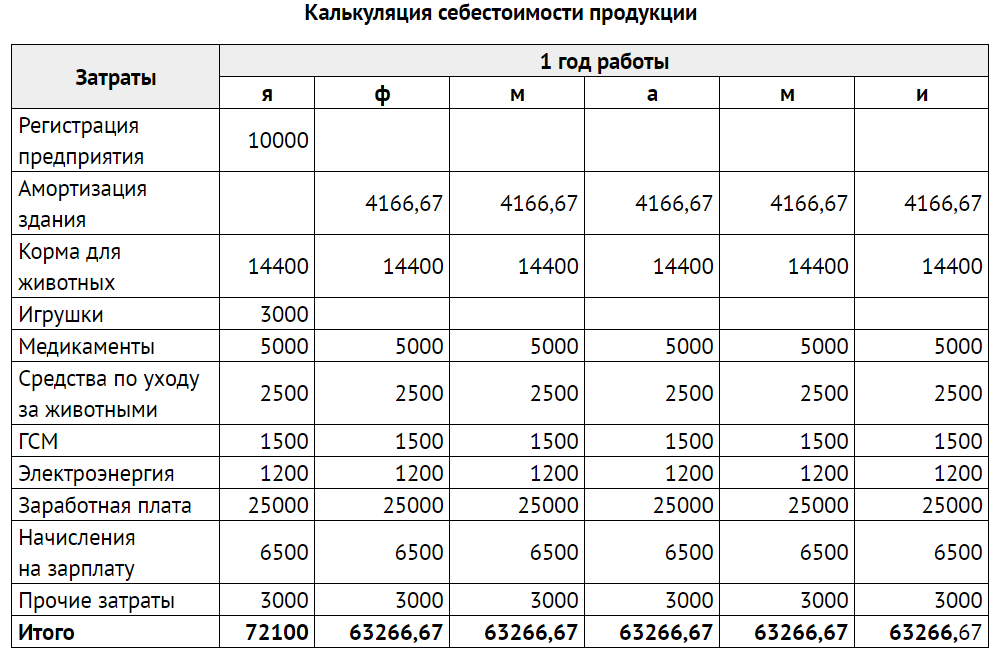
 Третичная упаковка – это оптовая упаковка для транспортировки.
Третичная упаковка – это оптовая упаковка для транспортировки. В то время как все компании могут иметь страховой запас, разделение запасов полезно, если части линии работают с разной скоростью, и применимо только к компаниям, производящим товары.
В то время как все компании могут иметь страховой запас, разделение запасов полезно, если части линии работают с разной скоростью, и применимо только к компаниям, производящим товары.
 Себестоимость проданных товаров (COGS) готового товара включает как его упаковку, так и труд, затраченный на его изготовление.
Себестоимость проданных товаров (COGS) готового товара включает как его упаковку, так и труд, затраченный на его изготовление. Помещение мешков с семенами льна в ящик для транспортировки и хранения является вторичной упаковкой. Третичная упаковка — это термоусадочная пленка, необходимая для транспортировки поддонов с товарными ящиками.
Помещение мешков с семенами льна в ящик для транспортировки и хранения является вторичной упаковкой. Третичная упаковка — это термоусадочная пленка, необходимая для транспортировки поддонов с товарными ящиками.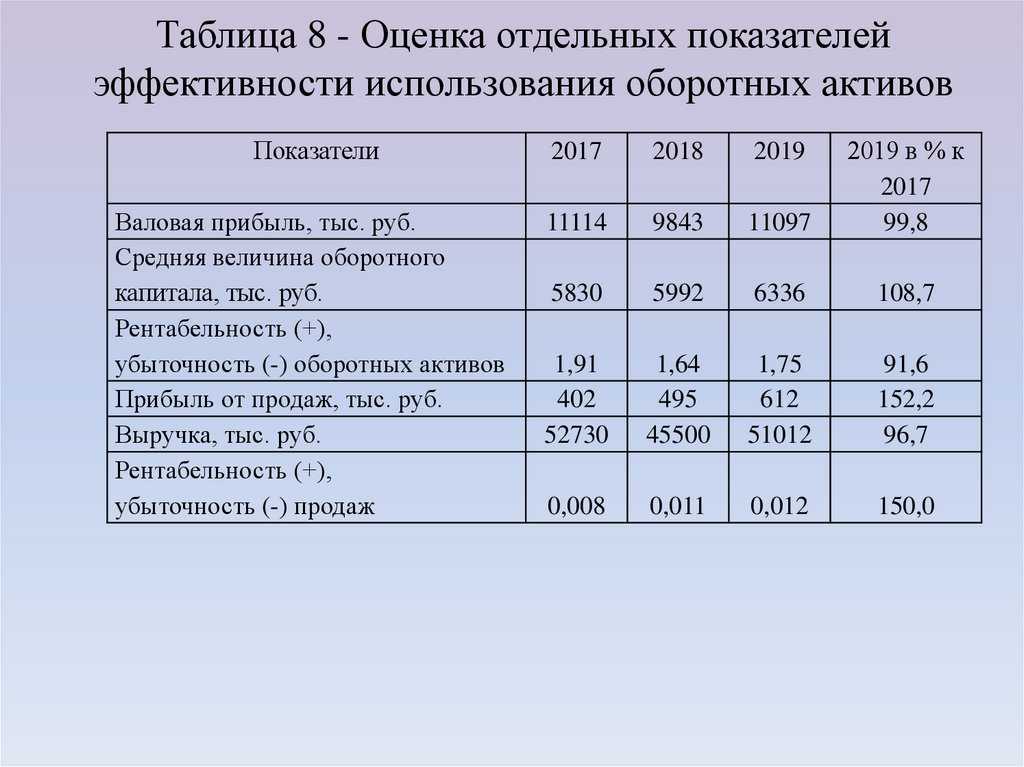 Поскольку цветы являются частью дизайна торта, если они закончатся у пекаря, он не сможет доставить готовый торт.
Поскольку цветы являются частью дизайна торта, если они закончатся у пекаря, он не сможет доставить готовый торт. «Теоретический запас» — это 4% продуктов, которые были потеряны или выброшены впустую.
«Теоретический запас» — это 4% продуктов, которые были потеряны или выброшены впустую. .
. Эти данные помогают организации быть более оперативной, актуальной и гибкой.
Эти данные помогают организации быть более оперативной, актуальной и гибкой.