Онлайн построение графиков функций с решением: Построение графика функции онлайн

Построение графика функции, содержащей модуль

МБОУ СОШ №11
пгт.Шерегеш
Материалы к ШМО
Учитель математики Белоусова М.А.
14.10.2019
Математика является одним из
наиболее важных предметов школьного
курса.
Статус математики как обязательного
государственного экзамена подтверждает
необходимость изучения
математики
каждым учащимся
14.10.2019
2
Каждый школьник в процессе обучения
должен иметь возможность получить
качественную подготовку к выпускным
экзаменам, освоить тот объём знаний,
умений и навыков, который необходим
для успешной сдачи ОГЭ в 9 классе,
дальнейшего обучения в 10-11 классах,
сдачи ЕГЭ и последующего обучения в
вузе.
14.10.2019
3

4. Результаты ГИА 2018-2019 по математике

35%
Результаты ГИА 2018-2019гг. по математике
100%
Общая
успеваемость
Качественная
успеваемость
13
14
12
7
10
Из них 4 ученика
набрали 22-24 балла
8
6
4
2
0
Оценка «3»
14. 10.2019
Оценка»4-5″
4

5. «Западающие темы»

Геометрические
задачи
Текстовые
задачи
Графики функций
Неравенства
14.10.2019
Формулы
сокращенного
умножения
5
Цели и задачи
Цели:
– Подготовка учащихся к успешной сдачи ОГЭ по
математике
Задачи:
– Обучить строить графики функции, содержащей
модуль, посредством алгоритмизации шагов;
– Углубить знания по математике, предусматривающие
формирование у учащихся устойчивого интереса к
предмету;
– Расширить математические представления учащихся о
приёмах и методах решения задач с модулями;
6
14.10.2019

7. Краткое описание работы

Презентация
содержит
алгоритмы
построения графиков функций, содержащих
модуль, семь примеров построения графиков
функции.
Формат презентации дает возможность
учителю обсудить шаги выполнения задания с
обучающимися, дать возможность самим
обучающимся выполнить действие, а потом
уже проконтролировать, используя анимацию.
14.11.2017
7

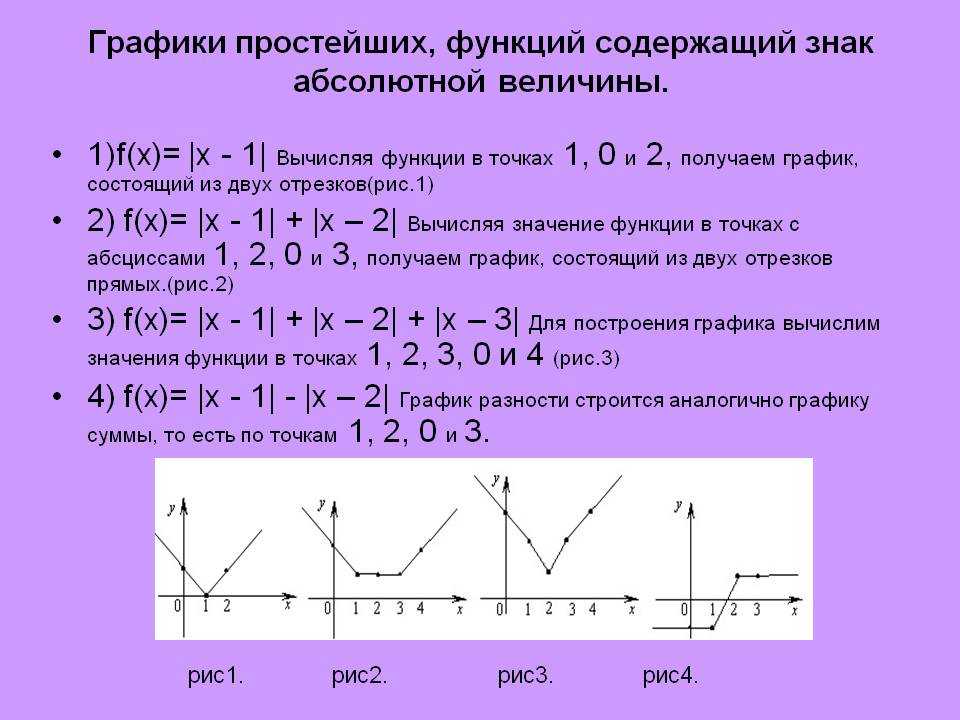
8. Построение графиков функций с выражениями под знаком модуля

Построение
графиков,
содержащих
осуществляется двумя способами:
модуль,
На основании определения модуля;
На основании правил геометрического
преобразования графиков функций.
По определению модуля числа:
14.11.2017
8

9. Построение графика линейной функции y = (f |x|)

Построение графика функции
Пример 1.
14.10.2019
9

10. Построение графика линейной функции y = |f (x)|

Пример 2.
Алгоритм построения:
Найдем нули выражения, стоящего под знаком
модуля.
Раскроем модуль на промежутках:
и
14.10.2019
10

11. Построение графика линейной функции y = |f (x)|

Пример 3.
Построить график функции
Найдем нули выражений, стоящих под знаком
модуля.
Получим три промежутка:
Расставим знаки для подмодульных выражений на
координатной прямой:
14.10.2019
11

12. Пример 3.

Построение графика линейной функции y = |f (x)|Раскроем знаки модуля на промежутках:
Раскрыв скобки и выполнив тождественные
преобразования, получим:
Строим график:
0
х
-7
14.10.2019
12

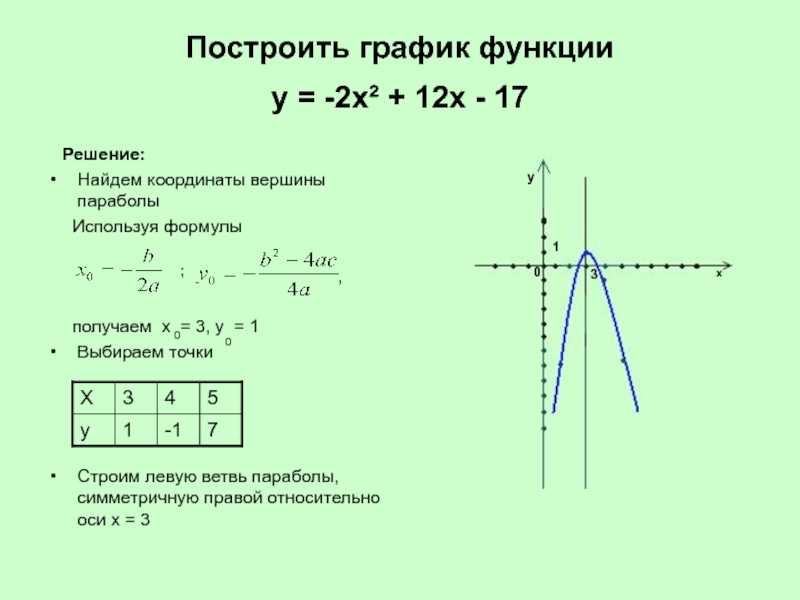
13. Построение графиков функций у = |ах2+bх+с| и у = ах2+b|х|+с

На основании правил геометрического
преобразования графиков функций.
Алгоритм построения графика:
1. Постройте график функции у = ах2+bх + с (I) любым
способом.
2. Если парабола пересечет ось Ох,
то всю часть графика, которая
расположена под осью Ox,
отобразите симметрично оси Ox,
т.к. |y| ≥ 0.
14.10.2019
13

14. Построение графиков функций у = |ах2+bх+с| и у = ах2+b|х|+с

3. Если парабола расположена над осью Ох,
то |ах2+bх+с| = ах2+bх+с при всех значениях х,
а значит, весь график сохранит свое положение.
4. Если вся парабола (I) расположена под осью Ох,
( а < 0; D < 0), то графиком функции у = |ах2+bх+с| будет
парабола,
расположенная
над
осью
Ох
симметрично параболе (I) относительно оси Ох.
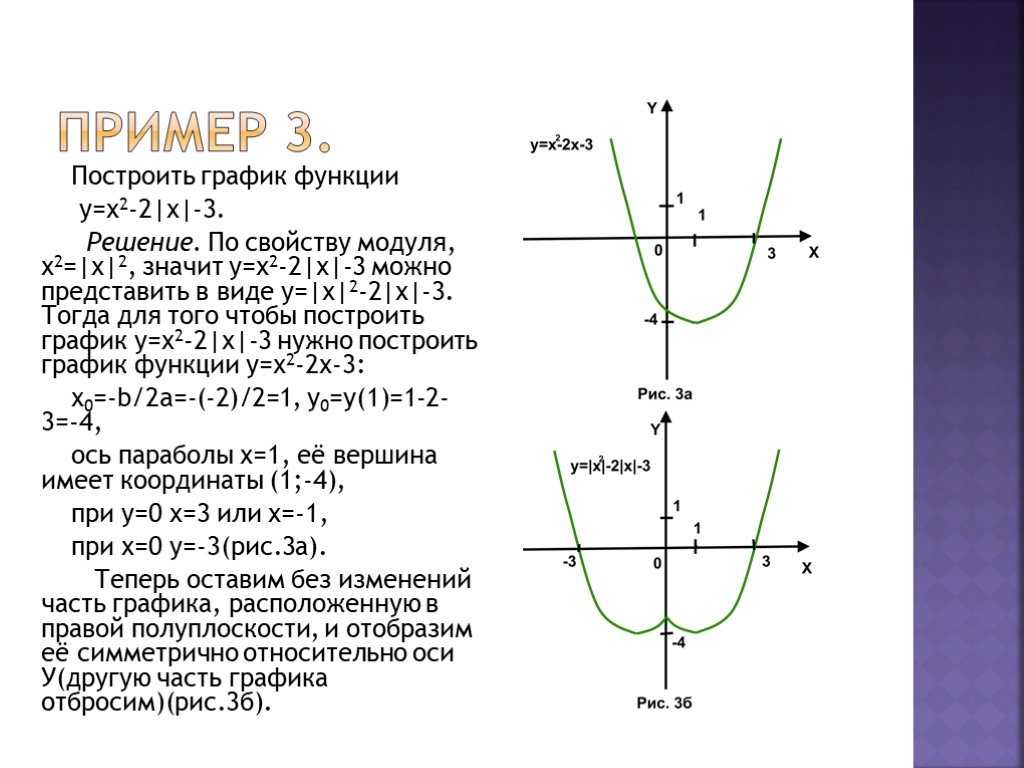
5. Если надо построить график функции у = ах2+b|х| + с ,
то всю часть графика (I), которая справа от оси Оу,
отобразите симметрично оси ОУ, а левую часть
графика (I) относительно оси ОУ стройте пунктиром.
14.10.2019
14

15. Пример 4. Построение графика функции у = |ах2+bх+с|

.-
Пример 4. Построение графика функции
у = |ах2+bх+с|
Построение
1) Найдем координаты вершины
параболы:
1) Постройте график
функции
у =ах2+bх+с (I) любым
способом.
Подставим
в трехчлен и найдем
— вершина параболы
14.11.2017
15

16. Пример 4. Построение графика функции у = |ах2+bх+с|

2)
— ось симметрии;
3) Точки пересечения с осью Ох:
— точки пересечения с осью Ох.
14.11.2017
16

17. Пример 4. Построение графика функции

4) Точка пересечения с осью Оу:
— точка пересечения с осью Оу;
Строим график,
отображая нижнюю часть
графика симметрично оси Ох:
14.10.2019
17

18.

Пример 5. Построение графика функции у = ах2+b|х|+сПостроим график функции
1. Найдем координаты вершины параболы:
:
— вершина параболы
2.
— ось симметрии
3. Точки пересечения с осью Ох:
— нет корней, точек пересечения с осью Ох нет
4. Точка пересечения с осью Оу:
— точка пересечения с осью Оу
14.10.2019
18

19. Алгоритм. Построение графика функции у = |ах2+b|х|+с|

1. Постройте график функции у = ах2+bх+с .
2. Постройте график функции у = ах2+b|х|+с.
Для этого постройте симметрично оси Оу ту
часть графика, которая справа от оси Оу.
3. Постройте симметрично оси Ох ту часть
графика, которая находится под осью Ох.
Построенный график является графиком
функции у = |ах2+b|х|+с|
14.10.2019
18

20. Построение графика функции у = |ах2+b|х|+с | Пример 6. Постройте график функции

1) Постройте график функции
(I).
Например, способом выделения полного квадрата:
Вершина в точке
.
Корни:
;
.
Ось симметрии:
2) Постройте график функции
3) Постройте симметрично оси Оx
ту часть графика, которая находится
под осью Ох, получим искомый график функции
14.10.2019
19

21. Пример 7.Постройте график функции

1 х 3,5
х 3,5
y (
)
2 3,5 х 3,5 х
1 х 3,5
х 3,5 1 х 2 3,52 х 2 3,52
y (
) (
)
2 3,5 х 3,5 х
2
3,5х
3,5х
х 2 3,52
( х 3,5)( х 3,5)
3,5 х
3,5 х
y
—
+
-3,5
0
+
3,5
1
х
3,5
х
3,5
(
)
2 3,5
х
3,5
х
1 х 2 3,5 2
х 2 3,5 2
(
)
2
3,5 х
3,5 х
1 2х2
х
, х 3,5;0 3,5;
3,5
2 3,5 х
2
1 2 3,5 3,5 , х ; 3,5 0;3,5
3,5 х
х
2
14.10.2019
20

22. Пример 7.Постройте график функции

х
, х 3,5;0 3,5;
3,5
y
3,5 , х ; 3,5 0;3,5
х
1 х 3,5
х 3,5
y (
)
2 3,5 х 3,5 х
у
3,5
0 1
14.10.2019
3,5
21
х

23.

Использованные материалы и литература:1.
Алгебра.7-9 класс: учеб.для общеобразоват.
организаций/Ю.Н.Макарычев, Н.Г.Миндюк,
К.Нешков,С.Б.Суворова; под ред.С.А.Теляковского.-4-е
изд.-М.:Просвещение, 2015
2.
Башмаков М.И. Уравнения и неравенства.
3.
Михайлова Ж.Н. Алгоритмы — ключ к решению задач:
Алгебра. 7-9 классы.-СПб.:Издательский дом
«Литера»,2014. — 448 с.: ил..-(Серия «Средняя школа»)
4.
http://www.fipi.ru/ http://reshuege.ru/ Сайт Федерального
института педагогических измерений (ФИПИ)
14.10.2019
23
14.10.2019

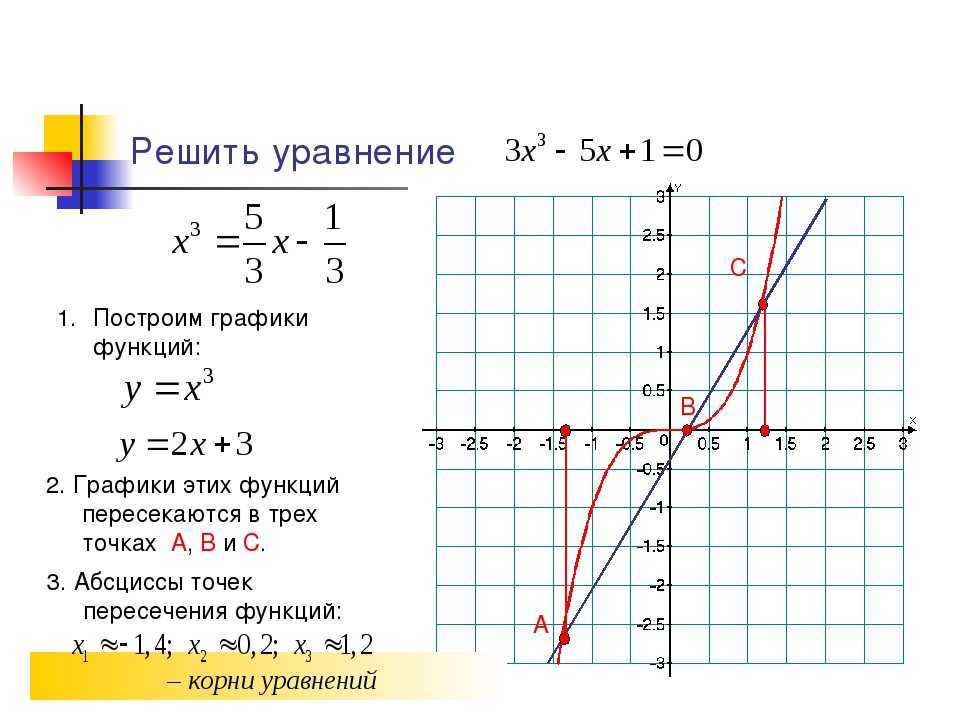
График уравнения на координатной плоскости. Построение графиков онлайн. Тема: Системы уравнений

Пусть задано уравнение с двумя переменными F(x; y) . Вы уже познакомились со способами решения таких уравнений аналитически. Множество решений таких уравнений можно представить и в виде графика.

Графиком уравнения F(x; y) называют множество точек координатной плоскости xOy, координаты которых удовлетворяют уравнению.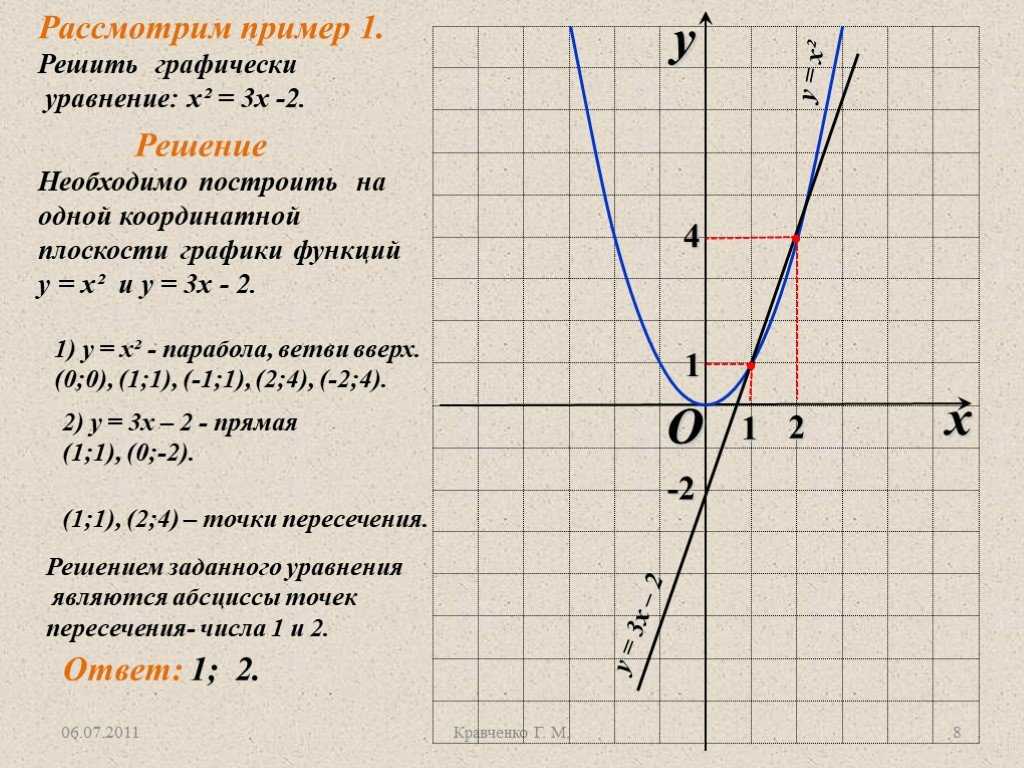

Для построения графика уравнения с двумя переменными сначала выражают в уравнении переменную y через переменную x.

Наверняка вы уже умеете строить разнообразные графики уравнений с двумя переменными: ax + b = c – прямая, yx = k – гипербола, (x – a) 2 + (y – b) 2 = R 2 – окружность, радиус которой равен R, а центр находится в точке O(a; b).

Пример 1.

Построить график уравнения x 2 – 9y 2 = 0.

Решение.

Разложим на множители левую часть уравнения.

(x – 3y)(x+ 3y) = 0, то есть y = x/3 или y = -x/3.

Ответ: рисунок 1.

Особое место занимает задание фигур на плоскости уравнениями, содержащими знак абсолютной величины, на которых мы подробно остановимся. Рассмотрим этапы построения графиков уравнений вида |y| = f(x) и |y| = |f(x)|.

Первое уравнение равносильно системе

{f(x) ≥ 0,
{y = f(x) или y = -f(x).

То есть его график состоит из графиков двух функций: y = f(x) и y = -f(x), где f(x) ≥ 0.

Для построения графика второго уравнения строят графики двух функций: y = f(x) и y = -f(x).

Пример 2.

Построить график уравнения |y| = 2 + x.

Решение.

Заданное уравнение равносильно системе

{x + 2 ≥ 0,
{y = x + 2 или y = -x – 2.

Строим множество точек.

Ответ: рисунок 2.

Пример 3.

Построить график уравнения |y – x| = 1.

Решение.

Если y ≥ x, то y = x + 1, если y ≤ x, то y = x – 1.

Ответ: рисунок 3.

При построении графиков уравнений, содержащих переменную под знаком модуля, удобно и рационально использовать метод областей , основанный на разбиении координатной плоскости на части, в которых каждое подмодульное выражение сохраняет свой знак.

Пример 4.

Построить график уравнения x + |x| + y + |y| = 2.

Решение.

В данном примере знак каждого подмодульного выражения зависит от координатной четверти.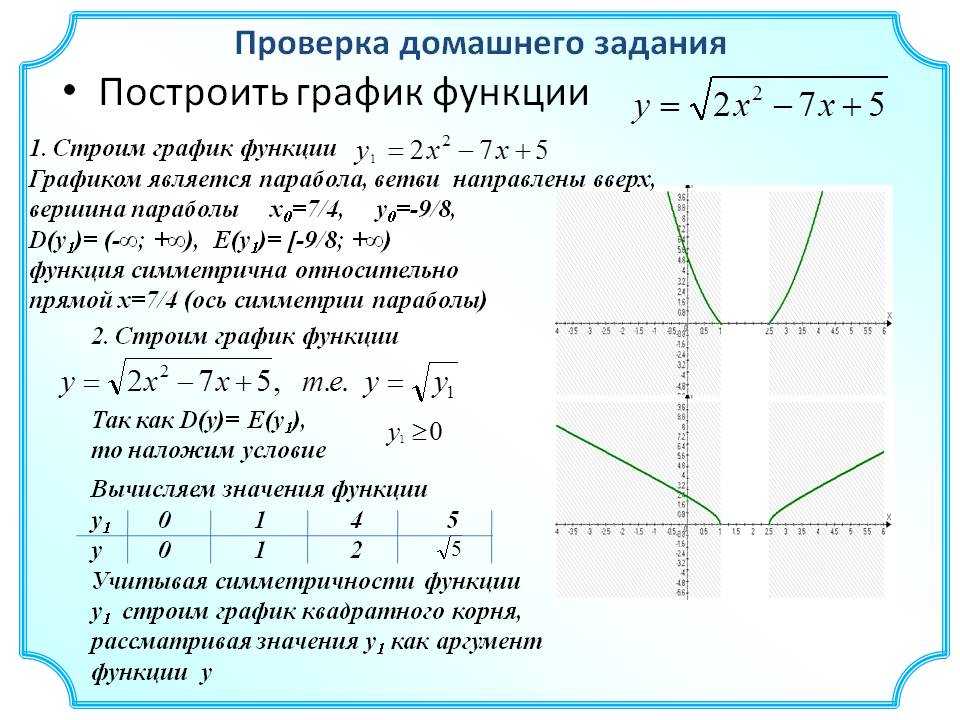

1) В первой координатной четверти x ≥ 0 и y ≥ 0. После раскрытия модуля заданное уравнение будет иметь вид:

2x + 2y = 2, а после упрощения x + y = 1.

2) Во второй четверти, где x

3) В третьей четверти x

4) В четвертой четверти, при x ≥ 0, а y

График данного уравнения будем строить по четвертям.

Ответ: рисунок 4.

Пример 5.

Изобразить множество точек, у которых координаты удовлетворяют равенству |x – 1| + |y – 1| = 1.

Решение.

Нули подмодульных выражений x = 1 и y = 1 разбивают координатную плоскость на четыре области. Раскроем модули по областям. Оформим это в виде таблицы.

Область	Знак подмодульного выражения	Полученное уравнение после раскрытия модуля
I	x ≥ 1 и y ≥ 1	x + y = 3
II	x	-x + y = 1
III	x	x + y = 1
IV	x ≥ 1 и y	x – y = 1

Ответ: рисунок 5.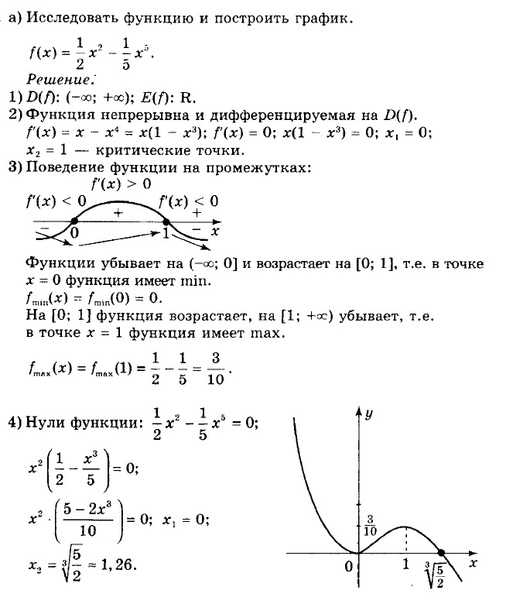

На координатной плоскости фигуры могут задаваться и неравенствами .

Графиком неравенства с двумя переменными называется множество всех точек координатной плоскости, координаты которых являются решениями этого неравенства.

Рассмотрим алгоритм построения модели решений неравенства с двумя переменными :

1. Записать уравнение, соответствующее неравенству.
2. Построить график уравнения из пункта 1.
3. Выбрать произвольную точку в одной из полуплоскостей. Проверить, удовлетворяют ли координаты выбранной точки данному неравенству.
4. Изобразить графически множество всех решений неравенства.

Рассмотрим, прежде всего, неравенство ax + bx + c > 0. Уравнение ax + bx + c = 0 задает прямую, разбивающую плоскость на две полуплоскости. В каждой из них функция f(x) = ax + bx + c сохраняет знак. Для определения этого знака достаточно взять любую точку, принадлежащую полуплоскости, и вычислить значение функции в этой точке.

Если знак функции совпадает со знаком неравенства, то эта полуплоскость и будет решением неравенства.

Рассмотрим примеры графического решения наиболее часто встречающихся неравенств с двумя переменными.

1) ax + bx + c ≥ 0. Рисунок 6 .

2) |x| ≤ a, a > 0. Рисунок 7 .

3) x 2 + y 2 ≤ a, a > 0. Рисунок 8 .

4) y ≥ x 2 . Рисунок 9.

5) xy ≤ 1. Рисунок 10.

Если у вас появились вопросы или вы хотите попрактиковаться изображать на плоскости модели множества всех решений неравенств с двумя переменными с помощью математического моделирования, вы можете провести бесплатное 25-минутное занятие с онлайн репетитором после того, как зарегистрируетесь . Для дальнейшей работы с преподавателем у вас будет возможность выбрать подходящий для вас тарифный план.

Остались вопросы? Не знаете, как изобразить фигуру на координатной плоскости?
Чтобы получить помощь репетитора – зарегистрируйтесь .
Первый урок – бесплатно!

сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Линейное уравнение с двумя переменными — любое уравнение, которое имеет следующий вид: a*x + b*y =с . Здесь x и y есть две переменные, a,b,c — некоторые числа.

Решением линейного уравнения a*x + b*y = с, называется любая пара чисел (x,y) которая удовлетворяет этому уравнению, то есть обращает уравнение с переменными x и y в верное числовое равенство. Линейное уравнение имеет бесконечное множество решений.

Если каждую пару чисел, которые являются решением линейного уравнения с двумя переменными, изобразить на координатной плоскости в виде точек, то все эти точки образуют график линейного уравнения с двумя переменными. Координатами точками будут служить наши значения x и у. При этом значение х будет являться абсциссой, а значение у — ординатой.

График линейного уравнения с двумя переменными

Графиком линейного уравнения с двумя переменными называется множество всевозможных точек координатной плоскости, координаты которых будут являться решениями этого линейного уравнения.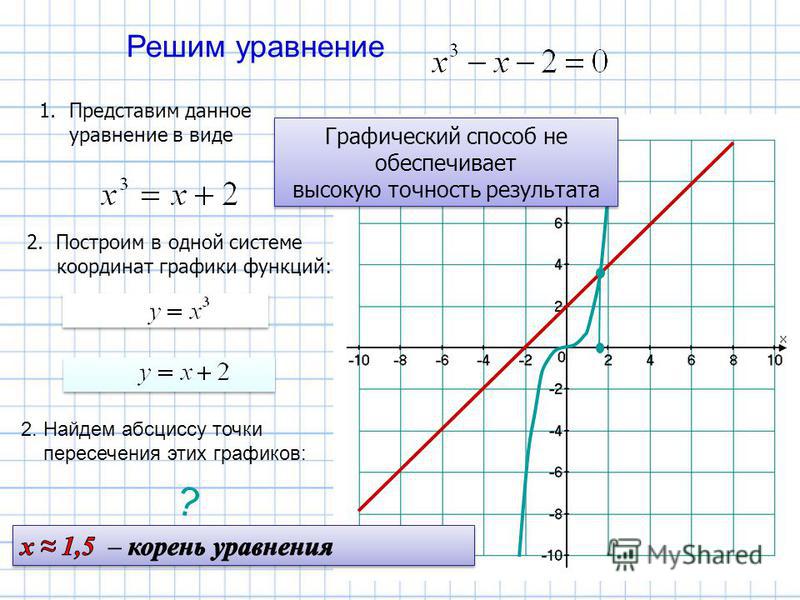 Несложно догадаться, что график будет представлять собой прямую линию. Поэтому такие уравнения и называются линейными.

Алгоритм построения

Алгоритм построения графика линейного уравнения с двумя переменным.

1. Начертить координатные оси, подписать их и отметить единичный масштаб.

2. В линейном уравнении положить х = 0, и решить полученное уравнение относительно у. Отметить полученную точку на графике.

3. В линейном уравнении в качестве у взять число 0, и решить полученное уравнение относительно х. Отметить полученную точку на графике

4. При необходимости взять произвольное значение х, и решить полученное уравнение относительно у. Отметить полученную точку на графике.

5. Соединить полученные точки, продолжить график за них. Подписать получившуюся прямую.

Пример: Построить график уравнения 3*x — 2*y =6;

Положим х=0, тогда — 2*y =6; y= -3;

Положим y=0, тогда 3*x = 6; x=2;

Отмечаем полученные точки на графике, проводим через них прямую и подписываем её.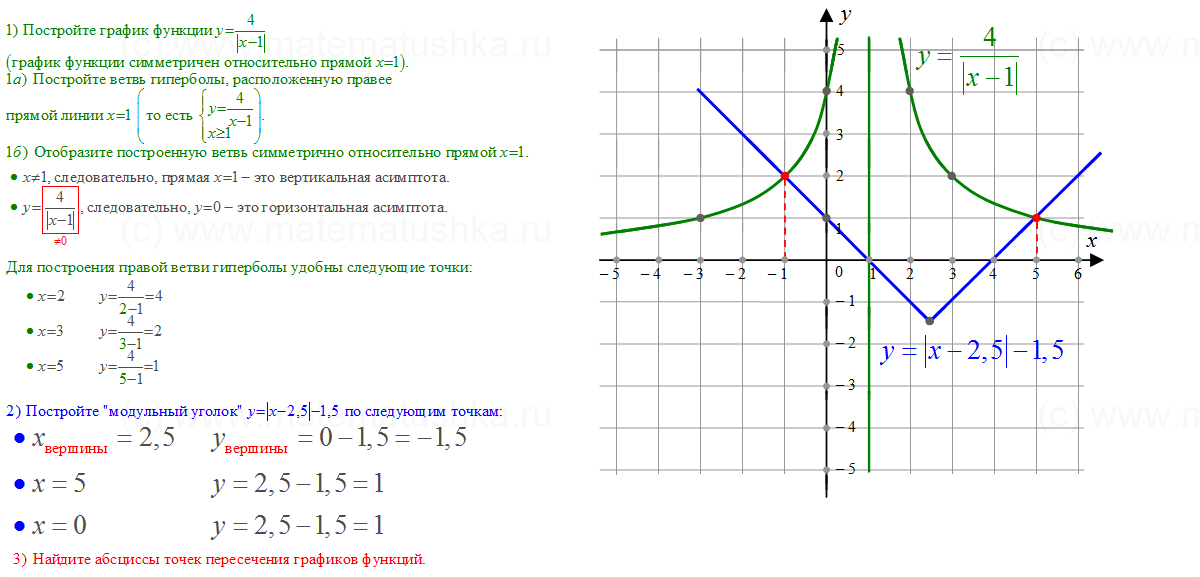 Посмотрите на рисунок ниже, график должен получиться именно таким.

На этом уроке мы подробно рассмотрим построение графиков уравнений. Вначале вспомним, что такое рациональное уравнение и множество его решений, образующее график уравнения. Подробно рассмотрим график линейного уравнения и свойства линейной функции, научимся читать графики. Далее рассмотрим график квадратного уравнения и свойства квадратичной функции. Рассмотрим гиперболическую функцию и ее график и график уравнения окружности. Далее перейдем к построению и изучению совокупности графиков.

Тема: Системы уравнений

Урок: Графики уравнений

Мы рассматриваем рациональное уравнение вида и системы рациональных уравнений вида

Мы говорили, что каждое уравнение в этой системе имеет свой график, если конечно имеются решения уравнений. Мы рассмотрели несколько графиков различных уравнений.

Сейчас мы систематически рассмотрим каждое из известных нам уравнений, т.е. выполним обзор по графикам уравнений .

1. Линейное уравнение с двумя переменными

x, y — в первой степени; a,b,c — конкретные числа.

Пример:

Графиком этого уравнения является прямая линия.

Мы действовали равносильными преобразованиями — y оставили на месте, всё остальное перенесли в другую сторону с противоположными знаками. Исходное и полученное уравнения равносильны, т.е. имеют одно и то же множество решений. График этого уравнения мы умеем строить, и методика его построения такова: находим точки пересечения с координатными осями и по ним строим прямую.

В данном случае

Зная график уравнения, мы можем многое сказать о решениях исходного уравнения, а именно: если сли

Эта функция возрастает, т.е. с увеличением x увеличивается y. Мы получили два частных решения, а как записать множество всех решений?

Если точка имеет абсциссу x, то ордината этой точки

Значит, чисел

У нас было уравнение, мы построили график, нашли решения. Множество всех пар — сколько их? Бесчисленное множество.

Это рациональное уравнение,

Найдем y, равносильными преобразованиями получаем

Положим и получаем квадратичную функцию, ее график нам известен.

Пример: Построить график рационального уравнения.

Графиком является парабола, ветви направлены вверх.

Найдем корни уравнения:

Схематически изобразим график (Рис. 2).

С помощью графика мы получаем всевозможные сведения и о функции, и о решениях рационального уравнения. Мы определили промежутки знакопостоянства, теперь найдем координаты вершины параболы.

У уравнения бесчисленное множество решений, т.е. бесчисленное множество пар , удовлетворяющих уравнению, но все А каким может быть x? Любым!

Если мы зададим любое x, то получим точку

Решением исходного уравнения является множество пар

3. Построить график уравнения

Необходимо выразить y. Рассмотрим два варианта.

Графиком функции является гипербола, функция не определена при

Функция убывающая.

Если мы возьмем точку с абсциссой , то ее ордината будет равна

Решением исходного уравнения является множество пар

Построенную гиперболу можно сдвигать относительно осей координат.

Например, график функции — тоже гипербола — будет сдвинут на единицу вверх по оси ординат.

4. Уравнение окружности

Это рациональное уравнение с двумя переменными. Множеством решений являются точки окружности. Центр в точке радиус равен R (Рис. 4).

Рассмотрим конкретные примеры.

a.

Приведем уравнение к стандартному виду уравнения окружности, для этого выделим полный квадрат суммы:

— получили уравнение окружности с центром в .

Построим график уравнения (Рис. 5).

b. Построить график уравнения

Вспомним, что произведение равно нулю тогда и только тогда, когда один из сомножителей равен нулю, а второй существует.

График заданного уравнения состоит из совокупности графиков первого и второго уравнений, т.е. двух прямых.

Построим его (Рис. 6).

Построим график функции Прямая будет проходить через точку (0; -1). Но как она пройдет — будет возрастать или убывать? Определить это нам поможет угловой коэффициент, коэффициент при x, он отрицательный, значит функция убывает. Найдем точку пересечения с осью ox, это точка (-1; 0).

Аналогично строим график второго уравнения. Прямая проходит через точку (0; 1), но возрастает, т.к. угловой коэффициент положителен.

Координаты всех точек двух построенных прямых и являются решением уравнения.

Итак, мы проанализировали графики важнейших рациональных уравнений, они будут использоваться и в графическом методе и в иллюстрации других методов решения систем уравнений.

1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений.- 4-е изд. — М.: Мнемозина, 2002.-192 с.: ил.

2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.

3. Макарычев Ю. Н. Алгебра. 9 класс: учеб. для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.

4. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16-е изд. — М., 2011. — 287 с.

5. Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 12-е изд., стер. — М.: 2010. — 224 с.: ил.

6. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.: ил.

1. Раздел College.ru по математике ().

2. Интернет-проект «Задачи» ().

3. Образовательный портал «РЕШУ ЕГЭ» ().

1. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил. № 95-102.

Прямоугольная система координат это пара перпендикулярных координатных линий, называемых осями координат, которые размещены так, что они пересекаются в их начале.

Обозначение координатных осей буквами х и у является общепринятым, однако буквы могут быть любые. Если используются буквы х и у, то плоскость называется xy-плоскость . В различных приложениях могут применяться отличные от букв x и y буквы, и как показано с нижерасположенных рисунках, есть uv-плоскости и ts-плоскости .

Упорядоченная пара

Под упорядоченной парой действительных чисел мы имеем в виду два действительных чисел в определённом порядке. Каждая точка P в координатной плоскости может быть связана с уникальной упорядоченной парой действительных чисел путём проведения двух прямых через точку P: одну перпендикулярно оси Х, а другую — перпендикулярно оси у.

Например, если мы возьмём (a,b)=(4,3), тогда на координатной полоскости

Построить точку Р(a,b) означает определить точку с координатами (a,b) на координатной плоскости. Например, различные точки построены на рисунке внизу.

В прямоугольной системе координат оси координат делят плоскость на четыре области, называемые квадрантами. Они нумеруются против часовой стрелки римскими цифрами, как показано на рисунке

Определение графика

Графиком уравнения с двумя переменными х и у, называется множество точек на ху-плоскости, координаты которых являются членами множества решений этого уравнения

Пример: нарисовать график y = x 2

Из-за того, что 1/x не определено, когда x=0, мы можем построить только точки, для которых x ≠0

Пример: Найдите все пересечения с осями
(a) 3x + 2y = 6
(b) x = y 2 -2y
(c) y = 1/x

Пусть y = 0, тогда 3x = 6 or x = 2

является искомой точкой пересечения оси x.

Установив, что х=0, найдем что точкой пересечения оси у является точка у=3.

Таким эе образом вы можете решить уравнение (b), а решения для (c) приведено ниже

x-пересечение

Пусть y = 0

1/x = 0 => x не может быть определено, то есть нет пересечения с осью у

Пусть x = 0

y = 1/0 => y также не определено, => нет пересечения с осью y

На рисунке внизу точки (x,y), (-x,y),(x,-y) и (-x,-y) обозначают углы прямоугольника.

График симметричен относительно оси х, если для каждой точки (x,y) графика, точка (x,-y) есть также точкой на графике.

График симметричен относительно оси y, если для каждой точки графика (x,y) точка (-x,y) также принадлежит графику.

График симметричен относительно центра координат, если для каждой точки (x,y) графика, точка (-x,-y) также принадлежит этому графику.

Определение:

График функции на координатной плоскости определяется как график уравнения y = f(x)

Постройте график f(x) = x + 2

Пример 2. Постройте график f(x) = |x|

График совпадает с линией y = x для x> 0 и с линией y = -x

для x

graph of f(x) = -x

Соединяя эти два графика, мы получаем

график f(x) = |x|

Пример 3. Постройте график

t(x) = (x 2 — 4)/(x — 2) =

= ((x — 2)(x + 2)/(x — 2)) =

= (x + 2) x ≠ 2

Следовательно, эта функция может быть записана в виде

y = x + 2 x ≠ 2

График h(x)= x 2 — 4 Or x — 2

график y = x + 2 x ≠ 2

Пример 4.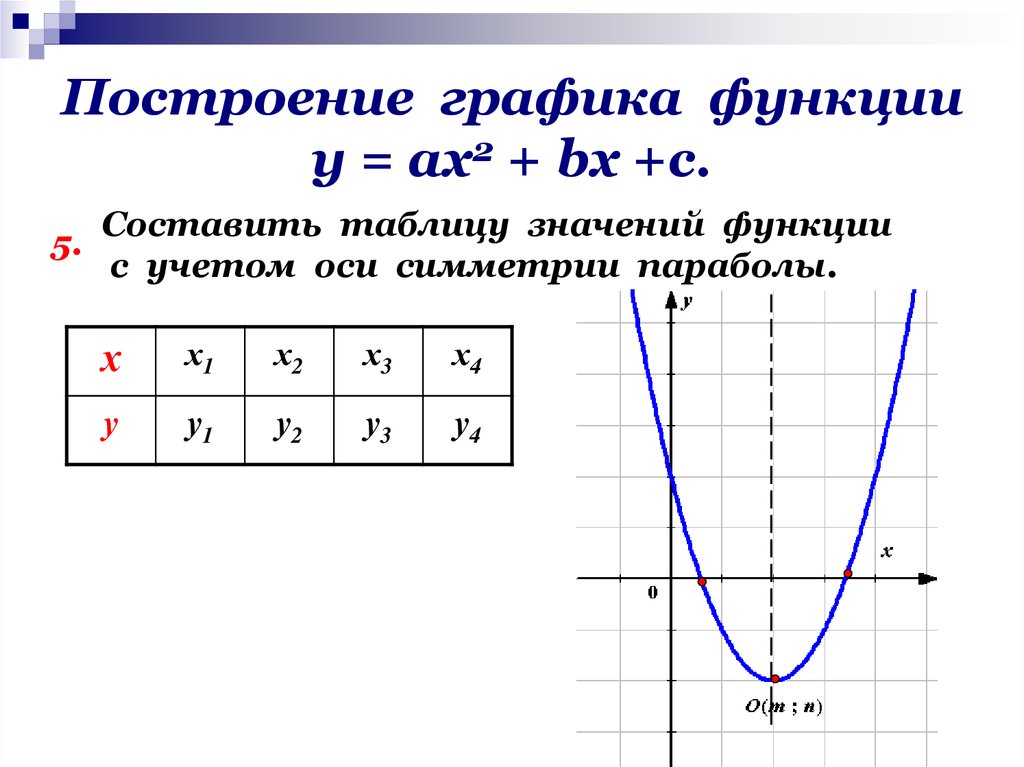 Постройте график

Графики функций с перемещением

Предположим, что график функции f(x) известен

Тогда мы можем найти графики

y = f(x) + c — график функции f(x), перемещённый

ВВЕРХ на c значений

y = f(x) — c — график функции f(x), перемещённый

ВНИЗ на c значений

y = f(x + c) — график функции f(x), перемещённый

ВЛЕВО на c значений

y = f(x — c) — график функции f(x), перемещённый

Вправо на c значений

Пример 5. Постройте

график y = f(x) = |x — 3| + 2

Переместим график y = |x| на 3 значения ВПРАВО, чтобы получить график

Переместим график y = |x — 3| на 2 значения ВВЕРХ, чтобы получить график y = |x — 3| + 2

Постройте график

y = x 2 — 4x + 5

Преобразуем заданное уравнение следующим образом, прибавив к обеим частям 4:

y + 4 = (x 2 — 4x + 5) + 4 y = (x 2 — 4x + 4) + 5 — 4

y = (x — 2) 2 + 1

Здесь мы видим, что этот график может быть получен перемещением графика y = x 2 вправо на 2 значения, потому что x — 2, и вверх на 1 значение, потому что +1.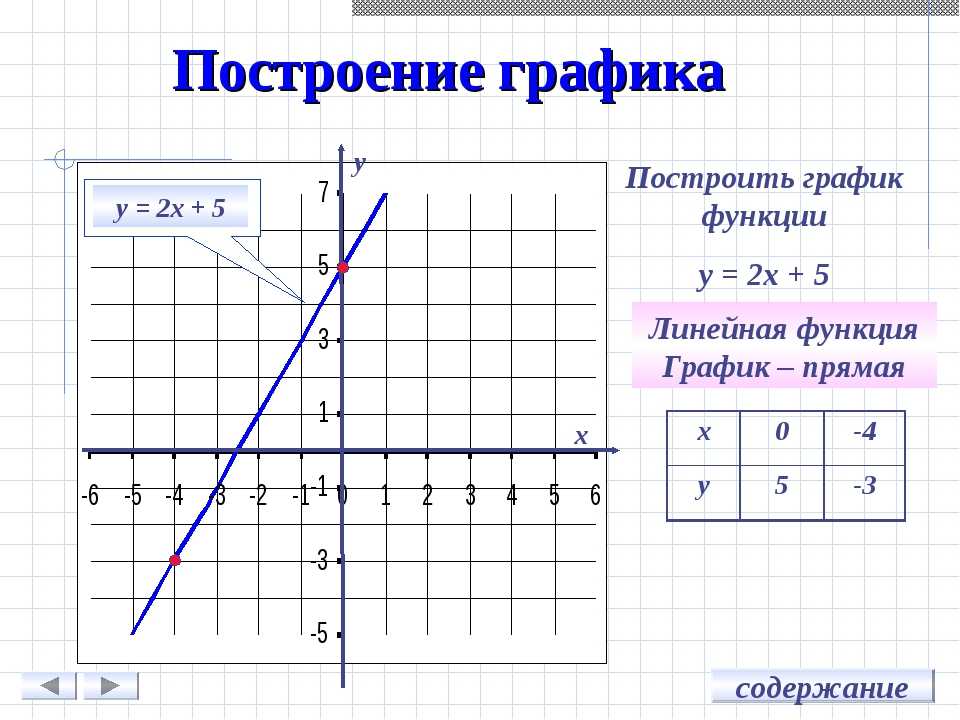

y = x 2 — 4x + 5

Отражения

(-x, y) есть отражением (x, y) относительно оси y

(x, -y) есть отражением (x, y) относительно оси x

Графики y = f(x) и y = f(-x) являются отражением друг друга относительно оси y

Графики y = f(x) и y = -f(x) являются отражением друг друга относительно оси x

График может быть получен отражением и перемещением:

Нарисуйте график

Найдём его отражение относительно оси y, и получим график

Переместим этот график вправо на 2 значения и получим график

Вот искомый график

Если f(x) умножена на положительною постояную c, то

график f(x) сжимается по вертикали, если 0

график f(x) растягивается по вертикали, если c > 1

Кривая не является графиком y = f(x) для любой функции f

Алгебра — Графика

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Уведомление для мобильных устройств

Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы наверное на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 3.1: Графики

В этом разделе нам необходимо рассмотреть некоторые основные идеи построения графиков. Предполагается, что вы видели некоторые графики до этого момента, поэтому мы не будем здесь вдаваться в подробности. Мы рассмотрим только некоторые из основных идей.

Мы начнем с прямоугольной или декартовой системы координат. Это просто стандартная система осей, которую мы используем при наброске наших графиков. Вот декартова система координат с нанесенными точками.

Горизонтальная и вертикальная оси, обычно называемые осью \(x\) и осью \(y\) соответственно, делят систему координат на квадранты, как показано выше.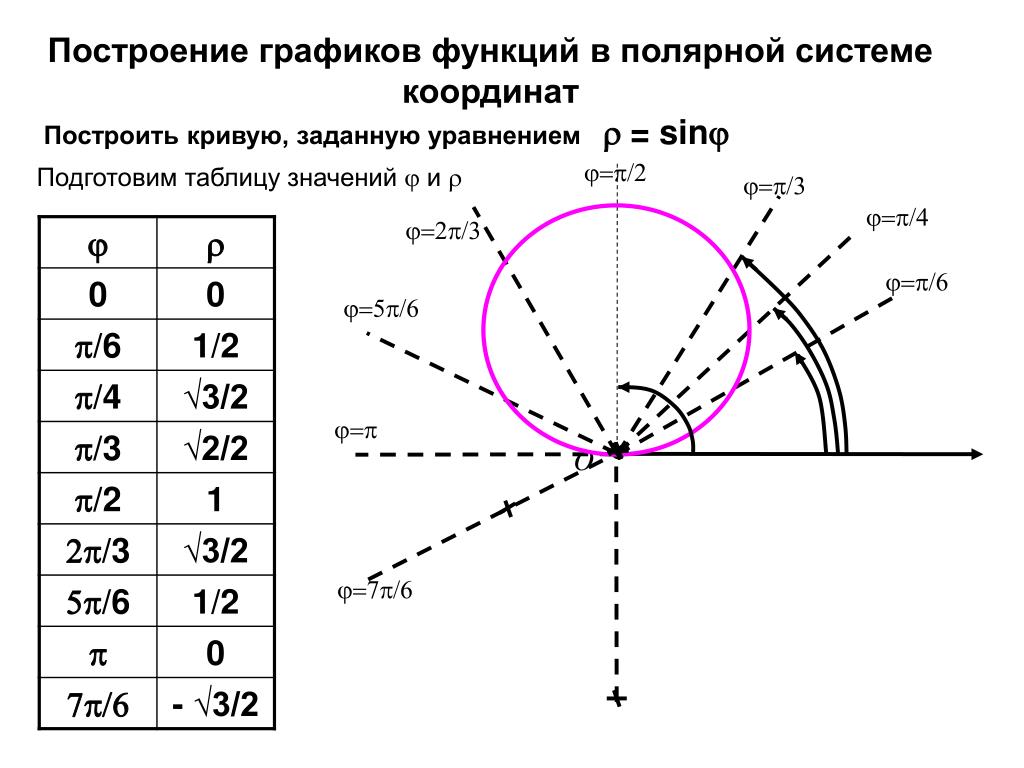 В каждом квадранте у нас есть следующие знаки для \(x\) и \(y\).

Квадрант I	\(x > 0\), или \(x\) положительный	\(y > 0\) или \(y\) положительный
Квадрант II	\(x < 0\) или \(x\) минус	\(y > 0\) или \(y\) положительный
Квадрант III	\(x < 0\), или \(x\) минус	\(y < 0\) или \(y\) минус
Квадрант IV	\(x > 0\), или \(x\) положительный	\(y < 0\) или \(y\) минус

Каждая точка в системе координат определяется упорядоченной парой вида \(\left( {x,y} \right)\). Первое указанное число — это \(x\)-координата точки, а второе указанное число — это \(y\)-координата точки. Упорядоченная пара для любой заданной точки \(\left({x,y} \right)\) называется координатами точки.

Точка пересечения двух осей называется началом координат и имеет координаты \(\left( {0,0} \right)\).

Также обратите внимание, что порядок координат важен. Например, точка \(\left( {2,1} \right)\) — это точка, которая находится на две единицы правее начала координат, а затем на 1 единицу выше, а точка \(\left( {1, 2} \right)\) — это точка, которая находится на 1 единицу правее начала координат, а затем на 2 единицы выше. 92} — 4\\ 5 & \ne — 4\hspace{0,25 дюйма}{\mbox{НЕ ОК}}\end{выравнивание*}\]

Координаты этой точки НЕ удовлетворяют уравнению, поэтому этой точки нет на графике.

Теперь, как мы нарисуем график уравнения? Конечно, ответ на этот вопрос зависит от того, насколько хорошо вы знаете об уравнении для начала. Например, если вы знаете, что уравнение представляет собой линию или окружность, у нас есть простые способы определить график в этих случаях. Есть также много других типов уравнений, график которых мы обычно можем получить из уравнения без особых усилий. Мы увидим многие из них в следующей главе.

Однако давайте предположим, что мы не знаем заранее, что это за уравнение, или какие-либо способы быстрого наброска графика. В этих случаях нам нужно будет напомнить, что график — это просто все точки, удовлетворяющие уравнению. Итак, все, что мы можем сделать, это сюжетные точки. Мы выберем значения \(x\), вычислим \(y\) из уравнения, а затем построим упорядоченную пару, заданную этими двумя значениями.

Как определить, какие значения \(х\) выбрать? К сожалению, ответ есть мы догадываемся. Мы выбираем некоторые значения и смотрим, что мы получаем для графика. Если кажется, что у нас есть довольно хороший эскиз, мы останавливаемся. Если нет, мы выбираем еще. Знание значений \(х\) для выбора на самом деле является чем-то, что мы можем получить только с опытом и некоторым знанием того, каким будет график уравнения.2}-4\).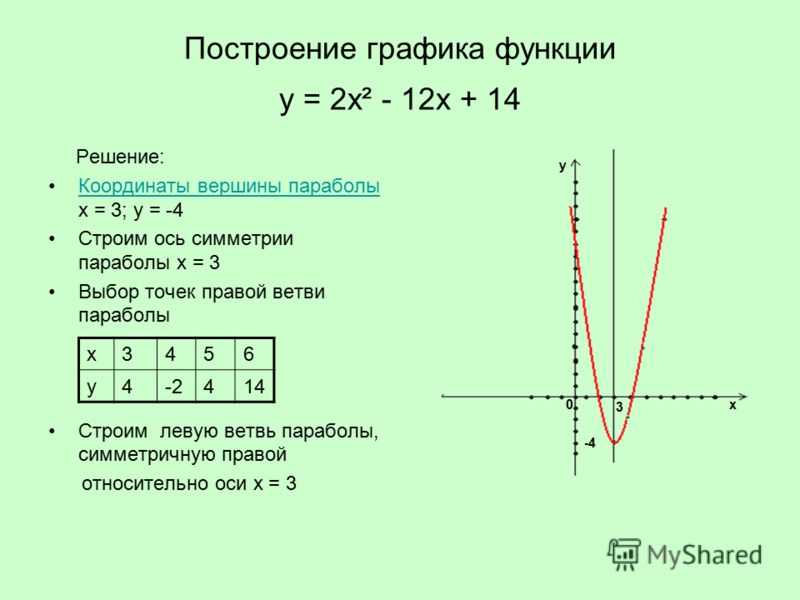

Показать решение

Теперь это парабола, и после следующей главы вы сможете быстро изобразить ее на графике без особых усилий. Однако мы еще не зашли так далеко, поэтому нам нужно будет выбрать некоторые значения \(x\), подставить их и вычислить значения \(y\).

Как упоминалось ранее, полезно иметь представление о том, как может выглядеть этот график при выборе значений \(x\). Итак, не беспокойтесь на данный момент, почему мы выбрали те значения, которые мы сделали. После следующей главы вы также сможете выбирать эти значения \(x\).

Вот таблица значений этого уравнения.

\(х\)	\(у\)	\(\влево({х,у} \вправо)\)
-2	5	\(\влево( { — 2,5} \вправо)\)
-1	0	\(\влево( { — 1,0} \вправо)\)
0	-3	\(\влево( {0, — 3} \вправо)\)
1	-4	\(\влево( {1, — 4} \вправо)\)
2	-3	\(\влево( {2, — 3} \вправо)\)
3	0	\(\влево( {3,0} \вправо)\)
4	5	\(\влево({4,5} \вправо)\)

Давайте проверим первое, а остальные предоставим вам для проверки.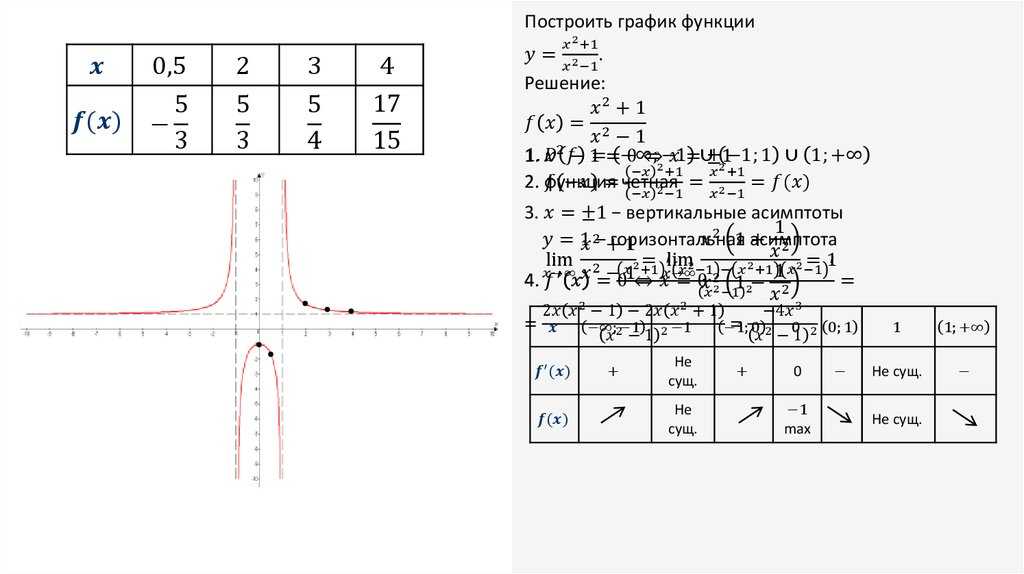 2} — 4\ \ & = 9- 4\\ & = 5\конец{выравнивание*}\]

Вот график этого уравнения.

Обратите внимание, что когда мы настраиваем систему координат в этом примере, мы настраиваем ровно столько, сколько нам нужно. Например, поскольку мы не превышали -2 в наших вычислениях, мы не превышали это значение и в нашей системе координат.

Также обратите внимание, что мы использовали разные масштабы для каждой из осей. По горизонтальной оси мы увеличили на 1, а по вертикальной оси увеличили на 2. Часто это делается для того, чтобы упростить набросок.

Последняя тема, которую мы хотим обсудить в этом разделе, это перехватов . Обратите внимание, что график в приведенном выше примере пересекает ось \(x\) в двух местах и ​​ось \(y\) в одном месте. Все эти три точки называются перехватами. Однако мы можем и часто будем более конкретными.

Нам часто нужно знать, пересекает ли точка пересечения ось \(x\) или \(y\) конкретно. Итак, если отрезок пересекает ось \(x\), мы будем называть его \(x\)-перехватом .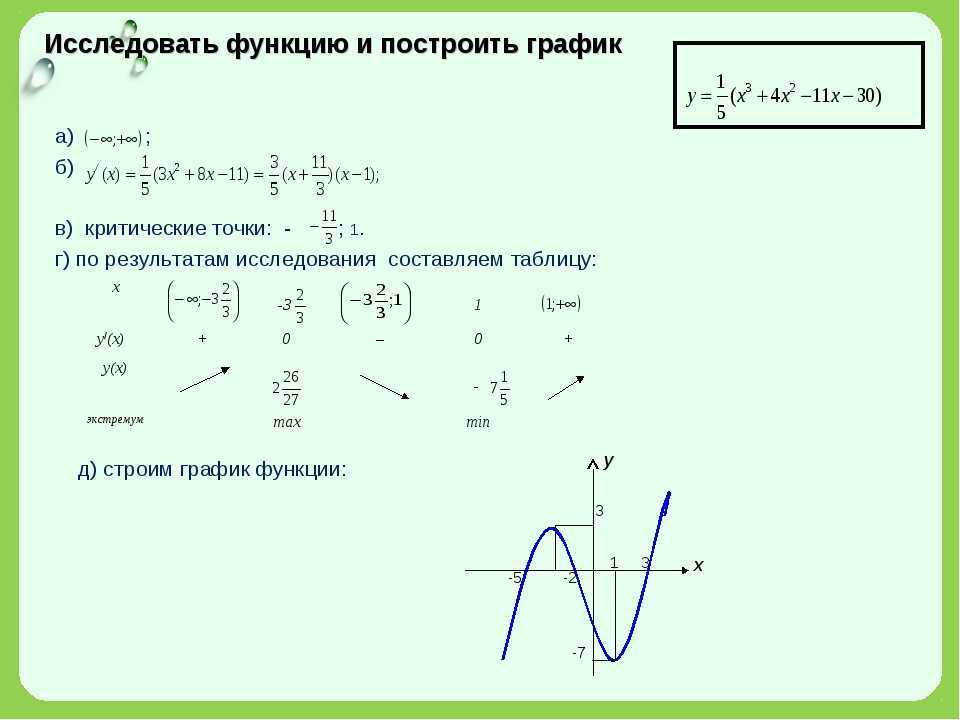 Точно так же, если отрезок пересекает ось \(y\), мы будем называть его \(y\)-перехватом .

Теперь, поскольку точка пересечения \(x\) пересекает ось \(x\), то координаты \(y\) точки пересечения \(x\) будут равны нулю. Кроме того, координата \(x\) точки пересечения \(y\) будет равна нулю, так как эти точки пересекают ось \(y\). Эти факты дают нам способ определить точки пересечения для уравнения. Чтобы найти \(x\)-перехваты для уравнения, все, что нам нужно сделать, это установить \(y = 0\) и решить для \(x\). Аналогичным образом, чтобы найти \(y\)-перехваты для уравнения, нам просто нужно установить \(x = 0\) и решить для \(y\). 92}\hspace{0,25 дюйма} \Rightarrow \hspace{0,25in}x = — 1\hspace{0,25in} \Rightarrow \hspace{0,25in}\left( { — 1,0} \right)\]

В этом случае мы имеем одиночный \(x\)-перехват.

Вот набросок графика для этого уравнения.

Теперь обратите внимание, что в этом случае график фактически не пересекает ось \(x\) в точке \(x = — 1\).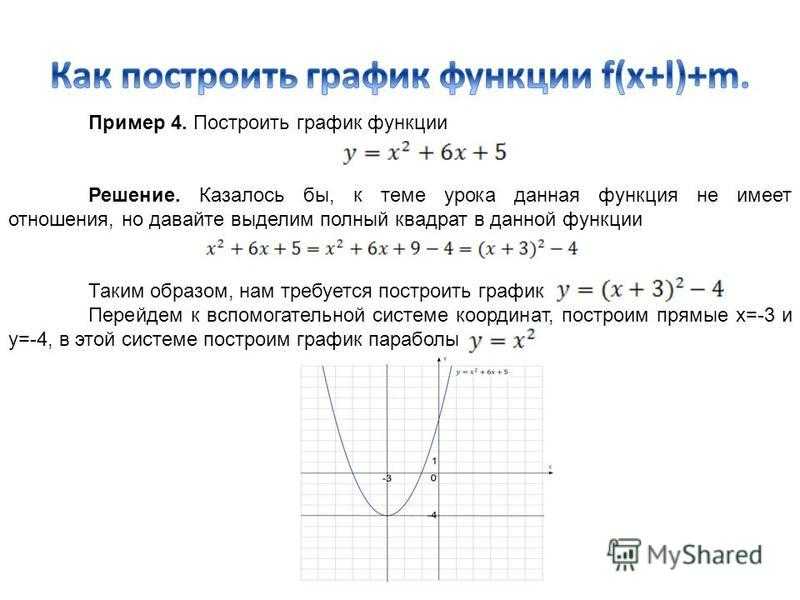 Однако эта точка по-прежнему называется \(x\)-перехватом.

Мы должны сделать последний комментарий, прежде чем покинуть этот раздел. В предыдущем наборе примеров все уравнения были квадратными уравнениями. Это было сделано только потому, что они демонстрировали диапазон поведения, который мы искали, и мы также могли выполнять эту работу. Вы не должны уходить от этого обсуждения перехватов с идеей, что они будут иметь место только для квадратных уравнений. Они могут возникать и возникают для многих различных уравнений.

легкий вопрос — Какой ваш любимый онлайн-инструмент для построения графиков?

спросил 12 лет, 4 месяца назад

Изменено 1 год, 4 месяца назад

Просмотрено 9к раз

$\begingroup$

Я ищу хороший, быстрый онлайн-инструмент для построения графиков. Возможность ссылки или встраивания вывода также была бы удобна.

• программный вопрос
• математическое программное обеспечение

$\endgroup$

0

$\begingroup$

desmos.com Это, безусловно, лучшее.

$\endgroup$

2

$\begingroup$

Ну, я не уверен, куда вы хотите встроить графики, но Wolfram Alpha очень удобен для построения графиков. Он имеет большинство функций Mathematica, может обрабатывать 3D-функции, причудливое масштабирование и тому подобное. Я очень рекомендую это.

$\endgroup$

1

$\begingroup$

Мне очень нравится Geogebra как веб-инструмент для построения графиков (требуется Java).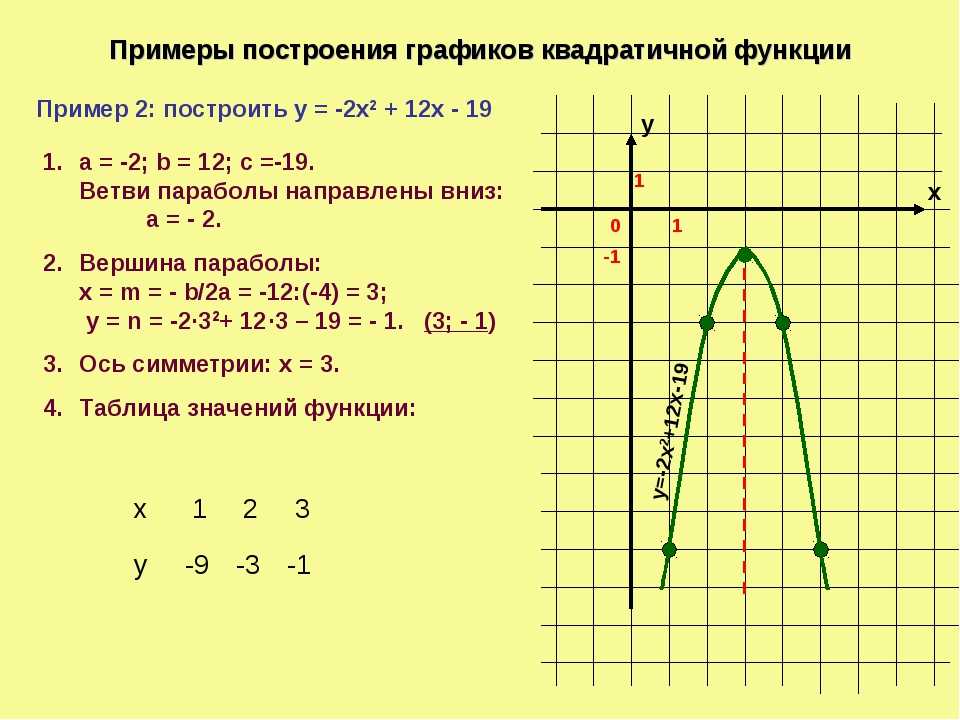

$\endgroup$

4

$\begingroup$

Несколько хороших вариантов:

• Диаграммы Livegap
• Инструмент онлайн-диаграмм
• Инструмент GraphFunc

$\endgroup$

1

$\begingroup$

Я искал хорошие интерактивные диаграммы без флэш-памяти (простой HTML + Javascript) и обнаружил, что http://DIYcharts.com является наиболее удобным и простым в использовании, очень похожим на Google Charts.

$\endgroup$

$\begingroup$

Я создал инструмент для рисования графики и опубликовал его несколько часов назад.

https://www.youtube.com/watch?v=xD080qQVaD8&feature=youtu.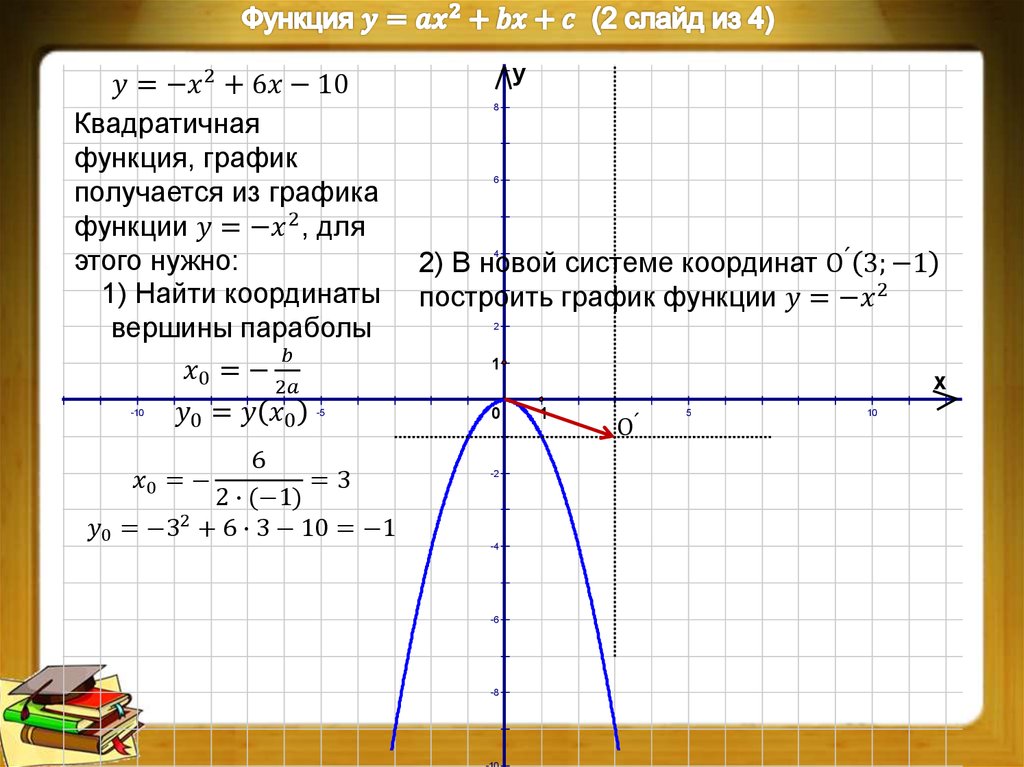 be

https://github.com/burlachenkok/plotter_plusplus

Чтобы использовать этот инструмент, вы можете использовать настольный компьютер для показа графики и прослушивания доходные соединения по сети.

Ваш целевой проект можно запустить в любом месте на любом языке на любой платформе — для обновления графики просто отправьте данные по сети.

$\endgroup$

3

$\begingroup$

Вот онлайн-инструменты, которые я ежедневно использую для построения графиков, а также для построения графиков геометрии:

1. Desmos (отличное удобство использования, потрясающие функции)

2. Plotlux (мощный плоттер, основанный на fooplot)

3. Graph.tk (быстрый и простой плоттер)

4. JSXGraph (мощный инструмент для построения графиков и геометрии, однако необходимо знать javascript)

5. Геодрафт (графическое построение простых геометрических фигур)

6. Геосервант 3D (графическое построение простых 3D объектов)

7. Geogebra (мощный, всеобъемлющий, но не может использоваться в коммерческих целях)

8. Скетчометрия (геометрические объекты, интересные возможности использования)

Как только я обнаруживаю новые инструменты, я обновляю свой пост.