Г.И. Запорожец. Руководство к решению задач по математическому анализу
Г.И. Запорожец. Руководство к решению задач по математическому анализуНа главную страницу | Математический анализ
Титул
Оглавление
Предисловие
Глава I. Введение в анализ
§ 1. Переменные величины и функции, их обозначение
§ 2. Область определения (существования) функции
§ 3. Построение графика функции по точкам
§ 4. Построение графика функции путем сдвига и деформации известного графика другой функции
§ 5. Переменная как упорядоченное числовое множество. Предел переменной. Бесконечно малые и бесконечно большие величины. Предел функции
§ 6. Теоремы о бесконечно малых и о пределах
§ 7. Вычисление пределов
§ 8. Смешанные задачи на нахождение пределов
Смешанные задачи на нахождение пределов
§ 9. Сравнение бесконечно малых
§ 10. Непрерывность и точки разрыва функции
Глава II. Производная и дифференциал функции
§ 1. Производная функции и её геометрическое значение. Непосредственное нахождение производной
§ 2. Производные простейших алгебраических и тригонометрических функций
§ 3. Производная сложной функции
§ 4. Производные показательных и логарифмических функций
§ 5. Производные обратных тригонометрических функций
§ 6. Смешанные задачи на дифференцирование
§ 7. Логарифмическое дифференцирование
§ 8. Производные высших порядков
§ 9. Производные неявной функции
§ 10. Производные от функции, заданной параметрически
§ 11.
§ 12. Скорость изменения переменной величины. Скорость и ускорение прямолинейного движения
§ 13. Дифференциал функции
§ 14. Вектор-функция скалярного аргумента и ее дифференцирование. Касательная к пространственной кривой
§ 15. Скорость и ускорение криволинейного движения
Глава III. Исследование функций и построение их графиков
§ 1. Теорема (формула) Тейлора
§ 2. Правило Лопиталя и применение его к нахождению предела функции
§ 3. Возрастание и убывание функции
§ 4. Максимум и минимум (экстремум) функции
§ 5. Наибольшее и наименьшее значения функции
§ 6. Задачи о наибольших или наименьших значениях величин
§ 7. Направление выпуклости кривой и точки перегиба
 Асимптоты
Асимптоты
§ 9. Общая схема исследования функций и построения их графиков
§ 10. Приближенное решение уравнений
§ 11. Кривизна плоской кривой
Глава IV. Неопределенный интеграл
§ 1. Первообразная функция и неопределенный интеграл. Основные формулы интегрирования
§ 2. Интегрирование посредством разложения подынтегральной функции на слагаемые
§ 3. Интегрирование посредством замены переменной
§ 4. Интегрирование по частям
§ 5. Интегралы от функций, содержащих квадратный трехчлен
§ 6. Интегрирование тригонометрических функций
§ 7. Интегрирование рациональных функций
§ 8. Интегрирование некоторых иррациональных функций
§ 9. Интегрирование некоторых трансцендентных (неалгебраических) функций
§ 10. Смешанные задачи на интегрирование
Смешанные задачи на интегрирование
Глава V. Определенный интеграл
§ 1. Определенный интеграл как предел интегральных сумм, его свойства и связь с неопределенным интегралом
§ 2. Замена переменной в определенном интеграле
§ 3. Схема применения определенного интеграла к вычислению различных величин. Площадь плоской фигуры
§ 4. Объем тела по площадям его параллельных сечений
§ 5. Объем тела вращения
§ 6. Длина дуги плоской кривой
§ 7. Площадь поверхности вращения
§ 8. Физические задачи
§ 9. Координаты центра тяжести
§ 10. Несобственные интегралы
Глава VI. Функции многих переменных
§ 1. Функции многих переменных, их обозначение и область определения
§ 2. Предел функции многих переменных. Непрерывность
Предел функции многих переменных. Непрерывность
§ 3. Частные производные функции многих переменных
§ 4. Дифференциалы функции многих переменных
§ 5. Дифференцирование сложных функций
§ 6. Дифференцирование неявных функций
§ 7. Частные производные высших порядков
§ 8. Касательная плоскость и нормаль к поверхности
§ 9. Экстремум функции многих переменных
§ 10. Наибольшее и наименьшее значения функции
Глава VII. Кратные, криволинейные и поверхностные интегралы
§ 1. Двойной интеграл, его вычисление двукратным интегрированием
§ 2. Двойной интеграл в полярных координатах
§ 3. Вычисление площади посредством двойного интеграла
§ 4. Вычисление объема тела
§ 5. Масса, центр тяжести и моменты инерции
§ 6. Тройной интеграл, его вычисление трехкратным интегрированием
Тройной интеграл, его вычисление трехкратным интегрированием
§ 7. Вычисление величин посредством тройного интеграла
§ 8. Криволинейные интегралы, их вычисление и условие независимости от линии интегрирования
§ 9. Вычисление величин посредством криволинейных интегралов
§ 10. Нахождение функции по ее полному дифференциалу
§ 11. Интегралы по поверхности, их вычисление сведением к двойным интегралам
§ 12. Вычисление величин посредством поверхностных интегралов
Глава VIII. Элементы теории поля
§ 1. Скалярное поле. Производная по направлению. Градиент
§ 2. Векторное поле. Поток и дивергенция поля
§ 3. Циркуляция и вихрь векторного поля
Глава IX. Ряды
§ 1. Числовые ряды сходящиеся и расходящиеся. Необходимый признак сходимости ряда. Достаточные признаки сходимости рядов с положительными членами
Достаточные признаки сходимости рядов с положительными членами
§ 2. Абсолютная и неабсолютная сходимость знакопеременного ряда. Признак сходимости знакочередующегося ряда
§ 3. Функциональные ряды
§ 4. Ряды Тейлора
§ 5. Действия со степенными рядами. Применение рядов к приближенным вычислениям
§ 6. Числовые и степенные ряды с комплексными членами
§ 7. Ряды Фурье
§ 8. Интеграл ФурьеГлава X. Дифференциальные уравнения
§ 1. Дифференциальные уравнения, их порядок, общий и частные интегралы
§ 2. Уравнения с разделяющимися переменными
§ 3. Однородные уравнения первого порядка
§ 4. Линейные уравнения первого порядка и уравнения Бернулли
§ 5. Уравнения в полных дифференциалах
§ 6. Уравнения высших порядков, допускающие понижение порядка
Уравнения высших порядков, допускающие понижение порядка
§ 7. Линейные однородные уравнения высших порядков с постоянными коэффициентами
§ 8. Линейные неоднородные уравнения высших порядков с постоянными коэффициентами
§ 9. Смешанные задачи на интегрирование уравнений разных типов
§ 10. Задачи, приводящие к дифференциальным уравнениям
§ 11. Метод Эйлера приближенного интегрирования уравнений первого порядка
§ 12. Интегрирование уравнений при помощи рядов
§ 13. Системы линейных дифференциальных уравнений
§ 14. Уравнения математической физики
Ответы
На главную страницу | Математический анализ
Используются технологии uCoz
Онлайн калькуляторы и программы для построения графиков функций
Онлайн калькуляторы и программы для построения графиков функций
В статье рассматриваются назначение и особенности
онлайн калькуляторов и программ для построения графиков функций, таких как
линейная, квадратичная, тригонометрическая.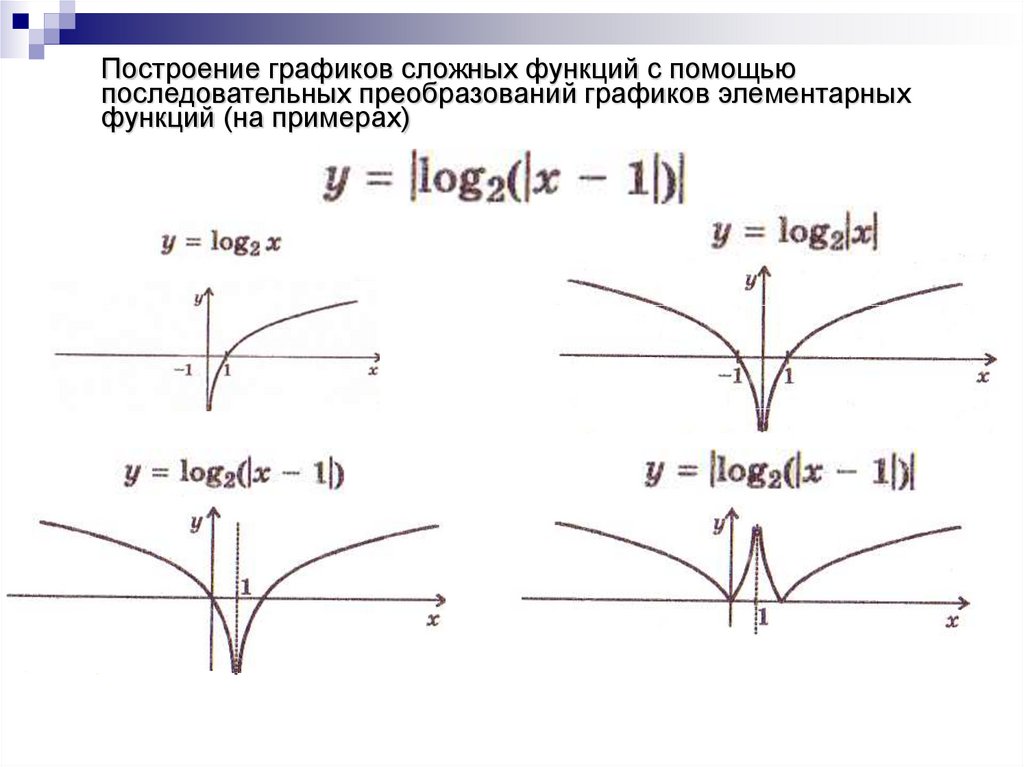 Определены основные геометрические
преобразования графиков данных функций и приведены примеры и алгоритмы их
построения с помощью онлайн калькуляторов и программ.
Определены основные геометрические
преобразования графиков данных функций и приведены примеры и алгоритмы их
построения с помощью онлайн калькуляторов и программ.
Понятие функции является одним из основных понятий в школьном курсе математики. Изучение функций одной переменной начинается с 7 класса. В рамках школьной программы учащиеся не только знакомятся с понятием функции одной переменной, но и строят графики функций. Существует ряд геометрический преобразований графиков функций, к которым относятся сдвиг, параллельный перенос, сжатие, растяжение. В школьном курсе математики данным преобразованиям уделяется внимание в связи с этим необходимо предлагать разные средства для их изучения. Одним из таких средств являются онлайн калькуляторы и математические программы. Рассмотрим ряд таких средств для проведения геометрических преобразований графиков функций, выделив их преимущества и недостатки.
Онлайн калькулятор, располагающийся по
адресу http://www.webmath.ru/ [3]
имеет следующие особенности: в нем дан список функций и констант для правильного ввода; для построения
графиков функции можно указать интервалы по осям координат; возможно построение
нескольких графиков на одной координатной плоскости; есть возможность изменять
масштаб; имеется удобная сетка, показаны промежуточные значения; есть
возможность посмотреть решения типовых задач; можно строить графики функций,
заданных параметрически; не дает информации об исследовании функции.
Онлайн калькулятор по адресу http://graph.reshish.ru/ [6] имеет следующие особенности: можно изменять масштаб графика, а так же передвигаться по координатной плоскости для детального изучения поведения графика функции. Представлена удобная сетка для отслеживания точек пересечения, указаны все промежуточные значения, есть возможность построения нескольких графиков функций на одной координатной плоскости.
Простой и удобный интерфейс в онлайн калькуляторе, который находится по адресу http://www.yotx.ru/. [5] В нем приведена справка ввода функций. Он позволяет строить график функции не только заданной аналитически, но и по точкам, в полярной системе координат и заданной параметрически. Добавлены и другие функции, например, можно выбрать цвет графика и интервал, на котором он будет построен. Так же на сайте можно открыть учебник.
При вводе функции на
сайте онлайн калькулятора http://grafikus.ru/ [1] необходимо использовать только простую функцию,
при вводе сложной были выявлены ошибки. График построенной функции можно
скачать на компьютер или распечатать. Есть возможность построения нескольких
графиков на одной координатной плоскости. Но также можно увидеть
предупреждение, что правильность результатов не гарантируется.
График построенной функции можно
скачать на компьютер или распечатать. Есть возможность построения нескольких
графиков на одной координатной плоскости. Но также можно увидеть
предупреждение, что правильность результатов не гарантируется.
На главной странице другого онлайн калькулятора http://easyto.me/services/graphic/ [2] расположена подробная инструкция, как ввести функцию с таблицей ввода основных видов функций. Перед построением графика функции необходимо выбрать цвет и толщину линий. Координатная плоскость стандартная, позволяет изменять масштаб, двигать курсив по осям координат. Есть возможность построения нескольких графиков на одной плоскости, в таком случае приведена таблица с историей всех ранее построенных графиков.
На сайте онлайн калькулятора http://function-graph.ru/
[7] график строится быстро, после его построения можно менять цвет линий,
интервал осей координат. Есть возможность скачать график в формате рисунка.
Дано подробное описание, как работать с этим онлайн-сервисом, приведена таблица
поддерживаемых функций.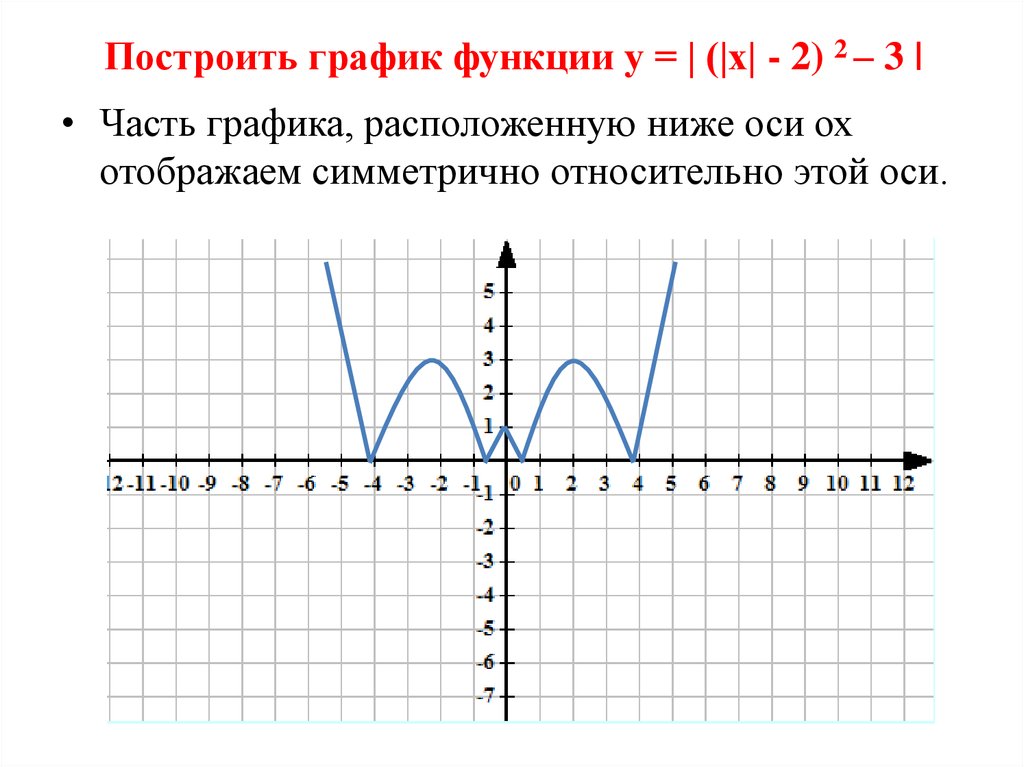 Неудобно то, что становится непонятно, обновилась ли
страница, или мы видим предыдущий график, если графиков нужно построить
несколько.
Неудобно то, что становится непонятно, обновилась ли
страница, или мы видим предыдущий график, если графиков нужно построить
несколько.
Теперь рассмотрим несколько математических пакетов, работающих в оффлайн-режиме.
Graph. Программа предназначена для построения графиков функций. Поддерживает все известные функции, позволяет выбирать цвет и толщину линий, интервалы. После построения графика можно выделять некоторые его части, сохранять его в виде рисунка, а также копировать в документы с координатной плоскостью. Поддерживает возможность импорта данных из других документов. Выводит координаты необходимых точек, позволяет оставлять комментарии на графиках.
1C Математический конструктор. Программа предлагает решение ряда математических задач: как
алгебраических, так и геометрических. Обратим внимание только на ту часть,
которая позволяет строить графики функций и работать с ними. При построении
графика функции с помощью геометрических преобразований пользователь сам увидит
все этапы его построения на графике и формулы в общем виде рядом с этими
графиками, что является познавательным и интересным.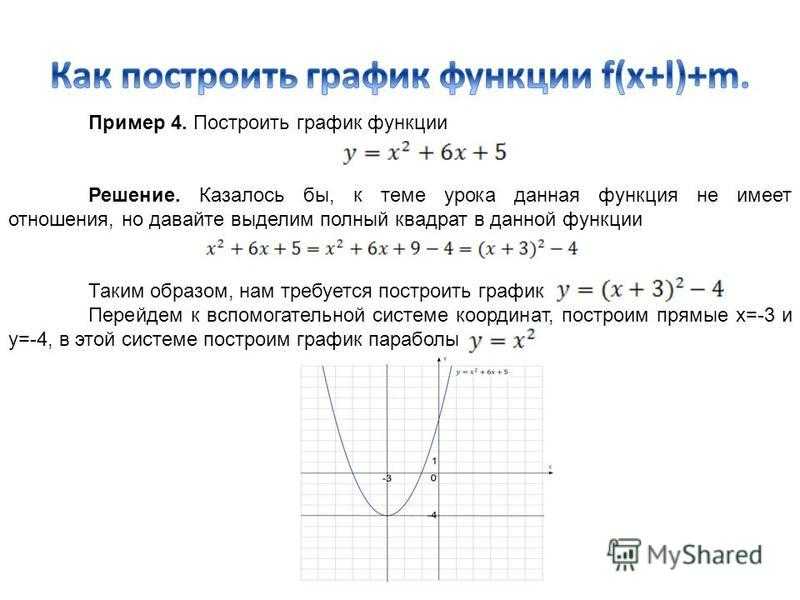 Как и в любых других
математических пакетах, в этой программе с графиками можно работать, находя
нужные точки, двигая, увеличивая, меняя цвет линий.
Как и в любых других
математических пакетах, в этой программе с графиками можно работать, находя
нужные точки, двигая, увеличивая, меняя цвет линий.
Grapher. Приложение позволяет строить графики различных функций и математических выражений. Есть возможность ввода параметрических графиков функций, а также строить графики функций в полярной системе координат. Программа позволяет строить несколько графиков функций подряд, при этом можно выбрать разные цвета линий. В программе имеется каталог с уже готовыми графиками функций, при этом ведется история ваших построенных графиков. При возникших сложностях можно обратиться с помощью к каталогу с описанием типов графиков и их примерами.
Рассмотрим геометрические преобразования графиков функций, таких как линейная, квадратичная, тригонометрические, и как с помощью этих программ их производить.
Выделяют всего три основных вида геометрических преобразований графиков функций:
1) Растяжение или сжатие.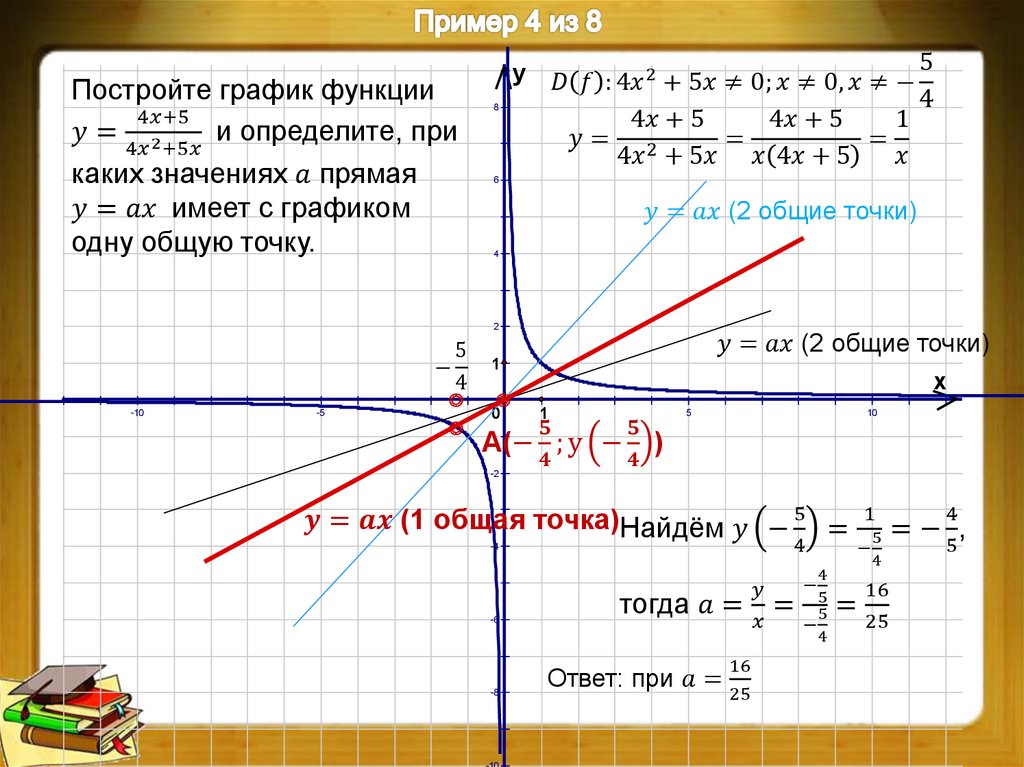
1.1) Растяжение или сжатие вдоль оси OY.
Общий вид: , k – const, k>0. Алгоритм построения: → при k>0 растягиваем график в k раз вдоль оси ординат, при 0< k<1 сжимаем график в раз вдоль оси ординат.
Например: построим график функции .
Алгоритм построения: → .
Используем для выполнения задания онлайн калькулятор «webmath». Так, как на этом сайте есть возможность строить несколько графиков одновременно, то мы увидим два графика: и (рис.1). Второй график получился путем растяжения исходного вдоль оси OY. Аналогичный алгоритм построения графика функции .
Рис.1. Графики функций , . в онлайн калькуляторе «webmath»
1.2) Растяжение или сжатие вдоль оси OX./Tablitsy%20s%20formulami/Grafiki%20elementarnyh%20funkciy.jpg)
Общий вид , k – const, k>0. Алгоритм построения: → при k>0 сжимаем график в k раз вдоль оси абцисс, при 0< k<1 растягиваем график в раз вдоль оси абцисс.
Пример: построим график функции с помощью онлайн калькулятора «graph.reshish.ru».
Алгоритм построения: →.
Онлайн калькулятор «graph.reshish.ru» также позволяет построить два графика на одной координатной плоскости и (рис.2). Второй график получился путем растяжения исходного вдоль оси OX. Аналогичный алгоритм построения графика функции .
Рис. 2. Графики функций , в онлайн калькуляторе «graph.reshish.ru»
2) Симметричное отображение.
2.1) Симметричное отображение относительно оси OX.
Общий вид . Алгоритм построения: → отображаем график симметрично относительно оси абцисс.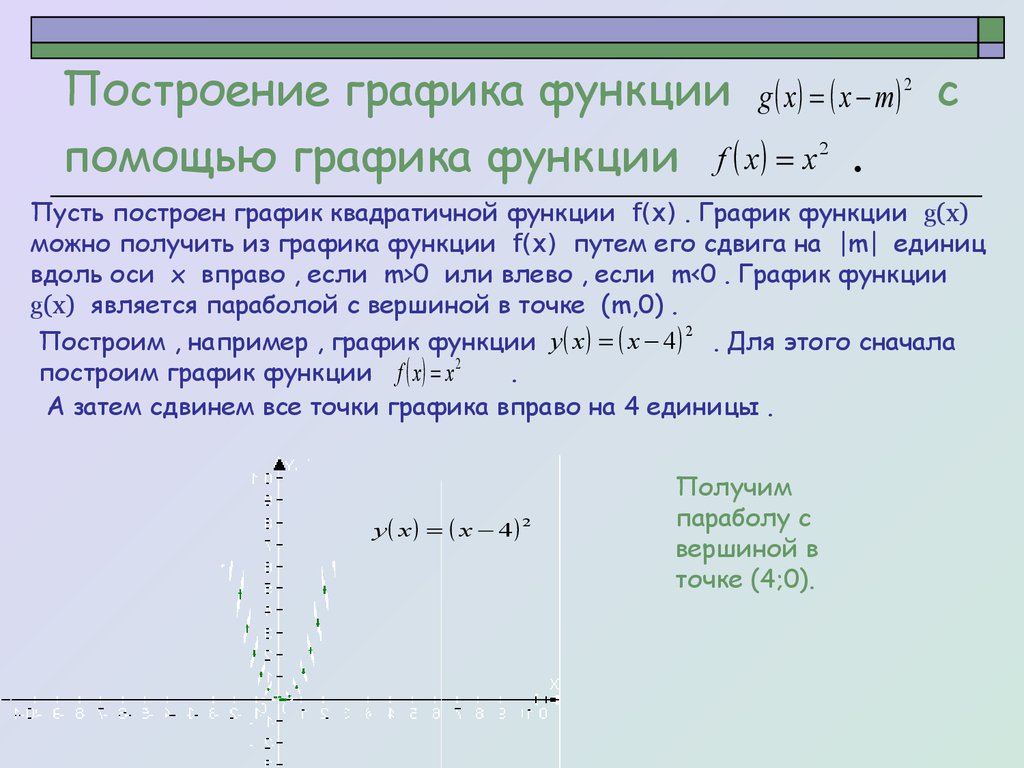
Пример: необходимо построить график функции в онлайн калькуляторе «yotx.ru».
Алгоритм построения: →
В онлайн калькуляторе «yotx.ru» невозможно построить два графика одновременно, поэтому построим сначала график функции (рис.3), а затем выполним преобразование, а именно, построим график функции (рис. 4).
Рис. 3. График функции в онлайн калькуляторе «yotx.ru»
Рис. 4. График функции в онлайн калькуляторе «yotx.ru»
2.2) Симметричное отображение относительно оси OY.
Общий вид . Алгоритм построения: → отображаем график симметрично относительно оси ординат.
Пример: необходимо построить график функции в онлайн калькуляторе «easyto.me/services/graphic».
Алгоритм построения: →
В онлайн калькуляторе «easyto.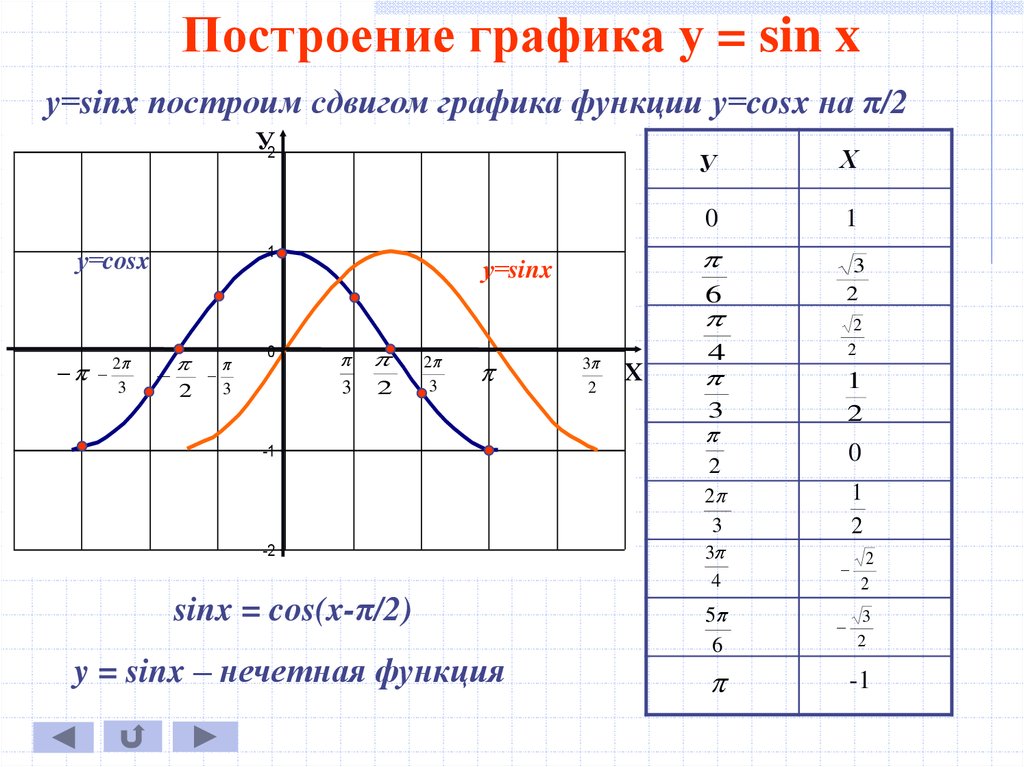 me/services/graphic» очень легко
построить два графика на одной координатной плоскости, причем при вводе функций
всплывают подсказки.
me/services/graphic» очень легко
построить два графика на одной координатной плоскости, причем при вводе функций
всплывают подсказки.
Рис. 5. Графики функций , в онлайн калькуляторе «easyto.me/services/graphic»
3) Параллельный перенос (сдвиг) вдоль осей координат.
3.1) Параллельный перенос по оси OY.
Общий вид , A-const. Алгоритм построения: → При А>0 поднимаем график на А единиц вверх по оси ординат, при А<0 опускаем график вниз по оси ординат.
Пример: построим график функции при помощи онлайн калькулятора «function-graph.ru».
Алгоритм построения: →
В этом онлайн калькуляторе все графики обновляются самостоятельно. Добавляем построение еще одного графика и вводим две функции. Два графика строятся на одной координатной плоскости (рис. 6).
Рис.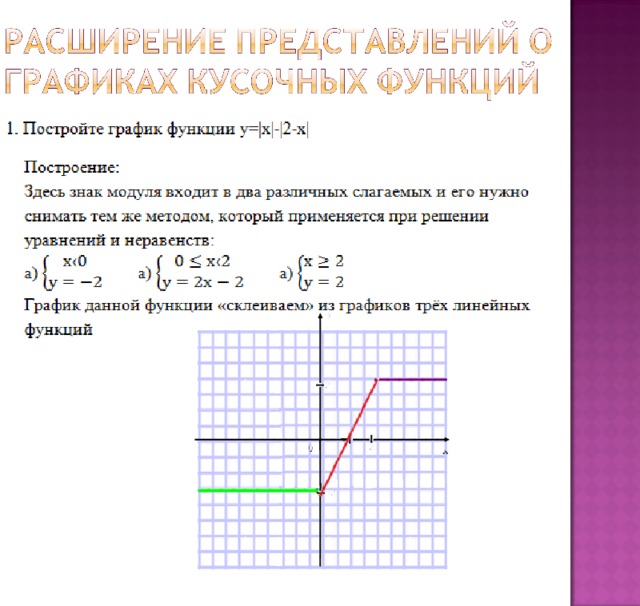 6 Графики функций ,
в онлайн калькуляторе «function-graph.ru»
6 Графики функций ,
в онлайн калькуляторе «function-graph.ru»
3.2) Параллельный перенос по оси OX.
Общий вид , a-const. Алгоритм построения: → При a >0 сдвигаем график на a единиц вправо по оси абцисс, при a <0 сдвигаем график влево по оси абцисс.
Пример: построим график функции c помощью программы Graph.
Алгоритм построения: →
Для построения графиков необходимо на панели задач выбрать Функции →Добавить и ввести необходимую функцию Для наглядности выбираем разный цвет для разных графиков.
В этой программе позволено строить несколько графиков функций на одной координатной плоскости (рис.7).
Рис. 7. Графики функций , в программе Graph
Построим
несколько графиков функций в программе 1С Математический конструктор.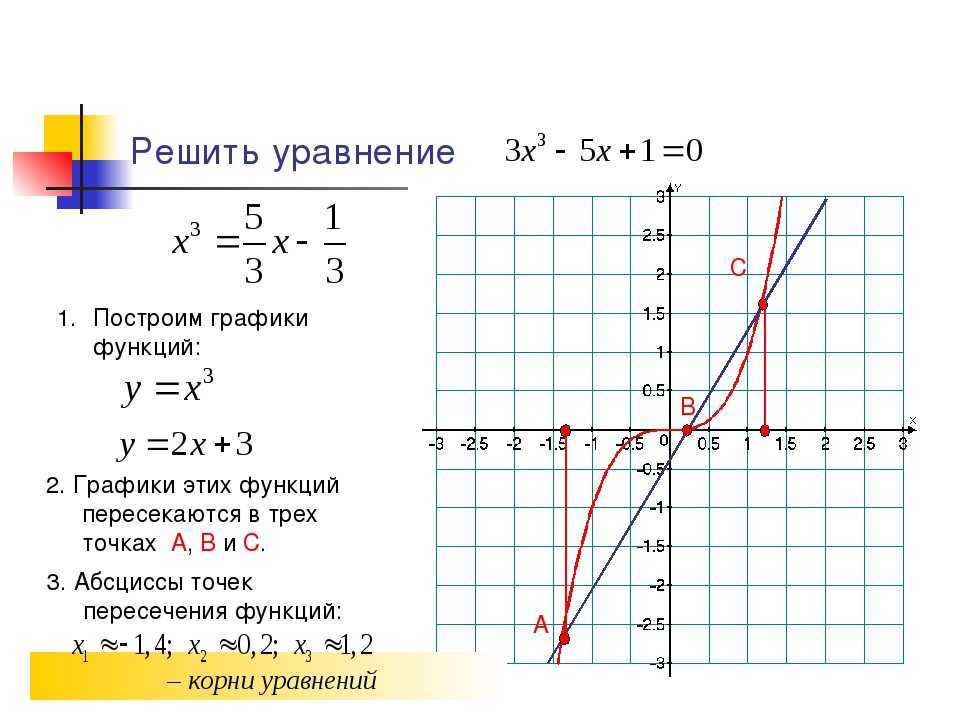 Например, , , .
Например, , , .
Выбираем необходимый вид графика на панели команд, вводим заданные константы, благодаря которым происходит сдвиг или симметричное отображение графиков. Формулы в общем виде можно увидеть слева от графиков на рисунке 8.
Рис. 8. Графики функций , , в программе 1С Математический конструктор
Построим график сложной функции с помощью программы Grapher.
Для начала дадим определение сложной функции:
Сложная функция — функция от функции. Если величина y является функцией от u, то есть , а u, в свою очередь, функцией от x, то есть , то является сложной функцией. [4]
Пусть задана функция . Для построения графика в программе необходимо выбрать на панели задач Графики →Добавить и вводим функцию, выбираем цвет и толщину линии. Результат на рисунке 9.
Рис. 9. График функции в программе Grapher
9. График функции в программе Grapher
Таким образом, был рассмотрен ряд онлайн калькуляторов и программ, с помощью которых можно не только построить графики простых и сложных функций, но и производить различные геометрические преобразования этих графиков. Был проведен анализ этих программ на наличие достоинств и недостатков, а так же выведены алгоритмы построения графиков функций, рассмотрены основные геометрические преобразования, приведены примеры функций, графики которых и были построены в тестируемых программах и онлайн калькуляторах.
В заключении можно отметить, что большинство анализируемых в статье онлайн калькуляторов и программ являются многофункциональными и позволяют не только строить графики сложных функций, но и выполнять геометрические преобразования над ними.
Список используемой литературы
1. Графики
онлайн. Построить график функции [Электронный ресурс] // математический онлайн
калькулятор URL: http://grafikus.ru/ (дата обращения: 07.12.2015)
Графики
онлайн. Построить график функции [Электронный ресурс] // математический онлайн
калькулятор URL: http://grafikus.ru/ (дата обращения: 07.12.2015)
2. Лучший построитель графиков функций [Электронный ресурс] // математический онлайн калькулятор URL: http://easyto.me/services/graphic/ (дата обращения: 07.12.2015)
3. Образовательные онлайн сервисы. Построение графиков функций онлайн [Электронный ресурс] // математический онлайн калькулятор URL: http://www.webmath.ru/web/prog31_1.php (дата обращения: 06.12.2015)
4. Общий толковый словарь русского языка http://tolkslovar.ru/ [Электронный ресурс] // математический онлайн калькулятор URL: (дата обращения: 10.12.2015)
5. Построение графиков функций онлайн [Электронный ресурс] // математический онлайн калькулятор URL: http://www.yotx.ru/ (дата обращения: 06.12.2015)
6.
Построить график функции онлайн [Электронный ресурс] //
математический онлайн калькулятор URL: http://graph.reshish. ru/ (дата обращения:
07.12.2015)
ru/ (дата обращения:
07.12.2015)
7. Построить график функции онлайн [Электронный ресурс] // математический онлайн калькулятор URL: http://function-graph.ru/ (дата обращения: 07.12.2015)
Исчисление I — неявное дифференцирование
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Мобильное уведомление
Похоже, вы находитесь на устройстве с «узкой» шириной экрана ( т.е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана. 2}}}\]
2}}}\]
Итак, это достаточно просто сделать. Однако есть некоторые функции, для которых это сделать нельзя. Вот тут-то и вступает в игру второй метод решения.
Решение 2 :
В этом случае мы собираемся оставить функцию в том виде, который нам дали, и работать с ним в этом виде. Однако давайте вспомним из первой части этого решения, что если бы мы могли найти \(y\), то мы получили бы \(y\) как функцию \(x\). Другими словами, если бы мы могли найти \(y\) (что мы могли бы сделать в этом случае, но не всегда сможем), мы получили бы \(y = y\left( x \right)\). Давайте перепишем уравнение, чтобы отметить это.
\[xy = x\,y\влево( x \вправо) = 1\]
Будьте осторожны и обратите внимание, что когда мы пишем \(y\left( x \right)\), мы не имеем в виду \(y\) умножить на \(x\). Здесь мы отмечаем, что \(y\) есть некоторая (вероятно, неизвестная) функция \(x\). Это важно помнить, выполняя эту технику решения.
Это важно помнить, выполняя эту технику решения.
Следующим шагом в этом решении является дифференцирование обеих сторон по \(x\) следующим образом:
\[\frac{d}{{dx}}\left( {x\,y\left( x \right)} \right) = \frac{d}{{dx}}\left( 1 \right)\ ]
Правая сторона проста. Это просто производная от константы. Левая сторона тоже проста, но мы должны признать, что здесь у нас действительно есть произведение, \(x\) и \(y\left( x \right)\). Итак, чтобы получить производную от левой части, нам нужно выполнить правило произведения. Выполнение этого дает,
\[\left( 1 \right)y\left( x \right) + x\frac{d}{{dx}}\left( {y\left( x \right)} \right) = 0\]
Теперь вспомним, что у нас есть следующий способ записи производной.
\[\frac{d}{{dx}}\left( {y\left( x \right)} \right) = \frac{{dy}}{{dx}} = y’\]
Используя это, мы получаем следующее,
\[у + ху’ = 0\]
Обратите внимание, что мы опустили \(\left( x \right)\) на \(y\), так как это было только для того, чтобы напомнить нам, что \(y\) является функцией \(x\) и теперь, когда мы взяли производную, она больше не нужна. Мы просто хотели, чтобы в уравнении учитывалось правило произведения, когда мы брали производную.
Мы просто хотели, чтобы в уравнении учитывалось правило произведения, когда мы брали производную.
Итак, давайте теперь вспомним, что нам нужно. Мы искали производную \(y’\) и заметили, что теперь в уравнении есть \(y’\). Итак, чтобы получить производную, все, что нам нужно сделать, это решить уравнение для \(y’\).
\[y’ = — \frac{y}{x}\]
Вот оно. Используя второй метод решения, это наш ответ. Однако это не то, что мы получили из первого решения. Или, по крайней мере, это не похоже на ту же производную, которую мы получили из первого решения. Однако вспомните, что мы действительно знаем, что такое \(y\) в терминах \(x\), и если мы подставим это, мы получим 9{2}}}\]
, что мы получили из первого решения. Независимо от используемого метода решения мы должны получить одну и ту же производную.
Процесс, который мы использовали во втором решении предыдущего примера, называется неявным дифференцированием и является предметом данного раздела. В предыдущем примере мы смогли просто найти \(y\) и избежать неявного дифференцирования. Однако в остальных примерах этого раздела мы либо не сможем найти \(y\), либо, как мы увидим в одном из приведенных ниже примеров, ответ будет не в той форме, которую мы может справиться.
В предыдущем примере мы смогли просто найти \(y\) и избежать неявного дифференцирования. Однако в остальных примерах этого раздела мы либо не сможем найти \(y\), либо, как мы увидим в одном из приведенных ниже примеров, ответ будет не в той форме, которую мы может справиться.
Во втором решении выше мы заменили \(y\) на \(y\left( x \right)\), а затем вычислили производную. Напомним, что мы сделали это, чтобы напомнить себе, что \(y\) на самом деле является функцией \(x\). Мы будем делать это довольно часто в этих задачах, хотя на самом деле мы редко пишем \(y\left( x \right)\). Итак, прежде чем мы на самом деле будем работать над проблемами неявного дифференцирования, давайте сделаем быстрый набор «простых» производных, которые, мы надеемся, помогут нам в вычислении производных функций, которые также содержат \(y\left( x \right)\). 9{у\влево(х\вправо)}}\)
Показать все решения Скрыть все решения
Они написаны немного иначе, чем мы привыкли видеть здесь. Это потому, что мы хотим сопоставить эти проблемы с тем, что мы будем делать в этом разделе. Кроме того, каждая из этих частей имеет несколько функций, которые можно различать, начиная с конкретной функции, за которой следует общая функция. Это снова поможет нам с некоторыми конкретными частями процесса неявной дифференциации, который мы будем выполнять. 92} — 7} \справа)\]
Это потому, что мы хотим сопоставить эти проблемы с тем, что мы будем делать в этом разделе. Кроме того, каждая из этих частей имеет несколько функций, которые можно различать, начиная с конкретной функции, за которой следует общая функция. Это снова поможет нам с некоторыми конкретными частями процесса неявной дифференциации, который мы будем выполнять. 92} — 7} \справа)\]
и это просто правило цепочки. Мы продифференцировали внешнюю функцию (показатель числа 5), а затем умножили ее на производную внутренней функции (элемент в скобках).
Для второй функции мы собираемся сделать то же самое. Нам нужно будет использовать цепное правило. Внешняя функция по-прежнему является показателем степени 5, а внутренняя функция на этот раз просто \(f\left( x \right)\). У нас здесь нет конкретной функции, но это не значит, что мы не можем хотя бы записать правило цепочки для этой функции. Вот производная этой функции, 94}f’\влево( х \вправо)\]
На самом деле мы не знаем, что такое \(f\left( x \right)\), поэтому, когда мы вычисляем производную внутренней функции, все, что мы можем сделать, это записать обозначение для производной, , т. е. \(f ‘\влево(х\вправо)\).
е. \(f ‘\влево(х\вправо)\).
В последней функции здесь мы просто заменили \(f\) во второй функции на \(y\), так как большая часть нашей работы в этом разделе будет включать \(y\) вместо \(f\ ) х. В остальном эта функция идентична второй. Итак, производная равна 9.4}у’\влево( х \вправо)\]
b \(\sin \left( {3 — 6x} \right)\), \(\sin \left( {y\left( x \right)} \right)\) Показать решение
Первая функция, которую нужно здесь отличить, — это просто задача быстрого правила цепи, так что вот ее производная,
\[\ frac{d}{{dx}}\left[ {\sin\left({3 — 6x} \right)} \right] = — 6\cos \left({3 — 6x} \right)\ ]
Для второй функции на этот раз мы не стали использовать \(f\left( x \right)\) и сразу перешли к \(y\left( x \right)\) для общей версии. Это всего лишь общая версия того, что мы сделали для первой функции. Внешняя функция по-прежнему является синусом, а внутренняя задается как \(y\left( x \right)\), и хотя у нас нет формулы для \(y\left(x \right)\), поэтому мы на самом деле не может взять его производную, у нас есть обозначение для его производной.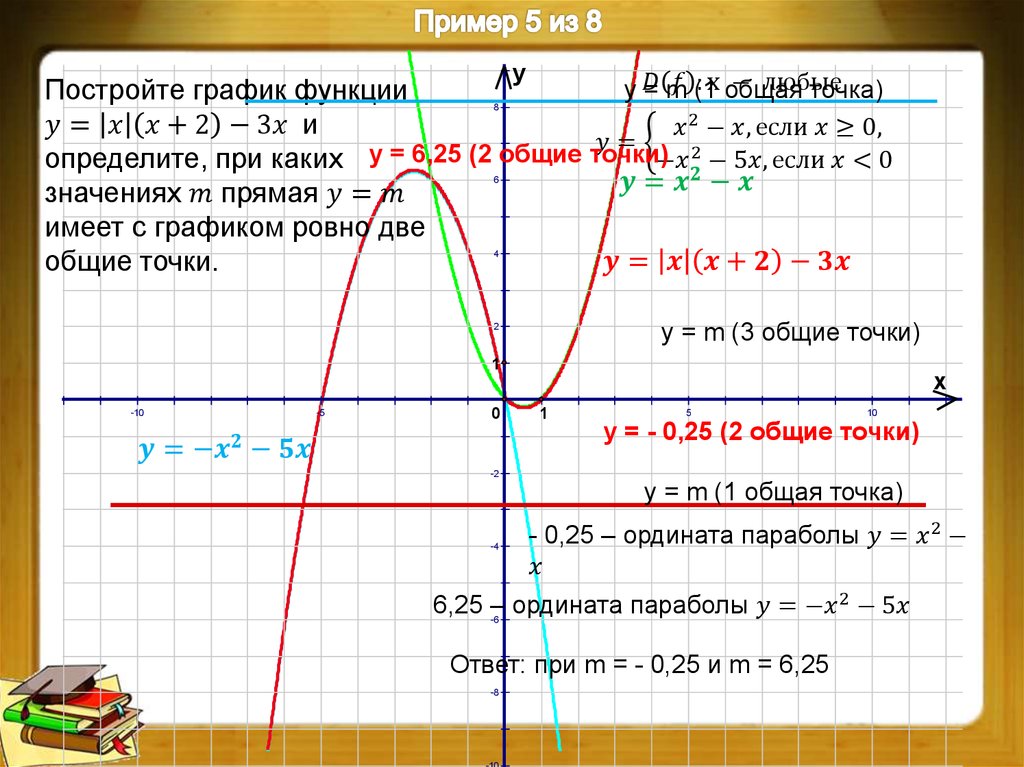 Вот производная этой функции, 9{у\влево(х\вправо)}}\]
Вот производная этой функции, 9{у\влево(х\вправо)}}\]
Итак, в этом наборе примеров мы просто решали некоторые задачи с цепным правилом, где внутренней функцией была \(y\left( x \right)\), а не конкретная функция. Такого рода производные постоянно появляются при выполнении неявного дифференцирования, поэтому нам нужно убедиться, что мы можем их выполнять. Также обратите внимание, что мы сделали это только для трех типов функций, но здесь мы могли бы использовать гораздо больше функций.
Итак, пришло время решить нашу первую задачу, где требуется неявное дифференцирование, в отличие от первого примера, где мы могли бы избежать неявного дифференцирования, найдя \(y\). 92}} \]
Перед тем, как приступить к этой задаче, мы заявили, что здесь нам нужно провести неявное дифференцирование, потому что мы не можем просто найти \(y\), и тем не менее это то, что мы только что сделали. Итак, почему мы не можем использовать здесь «нормальную» дифференциацию? Проблема в «\(\pm\)».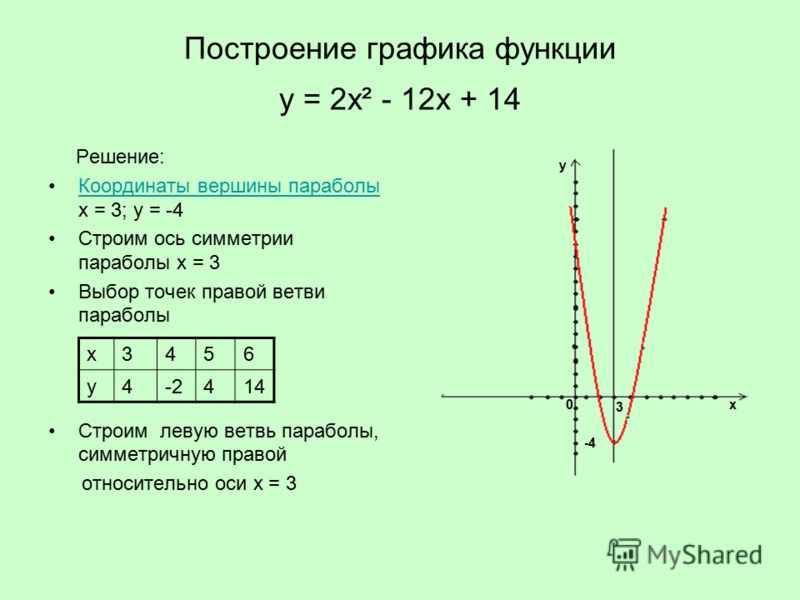 1} у ‘\ влево ( х \ вправо) = 0 \]
1} у ‘\ влево ( х \ вправо) = 0 \]
В этот момент мы можем опустить часть \(\left( x \right)\), так как это было только в задаче, чтобы облегчить процесс дифференцирования. Последний шаг — просто решить полученное уравнение относительно \(y’\).
\[\begin{align*}2x + 2yy’ & = 0\\ y’ & = — \frac{x}{y}\end{align*}\]
В отличие от первого примера, мы не можем просто подставить \(y\), так как не будем знать, какую из двух функций использовать. Большинство ответов от неявной дифференциации будут включать как \(x\), так и \(y\), так что не радуйтесь этому, когда это произойдет. 92} = 9\]
в точке \(\left( {2,\,\,\sqrt 5 } \right)\).
Показать решение
Во-первых, обратите внимание, что в отличие от всех других задач касательной, которые мы решали в предыдущих разделах, нам нужно задать значения \(x\) и \(y\) точки. Обратите также внимание, что эта точка действительно лежит на графике окружности (вы можете проверить, подставив точки в уравнение), и поэтому можно говорить о касательной в этой точке.
Обратите также внимание, что эта точка действительно лежит на графике окружности (вы можете проверить, подставив точки в уравнение), и поэтому можно говорить о касательной в этой точке.
Напомним, что для записи касательной нам нужен только наклон касательной, а это не что иное, как производная, вычисленная в данной точке. У нас есть производная от предыдущего примера, поэтому все, что нам нужно сделать, это подставить заданную точку.
\[м = {\ влево. {y’} \right|_{x = 2,\,y = \sqrt 5}} = — \frac{2}{{\sqrt 5}}\]
Тогда касательная.
\[y = \sqrt 5 — \frac{2}{{\sqrt 5}}\left( {x — 2} \right)\]
Теперь давайте поработаем еще над несколькими примерами. В оставшихся примерах мы больше не будем писать \(y\left( x \right)\) вместо \(y\). Это просто то, что мы делали, чтобы напомнить себе, что \(y\) на самом деле является функцией \(x\), чтобы помочь с производными. Вид \(y\left( x \right)\) напомнил нам, что нам нужно выполнить цепное правило для этой части задачи. С этого момента мы будем оставлять \(y\) записанными как \(y\) и в нашей голове нам нужно помнить, что они на самом деле \(y\left( x \right)\ ) и что нам нужно выполнить цепное правило.
Вид \(y\left( x \right)\) напомнил нам, что нам нужно выполнить цепное правило для этой части задачи. С этого момента мы будем оставлять \(y\) записанными как \(y\) и в нашей голове нам нужно помнить, что они на самом деле \(y\left( x \right)\ ) и что нам нужно выполнить цепное правило.
Есть простой способ запомнить, как выполнять цепное правило в этих задачах. Цепное правило действительно говорит нам дифференцировать функцию, как обычно, за исключением того, что нам нужно добавить производную внутренней функции. При неявном дифференцировании это означает, что каждый раз, когда мы дифференцируем терм с \(y\) в нем, внутренней функцией является \(y\), и нам нужно будет добавить \(y’\) к терму, так как это будет быть производной внутренней функции.
Давайте посмотрим на пару примеров. 93} + 1\) Показать решение
Сначала продифференцируйте обе части относительно \(x\) и помните, что каждый \(y\) на самом деле \(y\left( x \right)\), просто мы больше не будем писать его так.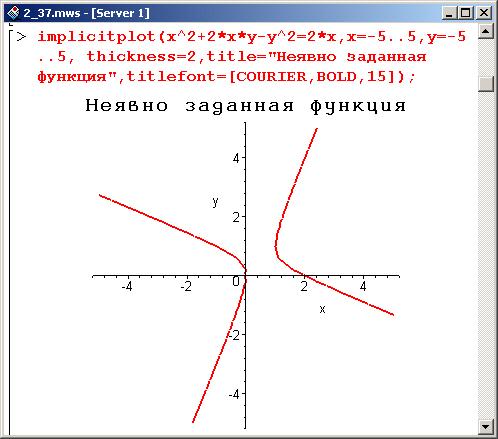 Это означает, что первый член слева будет правилом произведения.
Это означает, что первый член слева будет правилом произведения.
Мы дифференцировали эти виды функций, включающих \(y\), в степени с цепным правилом в Примере 2 выше. Также вспомните обсуждение до начала этой задачи. При решении такого рода задачи цепного правила все, что нам нужно сделать, это дифференцировать \(y\) как обычно, а затем добавить \(y’\), который является не чем иным, как производной «внутренней функции». ». 92}у’\]
Теперь нам нужно найти производную \(y’\). Это просто базовая алгебра решений, которую вы способны сделать. Основная проблема в том, что это может оказаться более грязным, чем то, к чему вы привыкли. Все, что нам нужно сделать, это получить все термины с \(y’\) в них с одной стороны и все термины без \(y’\) в них с другой. Затем вынесите \(y’\) из всех членов, содержащих его, и разделите обе части на «коэффициент» при \(y’\). Вот решение для этого, 93}} \right)\) Показать решение
Нам нужно быть осторожными с этой проблемой.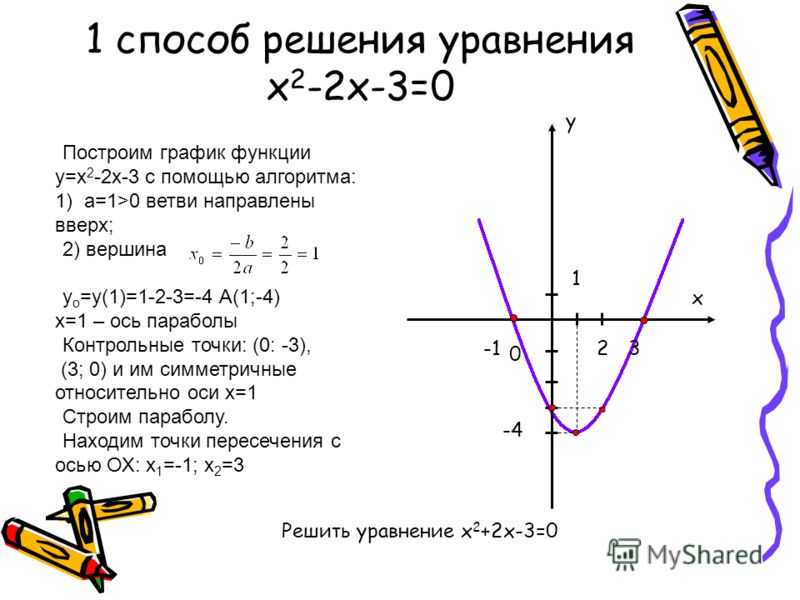 У нас есть пара цепных правил, с которыми нам придется иметь дело, которые немного отличаются от тех, с которыми мы имели дело до этой проблемы.
У нас есть пара цепных правил, с которыми нам придется иметь дело, которые немного отличаются от тех, с которыми мы имели дело до этой проблемы.
Как в экспоненте, так и в логарифме у нас есть «стандартное» цепное правило, заключающееся в том, что внутри экспоненты и логарифма есть нечто иное, чем просто \(x\) или \(y\). Итак, это означает, что здесь мы будем использовать цепное правило, как обычно, а затем, когда мы будем вычислять производную внутренней функции для каждого члена, нам придется иметь дело с дифференцированием \(y\). 9{- 1}}}}\end{выравнивание*}\]
Обратите внимание: чтобы производная хотя бы выглядела немного лучше, мы преобразовали все дроби в отрицательные степени.
Хорошо, мы видели одно применение неявного дифференцирования в примере с касательной выше. Однако есть еще одно применение, которое мы увидим в каждой задаче в следующем разделе.
В некоторых случаях у нас будет две (или более) функции, каждая из которых является функцией третьей переменной.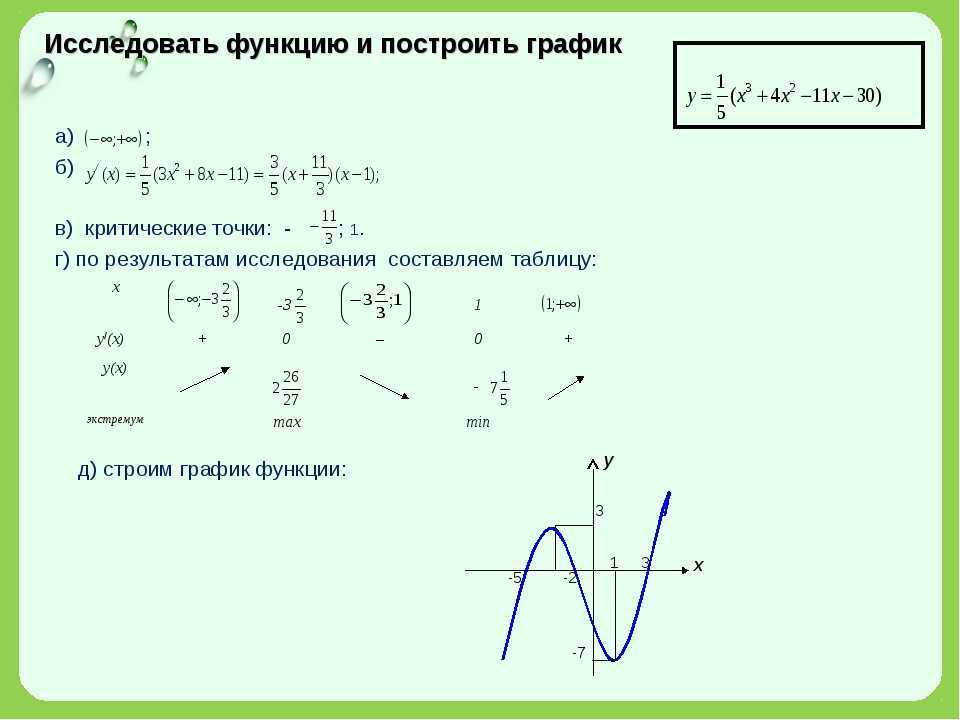 Таким образом, у нас могут быть, например, \(x\left( t \right)\) и \(y\left( t \right)\), и в этих случаях мы будем дифференцировать по \(t\) . Это просто неявное дифференцирование, как мы делали в предыдущих примерах, но, тем не менее, есть разница.
Таким образом, у нас могут быть, например, \(x\left( t \right)\) и \(y\left( t \right)\), и в этих случаях мы будем дифференцировать по \(t\) . Это просто неявное дифференцирование, как мы делали в предыдущих примерах, но, тем не менее, есть разница.
В предыдущих примерах у нас есть функции, включающие \(x\) и \(y\) и рассматриваемые \(y\) как \(y\left( x \right)\). В этих задачах мы дифференцировались по \(x\), поэтому, сталкиваясь с \(x\) в функции, мы дифференцировались как обычно, а когда сталкивались с \(y\), мы дифференцировались как обычно, за исключением того, что тогда добавил \(y’\) к этому термину, потому что мы действительно использовали цепное правило.
В новом примере, который мы хотим рассмотреть, мы предполагаем, что \(x = x\left( t \right)\) и что \(y = y\left( t \right)\) и дифференцируем по отношению к \(т\). Это означает, что каждый раз, когда мы сталкиваемся с \(x\) или \(y\), мы будем выполнять цепное правило. Это, в свою очередь, означает, что когда мы дифференцируем \(x\), нам нужно будет добавлять \(x’\), и всякий раз, когда мы дифференцируем \(y\), мы добавляем \(y’\).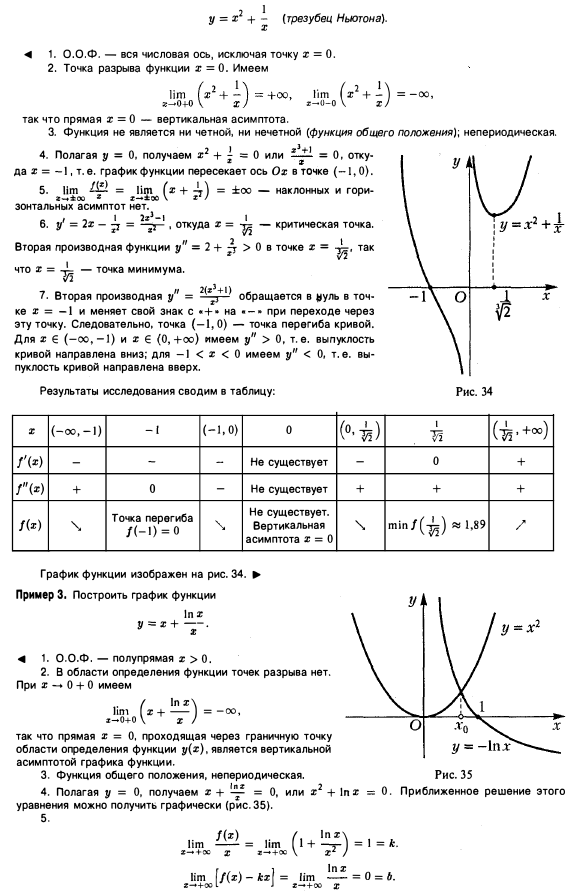 9{1 — x}} + 5y’\sin\left( {5y} \right) = 2yy’\]
9{1 — x}} + 5y’\sin\left( {5y} \right) = 2yy’\]
На самом деле в этой проблеме нет ничего особенного. Поскольку в задаче две производные, мы не будем утруждать себя решением одной из них. Когда мы решим такую задачу в следующем разделе, она будет подразумевать, какую из них нам нужно решить.
На данный момент, кажется, нет никакой реальной причины для решения такого рода задач, но, как мы увидим в следующем разделе, каждая задача, которую мы будем решать, будет включать такого рода неявное дифференцирование.
Как построить график неявных функций на TI-83 Plus
Что говорят наши клиенты…
Тысячи пользователей используют наше программное обеспечение, чтобы справиться со своими домашними заданиями по алгебре. Вот некоторые из их опытов:
Я считаю это программное обеспечение заменой репетитора по алгебре. Это тоже по очень доступной цене.
Victoria Hill, CO
Прошло много времени с тех пор, как мне нужно было разбираться в алгебре, и когда пришло время помочь моему сыну, я не мог этого сделать. Теперь, с вашим программным обеспечением по алгебре, мы оба учимся вместе.
Теперь, с вашим программным обеспечением по алгебре, мы оба учимся вместе.
George Miller, LA
Это программное обеспечение очень помогло мне с дробями. Что-то, с чем я боролся годами. Я попросил родителей о помощи, но они говорят, что вся математика сейчас выглядит иначе, чем когда они учились в школе. Теперь мне не нужно больше спрашивать, потому что программа все объясняет.
Чарльз Б., Висконсин
Поисковые фразы, использованные 23 мая 2009 г.:
Студенты, борющиеся со всевозможными задачами по алгебре, узнают, что наше программное обеспечение может спасти им жизнь. Вот поисковые фразы, которые сегодняшние поисковики использовали, чтобы найти наш сайт. Сможете ли вы найти среди них свою?
- онлайн-калькуляторы для решения систем уравнений
- +2 к рабочему листу 2 степени
- читы на кс2 сац
- Планы уроков по линейным функциям 7 класса
- Алгебра 2 вопроса и ответа
- нахождение области уравнения
- год 7 бесплатных листов по математике
- сложные задачи по уравнению окружностей
- Курс математики Glencoe/McGraw-Hill2 l 7-й класс
- Учебник по факторинговым полиномам
- Как узнать, что уравнение имеет бесконечно много решений? Как узнать, что уравнение не имеет решения?
- скачать бесплатно книгу МСФО
- решить уравнение квадратного корня для вас
- решение математических задач алгебра колледжа
- задача по алгебре вероятности
- Упрощение и решение комплексных чисел
- решение уравнений с помощью рабочего листа сложения и вычитания
- целочисленных рабочих листа для 7 класса
- бесплатных загрузок книг для подготовки к трудоустройству
- Рабочие листы по математике для 6-го класса
- ОБЪЯСНЕНИЕ МАТЕМАТИЧЕСКИХ РАДИКАЛОВ
- тест на способности и ответ
- преобразовать .


