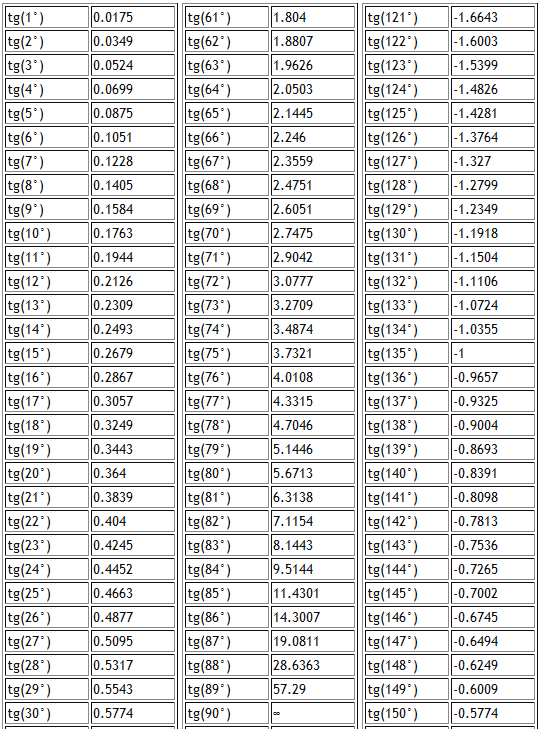
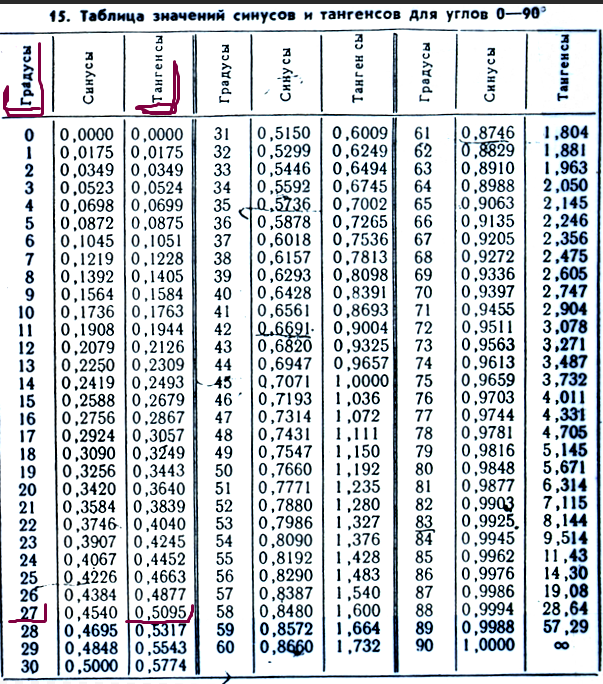
Быстро найти нужную формулу для расчета онлайн. Геометрия. Алгебра.
Свойства ромба:
1. Ромб — частный случай параллелограмма
2. Противоположные стороны — параллельны
3. Все четыре стороны — равны
4. Диагонали пересекаются под прямым углом (90°)
5. Диагонали являются биссектрисами
a — сторона ромба
D — большая диагональ
d — меньшая диагональ
α — острый угол
β — тупой угол
Формула стороны через диагонали, ( a ):
Формулы стороны через диагональ и угол, ( a ):
Формулы стороны через диагональ и половинный угол, ( a ):
Формулы стороны через диагонали и угол, ( a ):
Формулы стороны через площадь ромба ( S ) и угол, ( a
Формулы стороны через периметр ромба ( P ) и угол, ( a ):
Формулы площади ромба
Формула периметра ромба
Все формулы по геометрии
Рейтинг: 0 / 5
Свойства ромба:
1.
Ромб — частный случай параллелограмма
2. Противоположные стороны — параллельны
3. Все четыре стороны — равны
4. Диагонали пересекаются под прямым углом (90°)
5. Диагонали являются биссектрисами
a — сторона ромба
D — большая диагональ
d — меньшая диагональ
α — острый угол
β — тупой угол
Формулы косинуса углов через диагональ и сторону:
Формулы синуса углов через диагонали :
Формулы синуса углов через площадь S и сторону :
Формулы тангенса половинных углов через диагонали
Формулы соотношения острого и тупого углов:
Для определения величины угла в градусах или радианах, используем функции arccos или arcsin или arctg
Формулы площади ромба
Формула периметра ромба
Все формулы по геометрии
Рейтинг: 2 / 5
Свойства ромба:
1.
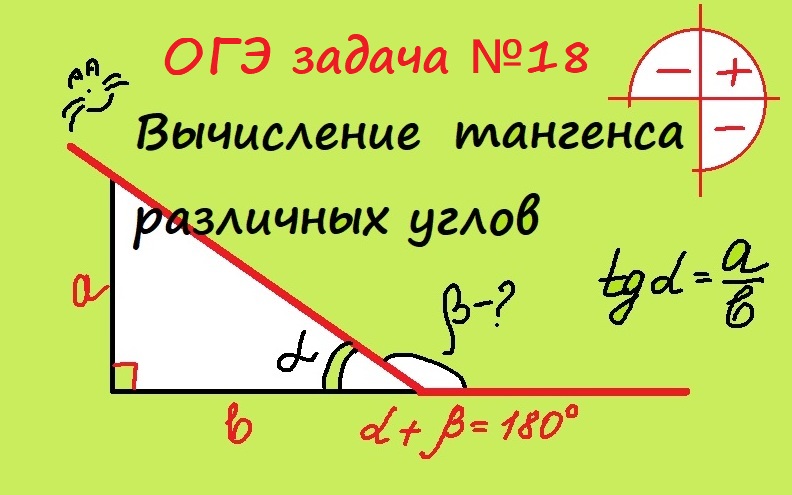Ромб — частный случай параллелограмма
2. Противоположные стороны — параллельны
3. Все четыре стороны — равны
4. Диагонали пересекаются под прямым углом (90°)
5. Диагонали являются биссектрисами
a — сторона ромба
D
d — меньшая диагональ
α — острый угол
β — тупой угол
Формулы диагоналей через сторону и угол, ( D d):
Формулы диагоналей через сторону и половинный угол, (D d):
Формулы диагоналей через сторону и другую диагональ, (D d):
Формулы диагоналей через угол и другую диагональ, (D d):
Формулы диагоналей через площадь (D d):
Формулы площади ромба
Формула периметра ромба
Все формулы по геометрии
Рейтинг: 4 / 5
Коэффициент трения
{\mu = \dfrac{F_{тр}}{mg}}
Найти коэффициент трения
через силу трения и массучерез угол наклона
Сила трения Fтрмикроньютонмиллиньютонньютонкилоньютонмеганьютонгиганьютонкилограмм-силакипдин
Масса m
микрограмммиллиграммграммкгцентнертонна
Ускорение свободного падения g
Виджет
Ссылка на расчет
Сообщить об ошибке
Сохранить расчет
Печатать
Приводим 2 варианта нахождения коэффициента трения — зная силу трения и массу тела или зная угол наклона.
Для обоих вариантов вы найдете удобные калькуляторы и формулы для расчета.
Коэффициент трения представляет собой безразмерную скалярную величину, которая равна отношению силы трения между двумя телами и силы, прижимающей их друг к другу, во время или в начале скольжения.
Коэффициент трения чаще всего обозначают греческой буквой µ («мю»).
Следует помнить, что коэффициент трения (μ) величина безразмерная, то есть не имеет единицы измерения.
Коэффициент трения зависит от качества обработки трущихся поверхностей, скорости движения тел относительно друг друга и материала соприкасающихся поверхностей. В большинстве случаев коэффициент трения находится в пределах от 0,1 до 0,5 (см. таблицу).
Содержание:
- калькулятор коэффициента трения
- формула коэффициента трения через силу трения и массу
- формула коэффициента трения через угол наклона
- таблица коэффициентов трения
- примеры задач
Формула коэффициента трения через силу трения и массу
\mu = \dfrac{F_{тр}}{mg}
Fтр — сила трения
m — масса тела
g — ускорение свободного падения (в большинстве задач можно принять g=9.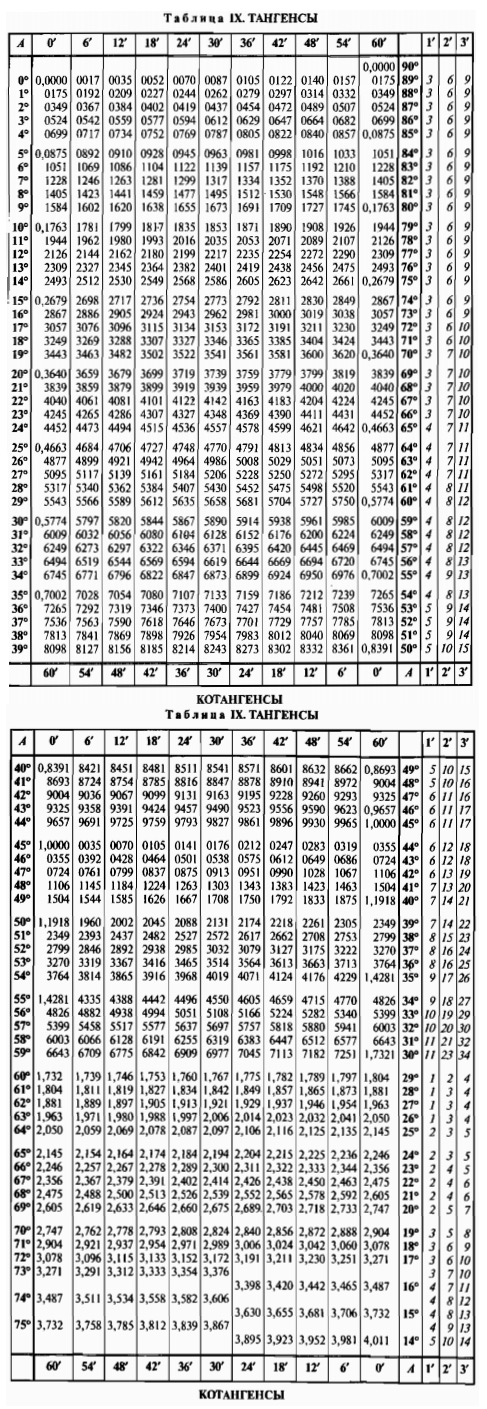
81 м/с²)
Формула коэффициента трения через угол наклона
\mu = \tg(\alpha)
α — угол наклона
Таблица коэффициентов трения скольжения для разных пар материалов
| Трущиеся материалы (при сухих поверхностях) | Коэффициенты трения | |
|---|---|---|
| покоя | при движении | |
| Резина по сухому асфальту | 0,95-1,0 | 0,5-0,8 |
| Резина по влажному асфальту | 0,25-0,75 | |
| Алюминий по алюминию | 0,94 | |
| Бронза по бронзе | 0,20 | |
| Бронза по чугуну | 0,21 | |
| Дерево по дереву (в среднем) | 0,65 | 0,33 |
| Дерево по камню | 0,46-0,60 | |
| Дуб по дубу (вдоль волокон) | 0,62 | 0,48 |
| Дуб по дубу (перпендикулярно волокнам) | 0,54 | 0,34 |
| Железо по железу | 0,15 | 0,14 |
| Железо по чугуну | 0,19 | 0,18 |
| Железо по бронзе (слабая смазка) | 0,19 | 0,18 |
| Канат пеньковый по деревянному барабану | 0,40 | |
| Канат пеньковый по железному барабану | 0,25 | |
| Каучук по дереву | 0,80 | 0,55 |
| Каучук по металлу | 0,80 | 0,55 |
| Кирпич по кирпичу (гладко отшлифованные) | 0,5-0,7 | |
| Колесо со стальным бандажем по рельсу | 0,16 | |
| Лед по льду | 0,05-0,1 | 0,028 |
| Метал по аботекстолиту | 0,35-0,50 | |
| Метал по дереву (в среднем) | 0,60 | 0,40 |
| Метал по камню (в среднем) | 0,42-0,50 | |
| Метал по металу (в среднем) | 0,18-0,20 | |
| Медь по чугуну | 0,27 | |
| Олово по свинцу | 2,25 | |
| Полозья деревянные по льду | 0,035 | |
| Полозья обитые железом по льду | 0,02 | |
| Резина (шина) по твердому грунту | 0,40-0,60 | |
| Резина (шина) по чугуну | 0,83 | 0,8 |
| Ремень кожаный по деревянному шкиву | 0,50 | 0,30-0,50 |
| Ремень кожаный по чугунному шкиву | 0,30-0,50 | 0,56 |
| Сталь по железу | 0,19 | |
| Сталь(коньки) по льду | 0,02-0,03 | 0,015 |
| Сталь по райбесту | 0,25-0,45 | |
| Сталь по стали | 0,15-0,25 | 0,09 (ν = 3 м/с)
0,03 (ν = 27 м/с) |
| Сталь по феродо | 0,25-0,45 | |
| Точильный камень (мелкозернистый) по железу | 1 | |
| Точильный камень (мелкозернистый) по стали | 0,94 | |
| Точильный камень (мелкозернистый) по чугуну | 0,72 | |
| Чугун по дубу | 0,65 | 0,30-0,50 |
| Чугун по райбесту | 0,25-0,45 | |
| Чугун по стали | 0,33 | 0,13 (ν = 20 м/с) |
| Чугун по феродо | 0,25-0,45 | |
| Чугун по чугуну | 0,15 | |
Примеры задач на нахождение коэффициента трения
Задача 1
Найдите коэффициент трения между полом и ящиком массой 20 кг, который равномерно двигают с силой 50 Н.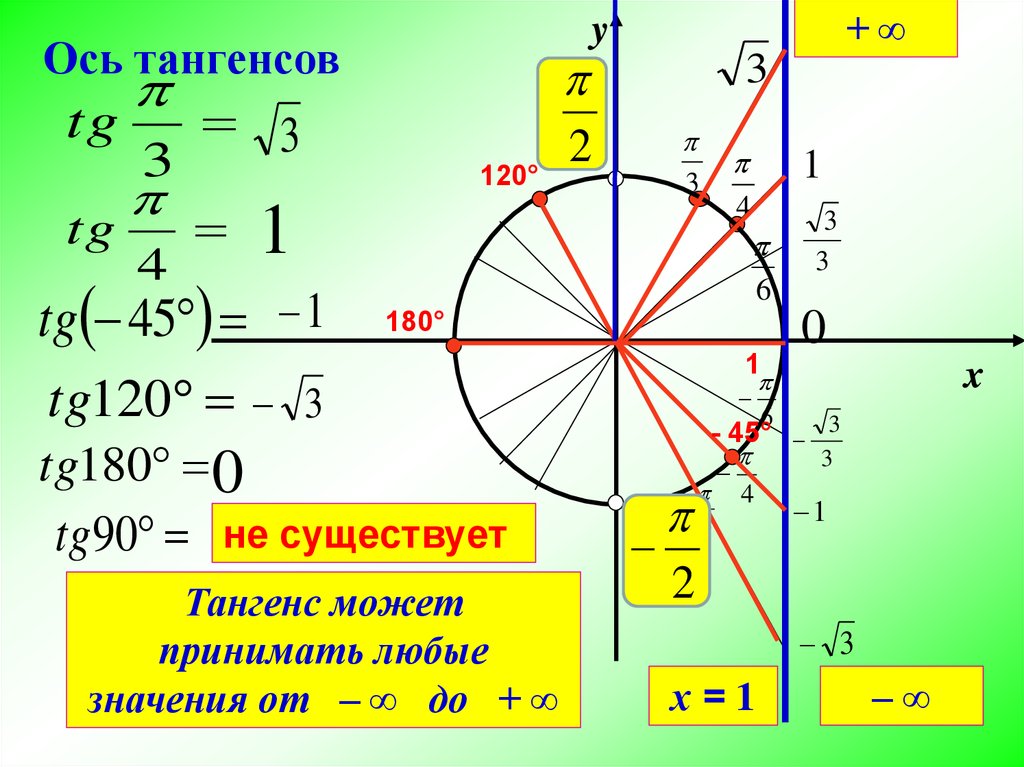
Решение
Для решения задачи воспользуемся формулой.
\mu = \dfrac{F_{тр}}{mg} = \dfrac{50}{20 \cdot 9.81} = \dfrac{50}{196.2} \approx 0.25484
Ответ: \approx 0.25484
С помощью калькулятора удобно проверить ответ.
Задача 2
Найдите коэффициент трения если угол наклона 30°.
Решение
Для решения этой задачи воспользуемся второй формулой.
\mu = \tg(\alpha) = \tg(30°) \approx 0.57735
Ответ: \approx 0.57735
Проверим полученный ответ с помощью калькулятора .
Тангенс-функция — онлайн калькулятор, формулы, график
Тангенс-функция — онлайн калькулятор, формулы, графикCalculat.org
- Функция тангенса определяется в прямоугольном треугольнике как отношение противоположной и прилежащей сторон.
- Функция определяется в диапазоне от 90 ° ± к · 180 °
до 270 °± к · 180 °
и принимает значения от −∞
до +∞.
График
Функция касательной αtan α[°][рад]090°180°270°360°0,5ππ1,5π2πКалькулятор
Введите 1 значение
α =
α 2 =
тангенс α =
±∞
Округлить до / десятичных разрядов
Формулы
Касательная функция
прямоугольный треугольник ABCabc α β$$ \tan\alpha = \frac{a}{b} $$
$$ \tan\beta = \frac{b}{a} $$
$$ \begin{выровнено} & \tan\alpha \cdot \cot\alpha = 1 \\Стрелка вправо\\ \\ & \cot\alpha = \frac{1}{\tan\alpha} \end{выровнено} $$
$$ \begin{выровнено} & \tan\alpha = \frac{\sin\alpha}{\cos\alpha} \\ \\ & \cot\alpha = \frac{\cos\alpha}{\sin\alpha} \end{выровнено} $$
$$ \begin{выровнено} & \tan(\alpha + \beta) = \frac{\tan\alpha + \tan\beta}{1 — \tan\alpha\tan\beta} \\ \\ & \ tan (\ alpha — \ beta) = \ frac {\ tan \ alpha — \ tan \ beta} {1 + \ tan \ alpha \ tan \ beta} \end{выровнено} $$ 92\альфа} \\ \\ & \left|\tan\frac{\alpha}{2}\right| = \ sqrt {\ frac {1- \ cos \ alpha} {1 + \ cos \ alpha}} \\ \\ & \тангенс(-\альфа) = -\тангенс\альфа \end{выровнено} $$
Рейтинг
★ ★ ★ ★ ★5,0/5 (1×)
9Калькулятор касательной линии 0000 — MathCracker.
comИнструкции: Используйте этот калькулятор, чтобы вычислить касательную для данной функции в заданной точке, показывая все шаги. Пожалуйста, введите функцию и соответствующий пункт в поле формы ниже.
Об этом калькуляторе касательной линии 92 — x + 1 и т. д. Точка может быть любым допустимым числовым выражением, например 1/2 например.
Затем, когда необходимая информация предоставлена и она действительна, вам нужно нажать «Рассчитать», чтобы получить все шаги уравнения касательной линии, показанные на ты.
Наука изобилует приложениями касательной прямой. Также называется первым порядком или линейным приближением,
это имеет действительно глубокое значение в физике и технике,
где идея основного вклада в изменение (часть первого порядка) раскрывает много информации о процессе.
Что такое касательная
Проще говоря, касательная — это линия, пересекающая кривую, но пересекающая ее только в одной точке (по крайней мере локально). Эта касательная построена зафиксировав точку \(x_0\), а затем взяв другую точку \(x_1\).
Затем, построив линию, проходящую через точки \((x_0, f(x_0))\) и \((x_1, f(x_1))\, мы получим то, что называется секущей , как показано на график ниже:
Наконец, мы приближаем точку \(x_1\) к \(x_0\), и получаем касательную:
Шаги для нахождения касательной геометрически
- Шаг 1: Определите функцию f(x), с которой вы хотите работать, и точку x0. Вам нужны оба
- Шаг 2: Точка (x0, f(x0)) будет на кривой функции f(x). Постройте это
- Шаг 3: Выберите точку (x1, f(x1)), для x1, которая отличается от x0 (может быть слева или справа от x). Сюжет
- Шаг 4: Нарисуйте линию, проходящую через точки (x0, f(x0)) и (x1, f(x1))
- Шаг 5: Выберите точку x2, которая находится посередине между x0 и x1, и проведите линию, проходящую через точки (x0, f(x0)) и (x2, f(x2))
- Шаг 6: Повторите этот процесс несколько раз
Этот графический метод поможет вам получить приблизительное представление о том, как выглядит касательная, но является приблизительным (если только функция f(x) не является линейной).
Формула касательной линии
Метод аппроксимации с использованием секущих может дать вам представление о том, что вы ищете, но, к счастью, существует точная формула для вычисления касательная к функции в точке \(x_0\). Формула:
\[\displaystyle y = f(x_0) + f'(x_0) (x — x_0) \]
Просто, да? Проще говоря, эта формула говорит о том, что касательная — это линия, проходящая через точку \((x_0, f(x_0))\) и имеет наклон \(m = f'(x_0)\)
Шаги для применения формулы касательной
- Шаг 1: Определите функцию f(x) и точку x0
- Шаг 2: Вычислить значение функции в точке x0, равное f(x0)
- Шаг 3: Вычислите производную f(x) в точке x0, поэтому вам нужно f'(x0)
- Шаг 4: Непосредственно применить формулу касательной \(y = f(x_0) + f'(x_0) (x — x_0)\)
Получив уравнение прямой, вы можете преобразовать его в формат, наиболее подходящий для данной ситуации.
Наклон касательной
Одним из основных выводов является то, что наклон касательной в точке \(x_0\) в точности равен \(f'(x_0)\), который является производной в точке \( х_0\). Это обеспечивает ясная и чрезвычайно полезная интерпретация производной в геометрических терминах.
Это соединение позволяет найти уравнение касательной к заданной кривой в заданной точке, просто взглянув на производную функции.
Пример: касательная 92-2x+1\) в точке \(x_0 = 2\) равно:
\[у = 2x-3 \]
Следующий график получен для данной функции и ее касательной в точке \(x_0 = 2\):
Пример: уравнение касательной линии
Что представляет собой касательная в точке x = 1/2 для функции \(f(x) = \sin(x) + 1\)?
Решение:
Была предоставлена следующая функция: \(\displaystyle f(x)=\sin\left(x\right)+1\), для которой нам нужно вычислить ее производную.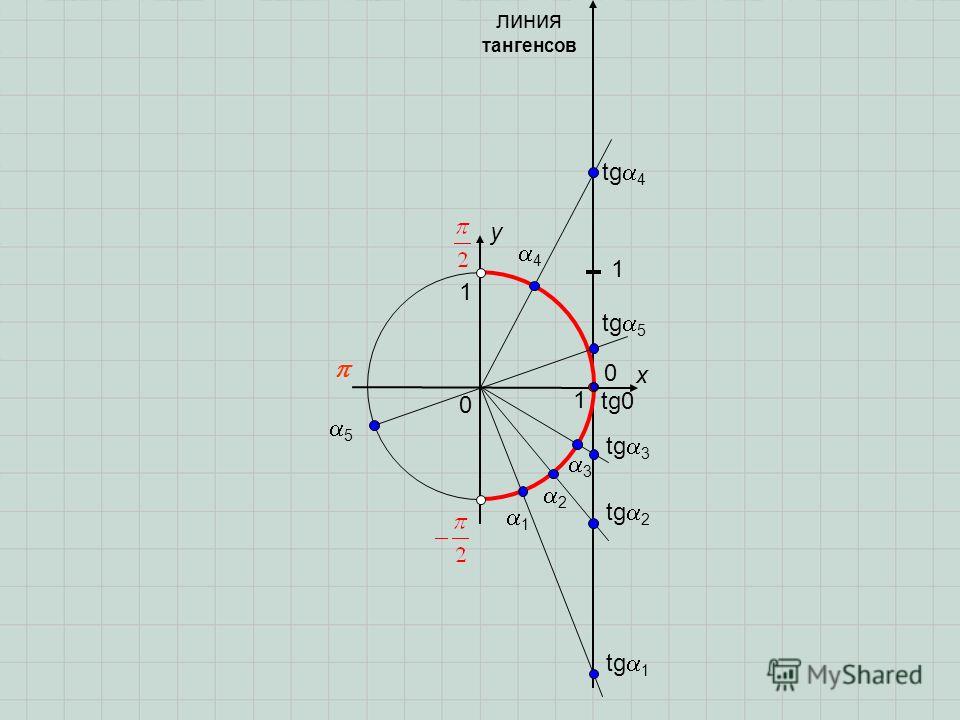
Функция пришла уже упрощенной, поэтому мы можем перейти непосредственно к вычислению ее производной:
\( \displaystyle \frac{d}{dx}\left(\sin\left(x\right)+1\right)\ )
По линейности мы знаем, что \(\frac{d}{dx}\left( \sin(x)+1 \right) = \frac{d}{dx}\left(\sin(x)\right )+\frac{d}{dx}\left(1\right)\), поэтому подставьте это:
\( \displaystyle = \,\,\)
\(\displaystyle \frac{d}{ dx}\left(\sin\left(x\right)\right)+\frac{d}{dx}\left(1\right)\)
Производная константы равна 0, тогда:
\( \displaystyle = \,\,\)
\(\displaystyle \frac{d}{dx}\left(\sin\left(x\right)\right)\)
Прямое дифференцирование: \ (\frac{d}{dx}\left( \sin\left(x\right) \right) = \cos\left(x\right)\)
\( \displaystyle = \,\,\)
\(\displaystyle \cos\left(x\right)\)
Касательная линия : Мы находим, что соответствующее уравнение касательной линии в точке \(x_0 = \frac{1}{2}\) дается по:
\[y = y_0 + f'(x_0)(x — x_0) \]
Но в этом конкретном случае \(\displaystyle y_0 = f(x_0)\), что означает, что нам нужно подставить значение точки \(x_0 = \frac{1}{2}\) в функция, поэтому мы получаем:
\[y_0 = f(x_0) = f\left(\frac{1}{2}\right) = \sin\left(\frac{1}{2}\right)+1\]
Теперь, проделывая то же самое с производной, для \(x_0 = \frac{1}{2}\) находим
\[f'(x_0) = f’\влево(\frac{1}{2}\right) = \cos\left(\frac{1}{2}\right) \]
Теперь нам просто нужно подставить значения, так что мы находим, что
\[y = y_0 + f'(x_0)(x — x_0) \]\[\Стрелка вправо y = \sin\left(\frac{1}{2}\right)+1+\cos\left(\frac {1}{2}\right)\left(x-\frac{1}{2}\right) = x\cos\left(\frac{1}{2}\right)-\frac{1}{ 2}\cos\left(\frac{1}{2}\right)+\sin\left(\frac{1}{2}\right)+1 \]
Вывод : Мы находим, что соответствующая касательная, которую мы ищем, в соответствующей точке \(x_0 = \frac{1}{2}\) задается как
\[y = x\cos\left(\frac{1}{2}\right)-\frac{1}{2}\cos\left(\frac{1}{2}\right)+\sin\ влево(\frac{1}{2}\вправо)+1 \]
Графически:
Пример: Другая касательная
Какова касательная в точке x = 0 для функции \(f(x) = \cos(x)\)? Имеет ли этот результат смысл?
Решение: Заметьте, что \(f'(x) = -\sin(x)\), поэтому \(f'(0) = -\sin(0) = 0\).
То есть касательная имеет наклон m = 0 при x = 0,
поэтому уравнение касательной выглядит просто \(y = y_0 = \cos(0) = 1\). Это имеет смысл, потому что в этом случае касательная является горизонтальной линией.
Другие калькуляторы дифференцирования
Некоторые люди могут утверждать, что дифференцирование является относительно простым упражнением и что использование калькулятора производных может не понадобиться, но на самом деле вычисление производных все еще может быть довольно громоздким и может потребовать длительных алгебраических вычислений.
Если у вас есть выражение с более чем одной переменной, чтобы найти производную, вам нужно будет определить, являются ли переменные независимыми друг от друга, и в этом случае вы используете частные производные, или если есть уравнение, связывающее переменные в этом случае вам нужно будет использовать неявное дифференцирование.
Две основные области дифференциального исчисления — интегрирование и дифференцирование, и обе они широко применяются повсюду.