Онлайн разложение вектора по векторам: Онлайн калькулятор. Разложение вектора по базису

Разложение вектора по трём некомпланарным векторам. Задачи 10 класс онлайн-подготовка на Ростелеком Лицей

 

 

Тема: Векторы в пространстве

 

Урок: Разложение вектора по трем некомпланарным векторам. Задачи

 

Основные определения по теме векторы

 

 

Определение:

 

Вектором называется направленный отрезок. У вектора  точка А – начало вектора, точка В – конец.

Для вектора важна не только длина, но и направление.

Определение:

Коллинеарными называют векторы, принадлежащие одной и той же или параллельным прямым.

Коллинеарные векторы могут быть сонаправленными и противонаправленными.

Определение:

Равными называют коллинеарные сонаправленные векторы, длины которых равны.

Любой вектор можно единственным образом отложить от произвольной точки.

Для сложения векторов применяются правила треугольника, параллелограмма, многоугольника и параллелепипеда.

При умножении вектора на положительное число его длина умножается на это число, а направление остается неизменным. При умножении вектора на отрицательное число его длина умножается на это число, а направление меняется на противоположное.

Новым для векторов в пространстве относительно векторов на плоскости является понятие компланарности.

Определение:

Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости.

 

Разложение вектора на плоскости и в пространстве

 

 

Мы знаем, что если заданы два неколлинеарных вектора на плоскости, то любой третий вектор на той же плоскости можно однозначно разложить по этим векторам (рис. 1, 2):

 

Рис. 1. Векторы на плоскости

Рис. 2. Разложение вектора через два неколлинеарных

Данный факт легко доказывается. Пусть . Из точки С проводим прямую CB, параллельно вектору . Получаем вектор , коллинеарный вектору . Аналогично из точки С проводим прямую CА, параллельно вектору . Получаем вектор , коллинеарный вектору . Это означает, что существуют такие два числа х и у, причем единственные, что:

Вопрос на понимание компланарности векторов. Если вектор  можно представить в виде , где х и у – конкретные числа, то векторы  и  компланарны.

Если заданы три некомпланарных вектора, то мы можем однозначно разложить любой заданный четвертый вектор через три заданных. Например, заданы некомпланарные векторы  и . Тогда любой вектор  можно представить в виде суммы: , где х, у и z – конкретные числа, причем для заданного вектора единственные. Эти числа называются коэффициентами разложения.

 

Решение задачи на разложение вектора по трем некомпланарным

 

 

Задача 1: дан куб  с ребром m. Точка К – середина ребра . Разложить вектор  по векторам  и найти его длину.

 

Решение: построим заданный куб (рис. 3).

Рис. 3. Куб, задача 1

Векторами  и  задается плоскость квадрата .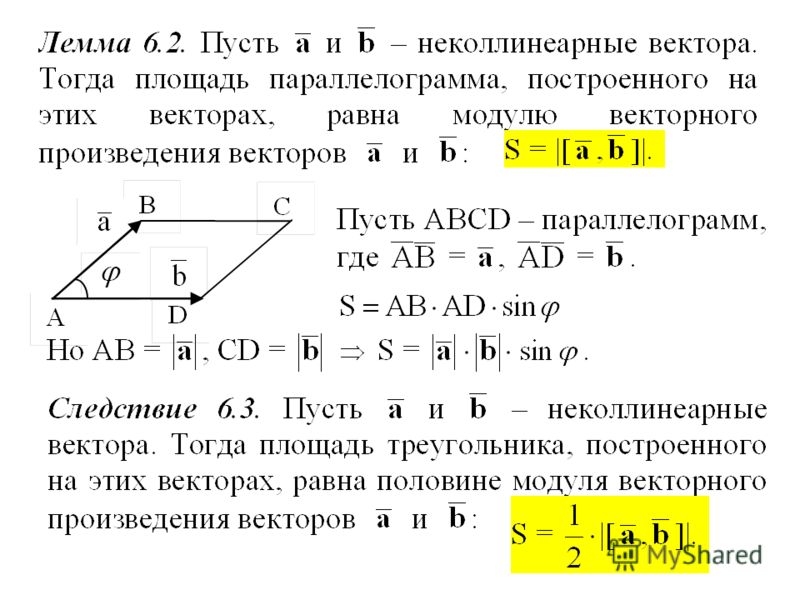 Третий вектор  не лежит в этой плоскости, отсюда заключаем, что три заданных вектора ,  и  некомпланарны, и мы можем выразить через них искомый вектор . Найдем вектор  по правилу многоугольника. Очевидно, что в данной задаче для этого есть множество способов, но мы выбираем самый короткий путь: . вектор  мы по условию обозначили как вектор . Вектор  согласно свойствам куба равен вектору , обозначенному за вектор .

вектор  составляет половину вектора , так как точка К – середина ребра  по условию: . Вектор  согласно свойствам куба, равен вектору , обозначенному как вектор . Имеем:

Так, заданный вектор выражен через три некомпланарных вектора. Осталось найти его длину. Здесь нужно применить теорему Пифагора. Рассмотрим прямоугольный треугольник . Он прямоугольный потому, что ребро  перпендикулярно всей плоскости основания , значит и любой прямой в этой плоскости, значит прямой . Один из катетов  равен m как ребро куба. Катет  найдем из другого прямоугольного треугольника – , где он уже является гипотенузой. Здесь катет  равен m как ребро куба. Катет  равен , так как точка К – середина ребра . Имеем:

Вернемся к первому треугольнику:

 

Задача на усвоение понятия компланарности

 

 

Задача 2: векторы ,  и  компланарны. Компланарны ли векторы ,  и ? Компланарны ли векторы ?

 

Решение: тот факт, что векторы ,  и  компланарны, означает, что, будучи отложенными от одной точки, они расположены в одной плоскости (рисунок 4.а). Это значит, что один из векторов, например, вектор , можно однозначно разложить по двум другим: . Очевидно, что векторы ,  и  тоже компланарны, т. к. умножение вектора на положительное число не меняет его направления, а меняет только длину, и векторы останутся в той же плоскости (рисунок 4.б).

Рис. 4. а

Рис. 4. б

Очевидно, что тройка векторов  также компланарна, потому что всякая линейная комбинация компланарных векторов есть вектор, им компланарный.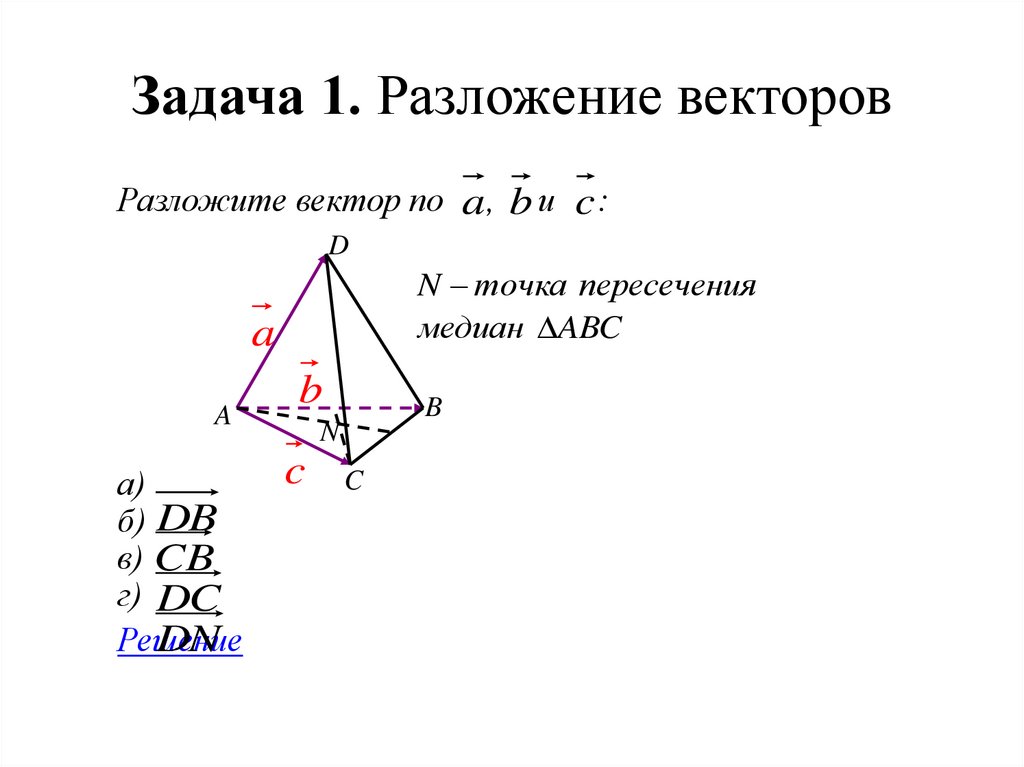

Мы имеем три вектора, компланарных заданным векторам, очевидно, что они компланарны между собой.

Итак, мы вспомнили все основные определения и теоремы касательно векторов в пространстве, подробно остановились на понятии компланарности векторов и рассмотрели типовые задачи на эту тему.

 

Список литературы

1. И. М. Смирнова, В. А. Смирнов. Геометрия. 10-11 класс: учебник для учащихся общеобразовательных учреждений (базовый и профильный уровни) / И. М. Смирнова, В. А. Смирнов. – 5-е изд., испр. и доп. – М.: Мнемозина, 2008. – 288 с.: ил.
2. Шарыгин И. Ф. Геометрия. 10-11 класс: Учебник для общеобразовательных учебных заведений / Шарыгин И. Ф. – М.: Дрофа, 1999. – 208 с.: ил.
3. Е. В. Потоскуев, Л. И. Звалич. Геометрия. 10 класс: Учебник для общеобразовательных учреждений с углубленным и профильным изучением математики /Е. В. Потоскуев, Л. И. Звалич. – 6-е изд., стереотип. – М.: Дрофа, 2008. – 233 с.: ил.

 

Домашнее задание

1.  – параллелепипед. М – точка пересечения  и . . Разложите вектор  по трем заданным векторам.
2. в тетраэдре DABC O – точка пересечения медиан треугольника АВС, точка F принадлежит ребру AD, причем . Разложите вектор  по векторам .
3. используя векторы, докажите, что диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал Webmath.exponenta.ru (Источник).
2. СтудопедиЯ (Источник).
3. Научная библиотека (Источник).

 

Разложение вектора по базису — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

Система
векторов
пространства Rn, если
называется
базисом
1
Векторы этой системы линейно независимы.
2
Любой вектор из этого пространства линейно
выражается через векторы этой системы.
ТЕОРЕМА
Линейно независимая система векторов
в пространстве Rn является базисом
тогда и только тогда, когда число
векторов этой системы равно

размерности пространства n.
ТЕОРЕМА
Разложение любого вектора в данном
базисе является единственным.
ДОКАЗАТЕЛЬСТВО:
Пусть система векторов
a1 , a2 …an
является базисом.
Предположим, что вектор b может быть
представлен в виде линейной комбинации
базисных векторов двумя способами:
b 1a1 2 a2 … n an
b 1a1 2 a2 … n an
Причем наборы чисел
1 , 2 . 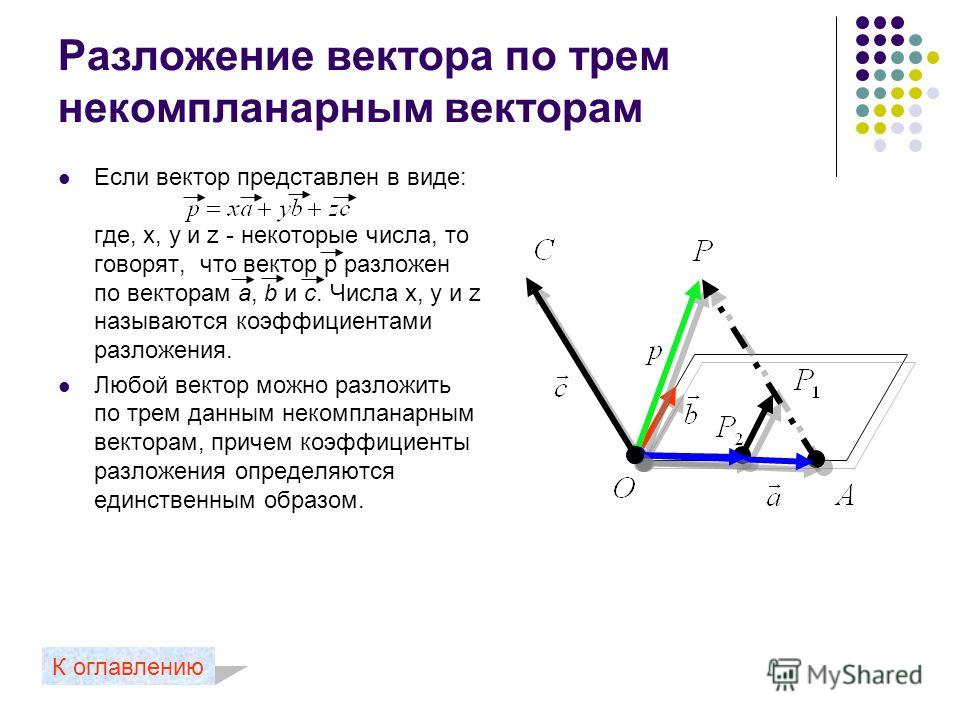.. n и 1 , 2 … n
не совпадают.
Вычтем одно равенство из другого:
( 1 1 )a1 ( 2 2 )a2 … ( n n )an 0
Получили, что линейная комбинация векторов
системы равна нулю, т.е. Система оказалась
линейно зависимой, что противоречит условию
теоремы.
Следовательно, разложение вектора в данном
базисе будет единственным.
Таким образом, в произвольном базисе
пространства Rn любой вектор из этого
пространства представим в виде разложения
по базисным векторам:
b 1a1 2 a2 … n an
Причем, это разложение является единственным
для данного базиса.
Числа
1 , 2 … n
называются координатами вектора b
в базисе
a1 , a2 …an
Чтобы найти коэффициенты разложения αi в
случае
произвольного
базиса,
нужно
приравнять соответствующие координаты
линейной комбинации и координаты вектора b
Пусть базисные вектора заданы в координатной
форме:
a1 (a11 , a12 …a1n )
…
an (an1 , an 2 …ann )
И задан вектор
b (b1 , b2 . 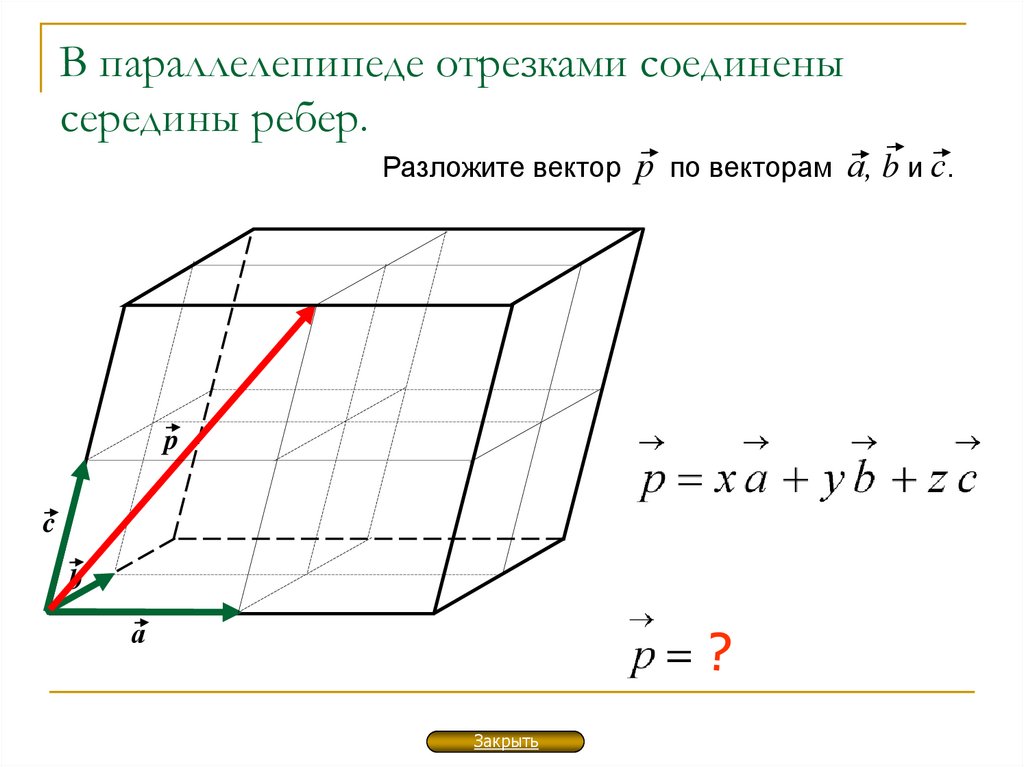..bn )
Тогда получим систему линейных уравнений:
1a11 2 a12 … n a1n b1
a a … a b
1 21
2 22
n 2n
2
…
1an1 2 an 2 … n ann bn
Решая эту систему,
разложения
находим
1 , 2 … n
коэффициенты
Рассмотрим базис пространства Rn , в котором
каждый вектор ортогонален остальным
векторам базиса:
e1 , e2 …en
(ei , e j ) 0 i j
i, j 1,2…n
Такой базис называется ортогональным.
Они хорошо представимы на плоскости и в
пространстве:
e3
e2
e1
e1
e2
Найдем разложение вектора b
в ортогональном базисе:
b 1e1 2e2 … n en
Умножим обе части равенства на e1
(b , e1 ) 1 (e1 , e1 ) 2 (e2 , e1 ) … n (en , e1 )
Поскольку
все
вектора
ортогональны, то
(ei , e j ) 0
базиса
i j
взаимно
Имеем:
(b , e1 ) 1 (e1 , e1 )
(b , e1 ) (b , e1 )
1 2
(e1 , e1 )
e1
В общем случае:
(b , ei )
i 2
ei
Частным случаем ортогонального
является ортонормированный базис.
базиса
В этом случае все базисные вектора имеют
единичную длину:
ei 1
Тогда коэффициенты разложения имеют вид:
i (b , ei )
i 1,2…n

English     Русский Правила

Задания на векторную декомпозицию онлайн

Найти величину вектора v⃗=(−3,4)?\vec{v}=(-3,4)?v=(−3,4)?

555 262\кв{6}26​ 666 363\кв{6}36​

Показать объяснение

View wiki

Точка P лежит на стороне BC и делит ее внутренне в отношении 1 : 4 в равностороннем треугольнике ABCABCABC ниже. Пусть AB⃗=a⃗,\vec{AB}=\vec{a},AB=a, AC⃗=b⃗,\vec{AC}=\vec{b},AC=b, AP⃗=c⃗.\vec{AP} =\vec{c}. AP=c. затем c⃗\vec{c}c можно выразить как xa⃗+yb⃗.x\vec{a}+y\vec{b}.xa+yb. Какое из следующих чисел равно x×yx\times yx×y?

14\dfrac{1}{4}41​ 15\dfrac{1}{5}51​ 425\dfrac{4}{25}254​ 45\dfrac{4}{5}54​

Показать объяснение

View wiki

GGG — центр тяжести треугольника OABOABOAB, показанного ниже. Пусть OA⃗=a⃗,OB⃗=b⃗,\vec{OA}=\vec{a}, \vec{OB}=\vec{b},OA=a,OB=b и GA⃗=c⃗\vec{GA} =\vec{c}GA=c. Тогда c⃗\vec{c}c можно представить как xa⃗−yb⃗.x\vec{a}-y\vec{b}.xa−yb. Что из следующего равно x−yx — ​​yx−y?

12\dfrac{1}{2}21​ 13\dfrac{1}{3}31​ 23\dfrac{2}{3}32​ 32\dfrac{3}{2}23​ 9\circ∘ к югу от востока, то на сколько градусов к северу от востока пилот должен наклонить самолет, тем самым противодействуя скорости ветра, чтобы самолет летел прямо на восток?

ПРИМЕЧАНИЕ. 2×2+y2+z2.

Показать объяснение

Просмотр вики

Калькулятор тензорного произведения ⊗ Вектор/Матрица

Поиск инструмента

Найдите инструмент в dCode по ключевым словам:

Просмотрите полный список инструментов dCode

Tensor Product

Инструмент для выполнения вычисления тензорного произведения, своего рода умножения, применимого к тензорам, векторам или матрицам.

Результаты

Тензорный продукт — dCode

Теги: Матрица

Поделиться

dCode и многое другое

dCode бесплатен, а его инструменты являются ценным подспорьем в играх, математике, геокэшинге, головоломках и задачах, которые нужно решать каждый день!
Предложение ? обратная связь? Жук ? идея ? Запись в dCode !

Векторный тензорный продукт ⊗

Вектор 1

Загрузка…
(если это сообщение не исчезнет, ​​попробуйте обновить эту страницу)

Вектор 2

Идет загрузка. ..
(если это сообщение не исчезнет, ​​попробуйте обновить эту страницу)

См. также: Матричный продукт — продукт Кронекера

Матричный тензорный продукт ⊗

Матрица 1

Загрузка…
(если это сообщение не исчезнет, ​​попробуйте обновить эту страницу)

Матрица 2

Загрузка…
(если это сообщение не исчезнет, ​​попробуйте обновить эту страницу)

См. также: Калькулятор матриц — Продукт Кронекера

Ответы на вопросы (FAQ)

Что такое тензорное произведение? (Определение)

тензорное произведение — это метод умножения линейных карт, который вычисляет внешнее произведение каждой пары тензоров.

Для матриц/векторов/тензоров тензорное произведение также называется произведением Кронекера.

Как вычислить тензорное произведение матриц?

Из 2 матриц $ A=\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix} $ и $ B=\begin{bmatrix}b_{11} &b_{12}\\b_{21}&b_{22}\end{bmatrix} $ тензорное произведение отмечено $ \otimes $ рассчитывается $$ A \otimes B = \begin{bmatrix}a_{11}\begin{bmatrix}b_{11}&b_{12}\\b_{21}&b_{22}\end{ bmatrix}&a_{12}\begin{bmatrix}b_{11}&b_{12}\\b_{21}&b_{22}\end{bmatrix} \\ a_{21}\begin{bmatrix}b_{11}&b_ {12}\\b_{21}&b_{22}\end{bmatrix} & a_{22}\begin{bmatrix}b_{11}&b_{12}\\b_{21}&b_{22}\end{bmatrix }\end{bmatrix} = \begin{bmatrix}a_{11}b_{11}&a_{11}b_{12}&a_{12}b_{11}&a_{12}b_{12}\\a_{11} b_{21}&a_{11}b_{22}&a_{12}b_{21}&a_{12}b_{22}\\a_{21}b_{11}&a_{21}b_{12}&a_{22} b_{11}&a_{22}b_{12}\\a_{21}b_{21}&a_{21}b_{22}&a_{22}b_{21}&a_{22}b_{22}\end{bmatrix } $$ 9T $ путем преобразования векторов в матрицы путем транспонирования второго вектора, чтобы иметь вектор-строку и вектор-столбец.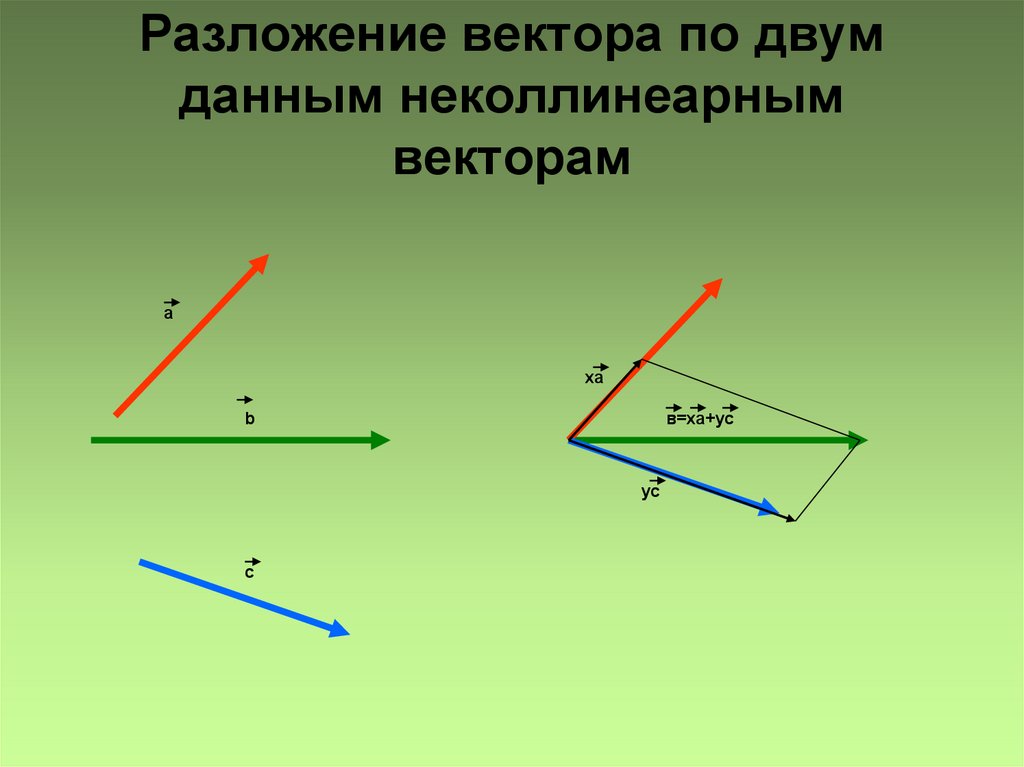

Результирующий тензор будет иметь размерность произведения количества элементов в исходных векторах.

$$ \vec{a} \otimes \vec{b} = \begin{bmatrix}a_1 b_1 & a_1 b_2 & \cdots &a_1 b_m \\ a_2 b_1 & a_2 b_2&\cdots &a_2 b_m \\ \vdots & \vdots & \ddots & \vdots \\ a_n b_1 & a_n b_2 & \cdots & a_n b_m \end{bmatrix} $$

Пример: $$ \begin{bmatrix} 1 \\ 2 \end{bmatrix} \otimes \begin{bmatrix} 3 & 4 \end{bmatrix} = \begin{bmatrix} 3 & 4 \\ 6 & 8 \end{bmatrix} $$

Исходный код

dCode сохраняет за собой право собственности на исходный код «Tensor Product». За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Tensor Product», апплета или фрагмента (конвертер, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор) или «Tensor Product» функции (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т.