Точка разрыва 1 рода: Точки разрыва функции онлайн

5.09.2 Разрывы функции и их классификация

Признаком непрерывности функции в точке служит равенство , которое подразумевает наличие трех условий:

1) определена в точке ;

2) ;

3) .

Если хотя бы одно из этих требований нарушено, то называют точкой разрыва функции. Другими словами, точкой разрыва называется точка, в которой эта функция не является непрерывной. Из определения точек разрыва следует, что точками разрыва функции являются:

А) точки, принадлежащие области определения функции, в которых теряет свойство непрерывности,

Б) точки, не принадлежащие области определения , которые являются смежными точками двух промежутков области определения функции.

Например, для функции точка есть точка разрыва, так как функция в этой точке не определена, а функция имеет разрыв в точке , являющейся смежной для двух промежутков и области определения и не существует (см пункт 5.7.2).

Для точек разрыва принята следующая классификация.

1) Если в точке имеются конечные и , но , то называется

Точкой разрыва первого рода, при этом называют Скачком функции.

Пример 2. Рассмотрим функцию

Разрыв функции возможен только в точке (в остальных точках она непрерывна как всякий многочлен).

Найдем , . Так как односторонние пределы конечны, но не равны друг другу, то в точке функция имеет разрыв первого рода. Заметим, что , следовательно функция в этой точке непрерывна справа (рис. 2).

2) Точками разрыва второго рода называются точки, в которых хотя бы один из односторонних пределов равен или не существует.

Пример 3. Функция непрерывна для всех значений , кроме . Найдем односторонние пределы: , , следовательно – точка разрыва второго рода (рис. 3).

3) Точка называется Точкой устранимого разрыва, если .

Разрыв «устраним» в том смысле, что достаточно изменить (доопределить или переопределить) значение функции в этой точке, положив , и функция станет непрерывной в точке .

Пример 4. Известно, что , причем этот предел не зависит от способа стремления к нулю. Но функция в точке не определена. Если доопределим функцию, положив , то она окажется непрерывной в этой точке (в остальных точках она непрерывна как частное непрерывных функций и ).

Пример 5. Исследовать на непрерывность функцию .

Решение. Функции и определены и непрерывны всюду, в том числе и в указанных промежутках. Исследуем точку стыка промежутков :

, , . Получаем, что , откуда следует, что в точке функция непрерывна.

Определение. Функция, непрерывная на промежутке за исключением конечного числа точек разрыва первого рода или устранимого разрыва, называется кусочно-непрерывной на этом промежутке.

< Предыдущая		Следующая >

19. Точки разрыва функции и их классификация

Точки, в которых нарушается непрерывность функции, называются точками разрыва этой функции. Если х=х₀ — точка разрыва функции у=ƒ(х), то в ней не выполняется по крайней мере одно из условий первого определения непрерывности функции, а именно:

1. Функция определена в окрестности точки х₀, но не определена в самой точке х₀.

Например, функция у1/(x-2)  не определена в точке х₀=2 (см. рис. 120).

2. Функция определена в точке х₀ и ее окрестности, но не существует предела ƒ(х) при х→х₀. Например, функция

определена в точке х₀=2    (ƒ(2)=0), однако в точке х₀=2 имеет разрыв (см. рис. 121), т. к. эта функция не имеет предела при х→2:

3. Функция  определена в  точке  х₀ и  ее  окрестности,  существует но  этот  предел  не  равен  значению   функции  в  точке x₀:

Например, функция (см. рис. 122)

Здесь x₀=0 — точка разрыва:  a g(х₀)=g(0)=2.

Все точки разрыва функции разделяются на точки разрыва первого и второго рода. Точка разрыва х₀называется точкой разрыва первого рода функции у=ƒ(х), если в этой точке существуют конечные пределы функции слева и справа (односторонние пределы), т. е.

 

При этом:

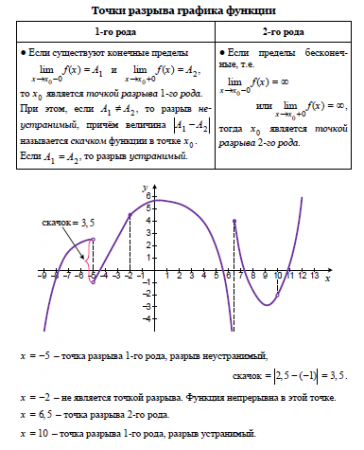
а) если А₁=А₂, то точка х₀ называется точкой устранимого разрыва; б) если А₁≠А₂, то точка х₀ называется точкой конечного разрыва.

Величину |A₁-А₂| называют скачком функции в точке разрыва первого рода.

Точка разрыва х₀ называется точкой разрыва второго рода функции у=ƒ(х), если по крайней мере один из односторонних пределов (слева или справа) не существует или равен бесконечности.

1. Обратимся к функциям, рассмотренным выше (см. рис. 120). у=1/(x-2)  x₀=2 -точка разрыва второго рода.

2. Для функции

х₀=2 является точкой разрыва первого рода, скачок функции равен |1-0|=1.

3. Для функции

х₀=0 является точкой устранимого разрыва первого рода. Положив g(х)=1 (вместо g(х)=2) при х=0, разрыв устранится, функция станет непрерывной

<< Пример 19. 3

Дана функция ƒ(х)=|x-3|/(x-3). Найти точки разрыва, выяснить их тип.

 Решение: Функция ƒ (х) определена и непрерывна на всей числовой оси, кроме точки х=3. Очевидно,

Следовательно,

Поэтому в точке х=3 функция имеет разрыв пещюго рода. Скачок функции в этой точке равен 1-(-1)=2.

1. Производной функции f(x) в точке x₀ называется предел отношения приращения функции Δf в этой точке к приращению аргумента Δх, когда последнее стремится к нулю (бесконечно мало). Lim_Δx→0 (Δf(x₀)/Δx)=lim_Δx→0 ((f(x+Δx)-f(x₀))/Δx)=f`(x₀)

Характеризует скорость изменения функции (в данной точке) – физический смысл.

ƒ'(х) = tga = k, производная ƒ'(х) β точке х равна угловому коэффициенту касательной к графику функции у = ƒ(х) в точке, абсцисса которой равна х. В этом заключается

геометрический смысл производной.

2. Если функция дифференцируема (имеет производную) в некоторой точке, то она непрерывна в ней (обратное не всегда верно).

Пусть функция у=ƒ(х) дифференцируема в некоторой точке х. Следовательно, существует предел

По теореме о связи функции, ее предела, имеем ∆y/∆x=ƒ'(х)+а, где α→0 при ∆х→0, то есть ∆у=ƒ'(х)•∆х+а•∆х. Переходя к пределу, при ∆х→0, получаем

А это и означает, что функция у=ƒ(х) непрерывна в точке х.

То есть бесконечно малому приращению аргумента соответствует бесконечно малое приращение ф-ции.

исчисление — Свойства набора разрывов 1-го рода

спросил 6 лет, 10 месяцев назад

Изменено 6 лет, 10 месяцев назад

Просмотрено 198 раз

$\begingroup$

Предположим, $f$: $[0, 1]\longrightarrow\mathbb{R}$ удовлетворяет $$\lim\limits_{x\longrightarrow a^-} f(x)=\lim\limits_{x\longrightarrow a^+} f(x)$$ везде, и что это значение конечно.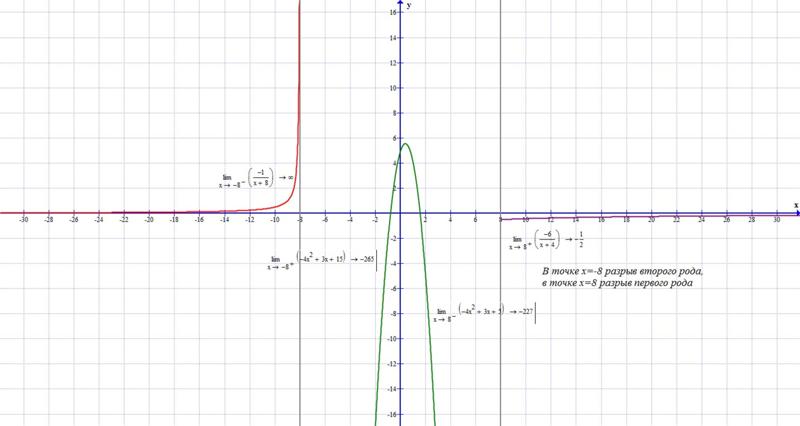

Множество разрывов $f$ должно быть счетным, но насколько большим (в любом другом смысле) оно может быть?

В частности, работает ли любое предписанное счетное $D\subset [0, 1]$?

• исчисление
• реальный анализ

$\endgroup$

3

$\begingroup$

Да, любое счетное множество $D\subset [0,1]$ работает. Если $D$ конечна, мы можем взять характеристическую функцию $\chi_D$, поэтому в дальнейшем будем считать $D$ бесконечной. Конструкция аналогична функции Тома.

Пусть $(d_n)_{n \in \mathbb{N}\setminus \{0\}}$ — перечисление $D$. Определите

$$f(x) = \begin{cases} \frac{1}{n} &, x = d_n \\ 0 &, x\notin D.\end{cases}$$

Тогда $f $ имеет всюду односторонний предел $0$ и разрывен во всех $x\in D$ (и нигде больше).

$\endgroup$

$\begingroup$

Вот ответ на связанный вопрос, основанный на этом.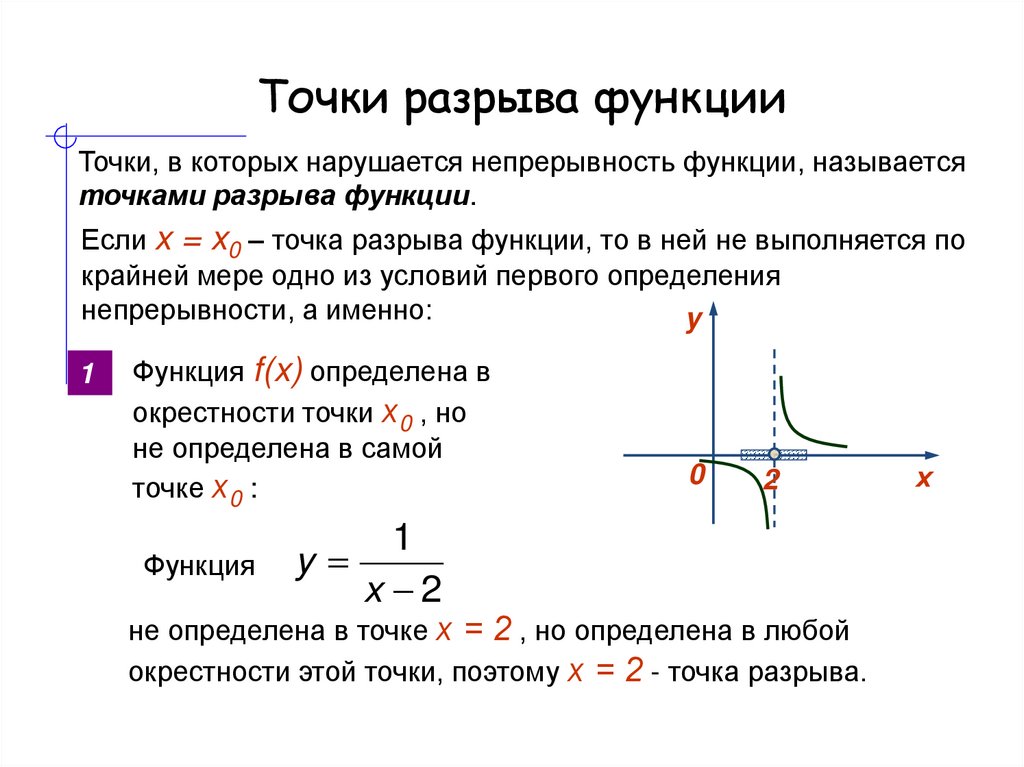 n}=f( а_н) $$

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

типов разрывов / разрывных функций

Содержание:

1. Что такое прерывистая функция?
2. График разрывной функции
3. Поиск разрывов
4. Типы разрывов
   • Основной разрыв (неустранимый)
   • Бесконечный разрыв
   • Прыжок (Шаг) Разрыв
   • Колеблющийся разрыв
   • Съемный (отверстие) разрыв

Прерывистая функция функция, которая не является непрерывной в одной или нескольких точках. Большинство функций, как это ни удивительно, так или иначе разрывны [1].

Быть «непрерывным в каждой точке» означает, что в каждой точке a:

1. Функция существует в этой точке. Если вы можете вставить x-значение в свою функцию, и она вернет значение, в этот момент она будет непрерывной.
2. Предел функции при переходе x в точку a существует. Другими словами, все значения функции, окружающие точку «а», приближаются к одному и тому же числу.
3. И (1), и (2) равны.

В обозначениях мы можем записать это как:

На простом языке это означает, что функция проходит через каждую точку, и каждая точка близка к следующей: нет резких скачков (в отличие от разрывов скачков) . Когда вы рисуете график, вы можете рисовать функцию слева направо, не отрывая карандаша от бумаги.

Прерывистая функция — это функция, для которой вы должны оторвать карандаш от бумаги хотя бы один раз во время рисования.

Скачок разрыва. Графически разрывная функция будет иметь либо дыру — одно пятно или несколько пятен, где функция не определена, — либо скачок, где значение f(x) быстро меняется («скачет») когда вы переходите из одного места в другое, бесконечно близкое.

Вертикальная асимптота. Функция будет приближаться к этой линии, но никогда не коснется ее. У нее также может быть асимптота, линия, где по мере приближения функция стремится к бесконечности. Функция никогда не сливается с этой линией, хотя может приближаться бесконечно близко.

Вернуться к началу

Если вашу функцию можно записать в виде рациональной функции (т. е. в виде дроби), любые значения x, при которых знаменатель стремится к нулю, будут разрывами вашей функции. Это места, где ваша функция не определена из-за деления на ноль.

Если у вас есть кусочная функция, точка, где заканчивается одна часть и другая часть, также является хорошим местом для проверки разрыва.

В противном случае самый простой способ найти разрывы в вашей функции — это построить ее график. Обратите внимание на любые дыры, асимптоты или скачки. Все они представляют собой разрывы, и достаточно одного разрыва, чтобы сделать вашу функцию разрывной.

Типы разрывов.

Классификация типов разрывов сложнее, чем кажется, из-за того, что разные авторы классифицируют их по-разному. Например:

• Некоторые авторы упрощают типы до двух общих терминов: съемный (отверстия) и неустранимый (скачки, бесконечные и существенные разрывы не могут быть удалены, поскольку они слишком далеко друг от друга или дикие в своем поведении). .
• Существенные разрывы (которые резко прыгают, когда функция приближается к пределу) иногда называют «неустранимый разрыв», исключающий скачки и бесконечность из определения неустранимого.
• Некоторые авторы также включают «смешанные» разрывы в качестве типа разрыва, где разрыв представляет собой комбинацию более чем одного типа.

Вывод: не существует «единой» системы классификации типов разрывов, с которой все согласны. Какую систему вы используете, будет зависеть от используемого вами текста и предпочтений вашего преподавателя. Следующий список следует воспринимать как руководство, а не как установленную систему классификации камней.

Вернуться к началу

1. Существенный разрыв
2. Существенная сингулярность

Существенный разрыв (также называемый вторым типом или неустранимым разрывом) — это разрыв, который резко скачет по мере приближения к пределу. Это затрудняет удаление разрыва (отсюда альтернативное название «неустранимый» разрыв) и выполнение любых вычислений функции.

Существенный разрыв считается «наихудшим» из видов разрыва. Это потому, что поведение вокруг пределов должно быть , но ненормально, невозможно вычислить, а иногда просто безумно. На очень коротком расстоянии может быть много разрывов прыжков, или вы вообще не сможете зафиксировать какое-либо поведение. Графические калькуляторы могут не помочь (из-за аберрантного поведения), и вам, возможно, придется прибегнуть к ручке и бумаге, чтобы понять график.

Подтипы

Существенные разрывы (т. е. неустранимые разрывы) можно далее разбить на два типа разрывов в зависимости от того, являются ли односторонние пределы ограниченными или неограниченными (Bauldry, 2011):

• Ограниченный : колебательный разрыв . Паттерн вблизи предела подпрыгивает вверх и вниз, никогда не формируя паттерн, который можно было бы зафиксировать.
• Неограниченный : бесконечный разрыв . Пределы существуют, но они бесконечны и становятся больше по мере приближения к пределу.

Простые (устранимые) разрывы также можно разделить на два подтипа:

• Устранимый разрыв имеет зазор, который можно легко заполнить, поскольку предел одинаков с обеих сторон.
• Разрыв прыжка в точке имеет существующие пределы, но разные по обе стороны от разрыва.

В любом из этих двух случаев можно количественно определить предел и устранить разрыв; Существенный разрыв не может быть определен количественно. Обратите внимание, что разрывы скачков, которые происходят на кривой , не могут быть удалены и поэтому необходимы (Rohde, 2012).

Вернуться к началу

Существенная сингулярность — это плохо работающая «дыра» в неаналитической сложной функции, которую невозможно удалить/отремонтировать. Другими словами, нет простого способа превратить функцию с существенной особенностью в непрерывную и дифференцируемую.

Этот тип сингулярности подобен своему вещественному аналогу: существенному разрыву. С этими типами сингулярностей/разрывов трудно иметь дело из-за их патологического поведения в определенный момент.

Существенные сингулярности являются одним из

трех типов сингулярностей в комплексном анализе. Два других — это полюса (изолированные сингулярности) и устранимые сингулярности, обе из которых ведут себя относительно хорошо. Существенных особенностей по исключению: если не полюс и не съемная сингулярность, то существенная.

Пример функции с существенной особенностью

Функция exp (1/z) имеет существенную особенность при z = 0, где функция не определена (из-за деления на ноль). На данный момент функция не имеет предела, поэтому убрать сингулярность невозможно.
График оттенка-яркости exp(1/z) с центром в основной сингулярности в нуле. Функция ведет себя по-разному в зависимости от того, с какой стороны вы приближаетесь к функции. Кредит: Функтор Салат | Викисклад./>

В терминах ряда Лорана

Существенные разрывы можно идентифицировать, глядя на поведение ряда Лорана, представляющего окрестности вокруг сингулярности. В частности, особенность существенна, если главная часть ряда Лорана имеет бесконечно много ненулевых членов (Крамер, nd).
Основная часть серии Laurent.

В начало

Бесконечный разрыв имеет один или несколько бесконечных пределов — значения, которые становятся все больше и больше по мере приближения к разрыву в функции. Бесконечный разрыв — это подтип существенных разрывов, которые представляют собой широкий набор плохо ведущих себя разрывов, которые нельзя удалить.
Типы разрывов. Бесконечный разрыв справа имеет значения функции, которые продолжают стремиться к бесконечности.

Эта функция стремится к бесконечности только при x = 0 с одной стороны (справа), но она по-прежнему классифицируется как бесконечная неоднородность. Важно отметить, что только одна сторона должна стремиться к ±бесконечности, чтобы разрыв должен быть классифицирован как бесконечный. Одна сторона может достигать определенного значения функции или быть неопределенной.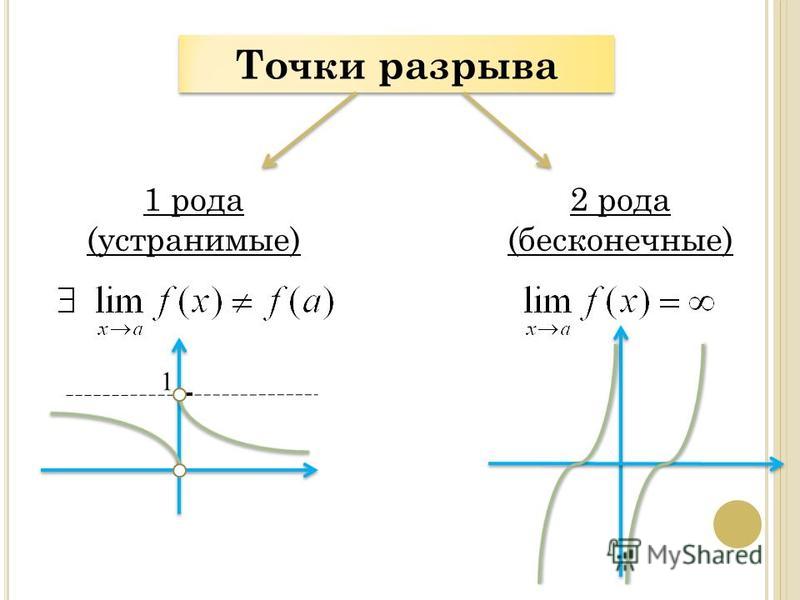 Но пока одна сторона представляет собой либо отрицательную бесконечность, либо положительную бесконечность, это бесконечный разрыв.

Бесконечность может быть положительной или отрицательной

Функция может двигаться к бесконечности в одном направлении или в разных направлениях. Например, функция может идти в направлении:

• Положительная бесконечность с обеих сторон,
• Отрицательная бесконечность с обеих сторон или
• Одна сторона может уйти в отрицательную бесконечность, а другая — в положительную бесконечность.

График y = 1/x, стремящийся как к отрицательной, так и к положительной бесконечности при x = 0,

График 1/x ² , который стремится к отрицательной бесконечности в обоих направлениях при x = 0. (Графики, сделанные с помощью калькулятора Desmos)

Наверх разрывность

или разрывность первого рода ) — разрыв в графе, который скачкообразно перескакивает.

Следующий график переходит в начало координат (x = 0).

Для того, чтобы разрыв был классифицирован как скачок, пределы должны:

1. существуют как (конечные) действительные числа по обе стороны от пробела, а
2. не могут быть равны. Если пределы равны , то это дыра, а не скачок (формальнее дыры называются устранимыми разрывами).

Разница между двумя пределами составляет скачка в этой точке (Сохраб, 2003). Удивительно, но количество прыжков в любой конкретной функции исчисляемо; Другими словами, невозможно иметь бесконечное количество переходов даже в непрерывных функциях (Сохраб, 2003).

Когда происходят прыжки?

Скачок разрыва обычно происходит только в кусочных или ступенчатых функциях.

Кусочные функции определяются на последовательности интервалов.

Пример ступенчатой ​​функции (красный график). Эта конкретная ступенчатая функция непрерывна справа.

Ступенчатые функции являются подвидом кусочных функций, в которых имеется ряд одинаковых «лестничных» шагов.

Обозначение разрывов скачка

В обозначениях разрыв скачка может быть определен в терминах пределов по обе стороны от скачка. Допустим, у вас есть функция f(t), которая имеет разрыв скачка при t = 10. Следующие обозначения описывают скачок:

Левый предел:

Правый предел:

Скачок можно определить через два предела:
f (10 +) – f (10 -) .

Прыжок против шага

Хотя термин «прерывистость ступени» является довольно распространенным, он имеет тенденцию быть неформальным. Обычное название такого типа разрыва — скачкообразный разрыв. Однако, когда это выглядит как физический шаг, имеет смысл называть его так (а не прыжком, который наводит на мысль о большом разрыве по горизонтальной оси, что не всегда так!). Какой термин вы используете, обычно зависит от вашего личного выбора или выбора вашего инструктора.

Примеры разрыва ступени / разрыва скачка

Функция

имеет разрыв скачка при x = 1. В этой точке нет единого предела; хотя существуют односторонние пределы L ^– и L ⁺ , потому что они не равны. Если бы вы представили, что идете по кривой, вам пришлось бы серьезно подпрыгнуть, когда вы доберетесь до нее. Это показано ниже.

На приведенном ниже графике есть разрыв шага в -4, потому что левый и правый пределы существуют и не бесконечны, но различны. В точке 2 имеется разрыв еще одной ступени; правый предел равен -1, а левый предел равен 5. Однако разрыв в точке 4 не является ступенчатым разрывом, поскольку левый и правый пределы равны. Это еще один тип разрыва — съемная несплошность .

Вернуться к началу

Колеблющийся разрыв (также называемый бесконечно колеблющимся разрывом ) резко прыгает (т.е. колеблется) по мере приближения к пределу; нет никакого способа «починить» разрыв. Его часто определяют методом исключения: это не устранимый разрыв, разрыв скачка или бесконечный разрыв. Поэтому вы можете увидеть, что его называют «другим» типом разрыва.

Ограниченные и неограниченные функции

Осциллирующие разрывы ограничены. Другими словами, их колебания остаются между определенными линиями. Например, функция может быть ограничена между верхней точкой y = 3 и нижней точкой y = -3. Если функция неограничена с одной или обеих сторон, это бесконечный разрыв. Другими словами, функция должна быть полностью ограничена во всех точках, чтобы имел место осциллирующий разрыв. Кроме того, односторонних ограничений вообще не существует.

Пример

Возможно, неудивительно, что многие осциллирующие функции имеют по крайней мере один осциллирующий разрыв.
Невозможно определить предел функции sin(1/x) в нуле.

Осциллирующие разрывы являются подтипом существенных или неустранимых разрывов.

Как найти колеблющийся разрыв

Самый простой способ определить этот тип разрыва — непрерывно увеличивать график: независимо от того, сколько раз вы увеличиваете масштаб, функция будет продолжать колебаться вокруг предела.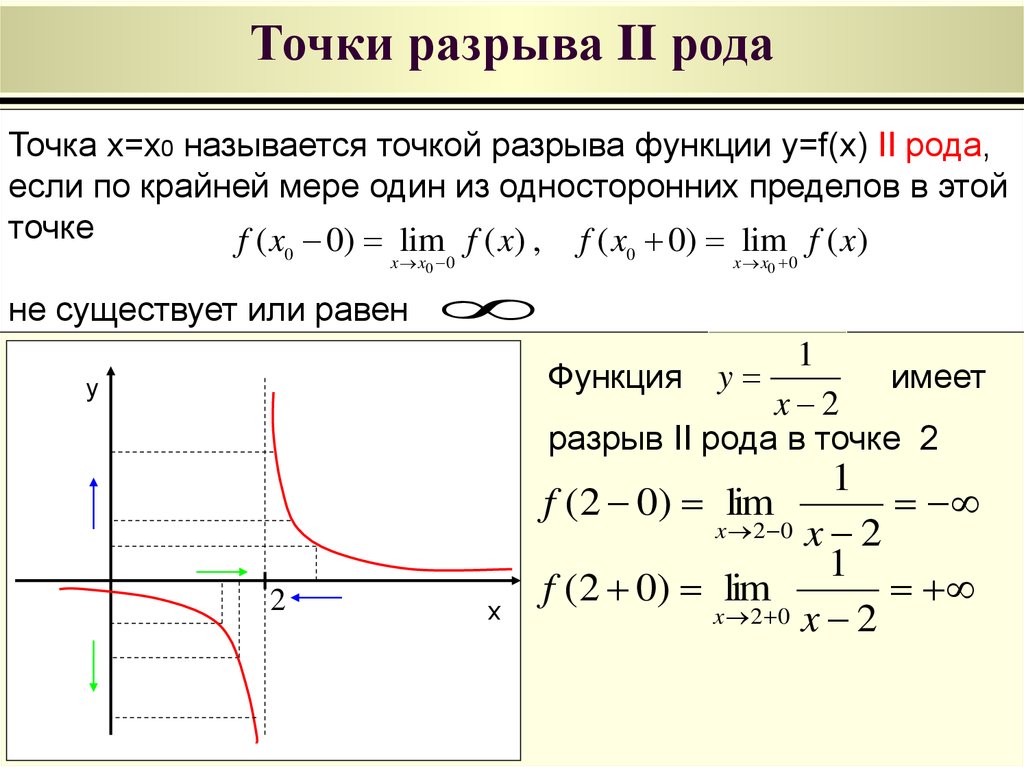

На TI-89 постройте график функции в маленьком окне (например, окно [-2,2,1]*[-2, 2, 1]. Нажмите клавишу Zoom, выберите функцию Zoom Box ( 1:ZBox) и нажмите Enter. Отметьте верхний левый угол поля, нажав Enter, затем увеличьте поле с помощью клавиш со стрелками. Нажмите Enter еще раз. Повторяйте до бесконечности. Полные инструкции и изображения того, как это сделать, см. в разделе Модуль 8: Непрерывность на веб-сайте TI

Вернуться к началу

съемная неоднородность (также называемая разрыв отверстия ) имеет зазор, который можно легко заполнить, поскольку предел одинаков с обеих сторон. Вы можете думать об этом как о маленьком отверстии на оси X.

Устранимый разрыв иногда называют точечным разрывом , потому что функция не определена в одной (крохотной точке).

Удаление отверстия

Отверстие называется устранимым разрывом, потому что его можно заполнить или удалить, немного переопределив значения функции. Просто заменить значение функции в отверстии значением предела.

Пример

Возьмем следующую кусочную функцию:

На графике функция выглядит так:

Обратите внимание на небольшое отверстие в точке x = 0,5. Значение функции здесь (то есть значение y) равно 4, что создает проблему, если мы хотим выполнить дальнейшие вычисления с функцией (например, интегрирование).

На графике вы можете просто нарисовать дырку и удалить точку в (0,5, 4). Математически, если мы возьмем значения y очень близко к дыре, мы сможем заполнить ее таким образом. Кусочная функция задается как h(x) = 1,5 + 1/(x + 0,25) для каждой точки , кроме 0.5, так что мы можем игнорировать эту причуду и просто использовать функцию, чтобы заполнить дыру. Подставляя x = 0,5 в функцию, получаем:
h(x) = 1,5 + 1 / (0,5 + 0,25) = 17/6 &приблизительно; 2.83.

Типы разрывов: Ссылки

Изображение: Functor Salad [CC BY-SA 3.0 (http://creativecommons.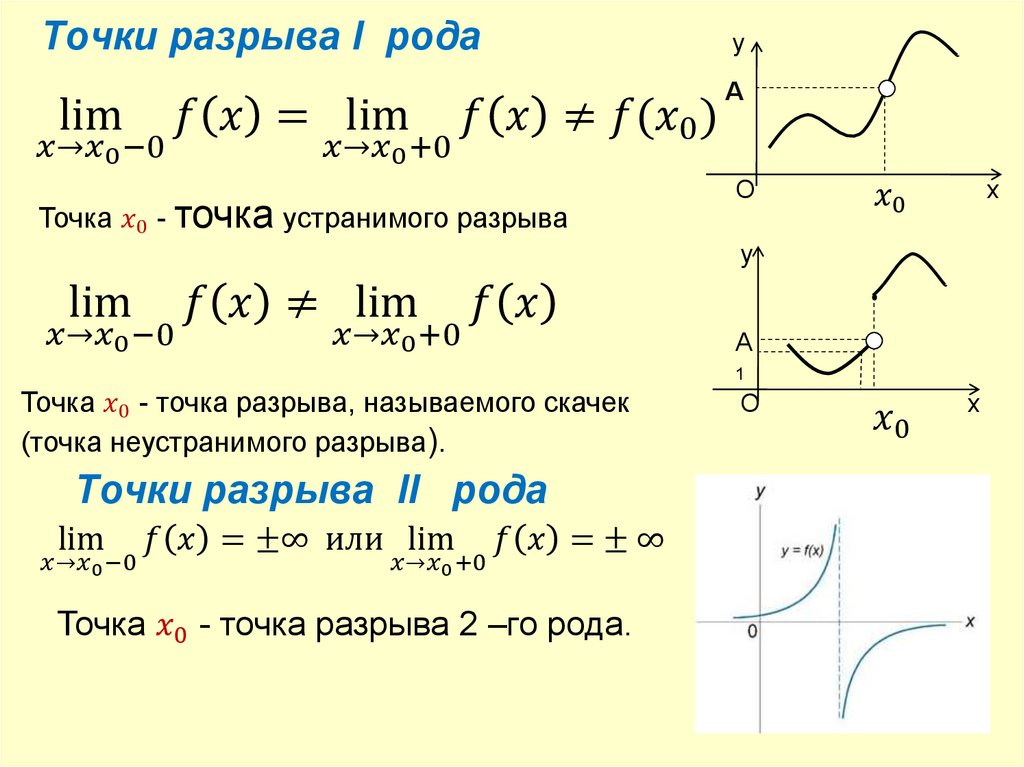 org/licenses/by-sa/3.0/)]

[1] Drago et. др. «Букет» разрывных функций для начинающих в математическом анализе. Получено 13 июля 2021 г. с: http://ceadserv1.nku.edu/longa//classes/mat420/days/highlights/PathologicalFunctions.pdf
[2] Раздел 1.4. Непрерывность. Получено 13 июля 2021 г. с: https://www.math.uh.edu/~beatrice/143114.pdf

Bauldry, W. (2011). Введение в реальный анализ: образовательный подход. Джон Уайли и сыновья.
Богли, В. (1996). Устранимые разрывы. Получено 28 октября 2019 г. с: https://oregonstate.edu/instruct/mth351/cq/Stage4/Lesson/removable.html
Григориу, М. Стохастическое исчисление: приложения в науке и технике.
Бесконечный разрыв. Проверено 29 октября., 2019 г. из: http://www-math.mit.edu/~djk/18_01/chapter02/example03.html
Бесконечные разрывы. Получено 28 октября 2019 г. с: https://ocw.mit.edu/courses/mathematics/18-01sc-single-variable-calculus-fall-2010/1.-дифференциация/part-a-definition-and-basic- rules/session-5-discontinuity/MIT18_01SCF10_Ses5c.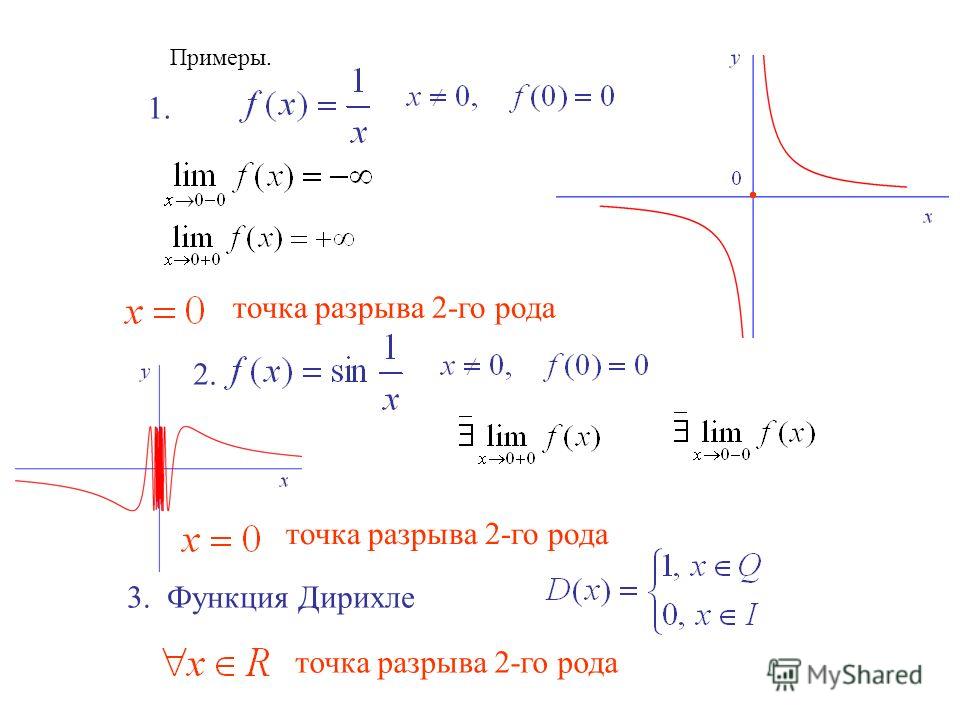 pdf
Кнопп, К. «Существенные и несущественные особенности или полюса». § 31 в Теории функций, части I и II, два тома, связанные как один, часть I. Нью-Йорк: Дувр, стр. 123–126, 19.96.
Крамер, П.Л.С. Примеры. Получено 22 августа 2020 г. с: http://eaton.math.rpi.edu/faculty/Kramer/CA13/canotes111113.pdf
Кранц С.Г. «Устранимые особенности, полюса и существенные особенности». §4.1.4 в Справочнике комплексных переменных. Бостон, Массачусетс: Биркхойзер, с. 42, 1999.
Rohde,U. и другие. (2012). Введение в дифференциальное исчисление: систематические исследования с инженерными приложениями для начинающих. Джон Уайли и сыновья.
Сохраб, Х. (2003). Базовый реальный анализ. Springer Science and Business Media.
Томсон, Б. и др., (2008). Элементарный реальный анализ, Том 1. ClassicalRealAnalysis.com.
Вайнман, А. и Раджагопал, К. (2000). Механическая реакция полимеров: введение. Издательство Кембриджского университета.

Калькулятор Desmos.

УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен .