MathOnWeb — Электронная книга по алгебре — Pre-Algebra
- Факторы числа
- Наибольший общий делитель двух чисел
- Наименьшее общее кратное двух чисел
- Дроби и как их складывать, вычитать, умножать и делить
- Десятичная запись
- Экспоненциальное представление
- Порядок действий
- Невидимые кронштейны
1.1 — Факторы числа
Числа, которые нас интересуют факторингом, натуральные числа 1, 2, 3, … Используется слово фактор как существительное и глагол. факторов (существительное) числа числа, которые делятся без остатка на число. Например, делителями числа 12 являются числа 1, 2, 3, 4, 6 и 12. (Обратите внимание, что наименьший множитель всегда равен 1, а наибольший множитель равен всегда само число.)
К коэффициенту (глагол) число означает его выражение
как произведение меньших чисел.
Число, которое нельзя разложить на множители, называется 9.0026 простое число . Разложить число на , значит записать его как произведение простых чисел. Это также называется простой факторизацией .
Вот несколько примеров чисел в полностью факторизованной форме:
100 = 2 · 2 · 5 · 518 = 2 · 3 · 3
29 = 29 (29 — простое число)
Наибольший общий делитель (НОД) двух чисел
Если мы посмотрим на два или более числа, то у них будут общие множители. Например
множители 40 равны 1, 2, 4, 5, 8, 10, 20 и 40,и множители 50 равны 1, 2, 5, 10, 25 и 50.
Мы показали общие факторы красным цветом. наибольший общий делитель является наибольшим из всех общие факторы. Наибольший общий делитель 40 и 50 равен 10. Вот еще несколько примеров величайших общих факторов:
GCF 24 и 30 равен 6GCF 24, 30 и 33 равен 3
GCF 7 и 21 равен 7
GCF 7 и 13 равен 1
Вот процедура для нахождения наибольшего общего делителя двух или более числа. Проиллюстрируем числами 24 и 30. Разложите числа полностью и выстройте их множители. (Этим мы имеем в виду поставить общие множители друг под другом, и когда любое число отсутствует множитель, тогда оставьте для него место.)
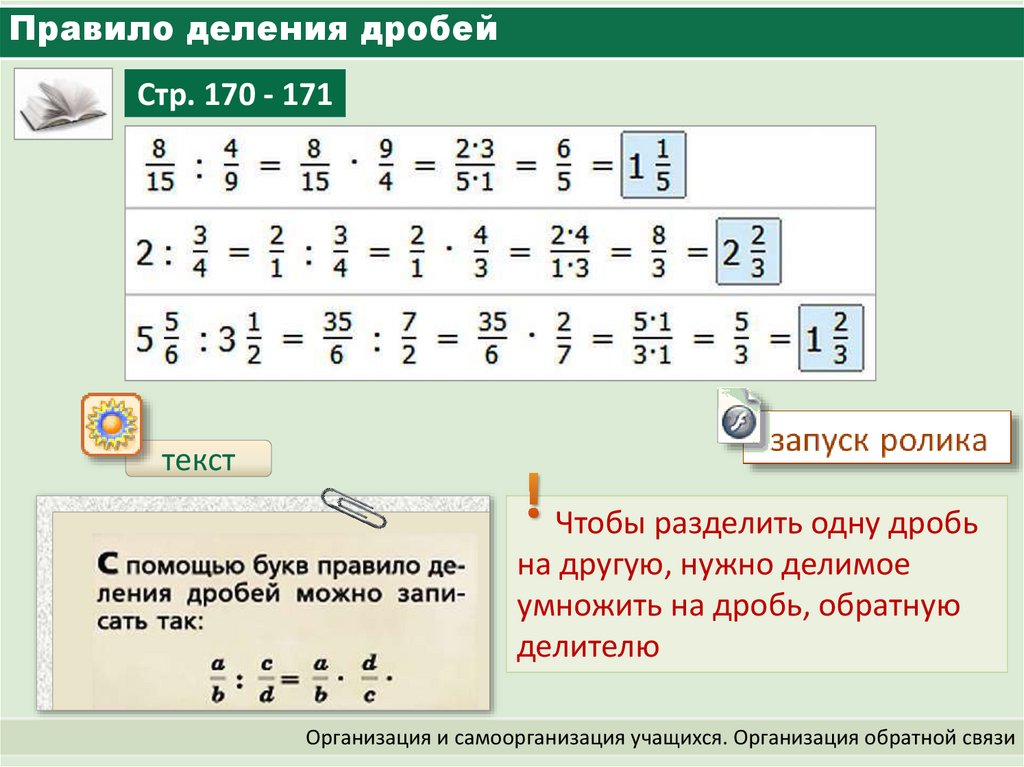
Наименьшее общее кратное (НОК) двух чисел
Кратные числа — это числа, которые имеют это число в качестве множителя. Например, числа, кратные 5, равны 5, 10, 15, 20, 25, …
. Если мы посмотрим на два или более числа, то у них будут общие кратные. Например
числа, кратные 3, равны 3, 6, 9, 12, 15, 18, 21, 24, 27, …, а числа, кратные 4, равны 4, 8, 12, 16, 20, 24, 28, …
Мы показали красным цветом общие кратные чисел 3 и 4. Их 12, 24, … Самые маленькие из общее кратное называется наименьшим общим кратным . Вот еще несколько примеров наименьших общих кратных:
LCM 9 и 20 равен 180LCM 2, 3 и 5 равен 30
LCM 7 и 21 равен 21
Вот процедура, чтобы найти наименьшее общее кратное двух или более
числа. Проиллюстрируем числами 24 и 30.
Разложите числа полностью и выстройте их множители. (Этим
мы имеем в виду поставить общие множители друг под другом, и когда любое число
отсутствует множитель, тогда оставьте для него место.)
Наименьшее общее кратное должно содержать все делители, которые в том или ином числе, но множители не используются дважды, когда они являются общими для обоих чисел. Выстроились вот так легко определить общие факторы. Наименьшее общее кратное должно быть 2 · 3 · 2 · 2 · 5 = 120,
Вам часто нужно найти факторы, которые каждый из исходных числа должны быть умножены, чтобы получить LCM. Выстроились вот так их легко заметить. Они просто отсутствуют факторы. В этом примере 24 нужно умножить на недостающие 5, и 30 нужно умножить на недостающие 2 · 2 или 4.
1.2 — Дроби и как их складывать, вычитать, умножать и делить
Обозначение дробей
Дроби (или обыкновенных дробей ) используются для описания части целого объекта.
Существует несколько обозначений дробей:
a называется числителем , а b называется знаменателем . Обозначение означает, что мы разбиваем объект на b равных частей и у нас есть и таких штук. Часть или часть объекта, который у нас есть это / б . Например, если мы разобьем пирог на 4 равных куска и берем 1 кусок то у нас получается 1/4 часть пирога:
Эквивалентные дроби
Обратите внимание, что мы получаем одинаковое количество пирога как в предыдущем примере, если разделить пирог на 8 равных частей и получить 2 из них:
Такие дроби, как 1/4 и 2/8, имеющие одинаковое значение, называются эквивалентные дроби . Этот пример предлагает следующий метод для
проверка на равенство двух дробей.
| Две дроби равны , если умножить числитель и знаменатель одной дроби на то же целое число дает другая дробь. |
Например, 4/5 и 24/30 эквивалентны, потому что мы можем начать с 4/5. и умножьте числитель и знаменатель на 6, чтобы получить 24/30:
Движение в обратном направлении (от 24/30 до 4/5) предполагает следующий метод. для сокращения дроби до младших членов или до простейшей эквивалентной дроби :
| Приведение дроби к наименьшему члену или к простейшей эквивалентной дроби , полностью разложить как числитель, так и знаменатель (т. е. на простые числа). Затем сократите каждый множитель, который встречается как в числителе, так и в числителе.  и знаменатель. Осталось простейшая эквивалентная дробь . |
Например вот как уменьшить дробь 24/42 это самое простое эквивалентная дробь, а именно 4/7:
Неправильные дроби, смешанные дроби и длинное деление
Дробь, у которой числитель меньше знаменателя, называется правильной дробью и дробь, у которой числитель больше знаменателя, называется неправильная дробь . Пример неправильной дроби 7/4. Используя пример пирога, это означает, что вы сломали множество пирогов, каждый из которых разделен на 4 равные части, и у вас есть 7 таких частей:
Неправильные дроби иногда выражаются в виде смешанной дроби , которая представляет собой сумму
целое число и правильная дробь, но без знака +. Например, 7/4 в обозначении смешанной дроби.
выглядит так:
Обозначение смешанной дроби не используется в этой книге Algebra Help
Длинное деление — это метод преобразования неправильной дроби в смешанную. Проиллюстрируем метод на дроби . Выполните следующие шаги:
- Установите формат длинного деления, а именно .
- Так как 5 в 9 идет 1 раз, напишите «1» над 9, напишите 1 × 5 или «5» ниже 9 и вычтите 5 из 9, чтобы получить разницу в 4, например:
- Затем опустите 2 следующим образом: Вот что мы на самом деле сделали: «1» и «5» находятся в
десятки место, поэтому они
на самом деле представляют числа 10 и 50, как показано здесь: Поэтому мы фактически показали, что
.
- Теперь повторите весь процесс с остатком 42. Поскольку 5 в 42 идет 8 раз, напишите «8» над 2, напишите 8 × 5 или «40» ниже 42, и вычтите 40 из 42, чтобы получить остаток 2, например:
- Это показывает, что . Поскольку остаток 2 меньше делителя 5, это наш окончательный вариант. результат смешанной фракции.
Некоторые специальные дроби
Есть несколько специальных дробей, которые важно распознать:
- . Любое число n можно превратить в дробь, написав ее над знаменателем 1.
- . Все, что делится само на себя, равно 1. Мы называем это UFOO (a u seful f orm o f o ne). Подробнее об НЛО позже.
- Если числитель дроби кратен знаменателю то дробь равна целому числу. Примером является .
- не определено для любого числителя n . Деление на ноль в математике запрещено.
- . Нулевой числитель не является проблемой. Эта дробь равна 0, .
Деление на ноль в математике запрещено.Сложение или вычитание дробей
На этом рисунке показано, что 2/8 пирога плюс 3/8 пирога равняются 5/8 пирога:
Дроби, имеющие одинаковые знаменатели, называются , как и дроби . Если подумать об этом примере, то следующая процедура добавления или вычитание одинаковых дробей очевидно:
| Чтобы сложить или вычесть одинаковые дроби (дроби, имеющие общий знаменатель) , просто сложите или вычтите числители и приведите результат к общему знаменателю, так: |
Но что, если дроби не имеют общего знаменателя?
Ответ заключается в том, что они должны быть затем преобразованы
к эквивалентным дробям, которые делают имеют общий знаменатель.
Процедура проиллюстрирована на этом примере:
Шаги:
- Найдите наименьшее общее кратное двух знаменатели 24 и 30. Применительно к дробям это число называется наименьшим общим знаменатель (ЖК-дисплей). В этом примере ЖК-дисплей равен 120, .
- Преобразуйте каждую дробь в эквивалентную дробь, имеющую ЖК 120 в знаменателе. Для этого в данном примере умножьте числитель и знаменатель первой дроби на 5, а числитель и знаменатель второй дроби на 4 (показаны красным).
- Сложите числители и поместите над общим знаменателем.
Иногда есть еще один шаг. Результат всегда должен быть выражен как простейшая эквивалентная дробь, например:
Вот еще несколько примеров:
Умножение дробей
| Умножение дробей производит новую фракцию.  Умножьте числители, чтобы получить
новый числитель и умножить знаменатели, чтобы получить новый знаменатель,
так: Затем упростите, сократив новую дробь до наименьших членов.Чтобы умножить дробь на целое число, просто умножьте числитель дроби на целое число, чтобы получить новый числитель, например: Затем упростите, сократив новую дробь до наименьших членов. |
Вот пример того, почему работает первая процедура. Предположим, что есть половина пирога (т. дробь 1/2), как показано слева. Теперь предположим, что вы взяли 2/3 из этой половины пирога. (Слово «из» переводится как математическая операция «умножить».) Это означает, что вы разрезаете половину пирога на 3 равные части и берете 2 из них. В результате получается 2/6 части пирога.
Вот пример того, почему вторая процедура работает.
Предположим, вы съели 1/4 часть пирога.
и что твой друг съел в 3 раза больше пирога, чем ты. Это означает, что ваш друг
съел 3/4 пирога.
Вот еще несколько примеров умножения:
Обратные числа и деление дробей
Обратные числа играют важную роль при делении дробей. Говорят, что два числа или дроби равны 9.0026 обратны друг друга если их произведение равно 1. Например:
4/5 и 5/4 обратны, потому что8 и 1/8 обратны, потому что
| Деление дробей: Процедура заключается в замене деления на дробь на умножение на обратную дробь , например: |
Обратите внимание, что вы берете обратная дробь на дне!
| Вот почему эта процедура работает: Суть в том, что вместо того, чтобы видеть дробь, деленную на дробь, ищите одну дробь, числитель и знаменатель которой являются дробями.  На первом шаге мы умножили эту дробь на UFOO
числитель и знаменатель которого являются дробями. НЛО был
выбран так, чтобы дроби в знаменателе сокращались и давали 1. После другого
упрощение, оставившее только окончательное умножение дробей. |
Пример 1: дробь, деленная на дробь :
Пример 2: дробь, деленная на число. Обратите внимание, что мы нарисовали одну разделительную линию. длиннее другого, чтобы вы могли сказать, какая дробь и какой это номер. Первый шаг — преобразовать целое число 4 в дробь 4/1. После нескольких шагов вы получите выражение, показанное синим цветом. Если сравнить это выражение с исходным вы заметите хороший ярлык. Число 4, на которое вы делите дробь, просто становится новый множитель в знаменателе дроби.
Пример 3: Число, разделенное на дробь.
Проверьте действия. Этот пример сильно отличается от предыдущего!
1.3 — Десятичная запись
Слово десятичное означает десять . Десятичная система счисления знакома система, которая использует всего десять символов (цифр) для создания любого целого числа, независимо от того, насколько большой. Эти символы, конечно же, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.. (В отличие от двоичная система счисления использует только два символа 0 и 1 и шестнадцатеричная система счисления использует шестнадцать символов 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, чтобы создать любое число. Двоичный и шестнадцатеричный системы счисления, используемые в компьютерах.)
Для создания чисел больше 9 в десятичной системе используется разрядных значений .
Например, диаграмма разрядности справа показывает, что 3528 означает 9.
0030
| 3528 =
3 · 1000 + 5 · 100 +
2 · 10 + 8 · 1 Это потому, что 3 стоит в разряде тысяч, а 5 — в разряде тысяч. разряд сотен, 2 в разряде десятков и 8 в разряде единиц место. Обратите внимание, что по мере того, как мы двигаемся справа налево в таблице разрядов, стоимость каждого места в десять раз превышает стоимость места вправо. |
Если мы продолжим этот шаблон до справа , то мы получим показанная здесь расширенная диаграмма места:
Десятичная точка используется для отделения цифры в разряде единиц от цифры справа от него. Десятичное число 3528,74 означает:
Преобразование десятичных чисел в обозначение дроби:
Мы уже видели, что целые числа можно преобразовать в дроби.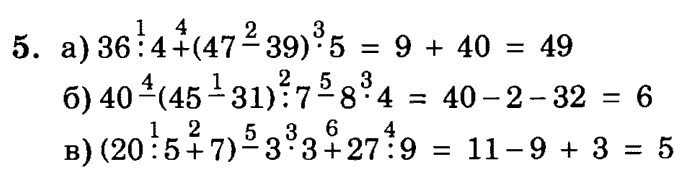
записи, просто поместив их над 1.
Десятичные числа с цифрами справа от запятой могут преобразовать в дробную форму, умножив их на УФО. Сначала определите разрядное значение самой правой цифры. Если разрядное значение — десятые, тогда умножьте на 10/10, если это сотые доли затем умножьте на 100/100 и т. д. Затем упростите числитель. Это превращает числитель в целое число. Вот некоторые примеры:
Экспоненциальное представление
Экспоненциальное представление является удобным сокращением для повторяющихся умножение. Экспоненциальное число b n означает умножить b раза на себя n раза:
b называется основанием , n называется показателем степени ,
а мы говорим что нас «повышение b до n th мощности» (кроме случаев, когда n равно 2, мы говорим, что «возводим в квадрат b »
а когда n равно 3, мы говорим, что мы «возводим в куб b »).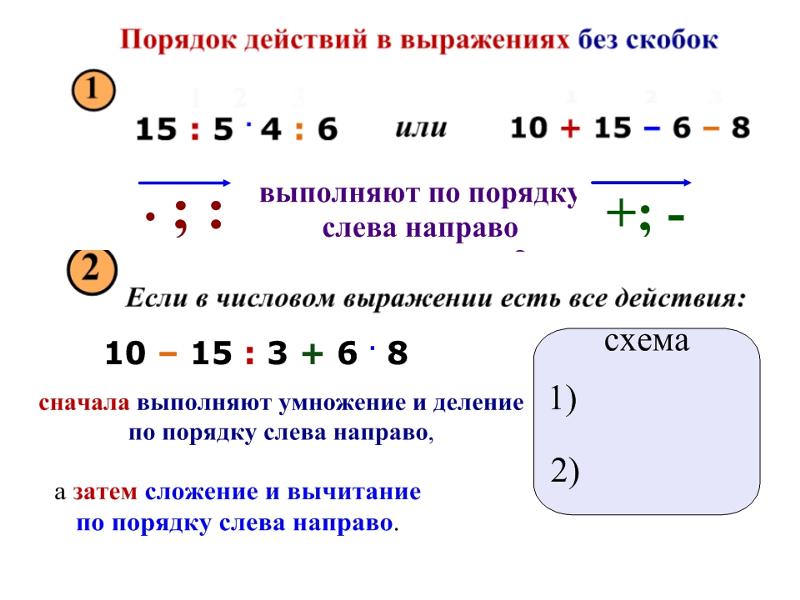
Вот два примера:
3 4 = 3 · 3 · 3 · 3 = 814 3 = 4 · 4 · 4 = 64
Важно: во избежание путаницы убедитесь, что вы пишете показательную цифру аккуратно , с показателем меньше и выше , чем основание. Например, написал ли этот человек экспоненту 3 4 или просто номер 34 ???
1.4 — Порядок действий
Выражение представляет собой набор чисел, которые объединяются с помощью таких операций, как как сложение, вычитание, умножение, деление, возведение в степень и т. д. Пример выражения:
4 + 5 · 2 3 .
В этом выражении числа 4, 5, 2 и 3 объединяются операциями сложение, умножение и возведение в степень.
В выражениях часто используются скобки ( ) как символы группировки.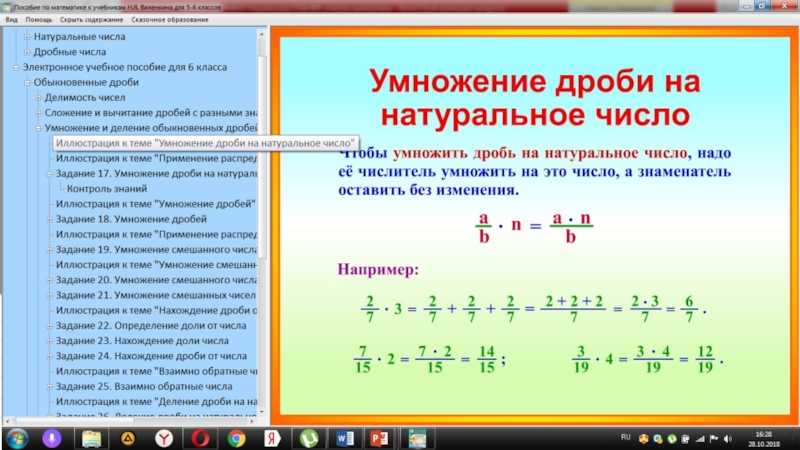
В скобках содержится
свои собственные подвыражения (таким образом создавая выражения внутри выражений).
Пример:
3 (4 + 5) + 2.
Здесь подвыражение 4 + 5. Более сложный пример:
10 (3 (4 + 5) + 2)
Это предыдущее выражение, умноженное на 10. Это выражение содержит подвыражение который сам содержит подвыражение! Тогда возникает вопрос: в каком порядке мы выполняем эти операции? Ответ дан в этой таблице:
| Порядок действий:
|
Таким образом, приведенные выше примеры упрощаются следующим образом:
Пример: 4 + 5 · 2 3 → 4 + 5 · 8 → 4 + 40 → 44
Пример: 3 (4 + 5) + 2 → 3 · 9 + 2 → 27 + 2 → 29
Пример: 10 (3 (4 + 5) + 2) → 10 (3 · 9 + 2) → 10 (27 + 2) → 10 · 29 → 290
Есть несколько сокращений, которые люди используют, чтобы запомнить таблица порядка операций. Один из них BEDMAS , что означает порядок: скобки, возведение в степень, деление и умножение, Сложение и вычитание.
Другой номер PEMDAS означает заказ: скобки, возведение в степень, Умножение и деление, Сложение и вычитание. Используйте любую аббревиатуру, которая вам больше нравится.
Невидимые кронштейны
Есть три места, где скобки обычно не отображаются, но вы должны представить, что они там есть.
Одно место является показателем в экспоненте. Два других — числитель выше
горизонтальная линия раздела и знаменатель под горизонтальной линией раздела.
Вот два примера, показывающие выражения, первый с невидимыми скобками,
а затем с видимыми скобками (показаны красным). Мы также показываем, что оценивают выражения.
Пример 1:
В этой экспоненте вы знаете, что «+2» находится в экспоненте вместе с «3». потому что оно написано меньше и выше основания и прямо возле «3». Это означает, что показатель степени должен быть равен «3+2» и должен храниться вместе, как если бы он был скобки вокруг него.
Пример 2:
В этой дроби вы знаете, что «+5» стоит в числителе вместе с «7».
потому что это написано прямо рядом с «7», а разделительная линия проходит прямо через
под оба. То же самое касается «+4» в знаменателе.
Это означает, что в числителе «7+5», а в знаменателе
«2+4», и оба должны быть вместе, как если бы вокруг них были скобки.
Примечание:
- Сравните следующие два примера с двумя приведенными выше. Разница лишь в том, что некоторые числа были немного перемещены или увеличены: Заключение: Аккуратность имеет значение!
- В приведенных выше примерах мы могли сказать, что число находится в показателе степени или в знаменателе с помощью насколько велика она была или где она была написана. Однако при вводе одного из этих выражений в В Algebra Coach (или в любой другой программе по алгебре) нельзя сделать числа меньше или больше. Все должно быть введено в одну строку, поэтому вы должны использовать квадратные скобки.
python — Преобразование дроби в строку с повторяющимися десятичными знаками в скобках
Я считаю, что неправильно то, что вы должны только проверять, является ли число ранее увиденных десятичных знаков числом длины цикла, и оно было замечено только что ранее на эту длину.
Я думаю, что лучший способ сделать это — использовать старую добрую математику.
Давайте попробуем найти способ найти десятичное представление дробей и как узнать, когда будут повторяющиеся десятичные дроби.
Лучший способ узнать, завершится ли дробь (или повторится), — это посмотреть на факторизацию (сложная задача) знаменателя.
Есть много способов найти разложение на множители, но на самом деле мы хотим знать, имеет ли это число простой делитель, отличный от 2 или 5. Почему? Ну, десятичное расширение — это просто какое-то число a / 10 * b. может быть 1/2 = 0,5 = 5/10. 1/20 = 0,05 = 5/100. и т. д.
Таким образом, делители числа 10 равны 2 и 5, поэтому мы хотим выяснить, есть ли у него какие-либо другие делители, кроме 2 и 5. Отлично, это просто, просто продолжайте делить на 2, пока оно не перестанет делиться на 2. , чем сделать то же самое с 5. Или наоборот.
Сначала мы можем захотеть узнать, делится ли оно на 2 или 5, прежде чем мы начнем серьезную работу.
def div_by_a_or_b( a, b, число):
вернуть нет (число % a) или нет (число % b)
Затем мы разделяем все пятерки, затем все двойки и проверяем, равно ли число 1
def powers_of_only_2_or_5(number):
number_to_check = [ 2, 5 ]
для n в number_to_check:
в то время как не число % n: # пока оно все еще делится на n
число = число // n # разделить на n
return number == 1 # если это 1, то оно делится только на числа в number_to_check
Я сделал это немного более полиморфным, чтобы вы могли изменить это, если хотите изменить основу. (все, что вам нужно, это множители этой базы, например, в базе 14 вы проверяете 2 и 7 вместо 2 и 5)
Теперь все, что осталось сделать, это выяснить, что мы делаем в случае незавершающегося/повторяющегося дроби.
Теперь это супер теория чисел, поэтому я оставлю вас с алгоритмом и позволю вам решить, хотите ли вы узнать больше на mathforum.org или wolfram alpha
Теперь мы можем легко сказать, будет ли дробь заканчиваться, а если нет, то какова будет длина ее цикла повторяющихся цифр.
Теперь все, что осталось сделать, это найти цикл или количество цифр, с которых он будет начинаться.
В поисках эффективного алгоритма я нашел этот пост на https://softwareengineering.stackexchange.com/, который должен быть полезен.
великое озарение — «Когда рациональное число m/n с (m,n)=1 расширяется, период начинается после s членов и имеет длину t, где s и t — наименьшие числа, удовлетворяющие 9(s+t) (mod n). »
Итак, все, что нам нужно сделать, это найти s и t:
def length_of_cycle(знаменатель):
моды = {}
для я в диапазоне (знаменатель):
ключ = 10**i % знаменатель
если ключ в модах:
вернуть [моды[ключ], я]
еще:
моды [ключ] = я
Давайте сгенерируем числа расширения
def expasionGenerator( числитель, знаменатель ):
в то время как числитель:
доходность числитель // знаменатель
числитель = (числитель % знаменатель) * 10
Будьте осторожны, используя это, так как это создаст бесконечный цикл в повторяющемся расширении (как и должно быть).
Теперь, я думаю, у нас есть все инструменты для написания нашей функции:
def the_expansion( числитель, знаменатель ):
# вернет список из двух элементов, первый из которых является расширением
# вторая - это повторяющиеся цифры после
# первый элемент первый
integer_part = [числитель // знаменатель]
числитель %= знаменатель
если div_by_a_or_b(2, 5, знаменатель) и power_of_only_2_or_5(знаменатель):
return [integer_part, [n вместо n в expasionGenerator(числитель, знаменатель)][1:],[0]]
# если нет, то повторяется
из itertools импортировать islice
length_of_cycle = длина цикла (знаменатель)
генератор = расширениеГенератор (числитель * 10, знаменатель)
# умножаем на 10, так как мы хотим пропустить части перед запятой
list_of_expansion = [n вместо n в islice (генератор, length_of_cycle[0])]
list_of_repeating = [n вместо n в islice (генератор, length_of_cycle[1])]
вернуть [целая_часть, список_расширений, список_повторяющихся]
Осталось только распечатать, это не так уж и плохо.