Онлайн решение системы неравенств с двумя переменными – Решение системы неравенств · Калькулятор Онлайн

Системы неравенств с двумя переменными

Решением неравенства с двумя переменными называется пара значений переменных, обращающие данное неравенство в верное числовое неравенство.

Определение:

Решением системы неравенств называются пара значений переменных, обращающая каждое неравенство системы в верное числовое неравенство.

Проверим, являются ли решениями системы пары чисел. Система состоит из двух неравенств, подставим значения в систему:

Получаем, что пара чисел системы а) и г) являются решениями, а пара чисел системы б) и в) — не являются решениями.

Понятно, что если каждое неравенство может иметь множество решений, то и общих решений может найтись большое количество.

Изобразим на координатной плоскости множество решений системы неравенств:

Найдём множество решений первого неравенства:

Изобразим график:

Решением будет множество точек расположенных ниже прямой.

Найдём множество решений второго неравенства:

Изобразим график уравнения:

Решением будет множество точек расположенных ниже прямой.

Изобразим множества решений неравенств в одной координатной плоскости:

Видим их общие решения, которые являются решением системы неравенств.

Изобразим на координатной плоскости множество решений системы неравенств:

Изобразим множество решений первого неравенства:

Изобразим график уравнения:

Решением неравенства будет множество точек находящихся ниже прямой.

Перейдём ко второму неравенству системы:

Изобразим график:

Решением неравенства будет множество внутренних точек круга.

Пересечение полученных множеств и является решением данной системы неравенств.

 

Изобразим на координатной плоскости множество решений системы неравенств:

Решением первого неравенства будет множество внутренних точек круга:

Решением второго неравенства будет множество, состоящее из точек, находящихся вне круга.

Пересечение полученных множеств и является решением данной системы:

Изобразим на координатной плоскости множество решений системы неравенств:

Изобразим множество решений ещё одной системы неравенств.

Решением первого неравенства будет множество точек находящихся между ветвями гиперболы. Решением второго неравенства будет множество внутренних точек круга.

Фигура, полученная в результате пересечения двух решений, представляет собой множество решений данной системы.

videouroki.net

33. Неравенства с двумя переменными и их системы

Неравенством с двумя переменными х и у Называется неравенство вида

(или знак ),

Где – некоторое выражение с данными переменными.

Решением неравенства с двумя переменными называют упорядоченную пару чисел при которой это неравенство обращается в верное числовое неравенство.

Решить неравенство – значит найти множество всех его решений. Решением неравенства с двумя переменными является некоторое множество точек координатной плоскости.

Основным методом решений данных неравенств является Графический. Он заключается в том, что строят линии границ (если неравенство строгое, линии строят пунктиром). Уравнение границы получают, если в заданном неравенстве заменяют знак неравенства на знак равенства. Все линии в совокупности разбивают координатную плоскость на части. Искомое множество точек, которое соответствует заданному неравенству или системе неравенств, можно определить, если взять контрольную точку внутри каждой области.

Системы, содержащие неравенства с двумя переменными, вида

Называются Системами неравенств с двумя переменными. Решением данных систем является пересечение решений всех неравенств, входящих в систему.

Совокупность неравенств с двумя переменными имеет вид

Решением совокупности является объединение всех решений неравенств.

Пример 1. Решить систему

Решение. Построим в системе Оху соответствующие линии (рис. 4.24):

Рис. 4.24

Уравнение задает окружность с центром в точке О¢(0; 1) и R = 2.

Уравнение определяет параболу с вершиной в точке О(0; 0).

Найдем решения каждого из неравенств, входящих в систему. Первому неравенству соответствует область внутри окружности и сама окружность (в справедливости этого убеждаемся, если подставим в неравенство координаты любой точки из этой области). Второму неравенству соответствует область, расположенная под параболой.

Решение системы – пересечение двух указанных областей (на рис. 4.24 показано наложением двух штриховок).

< Предыдущая		Следующая >

matica.org.ua

19.2. Решение систем mлинейных неравенств с двумя переменными

Дана система т линейных неравенств с двумя переменными

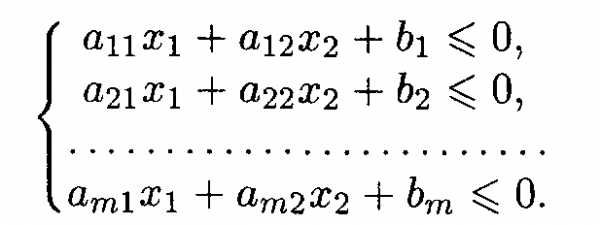
Знаки некоторых или всех неравенств могут быть ≥.

Рассмотрим первое неравенство в системе координат Х₁ОХ₂. Построим прямую

которая является граничной прямой.

Эта прямая делит плоскость на две полуплоскости 1 и 2 (рис. 19.4).

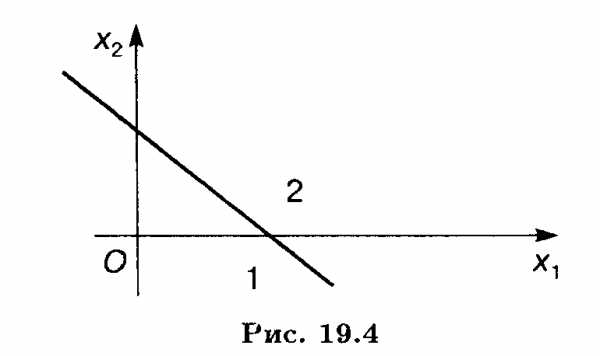
Полуплоскость 1 содержит начало координат, полуплос­кость 2 не содержит начала координат.

Для определения, по какую сторону от граничной прямой расположена заданная полуплоскость, надо взять произволь­ную точку на плоскости (лучше начало координат) и подста­вить координаты этой точки в неравенство. Если неравенство справедливо, то полуплоскость обращена в сторону этой точки, если не справедливо, то в противоположную от точки сторону.

Направление полуплоскости на рисунках показываем стрел­кой.

Определение 15. Решением каждого неравенства систе­мы является полуплоскость, содержащая граничную прямую и расположенная по одну сторону от нее.

Определение 16. Пересечение полуплоскостей, каждая из ко­торых определяется соответствующим неравенством системы, называется областью решения системы (ОР).

Определение 17. Область решения системы, удовлетворяю­щая условиям неотрицательности (x_j ≥ 0, j = ), называ­ется областью неотрицательных, или допустимых, решений (ОДР).

Если система неравенств совместна, то ОР и ОДР могут быть многогранником, неограниченной многогранной облас­тью или одной точкой.

Если система неравенств несовместна, то ОР и ОДР — пус­тое множество.

Пример 1. Найти ОР и ОДР системы неравенств и опреде­лить координаты угловых точек ОДР

Решение. Найдем ОР первого неравенства: х₁ + 3x₂ ≥ 3. Построим граничную прямую х₁ +3x₂ – 3 = 0 (рис. 19.5). Под­ставим координаты точки (0,0) в неравенство: 1∙0 + 3∙0 > 3; так как координаты точки (0,0) не удовлетворяют ему, то решени­ем неравенства (19.1) является полуплоскость, не содержащая точку (0,0).

Аналогично найдем решения остальных неравенств систе­мы. Получим, что ОР и ОДР системы неравенств является выпуклый многогранник ABCD.

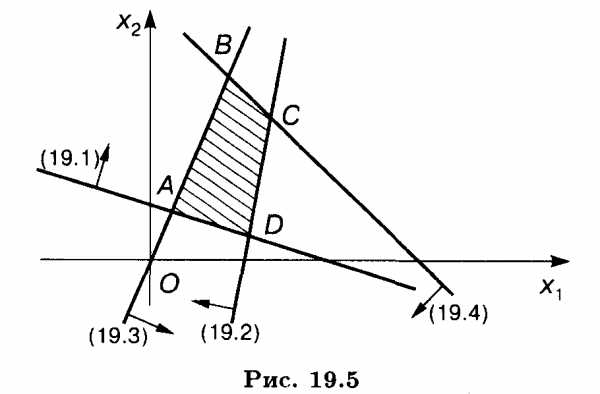
Найдем угловые точки многогранника. Точку А определим как точку пересечения прямых

Решая систему, получим А(3/7, 6/7).

Точку В найдем как точку пересечения прямых

Из системы получим B(5/3, 10/3). Аналогично найдем коорди­наты точек С и D: С(11/4; 9/14), D(3/10; 21/10).

Пример 2. Найти ОР и ОДР системы неравенств

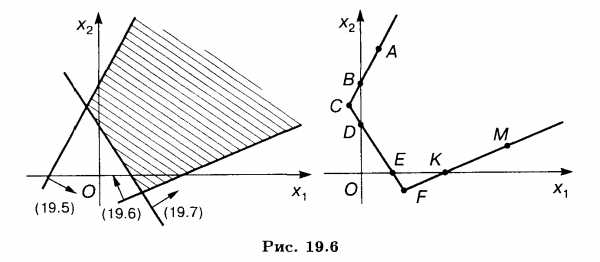
Решение. Построим прямые и определим решения не­равенств (19.5)-(19.7). ОР и ОДР являются неограниченные многогранные области ACFM и ABDEKM соответственно (рис. 19.6).

Пример 3. Найти ОР и ОДР системы неравенств

Решение. Найдем решения неравенств (19.8)-(19.10) (рис. 19.7). ОР представляет неограниченную многогранную область ABC; ОДР — точка В.

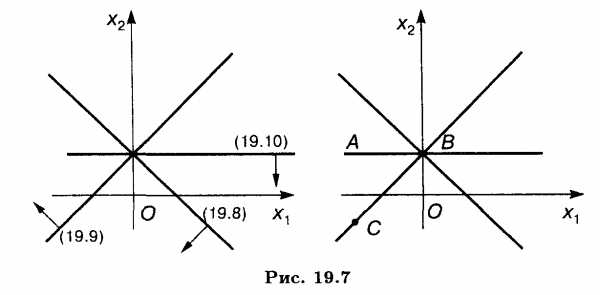
Пример 4. Найти OP и ОДР системы неравенств

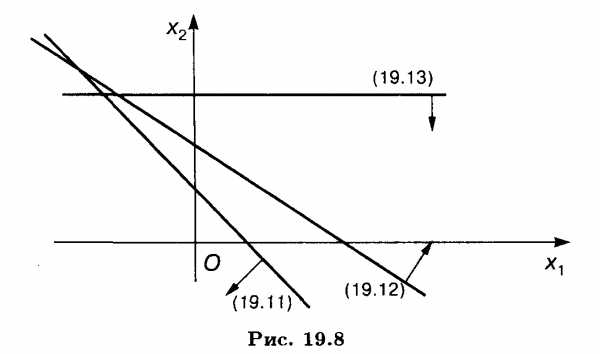
Решение. Построив прямые, найдем решения неравенств системы. ОР и ОДР несовместны (рис. 19.8).

Упражнения

Найти ОР и ОДР систем неравенств

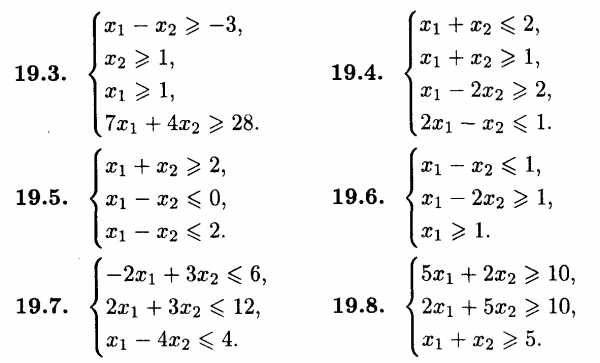
Глава 20. Графический метод

20.1. Постановка задачи

Наиболее простым и наглядным методом линейного про­граммирования является графический метод. Он применяется для решения задач ЛП с двумя переменными, заданными в не­канонической форме, и многими переменными в канонической форме при условии, что они содержат не более двух свободных переменных.

С геометрической точки зрения в задаче линейного про­граммирования ищется такая угловая точка или набор точек из допустимого множества решений, на котором достигается самая верхняя (нижняя) линия уровня, расположенная дальше (ближе) остальных в направлении наискорейшего роста.

Для нахождения экстремального значения целевой функ­ции при графическом решении задач ЛП используют вектор L() на плоскости Х₁ОХ₂, который обозначим . Этот вектор показывает направление наискорейшего изменения це­левой функции, он равен

где е₁ и е₂ — единичные векторы по осям OX₁ и ОX₂ соответ­ственно; таким образом, = (∂L/∂х₁, ∂L/∂х₂). Координатами вектора являются коэффициенты целевой функции L().

studfiles.net

19.2. Решение систем M линейных неравенств с двумя переменными

Дана система Т линейных неравенств с двумя переменными

Знаки некоторых или всех неравенств могут быть ≥.

Рассмотрим первое неравенство в системе координат Х1ОХ2. Построим прямую

Которая является Граничной прямой.

Эта прямая делит плоскость на две полуплоскости 1 и 2 (рис. 19.4).

Полуплоскость 1 содержит начало координат, полуплос­кость 2 не содержит начала координат.

Для определения, по какую сторону от граничной прямой расположена заданная полуплоскость, надо взять произволь­ную точку на плоскости (лучше начало координат) и подста­вить координаты этой точки в неравенство. Если неравенство справедливо, то полуплоскость обращена в сторону этой точки, если не справедливо, то в противоположную от точки сторону.

Направление полуплоскости на рисунках показываем стрел­кой.

Определение 15. Решением каждого неравенства систе­мы является полуплоскость, содержащая граничную прямую и расположенная по одну сторону от нее.

Определение 16. Пересечение полуплоскостей, каждая из ко­торых определяется соответствующим неравенством системы, называется Областью решения системы (ОР).

Определение 17. Область решения системы, удовлетворяю­щая условиям неотрицательности (Xj ≥ 0, J = ), называ­ется Областью неотрицательных, или допустимых, решений (ОДР).

Если система неравенств совместна, то ОР и ОДР могут быть многогранником, неограниченной многогранной облас­тью или одной точкой.

Если система неравенств несовместна, то ОР и ОДР — пус­тое множество.

Пример 1. Найти ОР и ОДР системы неравенств и опреде­лить координаты угловых точек ОДР

Решение. Найдем ОР первого неравенства: Х1 + 3X2 ≥ 3. Построим граничную прямую Х1 +3X2 – 3 = 0 (рис. 19.5). Под­ставим координаты точки (0,0) в неравенство: 1∙0 + 3∙0 > 3; так как координаты точки (0,0) не удовлетворяют ему, то решени­ем неравенства (19.1) является полуплоскость, не содержащая точку (0,0).

Аналогично найдем решения остальных неравенств систе­мы. Получим, что ОР и ОДР системы неравенств является выпуклый многогранник ABCD.

Найдем угловые точки многогранника. Точку А определим как точку пересечения прямых

Решая систему, получим А(3/7, 6/7).

Точку В найдем как точку пересечения прямых

Из системы получим B(5/3, 10/3). Аналогично найдем коорди­наты точек С и D: С(11/4; 9/14), D(3/10; 21/10).

Пример 2. Найти ОР и ОДР системы неравенств

Решение. Построим прямые и определим решения не­равенств (19.5)-(19.7). ОР и ОДР являются неограниченные многогранные области ACFM и ABDEKM соответственно (рис. 19.6).

Пример 3. Найти ОР и ОДР системы неравенств

Решение. Найдем решения неравенств (19.8)-(19.10) (рис. 19.7). ОР представляет неограниченную многогранную область ABC; ОДР — точка В.

Пример 4. Найти OP и ОДР системы неравенств

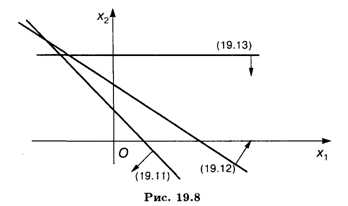
Решение. Построив прямые, найдем решения неравенств системы. ОР и ОДР несовместны (рис. 19.8).

< Предыдущая		Следующая >

matica.org.ua