Горизонтальная прямая это: Ошибка 404. Запрашиваемая страница не найдена

горизонтальная прямая — это… Что такое горизонтальная прямая?

горизонтальная прямая

мат. horizontal line

Большой англо-русский и русско-английский словарь. 2001.

• горизонтальная проекция
• горизонтальная развертка

Смотреть что такое «горизонтальная прямая» в других словарях:

• КОНИЧЕСКИЕ СЕЧЕНИЯ — плоские кривые, которые получаются пересечением прямого кругового конуса плоскостью, не проходящей через его вершину (рис. 1). С точки зрения аналитической геометрии коническое сечение представляет собой геометрическое место точек,… …   Энциклопедия Кольера

• Лазер —         источник электромагнитного излучения видимого, инфракрасного и ультрафиолетового диапазонов, основанный на вынужденном излучении (См.

  Вынужденное излучение) атомов и молекул. Слово «лазер» составлено из начальных букв (аббревиатура) слов… …   Большая советская энциклопедия

• горизонталь — (гр.; см. горизонт) 1) прямая линия, параллельная плоскости горизонта 1; 2) горизонтали иначе изогипсы геод, линии на географической карте, соединяющие точки с одинаковой высотой над уровнем моря и в совокупности отображающие рельеф местности.… …   Словарь иностранных слов русского языка

• Рычаг — одна из так называемых простых машин. Уже в сочинениях Аристотеля рассматривается действие Р. Действие равноплечих весов он объясняет правильно, представляя коромысло современных ему весов, не имевших еще чашек, в виде прямоугольной линейки,… …   Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

• SYPHACIA OBVELATA — (Rud, 1802). Нематода подсемейства Syphaciinae (отр. Oxyurata, сем. Oxyuridae), частый паразит грызунов. Космополит. У человека обнаружен 1 раз Ри ^ леем (Riley, 1919) в фе ,<^»»^ .

  «* , калиях ребенка с Фи липпинских островов (2 …   Большая медицинская энциклопедия

• Критическая температура — та, при которой видимое различие между жидкостью и ее паром исчезает. Явление наблюдается при нагревании жидкостей в запаянных трубках. При этом поверхность, ограничивающая жидкость, постепенно утрачивает кривизну, мениск становится плоским и,… …   Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

• Маятник Капицы — Одна из конструкция маятника Капицы: мотор приводит кривошип, который через шатун и рычаг передаёт вибрацию на перевёрнутый маятник. Маятником Капицы …   Википедия

• линия развертки — Линия на дисплее (например, экране ЭЛТ), расположение точек которой находится в определенной зависимости от времени или иного параметра (например, частоты, фазы и т.п). В ультразвуковом эходефектоскопе с разверткой типа А это горизонтальная… …   Справочник технического переводчика

• Пищеварительная система — обеспечивает усвоение организмом необходимых ему в качестве источника энергии, а также для обновления клеток и роста питательных веществ. Пищеварительный аппарат человека представлен пищеварительной трубкой, крупными железами пищеварительного… …   Атлас анатомии человека

• Асимптота — У этого термина существуют и другие значения, см. Асимптота (значения). Асимптота[1] (от греч. ασϋμπτωτος  несовпадающий, не касающийся) кривой с бесконечной ветвью прямая, обладающая тем свойством, что расстояние от точки кривой до этой… …   Википедия

• Средняя — периодическое увлажнение пола, при котором поверхность покрытия пола влажная или мокрая; покрытие пола пропитывается жидкостями. Источник: МДС 31 12.2007: Полы жилых, общественных и производственных зданий с применением м …   Словарь-справочник терминов нормативно-технической документации

Термины и определения начертательной геометрии

Содержание

1. Термины и определения;
2. Условные обозначения;
3. Способы задания плоскости на чертеже.

Термины и определения

Комплексный чертеж (эпюр Монжа) – чертеж, составленный из взаимосвязанных ортогональных проекций геометрической фигуры. Чтобы преобразовать пространственный макет в эпюр, нужно совместить плоскости проекций П₁ и П₃ с третьей плоскостью П₂, вращая П₁ вокруг оси x, а П₃ вокруг оси z.

Конкурирующие точки – точки, расположенные на одной проецирующей прямой, но при этом удаленные от плоскости проекций на разное расстояние.

Линии уровня – прямые, параллельные одной из плоскостей проекций.

• Горизонталь, h – прямая, параллельная горизонтальной плоскости;
• Фронталь, f – прямая, параллельная фронтальной плоскости;
• Профильная прямая, p – прямая, параллельная профильной плоскости.

Метрические задачи – это задачи, целью решения которых является нахождение натуральных величин отрезков, углов, расстояний.

Октант – часть пространства, ограниченная плоскостями проекций П₁, П₂, П₃. В начертательной геометрии выделяют восемь октантов, нумерация и взаимное расположение которых показаны на рисунке.

Отрезок – участок прямой, ограниченный двумя точками.

Плоскости общего положения – плоскости, которые не перпендикулярны ни одной из плоскостей проекций.

Плоскости уровня – плоскости, параллельные одной из плоскостей проекций.

Позиционные задачи – это задачи, целью решения которых является определение взаимного расположения фигур, нахождение точек и линий их пересечения.

Проецирующие плоскости – плоскости, перпендикулярные одной из плоскостей проекций.

Прямые общего положения – прямые, не параллельные ни одной из плоскостей проекций.

Проецирующие прямые – прямые, перпендикулярные одной из плоскостей проекций.

Следы плоскости – прямые, по которым данная плоскость пересекается с плоскостями проекций.

Следы прямой – точки пересечения прямой с плоскостями проекций.

Угол между прямой и плоскостью – угол между прямой и её проекцией на эту плоскость.

Условные обозначения

Оси координат:

• x – ось абсцисс;
• y – ось ординат;
• z – ось аппликат.

Проекции точек:

• A’, B’, C’ … Z’ или A₁, B₁, C₁ … Z₁ – горизонтальные;
• A», B», C» … Z» или A ₂, B₂, C₂ … Z₂ – фронтальные;
• A»’, B»’, C»’ … Z»’ или A₃, B₃, C₃ … Z₃ – профильные.

Проекции прямых:

• a’, b’, c’ … z’ или a₁, b₁, c₁ … z₁ – горизонтальные;
• a», b», c» … z» или a₂, b₂, c₂ … z₂ – фронтальные;
• a»’, b»’, c»’ … z»’ или a₃, b₃, c₃ … z₃ – профильные.

Плоскости проекций:

• П₁ или H – горизонтальная;
• П₂ или V – фронтальная;
• П₃ или W – профильная.

Следы плоскости α:

• h_0α – горизонтальный;
• f_0α – фронтальный;
• p_0α – профильный.

Следы прямой l:

• H_l – горизонтальный;
• F_l – фронтальный;
• W_l – профильный.

Способы задания плоскости на комплексном чертеже

Плоскость на комплексном чертеже может быть задана шестью различными способами:

1. Тремя точками, которые не лежат на одной прямой. На рисунке это т. A, B, C.
2. Прямой и точкой, не лежащей на этой прямой.
3. Двумя пересекающимися прямыми.
4. Двумя параллельными прямыми (пересекающимися в несобственной точке).
5. Отсеком плоской фигуры Ф.
6. Следами. Этот способ удобен тем, что позволяет наглядно представить расположение плоскости в пространстве.

Дополнительные материалы:

Вертикальная прямая (горизонтально-проецирующая)

ПРЯМЫЕ частного положения

Относительно плоскостей проекций прямые могут располагаться по разному. Если они параллельны или перпендикулярны плоскостям проекций, то говорят , что это прямые частного положения.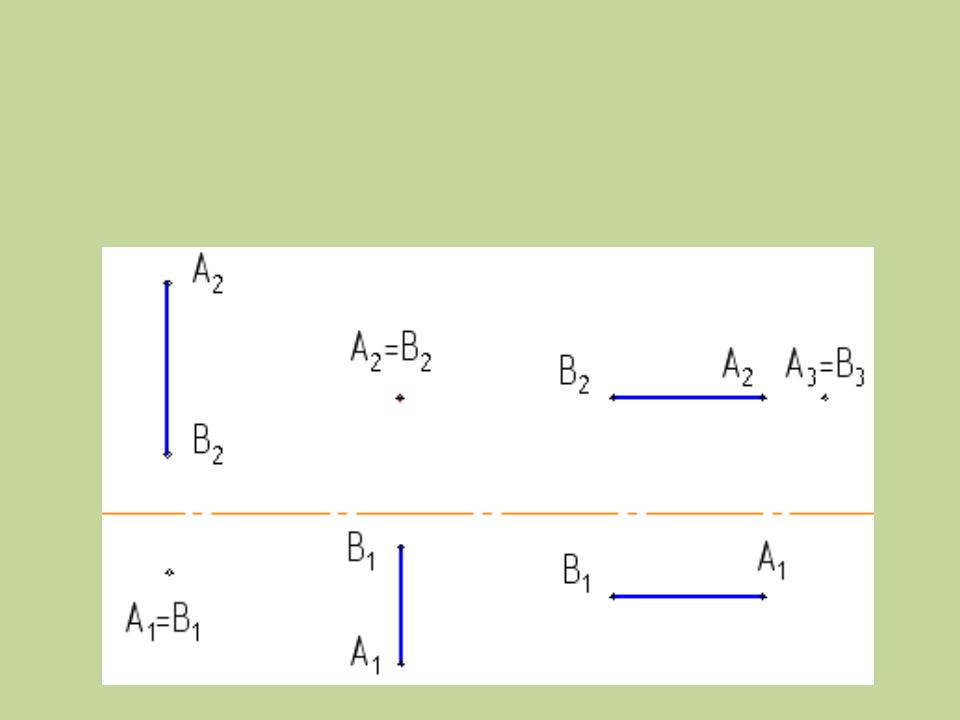

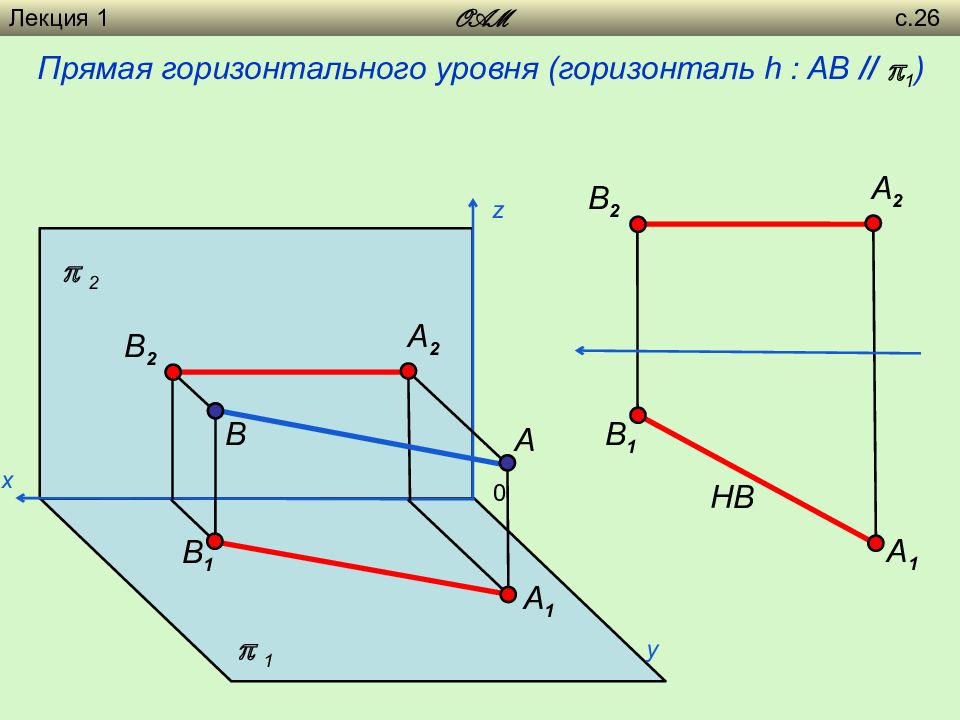
Горизонталь

Прямая, параллельная горизонтальной плоскости, называется горизонталью,h // Г (рисунок 2-1). На фронтальной проекции (виде спереди) она всегда перпендикулярна вертикальным линиям связи, а на виде сверху составляет с ними некоторый угол α(реконструкцией чертежа определяем положение прямой в пространстве). На виде сверху отрезок АВ, взятый на прямой, изображается в натуральную величину; здесь же можно определить угол α наклона прямой к фронтальной плоскости и угол γ — наклона ее к профильной плоскости.

На горизонтальной проекции (виде сверху) горизонталь проецируется без искажения.

4.2 Фронталь

 

Прямая, параллельная фронтальной плоскости, называется фронталью. f // Ф (рисунок 2-2). На горизонтальной проекции (виде сверху) фронталь всегда перпендикулярна вертикальным линиям связи, а на фронтальной проекции (виде спереди) составляет с ними некоторый угол. Отрезок СD, взятый на прямой, на виде спереди изображается без искажений. Здесь же определяются углы наклона прямой к горизонтальной плоскости b и к профильной плоскости П γ.

Фронталь проецируется без искажения на фронтальной проекции (виде спереди).

 

Профильная прямая

 

Прямая, параллельная профильной плоскости, называется профильной прямой р.р//П (рисунок 2-3). На видах спереди и сверху такая прямая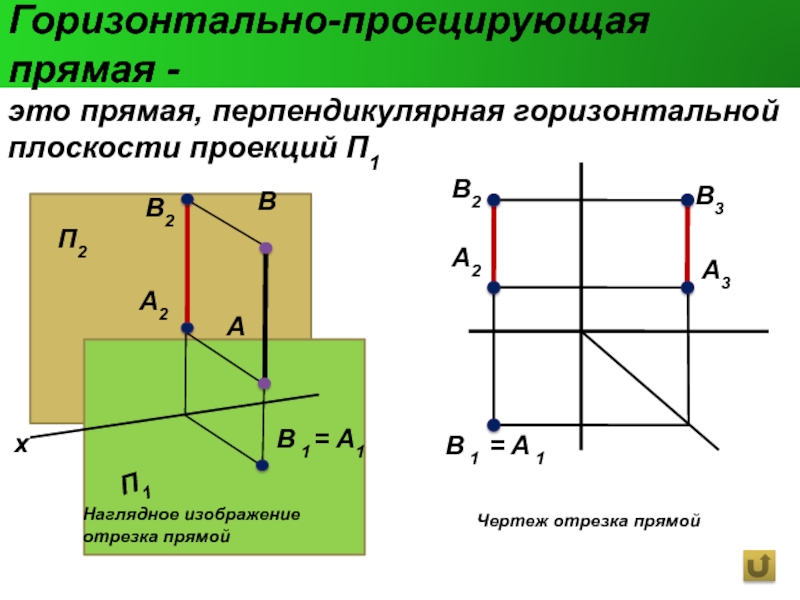

всегда совпадает по направлению с вертикальными линиями связи. Эти виды не определяют наглядно положение прямой в пространстве, поэтому необходимо построить ее изображение на виде слева, где определяются углы наклона прямой к фронтальной a и горизонтальной b плоскостям уровня. Отрезок EF, взятый на прямой р, на виде слева изображается в натуральную величину.

Положение прямой в пространстве определяется положением 2-х любых ее точек (например Е и F). Для построения точек Е и F на виде сверху необходимо наметить положение баз отсчета глубин, а затем, замерив глубины точек, отложить их на виде сверху. Удобно при выборе баз отсчета проводить их через одну из имеющихся точек. Так при выборе базы отсчета глубин ее проводят через дальнюю от наблюдателя точку — Е. Тогда задача построения 3-го вида упрощается — нужно строить на нем на одну точку меньше – F.

Профильная прямая проецируется без искажения на профильной проекции (виде слева).

Вертикальная прямая (горизонтально-проецирующая)

Это прямая, перпендикулярная горизонтальной плоскости Г.

Отрезок, отложенный на данной прямой, на видах спереди и слева изображается в натуральную величину (рисунок 2-4), а на виде сверху — как точка, совпадающая с проекцией прямой i. Точки А и В называются горизонтально-конкурирующими (совпадающими).

 

 

Узнать еще:

Чертежи точки , прямой и плоскости в системе прямоугольных проекций

1. Чертежи точки , прямой и плоскости в системе прямоугольных проекций

2. Оглавление

Чертежи точки , прямой и плоскости в системе
прямоугольных проекций
1. Чертеж точки
2. Чертёж отрезка прямой
3. Изображение плоскости на чертеже

3. 2.Чертежи точки , прямой и плоскости в системе прямоугольных проекций

Для получения обратимого, т.е. метрически
определенного чертежа любого предмета,
берут не одну, а две или три плоскости
проекций, которые образуют в
пространстве систему перпендикулярных
плоскостей
На главную

4. Система перпендикулярных плоскостей

•П2 — фронтальная
плоскость проекций,
•П1 — горизонтальная
плоскость проекций,
•П3- профильная
плоскость проекций
На главную

5.

Система перпендикулярных плоскостей z
V
II
VI
I -y
-х
О
О
x
III
y
VII
IV
VIII
-z
На главную

6. Знаки координат для точек октантов

Коорди
наты
I
X
Y
Z
+
+
+
Октанты
II III IV V VI VII VII
I
+ + + — — — — — + + — — +
+ — — + + — На главную
z
А2
A
-y
Аz
А3
А (a x; a y; a z)
Аx
x
Аy
А1
y
-z
z
-y
А2
A
Аz
А3
Аx
x
Аy
А1
-z
y
y
z
А2
-y
A
АzА
Аx
Аy
Аy
x
А1
3
y
y
z
А2
Аz
А3
Аy
Аx
x
А1
Аy
y
z
А2
Аz
Аx
x
А1
y
x
А3
у
А1
45°
П1
П3
z
А2
Аy
Аy
П2
А3
у
П2
Чертеж
точки
П3
z
А3
А2
x
у
А1
45°
П1
у

13.

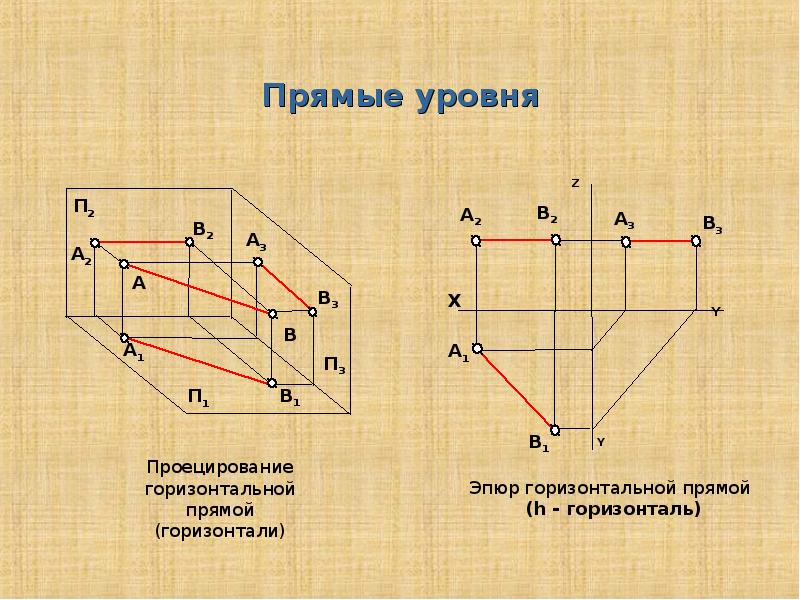Пример точка А (4; 2; 4)  I четверти Пример
точка А (4; 2; 4) I четверти
z
z
А2
Аz
А2
А3
A-y
х
-у
Аx
x
Аz
-Х
Аy
y
А1
Аx
А1
Аy
y
y
-z
Моисеева О.А.
13

14. Пример точка В (2; -3; -2) III четверти

Пример
точка В (2; -3; -2) III четверти
-y
-4
-3
b1
by
-2
-y
-1
b1
bx
Х
B
b2
bz
Х
b2
-z
Моисеева О.А.
-z
14

15. 2.2. Чертеж отрезка прямой

Чтобы построить чертеж прямой, надо
построить проекции лишь двух её точек
В2
В2
А2
В
А2
х
А
В1
х
А1
Наглядное изображение
отрезка прямой АВ
А1
В1
Чертеж отрезка прямой АВ
На главную

16. Прямые общего положения

— это прямые не параллельные и не перпендикулярные ни к
одной из плоскостей проекций
N=N2
A2
П2
N= N2
A2
B2
A
B2
N1
M2
N1
A1
П1
B
B1
M=M1
M2
A1
M =M1
B1
M (M1; M2) — горизонтальный
след прямой.
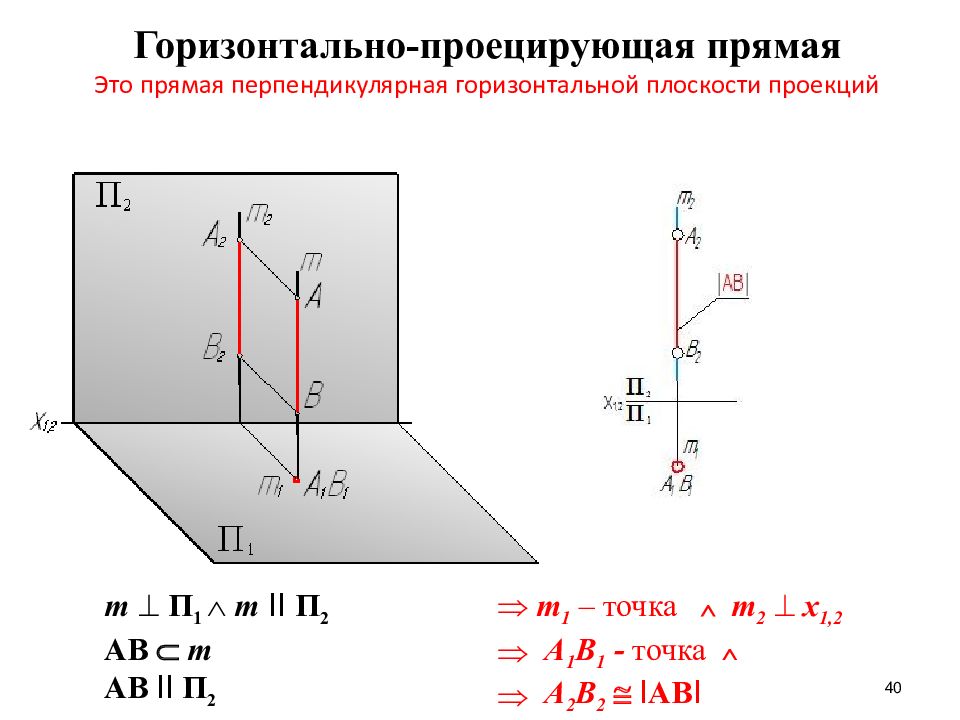
N (N1; N2) — фронтальный след
прямой.
На главную

17. Прямые частного положения

Прямая уровня
(прямая,
параллельная какойнибудь одной
плоскости
проекций):
•Горизонтальная
•Фронтальная
•Профильная
Проецирующая прямая
(прямая,
перпендикулярная к
какой-нибудь одной
плоскости проекций) :
•Горизонтальнопроецирующая;
•Фронтальнопроецирующая;
•Профильнопроецирующая.
На главную

18. Горизонтальная прямая уровня —

Горизонтальная прямая уровня это прямая, параллельная
горизонтальной плоскости проекций П1.
П2
A2
х
A2
B2
А
A1
Наглядное изображение
отрезка прямой
B2
В
х
B1
A1
Чертеж отрезка прямой
B1
Фронтальная прямая уровня это прямая, параллельная фронтальной
плоскости проекций П2.
П2
A2
B2
B2
A2
В
А
B1
х
A1
Наглядное изображение
отрезка прямой
х
A1
Чертеж отрезка прямой
B1

20.

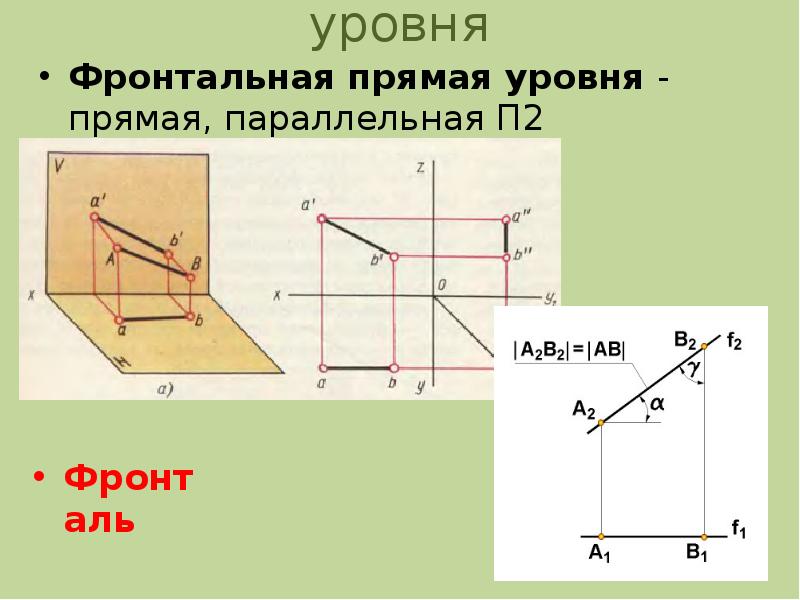Профильная прямая уровня — Профильная прямая уровня это прямая, параллельная профильной
плоскости проекций П3.
П2
П3
B2
B3
В
A2
х
A2
B3
A3
A3
А
A1
B2
A1
B1
Наглядное изображение
отрезка прямой
B1
Чертеж отрезка прямой

21. Горизонтально-проецирующая прямая —

Горизонтально-проецирующая
прямая это прямая, перпендикулярная горизонтальной
плоскости проекций П1
П2
B2
A2
х
В
B2
B3
A2
A3
А
B 1 = A1
Наглядное изображение
отрезка прямой
B1 = A1
Чертеж отрезка прямой

22. Фронтально-проецирующая прямая

это прямая, перпендикулярная фронтальной
плоскости проекций П2
П2
A2 =B2
A2 =B2
х
B3
A3
В
B1
А
B1
A1
A1
Наглядное изображение
отрезка прямой
Чертеж отрезка прямой

23. Профильно-проецирующая прямая

это прямая, перпендикулярная профильной
плоскости проекций П3
П2
A2
B2
B3 =A3
В
х
B1
B2
A2
B3 =A3
А
A1
Наглядное изображение
отрезка прямой
B1
A1
Чертеж отрезка прямой

24.

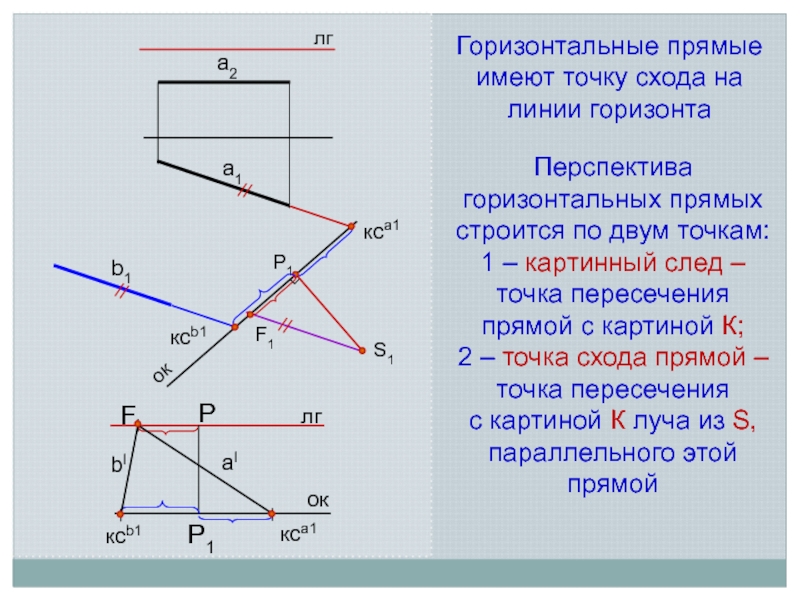Взаимное положение точки и прямой А2
Если точка в
пространстве
принадлежит
прямой, то ее
проекции
принадлежат
соответствующим А1
проекциям этой
прямой.
С2
К1
D2
В2
С1
•т. С АВ
•т. D АВ
•т. К АВ (III ч.)
Моисеева О.А.
D1
К2
В1
На главную

25. 2.3. Способы задания плоскости на чертеже

B2
B2
A2
A2
C1
A1
C2
A2
C2
C2
B1
B1
C1
а) три точки не
лежащие на одной
прямой
б) прямая и не
лежащая на ней
точка
A1
B2
A1
B1
C1
в) две
пересекающиеся
прямые
На главную

26. Способы задания плоскости на чертеже

f2
M2
N2
N1
M1
h3 = f1
h2
г) две параллельные
прямые
д) следы плоскости
На главную

27. Плоскость общего положения

П2
Fр=f2
h3=f1
Плоскость, не
параллельную и не
перпендикулярную
ни к одной из
плоскостей
проекций,
называют
плоскостью
общего положения.
Моисеева О.А.
Наглядное изображение
На главную

28. Плоскость общего положения

П2
Fр=f2
h3=f1
Моисеева О.А.
Наглядное изображение
На главную

29. Следы плоскости

Следом плоскости
называется линия ее
пересечения с
плоскостью проекций.
f2
k1 = k2
h3=f1
h2
Чертеж плоскости заданной следами
На главную

30. Плоскости частного положения

Плоскости, параллельные или
перпендикулярные к плоскостям проекций,
называют плоскостями частного положения.
Плоскость уровня
(плоскость, параллельная
какой-либо одной
плоскости проекций):
•Горизонтальная
•Фронтальная
•Профильная
Проецирующая плоскость
(плоскость,
перпендикулярная к какойлибо одной плоскости
проекций) :
•Горизонтальнопроецирующая;
•Фронтальнопроецирующая;
•Профильнопроецирующая.

31. Горизонтально-проецирующая плоскость —

Горизонтально-проецирующая
плоскость это плоскость, перпендикулярная горизонтальной
плоскости проекций П1
B2
B3
C2 C3
A3
A2
C1
B1
A1
Чертеж горизонтально-проецирующей плоскости

32.

Фронтально-проецирующая плоскость — Фронтально-проецирующая
плоскость это плоскость, перпендикулярная фронтальной
плоскости проекций П2
C2
C3
B2
B3
A2
A3
C1
A1
B1
Чертеж фронтально-проецирующей плоскости

33. Профильно-проецирующая плоскость —

Профильно-проецирующая
плоскость это плоскость, перпендикулярная профильной
плоскости проекций П3
B3
B
2
C2
A2
C3
A3
B1
C1
A1
Чертеж профильно-проецирующей плоскости

34. Горизонтальная плоскость уровня —

Горизонтальная плоскость уровня это плоскость, параллельная горизонтальной
плоскости проекций П1
A2
B2
C2
B3
C3
A3
B1
C1
A1
Чертеж горизонтальной плоскости уровня

35. Фронтальная плоскость уровня —

Фронтальная плоскость уровня это плоскость, параллельная фронтальной плоскости
проекций П2.
B2
B3
A3
A2
C2
A1
B1
C3
C1
Чертеж фронтальной плоскости уровня

36.

Профильная плоскость уровня — Профильная плоскость уровня это прямая, параллельная профильной плоскости
проекций П3.
A2
A3
C3
C2
B2
B3
C1
B1
A1
Чертеж профильной плоскости уровня

37. Информационные ресурсы по теме:

1. Гордон В.О., Семенцов-Огневский М.А. Курс
начертательной геометрии: учебное пособие/ под ред.
Ю.Б. Иванова. — 23-е изд., перераб. — М.: Наука,
1988. — 272 с.
2. Локтев О.В., Числов П.А. Задачник по начертательной
геометрии: учебное пособие для втузов. — М.: Высш.
шк., 1977. — 103.: ил.
3. Чекмарев АА. Начертательная геометрия и черчение:
учебник для студ. высш. учеб. заведений. — 2-е изд.,
перераб. и доп. — М.: Гуманит. изд. центр Владос,
2002. — 472 с.: ил.

38. Информационные ресурсы по теме:

Основная литература
1. Соломонов К.Н., Чиченёва О.Н., Бусыгина Е.Б. Основы начертательной
геометрии. -М.: МИСиС, 2003
2. Соломонов К.Н. , Чиченёва О.Н., Бусыгина Е.Б. Основы технического
черчения. – М.: МИСиС, 2004
3. Чекмарев А.А. Инженерная графика. М.: Высшая школа, 1998
4. Сборник «Национальные стандарты». ЕСКД .ГОСТ 2.301-68 2.321-84.-М.:
ИПК Издательство Стандартов,2004
Средства обеспечения освоения дисциплины
1.Пакет AutoCAD, Компас 3D, Симплекс
2.Курс лекций, созданный с использованием графического
«Power Point« и средств Internet.
редактора
38

Пошаговое руководство решения задачи №6

Пошаговое руководство решения задачи №6 — построение линии пересечения сферической поверхности от сквозного призматического выреза.

Необходимо построить линию пересечения сферической поверхности (шара) от сквозного призматического выреза, состоящего из четырех граней (проецирующих плоскостей). Фронтальная проекция линии пересечения заданных поверхностей (шара и многогранника) задана исходным чертежом, требуется построить ее в горизонтальную и профильную проекции.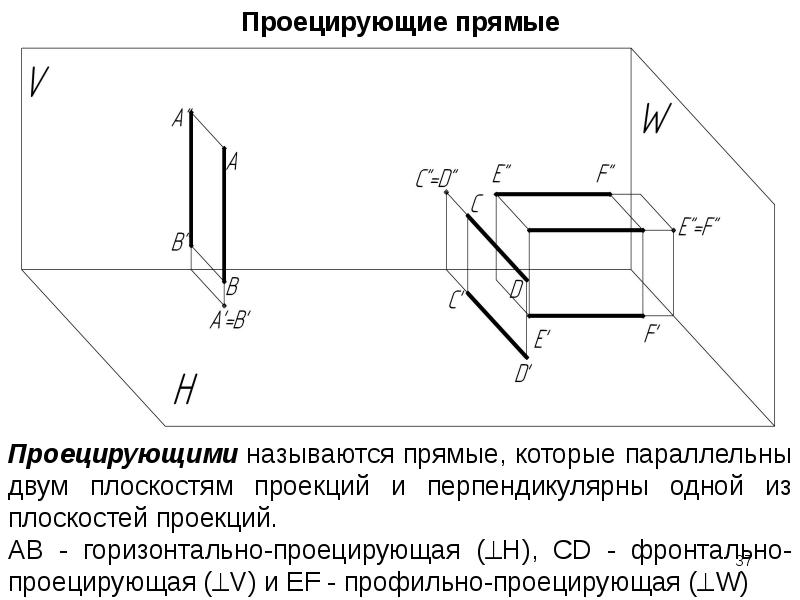

Для решения такой задачи по начертательной геометрии необходимо знать:

— построение трех проекций сферической поверхности (шара) по заданным координатам, на комплексном чертеже;

— построение линии пересечения шаровой поверхности с гранным телом;

— частные случаи построения линии пересечения шаровой поверхности с проецирующей плоскостью.

Порядок решения Задачи

Рис.6.1

1. В правой части листа формата A3 наносятся оси координат и согласно варианту задания строится фронтальная, горизонтальная и профильная проекции сферы (шара) заданного радиуса.

По координатам точек, взятым из таблицы по своему варианту, наносятся вершины сквозного четырехгранного выреза во фронтальной проекции (рис.6.1).

2. Решение задачи заключается в построении горизонтальной и профильной проекции линии пересечения данного выреза.

Прежде чем приступить к построению этих проекций, необходимо вспомнить некоторые частные случаи сечений шаровой поверхности от проецирующей плоскости (сквозное отверстие можно рассматривать как гранное тело, образованное четырьмя плоскостями), а именно:

(а) если плоскость во фронтальной проекции рассекает шаровую поверхность параллельно экватору, то в горизонтальной проекции это сечение проецируется в виде окружности с радиусом, взятым в этом сечении от оси вращения шара до очерка, а в профильной проекции это сечение проецируется в виде прямой линии;

(b)   если плоскость во фронтальной проекции рассекает шаровую поверхность перпендикулярно экватору, то в горизонтальной проекции это сечение проецируется в виде прямой линии, а в профильной — в виде окружности с радиусом, взятым тем же способом что и в первом случае;

(c)   если плоскость во фронтальной проекции рассекает шаровую поверхность под некоторым (отличным от 0 и 90 градусов) углом к экватору, то в горизонтальной и фронтальной проекциях это сечение будет проецироваться в виде эллипса. Построение эллипса осуществляется по опорным (характерным) и некоторым промежуточным, взятым произвольно, точкам;

(d)   все точки фронтальной проекции сферы, расположенные на очерке, в горизонтальной проекции будут проецироваться на экваторе, а в профильной — на главном меридиане;

(e)   все точки фронтальной проекции сферы, расположенные на экваторе, в горизонтальной проекции будут проецироваться на очерке, а в профильной — на экваторе;

(f)   все точки фронтальной проекции сферы, расположенные на главном меридиане, в горизонтальной проекции будут проецироваться также на главном меридиане, а в профильной — на очерке сферы.

Рис.6.2

3. С учетом приведенных частных случаев сечений построение выреза в горизонтальной и профильной проекциях не вызывает особых затруднений и начинается с определения характерных (опорных) точек сквозного выреза во фронтальной проекции. Этими точками являются А, В, С, D. Тогда берем проекцию стороны призмы B’C’ и рассматриваем ее как проецирующую плоскость ’, рассекающую шар параллельно экватору, — строим в горизонтальной проекции окружность с радиусом r₁ взятым в этой плоскости, от оси шара до очерка. Проецируем на эту окружность точки B’ и C’, получаем B и C — их горизонтальные проекции. Вполне очевидно, что этих точек будет по две (точки входа и выхода), т.к. отверстие сквозное.

Аналогичным способом строится проекция сечения плоскости А’D’. Берется радиус от оси сферы до очерка (разумеется не до точки A’) и в горизонтальной проекции проводится окружность этим радиусом.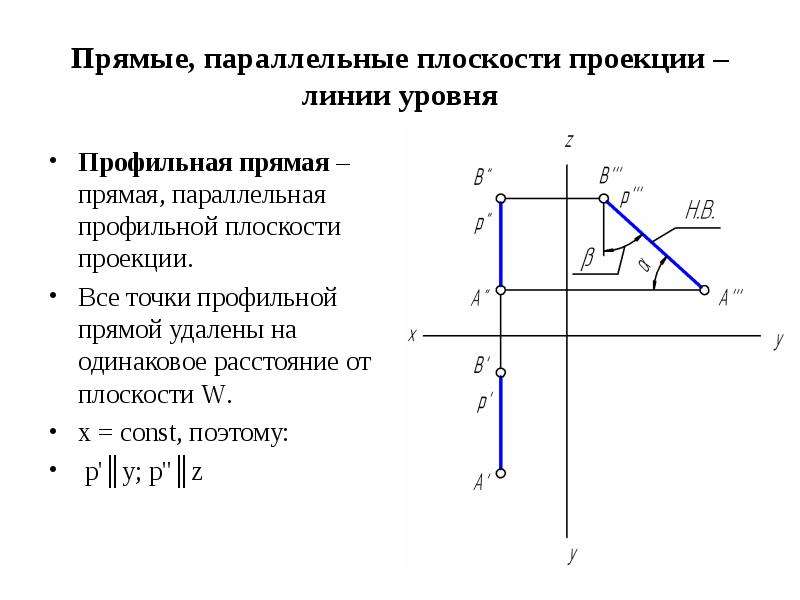 Проецированием находятся проекции точек D (их будет две — точка входа и точка выхода) — D и D₁ и промежуточной точки, расположенной на экваторе.

Рис.6.3

Сторона четырехугольника СD горизонтальной проекции проецируется в прямую линию, причем эта линия должна начинаться от очерка, т.к. во фронтальной проекции
она пересекает экватор шара и продолжается до точек С и D.

Рис.6.4

Горизонтальной проекцией сторон четырехугольника АВ будет эллипс, строим его по характерным (опорным) точкам. Проецируем точки, расположенные на меридиане, экваторе и очерке фронтальной проекции соответственно на меридиан, очерк и экватор горизонтальной проекции. Соединяя их по лекалу с уже имеющимися
проекциями точек B и B₁, и получаем искомую проекцию эллипса.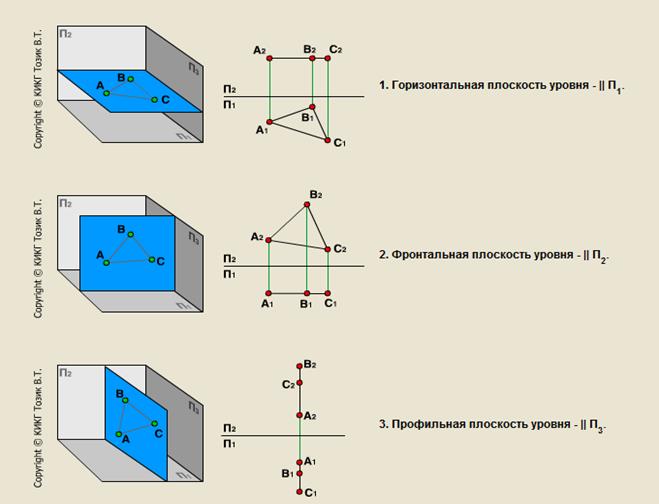

4. Аналогичным способом строится третья профильная проекция данного выреза (вид слева), поэтому нет надобности в подробном изложении четырехугольника ВС и АD будут проецироваться в прямые линии, СD – в окружность, AB – в эллипс.

Рис.6.5

5. Заключительным этапом в решении задачи является определение видимости сторон сквозного выреза, которая определяется из расположения их на сопряженной плоскости проекций. Тогда видимыми точками и линиями в горизонтальной плоскости будут точки и линии, которые во фронтальной — расположены выше экватора и на профильной проекции видимыми будут точки и линии которые на фронтальной плоскости расположены левее меридианы.

Экватор и меридиан являются границами видимости. Точки и линии, расположенные ниже экватора и правее меридиана во фронтальной проекции, в горизонтальной и профильной проекциях будут невидимыми.

Раздел: Начертательная геометрия / 

• Рекомендуем
• Комментарии
• Наши товары

Вспомогательные прямые в Компас 3D.

---

1  2  3  4  5  6  7  8  9  10  11  12  13  14  15  16  17

Урок №4. Вспомогательные прямые в Компас 3D.

Конструктора при разработке чертежей на кульмане всегда используют тонкие линии, их аналогом в Компас 3D выступают вспомогательные прямые. Они необходимы для предварительных построений и для задания проекционных связей между видами. При печати вспомогательные прямые Вспомогательная, изменить его невозможно.

Существует несколько способов построения вспомогательных прямых. В этом уроке рассмотрим некоторые из этих способов.

1. Произвольная прямая по двум точкам.

В основном меню программы последовательно нажимаем команды Инструменты-Геометрия-Вспомогательные прямые-Вспомогательная прямая.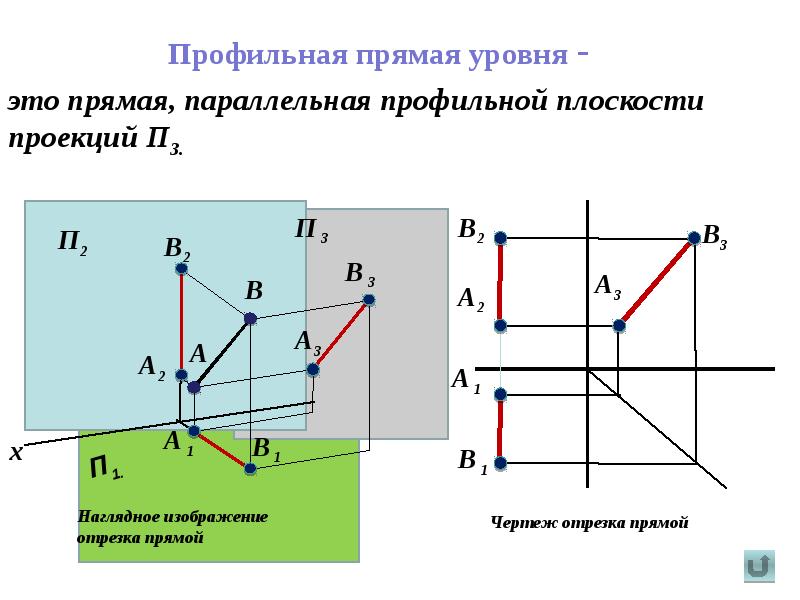

Или в компактной панели нажимаем кнопки Геометрия-Вспомогательная прямая.

Щелчком левой клавиши мыши указываем первую базовую точку (к примеру, начало координат). Теперь указываем вторую точку, через которую пройдет прямая. Угол наклона между прямой и осью абсцисс текущей системы координат, определится автоматически. Можно вводить угол, через панель свойств. Например введите угол 45º и нажмите клавишу Enter.

Для завершения построения необходимо нажать на значок «Прервать команду» в панели свойств. Данную команду можно осуществить, через контекстное меню, которое вызывается щелчком правой клавиши мыши.

Подобным образом через базовую точку, можно построить сколько угодно произвольных прямых под любым углом. Вы уже наверное обратили внимание что координаты точек можно вводить с клавиатуры используя панель свойств. Кроме того в панели свойств имеется группа Режимы, в которой есть два переключателя: «Не ставить точки пересечения» (активен по умолчанию) и «Ставить точки пересечения». Если вам нужно отметить точки пересечения прямой с другими объектами активируйте переключатель «Ставить точки пересечения», теперь система автоматически проставит точки пересечения со всеми графическими объектами в текущем виде.

Стиль точек будет- Вспомогательная. Для удаления всех вспомогательных элементов воспользуйтесь командами основного меню Редактор-Удалить-Вспомогательные кривые и точки. Как отметить точки пересечения не со всеми, а только с некоторыми объектами описано в уроке №3.

2.Горизонтальная прямая.

Для построения горизонтальной прямой вызываются команды Инструменты-Геометрия-Вспомогательные прямые-Горизонтальная прямая.

Или через компактную панель, нажатием кнопок: Геометрия-Горизонтальная прямая. Инструментальная панель для построения вспомогательных прямых, вся на экране не видна. Чтобы её увидеть, нажмите на кнопку вспомогательных прямых, активную на момент построения, и удерживайте несколько секунд.

Теперь достаточно, щелчком левой клавиши мыши указать точку, через которую пройдет горизонтальная прямая. Одновременно можно построить сколько угодно прямых. Для завершения построения необходимо нажать кнопку «Прервать команду» на панели свойств.

Необходимо помнить, что горизонтальная прямая параллельна оси абсцисс текущей системы координат. Горизонтальные, построенные в системе координат, повернутой относительно абсолютной системы, не будут параллельны горизонтальным сторонам листа.

3. Вертикальная прямая.

Построение аналогично построению горизонтальных прямых, поэтому разберетесь самостоятельно.

Необходимо помнить, что вертикальная прямая параллельна оси ординат текущей системы координат. Вертикальные, построенные в системе координат, повернутой относительно абсолютной системы, не будут параллельны вертикальным сторонам листа.

4. Параллельная прямая.

Для построения параллельной прямой нам потребуется объект параллельно которому она пройдет. В качестве таких объектов могут выступать: вспомогательные прямые, отрезки, звенья ломаной, стороны многоугольников, размерные линии и т.п. Давайте построим параллельную прямую для горизонтальной прямой, проходящей через начало координат.

Вызываем команды Инструменты-Геометрия-Вспомогательные прямые-Параллельная прямая.

Или через компактную панель, нажатием кнопок: Геометрия-Параллельная прямая.

Указываем базовый объект для построения параллельной прямой (в нашем случае горизонтальная прямая проходящая через начало координат). Задаем расстояние от базового объекта до параллельной прямой. Щелчком левой кнопки мыши указывается точка через которую прямая пройдет, либо вводится значение в соответствующее поле на панели свойств. Введем значение 30 мм, нажимаем клавишу Enter.

Системой будут предложены два фантома по обе стороны от базовой линии, каждый из них находится на заданном расстоянии от базового объекта. Обратите внимание на панель свойств, в группе «Количество прямых» активен переключатель «Две прямые». Для создания одной прямой можно включить переключатель «Одна прямая».

Чтобы зафиксировать фантом (активный фантом выделяется сплошной линией) нужно щелкнут на кнопке «Создать объект». Если Вы хотите зафиксировать оба фантома то повторно нажмите кнопку «Создать объект», а затем на кнопку «Прервать команду».

Иногда возникает необходимость сразу построить параллельную прямую для другого объекта, для этого служит кнопка «Указать заново». После её нажатия указывается новый базовый объект для построения параллельной прямой.

На этом пока все. В следующем уроке мы продолжим изучение вспомогательных прямых.

Если у Вас есть вопросы можно задать их ЗДЕСЬ.

1  2  3  4  5  6  7  8  9  10  11  12  13  14  15  16  17

Список последних уроков по программе Компас-3D

---

Автор: Саляхутдинов Роман

«БОСК 8.0» Познай Все Cекреты КОМПАС-3D Более 100 наглядных видеоуроков; Возможность быстрее стать опытным специалистом КОМПАС-3D; Умение проектировать 3D изделия (деталей и сборок) любой степени сложности; Гарантии доставки и возврата. >> Читать Полное Описание <<

---

Автор: Саляхутдинов Роман

«БОСК 5. 0″ Новый Видеокурс. «Твердотельное и Поверхностное Моделирование в КОМПАС-3D» Большая свобода в обращении с поверхностями; Возможность формирования таких форм, которые при твердотельном моделировании представить невозможно; Новый уровень моделирования; Гарантии доставки и возврата. >> Читать Полное Описание <<

---

Автор: Саляхутдинов Роман

«Эффективная работа в SolidWorks» Видеокурс. «Эффективная работа в SolidWorks» поможет Вам: Многократно сократить временя на освоение программы; Научит проектировать 3D изделия (деталей и сборок) любой степени сложности; создавать конструкторскую документацию; проводить инженерный анализ. Поможет быстрее стать грамотным специалистом; Гарантии доставки и возврата. >> Читать Полное Описание <<

---

Автор: Дмитрий Родин

«AutoCAD ЭКСПЕРТ» Видео самоучитель По AutoCAD 60 наглядных видеоуроков; Более 15 часов только AutoCAD; Создание проектов с нуля прямо у Вас на глазах; 365-дневная гарантия >> Читать Полное Описание <<

Фронтальная и горизонтальная проекции предмета. Способ прямоугольных проекций

Фронтальная и горизонтальная проекции предмета на чертеже связаны между собой вертикальными линиями связи. Фронтальная и профильная проекции связаны между собой горизонтальными линиями связи. Горизонтальная и профильная проекции связаны между собой горизонтально-вертикальными линиями связи, имеющими общую точку на так называемой постоянной прямой k₁₂₃ комплексного чертежа.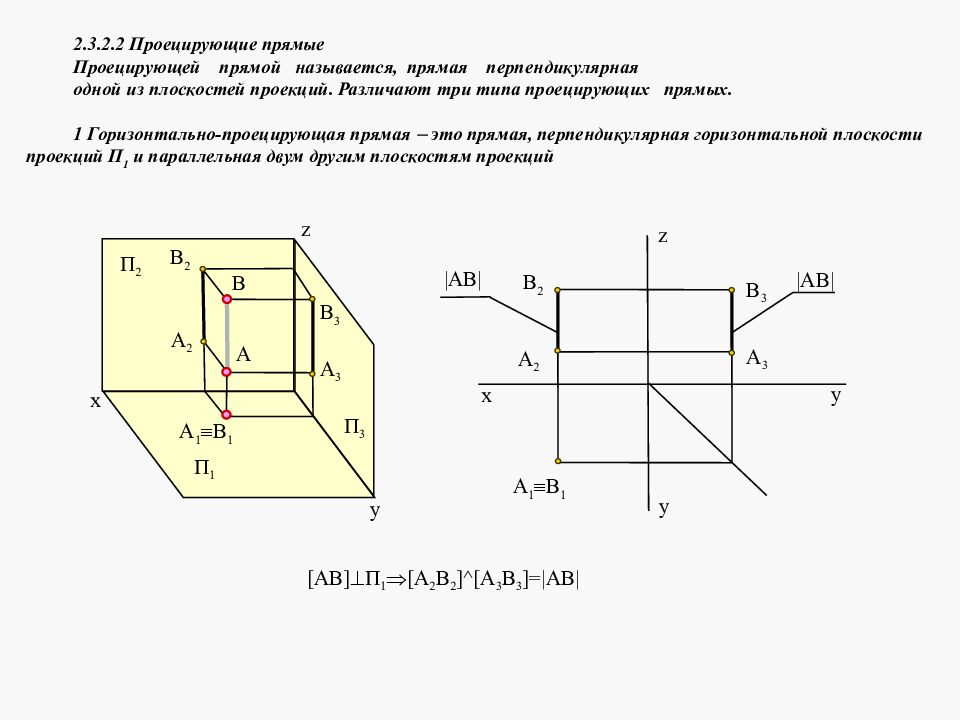 Эта прямая проходит под углами 45° к осям у₁ и у₃.

Способ прямоугольных проекций имеет меньшую наглядность, но зато отличается следующими положительными свойствами:

n
1. дает исчерпывающие сведения о предмете благодаря примененик нескольких видов и условных разрезов;
n
2. отличается простотой, так как каждый вид представляет собой изображение предмета лишь с одной стороны;
n
3. отличается точностью и удобством измерений.
n

Этот способ является поэтому основным для изображения предметен во всех отраслях техники. Только при изображении земной поверхности и производстве работ, связанных с ней, более удобен другой способ прямо угольных проекций, называемый способом проекций с числовыми отметками.
n
nTBegin—>TEnd—>n
n

Рис. 1

n

n

При этом способе используется одна горизонтальная плоскость проекций П₁. Высоты точек записываются с помощью числовых отметок (рис. 2, а).

Кроме числовых отметок, используются кривые линии — горизонтали которые Соединяют на чертеже проекции точек местности, имеющих одну и ту же высоту.

Приведенный план местности изображает возвышенность с наивысшей отметкой 84,4 м. Местность полого понижается вправо и более круто влево. Правая пониженная часть местности имеет отметку 81 м, что видно из записи, сделанной около крайней правой горизонтали. На рис. 2, б для наглядности нарисован участок местности. Проекции с числовыми отметками применяются в геодезии и топографическом черчении.

В рассматриваемой второй части курса, кроме основных сведений по начертательной геометрии, будет изложен раздел проекционного черчения. В этом разделе будут применяться и закрепляться способы изображений, изученные в начертательной геометрии. Причем если в начертательной геометрии объектами изучения являются точки, линии, плоскости и геометрические тела, то в проекционном черчении будут рассматриваться более сложные фигуры, являющиеся комбинацией геометрических тел. Кроме того, в этом разделе будут изучаться некоторые условности, принятые в практике технического черчения.

Этот раздел поможет подойти вплотную к изучению основной части курса — машиностроительного черчения.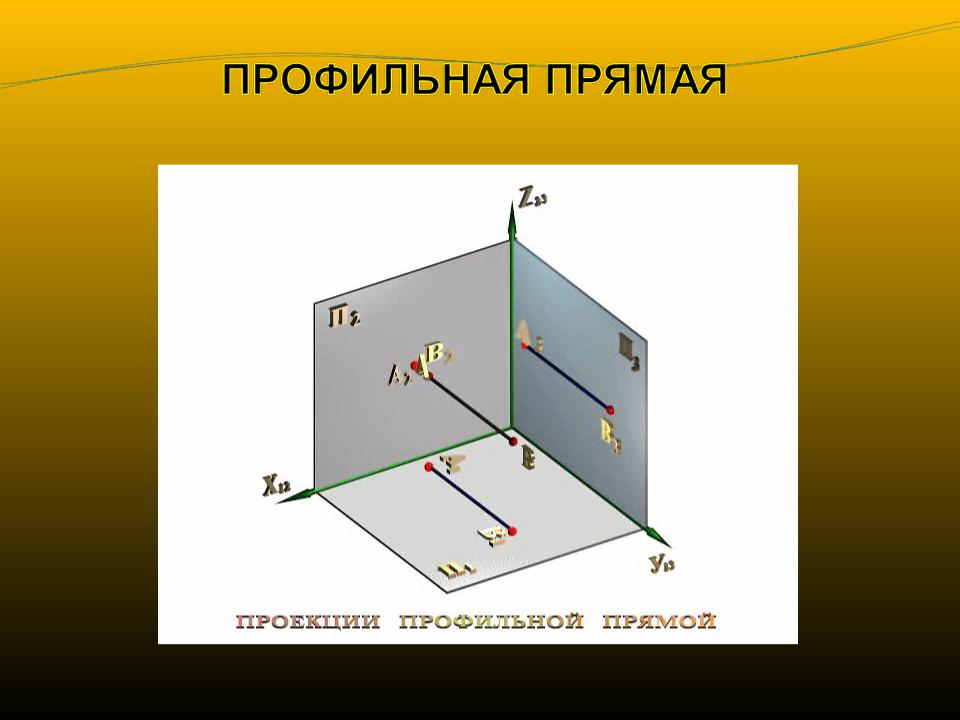

n

n

TBegin—>TEnd—>n
n

Рис. 2

Образование и обучение Сомали, искусство, экономика и инвестиции, политика, культура, программы лоббирования, фотогалерея на сайте www.sopri.org.

Горизонтальная линия — определение и примеры — Cuemath

Знаете ли вы, что подразумевается под горизонтом?

Горизонт — это линия, по которой кажется, что поверхность земли и небо встречаются (но на самом деле они не пересекаются).

Слово «горизонтальный» происходит от слова «горизонт».

«Горизонтально» означает «из стороны в сторону».

Горизонтальные линии — это линии, параллельные горизонту.

Давайте узнаем подробнее о горизонтальных линиях.

План урока

Что такое горизонтальные линии?

Определение горизонтальной линии

• Обычно горизонтальные линии — это спящие линии.
• Горизонтальные линии — это линии, параллельные горизонту.
• Горизонтальные линии в координатной геометрии — это линии, параллельные оси x.

---

Горизонтальные изображения

Примеры горизонтальных линий в реальной жизни

Вот несколько примеров горизонтальной линии в реальной жизни.

Другие популярные примеры включают ступеньки на лестнице, доски на железнодорожных путях и т. Д.

Примеры горизонтальных линий в геометрии

В геометрии мы можем найти горизонтальные линейные сегменты самых разных форм, например, четырехугольники, трехмерные формы и т. Д.

В координатной геометрии горизонтальные линии — это линии, параллельные оси x.

Вот несколько горизонтальных линий на координатной плоскости.

---

Что такое горизонтальные и вертикальные линии?

• «Горизонтальный» означает «из стороны в сторону», а горизонтальная линия — это не что иное, как линия сна.
• «Вертикаль» означает «вверх-вниз», а вертикальная линия — это не что иное, как стоячая линия.

«Горизонтальный» и «вертикальный» — слова, противоположные друг другу.

Горизонтальные и вертикальные линии перпендикулярны друг другу.

---

Как сделать горизонтальную линию?

Чтобы провести горизонтальную линию на простой бумаге, можно использовать линейку. Поместите его параллельно горизонтальному краю бумаги и проведите линию по линейке.

А как нарисовать горизонтальную линию на координатной плоскости? Посмотрим.

Чтобы нарисовать горизонтальную линию,

• Поместите точку в любую случайную точку на координатной плоскости, скажем, в (2, -3).
• Определите его координату y. Здесь координата Y равна -3.
• Постройте другие точки, координата Y которых совпадает с координатой точки на графике. Построим график (1, -3), (-2, -3) и т. Д.
• Соедините все точки и вытяните с обеих сторон, чтобы получилась горизонтальная линия.

---

Уравнение горизонтальной линии

В последнем разделе мы видим, что y-координаты всех точек на горизонтальной линии совпадают.

Таким образом, уравнение горизонтальной прямой, проходящей через любую точку \ ((a, b) \), имеет вид:

Здесь \ (x \) отсутствует. Это означает, что координата x может быть любой, тогда как координата y всех точек на линии должна быть только \ (b \).

Наклон горизонтальной линии равен 0, поскольку, сравнивая \ (y = b \) с \ (y = mx + b \), мы получаем наклон, равный \ (m = 0 \).

Вот пример:

Обратите внимание на некоторые точки на этой линии: (-5, 3), (-1, 3), (4, 3), (7, 3).

Вы можете видеть, что y-координата всех этих точек постоянна, то есть 3. Следовательно, уравнение этой прямой равно \ (y = 3 \).

---

Как использовать горизонтальную линию?

Горизонтальная линия симметрии

Горизонтальные линии используются для обозначения симметрии.

Горизонтальная линия симметрии — это горизонтальная линия, которая точно разделяет фигуру на две равные части, так что при складывании фигуры вдоль этой линии одна часть перекрывает другую.

На каждом из следующих рисунков пунктирная линия представляет собой горизонтальную линию симметрии.

Тест горизонтальной линии

Тест горизонтальной линии используется для определения, является ли функция однозначной.

Согласно тесту горизонтальной линии, функция НЕ является однозначной, если существует горизонтальная линия, которая проходит более чем через одну точку графика (функции).

Пример 1

Здесь \ (f (x) \) равно единице, потому что каждая горизонтальная линия проходит не более чем через одну точку графика.

Пример 2

Здесь \ (g (x) \) не один, так как существует горизонтальная линия, проходящая более чем через одну точку графика.

Важные примечания

1. Горизонтальная линия (кроме оси x) не имеет пересечений по оси x.
2. Уравнение горизонтальной прямой, проходящей через \ ((a, b) \), есть \ (y = b \).
3. Уравнение вертикальной прямой, проходящей через \ ((a, b) \), есть \ (x = a \).
4. Наклон горизонтальной линии равен 0, поскольку ее уравнение имеет форму \ (y = b \), и сравнивая его с формой пересечения наклона, мы получаем, что ее наклон равен \ (m = 0 \).
5. Тест вертикальной линии используется для определения, является ли отношение функцией, тогда как тест горизонтальной линии используется для определения, является ли функция однозначной.

Решенные примеры

Можем ли мы помочь Джейку найти уравнение следующей строки?

Решение

Данная линия представляет собой горизонтальную линию, проходящую через точку: \ [(a, b) = (1,3) \]

Мы знаем, что уравнение горизонтальной прямой, проходящей через точку \ ((a, b) \), есть \ (y = b \).

Следовательно, уравнение данной строки:

Можем ли мы помочь Аве определить заглавные алфавиты, у которых есть только горизонтальная линия симметрии, но нет вертикальной линии симметрии?

Решение

Давайте определим симметрию (горизонтальную / вертикальную) каждого алфавита.

Мы видим, что только алфавиты B, C, D, E и K имеют только горизонтальную линию симметрии, но не имеют вертикальной линии симметрии.2 \)

с) \ (ч (х) = | х | \)

г) \ (к (х) = \ ln х \)

Решение

Давайте изобразим каждую из этих функций и посмотрим, какая из них пройдет проверку горизонтальной линии.

Мы рисуем горизонтальную линию, чтобы увидеть, сколько графиков имеют не более одной точки пересечения с горизонтальной линией.

Здесь каждая из \ (h \) и \ (g \) имеет две точки пересечения с горизонтальной линией, и, следовательно, они не являются однозначными. Таким образом, у них не может быть обратного.

В то время как каждый из \ (f \) и \ (k \) имеет только одну точку пересечения с горизонтальной линией.

Следовательно, \ (f \) и \ (k \) однозначны и, следовательно, у каждого из них есть обратное. Следовательно,

\ (\ следовательно \) Только \ (f \) и \ (k \) имеют инверсию

---

Интерактивные вопросы

Вот несколько занятий для вас.

Выберите / введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.

Советы и хитрости

1. Всякий раз, когда мы видим уравнение вида \ (y = \) константа, мы должны понимать, что оно представляет собой уравнение горизонтальной линии.
2. Уравнение вида \ (y = \) константа представляет собой постоянную функцию.
3. Чтобы определить, есть ли у функции инверсия, используйте тест горизонтальной линии (потому что для того, чтобы функция имела инверсию, она должна быть один-один).

Подведем итоги

Мини-урок был посвящен увлекательной концепции «Горизонтальная линия». Математическое путешествие вокруг горизонтальной линии начинается с того, что студент уже знает, и переходит к творческому созданию новой концепции в молодых умах. Сделано таким образом, чтобы не только было понятно и легко понять, но и навсегда осталось с ними. В этом заключается магия Куэмат.

О компании Cuemath

В Cuemath наша команда экспертов по математике стремится сделать обучение интересным для наших любимых читателей, студентов!

Благодаря интерактивному и увлекательному подходу «обучение-обучение-обучение» учителя исследуют тему со всех сторон.

Будь то рабочие листы, онлайн-классы, сеансы сомнений или любые другие формы отношений, мы в Cuemath верим в логическое мышление и интеллектуальный подход к обучению.

---

Часто задаваемые вопросы по Горизонтальной линии

1. Есть ли наклон у горизонтальной линии?

Нет, горизонтальная линия не имеет наклона, т.е. наклон горизонтальной линии равен 0.

2. Что такое горизонтальная и вертикальная линия?

• Горизонтальная линия — это линия, параллельная оси x, и ее уравнение имеет вид \ (y = \) константа.
• Вертикальная линия — это линия, параллельная оси y, и ее уравнение имеет вид \ (x = \) постоянная.

3. Что такое вертикальная линия?

Вертикальная линия — это линия, параллельная оси y, и ее уравнение имеет вид \ (x = \) константа.

4. Как нарисовать горизонтальную линию?

Чтобы нарисовать горизонтальную линию на бумаге, используйте линейку. Поместите его параллельно горизонтальному краю бумаги и проведите линию по линейке.

Чтобы нарисовать горизонтальную линию на координатной плоскости,

• Поместите точку в любую случайную точку на координатной плоскости, скажем, в (2, -3).
• Определите его координату y. Здесь координата Y равна -3.
• Постройте другие точки, координата Y которых совпадает с координатой точки на графике. Построим график (1, -3), (-2, -3) и т. Д.
• Соедините все точки, чтобы получить горизонтальную линию.

5. Какое уравнение представляет собой горизонтальная линия?

Уравнение горизонтальной прямой, проходящей через точку (a, b): y = b.

6. Горизонтально из стороны в сторону или вверх-вниз?

Как мы узнали на этой странице, горизонталь — это линия из стороны в сторону.

7. Что подразумевается под горизонтальной линией?

• Горизонтальные линии — это линии, параллельные горизонту.
• Горизонтальные линии в координатной геометрии — это линии, параллельные оси x.
• Горизонтальные линии — это спящие линии.

8. Какой пример вертикальный?

Примером «вертикали» является электрический столб, перпендикулярный земле.

9. Как называются горизонтальные линии на земном шаре?

Горизонтальные линии на земном шаре называются «широтами».«

10. Как называются вертикальные линии на земном шаре?

Вертикальные линии на земном шаре называются «долготами».

Вертикальные и горизонтальные линии — Алгебра II

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Определение горизонтальной линии и пример

Что такое горизонтальная линия?

В техническом анализе на графике цены часто проводят горизонтальную линию, чтобы выделить области поддержки или сопротивления.

В геометрическом анализе горизонтальная линия проходит параллельно оси x. Другими словами, на идеально горизонтальной линии все значения в строке будут иметь одинаковое значение y.

Ключевые выводы

• Горизонтальная линия обычно используется в техническом анализе для обозначения областей поддержки или сопротивления.
• Горизонтальная линия проходит параллельно оси x.
• В техническом анализе горизонтальная линия обычно проводится по максимуму колебания или их серии, где каждый максимум в серии останавливается на одном и том же уровне.То же самое применимо и к минимумам колебаний.

Понимание горизонтальной линии

Горизонтальные линии обычно используются в техническом анализе, чтобы выделить области поддержки, где цена перестала падать, а затем отскакивала в предыдущих случаях, или сопротивления, когда цена перестала расти, а затем продолжала падать в предыдущих случаях.

Горизонтальная линия проводится путем соединения аналогичных минимумов колебания цены для создания горизонтальной линии поддержки. Для горизонтальной линии сопротивления связаны аналогичные максимумы колебаний.

Затем горизонтальная линия используется в аналитических или торговых целях. Например, если цена актива движется между горизонтальными линиями поддержки и сопротивления, то считается, что цена находится в пределах диапазона.

Движение ниже горизонтальной линии поддержки может указывать на дальнейшее снижение цены, но если поддержка удерживается и цена отскакивает выше, цены могут появиться. Те же принципы применимы к горизонтальной линии сопротивления. Если цена поднимется выше сопротивления, могут появиться более высокие цены.Если цена достигает сопротивления, а затем начинает снижаться, горизонтальная линия удерживается, и трейдеры будут следить за более низкими ценами.

Проще говоря, горизонтальная линия на любом графике — это место, где значения оси Y равны. Если он был нарисован, чтобы показать серию максимумов данных, точка данных, перемещающаяся над горизонтальной линией, будет указывать на рост значения оси Y по сравнению с последними значениями в выборке данных.

Фундаментальный горизонтальный анализ

Горизонтальный анализ используется для сравнения значений или цен с течением времени.Это аспект фундаментального анализа, в котором аналитик будет сравнивать различные отчеты о прибылях и убытках с течением времени. В этом виде анализа время функционирует как горизонтальная ось x и позволяет аналитикам вычислять процентные изменения во времени, что является полезным инструментом для представления степени изменения.

Горизонтальный анализ рассматривает тенденции финансовой отчетности за несколько периодов с использованием указанного базового периода и обычно показывает изменения по сравнению с базовым периодом в долларах и процентах.

Процентное изменение рассчитывается путем сначала деления изменения в долларах между годом сравнения и базовым годом на стоимость позиции в базовом году, а затем умножением частного на 100. Например, когда вы слышите, что кто-то говорит, что выручка увеличилась на 10%, это В прошлом квартале этот человек использовал горизонтальный анализ.

Горизонтальный анализ можно использовать по любой статье финансовых показателей компании, от выручки до прибыли на акцию (EPS), и он полезен при сравнении результатов деятельности различных компаний.

Горизонтальная линия относительно кривых спроса и предложения

Кривые спроса и предложения построены с ценой на вертикальной оси графика и объемом спроса на горизонтальной оси. При взгляде на кривые спроса и предложения идеально горизонтальная линия указывает на то, что товар обладает идеальной эластичностью или что его спрос немедленно реагирует на изменения цены. Когда цена совершенно эластичного товара или услуги превышает рыночную цену, объем спроса падает до нуля.При идеальной эластичности потребители просто не готовы тратить на товар или услугу больше, чем определенная цена.

Пример использования горизонтальной линии в техническом анализе

Проведение горизонтальной линии — одна из простейших форм технического анализа, но она также дает важную информацию. На графике ниже горизонтальная линия проведена на биржевом фонде (ETF) SPDR S&P 500 (SPY).

Изображение Сабрины Цзян © Investopedia 2021

Восходящий тренд — это когда цена достигает более высоких максимумов и более высоких минимумов колебаний.Следовательно, горизонтальная линия может выделять, когда цена делает новый максимум, в этом случае показывая признаки восходящего тренда. На приведенном выше графике SPY цена движется выше горизонтальной линии, что указывает на восходящий тренд. Если цена снова упадет ниже горизонтальной линии, это может предупредить о том, что восходящий тренд потерпел неудачу и может произойти снижение цен.

В этом смысле горизонтальная линия действует как линия на песке, где движение над линией является бычьим.

Разница между горизонтальной линией и линией тренда

Оба эти термина могут относиться к одному и тому же: нарисованным линиям на графике.В то время как горизонтальная линия является строго горизонтальной, линия тренда обычно проходит под углом и проводится вдоль восходящих минимумов колебаний во время восходящего тренда или вдоль падающих максимумов колебаний во время нисходящего тренда.

Ограничения использования горизонтальной линии в техническом анализе

Горизонтальная линия не является реальной преградой для цены. Это технический инструмент, который может помочь трейдерам определить, следует ли им быть более медвежьим или бычьим.

То, где проводится горизонтальная линия, субъективно.Не все трейдеры могут разместить горизонтальную линию по одной и той же цене.

При очень важных ценах, где может быть проведена горизонтальная линия, цена может развернуться вокруг нее. Это может вызвать путаницу или некоторые потенциально убыточные сделки, пока цена не сделает более решительное движение выше или ниже линии.

Значение, пример, правила и многое другое

Горизонтальная линия: Горизонтальная линия — это широко используемый термин в математике, а также в нашей повседневной жизни. В координатной геометрии линия называется горизонтальной, если две точки на линии имеют одинаковые координаты Y.Говоря простым языком, прямая линия, параллельная горизонту, называется горизонтальной линией. Горизонтальные линии также называют линиями сна. На оси X-Y горизонтальная линия всегда будет параллельна оси x и перпендикулярна оси y. В этой статье вы можете найти все о горизонтальных линиях, примерах, уравнениях и фактах. Читай дальше что бы узнать!

Горизонтальные линии

Горизонтальные линии в координатной геометрии — это линии, параллельные оси x. Другими словами, линия, имеющая точки в одинаковых точках координаты Y, называется горизонтальной линией.

Горизонтальная аналогия для понимания горизонтальной линии

Горизонт — это линия, по которой земля и небо встречаются. Слово «горизонтальный» происходит от слова «горизонт». Таким образом, простыми словами линия, параллельная горизонту, называется горизонтальной линией.

Как нарисовать горизонтальную линию?

Чтобы нарисовать горизонтальную линию с помощью графика, выполните следующие действия:

• — Для начала определите оси x и y и отметьте числа.
• — Выберите разные точки с разными координатами x, но с одинаковой координатой y.
• — Соедините все точки и вытяните их с обеих сторон, чтобы получить горизонтальную линию

Уравнение горизонтальной линии

В геометрии мы можем представить горизонтальную линию в форме уравнения. Составим уравнение для горизонтальной линии, проходящей через точку (0,2), как показано ниже:

Мы знаем, что прямая линия представлена ​​как y = mx + C

Для точки (0, 2) уравнение будет следующим:
y = (0) x + C
y = C
Линия пересекает ось y в точке (0, 2), таким образом, значение C = 2
Следовательно, y = 2
Следовательно, уравнение горизонтальной линии y = 2

Обратите внимание, что на приведенном выше графике даже для других точек, таких как (-3, 2), (3, 2) или (-6, 2), (6, 2) или любых других точек, координаты y всегда будет 2.В этой ситуации линия будет горизонтальной линией.

Использование горизонтальной линии

Горизонтальная линия может помочь визуализировать симметричность фигуры или трехмерного объекта. Чтобы проверить симметрию, визуализируйте горизонтальную линию, проходящую через ось фигуры и объекта, так что, когда они сложены по горизонтальной линии, обе равные части перекрываются.

Что такое горизонтальная и вертикальная линия

Горизонтальные линии — это линии, параллельные оси X, а точка пересечения оси Y всегда одинакова для всех точек на линии.Принимая во внимание, что вертикальные линии — это линии, параллельные оси Y, и точка пересечения по оси X будет такой же. Проверьте графическое изображение горизонтальных и вертикальных линий снизу:

Решенные примеры горизонтальной линии

Давайте рассмотрим несколько решенных примеров на горизонтальных линиях:

Пример 1: Проверьте, сколько алфавитов симметрично по горизонтали, по изображению, приведенному ниже:

Решение: Мы нарисовали горизонтальную линию поперек букв, чтобы определить, симметричны ли буквы.Алфавит «А» не симметричен по горизонтали, но симметричен по вертикали. Принимая во внимание, что алфавиты «B», «C» и «D» симметричны по горизонтали.

Пример 2: Проверьте, какое уравнение соответствует горизонтальной линии на приведенном ниже графике:

Решение: Уравнения линий следующие:

• y = x ² — 5
• y = x ²
• y = x
• y = 3
• x = 3

В вышеупомянутых уравнениях линия с таким же отрезком y во всех точках прямой y = 3.Для линии y = 3 точка пересечения по оси x изменяется, а точка пересечения по оси y остается постоянной. Следовательно, y = 3 — горизонтальная линия.

Бесплатные учебные материалы по Embibe

Воспользуйтесь следующими бесплатными учебными материалами Embibe, которые определенно помогут вам на экзаменах:

Часто задаваемые вопросы

Проверьте часто задаваемый вопрос ниже:

В. Какое правило для горизонтальной линии? А.Горизонтальная линия имеет следующие свойства: — линия, параллельная оси x координатной плоскости. — Наклон горизонтальной линии равен нулю — Пересечение оси Y горизонтальной линии является постоянным.

В. Как нарисовать горизонтальную линию? A. Чтобы нарисовать горизонтальную линию, координаты y должны быть постоянными, а координаты x могут изменяться. Постройте несколько точек с постоянными координатами y и нарисуйте линию, соединяющую их.

В. Что такое горизонтальная и вертикальная линия? A. Горизонтальная линия, параллельная оси x. В то время как вертикальная линия параллельна оси y.

В. Есть ли наклон у горизонтальной линии? A. Нет, горизонтальная линия не имеет наклона.

В. Какое уравнение представляет собой горизонтальную линию? A. Уравнение горизонтальной линии будет: y = постоянная.Константа будет соответствовать координате y.

В. Как называются горизонтальные линии на земном шаре? A. Горизонтальные линии на земном шаре называют широтой.

Надеемся, эта статья вам поможет. Если у вас есть какие-либо вопросы, не стесняйтесь задавать их в разделе комментариев ниже. Мы свяжемся с вами в ближайшее время.

579 Просмотры

Особые случаи линейного уравнения: горизонтальные линии

Уравнение горизонтальной линии

Горизонтальная линия проходит слева направо и параллельна оси x.Это также линейная линия, очень похожая на многие, с которыми вы сталкивались до сих пор (например, форма пересечения уклона, общая форма). Но что делает его таким особенным? Уравнение горизонтальной линии уникально, и вы скоро поймете, почему.

Какой наклон горизонтальной линии

Когда мы имеем дело с горизонтальными линиями, каков их наклон? Вы, вероятно, сможете ответить на этот вопрос, не вдаваясь в математику. Посмотрите на идеально горизонтальную линию на графике ниже.

Наклон говорит нам, насколько крута линия.Фактически, наклон можно определить по подъему / спуску, что помогает нам определить крутизну. Глядя на красную линию выше, насколько она крутая? Наклон горизонтальной линии на самом деле равен 0. Она никогда не поднимается (и не падает), поэтому, если бы мы нашли подъем / пробег, мы бы получили 0 / пробег. 0, деленный на что угодно, все равно равен 0, и, следовательно, наклон нашей горизонтальной линии равен 0.

Немного отступая, каково уравнение горизонтальной линии? Поскольку линия горизонтальна и проходит параллельно оси x, уравнение просто:

y = y-точка пересечения линии или, чаще y = b (где b = точка пересечения с y)

Примеры задач

Вопрос 1:

Определите линию уравнений из следующих точек.

я) (-5, 2), (3, 2)

Решение:

Еще раз взгляните либо на точки, либо на сам график. Обе координаты оси y равны 4. Линия проходит по y = 4. Ваш ответ будет заключаться в том, что уравнение y = 4.

iii) (б, м), (в, м)

Решение:

Теперь вы понимаете, что даже без чисел, координаты y могут рассказать вам уравнение линии. В этом случае уравнение = y = m.

Вопрос 2:

Напишите уравнение линии с заданной информацией:

Горизонтально, проходит через (4,7)

Решение:

Хотя нам не дают двух точек для наблюдения, предоставленная информация говорит нам все, что нам нужно знать.В нем говорится, что линия, с которой мы имеем дело, горизонтальна. Следовательно, мы можем взглянуть только на координату y данной точки, чтобы помочь нам определить уравнение горизонтальной линии. Вы должны обнаружить, что уравнение = y = 7.

Ищете, чем заняться дальше? Узнайте о параллельных и перпендикулярных линиях в линейных функциях и о том, как они должны выглядеть. Вы также можете узнать, как построить график линейных неравенств с двумя переменными или системы линейных неравенств. Еще многое предстоит узнать с точки зрения линейных функций, поэтому убедитесь, что вы усвоили этот урок о закреплении уклона горизонтальной линии, прежде чем двигаться дальше!

Координатная геометрия: вертикальные и горизонтальные линии

В последнем видео мы рассмотрели графические линии.Нет, мы подробнее рассмотрим вертикальные и горизонтальные линии, а также то, как мы можем найти их уравнения.

Как мы обсуждали в последнем видео, каждая линия в плоскости x-y имеет свое собственное уникальное уравнение. Самыми простыми уравнениями являются уравнения для горизонтальных и вертикальных линий.

Давайте представим типичную горизонтальную линию. Итак, вот горизонтальная линия, и я выделил точки на ней. Давайте просто подумаем о координатах этих точек.

Некоторыми точками на линии являются такие, как (0, -3), (1, -3), (2, -3) и т. Д. -1, -3, -2, -3 и т. Д. X -координата может быть любым числом в числовой строке, это может быть даже дробь. Я их не перечислял, но это тоже могут быть дроби. Но обратите внимание, что координата Y зафиксирована на месте. Координата y должна быть отрицательной 3.

Что ж, очень элегантный способ обозначить это условие — просто y = -3. Это уравнение линии, которое суммирует все, что вам нужно знать о линии.Чтобы квалифицироваться как точка на этой линии, эта точка должна иметь координату y, равную -3, а координата x может быть любой, какой она хочет. И это уравнение линии.

Общая форма горизонтальной линии

Другой способ подумать об этом: любая горизонтальная линия будет полностью состоять из точек на одной высоте, то есть на одинаковом расстоянии выше или ниже оси x. Если мы просто укажем эту высоту как место, где горизонтальная линия пересекает ось Y, тогда мы укажем все об этом.Таким образом, общая форма горизонтальной линии y = K, где K — высота линии.

И K также будет точной точкой на оси y, где линия пересекает ось y. Мы называем это перехватчиком y . Мы поговорим об этом подробнее в следующих видео. Например, эта линия здесь всегда имеет координату y, равную 2, и она пересекает ось y в точке 2. Итак, должно быть уравнение y = 2.

Что такое уравнение оси X?

Какое уравнение представляет собой сама ось абсцисс? Вот это интересно.Ось x представляет собой горизонтальную линию, поэтому у нее должно быть собственное уникальное уравнение. Каждая линия в плоскости x y имеет собственное уникальное уравнение, в то время как ось x выровнена, поэтому она должна иметь собственное уникальное уравнение. Теперь давайте подумаем об этом: ось x представляет собой горизонтальную линию с нулевой высотой.

Поскольку он проходит через ось y в начале координат, он проходит через ноль, ноль. Это означает, что уравнение оси x должно быть y = 0, и это уравнение оси x.

Вертикальные линии

Теперь поговорим о вертикальных линиях.Точно так же, как горизонтальные линии имеют одинаковые координаты y, вертикальные линии имеют одинаковые координаты x.

Итак, здесь мы видим, что линия пересекает ось x в точке 4. Мы также видим, что все точки выше и ниже нее находятся на одинаковом расстоянии справа от оси y. Таким образом, все они должны иметь координату x, равную 4. И, следовательно, хороший способ написать уравнение этой линии будет просто x = 4, а не слова, которые мы устанавливаем для этой линии, а именно: координата x должна быть быть 4.

Координаты Y могут быть где угодно, и если мы будем следовать этому правилу, мы всегда попадем на эту конкретную линию. Уравнение любой вертикальной линии, проходящей через ось x в точке K, должно быть x = K. Точно так же уравнение оси y, вертикальной линии, пересекающей ось x в нуле, должно быть x = 0.

Две точки с одинаковой координатой X или Y

Итак, уравнение оси x y = 0, уравнение оси y имеет вид x = 0. Любые две точки, которые имеют одну и ту же координату y, должны лежать на одной и той же горизонтальной линии.Это очень важная идея. И это то, что вам нужно распознать, потому что тест просто даст вам набор координат.

Вы должны будете распознать, что эти две координаты имеют одинаковую координату y. Значит, они должны быть на горизонтальной линии. Точно так же любые две точки с одинаковой координатой x должны лежать на одной и той же вертикальной линии. Если C имеет такую ​​же координату x, что и точка A, и такую ​​же координату y, что и точка B, тогда должно быть верно, что угол, ACB, является прямым углом, углом 90 градусов.

Потому что это угол между горизонтальной линией и вертикальной линией. Имейте в виду, что горизонтальная линия может проходить через первый и второй квадранты, то есть, если она выше оси x, или она может проходить через третий и четвертый квадранты, если она ниже оси x. Вертикальная линия может проходить через второй и третий квадранты, если она находится слева от оси y, или через четвертый и один квадранты, если она находится справа от оси y.

Большинство горизонтальных и вертикальных линий проходят через два квадранта.Как мы увидим, большинство наклонных линий проходят через три квадранта.

Вертикальные и горизонтальные линии: практическая задача

Вот практическая задача.

Прямоугольник образован линиями y = 1, y = 4, x = 2 и line = D. Когда диагональ построена, она образует у основания угол 30 градусов. Найдите уравнение линии D.

Итак, я предлагаю вам приостановить видео, поработать над этим, а затем мы поговорим об этом.

_{Изображение Новикова Алексея}

Ладно, ну во-первых, очевидно, что D — это вертикальная линия.Как и все вертикальные линии, у него должно быть уравнение в форме x = K. Давайте подумаем об этом, мы посмотрим на треугольник и дадим вершинам буквенные названия.

Итак, точку в 2, 1 мы будем называть A, точку в K, 4 мы будем называть B, а точку в C, в K, 1 мы будем называть C. И обратите внимание, что длина этой базы равна K-2, потому что, начиная с оси Y, мы переместились бы на два деления вправо, чтобы добраться до A, а затем, когда мы переместимся в C, мы пройдем K пробелов. Итак, маленькие 2 плюс нижняя ножка этого треугольника в сумме дают K.

Это должно означать, что основание K- 2. Итак, конечно, это треугольник 30-60-90. Мы изучали это на уроке геометрии и знаем, что можем установить соотношение: A над C = корень 3 над 1. Перекрестным умножением мы получаем AC = 3 корень 3. Итак, этот AC, который равен 3 корню 3, это равно K-2, как мы уже сказали.

Итак, теперь мы должны добавить 2, чтобы решить K, и мы получаем K = 2 + 3 корня над 3. И, следовательно, уравнение прямой x = 2 + 3 корня 3.

Резюме

Таким образом, горизонтальное прямые имеют общий вид y = K.Вертикальные линии имеют общий вид x = K. Ось x имеет уравнение y = 0.

Ось y имеет уравнение x = 0. Если две точки имеют одну и ту же координату x, они разделены по вертикали. Они лежат на одной вертикальной линии. И если две точки имеют одну и ту же координату y, то они разделены по горизонтали. Они лежат на одной горизонтальной линии.

О Майке МᶜГарри

Майк создает уроки для экспертов и практические вопросы, чтобы помочь студентам GMAT добиться успеха.У него есть степень бакалавра физики и магистра религии в Гарварде, а также более 20 лет опыта преподавания, специализирующегося на математике, естественных науках и стандартизированных экзаменах. Майк любит разбивать футбольные мячи на орбите, и, несмотря на отсутствие очевидной черепно-мозговой недостаточности, он настаивает на том, чтобы болеть за Нью-Йорк Метс.

Горизонтальные и вертикальные линии

Горизонтальные и вертикальные линии представляют собой уникальные линейные уравнения. Когда наклон равен нулю, линия горизонтальна. Если наклон не определен, линия вертикальная.Обратите особое внимание на то, что здесь означает undefined, наклон вертикальной линии не определен, потому что это линия, указывающая прямо вверх, что приближает ее к бесконечности как предельному значению.

Уравнение вертикальной линии , проходящей через точку \ (P (a, b) \): \ (x = a \)

Уравнение горизонтальной линии , проходящей через точку \ (P (a, б) \) равно \ (y = b \)

Обратите внимание, насколько упрощенно каждое уравнение. Давайте разберемся, почему они такие.

Вертикальные линии

Вертикальная линия указывает прямо вверх и вниз. Это линия, параллельная оси Y графика. Вертикальная линия, определяемая при каждом значении y, имеет только одно значение x. Его наклон не определен. Это затрудняет математическое описание с использованием общего уравнения линии, поскольку у нее нет наклона, который можно было бы описать.

Неопределенный наклон эквивалентен тому, что коэффициент наклона равен нулю.Общее уравнение прямой выглядит следующим образом:
$$ Ax + By = C $$
Если мы допустим \ (B = 0 \) и попытаемся преобразовать уравнение в форму точки с наклоном линии:
$$ \ begin {align} & Ax + 0y = C & \ text {уравнение с} B = 0 \\ [1em] & 0y = -Ax + C & \ text {вычтите Ax с обеих сторон} \\ [1em] & y = \ frac { -A} {0} x + \ frac {C} {0} & \ text {попытка деления на ноль} \ end {align} $$
Это показывает нам проблему с неопределенным уклоном. В случае, когда наклон не определен, потому что он делится на ноль, исходная общая форма уравнения с \ (B = 0 \) является правильным методом поиска вертикальной линии.
$$ x = \ frac {C} {A} $$
Вышесказанное является упрощением, если бы мы просто продолжили с \ (B = 0 \). Мы, конечно, не можем делить на ноль, поэтому пример попытки упростить до формы «точка-наклон» был нелепым занятием. Он был включен, чтобы показать, насколько странным является неопределенный наклон в линейном уравнении. Мы можем определить, что любое уравнение, где y равно константе, представляет собой вертикальную линию на графике.

Горизонтальные линии

Горизонтальная линия указывает слева направо.Это перпендикулярная линия к оси Y графика. Горизонтальная линия, определяемая для каждого значения x, имеет только одно значение y. Он имеет нулевой наклон. Вариант линии намного проще описать математически, используя общее уравнение линии, чем вертикальную линию. Нулевой наклон легко учесть, потому что он подразумевает \ (A = 0 \) в общем уравнении прямой.

$$ \ begin {align} & Ax + By = C & \ text {общее уравнение линии} \\ [1em] & By = -Ax + C & \ text {вычесть Ax с обеих сторон} \\ [1em] & y = \ frac {-A} {B} x + \ frac {C} {B} & \ text {разделите обе стороны на B, теперь в форме точечного уклона} \\ [1em] && \ text {если уклон равно нулю, что означает} \ frac {-A} {B} = 0 \\ [1em] & y = \ frac {C} {B} & \ text {уравнение горизонтальной линии} \ end {align} $$
Выше показано упрощение общего уравнения прямой до уравнения, в котором наклон равен нулю.Что мы можем определить, так это то, что любое уравнение, в котором x равно константе, представляет собой горизонтальную линию на графике.

Уравнение вертикальной линии , проходящей через точку \ (P (a, b) \): \ (x = a \)

Уравнение горизонтальной линии , проходящей через точку \ (P (a, b) \) равно \ (y = b \)

---

Об авторе

Джеймс Лоуман — прикладной математик, в настоящее время работает над докторской степенью. в области вычислительной гидродинамики в Университете Ватерлоо.Он является соучредителем компании Waterloo Standard, занимающейся онлайн-обучением по математике и естественным наукам.

Если вам нужна помощь по математике, запишитесь на сеанс у Джеймса.

.