доказать неравенство онлайн с подробным решением
доказать неравенство онлайн с подробным решениемВы искали доказать неравенство онлайн с подробным решением? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и иррациональные неравенства калькулятор онлайн, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «доказать неравенство онлайн с подробным решением».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает.
Где можно решить любую задачу по математике, а так же доказать неравенство онлайн с подробным решением Онлайн?
Решить задачу доказать неравенство онлайн с подробным решением вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Решение неравенств — ЕГЭ-апрель 2021
решить неравенство онлайн с подробным решением егэ
Шаг 1.
Введите неравенствоПодробно решает любые неравенства онлайн с возможностью изобразить неравенство на рисунке.
Примеры
Неравенства с модулем
С кубом (неравество третьей степени)
С кубическим корнем
С натуральным логарифмом
Иррациональные с квадратным корнем
С четвёртой степенью
Решение с целыми числами
Правила ввода выражений и функций
3.14159.. E Число E — основание натурального логарифма, примерно равно
2,7183.. I Комплексная единица Oo Символ бесконечности — знак для бесконечности
© Контрольная работа РУ — калькуляторы онлайн
С кубическим корнем
Подробно решает любые неравенства онлайн с возможностью изобразить неравенство на рисунке.
Примеры
Неравенства с модулем
С кубом (неравество третьей степени)
С кубическим корнем
С натуральным логарифмом
Иррациональные с квадратным корнем
С четвёртой степенью
Решение с целыми числами
Правила ввода выражений и функций
3.
= v$ или $x = — \frac>>$ $x_ = \frac> \left(- \log + \log \right)$ $x_ = \frac> \left(\log — \log\right)$ $x_ = \frac> \left(- \log + \log \right)$ $x_ = \frac> \left(\log — \log\right)$ Данные корни $x_ = \frac> \left(\log — \log\right)$ $x_ = \frac> \left(- \log + \log \right)$ являются точками смены знака неравенства в решениях.
Сначала определимся со знаком до крайней левой точки: $x_ 5$
Значит одно из решений нашего неравенства будет при:
$x \frac> \left(- \log + \log \right)$
Также вы будете иметь графическое решение показательного неравенства:
Тэги: Неравенство
© Контрольная работа РУ — примеры решения задач
Значит одно из решений нашего неравенства будет при:
$x \frac> \left(- \log + \log \right)$
Вы получите следующее подробное решение для неравенства.
Www. kontrolnaya-rabota. ru
18.08.2017 9:35:03
2017-08-18 09:35:03
Этот математический калькулятор онлайн поможет вам Решить тригонометрическое неравенство.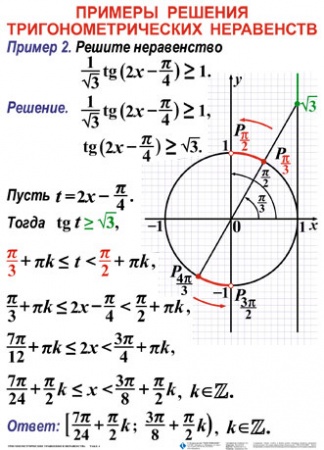
Программа для Решения тригонометрического неравенства не просто даёт ответ задачи, она приводит Подробное решение с пояснениями, т. е. отображает процесс получения результата.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> С 9 января 2019 года вводится новый порядок получения подробного решения некоторых задач.
Ознакомтесь с новыми правилами >> —> Введите тригонометрическое неравенство
Решить неравенство
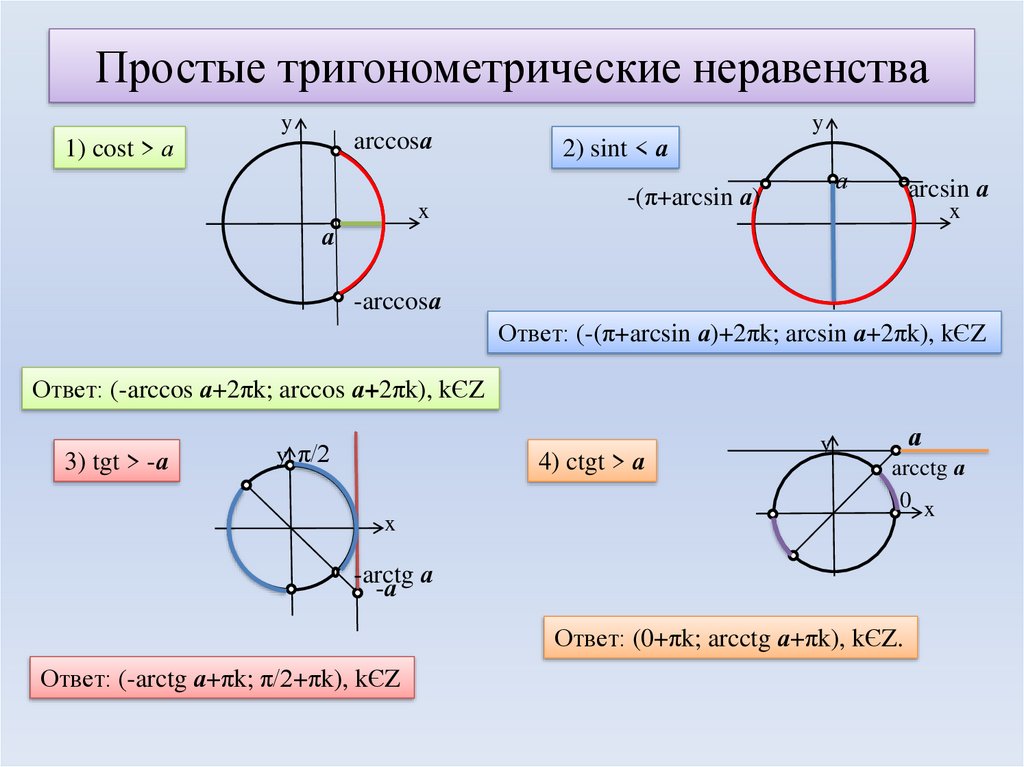
Тригонометрические неравенства
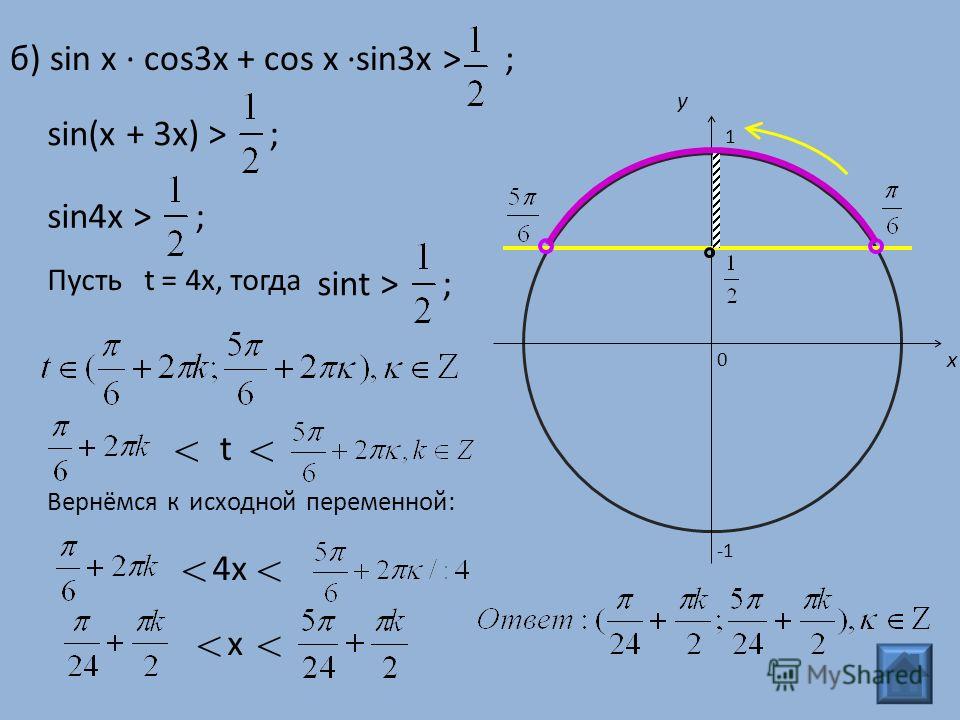
Неравенства вида \( \sin x > a \) и \( \sin x
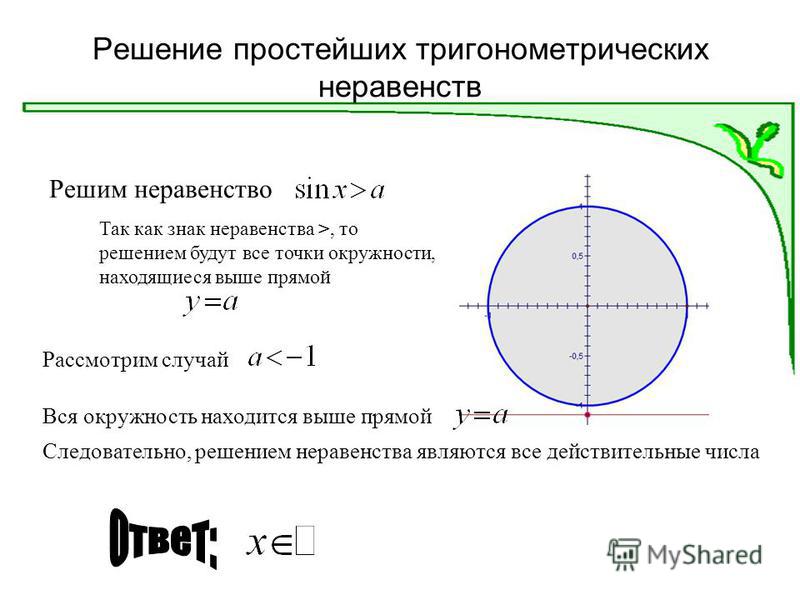
Пусть дано простейшее неравенство \( \sin x > a \).
1) При \(-1 1 \) решением неравенства является любое действительное число: \( x \in \mathbb \)
3) При \(а = 1 \) решением неравенства является любое действительное число, отличное от \( \frac + 2\pi k, \; k \in \mathbb \)
4) При \(а \leqslant -1 \) неравенство не имеет решений.
Неравенства вида \( \cos x > a \) и \( \cos x
Пусть дано простейшее неравенство \( \cos x > a \).
1) При \(-1 1\) решением неравенства является любое действительное число: \( x \in \mathbb \)
3) При \(a \leqslant -1\) неравенство не имеет решений.
4) При \(a = 1\) решением неравенства является любое действительное число, отличное от \( 2\pi k, \; k \in \mathbb \)
Неравенства вида \( tg \;x > a \) и \( tg \;x
Пусть дано простейшее неравенство \( tg \;x > a \).
Множество всех решений данного тригонометрического неравенства будем искать с помощью тригонометрического круга.
Из данного рисунка видно, что при любом \(a \in \mathbb \) решение неравенства будет таким:
$$ x \in \left(arctg \;a + \pi k; \;\; \frac + \pi k \right), \; k \in \mathbb $$
Пусть дано простейшее неравенство \( tg \;x
Неравенства вида \( ctg \;x > a \) и \( ctg \;x
Пусть дано простейшее неравенство \( ctg \;x > a \).
Множество всех решений данного тригонометрического неравенства будем искать с помощью тригонометрического круга.
Из данного рисунка видно, что при любом \(a \in \mathbb \) решение неравенства будет таким:
$$ x \in ( \pi k; \;\; arcctg \;a + \pi k ), \; k \in \mathbb $$
Пусть дано простейшее неравенство \( ctg \;x
Решение тригонометрических неравенств
ПРИМЕР 1. Решим неравенство \( \sin x > \frac \).
Так как \( -1 \frac \).
Так как \( -1 1 \).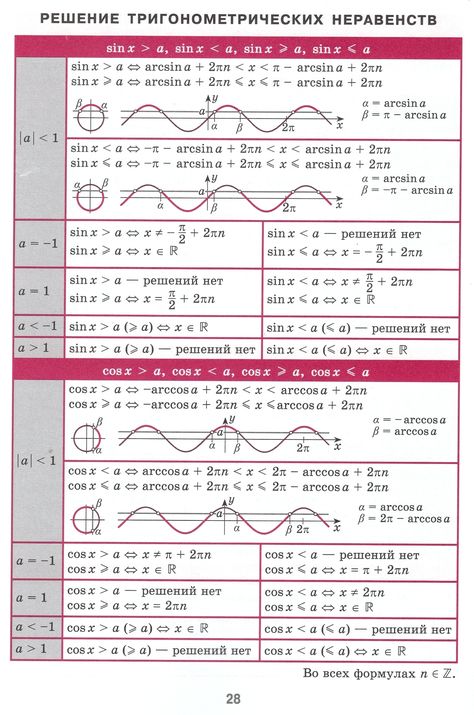
Очевидно, что решение неравенства будет таким:
$$ x \in \left(\frac + \pi k; \;\; \frac + \pi k\right), \; k \in \mathbb $$
ПРИМЕР 6. Решим неравенство \( tg \;x \frac \).
Очевидно, что решение неравенства будет таким:
$$ x \in \left( \pi k; \;\; \frac + \pi k \right), \; k \in \mathbb $$
ПРИМЕР 8. Решим неравенство \( ctg \;x
ПРИМЕР 1. Решим неравенство \( \sin x > \frac \).
Так как \( -1 \frac \).
Так как \( -1 1 \).
Очевидно, что решение неравенства будет таким:
$ x \in \left(\frac + \pi k; \;\; \frac + \pi k\right), \; k \in \mathbb $
Решение тригонометрических неравенств
ПРИМЕР 1. Решим неравенство \( \sin x > \frac \).
Так как \( -1 \frac \).
Так как \( -1 1 \).
Очевидно, что решение неравенства будет таким:
$ x \in \left(\frac + \pi k; \;\; \frac + \pi k\right), \; k \in \mathbb $
ПРИМЕР 6. Решим неравенство \( tg \;x \frac \).
Очевидно, что решение неравенства будет таким:
$ x \in \left( \pi k; \;\; \frac + \pi k \right), \; k \in \mathbb $
ПРИМЕР 8.
Решим неравенство \( ctg \;x
Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> С 9 января 2019 года вводится новый порядок получения подробного решения некоторых задач. Ознакомтесь с новыми правилами >> —> Введите тригонометрическое неравенство
Решить неравенство
Неравенства вида \( ctg \;x > a \) и \( ctg \;x
Решение тригонометрических неравенств.
Www. math-solution. ru
18.06.2020 4:37:58
2020-06-18 04:37:58
Источники:
Http://ramrepetitor. ru/shkala-perevoda-ballov-profilnogo-ege-po-matematike/
Https://www. kontrolnaya-rabota. ru/s/neravenstva/
Https://www. kontrolnaya-rabota. ru/diario/101-reshenie-pokazatelnyh-neravenstv-onlajn/
Https://www. math-solution. ru/math-task/trigonometry-inequality
Тригонометрические уравнения и неравенства — Умскул Учебник
На этой странице вы узнаете:- Как промежутку попасть цель?.
. - Есть ли универсальные решения в тригонометрии?
. Что общего у астрономии, компьютерной графики, архитектуры и медицины? Измерить расстояние до звезд или провести обследование сердца, спроектировать небоскреб в центре города и нарисовать локацию в игре – это и многое другое невозможно без решения задач тригонометрии.
Решение тригонометрических уравненийОсновные способы решения тригонометрических уравнений:
Введение новой переменной.
1) Рассмотрим следующее уравнение
3cos2x — 5cos x — 2 = 0
2) Введем новую переменную (не забудем указать, что cos x может принимать значения только от -1 до 1)
cos x = t, -1 ≤ t ≤ 1
3t2 — 5t — 2 = 0
3) Решим уравнение и получим
4) Первый корень не подходит, так как не находится на промежутке от -1 до 1.
Сделаем обратную замену
\(cos\:x = -\frac{1}{3}\)
\(x = \pm arccos \frac{1}{3} + 2 \pi k, k \in Z\)
Данная запись и является ответом.
Разложение на множители.
- Решим следующее уравнение
sin x * cos x — cos x = 0
- Вынесем общий множитель за скобку
cos x * (sin x — 1) = 0
- Перейдем к совокупности уравнений
- Решим
Так как решения второго уравнения одновременно являются и решениями первого уравнения, в ответ запишем следующее:
\(\large x = \frac{\pi}{2} + \pi k, k \in Z\)
Простейшие тригонометрические неравенстваТригонометрическое неравенство – это неравенство, в котором переменная содержится под знаком тригонометрической функции.
Как решаются тригонометрические неравенства?
Для их решения нужно ориентироваться в “Тригонометрической окружности и графиках функций”.
Этот навык очень пригодится нам в нахождении угла или значения угла заданной тригонометрической функции.
Рассмотрим на примерах простейших тригонометрических неравенств.
Пример 1:
\(cos x > \frac{1}{2}\)
Отметим значение \(\frac{1}{2}\) на оси косинусов и выделим промежуток, на котором значения больше \(\frac{1}{2}\). Далее выделим промежуток, для точек которого неравенство верно.
Важно: точки называем в соответствии с тригонометрической окружностью так, чтобы между ними можно было определить непрерывный промежуток.
Ответ:
\(\large (-\frac{\pi}{3} + 2 \pi k, k \in Z; \frac{\pi}{3} + 2 \pi k, k \in Z)\)
Пример 2:
\(cos x < \frac{1}{2}\)
Ответ:
\(\large (\frac{\pi}{3} + 2 \pi k, k \in Z; \frac{5\pi}{3} + 2 \pi k, k \in Z)\)
Пример 3:
\(sin x > \frac{1}{2}\)
Ответ:
\(\large (\frac{\pi}{6} + 2 \pi k, k \in Z; \frac{5\pi}{6} + 2 \pi k, k \in Z)\)
Пример 4:
\(sin x < \frac{1}{2}\)
Здесь, как и в примере 1, называем точки так, чтобы в итоге можно было записать непрерывный промежуток.
Ответ:
\(\large (-\frac{7 \pi}{6} + 2 \pi k, k \in Z; \frac{\pi}{6} + 2 \pi k, k \in Z)\)
Пример 5:
tg x > 1
Важно: тангенс не существует в точках \(\frac{\pi}{2}\) и \(\frac{3 \pi}{2}\), поэтому эти точки выкалываются.
Заметим, что получились диаметрально противоположные промежутки, таким образом можно записать только первый, но с периодом в половину окружности.
Ответ:
\(\large (\frac{\pi}{4} + \pi k, k \in Z; \frac{\pi}{2} + \pi k, k \in Z)\)
Пример 6:
tg x < 1
Выделяем нужный отрезок на прямой тангенсов, выкалываем несуществующие точки, обозначаем точки на одном витке по окружности и выделяем промежутки.
Ответ:
\(\large (-\frac{\pi}{2} + \pi k, k \in Z; \frac{\pi}{4} + \pi k, k \in Z)\)
Пример 7:
ctg x < 1
Важно: у котангенса не существуют точки 0 и \(\pi\).
Ответ:
\(\large (\frac{\pi}{4} + \pi k, k \in Z; \pi + \pi k, k \in Z)\)
Пример 8:
ctg x > 1
Ответ:
\(\large (\pi k, k \in Z; \frac{\pi}{4} + \pi k, k \in Z)\)
Алгоритм решения:
- Отметить промежуток на прямой тригонометрической функции;
- Найти граничные точки;
- Отметить дугу или дуги и записать в ответ промежуток.
Рассмотрим решение простейшего неравенства более детально
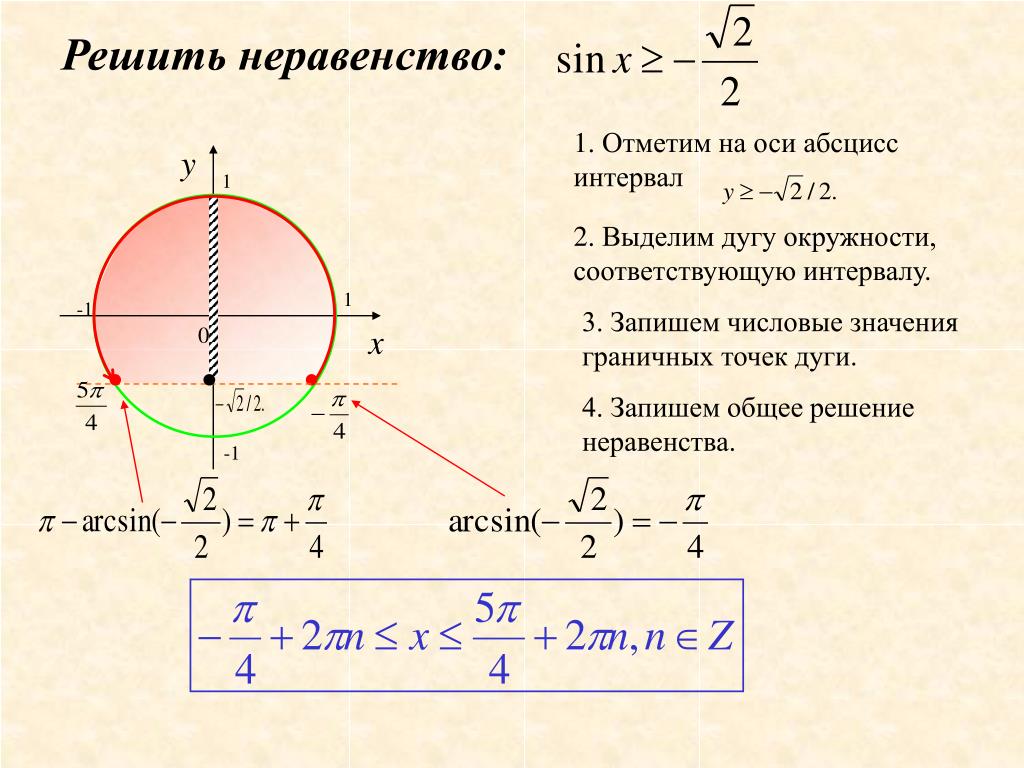
\(\large sin\:x > -\frac{1}{2}\)
- Нарисуем тригонометрическую окружность и отметим на ней промежуток, где синус больше \(-\frac{1}{2}\).
- Теперь найдем значения х, при которых синус х равен \(-\frac{1}{2}\), используя тригонометрический круг, знак неравенства строгий – точки выколоты.
- Отметим промежуток, который должен идти в ответ.
Ответ:
\(\large (-\frac{\pi}{6} + 2 \pi k, k \in Z; \frac{7 \pi}{6} + 2 \pi k, k \in Z)\)
Решение тригонометрических неравенствТригонометрические неравенства отличаются от тригонометрических уравнений только одним пунктом. В уравнениях ищутся отдельные решения, а в неравенствах — множество решений, которое чаще всего является промежутком(ами).
| Есть ли универсальные решения в тригонометрии? Для решения тригонометрических неравенств можно применять те же методы, что и для решения тригонометрических уравнений: |
Основные способы решения тригонометрических неравенств:
Введение новой переменной.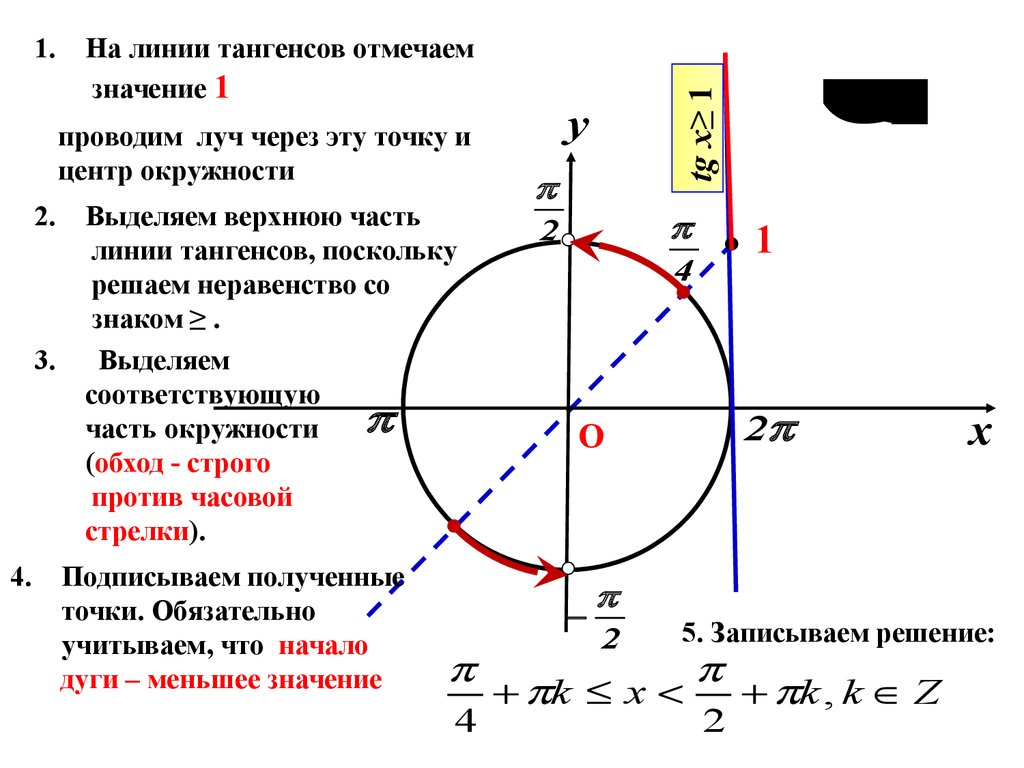
Отличается лишь тем, что после замены переменной, нужно решать обычное неравенство и далее рассматривать промежуток.
Для сравнения рассмотрим неравенство с той же левой частью, что и предыдущее уравнение
3cos2x — 5cos x — 2 < 0
- Введем новую переменную (не забудем указать, что cos x может принимать значения только от -1 до 1)
cos x = t, -1 ≤ t ≤1
3t2 — 5t — 2 < 0
- Решим неравенство и получим
\(-\frac{1}{3}<t<2\)
- Так как -1≤t≤1 , неравенство t<2 будет выполняться всегда, опустим эту часть и сделаем обратную замену
\(cos x > -\frac{1}{3}\)
А теперь решим простейшее тригонометрическое неравенство.
Ответ:
\((-arccos(-\frac{1}{3}) + 2 \pi k, k \in Z; arccos(-\frac{1}{3}) + 2 \pi k, k \in Z)\)
Данная запись и является ответом .
Разложение на множители.
Аналогично рассмотрим неравенство
sin x * cos x — cos x > 0
- Вынесем общий множитель за скобку
cos x * (sin x — 1) > 0
- Запишем совокупность
- У первой системы нет решений, так как синус не может быть больше 1.
Из второй системы получим
\((\frac{\pi}{2} + 2 \pi k, k \in Z; \frac{3 \pi}{2} + 2 \pi k, k \in Z)\)
Это и будет ответом.
Важно: Для решения квадратных, рациональных, дробно-рациональных и иррациональных тригонометрических неравенств сначала делается замена. Неравенство решается относительно новой переменной, используя методы решения неравенств данного типа. Далее совершается переход к изначальной переменной, и решается простейшее тригонометрическое неравенство.
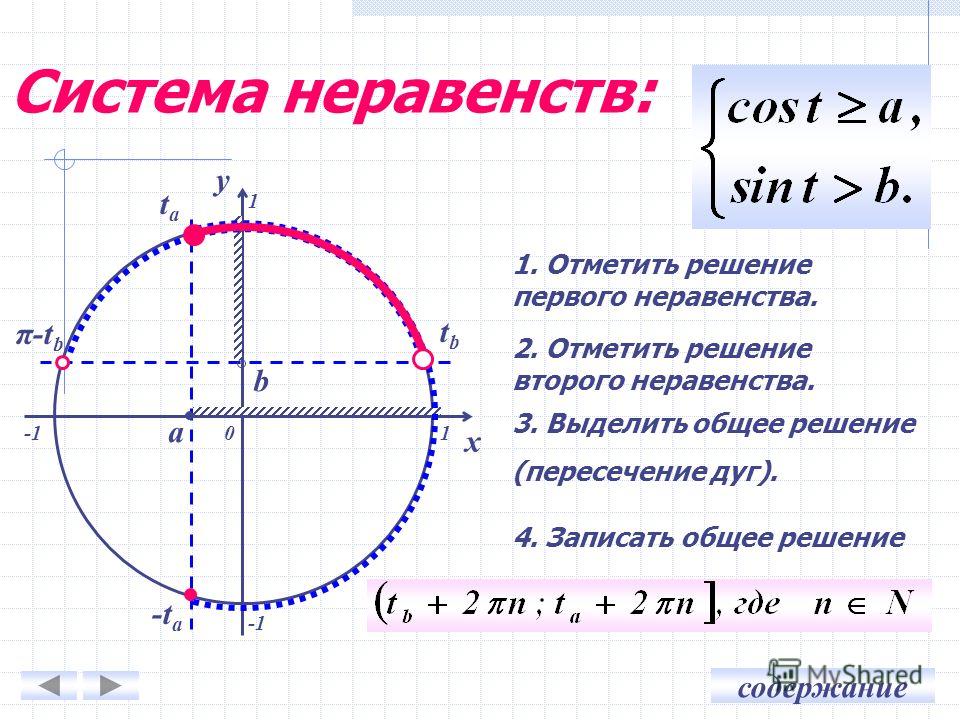
Системы тригонометрических неравенствЧтобы найти значение системы тригонометрических неравенств, нужно решить каждое неравенство отдельно и найти пресечение их решений.
| Как промежутку попасть цель?.. …то есть в ответ системы тригонометрических неравенств. |
Рассмотрим следующий пример
Решим каждое уравнение отдельно
- cos x >0
Получим промежуток
\(\large (-\frac{\pi}{2} + 2 \pi k, k \in Z; \frac{\pi}{2} + 2 \pi k, k \in Z)\)
- 2sin2x — 3sin x -2 ≤ 0
Сделаем замену sin x = t, -1 ≤ t ≤ 1
2t2 — 3t — 2 ≤ 0
Решим и получим следующий промежуток
\(-\frac{1}{2} ≤ t ≤ 2\)
Сделаем обратную замену
\(-\frac{1}{2} ≤ sin\:x ≤ 2\)
Так как sin x всегда меньше двух, опустим правую часть и решим простейшее тригонометрическое неравенство
-\(-\frac{1}{2} ≤ sin\:x\)
Получим промежуток
\(\large [-\frac{\pi}{6} + 2 \pi k, k \in Z; \frac{7 \pi}{6} + 2 \pi k, k \in Z]\)
Отметим оба промежутка и найдём их пересечение.
Запишем найденный промежуток.
Ответ:
\(\large [-\frac{\pi}{6} + 2 \pi k, k \in Z; \frac{\pi}{2} + 2 \pi k, k \in Z)\)
Фактчек- Тригонометрические уравнения и неравенства решаются методами введения новой переменной и разложения на множители.
- Квадратные, рациональные, дробно-рациональные и иррациональные тригонометрические неравенства решаются совершением замены. Затем используются методы решения неравенств данного типа, совершается переход к изначальной переменной, и решается простейшее тригонометрическое неравенство.
- Для решения системы уравнений сначала решается каждое неравенство отдельно, а потом находится пересечение.
Задание 1.
Решите неравенство cos x ≤-1
- Нет решений
- (-∞; +∞)
- π+2πk, k∈z
- 2πk, k∈z
Задание 2.
Решите неравенство ctg x ≥-1
- (k, kz; 4+k, kz ]
- (k, kz; 4+k, kz )
- Нет решений
- (+k, kz; 76+k, kz )
Задание 3.
Решите уравнение 2cos x +4cos x sin x =0
- -2+k, kz
- -56+2k, kz;-6+2k, kz;-2+k, kz
- Нет решений
- При любом х
Задание 4.
Решите неравенство 2sin2x -3sin x <0
- (2k, kz; +2k, kz )
- (k, kz; +k, kz )
- k, kz
- +2k, kz
Задание 5.
Решите систему неравенств
- [2+2k, kz; 54+2k, kz ]
- Нет решений
- (2+2k, kz; +2k, kz )
- (2+2k, kz; 76+2k, kz ]
Ответы: 1. — 3; 2. — 1; 3. — 2; 4. — 1; 5. — 4
Решатель неравенств шаг за шагом онлайн
- Системы неравенства шаг за шагом
- Регулярные уравнения шаг за шагом
- Системы уравнений шаг за шагом
- Квадратное неравенство шаг за шагом
- Неравенство с модулем Step by Step
- Логарифмическое неравенство онлайн 92 — 1| — |х — 3| > 7
- Неравенства с параметром
sqrt(x - a) + sqrt(2a - x) + sqrt(a - 1) + sqrt(3 - a) >
- Иррациональные неравенства с квадратным корнем
кв (х + 1) - кв (2 - х)
- Тригонометрические неравенства
2*sin(x)
- Линейные неравенства 92 + 3x + 1) > 0
Приведенные выше примеры также содержат:
- модуль или абсолютное значение: absolute(x) или |x|
- квадратные корни sqrt(x),
кубических корней cbrt(x) - тригонометрические функции:
sinus sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x) - экспоненциальные функции и показатели exp(x)
- обратные тригонометрические функции:
арксинус asin(x), арккосинус acos(x), арктангенс atan(x), арккотангенс acot(x) - натуральные логарифмы ln(x),
десятичные логарифмы log(x) - гиперболические функции:
гиперболический синус sh(x), гиперболический косинус ch(x), гиперболический тангенс и котангенс tanh(x), ctanh(x) - обратные гиперболические функции:
гиперболический арксинус asinh(x), гиперболический арккосинус acosh(x), гиперболический арктангенс ath(x), гиперболический арккотангенс acoth(x) - другие тригонометрические и гиперболические функции: секанс
сек(х), косеканс csc(x), арксеканс asec(x), арккосеканс acsc(x), гиперболический секанс sech(x), гиперболический косеканс csch(x), гиперболический арксикансек asech(x), гиперболический арккосеканс acsch(x) - функции округления:
округлить до пола(x), округлить до потолка(x) - знак числа:
знак(х) - по теории вероятностей:
функция ошибок erf(x) (интеграл вероятности), Функция Лапласа laplace(x) - Факториал х :
х! или факториал(х) - Гамма-функция gamma(x)
- Функция Ламберта LambertW(x)
- Тригонометрические интегралы: Si(x), Ci(х), Ши(х), Чи(х)
Правила вставки
Следующие операции могут быть выполнены 95
Константы
- Пи
- — число Пи
- и
- — основание натурального логарифма
- и
- — комплексный номер
- оо
- — символ бесконечности
Чтобы увидеть подробное решение, поделитесь им со всеми своими друзьями-студентами
Решение тригонометрических уравнений и неравенств
Все ресурсы по предварительному исчислению
12 диагностических тестов 380 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущий 1 2 Далее →
Справка по предварительному исчислению » Тригонометрические тождества » Решение тригонометрических уравнений и неравенств
Используйте тригонометрические тождества, чтобы решить следующее уравнение для:
Возможные ответы:
Правильный ответ:
9
9 Объяснение:
Используйте тригонометрические тождества, чтобы заменить сек на тангенс:
, следовательно,
Таким образом, у нас есть , что делает
Следовательно, решение для n равно любому целому числу.
Сообщить об ошибке
Что из следующего не является решением для
Возможные ответы:
Правильный ответ:
Объяснение:
Начнем с того, что приравняем правую часть уравнения к 0.
Уравнение может быть проще разложить на множители, используя следующую замену.
Это приведет следующие
Это можно учитывать следующим образом
Поэтому
Заменяя наше замене. Поэтому мы сработали.
когда
когда
Таким образом, единственным неверным выбором является
Сообщить об ошибке
Найдите одно возможное значение .
Возможные ответы:
Правильный ответ:
Объяснение:
Начните с выделения касательной стороны уравнения:
Затем возьмите арктангенс обеих сторон:
Разделите на пять, чтобы получить окончательный ответ:
4 Сообщите об ошибке
4
Используйте тригонометрические тождества для определения значения угла.
Возможные ответы:
Правильный ответ:
Объяснение:
Есть два способа решить эту проблему. Первый включает два тригонометрических тождества:
Второй метод позволяет нам использовать только первое тригонометрическое тождество:
Сообщить об ошибке
Используйте тригонометрические тождества для решения уравнения для значения угла.
Возможные ответы:
Правильный ответ:
Объяснение:
Самый простой способ решить эту задачу — использовать тождество двойного угла для косинуса.
Подстановка этого значения в исходное уравнение дает нам:
Сообщить об ошибке
Согласно тригонометрическим тождествам,
Возможные ответы:
3 2 Правильный ответ30039
Объяснение:
Тригонометрическое тождество важно запомнить.
Некоторые другие личности, которые важны для знания:
Отчет о ошибке
Если существует в домене, решить следующее:
.
Объяснение:
Факторизация .
Приравняйте оба члена к нулю и решите.
Это значение не входит в домен.
Это единственное правильное значение в домене.
Сообщить об ошибке
Решите для в уравнении на интервале .
Возможные ответы:
Правильный ответ:
Объяснение:
Если вы подставите, вы получите узнаваемое квадратное уравнение, которое можно решить для ,
.
Затем мы можем снова подключиться к нашему уравнению и использовать единичный круг, чтобы найти это
.
Сообщить об ошибке
Учитывая, что тета существует из , решите:
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы правильно решить, не разделяйте на обе стороны. Эффект устранит один из корней этой триггерной функции.
Вычтите с обеих сторон.
Фактор левой части уравнения.
Приравняйте каждый член к нулю и найдите тета с ограничением .
. Правильный ответ:
Отчет о ошибке
Solve для
. Ошибка
Solve для
. Ошибка
Solve для
.
Правильный ответ:
Нет решения.
Объяснение:
Вычитая из обеих частей исходного уравнения, мы получаем .