Неоднородные дифференциальные уравнения 2ого порядка
Онлайн калькуляторы
На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.
Справочник
Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!
Заказать решение
Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!
Главная Справочник Дифференциальные уравнения Неоднородные дифференциальные уравнения второго порядка
Определение и формулы неоднородных ДУ второго порядка
Нахождение решения однородного уравнения (2) можно посмотреть тут — решение дифференциальных уравнений второго порядка и линейные неоднородные дифференциальные уравнения второго порядка.
Методы нахождения частного решения неоднородных ДУ второго порядка
Существует несколько методов нахождения частного решения линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами (1).
Эти методы выбираются в зависимости от вида правой части – функции .
1) Если функция представляет собой многочлен n-ой степени
то частное решение уравнения (1) ищется в виде
Здесь – многочлен степени n с неопределенными коэффициентами (которые подлежат определению), а s – кратность корня характеристического уравнения однородного уравнения (2) (или то есть количество корней характеристического уравнения, равных нулю).
Так как – частное решение уравнения (1), то коэффициенты, определяющие многочлен , можно найти методом неопределенных коэффициентов из равенства
использовав тот факт, что два многочлена равны, если равны коэффициенты при соответствующих степенях независимой переменной.
2) Если функция , стоящая в правой части уравнения (1), имеет вид
то есть представляет собой произведение многочлена степени n и экспоненты, то частное решение этого уравнения ищется в виде
где – многочлен степени n с неопределенными коэффициентами, а s – кратность корня в характеристическом уравнении соответствующего однородного уравнения (2) (или то есть количество корней характеристического уравнения, равных a).
3) Если правая часть неоднородного дифференциального уравнения (1) имеет вид:
то частное решение в этом случае ищем в виде:
Здесь s – число комплексно сопряженных пар корней характеристического уравнения – многочлены степени k с неизвестными коэффициентами. Коэффициенты этих многочленов определяются из равенства (3).
Если правая часть имеет отличную, от описанных выше, структуру, то для нахождение решения уравнения (1) применяют метод вариации произвольной постоянной:
1) находится общее решение соответствующего линейного однородного уравнения (2) в виде
где – линейно независимые частные решения линейного однородного дифференциального уравнения (2), – некоторые произвольные постоянные;
2) варьируются произвольные постоянные, то есть считается, что они являются функциями независимой переменной x:
А в качестве общего решения исходного дифференциального уравнения (1) рассматривается функция
Функции (точнее их производные ) являются решением системы
Тогда сами неизвестные функции находятся с помощью интегрирования.
| Понравился сайт? Расскажи друзьям! | |||
Определить тип и решить дифференциальное уравнения.
Пример 1:
Определить тип дифференциального уравнения и найти его решение:
Решение от преподавателя:
Пример 2:
Определить тип дифференциального уравнения первого порядка и найти его общее решение:
Решение от преподавателя:
Пример 3:
Определить тип дифференциального уравнения и найти его решение:
Решение от преподавателя:
Пример 4:
Дано дифференциальное уравнение 1-го порядка. Определить тип дифференциального уравнения и найти его общее решение.
Решение от преподавателя:
Это однородное дифференциальное уравнение 1-го порядка, так как множители при dx и dy – одинаковой 2-й степени.
Сделаем замену переменных
Пример 5:
Определить тип дифференциального уравнения и найти его решение:
Решение от преподавателя:
Пример 6:
Определить тип дифференциального уравнения первого порядка и найти его общее решение:
y» + 4y’ = 2sin 5x .
Решение от преподавателя:
Решение уравнения будем искать в виде y = erx. Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
r2 +4 r + 0 = 0
D=42 — 4*1*0=16
Корни характеристического уравнения:
r1 = 0
r2 = -4
Следовательно, фундаментальную систему решений составляют функции:
y1 = e0x
y2 = e-4x
Общее решение однородного уравнения имеет вид:
Рассмотрим правую часть:
f(x) = 2*sin(5*x)
Поиск частного решения.
Здесь P(x) = 0, Q(x) = 2, α = 0, β = 5.
Следовательно, число α + βi = 5i не является корнем характеристического уравнения.
Уравнение имеет частное решение вида:
y = Acos(5x) + Bsin(5x)
Вычисляем производные:
y’ = -5Asin(5x)+5Bcos(5x)
y» = -25(Acos(5x)+Bsin(5x))
которые подставляем в исходное дифференциальное уравнение:
y» + 4y’ = (-25(Acos(5x)+Bsin(5x))) + 4(-5Asin(5x)+5Bcos(5x)) = 2sin(5x)
или
-20Asin(5x)-25Acos(5x)-25Bsin(5x)+20Bcos(5x) = 2sin(5x)
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
1: -20A -25B = 2
1: -25A + 20B = 0
Решая ее, находим:
A = -8/205;B = -2/41;
Частное решение имеет вид:
y=-8/205cos(5x) —2/41sin(5x)
Таким образом, общее решение дифференциального уравнения имеет вид:
Пример 7:
Определить тип дифференциального уравнения и найти его решение:
Решение от преподавателя:
Пример 8:
Определить тип и решить дифференциальное уравнения:
Решение от преподавателя:
Пример 9:
Определить тип дифференциального уравнения и найти его решение:
Решение от преподавателя:
Пример 10:
Дано дифференциальное уравнение 2-го порядка и начальные условия.
Определить тип дифференциального уравнения инайти его частное решение, удовлетворяющее заданным начальным условиям.
Решение от преподавателя:
Это дифференциальное уравнение 2-го порядка, допускающее понижение порядка, так как в него не входит искомая функция у. Порядок уравнения понижаем, взяв за новую неизвестную функцию первую производную, т.е.
Тогда
частное решение, удовлетворяющее заданным начальным условиям.
Пример 11:
Определить тип дифференциального уравнения и найти его решение:
Решение от преподавателя:
Пример 12:
Определить тип и решить дифференциальное уравнения:
Решение от преподавателя:
Пример 13:
Определить тип дифференциального уравнения и найти его решение:
Решение от преподавателя:
Это неоднородное уравнение.
Сделаем замену переменных:
y=u*v, y’ = u’v + uv’.
u*v/x+u*v’+u’v = ln(x)
или
u(v/x+v’) + u’v= ln(x)
Выберем переменную v так, чтобы выполнялись условия:
1. u(v/x+v’) = 0
2. u’v = ln(x)
1. Приравниваем u=0, находим решение для:
v/x+v’ = 0
Представим в виде:
v’ = -v/x
Преобразуем уравнение так, чтобы получить уравнение с разделяющимися переменными:
Интегрируя, получаем:
ln(v) = -ln(x)
v = 1/x
2. Зная v, Находим u из условия: u’*v = ln(x)
u’/x = ln(x)
u’ = x*ln(x)
Интегрируя, получаем:
Из условия y=u*v, получаем:
y = u*v = 1/x(C+x2/2ln(x)-x2/4)
или
y = C/x+x/2ln(x)-x/4
Пример 14:
Дано дифференциальное уравнение 2-го порядка. Определить тип дифференциального уравнения и найти его общее решение, используя метод вариации произвольных постоянных.
Решение от преподавателя:
Составим и решим характеристическое уравнение для однородного уравнения:
Пример 15:
Определить тип дифференциального уравнения и найти его решение:
Решение от преподавателя:
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = erx. Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
r2 +0 r + 0 = 0
D=02 — 4*1*0=0
Корни характеристического уравнения:
Корень характеристического уравнения r1 = 0 кратности 2.
Следовательно, фундаментальную систему решений составляют функции:
y1 = e0x
y2 = xe0x
Общее решение однородного уравнения имеет вид:
Поиск частного решения методом вариации произвольной постоянной.
Для нахождения производных C’i составляем систему уравнений:
C’1 + C’2 x = 0
C’1(0) + C’2(1) = x*sin(x)
Выразим C’1 из первого уравнения:
C’1 = -c2x
и подставим во второе. В итоге получаем:
C’1 = -x2sin(x)
C’2 = x*sin(x)
Интегрируем полученные функции C’i:
C1 = x2cos(x)-2x*sin(x)-2cos(x) + C1
C2 = -x*cos(x)+sin(x) + C2
Записываем полученные выражения в виде:
C1 = x2cos(x)-2x*sin(x)-2cos(x) + C11
C2 = x(-x*cos(x)+sin(x)) + C2x
Таким образом, общее решение дифференциального уравнения имеет вид:
y = C1 + C2 = C1 + C2 x -x*sin(x)-2cos(x)
Найдем частное решение при условии: y(0) = 1, y'(0) = 1
Поскольку y(0) = c1-2, то получаем первое уравнение:
c1-2 = 1
Находим первую производную:
y’ = c2-x*cos(x)+sin(x)
Поскольку y'(0) = c2, то получаем второе уравнение:
c2 = 1
В итоге получаем систему из двух уравнений:
c1-2 = 1
c2 = 1
т.
е.:
c1 = 3, c2 = 1
Тогда частное решение при заданных начальных условиях можно записать в виде:
Пример 16:
Определить тип и решить дифференциальное уравнения:
Решение от преподавателя:
Пример 17:
Определить тип дифференциального уравнения и найти его решение:
Решение от преподавателя:
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = erx. Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
r2 +0 r + 1 = 0
D=02 — 4*1*1=-4
Корни характеристического уравнения:
(комплексные корни):
r1 = i
r2 = — i
Следовательно, фундаментальную систему решений составляют функции:
Общее решение однородного уравнения имеет вид:
Поиск частного решения методом вариации произвольной постоянной.
Для нахождения производных C’i составляем систему уравнений:
C’1cos(x) + C’2sin(x) = 0
C’1(-sin(x)) + C’2(cos(x)) = (x+2)*e-x
Выразим C’1 из первого уравнения:
C’1 = -c2tg(x)
и подставим во второе. В итоге получаем:
C’1 = -(x+2)*e-xsin(x)
C’2 = (x+2)*e-xcos(x)
Интегрируем полученные функции C’i:
Записываем полученные выражения в виде:
или
Таким образом, общее решение дифференциального уравнения имеет вид:
Пример 18:
Дано дифференциальное уравнение 2-го порядка. Определить тип дифференциального уравнения и найти его общее решение, используя метод неопределенных коэффициентов.
Решение от преподавателя:
Пример 19:
Определить тип дифференциального уравнения и найти его решение:
Решение от преподавателя:
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = erx. Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
r2 -4 r + 4 = 0
D=(-4)2 — 4*1*4=0
Корни характеристического уравнения:
Корень характеристического уравнения r1 = 2 кратности 2.
Следовательно, фундаментальную систему решений составляют функции:
y1 = e2x
y2 = xe2x
Общее решение однородного уравнения имеет вид:
Поиск частного решения методом вариации произвольной постоянной.
Для нахождения производных C’i составляем систему уравнений:
C’1(2e2x) + C’2(2x*e2x+e2x) = cos(x)+10sin(x)
Выразим C’1 из первого уравнения:
C’1 = -c2x
и подставим во второе. В итоге получаем:
C’1 = -x(10sin(x)+cos(x))*e-2x
C’2 = (10sin(x)+cos(x))*e-2x
Интегрируем полученные функции C’i:
=
Записываем полученные выражения в виде:
=
или
Таким образом, общее решение дифференциального уравнения имеет вид:
Найдем частное решение при условии: y(0) = 0, y'(0) = 2
Поскольку y(0) = c1+43/25, то получаем первое уравнение:
c1+43/25 = 0
Находим первую производную:
y’ = 2c1e2x+2c2x*e2x+c2e2x-43/25sin(x)+26/25cos(x)
Поскольку y'(0) = 2*c1+c2+26/25, то получаем второе уравнение:
2c1+c2+26/25 = 2
В итоге получаем систему из двух уравнений:
c1+43/25 = 0
2c1+c2+26/25 = 2
т.
е.:
c1 = -43/25, c2 = 22/5
Тогда частное решение при заданных начальных условиях можно записать в виде:
Пример 20:
Установить тип ДУ, найти его общее и частное решения.
Решение от преподавателя:
Данное уравнение является линейным дифференциальным уравнением (ЛДУ) первого порядка, так как его можно записать в виде y‘=p(x)y = q(x), где p(x) = , q(x)= .
Сделаем замену переменных: y=u*v, y’ = u’v + uv’.
-u*v*ctg(x)+u*v’+u’v = 2x*sin(x)
или
u(-v*ctg(x)+v’) + u’v= 2x*sin(x)
Выберем переменную v так, чтобы выполнялись условия:
1. u(-v*ctg(x)+v’) = 0
2. u’v = 2x*sin(x)
1. Приравниваем u=0, находим решение для:
-v*ctg(x)+v’ = 0
Представим в виде:
v’ = v*ctg(x)
Преобразуем уравнение так, чтобы получить уравнение с разделяющимися переменными:
Интегрируя, получаем:
ln(v) = ln(sin(x))
v = sin(x)
2.
Зная v, Находим u из условия: u’*v = 2*x*sin(x)
u’sin(x) = 2x*sin(x)
u’ = 2x
Интегрируя, получаем:
Из условия y=u*v, получаем:
y = u*v = (C+x2)*sin(x)
или
y = C*sin(x)+x2sin(x)
Найдем частное решение при условии: y(π/2)=0
y(π/2)= C*sin(π /2)+ π /22sin(π /2) = 0
Откуда:
c1 = -π/4
Таким образом, частное решение имеет вид:
y(π/2)= -π/4sin(x)+x2sin(x)
Ответ:
Пример 21:
Установить тип ДУ первого порядка и найти его общее решение.
Решение от преподавателя:
Пример 22:
Установить тип ДУ первого порядка и найти его общее решение.
Решение от преподавателя:
Работа вам нужна срочно. Не волнуйтесь, уложимся!
Заполните, пожалуйста, данные для автора:
- 22423 авторов готовы помочь тебе.
- 2402 онлайн
Калькулятор дифференциальных уравнений второго порядка
Бесплатный онлайн-калькулятор дифференциальных уравнений второго порядка предназначен для проверки дифференциала второго порядка заданного выражения и отображения результата в течение нескольких секунд.
Укажите свое уравнение в качестве входного значения и нажмите кнопку расчета, чтобы получить производные второго порядка вместе с работой.
Калькулятор дифференциального уравнения второго порядка: Дифференциальное уравнение второго порядка — это обыкновенное дифференциальное уравнение с функцией производной 2. Перейдите к разделам ниже, чтобы узнать пошаговый процесс изучения дифференциального уравнения второго порядка на примере. Инструмент Handy Calculator предоставит вам результат без промедления. 92=f”’(x)=y’’. Взгляните на следующие шаги и используйте их при решении дифференциального уравнения второго порядка.
- Возьмем любое уравнение с дифференциальным уравнением второго порядка
- Примем dy/dx как переменную r
- Подставим переменную r в данное уравнение
- Получится биномиальное уравнение
- Решим уравнение и найдем его множители
- Найдите значение y
Пример:
Вопрос: Решите d^2y/dx^2-10dy/dx+25y=0?
Ответ:
Уравнение.
RX
D 2 Y/DX 2 = R 2 E RX
Замените эти значения в уравнении
R 2 E RX -10RE 2 E RX -10RE + + + + + +. =0
e rx (r 2 -10r+25)=0
r 2 -10r+25=0
r 2 -5r-5r+25=0
r(r-5)-5(r-5)=0
(r-5)( R-5) = 0
R = 5
Итак, мы можем сказать, что Y = E 5x
DY/DX = 5E 5x
D 2 Y/DX 2 = 25E 5x
SO,
D 2 Y/DX 2 -10DY/DX +25Y
= 25E 5x -10*5E 5X +25E 5X
= 25E +25E 9003 = 25E +25E 9003 = 25E . -50e 5x +25e 5x=0
Итак, в этом случае наше решение
y=Ae 5x +Bxe 5x
Вы можете легко вычислить с помощью нашего дифференциального калькулятора второго порядка входя в уравнение.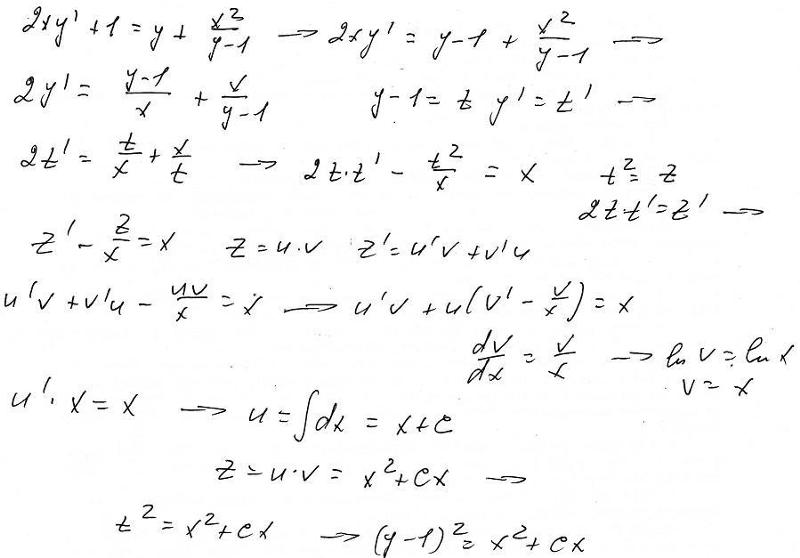
Если вы ищете другие калькуляторы математических понятий, зайдите на Onlinecalculator.guru и изучите другие темы.
сообщите об этом объявлении
1. Сколько решений имеет дифференциальное уравнение второго порядка?
Чтобы построить общее решение уравнения второго порядка, нужно взять два независимых решения. Итак, у него есть 2 решения.
2. Как решить дифференциальное уравнение второго порядка?
Рассмотрим любую переменную для производной и подставим это значение в уравнение. Найдите корни этой переменной и подставьте значения в данное уравнение.
3. Как написать дифференциальное уравнение второго порядка?
Стандартная форма дифференциального уравнения второго порядка: pd 2 y/dx 2 +qdx/dy+r=0. Математический оператор может быть как плюсом, так и минусом.
4. Чем отличаются дифференциальные уравнения первого и второго порядка?
Уравнение, имеющее только первые производные, называется дифференциальным уравнением первого порядка, а уравнение, содержащее вторую производную, называется дифференциальным уравнением второго порядка.
Дифференциальное уравнение первого порядка представляется как dy/dx, а дифференциальное уравнение второго порядка представляется как d 2 года / дх 2 .
Калькулятор дифференциальных уравнений второго порядка
D 2 Y/DX 2 = R 2 E RX
Замените эти значения в уравнении
R 2 E RX -10RE 2 E RX -10RE + +
+ + + +. =0e rx (r 2 -10r+25)=0
r 2 -10r+25=0
r 2 -5r-5r+25=0
r(r-5)-5(r-5)=0
(r-5) (r-5)=0
r=5
Итак, мы можем сказать, что y=e 5x
dy/dx=5e 5x
d 2 50e 0 y/38 0 5x
SO,
D 2 Y/DX 2 -10DY/DX +25Y
= 25E 5x -10*5E 5x +25E 5X
9003 9003 . -50e 5x +25E 5x= 0
Итак, в этом случае наше решение составляет
y = AE 5x +BXE 5x
Найдите разнообразие других математических каллеров, которые спасут ваше время.
выполняя сложные расчеты и получая пошаговые решения всех ваших проблем за считанные секунды.
Часто задаваемые вопросы о калькуляторе дифференциальных уравнений второго порядка
1. Сколько решений имеет дифференциальное уравнение второго порядка?
Чтобы построить общее решение уравнения второго порядка, нужно взять два независимых решения. Итак, у него есть 2 решения.
2. Как решить дифференциальное уравнение второго порядка?
Рассмотрим любую переменную для производной и подставим это значение в уравнение. Найдите корни этой переменной и подставьте значения в данное уравнение.
3. Как написать дифференциальное уравнение второго порядка?
Стандартная форма дифференциального уравнения второго порядка: pd 2 y/dx 2 +qdx/dy+r=0. Математический оператор может быть как плюсом, так и минусом.
4. Чем отличаются дифференциальные уравнения первого и второго порядка?
Уравнение, имеющее только первые производные, называется дифференциальным уравнением первого порядка, а уравнение, содержащее вторую производную, называется дифференциальным уравнением второго порядка.