Онлайн решить уравнение с дробью: Решение уравнений с дробями онлайн · Как пользоваться Контрольная Работа РУ

Уравнение плоскости, проходящей через точку и прямую онлайн

С помощю этого онлайн калькулятора можно построить уравнение плоскости, проходящей через данную точку и через данную прямую (точка не лежит на этой прямой). Дается подробное решение с пояснениями. Для построения уравнения плоскости задайте вид уравнения прямой (канонический или параметрический) введите координаты точки и коэффициенты уравнения прямой в ячейки и нажимайте на кнопку «Решить».

Очистить все ячейки?

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

 

Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат задана прямая L:

и точка M₀(x₀, y₀, z₀), которая не находится на этой прямой.

Задача заключается в построении уравнения плоскости α, проходящей через точку M₀ и и через прямую L(Рис.1).

Решение. Уравнение плоскости, проходящей через точку M₀ и имеющий нормальный вектор n={A, B, C} имеет следующий вид:

A(x−x0)+B(y−y0)+C(z−z0)=0.

(2)

Направляющий вектор прямой L имеет вид q={m, p, l}. Поскольку плоскость проходит через прямую L, то она проходит также через точку M₁(x₁, y₁, z₁). Тогда уравнение плоскости, проходящей через точку M₁(x₁, y₁, z₁) имеет вид:

A(x− x1)+B(y−y1)+C(z−z1)=0.

(3)

Для того, чтобы плоскость проходила через прямую L, нормальный вектор плоскости n={A, B, C} должен быть ортогональным направляющему вектору q прямой L, т.е. скалярное произведение этих векторов должен быть равным нулю:

Am+Bp+Cl=0

(4)

Вычитая уравнение (3) из уравнения (2), получим:

A(x1−x0)+B(y1−y0)+C(z1−z0)=0.

(5)

Решая совместно уравнения (4) и (5) отностительно коэффициентов

A, B, C получим такие значения A, B, C, при которых уравнение (2) проходит через точку M₀ и через прямую (1). Для решения систему уравнений (4), (5), запишем их в матричном виде:

Как решить систему линейных уравнений посмотрите на странице метод Гаусса онлайн.

Получив частное решение уравнения (6) и подставив полученные значения A, B, C в (2), получим решение задачи.

Пример 1.Найти уравнение плоскости α, проходящей через точку M₀(x₀, y₀, z₀)=M₀(1, 2, 5) и через заданную прямую L:

Решение. Уравнение плоскости α, проходящей через точку M₀(x₀, y₀, z₀)=M₀(1, 2, 5) и имеющий нормальный вектор

n={A, B, C} представляется формулой (2).

Уравнение плоскости α, проходящей через точку M₁(x₁, y₁, z₁)=M₁(2, 1, −3) и имеющий нормальный вектор n={A, B, C} представляется формулой (3).

Вычитая уравнение (3) из уравнения (2), получим:

A(x1−x0)+B(y1−y0)+C(z1−z0)=0.

(8)

Направляющий вектор прямой L имеет следующий вид:

q={m, p, l}={−3, 1, 4}

Для того, чтобы плоскость проходила через прямую L, нормальный вектор плоскости

n={A, B, C} должен быть ортогональным направляющему вектору q прямой L, т.е. скалярное произведение этих векторов должен быть равным нулю:

Am+Bp+Cl=0

(9)

Подставим значения m, p, l, x₀, y₀, z₀, x₁, y₁, z₁ в (8) и (9):

Решим систему линейных уравнений (10) и (11) отностительно A, B, C. Для этого представим эти уравнения в матричном виде:

Решив однородную систему линейных уравнений (12) используя метод Гаусса, найдем следующее частное решение:

Подставляя значения коэффициентов A, B, C в уравнение плоскости (2), получим:

Упростим уравнение (13):

Ответ: Уравнение плоскости, проходящей через точку M₀(1, 2, 5) и через прямую (7) имеет вид (14).

Пример 2. Найти уравнение плоскости α, проходящую через точку M₀(4, 3, −6) и через прямую L, заданной параметрическим уравнением:

Решение. Приведем параметрическое уравнение (15) к каноническому виду:

Уравнение плоскости α, проходящей через точку M₀(x₀, y₀, z₀) и имеющий нормальный вектор n={A, B, C} представляется формулой:

A(x−x0)+B(y−y0)+C(z−z0)=0.

(17)

Поскольку плоскость проходит через прямую L, то она проходит также через точку M₁(x₁, y₁, z₁)=(0, 2, 4). Тогда уравнение плоскости, проходящей через точку

M₁(x₁, y₁, z₁) имеет вид:

A(x−x1)+B(y−y1)+C(z−z1)=0.

(18)

Вычитая уравнение (18) из уравнения (17), получим:

A(x1−x0)+B(y1−y0)+C(z1−z0)=0.

(19)

Направляющий вектор прямой L имеет следующий вид:

q={m, p, l}={−7, 4, 0}

Для того, чтобы плоскость проходила через прямую L

, нормальный вектор плоскости n должен быть ортогональным направляющему вектору прямой L :

Am+Bp+Cl=0.

(20)

Подставим значения m, p, l, x₀, y₀, z₀, x₁, y₁, z₁ в (19) и (20):

Решим систему линейных уравнений (21) и (22) отностительно A, B, C. Для этого представим эти уравнения в матричном виде:

Решив однородную систему линейных уравнений (23) используя метод Гаусса, найдем следующее частное решение:

Подставляя значения коэффициентов A, B, C в уравнение плоскости (17), получим:

Упростим уравнение (24):

Уравнение плоскости можно представить более упрощенном виде, умножив на число 23.

Ответ: Уравнение плоскости, проходящей через точку

M₀(4, 3, −6) и через прямую (16) имеет вид (26).

Решение рациональных уравнений — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике.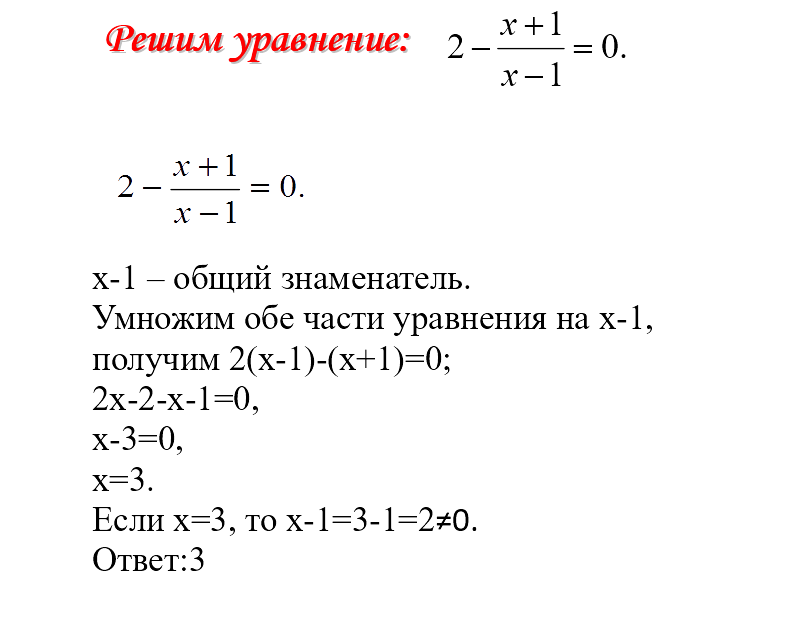 Базовый уровень Сложные задачи

2. Задача

• Моторная лодка, двигаясь по течению реки,
проходит от пристани А до пристани В
расстояние, равное 24км, на полчаса быстрее,
чем то же расстояние против течения. Какую
скорость развивает лодка в стоячей воде,
если скорость течения реки равна 2км/ч?
24
24
1
.
х 2 х 2 2

3. задача

• Лодка прошла 10км по течению реки и
6км против течения, затратив на весь путь
2ч. Чему равна собственная скорость
лодки, если скорость течения реки равна
2км/ч?
10
6
2.
х 2 х 2

4. Когда дробь равна нулю?

a 0,
a
0
b
0
.
b

5. При каком значении переменной значение дроби равно нулю?

1группа
2 группа
х
;
312
6х 3
2)
;
х 5
х 2 25
3)
;
2
( х 5)
х 7
1)
;
2х
х2 9
2)
;
х 3
( х 4) 2
3) 2
;
х 4х
16с 4
4)
.
3с 15
1)
4с 2 9
4)
.
2с 3
3группа
4х 8
;
х 6
100 х 2
2)
;
х 10
18а 18
3)
;
13а 18
4 у 2 25
4)
.
2у 5
1)

6. ответы

• 0; -0,5; -5; 1,5 — 1 группа
• 7; 3; -4; -0,25 – 2 группа
• 2; -10; -1; -2,5 – 3 группа
0;
Л;
7;
Е;
-5;
А;
-4;
Ц;
2;
Н;
-1;
О;
-0,5;
Н;
3;
О;
1,5; -0,25;
Ь;
А;
-10
Р
-2,5
и

8. -10;-5;-4;-2,5;-1;-0,5;-0,25; 0;1,5;2;3;7.

РАЦИОНАЛЬНОЕ

9. Первые представления о решении рациональных уравнений

10. алгоритм

Алгоритм решения
рационального уравнения
24
24
1
х 2 х 2 2
24
24
1
0
х 2
х 2
2
24
х 2
\2 х 4
24
х 2
\2 х 4
1
2
х 2 4
0
48х 96 48х 96 х 2 4
0
2 х 2 х 2
196 х 2
0
2 х 2 х 2
196 х 2 0
14 х 14 х 0
х 14, х 14
1)2 14 2 14 2 2 12 16 384 0
2)2 14 2 14 2 2 16 12 384 0
Ответ : 14,14.
Р х
Получили уравнение Q х 0 .
Для решения такого уравнения
нужно:
Алгоритм решения
рационального
уравнения
24
24 1
х 2 х 2 2
24
24 1
0
х 2 х 2 2
\2 х 4
\ 2 х 4
Перенести все члены
уравнения в левую
часть
\ х2 4
24
24
1
0
х 2
х 2
2
2
48 х 96 48 х 96 х 4
0
2 х 2 х 2
Привести дроби к
общему
знаменателю
Упростить
полученное
выражение
196 х 2
0
2 х 2 х 2
196 х 2 0
Р х
0.
Получили уравнение
Q х
Для решения такого
уравнения нужно:
Решить уравнение
Р(х) = 0
х 14.х 14
1)2 14 2 14 2 384 0
2)2 14 2 14 2 384 0
Ответ : 14,14
Выяснить, какие из
найденных корней
уравнения Р(х) = 0 не
обращают знаменатель
дроби в нуль
Записать эти значения в
ответ

13. Решите уравнение

10
6
2
х 2 х 2

14. Алгоритм решения рационального уравнения

• Перенести все члены уравнения в левую часть.
• Привести дроби к общему знаменателю.
• Упростить полученное выражение.
Р х
• Получили уравнение Q х 0 .
Для решения такого уравнения нужно:
• Решить уравнение Р(х) = 0.
• Выяснить, какие из найденных корней уравнения Р(х) = 0
не обращают знаменатель
дроби в нуль.
• Записать эти значения в ответ.
10
6
2
х 2
х 2
\ х 2
\ х 2
10
6
\ х 2 4
2
0
х 2
х 2
10 х 20 6 х 12 2 х 2 8
0
х 2 х 2
2 х 2 16 х
0
х 2 х 2
2 х 2 16 х 0
2х х 8 0
х 0, х 8
1) 0 2 0 2 4 0
2) 8 2 8 2 60 0
Ответ : 0,8

16. Решите уравнение

1группа
2 группа
3
7
10
х 2 х 2 х
1
5
4
у у 2 у 3
3группа
1
1
0
10с 1 5с 2

17. Задача

• Моторная лодка, двигаясь по течению реки,
проходит от пристани А до пристани В
расстояние, равное 24км, на полчаса быстрее,
чем то же расстояние против течения. Какую
скорость развивает лодка в стоячей воде,
если скорость течения реки равна 2км/ч?
24
24
1
.
х 2 х 2 2

18. задача

• Лодка прошла 10км по течению реки и
6км против течения, затратив на весь путь
2ч. Чему равна собственная скорость
лодки, если скорость течения реки равна
2км/ч?
10
6
2.
х 2 х 2

19. Домашнее задание

П.7 стр. 29 – 32.Пример 1 – 4.
№258(в) — №261(в).
Алгоритм

20. Решите уравнение

2
х
х 1

22. Характеристика взаимодействий.

Одинаковые задания
1
1
1
1
Индивидуально-групповое
взаимодействие.

English     Русский Правила

Решатель индексов онлайн с пошаговым решением

	Дом
	Системы линейных уравнений и решение задач
	Решение квадратных уравнений
	Решение абсолютных неравенств
	Решение квадратных уравнений
	Решение квадратных неравенств
	Решающие системы сокращения строк уравнений
	Решение систем линейных уравнений с помощью графиков
	Решение квадратных уравнений
	Решение систем линейных уравнений
	Решение линейных уравнений. Часть II
	Решение уравнений I
	Итоговая оценка результатов решения проблем и навыков
	Решение математических задач: длинное деление лица
	Решение линейных уравнений
	Системы линейных уравнений с двумя переменными
	Решение системы линейных уравнений с помощью графика
	Ti-89 Решение одновременных уравнений
	Системы линейных уравнений с тремя переменными и матричные операции
	Решение рациональных уравнений
	Решение квадратных уравнений методом факторинга
	Решение квадратных уравнений
	Решение систем линейных уравнений
	Системы уравнений с двумя переменными
	Решение квадратных уравнений
	Решение экспоненциальных и логарифмических уравнений
	Решение систем линейных уравнений
	Решение квадратных уравнений
	Математическая логика и решение задач с отличием
	Решение квадратных уравнений методом факторинга
	Решение буквенных уравнений и формул
	Решение квадратных уравнений путем заполнения квадрата
	Решение экспоненциальных и логарифмических уравнений
	Решение уравнений с дробями
	Решение уравнений
	Решение линейных уравнений
	Решение линейных уравнений с одной переменной
	Решение линейных уравнений
	РЕШЕНИЕ КВАДРАТИЧНЫХ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ КВАДРАТИЧНОЙ ФОРМУЛЫ
	РЕШЕНИЕ ЛИНЕЙНЫХ УРАВНЕНИЙ

 

Выражение Уравнение Неравенство Свяжитесь с нами Упрощение Фактор Расширение GCF LCM Решение График Система SOLVE График Система . Наших пользователей: Моя мать всегда пристает ко мне по поводу игр на компьютере, потому что считает это пустой тратой времени, но я доказал ее неправоту, когда мне удалось улучшить свои оценки по алгебре с помощью вашей программы. Это действительно настоящий помощник. Кандида Барни, MT Квадратные уравнения действительно доставляли мне неприятности. Затем у меня появился Алгебратор, и он помог мне не только с квадратичными уравнениями, но и с практически любым уравнением или выражением, которое я только мог придумать! Кен Роджерс, Лос-Анджелес. ВОТ ЭТО ДА!!! Это круто!! Нравится обновленная версия, она делает вещи ГЛАДКИМИ!!! Т.П., Вайоминг В течение многих лет я платил за дорогую программу для своей дочери, которая была не чем иным, как прославленным репетиторством. По совету учителей дочери я купил вашу программу. Она уже стала настолько лучше, что я понимаю, что должен был купить ее давным-давно и сэкономить деньги! Оуэн Паттон, Юта. Студенты, борющиеся со всевозможными задачами по алгебре, узнают, что наше программное обеспечение может спасти им жизнь. Вот поисковые фразы, которые сегодняшние поисковики использовали, чтобы найти наш сайт. Сможете ли вы найти среди них свою? Поисковые фразы, использованные 10 мая 2012 г.: Marh Рабочие листы дробей в процентах КАЛЬКУЛЯТОР ДЕСЯТИЧНЫХ ДОЛЯ алгебра балдор 3 переменных одновременное решение уравнений фото переменных и математических выражений одновременных уравнения в повседневной жизни рабочие листы по математике для 10 класса «лист перестановок» Калькулятор решения рациональных уравнений теорема Силова десятичная в двоичную ti89 ти-89+скачать Рабочий лист дробей промежуточный Руководство пользователя калькулятора ti-85 «Решение алгебраического уравнения» Дроби 8 и 9 классов и алгебра элементарная математика для подростков как использовать квадратные корни TI-83 Plus целочисленный рабочий лист Рабочие листы пропорций 5-го класса бесплатных печатных рабочих листа с использованием алгебраических шаблонов Техасские планы уроков для первого класса математические стихи математические формулы наименьшее общее кратное практика Математическое упражнение упрощение радикальных выражений ответы каковы ответы на мои математические задачи, которые решают системы подстановкой дроби «упростить» калькулятор как решать подкоренные выражения деления факторинг для gcSE классификация алгебраических квадратных корней простой способ сделать 7 класс по алгебре рабочих листа для 4-х классов найти наименьший общий знаменатель Скачать тест Макдугала Литтелла ввод неопределенных интегралов в TI-85 алгебраических выражения в повседневной жизни найти ответы на дискретные математические задачи т1 84 игры интерактивный график квадратных уравнений радикальный калькулятор Образец бумаги для теста способностей алгебра I eoct информационный бюллетень Калькулятор квадратного корня множителя Рабочий лист по экспоненциальной функции в предварительном исчислении сол-грамматический тест манекен для предварительной алгебры аналитическая тригонометрия с приложениями 9 издание +ответы Рабочий лист по неравенству объективная математика Распространенные ошибки TI-89 Формула изменения разницы в последовательности математика со вкусом Рабочие листы пересмотра ks3 maple plot многомерное выражение algerbra. com загружаемых математических листа для типов углов парабола, линейная, кубическая, рациональная, обратная программирование ти-84 бесплатный базовый тест математических способностей «примеры задач с формулой расстояния» Калькулятор умножения рациональных выражений Объяснение алгебраических выражений предварительный расчет для чайников математический писк ответы aptitude+пример+документы+скачать «бесплатные электронные книги» + c +программирование электронная книга по математике бесплатно вопросы для печати ks3 sats по математике решены вопросы о способностях Рабочий лист уравнения алгебраических дробей Sat2 учебник по математике скачать бесплатно вычитание подкоренных выражений сложение и вычитание целых чисел бесплатные рабочие листы решение нескольких уравнений в Matlab карман + электронная книга с преобразованием Фурье Буклет ответов по бухгалтерскому учету Glencoe подстановка формулы счета примеров упрощения тригонометрических выражений найти наибольший общий делитель чисел 12 и 18 викторина с несколькими вопросами (гидромеханика) квадратичная формула онлайн-решатель печатные отрицательные и положительные целые числа решение алгебраических уравнений решатель булевой алгебры Рабочий лист периметра области ks2 Решатель одновременных уравнений с 3 переменными Java ПО для алгебры Журнал + ТИ-84 Предыдущий Следующий

‎Решатель уравнений 4 в 1 в App Store

Описание

Equation Solver 4-in-1 — это универсальное приложение, помогающее решать линейные уравнения с одной переменной, квадратные уравнения с вещественными и комплексными корнями, уравнения кубической и четвертой степени.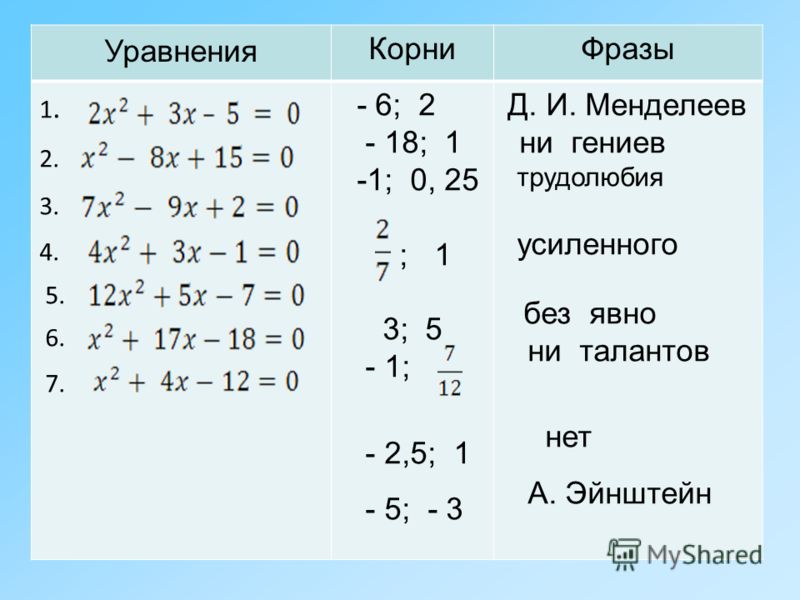 Он интуитивно понятен и прост в использовании. Просто введите любое уравнение, которое вы хотите решить, и калькулятор уравнений покажет вам результат.

Все, что вам нужно для решения уравнений или проверки результатов!

Особенности:

• Решатель линейных уравнений.
• Решатель квадратных уравнений.
• Решатель кубических уравнений.
• Решатель уравнений четвертой степени.
• Решает уравнения с дробями и скобками. Примечание: приложение пока не поддерживает уравнения с переменной в знаменателе.
• Поддерживает целые числа, дроби и десятичные дроби, включая отрицательные значения.
• Предопределенные форматы.
• Подробные пошаговые инструкции для линейных уравнений и квадратных уравнений.
• Сохраняет историю с возможностью вызова предыдущих уравнений.
• Кнопки «Назад» и «Вперед» для проверки и вызова последних уравнений.
• Отправляет результаты и историю по электронной почте.

000Z» aria-label=»February 10, 2020″> 10 февраля 2020 г.

Версия 4.1.5

Добавлены чешская и польская локализации.
Обновлен интерфейс для iPhone XR.

Рейтинги и обзоры

Приложение решает все… буквально

Обычно вы бы использовали калькулятор, чтобы получить ответ. Ну, это заставляет вас дать ответ. Не уверен, что они собирались здесь, но разве это не было бесполезно

ПОТРЯСАЮЩИЕ!

Это спасло меня. Сдавать алгебру в колледже через 10 лет после окончания школы — это все равно, что заново учить язык. Мне нравится тот факт, что он показывает вам решения, так что вы также можете изучить различные проблемы.

Моя единственная рекомендация для программистов — разрешить вводить больше переменных в расширенном режиме. Если эта функция уже здесь, я ее не нашел.

Идеальный

ЭТО ПОТРЯСАЮЩЕЕ ПРИЛОЖЕНИЕ перейдите в расширенное раскрывающееся меню и введите свою математическую задачу из книги. И ЭТО ДАЖЕ ПОКАЗЫВАЕТ СВОЮ РАБОТУ!!!! просто потрясающе. получить это приложение!!

Разработчик, Intemodino Group s.r.o., не предоставил Apple подробностей о своей политике конфиденциальности и обработке данных. Для получения дополнительной информации см. политику конфиденциальности разработчика.

Сведения не предоставлены

Разработчик должен будет предоставить сведения о конфиденциальности при отправке следующего обновления приложения.

Информация

Продавец

Интермодино Групп с.р.о.

Размер

No related posts.