Тангенс график: График тригонометрических функций. Тангенс. Котангенс

.3. СВОЙСТВА ФУНКЦИИ y=tg⁡x И ЕЕ ГРАФИК

Объяснение и обоснование

Напомним, что . Таким образом, областью определения функции y=будут все значения аргумента, при которых , то есть все значения x, kZ. Получаем

Этот результат можно получить и геометрически. Значения тангенса – это ордината соответствующей точки  на линии тангенсов (рис.91). Поскольку точки Aи B единичной окружности лежат на прямых ОА и ОВ, параллельных линии тангенсов, мы не сможем найти значение тангенса дляx, kZ.

Для всех других значений аргумента мы можем найти соответствующую точку на линии тангенсов и ее ординату — тангенс. Следовательно, все

Значенияx входят в область определения функции y=tgx.

Для точек единичной окружности (которые не совпадают с точками А и В) ординаты соответствующих т

очек на линии тангенсов принимают

все значения до +, поскольку для любого действительного числа

мы можем указать соответствующую точку на оси ординат, а значит, и соответствующую точку на оси тангенсов.

Учитывая, что точка О лежит

внутри окружности, а точка   вне ее (или на самой окружности), получаем, что прямая  имеет с окружностью хотя бы одну общую точку

(на самом деле их две). Следовательно, для любого действительного числа

найдется аргумент х, такой, что tan x равен данному действительному числу.

Поэтому область значений функции y= tg x — все действительные числа,

то есть R. Это можно записать так: E (=tgx) = R. Отсюда следует, что наибольшего и наименьшего значений функция tan x не имеет.

Как было показано в § 13, тангенс — нечетная функция:tg(-x)=tg x, следовательно, ее график симметричен относительно начала координат.

Тангенс — периодическая функция с наименьшим положительным периодом

Поэтому при построении графика

этой функции достаточно построить график на любом промежутке длиной π,

а потом полученную линию перенести параллельно вправо и влево вдоль оси

Ox на расстоянияkT = πk, где k — любое натуральное число.

Чтобы найти точки пересечения графика функции с осями координат,

напомним, что на оси Oy значение x = 0. Тогда соответствующее значение

y = tg 0 = 0, то есть график функции y = tg x проходит через начало координат.

На оси Ox значение y = 0. Поэтому необходимо найти такие значения x,

при которых tg x, то есть ордината соответствующей точки линии тангенсов, равна нулю. Это будет тогда и только тогда, когда на единичной окружности будут выбраны точки C или D, то есть при x = πk, k ∈ Z.

Промежутки знакопостоянства. Как было обосновано в § 13, значения

функции тангенс положительны (то есть ордината соответствующей точкилинии тангенсов положительна) в І и ІІІ четвертях. Следовательно, tgx > 0 при

а также, учитывая период, при всех

Значения функции тангенс отрицательны (то есть ордината соответствующей точки линии тангенсов отрицательна) во ІІ и ІV четвертях. Такимобразом,

Промежутки возрастания и убывания.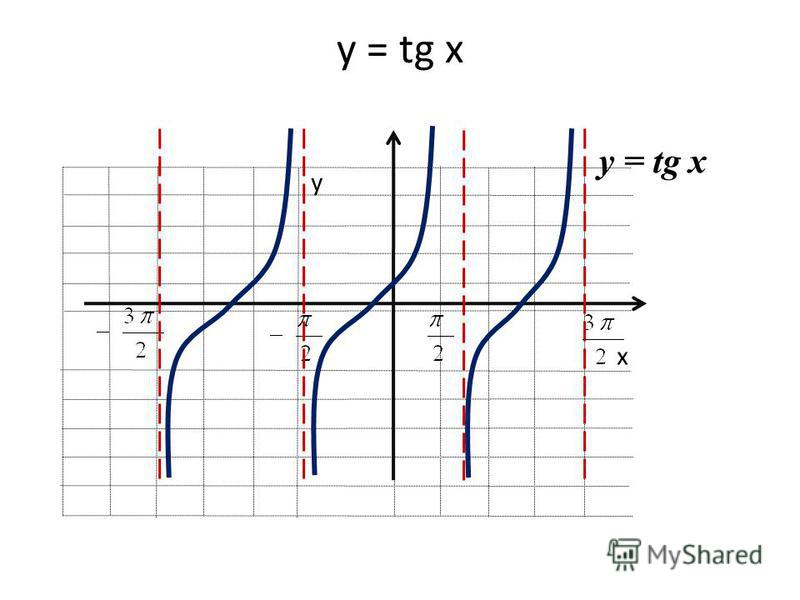           

 Учитывая периодичность функции tgx (период T = π), достаточно исследовать ее на возрастание и убывание на любом промежутке длиной π,

например на промежутке . Если x (рис. 92), то при увеличении аргумента x (x2>x1) ордината соответствующей точки линии

тангенсов увеличивается (то есть tgx2>tgx1). Таким образом, на этом

промежутке функция tgx возрастает. Учитывая периодичность функции

tgx, делаем вывод, что она возрастает также на каждом из промежутков

Проведенное исследование позволяет обоснованно построить график

функции y = tg x. Учитывая периодичность этой функции (с периодом π),

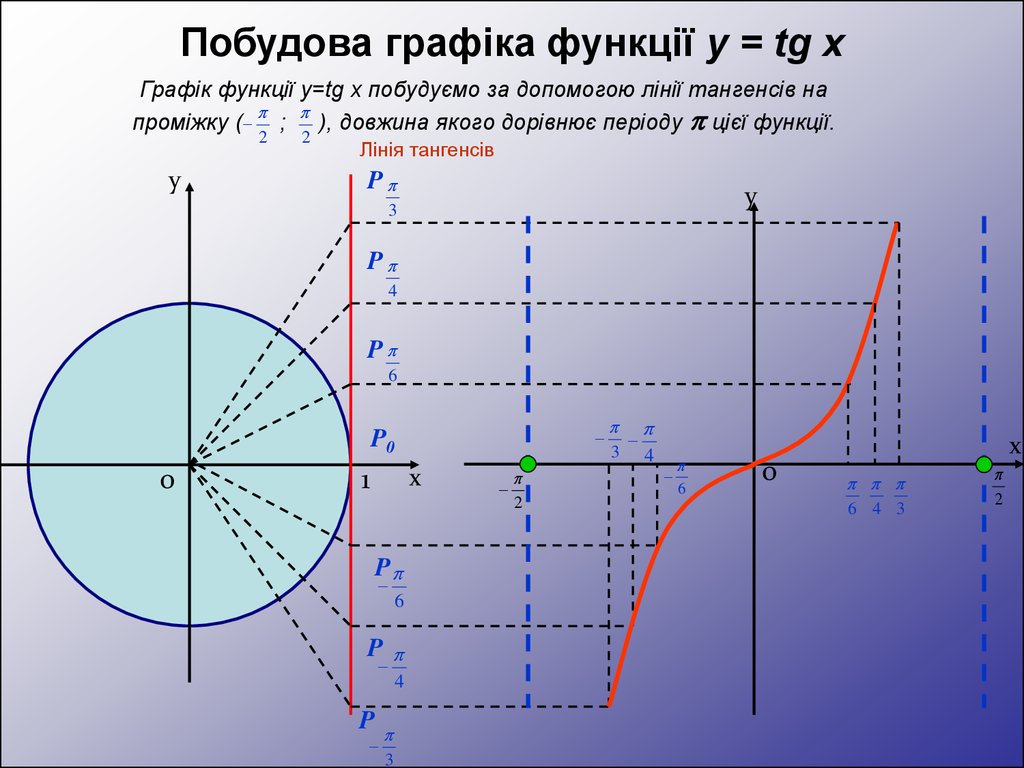
сначала построим график на любом промежутке длиной π, например на промежутке . Для более точного построения точек графика воспользуемся также тем, что значение тангенса — это ордината соответствующей точки

линии тангенсов. На рисунке 93 показано построение графика функции

y = tg x на промежутке.

Далее, учитывая периодичность тангенса (с периодом π), повторяем вид

графика на каждом промежутке длиной π (то есть параллельно переносим

график вдоль оси Ох на πk, где k — целое число).

Получаем график, приведенный на рисунке 94, который называется тангенсоидой.

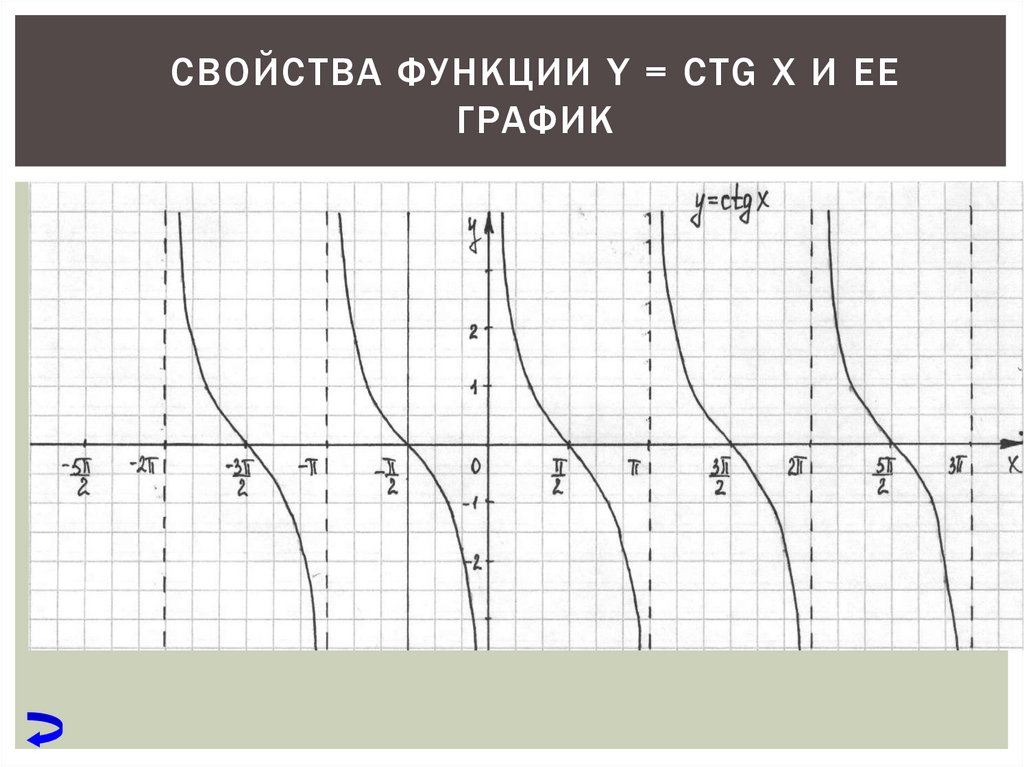
14.4. СВОЙСТВА ФУНКЦИИ y = ctg x И ЕЕ ГРАФИК

Объяснение и обоснование

Так как  =, то областью определения котангенса будут все значения аргумента, при которых sin х ≠ 0, то есть x ≠ πk, k ∈ Z. Такимобразом,

D (ctg x): x ≠

πk, k ∈ Z.

Тот же результат можно получить, используя геометрическую иллюстрацию. Значение котангенса — это абсцисса соответствующей точки на линии

котангенсов (рис. 95).

 Поскольку точки А и В единичной окружности лежат на прямых ОА

и ОВ, параллельных линии котангенсов, мы не можем найти значение котангенса для x = πk, k ∈ Z. Длядругихзначенийаргументамыможемнайтисоответствующуюточкуна линии котангенсов и ее абсциссу — котангенс. Поэтому все значения x ≠ πk входят в область определения функции у = ctg х.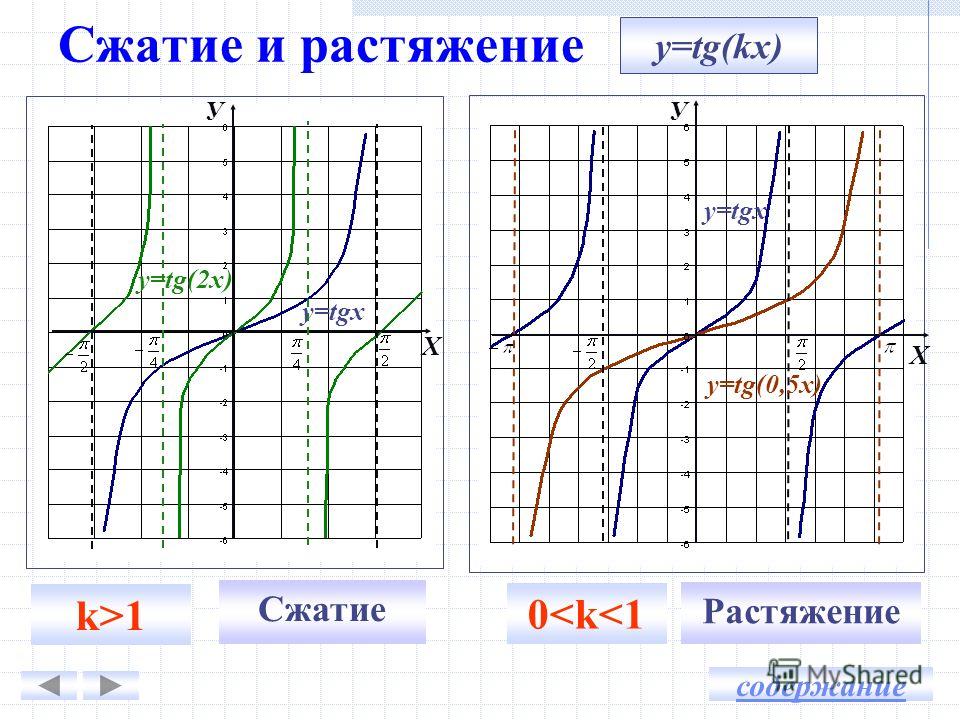

Для точек единичной окружности (которые не совпадают с точками А и В) абсциссы соответствующих точек на линии котангенсов принимают все значения от –× до +×, поскольку для любого действительного числа мы можем указать соответствующую точку на оси абсцисс, а значит, и соответствующую точку Qх на оси котангенсов. Учитывая, что точка О лежит внутри окружности, а точка Qх — вне ее (или на самой окружности), получаем, что прямая ОQх имеет с окружностью хотя бы одну общую точку (на самом деле их две). Следовательно, для любого действительного числа найдется аргумент х, такой, что сtg x равен данному действительному числу. Таким образом,

область значений функции y = ctg x — все действительные числа, то есть R.

Это можно записать так: E (ctgx) = R.Из приведенных рассуждений также вытекает, что наибольшего и наименьшего значений функция ctgxне имеет.

Как было показано в § 13, котангенс — нечетная функция: ctg (-x) = -ctgx, поэтому ее график симметричен относительно начала координат.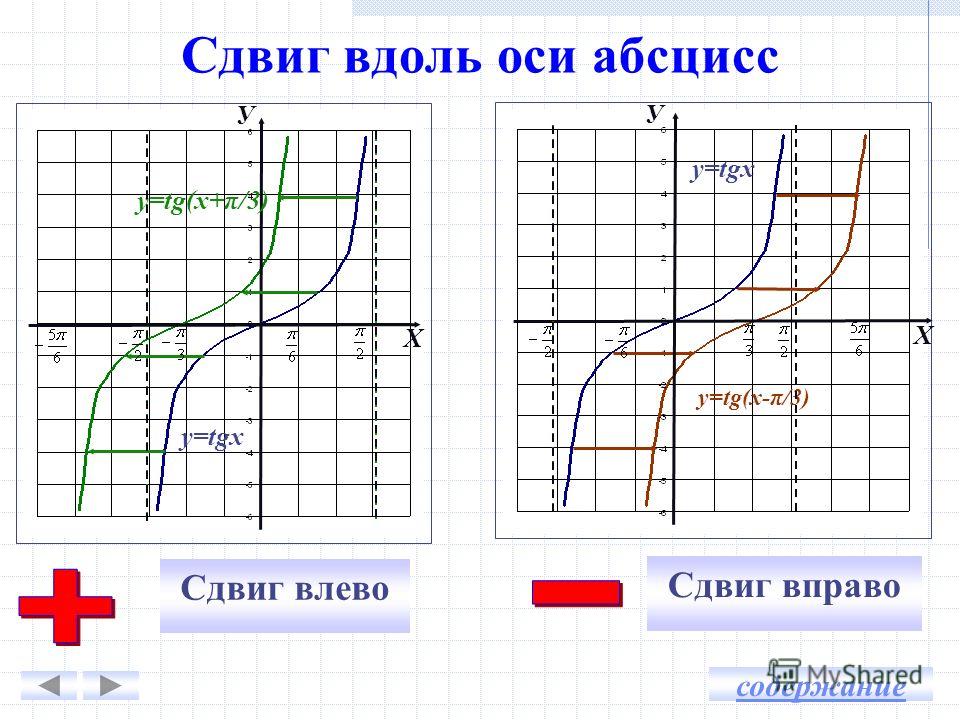

Там же было обосновано, что котангенс — периодическая функция с наи­меньшим положительным периодом T= : ctg (x+ ) = ctg x, поэтому через промежутки длиной п вид графика функции ctgxповторяется.

Чтобы найти точки пересечения графика функции с осями координат, напомним, что на оси Oyзначение x= 0. Но ctg0 не существует, значит, график функции y= ctg x не пересекает ось Oy.

На оси Оx значение y= 0. Поэтому необходимо найти такие значения x, при которых ctgx, то есть абсцисса соответствующей точки линии котанген­сов, равна нулю. Это будет тогда и только тогда, когда на единичной окруж­ности будут выбраны точки C или D(рис. 95), то есть при

Промежутки знакопостоянства. Как было обосновано в § 13, значения функции котангенс положительны (то есть абсцисса соответствующей точки линии котангенсов положительна) в I и III четвертях (рис. 96). Тогда ctgx> 0 при всех . Учитывая период, получаем, что ctgx> 0 при всех

         Значения функции котангенс отрицательны (то есть абсцисса соответ­ствующей точки линии котангенсов отрицательна) во II и IV четвертях, та­ким образом, ctgx< 0 при .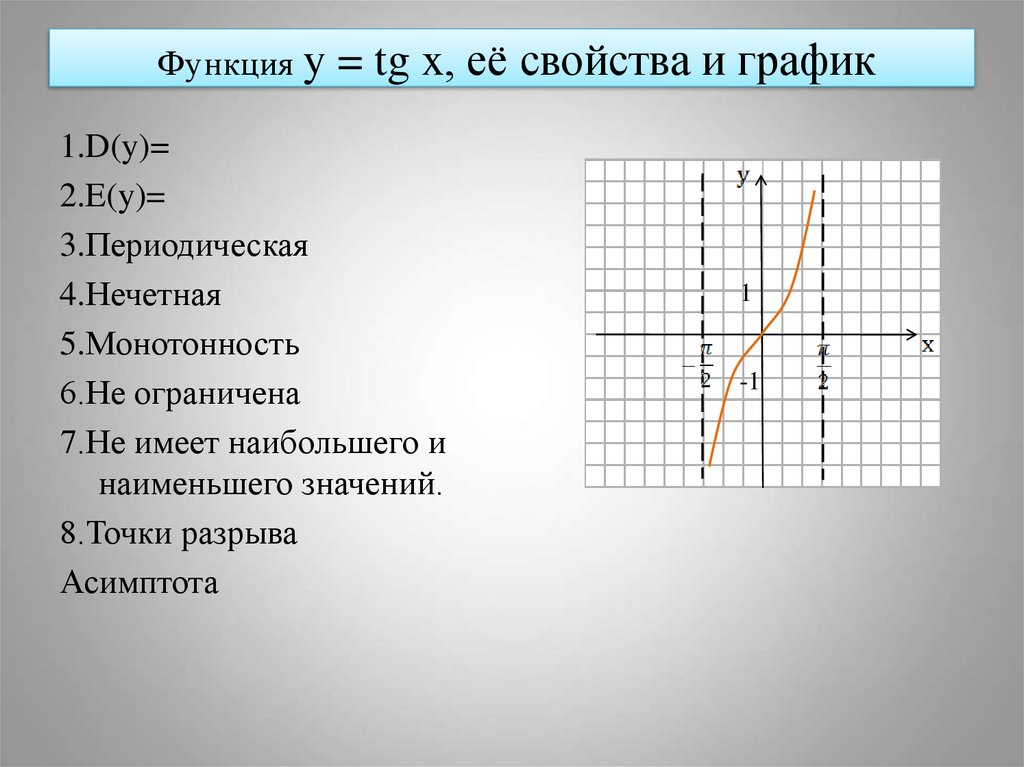

 

     Промежутки возрастания и убывания

 Учитывая периодичность функции ctg x (наименьший положительный период T = ), достаточно исследовать ее на возрастание и убывание на любом промежутке длиной , например на промежутке (0; ). Если (0; ) (рис. 97), то при увеличении аргумента x (x₂>x₁) аб­сцисса соответствующей точки линии котангенсов уменьшается (то есть ctgx₂<ctgx₁), следовательно, на этом промежутке функция ctg x убывает. Учитывая периодичность функции y= ctgx, делаем вывод, что она также убывает на каждом из промежутков

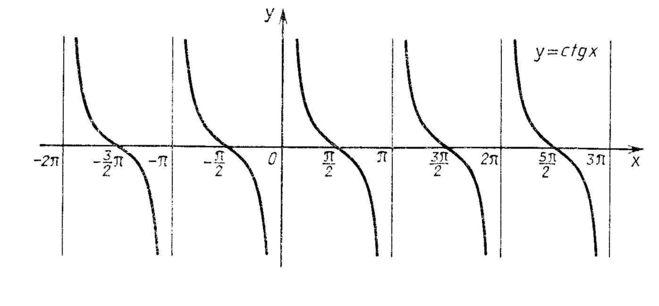
 Проведенное исследование позволяет построить график функции y= ctg x аналогично тому, как был построен график функции y= tg x. Но график функции у = ctg x можно получить также с помощью геометрических пре­образований графика функции у = tg х. По формуле, приведенной на с. 172, , то есть Поэтому график функции у = ctg x можно получить из графика функции у = tg х параллельным переносом вдоль оси Ох на (− ) и симметричным отображением полученного графика относительно оси Ох.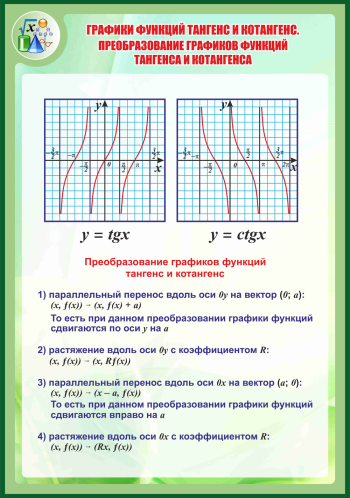

Получаем график, который называется котангенсоидой (рис. 98).

 

Функция y = tg x, свойства и график косинуса с примерами

1. Развертка тангенса движения точки по числовой окружности в функцию от угла
2. Свойства функции y=tgx
3. Примеры

п.1. Развертка тангенса движения точки по числовой окружности в функцию от угла

При движении точки по числовой окружности на вертикальной касательной, проведенной через точку (1;0), отображаются значения тангенсов соответствующих углов (см. §3 данного справочника).

Рассмотрим, как изменяется тангенс, если точка описывает полный круг, и угол x изменяется в пределах: 0≤x≤2π и построим график y=tgx на этом отрезке.

Если мы продолжим движение по окружности для углов x > 2π, кривые продолжатся вправо; если будем обходить числовую окружность в отрицательном направлении (по часовой стрелке) для углов x<0, кривые продолжатся влево.

В результате получаем график y=tgx для для всех x из области допустимых значений.

График y=tgx называют тангенцоидой.
Часть тангенцоиды c \(-\frac\pi2\lt x\lt \frac\pi2\) называют главной ветвью тангенцоиды.

п.2. Свойства функции

y=tgx⁡

1. Область определения \(x\ne\frac\pi2+\pi k\) — множество действительных чисел, кроме точек, в которых \(cosx=0\).

2. Функция не ограничена сверху и снизу. Область значений \(y\in\mathbb{R}\)

3. Функция нечётная $$ tg(-x)=-tgx $$

4. Функция периодическая с периодом π $$ tg(x+\pi k)=tgx $$

5. Функция стремится к \(+\infty\) при приближении слева к точкам \(x=\frac\pi2+\pi k\).
Приближение к точке a слева записывается как \(x\rightarrow a-0\) $$ \lim_{x\rightarrow\frac\pi2+\pi k-0} tgx=+\infty $$ Функция стремится к \(-\infty\) при приближении справа к точкам \(x=\frac\pi2+\pi k\).
Приближение к точке a справа записывается как \(x\rightarrow a+0\) $$ \lim_{x\rightarrow\frac\pi2+\pi k+0} tgx=-\infty $$ Нули функции \(y_{0}=0\) достигаются в точках \(x_0=\pi k\)

6.  Функция возрастает на всей области определения.

7. Функция имеет разрывы в точках \(x=\frac\pi2+\pi k\), через эти точки проходят вертикальные асимптоты. На интервалах между асимптотами \(\left(-\frac\pi2+\pi k;\ \frac\pi2+\pi k\right)\) функция непрерывна.

п.3. Примеры

Пример 1.Найдите наименьшее и наибольшее значение функции y=tgx на заданном промежутке:

a) \(\left[\frac{2\pi}{3}; \frac{3\pi}{2}\right)\) $$ y_{min}=tg\left(\frac{2\pi}{3}\right)=-\sqrt{3},\ \ y_{max}=\lim_{x\rightarrow\frac{3\pi}{2}-0}tgx=+\infty $$ б) \(\left(\frac{\pi}{2}; \pi\right]\) $$ y_{min}=\lim_{x\rightarrow\frac{\pi}{2}+0}tgx=-\infty,\ \ y_{max}=tg(\pi)=0 $$ в) \(\left[\frac{3\pi}{4}; \frac{7\pi}{6}\right]\) $$ y_{min}=tg\left(\frac{3\pi}{4}\right)=-1,\ \ y_{max}=tg\left(\frac{7\pi}{6}\right)=\frac{1}{\sqrt{3}} $$

Пример 2. Решите уравнение:
a) \(tgx=-\sqrt{3}\)
Бесконечное множество решений: \(x=\frac{2\pi}{3}+\pi k,\ k\in\mathbb{Z}\)

б) \(tg\left(x-\frac\pi2\right)=0\)
\(x-\frac\pi2=\pi k\)
Бесконечное множество решений: \(x=\frac{\pi}{2}+\pi k,\ k\in\mathbb{Z}\)

в) \(tg(2x)=1\)
\(2x=\frac\pi4+\pi k\)
Бесконечное множество решений: \(x=\frac{\pi}{8}+\frac{\pi k}{2},\ k\in\mathbb{Z}\)

г) \(tg\left(\frac{x}{3}-1\right)=-1\)
\(\frac{x}{3}-1=-\frac{\pi}{4}+\pi k\)
\(\frac{x}{3}=1-\frac{\pi}{4}+\pi k\)
Бесконечное множество решений: \(x=3-\frac{3\pi}{4}+3\pi k,\ k\in\mathbb{Z}\)

Пример 3.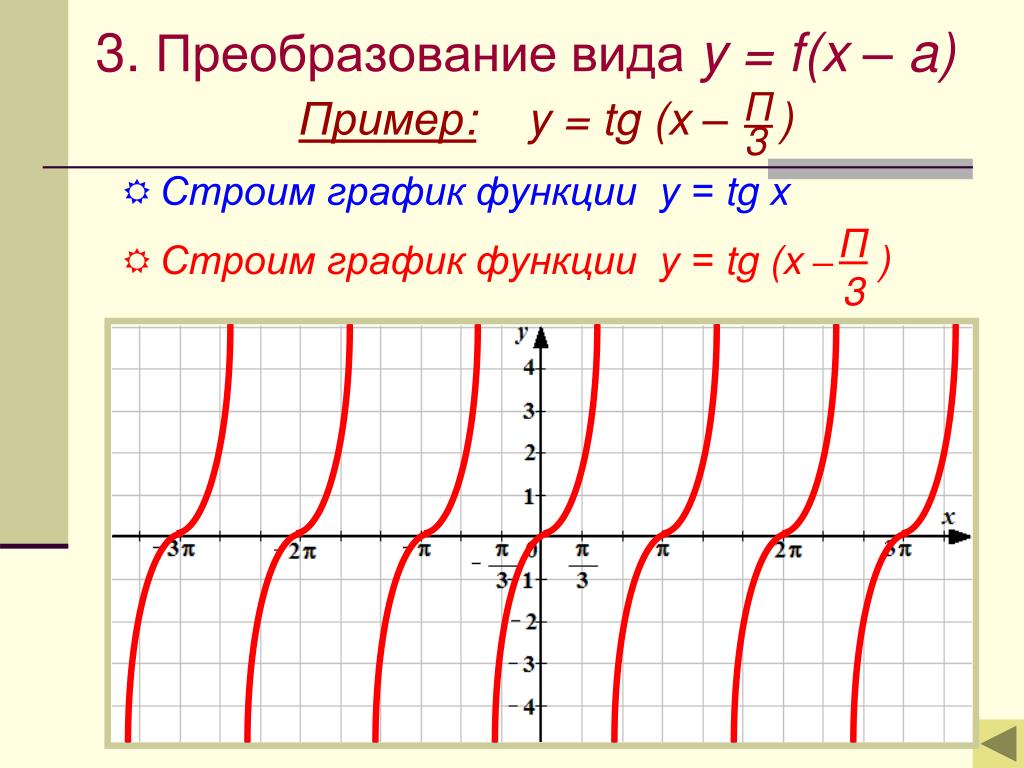 2+tgx\ne \left[ \begin{array} -y(x)\\ y(x) \end{array} \right. $$ Функция ни чётная, ни нечётная.

Пример 4. Если \(tg(7\pi-x)=\frac34\), то чему равны \(tgx,\ \ ctgx\)?
Т.к. период тангенса равен π, получаем: \begin{gather*} tg(7\pi-x)=tg(-x)=-tgx=\frac34\Rightarrow tgx=-\frac34\\ ctgx=\frac{1}{tgx}=-\frac43 \end{gather*} Ответ: \(-\frac34,\ \ -\frac43\)

График функции тангенса — Тригонометрия

График функции тангенса — Тригонометрия — Открытый справочник по математике

Открытый справочник по математике

Главная Контакт О Тематический указатель

Тангенс угла строится относительно этой меры угла.

Попробуйте это Перетащите вершину треугольника и посмотреть, как функция тангенса зависит от угла.

Чтобы построить график функции тангенса, мы отмечаем угол вдоль горизонтальной оси x, и для каждого угла мы помещаем тангенс этого угла на вертикальную ось y. В результате, как видно выше, получается довольно неровная кривая, уходящая в положительную бесконечность в одном направлении и отрицательную бесконечность в другом.

На диаграмме выше перетащите точку A по круговой траектории, чтобы изменить угол CAB. При этом точка на графике перемещается в соответствии с углом и его касательной. (Если вы установите флажок «прогрессивный режим», кривая будет рисоваться при перемещении точки A вместо отслеживания существующей кривой.)

Область определения касательной функции имеет дыры

Когда вы перетаскиваете точку A, обратите внимание, что после полного поворота вокруг точки B форма графика повторяется. Форма касательной одинакова для каждого полного поворота угла, поэтому функция называется «периодической». Период функции составляет 360° или 2π радиан. Вы можете вращать точку столько раз, сколько захотите.

Это означает, что вы можете найти тангенс любого угла, независимо от того, насколько он велик, за одним исключением. Если вы посмотрите на график выше, вы увидите, что tan90° не определено, потому что требует деления на ноль. Следовательно, такие углы не входят в область функций тангенса и дают неопределенный результат.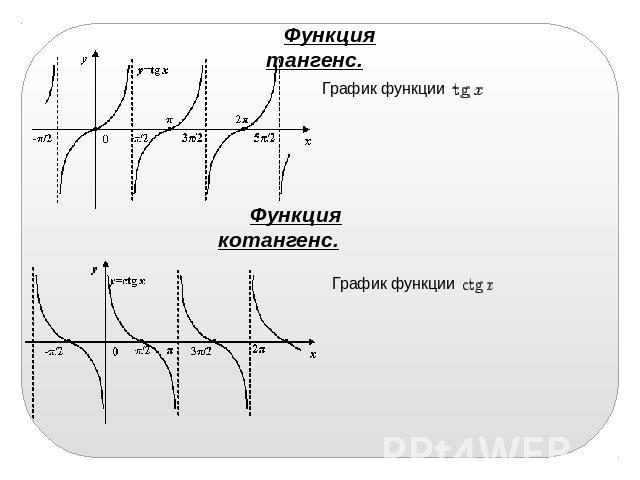 Пытаться tan90 ° на вашем калькуляторе, и вы получите ошибку, тогда как, скажем, 89,99 будет работать.

Таким образом, областью определения функции тангенса является множество всех действительных чисел , кроме 9.0026 90°, -90°, 270°, -270° и т. д. (или эквивалент в радианах: плюс/минус пи больше 2, 3 пи больше 2 и т. д.).

Диапазон

Диапазон функции — это набор значений результата, которые она может произвести. Функция тангенса имеет диапазон от положительной бесконечности до отрицательной бесконечности.

Чтобы понять, почему это происходит, нажмите «Сброс», затем перетащите точку А против часовой стрелки. Когда он приближается к точке 90°, когда AB почти вертикальна, вы можете видеть, что BC становится очень маленьким. Поскольку тангенс угла равен «Противоположный над смежным» (TOA), результат деления числа на очень маленькое число дает очень большое число. В конце концов, сторона BC стремится к нулю, а результат приближается к бесконечности.

То же самое происходит во втором квадранте, за исключением того, что тогда BC становится отрицательным, и поэтому функция приближается к отрицательной бесконечности.

Бесконечность не является реальным числом, поэтому tan90° на самом деле не определено. Однако, когда угол приближается к 90°, функция будет возвращать очень большие числа. Например, загар (89,999°) больше 57 000.

Функция арктангенса

Что, если бы нас попросили найти арктангенс числа, скажем, 4,0? Другими словами, мы ищем угол, тангенс которого равен 4,0.

Если мы посмотрим на кривую выше, мы увидим четыре угла, тангенс которых равен 4,0 (красные точки). На самом деле, поскольку график бесконечно продолжается в обоих направлениях, существует бесконечное количество углов, тангенс которых имеет заданное значение.

Так что же говорит калькулятор?

Если вы попросите калькулятор определить арктангенс (tan ^-1 или atan) числа, он не сможет вернуть бесконечно длинный список углов, поэтому по соглашению он найдет только первый из них. Но помните, что их намного больше.

Другие темы по тригонометрии

Уголки

• Определение угла, свойства углов
• Стандартное положение на углу
• Начальная сторона угла
• Конечная сторона уголка
• Четырехугольники
• Котерминальные уголки
• Опорный уголок

Тригонометрические функции

• Знакомство с шестью триггерными функциями
• Функции больших и отрицательных углов
• Инверсные триггерные функции
• SOH CAH TOA Память


• Синусоидальная функция (sin) в прямоугольных треугольниках
• Функция обратного синуса (арксинус)
• График функции синуса
• Синусоидальные волны


• Функция косинуса (cos) в прямоугольных треугольниках
• Функция арккосинуса (arccos)
• График функции косинуса


• Касательная функция (тангенс) в прямоугольных треугольниках
• Функция арктангенса (арктангенс)
• График функции касательной


• Функция котангенса cot (в прямоугольных треугольниках)
• Функция секанса сек (в прямоугольных треугольниках)
• Функция косеканса csc (в прямоугольных треугольниках)

Решение задач по тригонометрии

• Общий подход
• Определение наклонного расстояния вдоль склона или пандуса
• Определение угла наклона или пандуса

Исчисление

• Производные тригонометрических функций

(C) 2011 Copyright Math Open Reference.
Все права защищены

График загара — GCSE по математике

Введение

Что такое график загара?

Как построить график загара

Единичный круг

Когда мы получаем положительные и отрицательные значения для tan(θ)

Что такое асимптота?

График функции тангенса

Как интерпретировать касательные графики

Рабочий лист касательного графика

Распространенные заблуждения

Похожие уроки

Практические вопросы по касательным графикам

Касательные графы Вопросы GCSE

Контрольный список обучения

Следующие уроки

Все еще застряли?

Индивидуальные математические занятия, созданные для успеха KS4

Еженедельные онлайн-уроки повторения GCSE по математике теперь доступны

Узнать больше

Введение

Что такое график загара?

Как построить график загара

Единичный круг

Когда мы получаем положительные и отрицательные значения для tan(θ)

Что такое асимптота?

График функции тангенса

Как интерпретировать касательные графики

Рабочий лист касательного графика

Распространенные заблуждения

Похожие уроки

Практические вопросы по касательным графикам

Касательные графы Вопросы GCSE

Контрольный список обучения

Следующие уроки

Все еще застряли?

Здесь мы узнаем о графиках касательной , в том числе о том, как распознавать график функции тангенса, рисовать кривую тангенса и обозначать важные значения, а также интерпретировать график тангенса.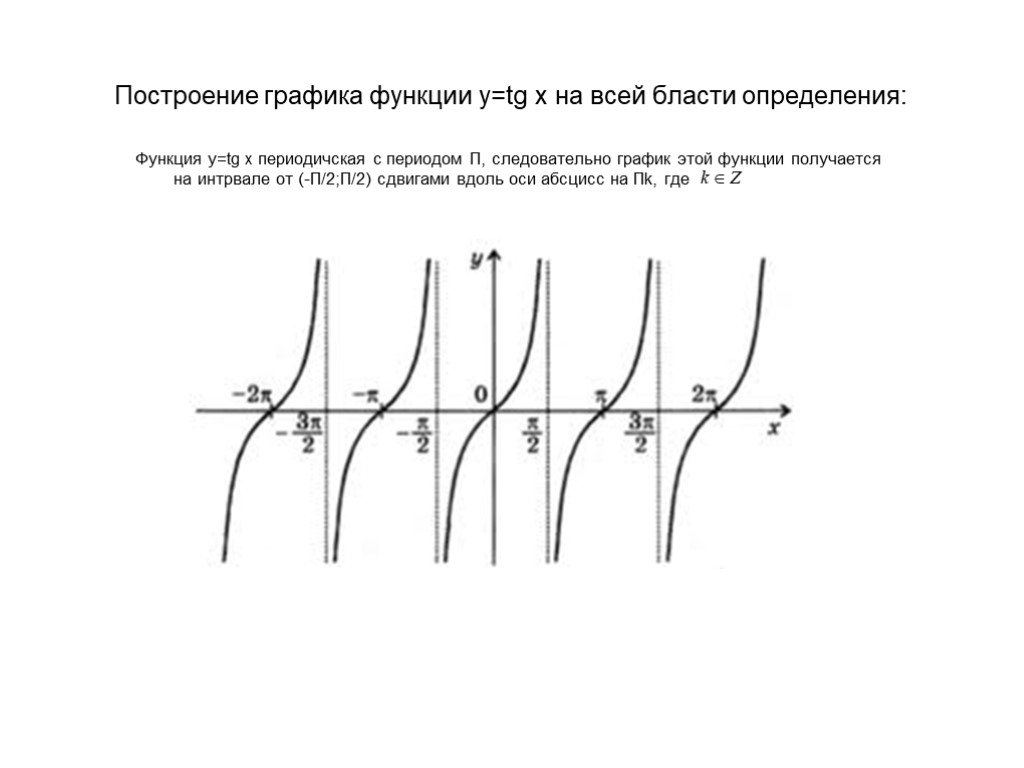

Также есть рабочие листы касательного графика , основанные на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли.

Что такое график загара?

График тангенса представляет собой визуальное представление функции тангенса для заданного диапазона углов.

Горизонтальная ось тригонометрического графика представляет угол, обычно записываемый как \theta , а ось y представляет собой тангенс функции этого угла.

9o

В этом уроке мы рассмотрим график функции тангенса только для углов в градусах, хотя его также можно представить в радианах.

Что такое танграф?

Как построить график тангенса

Помните, что \tan(\theta) — это отношение между противоположной стороной и прилежащей стороной прямоугольного треугольника:

Давайте посмотрим на 3 треугольника, где мы использовали бы отношение касательной для вычисления размера угла \theta . Для каждого треугольника смежная сторона одинакова, но длина противоположной стороны и связанный с ней угол меняются.

Здесь мы видим, что, поскольку \tan(\theta)=\frac{opp}{adj} , с увеличением угла \theta увеличивается и длина стороны, противоположной углу. Итак, для каждого треугольника имеем:

• Треугольник 1: \tan(\theta)=\frac{3}{10}=0,3
• Треугольник 2: \tan(\theta)=\frac{9}{10} =0,9
• Треугольник 3: \tan(\theta)=\frac{15}{10}=1,5

Итак, что произойдет, если сторона, противоположная углу, будет равна 10?

\тангенс(\тета)=\фракция{10}{10}=1 9о . Для любых больших или меньших углов нам нужно смотреть на единичный круг.

Объясните, как построить график тангенса

Единичная окружность

Единичная окружность — это окружность радиусом 1 с центром в начале координат. Мы можем пометить значения, в которых окружность пересекает оси, потому что мы знаем, что радиус единичной окружности равен 1 единице.

Мы все еще можем построить треугольник внутри единичного круга с углом, начинающимся с положительной оси x.

Глядя на тригонометрические соотношения синуса и косинуса, мы можем сказать, что:

• \sin(\theta)=\frac{a}{1} \; \текст{так} \; a=\sin(\theta)
• \cos(\theta)=\frac{b}{1} \; \текст{так} \; b=\cos(\theta)
• \tan(\theta)=\frac{a}{b} \; \текст{так} \; \tan(\theta)=\frac{\sin(\theta)}{\cos(\theta)}

Это означает, что ширина треугольника равна \cos(\theta), а высота треугольник равен \sin(\theta) . Таким образом, точка на единичной окружности является координатой ( \cos(\theta) , \; \sin(\theta) ): 9o

Кривая всегда имеет положительный градиент

В отличие от графиков функций синуса и косинуса, функция тангенса не является волной. Это потому, что граф не является непрерывным .

Следовательно, у волны нет амплитуды, так как нет максимального или минимального значения .

Касательная функция может измениться при преобразовании функции. Подробнее читайте в уроке преобразований тригонометрических функций. 9{-1}(\ theta) по математике GCSE. Степень -1 здесь используется как обозначение обратной функции, а не обратной. На уровне математики мы узнаем, что обратная величина к \tan(\theta) называется котангенсом или \cot(\theta), где \cot(\theta)=\frac{1}{\tan(\theta)}=\ гидроразрыва {\ соз (\ тета)} {\ грех (\ тета)} . Чтобы не путаться с обозначением обратной функции, мы называем обратную \tan(\theta) \arctan(\theta). Мы делаем то же самое с обратными функциями синуса и косинуса, \arcsin(\theta) и \arccos(\theta).

Как интерпретировать графики касательной

Чтобы интерпретировать графики касательной:

1. Проведите прямую линию от оси известного значения до кривой касательной.
2. Нарисуйте прямую перпендикулярную линию в точке пересечения с другой осью .
3. Считайте значение, где перпендикулярная линия пересекает другую ось.

Рабочий лист касательного графика

Получите бесплатный рабочий лист с более чем 20 вопросами и ответами. Включает рассуждения и прикладные вопросы. 9o считывается с графика.

• Графики синуса и косинуса перепутаны

Графики синуса и косинуса очень похожи, и их легко спутать друг с другом. Совет, который следует помнить, заключается в том, что вы «синусируете вверх» от 0 для синусоидального графика, поэтому линия увеличивается, тогда как вы «косинусируете вниз» от 1, поэтому линия уменьшается для косинусного графика.

• Неправильно построены асимптоты для графика касательной функции 9о и так далее.
  • Графики рисуются с помощью линейки

  Каждый тригонометрический график представляет собой кривую, поэтому единственный раз, когда вам требуется использовать линейку, — это начертить набор осей. Потренируйтесь рисовать каждую кривую от руки и отмечайте важные значения на каждой оси.

  • Значение, указанное вне диапазона

  При нахождении значения \theta с помощью тригонометрического графика необходимо убедиться , что значение \theta находится в пределах диапазона, указанного в вопросе. 9о тоже верно.

  Диаграмма тангенса является частью нашей серии уроков по тригонометрии. Возможно, вам будет полезно начать с основного урока по тригонометрии, чтобы получить общее представление о том, чего ожидать, или использовать пошаговые руководства ниже для получения более подробной информации по отдельным темам. Другие уроки этой серии включают:

  • Тригонометрия
  • График Cos
  • График Sin
  • Тригонометрические функции
  • Трехмерная тригонометрия
  • Площадь треугольника тригонометрия 9о

    \tan(150)=-0,8

    \tan(150)=0,6

    \tan(150)=-0,6

    \tan(150)=-0,2

    3 \tan(150)=-0,2

    3 320)=0,8

    \tan(-320)=-0,5

    \tan(-320)=-0,8

    \tan(-320)=0,5

    \tan(240)= \tan(- 120)

    \tan(240) = \tan(-240)

    \tan(240) = \tan(120)

    \tan(240) = \tan(60)

    Касательные графы Вопросы GCSE

    1.

    No related posts.