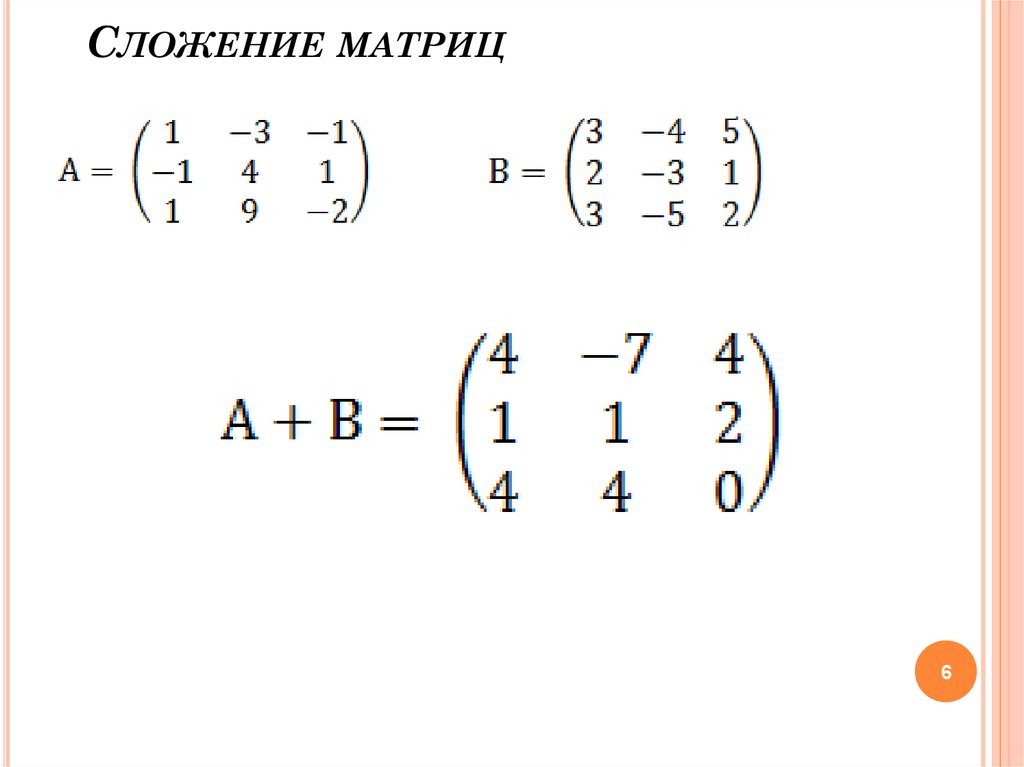умножение на число, сложение, вычитание, умножение матриц. Свойства операций над матрицами.
Сложение матриц:
Вычитание и сложение матриц сводится к соответствующим операциям над их элементами. Операция сложения матриц вводится только для матриц одинакового размера, т. е. для матриц, у которых число строк и столбцов соответственно равно. Суммой матриц А и В, называется матрица С, элементы которой равны сумме соответствующих элементов. С = А + В cij = aij + bij Аналогично определяется разность матриц.
Умножение матрицы на число:
Операция умножения (деления) матрицы любого размера на произвольное число сводится к умножению (делению) каждого элемента матрицы на это число. Произведением матрицы А на число k называется матрица В, такая что
bij = k × aij. В
= k × A
b
В
= k × A
b
Свойства сложения матриц и умножения матрицы на число:
Операции сложения матриц и умножения матрицы на число обладают следующими свойствами: 1. А + В = В + А; 2. А + (В + С) = (А + В) + С; 3. А + 0 = А; 4. А — А = 0; 5. 1 × А = А; 6. α × (А + В) = αА + αВ; 7. (α + β) × А = αА + βА; 8. α × (βА) = (αβ) × А; , где А, В и С — матрицы, α и β — числа.
Умножение матриц (Произведение матриц):
Операция
умножения двух матриц вводится только для случая, когда число
столбцов первой матрицы равно числу строк второй матрицы. Произведением матрицы Аm×n на матрицу Вn×p,
называется матрица Сm×p такая, что
сik = ai1 × b1k + ai2 × b2k + .
Свойства умножения матриц:
Умножение матриц не коммутативно, т.е. АВ ≠ ВА даже если определены оба произведения. Однако, если для каких — либо матриц соотношение АВ=ВА выполняется, то такие матрицы называются перестановочными. Самым характерным примером может служить единичная матрица, которая является перестановочной с любой другой матрицей того же размера. Перестановочными могут быть только квадратные
Умножение
матриц обладает
следующими свойствами:
1. А × (В × С) =
(А × В) × С;
2. А × (В + С) = АВ + АС;
3. (А + В)
× С = АС + ВС;
4. α × (АВ) = (αА) × В;
5. А × 0
= 0; 0 × А = 0;
6. (АВ)Т = ВТАТ;
7.
(АВС)Т = СТВТАТ;
8.
(А + В)Т = АТ + ВТ;
А × (В × С) =
(А × В) × С;
2. А × (В + С) = АВ + АС;
3. (А + В)
× С = АС + ВС;
4. α × (АВ) = (αА) × В;
5. А × 0
= 0; 0 × А = 0;
6. (АВ)Т = ВТАТ;
7.
(АВС)Т = СТВТАТ;
8.
(А + В)Т = АТ + ВТ;
Определителем матрицы второго порядка, или определителем второго порядка, называется число, которое вычисляется по формуле:
Определителем матрицы третьего порядка, или определителем третьего порядка, называется число, которое вычисляется по формуле:
Это число представляет алгебраическую сумму, состоящую из шести слагаемых. В каждое слагаемое входит ровно по одному элементу из каждой строки и каждого столбца матрицы. Каждое слагаемое состоит из произведения трех сомножителей.
Знаки,
с которыми члены определителя
матрицы входят в
формулу нахождения
определителя матрицы третьего порядка можно определить,
пользуясь приведенной схемой, которая
называется правилом треугольников или
правилом Сарруса. Первые три слагаемые
берутся со знаком плюс и определяются
из левого рисунка, а последующие три
слагаемые берутся со знаком минус и
определяются из правого рисунка.
Первые три слагаемые
берутся со знаком плюс и определяются
из левого рисунка, а последующие три
слагаемые берутся со знаком минус и
определяются из правого рисунка.
Определить количество слагаемых, для нахождения определителя матрицы, в алгебраической сумме, можно вычислив факториал: 2! = 1 × 2 = 2 3! = 1 × 2 × 3 = 6
Свойства определителей матриц
Свойства определителей матриц:
Свойство № 1:
Определитель матрицы не изменится, если его строки заменить столбцами, причем каждую строку столбцом с тем же номером, и наоборот (Транспонирование). |А| = |А|Т
Следствие:
Столбцы и строки определителя матрицы равноправны, следовательно, свойства присущие строкам выполняются и для столбцов.
Свойство № 2:
При
перестановке 2-х строк или столбцов определитель матрицы изменит знак на противоположный, сохраняя
абсолютную величину, т. е.:
е.:
Свойство № 3:
Определитель матрицы, имеющий два одинаковых ряда, равен нулю.
Свойство № 4:
Общий множитель элементов какого-либо ряда определителя матрицы можно вынести за знак определителя.
Следствия из свойств № 3 и № 4:
Если все элементы некоторого ряда (строки или столбца) пропорциональны соответствующим элементам параллельного ряда, то такой определитель матрицы равен нулю.
Свойство № 5:
Если все элементы какой–либо строки или столбца определителя матрицы равны нулю, то сам определитель матрицы равен нулю.
Свойство № 6:
Если
все элементы какой–либо строки или
столбца определителя представлены в виде суммы 2-х слагаемых,
то
Свойство № 7:
Если
к какой–либо строке (или столбцу) определителя прибавить соответствующие элементы
другой строки (или столбца), умноженные
на одно и тоже число, то определитель
матрицы не
изменит своей величины.
Пример применения свойств для вычисления определителя матрицы:
Как складывать и вычитать матрицы? (+ БЕСПЛАТНЫЙ рабочий лист!)
В этом пошаговом руководстве вы узнаете, как складывать или вычитать матрицы, используя примеры с подробными решениями.
См. также
- Как умножить матрицу
Пошаговое руководство по сложению и вычитанию матриц
- Матрица (множественное число: матрицы) представляет собой прямоугольный массив чисел или переменных, расположенных в строках и столбцах.
- Мы можем сложить или вычесть две матрицы, если они имеют одинаковые размеры.
- Для сложения или вычитания сложите или вычтите соответствующие записи и поместите результат в соответствующую позицию результирующей матрицы.
Сложение и вычитание матриц – Пример 1:
\(\begin{bmatrix} 2 & -5 & -3 \end{bmatrix}+ \begin{bmatrix}1 & -2 & -3 \end{bmatrix} \)
Решение:
Добавьте элементы в соответствующие позиции: \(\begin{bmatrix} 2+1 & -5+(-2) & -3+(-3) \end{bmatrix}= \begin{bmatrix}3 & -7 & -6 \end{bmatrix}\)
Сложение и вычитание матриц – Пример 2:
\(\begin{bmatrix}3 & 6 \\-1 & -3 \\-5 & -1\end{bmatrix}+ \begin{bmatrix}0 & — 1 \\6 & 0 \\2 & 3\end{bmatrix} \)
Решение :
Добавьте элементы в соответствующие позиции: \(\begin{bmatrix}3+0 & 6+(- 1) \\-1+6 & -3+0 \\-5+2 & -1+3\end{bmatrix} = \begin{bmatrix}3 & 5 \\5 & -3 \\-3 & 2 \end{bmatrix} \)
Сложение и вычитание матриц – Пример 3:
\(\begin{bmatrix}2 & -1 \\0 & 1 \end{bmatrix}+\begin{bmatrix}3 & 1 \\5 & -2 \end{bmatrix}\)
Решение :
Добавьте элементы в соответствующие позиции: \(\begin{bmatrix}2+3 и -1+1 \\0+5 и 1+(-2) \end{bmatrix}=\begin{bmatrix} 5 & 0 \\5 & -1 \end{bmatrix}\)
Сложение и вычитание матриц – Пример 4:
\(\begin{bmatrix}-1 & 2 \\3 & 4 \\0 & -2 \end{bmatrix}- \begin{bmatrix}5 & -2 \\6 & 1 \\-3 & 4\end{bmatrix} \)
Решение :
Вычтите элементы в совпадающих позициях: \(\begin{bmatrix}-1-5 & 2-(-2) \\3-6 & 4-1 \\0-(- 3) & -2-4\end{bmatrix}= \begin{bmatrix}-6 & 4 \\-3 & 3 \\3 & -6\end{bmatrix}\)
youtube.com/embed/WR9qCSXJlyY» allowfullscreen=»»/>Упражнения на сложение и вычитание Матрицы
- \(\color{blue}{\begin{bmatrix}6 и 8 \\-14 и 33 \end{bmatrix}-\begin{bmatrix}12 и 5 \\-27 & -8 \end{ bmatrix}}\)
- \(\color{blue}{\begin{bmatrix}12 и 21 \\-17 и 33 \end{bmatrix}-\begin{bmatrix}5&-8 \\2 & 19\end{bmatrix}}\)
- \(\color{blue}{\begin{bmatrix}-5 & 2& -2 \\4 & -2&0 \end{bmatrix}-\begin{bmatrix}6 & -5& -6 \\1 & 3&-3 \end{bmatrix}}\)
- \(\color{blue}{\begin{bmatrix}-6r+t \\-r\\6s \end{bmatrix}+\ begin{bmatrix}6r \\-4t\\-3r+2 \end{bmatrix}}\)
- \(\color{blue}{\begin{bmatrix}16 & -4 \\-38 & 24 \end {bmatrix}+\begin{bmatrix}9 и -6 \\5& 2 \end{bmatrix}}\)
- \(\color{blue}{\begin{bmatrix}18 и -5 \\-32 и 14 \end{bmatrix}+\begin{bmatrix}11& -6 \\7 & 2 \end{bmatrix}}\)
- \(\color{синий}{\begin{bmatrix}-4n & n+m \\-2n & -4m\end{bmatrix}+\begin{bmatrix}4 & -5 \\3 & 0 \end {bmatrix}}\)
- \(\color{blue}{\begin{bmatrix}z-5 \\-6\\-1-6z\\3y \end{bmatrix}+\begin{bmatrix}-3y \\3z\\5+z\\4z \end{bmatrix}}\)
Решить.

- \(\color{blue}{\begin{bmatrix}-6 & 3 \\13 & 41 \end{bmatrix}}\)
- \(\color{blue}{\begin{bmatrix}7 & 29 \\-19 & 14 \end{bmatrix}}\)
- \(\color{blue}{\begin{bmatrix}-11 & 7&4 \\3 & -5&3 \end{bmatrix}}\)
- \(\color{blue}{\begin{bmatrix}t \\-r-4t\\6s-3r+2 \end{bmatrix}} \)
- \(\color{blue}{\begin{ bmatrix}25 и -10 \\-33 и 26 \end{bmatrix}}\)
- \(\color{blue}{\begin{bmatrix}29 и -11 \\-25 и 16 \end{bmatrix} }\)
- \(\color{синий}{\begin{bmatrix}-4n+4 & n+m-5 \\-2n+3 & -4m\end{bmatrix}}\)
- \(\ color{blue}{\begin{bmatrix}z-5-3y \\-6+3z\\4-5z\\3y+4z \end{bmatrix}} \)
Реза
Реза опытный преподаватель математики и эксперт по подготовке к экзаменам, который обучает студентов с 2008 года. Он помог многим студентам повысить свои баллы по стандартизированным тестам и поступить в колледжи своей мечты. Он работает со студентами индивидуально и в группах, ведет как живые, так и онлайн-курсы по математике, а также математическую часть стандартизированных тестов.
Сложение и вычитание матриц Как складывать и вычитать матрицы
Другие математические статьи
- О нас
- Свяжитесь с нами
- Оптовые заказы
- Политика возврата
Математика без усилий: мы помогаем учащимся полюбить математику — © 2023
Сложение и вычитание матриц: расчет
Вы знакомы с операциями сложения и вычитания между двумя числами, то есть знаете, что 2 + 4 равно 6 или 8 — 7 равно 1. Теперь нас интересуют операции сложения и вычитания между двумя матрицами. Вы увидите, что мы сможем сделать это, зная эти самые операции между числами.
Но зачем нам вообще складывать или вычитать две матрицы?
Мы видели, что матрицы помогают нам представлять данные упорядоченным образом. Предположим, что есть две матрицы, отображающие оценки, выставленные двумя судьями двум участникам конкурса пения и рисунка.
Предположим, что есть две матрицы, отображающие оценки, выставленные двумя судьями двум участникам конкурса пения и рисунка.
Судья А ставит 1 st участнику 5 баллов за пение и 4 балла за рисунок. Точно так же подсчитывается 2 -й участник, и мы представляем его матрицей, где каждая строка представляет каждого участника. Судья Б также обращается к тем же участникам и ставит им оценки за пение, рисование и танцы.
Судья A = , Судья B = .
Допустим, я хочу узнать общую оценку судьи для участника 1 по пению. Из нашей информации мы знаем, что судья А поставил 5 баллов, а судья Б поставил 4 балла участнику 1 за пение. Таким образом, общая сумма баллов первого участника равна 9.. Мы добавили A (1, 1) с B (1, 1). В общем, если мы проделаем то же самое для соответствующих элементов в матрице, мы получим матрицу, являющуюся суммой матриц A и B. два конкурса. Чтобы сложить соответствующие элементы двух матриц, мы сразу видим, что порядки матриц должны совпадать. Например, мы не можем сложить матрицу порядка с другой матрицей порядка.
Например, мы не можем сложить матрицу порядка с другой матрицей порядка.
Чтобы выполнить сложение или вычитание двух матриц, правило состоит в том, что они имеют совпадающие порядки.
Рассмотрим две матрицы. Порядок А такой, а порядок Б такой. Порядок матриц не совпадает, поэтому вы не можете складывать или вычитать эти матрицы.
Сложение матриц
Матрица может быть сложена с другой матрицей тогда и только тогда, когда порядок матриц одинаков и сложение будет происходить между соответствующими элементами матриц. Результатом сложения двух матриц снова является матрица того же порядка, что и две матрицы.
Например, вам даны две матрицы.
Обе эти матрицы одного порядка. Сложение этих матриц C = A + B также является матрицей порядка. Его элементы можно получить, сложив соответствующие элементы этих двух матриц. Под этим понимается C(1, 1) = A(1, 1) + B(1, 1) = a + e, C(1, 2) = A(1, 2) + B(1, 2) = б + ж и так далее. Поэтому у нас есть
.
1. Рассмотрим две матрицы . Две матрицы имеют одинаковый порядок. Их сложение равно
.
2. Теперь рассмотрим матрицы . Две матрицы имеют одинаковый порядок. Их дополнение есть.
3. Рассмотрим две матрицы . Порядок E и F равен . Поскольку матрицы разного порядка, мы не можем их сложить.
Вычитание матриц
Матрица может быть вычтена из другой матрицы тогда и только тогда, когда порядок матриц одинаков и вычитание будет происходить между соответствующими элементами матриц. В результате снова получается матрица того же порядка.
Например, вам даны две матрицы.
Обе эти матрицы одного порядка. Вычитание этих матриц C = A – B является матрицей порядка . Его элементы можно получить, вычитая соответствующие элементы этих двух матриц. Под этим понимается C(1, 1) = A(1, 1) – B(1, 1) = i – m, C(1, 2) = A(1, 2) – B(1, 2) = j-n и так далее.
.
1. Рассмотрим матрицы . Матрицы имеют порядок . Вычитание матрицы B из A равно
Рассмотрим матрицы . Матрицы имеют порядок . Вычитание матрицы B из A равно
.
2. Рассмотрим матрицы. Обе эти матрицы имеют порядок. Вычитание D из C равно
.
3. Рассмотрим матрицы . Порядок E равен , а порядок F равен . Поскольку они не одного порядка, мы не можем выполнить вычитание между этими матрицами.
Свойства сложения и вычитания матриц
Теперь рассмотрим некоторые свойства с точки зрения двух операций – сложения и вычитания. Предположим, у нас есть три матрицы A, B и C.
Коммутативность
Сложение двух матриц коммутативно, т.е. Вычитание двух матриц не является коммутативным, т.е.
Допустим . Две матрицы одного порядка.
Теперь проверим коммутативность сложения.
Следовательно, .
Теперь проверим коммутативность вычитания.
Мы видим, что две приведенные выше матрицы не совпадают. Следовательно, .
Ассоциативность
Сложение трех матриц ассоциативно, т. е. Вычитание трех матриц не является ассоциативным, т.е.
е. Вычитание трех матриц не является ассоциативным, т.е.
Имея три матрицы одного порядка, мы проверим свойство ассоциативности сложения и вычитания.
Приведенные выше две матрицы одинаковы. Следовательно, .
Приведенные выше две матрицы не совпадают. Поэтому мы видим.
Аддитивная идентичность
Матрица, которая при добавлении к любой матрице дает вторую матрицу, называется аддитивной матрицей идентичности. Аддитивная идентичность — это нулевая матрица или нулевая матрица в любом заданном порядке.
Аддитивная единичная матрица, добавленная к матрице, является нулевой матрицей того же порядка, то есть .
Следовательно,
.
Аддитивная обратная
При сложении двух заданных матриц, в результате чего получается нулевая матрица, одна из матриц называется аддитивной обратной по отношению к другой. Для матрицы A аддитивной обратной является –A, поскольку A – A дает нулевую матрицу.
Аддитивная обратная матрица . Поскольку сложение этих двух матриц дает нулевую матрицу. .
Поскольку сложение этих двух матриц дает нулевую матрицу. .
.
Сложение и вычитание матриц – Основные выводы
- Сложение матриц: Матрица может быть сложена с другой матрицей тогда и только тогда, когда порядок матриц одинаков и сложение будет происходить между соответствующими элементами матриц.
- Вычитание матриц: Матрица может быть вычтена из другой матрицы тогда и только тогда, когда порядок матриц одинаков и вычитание будет происходить между соответствующими элементами матриц.
- Свойства сложения и вычитания матриц:
- Коммутативность: .
- Ассоциативность: .
- Аддитивная идентичность: Аддитивная обратная матрица — это нулевая или нулевая матрица того же порядка.
- Обратная аддитивная матрица: Обратная аддитивная матрица — это матрица с одинаковыми элементами с противоположным знаком, так что при сложении этих двух матриц получается нулевая матрица.