Уравнение прямой по двум точкам
УчебаМатематика
Данный онлайн калькулятор находит формулы параметрического уравнения прямой и уравнения прямой с угловым коэффициентом по координатам двух точек, принадлежащих прямой.
На этой странице вы найдете два калькулятора, которые строят уравнение прямой по координатам двух точек, принадлежащих этой прямой.
Первый калькулятор находит уравнение прямой с угловым коэффициентом, то есть уравнение в форме . Также он строит график и отдельно выводит угловой коэффициент и значение y в месте пересечения прямой с осью ординат.
Второй калькулятор находит параметрические уравнения прямой, то есть систему уравнений вида . Он также строит график и отдельно выводит направляющий вектор.
Формулы расчета можно найти под калькуляторами.
Уравнение прямой с угловым коэффициентом по двум точкам
Первая точка
Вторая точка
Уравнение прямой
Угловой коэффициент
Значение y в точке пересечения с осью ординат
Точность вычисления
Знаков после запятой: 2
Параметрическое уравнение прямой
Первая точка
Вторая точка
Параметрическое уравнение для x
Параметрическое уравнение для y
Направляющий вектор
Точность вычисления
Знаков после запятой: 2
Уравнение прямой с угловым коэффициентом
Найдем уравнение прямой с угловым коэффициентом по двум известным точкам и .
Нам надо найти угловой коэффициент a и y координату точки пересечения прямой с осью ординат b.
Мы можем составить следующие уравнения для двух точек относительно a и b
Вычитаем первое из второго
Откуда
b можно найти как
Таким образом, как только мы нашли а, для расчета b достаточно только подставить значения или в выражение выше.
Параметрическое уравнение прямой
Найдем параметрическое уравнение прямой по двум известным точкам и .
Нам надо найти компоненты направляющего вектора.
Этот вектор описывает величину и направление воображаемого движения по прямой от первой до второй точки.
Имея направляющий вектор, легко записать параметрические уравнения прямой
Обратите внимание, что если , то и если , то
Ссылка скопирована в буфер обмена
Похожие калькуляторы
- • Уравнения прямой, проходящей через две точки в трехмерном пространстве
- • Нахождение уравнений прямой, заданной пересечением двух плоскостей
- • Условия параллельности и перпендикулярности прямых на плоскости
- • Уравнение окружности по заданному центру и радиусу в различных формах
- • Решение системы двух уравнений первой степени с двумя неизвестными
- • Раздел: Математика ( 265 калькуляторов )
#математика #Прямая Математика Математикая направляющий вектор параметрическое уравнение параметрическое уравнение прямой прямая угловой коэффициент уравнение уравнение прямой уравнение прямой с угловым коэффициентом
PLANETCALC, Уравнение прямой по двум точкам
Timur2020-11-03 14:19:37
каноническое уравнение прямой калькулятор онлайн
Вы искали каноническое уравнение прямой калькулятор онлайн? На нашем сайте вы можете получить ответ на любой математический вопрос здесь.
Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и каноническое уравнение прямой онлайн, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «каноническое уравнение прямой калькулятор онлайн».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как каноническое уравнение прямой калькулятор онлайн,каноническое уравнение прямой онлайн,каноническое уравнение прямой онлайн калькулятор,написать каноническое уравнение прямой онлайн калькулятор,онлайн калькулятор каноническое уравнение прямой,онлайн калькулятор написать каноническое уравнение прямой,онлайн калькулятор уравнение прямой в отрезках,онлайн составить уравнение прямой,онлайн составить уравнение прямой проходящей через две точки,онлайн уравнение прямой по двум точкам,онлайн уравнение прямой проходящей через две точки,онлайн уравнение прямой через две точки,составить уравнение прямой онлайн,составить уравнение прямой проходящей через две точки онлайн,уравнение прямой в отрезках онлайн калькулятор,уравнение прямой калькулятор,уравнение прямой калькулятор онлайн,уравнение прямой онлайн,уравнение прямой онлайн калькулятор,уравнение прямой онлайн по двум точкам,уравнение прямой по двум точкам онлайн,уравнение прямой проходящей через 2 точки онлайн,уравнение прямой проходящей через две точки онлайн,уравнение прямой составить онлайн,уравнение прямой через две точки онлайн.
Где можно решить любую задачу по математике, а так же каноническое уравнение прямой калькулятор онлайн Онлайн?
Решить задачу каноническое уравнение прямой калькулятор онлайн вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Equation of Line Calculator — Онлайн калькулятор уравнения линии
Equation of Line Calculator — это онлайн-инструмент, который помогает рассчитать уравнение линии.
Он использует форму линии с пересечением наклона для получения уравнения. Таким образом, нам нужно знать наклон и точку пересечения линии по оси Y.
Что такое уравнение линейного калькулятора?
Калькулятор уравнения линии поможет вам вычислить уравнение линии, если заданы ее наклон и точка пересечения с осью y. Уравнение линии представлено линейным уравнением, заданным y = mx + c. Чтобы использовать уравнение линейного калькулятора , введите значения наклона и точки пересечения в поля ввода.
Уравнение линейного калькулятора
ПРИМЕЧАНИЕ. Введите значения, не превышающие трех цифр.
Как пользоваться калькулятором уравнения линии?
Чтобы найти уравнение прямой с помощью калькулятора уравнения прямой, выполните следующие шаги:
- Шаг 1: Перейдите к онлайн-калькулятору уравнения прямой от Cuemath.
- Шаг 2: Введите наклон (м) и точку пересечения (с) в заданном поле ввода.
- Шаг 3: Нажмите на кнопку «Решить» , чтобы найти уравнение линии.
- Шаг 4: Нажмите кнопку «Сброс» , чтобы очистить поля и ввести другие значения.
Как работает калькулятор уравнения прямой?
Прямая линия образуется при соединении двух точек и бесконечном удлинении этого отрезка в обоих направлениях. Уравнение прямой — это функция, которой удовлетворяют все точки, лежащие на этой прямой. Точки, не лежащие на этой прямой, этой функции не удовлетворяют. Степень уравнения прямой всегда будет равна 1. Существует много способов найти уравнение прямой в зависимости от известных параметров. Это форма точки-наклона, форма с двумя точками, форма с пересечением наклона, форма с пересечением и нормальная форма. Форма уравнения линии с пересечением наклона широко используется, поскольку с ней проще всего работать. Существуют определенные важные термины, связанные с этой формой, как указано ниже:
- Наклон: Наклон используется для определения крутизны прямой по отношению к горизонтали. Наклон может быть как положительным, так и отрицательным. Его также можно определить как изменение отношения координат y по отношению к координатам x.
- Точка пересечения: Точка, в которой линия пересекает или пересекает оси x или y, называется точкой пересечения. Чтобы определить уравнение линии, используя форму пересечения наклона, нам нужно знать точку пересечения по оси y.
Наклон может быть как положительным, так и отрицательным. Его также можно определить как изменение отношения координат y по отношению к координатам x.Алгебраически линия определяется как линейное уравнение с двумя переменными.
Уравнение линии с использованием формы наклона и точки пересечения задается как
y = mx + c
где m — наклон линии, а c — точка пересечения с осью y
Хотите найти сложные математические вычисления решения за секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.
Забронировать бесплатный пробный урок
Решенные примеры на калькуляторе уравнения прямой
Пример 1:
Найдите уравнение прямой, если наклон равен 5, а ее точка пересечения равна 7.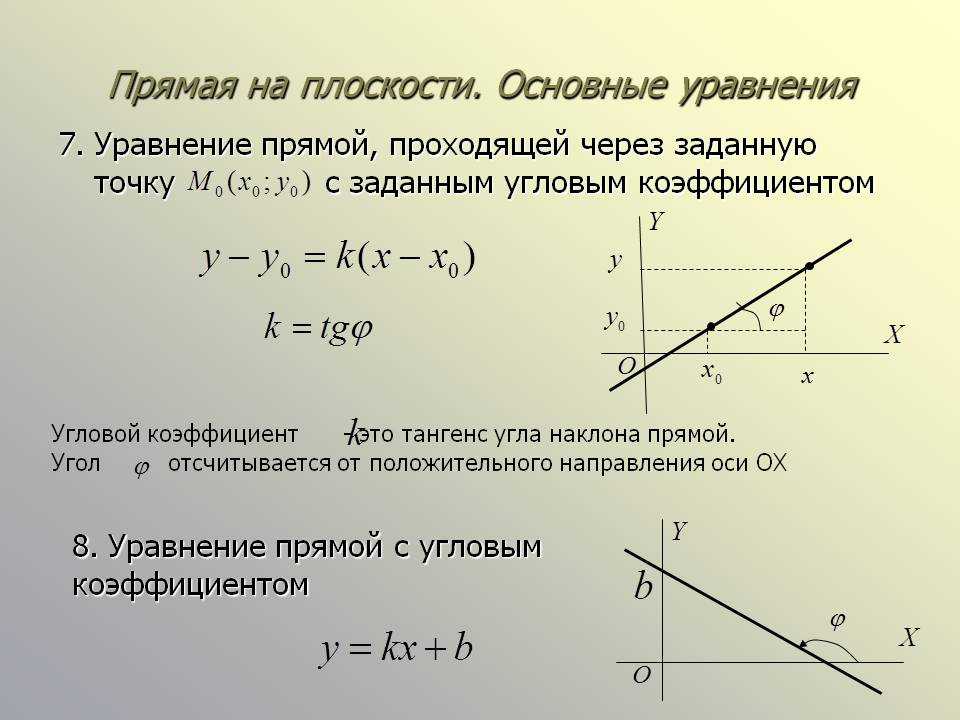
Решение:
Дано: Наклон (м) = 5, точка пересечения с Y = 7
Уравнение прямой: y = mx + c = 0
Следовательно, уравнение прямой 5x — y + 7 = 0
Пример 2:
Найдите уравнение прямой, если наклон равен 20, а точка пересечения равна 3. Проверьте это с помощью калькулятора уравнения прямой.
Решение:
Дано: Наклон (м) = 20, точка пересечения с Y = 3
Уравнение прямой: y = mx + c = 0
Следовательно, уравнение прямой 20x — y + 3 = 0
Точно так же вы можете попробовать калькулятор уравнения прямой, чтобы найти уравнение прямой для следующего:
- Наклон = 12, точка пересечения с осью Y = 7
- Наклон = 5, точка пересечения с осью Y = 8
- Уравнение прямой
- Форма пересечения уклонов
Калькулятор перехвата склона
, созданный Альваро Диэз и Богна Szyk
.
Обзор Dominik Czernia, PhD and Jack Bowater
Последний0022
Калькулятор формы пересечения наклона научит вас как найти уравнение прямой из любых двух точек, через которые проходит эта прямая. Это поможет вам найти коэффициенты наклона и точки пересечения по оси Y, а также точки пересечения по оси X, используя формулы пересечения наклона. Читайте дальше, чтобы узнать, что такое форма пересечения наклона линейного уравнения, как найти уравнение линии и важность уравнения формы пересечения наклона в реальной жизни.
Что такое форма пересечения склона?
Любая линия на плоскости может быть математически описывается как соотношение между вертикальным (ось Y) и горизонтальным (ось X) положением каждой из точек, составляющих линию. Это отношение можно записать как y = [что-то с x] . Конкретная форма [что-то с x] будет определять, какая у нас линия. Например, y = x² + x — это парабола, также называемая квадратичной функцией. С другой стороны, y = mx + b (с m и b , представляющий любые действительные числа) представляет собой отношение прямой линии.
В этом калькуляторе пересечения наклона мы сосредоточимся только на прямой линии . Вы можете проверить наш калькулятор средней скорости изменения, чтобы найти связь между переменными нелинейных функций.
Линейные уравнения, или уравнения прямых линий, можно быстро распознать, поскольку в них нет членов с показателями степени .
(Например, вы найдете x или y , но никогда x² .) Каждое линейное уравнение описывает прямую линию, которая может быть выражена с помощью уравнения формы пересечения наклона.
Как мы уже видели, уравнение любой прямой можно записать в виде y = mx + b . Это так называемая форма пересечения наклона, потому что она дает вам две важные части информации: уклон 90 179 м 90 180 и точку пересечения по оси Y 90 179 b 90 180 линии. Вы можете использовать эти значения для линейной интерполяции позже.
Термин уклон — это наклон или уклон линии. Он говорит нам, насколько изменится х при фиксированном изменении х . Если он положительный, значения y увеличиваются при увеличении x . Если оно отрицательное, y уменьшается с увеличением x . Подробнее об этом можно прочитать в описании нашего калькулятора уклона.
Точка пересечения y — это значение y , при котором линия пересекает ось y.
Чтобы его найти, нужно подставить x = 0 в линейное уравнение. Позже вы увидите, почему точка пересечения по оси y равна 9.0008 важный параметр в линейных уравнениях , и вы также узнаете физический смысл его значения на некоторых примерах из реальной жизни.
Вывод формулы пересечения наклона
Все еще нужно знать, как найти форму пересечения наклона линейного уравнения? Предположим, что вы знаете две точки , через которые проходит прямая. У первого будут координаты (x₁, y₁), а у второго (x₂, y₂). Ваши неизвестные — это наклон м и точка пересечения с координатой 9.0179 б .
Во-первых, подставьте координаты двух точек в уравнение пересечения наклона:
(1) y₁ = mx₁ + b
(2) y₂ = mx₂ + b
Затем вычтите из первого уравнения второе:
y₂ — y₁ = m(x₂ — x₁)
Наконец, разделите обе части уравнения на (x₂ — x₁) , чтобы найти наклон:
m = (y₂) — /(x₂ — x₁)
Как только вы нашли наклон, вы можете подставить его в первое или второе уравнение, чтобы найти точку пересечения с осью y:
y₁ = x₁(y₂ — y₁)/(x₂ — x₁) + b
b = y₁ — x₁(y₂ — y₁)/(x₂ — x₁)
3 ?
Калькулятор формы пересечения уклона позволяет найти уравнение линии в форме пересечения уклона .
Все, что вам нужно сделать, это указать две точки, через которые проходит линия. Вам необходимо следовать процедуре, описанной ниже.
Запишите координаты первой точки . Предположим, что это точка с х₁ = 1 и у₁ = 1 .
Запишите также координаты второй точки . Возьмем точку с x₂ = 2 и y₂ = 3 .
Используйте формулу пересечения наклона , чтобы найти уклон:
м = (y₂ — y₁)/(x₂ — x₁) = (3-1)/(2-1) = 2/1 = 2 .
Вычислить точку пересечения y . Вы также можете использовать x₂ и y₂ вместо x₁ и y₁ здесь.
б = у₁ — м × х₁ = 1 — 2×1 = -1
Сложите все эти значения вместе, чтобы построить форму точки пересечения наклона линейного уравнения:
у = 2х — 1 .
Вы также можете использовать калькулятор расстояний, чтобы найти расстояние между двумя точками.
Найти точку пересечения по осям x и y
Также всегда возможно найти точку пересечения по оси x линии . Это значение x, при котором прямая линия пересекает ось x (означает значение x , для которых y равно 0 ). Вы можете рассчитать его следующим образом:
0 = mx + b
x = -b/m
Наш калькулятор формы пересечения наклона отобразит значения пересечения по оси x и y для ты. Тем не менее, если вы хотите узнать о них больше, мы рекомендуем вам посетить наш калькулятор пересечения осей x и y.
Использование точек пересечения по оси y и по оси x в реальном мире
Мы уже видели, что такое форма точки пересечения наклона, но чтобы понять, почему уравнение формы точки пересечения настолько полезно, вы должны знать некоторые приложений в реальном мире .
Давайте посмотрим на пару примеров. Мы начнем с простых из физики, чтобы вы могли получить интуитивное представление о том, что означают точки пересечения y и x.
Представьте себе автомобиль , движущийся с фиксированной скоростью к вам . Его движение можно изобразить как зависимость времени от расстояния от вас до машины (как показано выше). Это означает, что ось X будет представлять прошедшее время, а ось Y — расстояние до автомобиля. Можно даже представить, что машина тронулась до того, как вы запустили таймер (то есть до 9 часов).0179 т = 0 ).
Теперь, если вы посмотрите на точку пересечения оси Y ( x = 0 ), точка, с которой вы начали отслеживать время, будет t = 0 . И так, значение y в этой точке будет указывать на начальную позицию (расстояние) автомобиля по отношению к вам. Это значение, как мы обсуждали ранее, такое же, как значение b в форме пересечения наклона уравнения прямой линии.
Глядя теперь на x-перехват ( y = 0 ), это будет точка, в которой расстояние от машины до вас будет 0 . Тогда значение x в этой точке будет время, когда вы и машина были в одном месте . Будем надеяться, что это означает, что вы были внутри машины, а не под ней.
Другие уравнения с точкой пересечения по оси y
Приведенный выше пример автомобиля очень прост и должен помочь вам понять, почему важна форма точки пересечения наклона и, в частности, значение перехватывает . В этой статье мы в основном будем говорить о прямых линиях, но точки пересечения могут быть рассчитаны для любой кривой (если она пересекает ось).
Фактически, приведенный выше пример не соответствует линейному уравнению и по-прежнему содержит обе точки пересечения. То же самое верно для любой другой параболы или другой формы.
Одно уравнение, которое гарантированно имеет точку пересечения по оси Y, но не обязательно точку пересечения по оси X, — это парабола.
Это уравнение показано на изображении выше. Он имеет максимум или минимум (в зависимости от ориентации). Если этот максимум ниже оси x или минимум выше оси x, никогда не будет x-перехвата .
Однако, в отличие от людей, не все уравнения равны . Некоторые формулы описывают кривые, которые никогда не пересекаются с осью x, осью y или обеими. Давайте посмотрим подробнее, как это может быть.
Уравнения без точки пересечения (асимптоты)
Мы можем различать 3 группы уравнений в зависимости от того, имеют ли они только точку пересечения по оси y, только точку пересечения по оси x или не имеют ни одной точки пересечения . Первая группа (только y-пересечение) может иметь почти любой тип уравнения, включая линейные уравнения. Хороший простой пример — y = 3 (или любое другое постоянное значение y, кроме 0 ), так как это прямая, параллельная оси x, и, таким образом, никогда не будет пересекать или пересекать ее.
Пожалуйста, не пытайтесь рассчитать эти типы точек пересечения на этом калькуляторе формы точки пересечения, поскольку эти типы уравнений потенциально могут сломать Интернет.
Вторую и третью группы уравнений немного сложнее представить, и чтобы их хорошо понять, нам нужно ввести понятие асимптоты . Асимптота — это линия (которая может быть выражена в виде линейного уравнения), к которой функция или кривая, о которой мы говорим, приближается и приближается, но никогда не пересекает эту линию и не касается ее.
Определение может показаться не совсем ясным, но если мы посмотрим на пример уравнения , у нас будет меньше проблем с его пониманием. Возьмем уравнение y = 1/x . Если мы попытаемся найти точку пересечения с осью , подставив x = 0 , мы придем к тому, что называется числом 9.0008 математически неопределенное выражение так как нет смысла делить на 0 .
Если мы будем подбирать значения все ближе и ближе к 0 (что-то вроде 0,1 , затем 0,001 , 0,000001 .
..), мы увидим, что значение y увеличивается очень быстро. Таким образом, вокруг точки x = 0 мы знаем, что y будет иметь огромное значение, но из-за того, как работает математика, у него нет определенного значения для этой точной точки. Иногда люди могут сказать 1/0 = ∞ , но на самом деле бесконечность — это не число , а понятие .
В этом случае линейное уравнение x = 0 представляет собой асимптоту функции y = 1/x , что означает, что y = 1/x никогда не пересечет эту прямую и, следовательно, не будет иметь y-перехват. В общем, каждый раз, когда функция имеет асимптоту , лежащую на одной из осей, у нее будет отсутствовать по крайней мере одна из точек пересечения . Источник: Википедия По той же причине, что и раньше, y = 0 никогда не достижимо по формуле, потому что для этого потребовалось бы x = ∞ , и, как мы уже говорили ранее, невозможно добиться этого, поскольку бесконечность является понятием, а не числом .
Прежде чем мы перейдем к нашей следующей теме, важно отметить, что мы сделали крайних упрощений , когда речь идет о бесконечности, но мы считаем, что это хороший и быстрый подход для тех, кто не привык к концепции работы с бесконечностью в математике. Мы рекомендуем вам узнать больше о правильных способах бесконечности , начиная с неопределенных выражений в математике.
Пересечения и линейные уравнения в машинном обучении и науке
Можно легко подумать, что полезность линейных уравнений очень ограничена из-за их простоты. Однако реальность немного другая. Линейные уравнения лежат в основе некоторых из самые мощные методы решения задач минимизации и оптимизации .
Задачи на минимизацию — это тип задач, в которых нужно найти способ сделать одну из переменных как можно меньше. Эта переменная может быть, например, разницей между прогнозом, сделанным моделью, и реальностью. Эти типы проблем являются одними из 
Одним из наиболее распространенных и мощных методов нахождения минимального значения уравнения или формулы является так называемый Метод Ньютона , названный в честь гения, который его изобрел. Он работает с использованием производных, линейных уравнений и точек пересечения:
Пример использования метода Ньютона (Источник: Wikimedia) Этот метод состоит из выбора значения x для уравнения и вычисления производной уравнение в этой точке. Используя производную в качестве наклона линейного уравнения
(x, y) , затем вычисляется точка пересечения по оси x. Это одна из ситуаций, в которых пригодится форма пересечения наклона. После вычисления точки пересечения по оси x это значение x используется для повторения описанного выше процесса определенное количество раз , пока мы не придем к минимальному значению y (что означает, что производная будет 0 ).