Область определения функции, в которой есть дробь
Стр 1 из 12Следующая ⇒Как исследовать функцию и построить её график?
1) Область определения, непрерывность, четность/нечётность, периодичность функции.
2) Асимптоты графика функции.
3) Нули функции, интервалы знакопостоянства.
4) Возрастание, убывание и экстремумы функции.
5) Выпуклость, вогнутость и перегибы графика.
6) Дополнительные точки и график по результатам исследования.
Как найти область определения функции?
Примеры решений
Коротко о главном: речь идёт о функции одной переменной . Её область определения – это множество значений «икс», для которых существуют значения «игреков». Рассмотрим условный пример: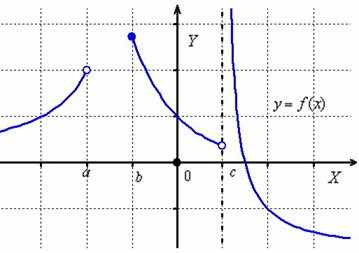
(для тех, кто позабыл: – значок объединения). Иными словами, если взять любое значение «икс» из интервала , или из , или из , то для каждого такого «икс» будет существовать значение «игрек».
Грубо говоря, где область определения – там есть график функции. А вот полуинтервал и точка «цэ» не входят в область определения, поэтому графика там нет.
Область определения функции, в которой есть дробь
Предположим, дана функция, содержащая некоторую дробь . Как вы знаете, на ноль делить нельзя: , поэтому те значения «икс», которые обращают знаменатель в ноль – не входят в область определения данной функции.
Не буду останавливаться на самых простых функциях вроде и т.п., поскольку все прекрасно видят точки, которые не входят в их области определения. Рассмотрим более содержательные дроби:
Пример 1
Найти область определения функции
Решение: в числителе ничего особенного нет, а вот знаменатель должен быть ненулевым. Давайте приравняем его к нулю и попытаемся найти «плохие» точки:
Полученное уравнение имеет два корня: . Данные значения не входят в область определения функции. Действительно, подставьте или в функцию и вы увидите, что знаменатель обращается в ноль.
Ответ: область определения:
Запись читается так: «область определения – все действительные числа за исключением множества, состоящего из значений ». Значок обратного слеша в математике обозначает логическое вычитание, а фигурные скобки – множество. Ответ можно равносильно записать в виде объединения трёх интервалов:
Найти область определения функции
Решение: попытаемся найти точки, в которых знаменатель обращается в ноль. Для этого решим квадратное уравнение:
Ответ: область определения:
©2015 arhivinfo.ru Все права принадлежат авторам размещенных материалов.
arhivinfo.ru
Область определения функции, в которой есть дробь
Итак, нам надо найти все допустимые значения икса для какой-то конкретной функции. Самый широкий набор значений, как правило — это все действительные числа. От -∞ до+∞. Перебирать все возможные числа мы не будем, да…) В математике поступают по-другому. Работаем в два этапа.
На первом этапе ищем в функции операции, которые могут оказаться недопустимыми при каких-то значениях икса. Т.е. ищем потенциально опасные операции.
На втором этапе определяем иксы, которые не приводят к запретному действию в этих самых операциях. Это и будет область определения функции.
Если эти этапы не очень понятны, читаем дальше, на примерах всё куда яснее будет.
Что такое потенциально опасные операции? Это операции, в которых существуют принципиальные ограничения. Не пугайтесь, таких операций всего ничего и вы их прекрасно знаете). Перечисляю:
До 9-го класса включительно:
1. Деление. Нельзя делить на ноль.
2. Извлечение корня. Нельзя извлекать корни чётной степени из отрицательных чисел.
В выпускных классах и ВУЗах:
3. Логарифмы. Ограничения в логарифмах: если logab = c, то а>0, a≠1, b>0.
4. Тригонометрия. Ограничения в тригонометрии: значения углов, для которых тангенс и котангенс не существуют, ограничения на выражения под знаком арксинуса, арккосинуса.
Предположим, дана функция, содержащая некоторую дробь . Как вы знаете, на ноль делить нельзя: , поэтому те значения «икс», которые обращают знаменатель в ноль – не входят в область определения данной функции.
Не буду останавливаться на самых простых функциях вроде и т.п., поскольку все прекрасно видят точки, которые не входят в их области определения. Рассмотрим более содержательные дроби:
Пример 1
Найти область определения функции
Решение: в числителе ничего особенного нет, а вот знаменатель должен быть ненулевым. Давайте приравняем его к нулю и попытаемся найти «плохие» точки:
Полученное уравнение имеет два корня: . Данные значения не входят в область определения функции. Действительно, подставьте или в функцию и вы увидите, что знаменатель обращается в ноль.
Ответ: область определения:
Запись читается так: «область определения – все действительные числа за исключением множества, состоящего из значений ». Напоминаю, что значок обратного слеша в математике обозначает логическое вычитание
, а фигурные скобки – множество. Ответ можно равносильно записать в виде объединения трёх интервалов:.
Пример 3
Найти область определения функции
Решение: попытаемся найти точки, в которых знаменатель обращается в ноль. Для этого решим квадратное уравнение:
Дискриминант получился отрицательным, а значит, действительных корней нет, и наша функция определена на всей числовой оси.
Ответ: область определения:
Определение.
Областью значений функции y = f(x) называется множество всех значений функции, которые она принимает при переборе всех x из области определения .
Пример.
Определите множество значений функции на интервале (-2; 2).
Решение.
Найдем точки экстремума функции, попадающие на промежуток (-2; 2):
Точка x = 0 является точкой максимума, так как производная меняет знак с плюса на минус при переходе через нее, а график функции от возрастания переходит к убыванию.
есть соответствующий максимум функции.
Выясним поведение функции при x стремящемся к -2 справа и при xстремящемся к 2 слева, то есть, найдем односторонние пределы:
Что мы получили: при изменении аргумента от -2 к нулю значения функции возрастают от минус бесконечности до минус одной четвертой (максимума функции при x = 0), при изменении аргумента от нуля к 2 значения функции убывают к минус бесконечности. Таким образом, множество значений функции на интервале (-2; 2) есть .
Как найти область значения функции y=3x(квадрат)-6x +1
1 способ.
Найдем x0. x0=-b/(2a)=-(-6)/(2*3)=1
Найдем значение y при x=1.
y=3*1^2-6*1+1=3-6+1=-2.Т.к. y=3x^2-6x+1 — это парабола, ветви направлены вверх, то область значений: [-2;+бесконечности)
2 способ.
Найдем производную функции. y’=6x-6. Приравним производную функции к нулю.
6x-6=0. Найдем точки экстремума. 6x=6, x=1. Т.к. y=3x^2-6x+1 — это парабола, ветви направлены вверх, то x=1- это точка минимума. Найдем значение функции наданной точке. y=3*1^2-6*1+1=3-6+1=-2. Т.к. y=3x^2-6x+1 — это парабола, ветви направлены вверх, то область значений: [-2;+бесконечности)
P.S. Если вы ещё не прошли производную, воспользуйтесь первым способом.
studopedya.ru
как найти область определения функции??
найти все х-удовлетворяющие данному условию
смотря какой, если есть квадратный корень, то под ним больше или =0 и т. д
При решении многих задач приходится искать область определения функции. Особенно это нужно знать при построении графика и исследовании функции. Именно поэтому я решил рассмотреть основные варианты, которые могут быть при нахождении области определения функции. Их не так много, наверняка, многие это знают и сами, но думаю, напомнить не будет лишним. И так, область определения функции – это множество всех тех значений переменной х, при каких функция f(x) имеет смысл. То есть значения переменной х, при которых функция от этой переменной существует, а могут быть и такие, при каких она не существует, нам нужны, только те, при которых – существует. Рассмотрим конкретные варианты, в каких случаях функция может существовать не при всех значениях переменной: Во-первых, когда есть дробь, в этом случае знаменатель дроби, недолжен быть равным нулю, потому, что такая дробь не может существовать. То есть, если ваша функция — дробь и в знаменателе есть переменная (потому, что если там только число, то оно никогда не станет нулём) то вам надо всё то выражение, что в знаменателе прировнять к нулю. И решив полученное уравнение, вы найдёте те значения переменной x, которые необходимо исключить с области определения. Во-вторых, когда есть корень чётной степени, думаю, вы знаете, что в поле вещественных чисел, корень чётной степени может быть только с положительного числа. То есть если в вас есть функция с корнем чётной степени, то что бы найти те числа, которые не будут попадать в область определения, вам надо решить неравенство, где выражение, что под корнем будет меньше нуля. В-третьих, когда есть логарифм. Здесь понятно, что область определения логарифма все числа, которые больше ноля. То есть что бы найти те значения переменной, которые надо исключить с области определения, вам надо составить и решить неравенство, где выражение, которое будет под логарифмом должно быть меньше нуля. В-четвёртых, не надо забыть о таких обратных тригонометрических функциях, как арксинус и арккосинус, которые определены, только на промежутке [-1;1]. Соответственно вам надо следить, что бы выражение, которое будет под этими функциями, также попадало в этот промежуток и исключить все значения переменной, которые туда не попадают. И в-пятых, в одном примере может быть несколько этих случаев. Надо разбирать всё, до мельчайших подробностей. Например, в знаменателе дроби, может быть корень из арксинуса, поэтому вам надо отобрать, только те значения переменной, при которых существует арксинус, при чём значение этого арксинуса должно не должно быть равное нулю (так как оно в знаменателе) и также не должно быть отрицательным (так как есть корень) .
touch.otvet.mail.ru
| Область визначення функції — це множина всіх значень незалежної змінної, при яких функція має зміст.
Для функцій, заданих формулою, область визначення знаходять виходячи з наступних принципів:.
| Область определения функции — это множество всех значений переменной х, при которых функция имеет смысл.
Для функций, заданных формулой, область определения находится исходя из следующих принципов:
| Область визначення функції — це множина допустимих значень аргументу функції. Вона позначається як D(y), якщо треба вказати область визначення функції y = f(x).
Якщо задані: числова множина та правило, що дозволяє поставити у відповідність кожному елементу з множини певне число, то говорять, що задана функція з областю визначення . Визначення області значень функції є необхідною умовою визначення функції.
Значення змінних, при яких значення функції має зміст, називають допустимими значеннями аргументу. Множину всіх допустимих значень аргументу називають областю допустимих значень аргументу функції . | Область определения функции — это множество допустимых значений аргумента функции. Она обозначается как D(y), когда нужно указать область определения функции y = f(x).
Если заданы: числовое множество и правило, которое позволяет сопоставить в соответствие каждому элементу из множества определенное число, говорят, что задана функция с областью определения. Определение области значений функции является необходимым условием определения функции.
Значения переменных, при которых значение функции имеет смысла, называют допустимыми значениями аргумента. Множество всех допустимых значений аргумента называют областью допустимых значений аргумента функции. |
profmeter.com.ua
