Упрощение логических выражений
Разделы: Информатика
Основная образовательная задача урока – научить учащихся умению упрощать логические выражения, правильно определять порядок выполнения операций в логическом выражении, устанавливать связи между различными частями сложных логических выражений, умение выбирать лучший вариант решения.
Под упрощением формулы, не содержащей операций импликации и эквиваленции, понимают равносильное преобразование, приводящее к формуле, которая либо содержит по сравнению с исходной меньшее число операций конъюнкции и дизъюнкции и не содержит отрицаний неэлементарных формул, либо содержит меньшее число вхождений переменных.
Обозначим: X – логическое высказывание, – инверсия, & – конъюнкция, – дизъюнкция, – импликация, – эквиваленция.
Применение основных законов логики для упрощения логических выражений.
Упростить логическое выражение:
1)
Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций:
Воспользуемся распределительным законом и вынесем за скобки общий множитель, затем операцией переменной с ее инверсией.
Воспользуемся распределительным законом и вынесем за скобки общий множитель, затем операцией переменной с ее инверсией, затем операцией с константами.
Таким образом,
2)
Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций. В выражении присутствуют два выражения в скобках, соединенных дизъюнкцией. Сначала преобразуем выражения в скобках.
В первой скобке воспользуемся распределительным законом, во второй скобке – раскроем инверсию по правилу де Моргана и избавимся от инверсии по закону двойного отрицания.
Воспользуемся операцией переменной с ее инверсией.
Таким образом,
3)
Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций. В выражении присутствуют два выражения в скобках, соединенных конъюнкцией. Сначала преобразуем выражения в скобках.
Раскроем инверсию по правилу де Моргана, избавимся от инверсии по закону двойного отрицания.
Воспользуемся переместительным законом и поменяем порядок логических сомножителей.
Применим закон склеивания
Воспользуемся распределительным законом, затем операцией переменной с ее инверсией, затем операцией с константами.
Таким образом,
4)
Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций.
В выражении присутствует импликация. Сначала преобразуем импликацию .
Воспользуемся правилом де Моргана, затем законом двойного отрицания, затем раскроем скобки.
Применим закон идемпотенции и перегруппируем логические слагаемые.
Воспользуемся распределительным законом и вынесем за скобки общий логический множитель.
Воспользуемся операцией с константами.
Таким образом,
5)
Рассмотрим 3 способа упрощения этого логического выражения.
1 способ. Перепишем выражение с помощью более привычных операций умножения и сложения.
Воспользуемся распределительным законом и раскроем скобки, затем операцией переменной с ее инверсией и законом идемпотенции.
Воспользуемся законом идемпотенции.
Таким образом,
2 способ. Перепишем выражение с помощью более привычных операций умножения и сложения.
Воспользуемся законом склеивания
Воспользуемся операцией переменной с ее инверсией.
Таким образом,
3 способ. Перепишем выражение с помощью более привычных операций умножения и сложения.
Повторим второй сомножитель , что разрешено законом идемпотенции.
Сгруппируем два первых и два последних сомножителя.
Воспользуемся законом склеивания
Таким образом,
6)
Рассмотрим 2 способа упрощения этого логического выражения.
1 способ. Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций.
Воспользуемся распределительным законом и вынесем общий логический множитель за скобки.
2 способ. Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций.
Введем вспомогательный логический сомножитель
Сгруппируем 1 и 4, 2 и 3 логические слагаемые. Вынесем общие логические множители за скобки.
Воспользуемся операцией с константами и операцией переменной с ее инверсией.
Таким образом,
Получили два логических выражения:
Теперь построим таблицы истинности и посмотрим, правильно ли упрощено логическое выражение
| X | Y | Z | ||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 1 |
| X | Y | Z | ||||
| 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| X | Y | Z | |||
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 1 | 1 |
| X | Y | Z | |||
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 |
Как видно из сравнения таблиц истинности формулы являются равносильными.
18.02.2012
urok.1sept.ru
Булева алгебра (алгебра логики)
На этом уроке знакомимся с алгеброй логики, одним из основателей которой стал английский математик Джордж Буль (1815-1864), который был из довольно бедной семьи, а в юности зарабатывал переводами сочинений древнегреческих философов. За этим занятием его и посетила мысль о том, что высказываниям можно присваивать значения 1 («истина») и 0 «ложь».
Итак, алгебра логики (булева алгебра) — это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними. Алгебра логики позволяет закодировать любые утверждения, истинность или ложность которых нужно доказать, а затем манипулировать ими подобно обычным числам в математике.
Создание алгебры логики в середине ХIХ века в трудах Джорджа Буля представляло собой попытку решать традиционные логические задачи алгебраическими методами.
Функция от n переменных называется логической или булевой или переключательной или функцией алгебры логики, если сама функция и любой из ее аргументов могут принимать значения только из множества {0, 1}. Описанную функцию часто называют также булевым вектором. Количество функций от n переменных равно 2 в степени n. То же самое можно сказать и иначе: число различных n-мерных булевых векторов равно 2 в степени n. А число различных функций алгебры логики от этих векторов равно уже .
Значениям переменной в булевой алгебре соответствуют состояниям элементов микросхем компьютера или любого другого электронного устройства: сигнал присутствует (логическая «1») или сигнал отсутствует (логический «0»).
На логических элементах, реализующих булевы функции, строятся логические схемы электронных устройств.
Законы булевой алгебры применяются и в программировании — при написании сложных логических условий и сложных запросов к базе данных. Один пример со скриптом на PHP приведён здесь (это статья о системе многокритериального поиска по сайту с базой данных). Ещё один пример — применение алгебры логики в создании многоуровневого меню сайта, в котором были бы открыты все пункты всех уровней, по которому пролегает путь к конечному открытому пункту меню.
Часто оказывается, что изначально построенное логическое выражение можно упростить, используя аксиомы, теоремы и законы алгебры логики.
Применяются следующие способы описания логических функций:
- словесный;
- табличный;
- числовой;
- аналитический;
- координатный;
- графический.
Пример табличного описания логических функций
| Номер набора | f |
| 0 | 0 |
| 1 | 1 |
| 2 | 0 |
| 3 | 0 |
| 4 | 1 |
| 5 | 1 |
| 6 | 0 |
| 7 | 1 |
| X1 | X2 | X3 | f |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
Приведённые выше таблицы имеют название таблиц истинности. Такие таблицы в практике необходимо строить для любой, сколь либо сложной булевой функции. Примеры таблиц истинности для булевых функций, реализованных в логических схемах — в материале Логические схемы и таблицы истинности.
Пример числового описания логических функций
или .
Пример аналитического описания логических функций
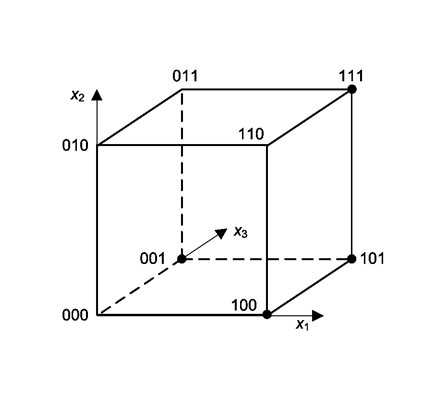
Пример координатного описания логических функций
Карта Карно
Пример графического описания логических функций
Логические функции одной переменной
| Переменная | Логические функции | |||
| x | ||||
| 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 |
Логические функции двух переменных
В логических схемах функции могут быть реализованы с произвольных количеством входных переменных, примеры — в материале Логические схемы и таблицы истинности.
Ответить на контрольные вопросы, а затем посмотреть ответы
Контрольный вопрос 1. Даны две переменные x1 и x2. Число различных булевых векторов и различных ФАЛ от полученных векторов равны соответственно:
- 8 и 16
- 8 и 32
- 4 и 8
- 4 и 16
Контрольный вопрос 2. Какие из функций не являются ФАЛ одной переменной (и одна, и вторая в варианте ответа):
- отрицание и сложение по модулю два
- эквивалентность и повторение x
- отрицание и импликация
- функция Шеффера и эквивалентность
- запрет по x2 и отрицание
Правильные ответы на вопрос 1 и вопрос 2.
Любую булеву функцию с произвольным количеством аргументов можно построить через подстановку элементарных функции вместо аргументов (суперпозицию). Набор простейших функций, с помощью которого можно выразить любые другие, сколь угодно сложные логические функции, называется функционально полным набором, или логическим базисом.
Инверсия (логическое отрицание, «НЕ»)
.
| 0 | 1 |
| 1 | 0 |
Конъюнкция (логическое умножение, «И»)
.
Дизъюнкция (логическое сложение, «ИЛИ»)
.
В булевом базисе обычно строятся логические схемы, которые реализуют сколь угодно сложные логические функции, примеры — в материале Логические схемы и таблицы истинности.
В качестве исходного описания сложных логических функций обычно используется таблица истинности, однако упрощение функций удобнее производить в аналитической форме. При аналитической записи функция алгебры логики представляется либо в виде логической суммы элементарных логических произведений (дизъюнкции элементарных конъюнкций), либо в виде логического произведения элементарных логических сумм (конъюнкции элементарных дизъюнкций). Первая форма записи имеет название дизъюнктивной нормальной формы (ДНФ), вторая — конъюнктивной нормальной формы (КНФ). В этих названиях термин «нормальная» означает отсутствие общей инверсии (отрицания) над несколькими перемнными сразу.
Дизъюнктивная нормальная форма
.
Конъюнктивная нормальная форма
.
Аксиомы конъюнкции
.
Аксиомы дизъюнкции
.
Аксиомы отрицания
если , то ; если , то .
Теоремы исключения констант
.
Теоремы идемпотентности (тавтологии, повторения)
.
для n переменных
.
Теорема противоречия
.
Теорема «исключённого третьего»
.
Теорема двойного отрицания (инволюции)
.
Ассоциативный (сочетательный) закон
.
Коммутативный (переместительный) закон
.
Дистибутивный (распределительный) закон
.
.
Законы де Моргана (законы общей инверсии или дуальности)
.
.
Закон поглощения (элиминации)
.
Закон склеивания (исключения)
.
function-x.ru
Упрощение логических выражений.
Тип ПОЛабораторная работа PASCOActivInspire (Promethean)SMART NotebookПрезентация PowerPointAнимационный Flash-роликУрок для ActivTableElite Panaboard (Panaboard)HitachiМастер-классMimioStudio™RM Easiteach Next Generation (TriumphBoard, Panaboard, Legamaster)Interwrite WorkSpace (Interwrite)IP board (IPBoard /Julong)Интересный материал
ПредметИЗОЧерчениеМузыкаФранцузский языкАстрономияИнформатикаГеографияОкружающий мирБиологияНемецкий языкОбщественные наукиМатематикаТатарский языкОРКСЭкономикаИностранный языкМХКВоспитательная работа (классный час)Русский языкОБЖГеометрияАнглийский языкТехнологияПриродоведениеОбществознаниеВнеурочное занятиеЕстественные наукиФизикаХимияЛитератураИсторияПравоДругое
Уровень образованияДошкольное образованиеНачальная школаСредняя школаСтаршая школаВысшая школаСредне-специальное образованиеСреднее образованиеПрофессиональное образованиеСпециальное образованиеДистанционное обучениеВнеурочные занятияДополнительное образование
Вид урокаМетодические рекомендацииРазработка урокаИграФрагмент урокаВнеурочные занятияДидактический материалШаблонСценарий
Классдошкольное1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 классне зависит от класса
Рекомендованные
Сбросить фильтрedcommunity.ru
