Закон распределения вероятностей дискретной случайной величины – Закон распределения дискретной случайной величины. Примеры решения задач

Закон распределения дискретной случайной величины

Определение. Соотношение между возможными значениями случайной величины и их вероятностями называется законом распределения дискретной случайной величины.

Закон распределения может быть задан аналитически, в виде таблицы или графически.

Таблица соответствия значений случайной величины и их вероятностей называется рядом распределения.

Графическое представление этой таблицы называется многоугольником распределения. При этом сумма все ординат многоугольника распределения представляет собой вероятность всех возможных значений случайной величины, а, следовательно, равна единице.

Пример 14 . По цели производится 5 выстрелов. Вероятность попадания для каждого выстрела равна 0,4. Найти вероятности числа попаданий и построить многоугольник распределения.



Вероятности пяти попаданий из пяти возможных, четырех из пяти и трех из пяти были найдены выше по формуле Бернулли и равны соответственно:

, ,

Аналогично найдем:

. 

Представим графически зависимость числа попаданий от их вероятностей.

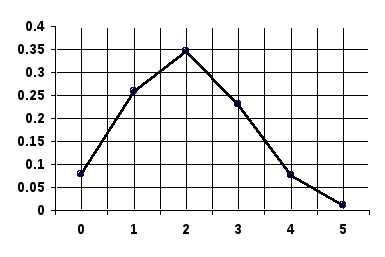При построении многоугольника распределения надо помнить, что соединение полученных точек носит условный характер. В промежутках между значениями случайной величины вероятность не принимает никакого значения. Точки соединены только для наглядности.

Биноминальное распределение

Если производится

независимых испытаний, в каждом из которых событиеможет появиться с одинаковой вероятностью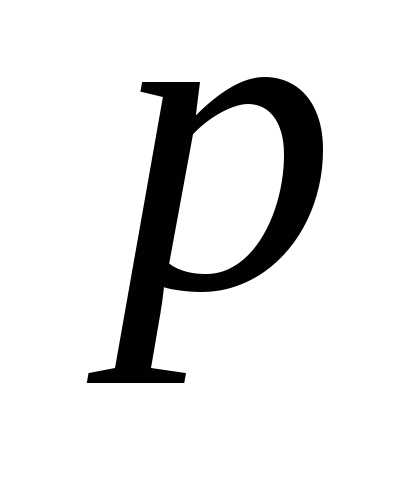в каждом из испытаний, то вероятность того, что событие не появится, равна.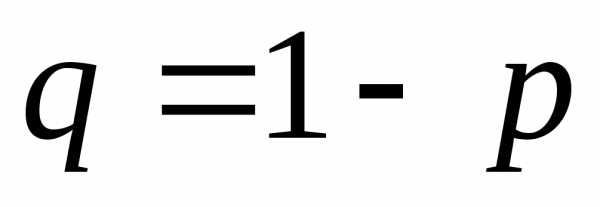

Примем число появлений события в каждом из испытаний за некоторую случайную величину .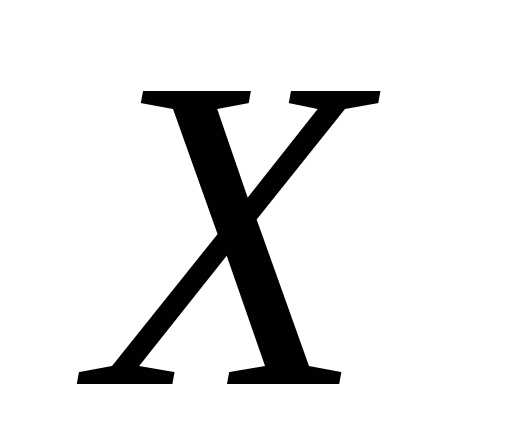

Чтобы найти закон распределения этой случайной величины, необходимо определить значения этой величины и их вероятности.

Значения найти достаточно просто. Очевидно, что в результате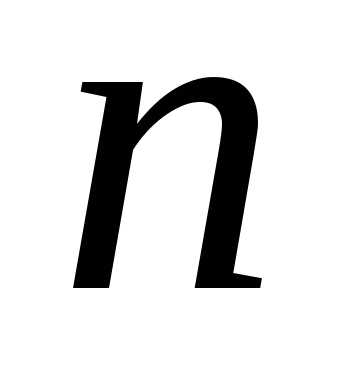

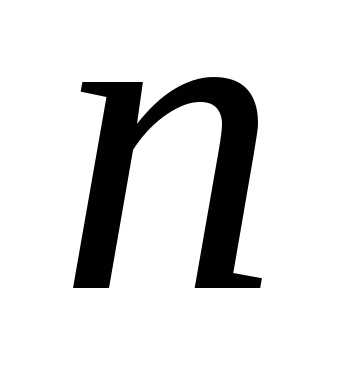испытаний событие может не появиться вовсе, появиться один раз, два раза, три и т.д. дораз.

Вероятность каждого значения этой случайной величины можно найти по формуле Бернулли.

Эта формула аналитически выражает искомый закон распределения. Этот закон распределения называется биноминальным.

Пример 15. В партии 10% нестандартных деталей. Наугад отобраны 4 детали. Написать биноминальный закон распределения дискретной случайной величины 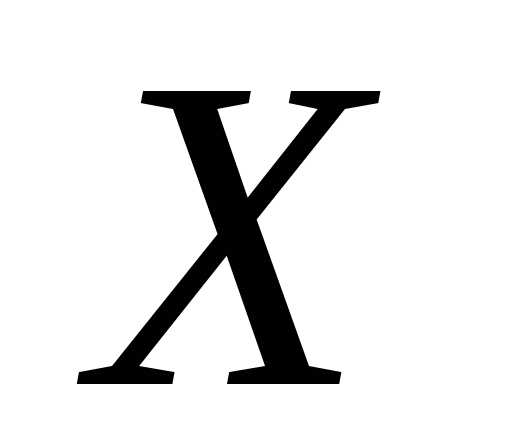– числа нестандартных деталей среди четырех отобранных и построить многоугольник полученного распределения.



Вероятность появления нестандартной детали в каждом случае равна 0,1.

Найдем вероятности того, что среди отобранных деталей:

1) Вообще нет нестандартных.

2) Одна нестандартная.

3) Две нестандартные детали.

4) Три нестандартные детали.

5) Четыре нестандартных детали.

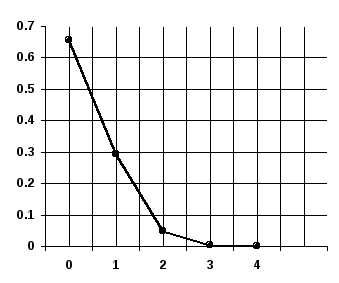Построим многоугольник распределения.

Пример 16 . Две игральные кости одновременно бросают 2 раза. Написать биноминальный закон распределения дискретной случайной величины 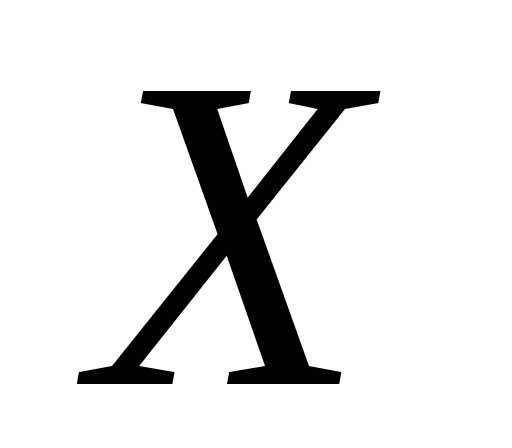– числа выпадений четного числа очков на двух игральных костях.



Каждая игральная кость имеет три варианта четных очков – 2, 4 и 6 из шести возможных, таким образом, вероятность выпадения четного числа очков на одной кости равна 0,5.

Вероятность одновременного выпадения четных очков на двух костях равна 0,25.

Вероятность того, что при двух испытаниях оба раза выпали четные очки на обеих костях, равна:

Вероятность того, что при двух испытаниях один раз выпали четные очки на обеих костях:

Вероятность того, что при двух испытаниях ни одного раза не выпаде четного числа очков на обеих костях:

. 

studfiles.net

Закон распределения дискретной случайной величины

Закон распределения дискретной случайной величины (ДСВ) представляет собой соответствие между значениями х

1, х₂,…,х_n этой величины  и их вероятностями p₁, p₂,…,p_n

 Может быть задан аналитически, графически или таблично.

Самый простой способ представления закона распределения дискретной случайной величины — в виде таблицы ряда распределения, то есть

X	x1	x2	……	xn
P	p1	p2	……	pn

х₁, х₂,…,х_n — значения дискретной случайной  величины;

p₁, p₂,…,p_n — вероятности значений X дискретной случайной  величина.

Также должно выполняться условия, что сумма вероятностей равна 1, то есть

∑p=p₁+p₂+ … +p_n=1

Рассмотрим примеры

---

Пример 1

Из корзины извлечено 4 белых шара, 6 черных, 8 синих и 2 красных шара. Найти закон распределения случайной величины X возможного выигрыша на один билет.

Решение

Объем выборки равен

n=4+6+8+2=20

X принимает следующие значения:

x₁=4; x₂=6; x₃=8; x₁=2

Найдем их вероятности:

  p₁(4)=4/20=0,2;

p₂(6)=6/20=0,3;

  p₃(8)=8/20=0,4;

p₄(2)=2/20=0,1

Получаем таблицу закона распределения дискретной случайной величины

X	4	6	8	2
P	0.2	0.3	0.4	0.1

---

Пример 2
Партия из 8 изделий содержит 5 стандартных. Наудачу отбираются 3 изделия. Составить таблицу закона распределения числа стандартных изделий среди отобранных.
Решение
Для составления закона распределения воспользуемся формулой комбинаторики сочетание без повторений, то есть всего 8 изделия, а отобрать необходимо 3 изделия получаем:

при P(X=0) — вероятность того, что среди трех отобранных изделий не окажется ни одного стандартного;
при P(X=1) — вероятность того, что среди трех отобранных изделий окажется одно стандартное и два нестандартных изделия;
при P(X=2) — вероятность того, что среди трех отобранных изделий окажется два стандартных и одно нестандартное изделие;

при P(X=3) — вероятность того, что среди трех отобранных изделий все три изделия стандартные.

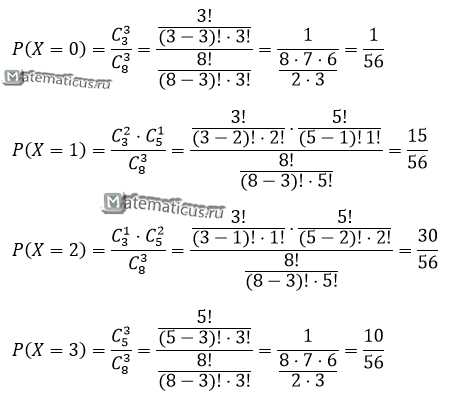
Составим таблицу распределения

X	0	1	2	3
P	0.018	0.268	0.536	0.178

---

Пример 3
По контрольной работе по математике школьники получили оценки:
удовлетворительно — 5 человек;
хорошо — 13 человек;
отлично — 7 человек.
Составьте таблицу закона распределения ДСВ
Решение

n=5+13+7=26

Вычислим вероятности:

  p₁(5)=5/25=0,2;

p₂(13)=13/25=0,52;

  p₃(7)=7/25=0,28

Таблица имеет вид:

X	5	13	8	2
P	0.2	0.52	0.28	0.1

---

Пример 4
Монета подбрасывается 10 раз, герб выпал 6 раз, а орел — 4 раза. Составить закон распределения дискретной случайной величины.
Решение

Вероятности равны:

p₁(6)=6/10=0,6;

p₂(4)=4/10=0,4

www.matematicus.ru

Закон распределения вероятностей дискретной двумерной случайной величины

Закон распределения двумерной случайной величины задан следующей таблицей:

Рисунок 2.

Найти законы распределения случайных величин $X,\ Y$, $X+Y$ и проверить в каждом случае выполнение равенства полной суммы вероятностей единице.

1. Найдем сначала распределение случайной величины $X$. Случайная величина $X$ может принимать значения $x_1=2,$ $x_2=3$, $x_3=5$. Для нахождения распределения будем пользоваться теоремой 1.

Найдем вначале сумму вероятностей $x_1$ следующим образом:

Рисунок 3.

\[P\left(x_1\right)=0,1+0,05+0,12=0,27\]

Аналогично найдем $P\left(x_2\right)$ и $P\left(x_3\right)$:

\[P\left(x_2\right)=0,2+0,14+0,08=0,42\] \[P\left(x_3\right)=0,15+0,11+0,05=0,31\]

Значит, закон распределения величины $X$ имеет следующий вид:

Рисунок 4.

Проверим выполнение равенства полной суммы вероятностей:

\[0,27+0,42+0,31=1-верно.\]

1. Найдем теперь распределение случайной величины $Y$. Случайная величина $Y$ может принимать значения $x_1=1,$ $x_2=3$, $x_3=4$. Для нахождения распределения будем пользоваться теоремой 1.

Найдем вначале сумму вероятностей $y_1$ следующим образом:

Рисунок 5.

\[P\left(y_1\right)=0,1+0,2+0,15=0,45\]

Аналогично найдем $P\left(y_2\right)$ и $P\left(y_3\right)$:

\[P\left(y_2\right)=0,05+0,14+0,11=0,3\] \[P\left(y_3\right)=0,12+0,08+0,05=0,25\]

Значит, закон распределения величины $X$ имеет следующий вид:

Рисунок 6.

Проверим выполнение равенства полной суммы вероятностей:

\[0,45+0,3+0,25=1-верно.\]

1. Осталось найти закон распределения случайной величины $X+Y$.

Обозначим её для удобства через $Z$: $Z=X+Y$.

Вначале найдем, какие значения может принимать данная величина. Для этого будем попарно складывать значения величин $X$ и $Y$. Получим следующие значения: 3, 4, 6, 5, 6, 8, 6, 7, 9. Теперь, отбрасывая совпавшие величины, получим, что случайная величина $X+Y$ может принимать значения $z_1=3,\ z_2=4,\ z_3=5,\ z_4=6,\ z_5=7,\ z_6=8,\ z_7=9.\ $

Найдем для начала $P(z_1)$. Так как значение $z_1$ единично, то оно находится следующим образом:

Рисунок 7.

\[P\left(z_1\right)=0,1\]

Аналогично находятся се вероятности, кроме $P(z_4)$:

\[P\left(z_2\right)=0,2,\ P\left(z_3\right)=0,05,\ P\left(z_5\right)=0,08,\ P\left(z_6\right)=0,11,\ P\left(z_7\right)=0,05\]

Найдем теперь $P(z_4)$ следующим образом:

Рисунок 8.

\[P\left(z_4\right)=0,12+0,14+0,15=0,41\]

Значит, закон распределения величины $Z$ имеет следующий вид:

Рисунок 9.

Проверим выполнение равенства полной суммы вероятностей:

\[0,1+0,2+0,05+0,41+0,08+0,11+0,05=1-верно.\]

spravochnick.ru

Ничего не найдено для Publ Teorija_Verojatnosti Sluchajnye_Velichiny Zakon_Raspredelenija_Diskretnoj_Sluchajnoj_Velichiny 82 1 0 268

It looks like nothing was found at this location. Maybe try a search or one of the links below?

Архивы Выберите месяц Июнь 2019 Май 2019 Апрель 2019 Март 2019 Февраль 2019 Январь 2019 Февраль 2014 Январь 2014 Апрель 2013 Март 2013 Февраль 2013 Январь 2013 Декабрь 2012 Ноябрь 2012 Октябрь 2012 Сентябрь 2012 Август 2012 Июнь 2012 Май 2012 Апрель 2012 Март 2012 Февраль 2012

РубрикиВыберите рубрику9_izmenenie_chisla_ehlektronov_na_vneshnem_ehnergeticheskom_urovne_atomov_khimicheskikh_ehlementovbinominalnoe_raspredeleniedelenie_otrezka_popolamExcelformula_bejesa_primery_s_reshenijamiformula_bernulli_primery_zadach_s_resheniemformula_polnoj_verojatnosti_primery_s_reshenijamiformuly_proizvodnyjgdz_onlajn_reshebnik_po_anglijskomu_jazyku_dlja_9_klassa_spotlight_anglijskij_v_fokuse_test_booklet_kontrolnye_zadanija_2012_ggeometricheskoe_opredelenie_verojatnostiGPSS Worlditogovoe_povtorenie_reshebnik_mordkovich_9_klass_chislovye_vyrazhenijakontrolnaja_rabota_po_teorii_verojatnosti_variant_7kontrolnye_raboty_po_algebre_7_klass_dudnicyn_tulchinskaja_pod_red_mordkovicha_8_e_izd_2006_g_i_dudnicyn_pod_red_mordkovicha_2_e_izd_2000najti_radius_i_centr_okruzhnostinormalnoe_raspredelenieobjom_parallelepipedaonlajn_gia_po_matematike_2014_gonlajn_gia_po_matematike_2017_gonlajn_reshebnik_algebra_7_klass_makarychevonlajn_reshebnik_algebra_7_klass_mordkovich_2010_gonlajn_reshebnik_algebra_9_klass_makarychev_2011_gonlajn_reshebnik_anglijskij_jazyk_3_klass_biboletova_denisenko_trubanevaonlajn_reshebnik_didakticheskie_materialy_po_algebre_7_klass_zvavich_kuznecova_2010_gonlajn_reshebnik_didakticheskim_materialam_po_matematike_6_klass_chesnokov_2011_gonlajn_reshebnik_didikticheskie_materialy_po_matematike_5_klass_chesnokov_neshkov_2003_g_2009_gonlajn_reshebnik_k_uchebniku_po_anglijskomu_jazyku_i_rabochej_tetradi_4_klass_biboletova_denisenko_trubanevaonlajn_reshebnik_matematika_6_klass_vilenkin_2010_gonlajn_reshebnik_po_anglijskomu_jazyku_3_klass_vereshhagina_pritykina_2009_gonlajn_reshebnik_po_fizike_sbornik_zadach_9_11_klassy_rymkevichonlajn_reshebnik_po_matematike_3_klass_istominaonlajn_reshebnik_po_matematike_3_klass_moroonlajn_reshebnik_po_matematike_4_klass_chast_1_i_chast_2_rudnickaja_judachevaonlajn_reshebnik_po_matematike_4_klass_chebotarjovskaja_t_m_drozda_v_l_stoljara_a_a_2010_gonlajn_reshebnik_po_matematike_4_klass_moro_bantova_beltjukovaonlajn_reshebnik_po_matematike_4_klass_peterson_2010_gonlajn_reshebnik_po_matematike_5_klass_dorofeev_peterson_2008_gonlajn_reshebnik_po_matematike_5_klass_kuznecova_muravjova_shneperman_i_dr_2009_gonlajn_reshebnik_po_matematike_6_klass_zubareva_mordkovich_2005_2010_gonlajn_reshebnik_po_russkomu_jazyku_dlja_9_klassa_barkhudarov_krjuchkov_maksimov_cheshko_25_e_izd_prosveshhenie_2011_gonlajn_reshebnik_russkij_jazyk_5_klass_razumovskaja_2010_gonlajn_reshebnik_russkij_jazyk_5_klass_razumovskaja_lekanta_2010_g_i_razumovskaja_lvova_kapinos_i_dr_2004_gonlajn_reshebnik_russkij_jazyk_6_klass_razumovskaja_2009_gotrezki_na_osjakhploskost_prokhodjashhaja_cherez_dannuju_tochku_parallelnoj_dannoj_ploskostiploskost_prokhodjashhaja_cherez_dannuju_tochku_perpendikuljarno_k_dvum_ploskostjamploskost_prokhodjashhaja_cherez_dve_tochki_perpendikuljarno_k_dannoj_ploskostipoljarnye_parametry_prjamojponjatie_o_vektoreprakticheskaja_rabota_2_nabljudenie_za_gorjashhej_svechojprakticheskaja_rabota_3_analiz_pochvy_i_vodyprakticheskaja_rabota_4_priznaki_khimicheskikh_reakcijprakticheskaja_rabota_5_prigotovlenie_rastvora_sakhara_i_raschet_ego_massovoj_doli_v_rastvoreprakticheskaja_rabota_8_svojstva_kislot_osnovanij_oksidov_i_solejprakticheskaja_rabota_9_reshenie_ehksperimentalnykh_zadachprivedenie_uravnenie_k_normalnomu_viduprivedenie_uravnenij_prjamoj_k_simmetrichnomu_viduprivedenie_uravnenija_ploskosti_k_normalnomu_viduraspredelenie_puassonareshebnik_kontrolnye_raboty_po_algebre_9_klass_dudnicyn_tulchinskaja_mordkovich_8_izd_2006_greshebnik_po_matematike_5_klass_kuznecova_muravjova_shneperman_2009_g_glavy_1_5reshebnik_po_matematike_5_klass_kuznecova_muravjova_shneperman_2009_g_glavy_6_10reshebnik_rabochaja_tetrad_po_anglijskomu_jazyku_3_klass_vereshhagina_pritykina_2009_gsimmetrichnye_uravnenija_prjamojslozhenie_vektorovteorema_slozhenija_verojatnostej_formuly_primery_s_reshenijamiteorema_umnozhenija_verojatnostej_formuly_primery_s_reshenijamiteorija_verojatnostiteorija_verojatnosti_sobytijaugol_mezhdu_dvumja_ploskostjamiumnozhenie_vektora_na_chislouravnenie_prjamoj_v_prostranstveuravnenija_prjamoj_prokhodjashhej_cherez_dve_dannye_tochkiverojatnost_pojavlenija_khotja_by_odnogo_sobytija_zadachi_s_reshenijamiverojatnost_pojavlenija_tolko_odnogo_iz_sobytij_primery_s_resheniemvychitanie_vektorovvyrazhenie_skaljarnogo_proizvedenija_cherez_koordinaty_soomnozhitelejvyrazhenie_vektornogo_proizvedenija_cherez_koordinaty_somnozhitelejWindowsWordАлгебраАналитическая геометрия в пространствеАналитическая геометрия на плоскостиАрифметикаГрафик онлайнДифференциальное исчислениеДокументыЖелезоЗаконы распределения случайной величиныИллюстрацииИнтегральное исчислениеИсследование функцииКомбинаторикаКомплексные числаЛинейная алгебраЛогарифмМатематическая статистикаПланиметрияПроизводнаяРядыСвязьСофтСтереометрияТаблицыТеория вероятностейТеория системТехникаТригонометрияФилософияЭлектроника

www.matematicus.ru

8. Основные законы распределения дискретных случайных величин.

1. Биномиальный закон распределения (биномиальное распределение) дискретных случайных величин.

Дискретная случайная величина Х распределена по биномиальному закону, если она принимает значения 0,1,2…,m…,n… с вероятностями, которые находятся по формуле Бернулли:

…………………………………………………

Теорема. Математическое ожидание дискретной случайной величины, распределенной по биномиальному закону, равняется произведению числа всех испытаний на вероятность наступления события в отдельном испытании, то есть

.

Дисперсия равняется произведению числа всех испытаний на вероятность наступления и не наступления события в отдельном испытании, то есть

.

Пример.

По статистическим данным известно, что вероятность рождения мальчика составляет: p = 0,515.

Составить закон распределения числа мальчиков в семье с пятью детьми. Найти математическое ожидание, дисперсию, среднее квадратическое отклонениеи моду.

Решение:

X ‒ случайная величина ‒ число мальчиков в семье с пятью детьми.

Составим закон распределения числа мальчиков в семье с пятью детьми:

	0	1	2	3	4	5
	0,026835	0,142475	0,302579	0,321296	0,170585	0,036227

Проверка:

1. Математическое ожидание:

2. Дисперсия:

3. Среднее квадратическое отклонение:

4. так как приm = 3 вероятность максимальная. Она составляет: p = 0,321296.

2. Геометрический закон распределения (геометрическое распределение) дискретных случайных величин.

Дискретная случайная величина распределена геометрически, если она принимает значения 1,2,…m …(бесконечное, но счетное количество раз) с вероятностями, находящимися по формуле общего члена геометрической прогрессии:

Случайная величина X = m, распределенная геометрически, представляет собой число испытаний (m) до первого положительного исхода.

Составим ряд распределения:

и т.д.

Теорема. Математическое ожидание и дисперсия случайной величины, распределенной геометрически, вычисляются по формулам:

Пример.

Охотник стреляет по дичи до первого попадания, но успевает сделать не более 4‒х выстрелов.

Составить закон распределения числа выстрелов, если вероятность попадания при одном выстреле равна p = 0,7. Найти математическое ожидание, дисперсию, среднее квадратическое отклонение и моду числа выстрелов.

Решение:

По условию

число выстрелов

Составим закон распределения числа выстрелов:

	1	2	3	4
	0,7	0,21	0,063	0,027

Проверка:

1. Математическое ожидание:

2. Дисперсия:

3. Среднее квадратическое отклонение:

4. так как приm = 1 вероятность максимальная, она составляет: p = 0,7.

Пример.

Вероятность поражения цели равна 0,6. Производится стрельба по мишени до первого попадания (число патронов не ограничено). Требуется составить ряд распределения числа сделанных выстрелов, найти математическое ожидание и дисперсию этой случайной величины. Определить вероятность того, что для поражения цели потребуется не более трёх патронов.

Решение:

Случайная величина X — число сделанных выстрелов — имеет геометрическое распределение с параметром p=0,6. Ряд распределения X имеет вид:

	1	2	3	…	m	…
	0,6	0,24	0,096	…	0,6·0,4m	…

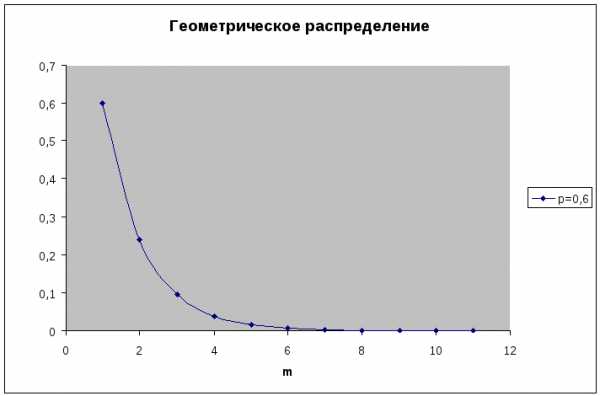
Вероятность того, что для поражения цели потребуется не более трёх патронов:

P(X ≤ 3) = P(X = 1) + P(X = 2) + P(X = 3) = 0,6+0,24+0,096 = 0,936.

studfiles.net

7. Дискретные случайные величины и их характеристика. Закон распределения вероятностей дсв. Математическое ожидание дсв. Свойства математического ожидания.

Наряду с понятием случайного события в теории вероятности используется и более удобное понятие случайной величины.

Случайной величиной называется величина, принимающая в результате опыта одно из своих возможных значений, причем заранее неизвестно, какое именно.

Будем обозначать случайные величины заглавными буквами латинского алфавита (Х, Y,Z,…), а их возможные значения – соответствующими малыми буквами (x_i, y_i,…).

Примеры: число очков, выпавших при броске игральной кости; число появлений герба при 10 бросках монеты; число выстрелов до первого попадания в цель; расстояние от центра мишени до пробоины при попадании.

Можно заметить, что множество возможных значений для перечисленных случайных величин имеет разный вид: для первых двух величин оно конечно ( соответственно 6 и 11 значений), для третьей величины множество значений бесконечно и представляет собой множество натуральных чисел, а для четвертой – все точки отрезка, длина которого равна радиусу мишени. Таким образом, для первых трех величин множество значений из отдельных (дискретных), изолированных друг от друга значений, а для четвертой оно представляет собой непрерывную область. По этому показателю случайные величины подразделяются на две группы: дискретные и непрерывные.

Случайная величина называется дискретной, если она принимает отдельные, изолированные возможные значения с определенными вероятностями.

Случайная величина называется непрерывной, если множество ее возможных значений целиком заполняет некоторый конечный или бесконечный промежуток.

Дискретные случайные величины.

Для задания дискретной случайной величины нужно знать ее возможные значения и вероятности, с которыми принимаются эти значения. Соответствие между ними называется законом распределения случайной величины. Он может иметь вид таблицы, формулы или графика.

Таблица, в которой перечислены возможные значения дискретной случайной величины и соответствующие им вероятности, называется рядом распределения:

xi	x1	x2	…	xn	…
pi	p1	p2	…	pn	…

Заметим, что событие, заключающееся в том, что случайная величина примет одно из своих возможных значений, является достоверным, поэтому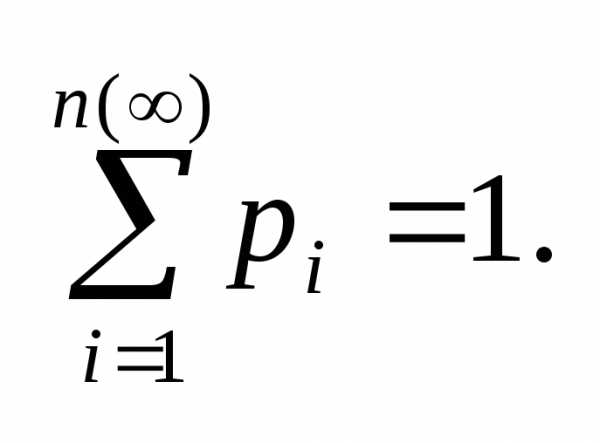

Графически закон распределения дискретной случайной величины можно представить в виде многоугольника распределения – ломаной, соединяющей точки плоскости с координатами (x_i, p_i).

x₁x₂x₃x₄x₅

Математическим ожиданием дискретной случайной величины называ-ется сумма произведений ее возможных значений на соответствующие им вероятности:

М(Х) = х₁р₁ + х₂р₂ + … + х_пр_п . (7.1)

Если число возможных значений случайной величины бесконечно, то 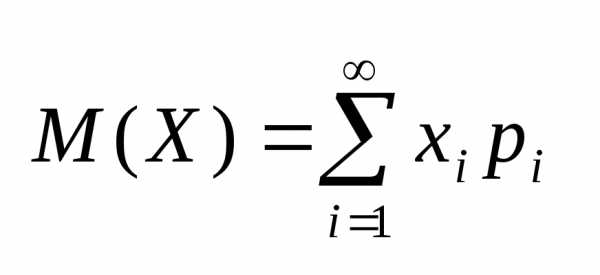, если полученный ряд сходится абсолютно.

Замечание 1. Математическое ожидание называют иногда взвешенным средним, так как оно приближенно равно среднему арифметическому наблюдаемых значений случайной величины при большом числе опытов.

Замечание 2. Из определения математического ожидания следует, что его значение не меньше наименьшего возможного значения случайной величины и не больше наибольше-го.

Замечание 3. Математическое ожидание дискретной случайной величины есть неслучай-ная (постоянная) величина. В дальнейшем увидим, что это же справедливо и для непре-рывных случайных величин.

Свойства математического ожидания.

1)Математическое ожидание постоянной равно самой постоянной:

М(С) = С. (7.2)

Доказательство. Если рассматривать С как дискретную случайную величину, принимающую только одно значение С с вероятностью р = 1, то М(С) = С·1 = С.

2)Постоянный множитель можно выносит за знак математического ожидания:

М(СХ) = С М(Х). (7.3)

Доказательство. Если случайная величина Х задана рядом распределения

xi	x1	x2	…	xn
pi	p1	p2	…	pn

то ряд распределения для СХ имеет вид:

Сxi	Сx1	Сx2	…	Сxn
pi	p1	p2	…	pn

Тогда М(СХ) = Сх₁р₁ + Сх₂р₂ + … + Сх_пр_п = С( х₁р₁ + х₂р₂ + … + х_пр_п) = СМ(Х).

Две случайные величины называются независимыми, если закон распределения одной из них не зависит от того, какие значения приняла другая. В противном случае случайные величины зависимы.

Назовем произведением независимых случайных величин Х и Y случайную величину XY, возможные значения которой равны произведениям всех возможных значений Х на все возможные значения Y, а соответствующие им вероят-ности равны произведениям вероятностей сомножителей.

1. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:

M(XY) = M(X)M(Y). (7.4)

Доказательство. Для упрощения вычислений ограничимся случаем, когда Х и Y принимают только по два возможных значения:

Тогда ряд распределения для XY выглядит так:

ХY	x1y1	x2y1	x1y2	x2y2
p	p1g1	p2 g1	p1g2	p2g2

Следовательно, M(XY) = x₁y₁·p₁g₁ + x₂y₁·p₂g₁ + x₁y₂·p₁g₂ + x₂y₂·p₂g₂ = y₁g₁(x₁p₁ + x₂p₂) + + y₂g₂(x₁p₁ + x₂p₂) = (y₁g₁ + y₂g₂) (x₁p₁ + x₂p₂) = M(X)·M(Y).

Замечание 1. Аналогично можно доказать это свойство для большего количества возможных значений сомножителей.

Замечание 2. Свойство 3 справедливо для произведения любого числа независимых случайных величин, что доказывается методом математической индукции.

Определим сумму случайных величин Х и Y как случайную величину Х + Y, возможные значения которой равны суммам каждого возможного значения Х с каждым возможным значением Y; вероятности таких сумм равны произведениям вероятностей слагаемых (для зависимых случайных величин – произведениям вероятности одного слагаемого на условную вероятность второго).

4) Математическое ожидание суммы двух случайных величин ( зависимых или незави-симых ) равно сумме математических ожиданий слагаемых:

M (X + Y) = M (X) + M (Y). (7.5)

Доказательство.

Вновь рассмотрим случайные величины, заданные рядами распределения, приведен-ными при доказательстве свойства 3. Тогда возможными значениями X + Y являются х₁ + у₁, х₁ + у₂, х₂ + у₁, х₂ + у₂. Обозначим их вероятности соответственно как р₁₁, р₁₂, р₂₁ и р₂₂. Найдем М( Х +Y ) = (x₁ + y₁)p₁₁ + (x₁ + y₂)p₁₂ + (x₂ + y₁)p₂₁ + (x₂ + y₂)p₂₂ =

= x₁(p₁₁ + p₁₂) + x₂(p₂₁ + p₂₂) + y₁(p₁₁ + p₂₁) + y₂(p₁₂ + p₂₂).

Докажем, что р₁₁ + р₂₂ = р₁. Действительно, событие, состоящее в том, что X + Y примет значения х₁ + у₁ или х₁ + у₂ и вероятность которого равна р₁₁ + р₂₂, совпадает с событием, заключающемся в том, что Х = х₁ (его вероятность – р₁). Аналогично дока-зывается, что p₂₁ + p₂₂ = р₂, p₁₁ + p₂₁ = g₁, p₁₂ + p₂₂ = g₂. Значит,

M(X + Y) = x₁p₁ + x₂p₂ + y₁g₁ + y₂g₂ = M (X) + M (Y).

Замечание. Из свойства 4 следует, что сумма любого числа случайных величин равна сумме математических ожиданий слагаемых.

studfiles.net

Закон распределения дискретной случайной величины

Пусть задана д.с.в. Х, которая в результате эксперимента может принять одно из своих возможных значений: х₁, х₂, … , x_n . Поскольку заранее неизвестно, какое значение примет с.в. Х, то, скажем, событие (Х=х₁), заключающееся в том, что с.в. Х в результате эксперимента примет значение х₁, есть случайное событие – оно может произойти или не произойти. Все, чем мы можем характеризовать случайное событие, это его вероятность как степень нашей уверенности, что это событие произойдет. Обозначим эту вероятность р₁=Р(Х=х₁). Аналогично, обозначим вероятности событий: р₂=Р(Х=х₂), …, р_n=P(Х=х_n). Тогда эти два набора чисел: { х₁, х₂, … , x_n } и {p₁, p₂, … , p_n} полностью характеризуют д.с.в. Х (и уже даже не важно, с каким именно экспериментом связана эта с.в. и что она в этом эксперименте означает). Законом (иногда говорят «рядом») распределения (вероятностей) дискретной случайной величины называется таблица, содержащая возможные значения этой с.в. и вероятности, с которыми эти значения принимаются. Если д.с.в. Х принимает значения { х₁, х₂, … , x_n } с вероятностями {p₁, p₂, … , p_n}, то закон распределения этой с.в. имеет вид:

Х	х1	х2	…	xn
Р	p1	p2	…	pn

Поскольку события (Х=х₁), (Х=х₂), … , (X=x_n) , очевидно, попарно несовместны, а событие (Х=х₁)+(Х=х₂)+… +(X=x_n) , заключающееся в том, что в результате испытания с.в. Х примет хотя бы одно из своих значений, является достоверным событием, то, используя свойства вероятности, получим:

1=Р((Х=х₁)+(Х=х₂)+… +(X=x_n))=Р(Х=х₁)+…+Р(Х=x_n)=р₁+ … +p_n .

Поэтому получаем важное свойство закона распределения:

Это свойство чаще всего используется для проверки правильности составленного закона распределения или для определения вероятности одного из значений с.в. при вычисленных вероятностях остальных значений.

Приведем примеры .

1. Х – число очков на подброшенном кубике:

Х	1	2	3	4	5	6
Р	1/6	1/6	1/6	1/6	1/6	1/6

2. В корзине 3 белых и 2 черных шара. Наугад вынимается 2 шара. С.в. Х – число белых шаров среди вынутых:

или

3. Вася с Петей затеяли такую игру. Если при подбросе кубика выпадет 6, то Вася дает Пете 4 рубля, а в противном случае Петя дает Васе 1 рубль. Пусть с.в. Х – величина Васиного выигрыша.

Тогда эта величина имеет следующий закон распределения:

Функция распределения случайной величины и ее свойства

Если Х − непрерывная случайная величина, то ее невозможно описать с помощью упомянутой выше таблицы, выражающей закон распределения вероятностей случайной величины, поскольку возможных значений слишком много (континуум). Поэтому появляется необходимость ввести понятие, которое бы полностью характеризовало случайную величину не зависимо от того, является ли она дискретной или непрерывной. Пусть дана с.в. Х (д.с.в. или н.с.в.). Фиксируем произвольное число х и рассмотрим событие (X<x) , заключающееся в том, что в результате эксперимента с.в. Х приняла значение, которое меньше взятого числа х (т.е. значение с.в. Х попало в интервал (−∞, х) ). Это событие в результате эксперимента может произойти или не произойти, т.е. является случайным событием. Вероятность этого события (т.е. Р(X<x) ) зависит от величины взятого нами числа х (чем больше х, тем шире интервал (−∞, х), тем вероятнее в него попасть), т.е. является функцией от х. Обозначим эту функцию F(x). Эта функция и называется функцией распределения. Итак, функцией распределения (функцией распределения вероятностей, интегральной функцией распределения) с.в. Х (дискретной или непрерывной) называется числовая функция F(x), заданная на всей числовой прямой следующей формулой:

F(x) = Р(X<x)

Посмотрим, как выглядит функция распределения для дискретной с.в. с заданным законом распределения. Пусть д.с.в. Х принимает значения { х₁, х₂, … , x_n } с вероятностями {p₁, p₂, … , p_n}, а потому имеет закон распределения следующего вида:

Х	х1	х2	…	xn
Р	p1	p2	…	pn

Возьмем произвольное значение х, меньшее или равное первого принимаемого случайной величиной значения х₁ : x<x₁. По определению F(x) =. Но при таком значениих в интервале (−∞, х) нет значений, принимаемых случайной величиной, поэтому событие является невозможным и. Итак, для всех :x<x₁ получается F(x)=0. Возьмем теперь произвольное значение х между первым и вторым значением, принимаемых с.в. Х : . При таком значениих в интервале (−∞, х) есть только одно значение (это х₁ ), принимаемое случайной величиной. Поэтому событие совпадает с событием (Х=х₁) , вероятность которого равна р₁. Таким образом, F(x) == р₁ для всех х: . Точно так же можно получить, что для всехх таких, что функция распределенияF(x) = р₁ +р₂ . И так далее. Для всех х таких, что функция распределенияF(x) = р₁ +р₂ +…+р_n-1 . Наконец, пусть х>x_n . Тогда интервал (−∞, х) содержит все значения, которые может принять случайная величина. Поэтому при любом исходе испытания событие происходит, т.е. является достоверным событием, вероятность которого равна 1. Поэтому для всехх>x_n : F(x)=1. Таким образом, функция распределения для дискретной случайной величины Х с законом распределения

Х	х1	х2	…	xn
Р	p1	p2	…	pn

имеет следующий вид:

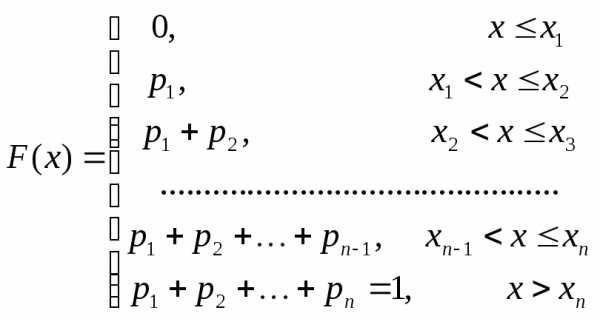
График такой ступенчатой функции состоит из отрезков горизонтальных прямых, расположенных над соответствующими отрезками оси х на соответствующей высоте.

Пример. В корзине 3 белых и 2 черных шара. Наугад вынимается 2 шара. Найти функцию распределения с.в. Х – числа белых шаров среди вынутых. Построить график этой функции.

Решение. Выше мы уже нашли вид закона распределения этой с.в. :

Учитывая выписанную выше общую формулу, получаем:

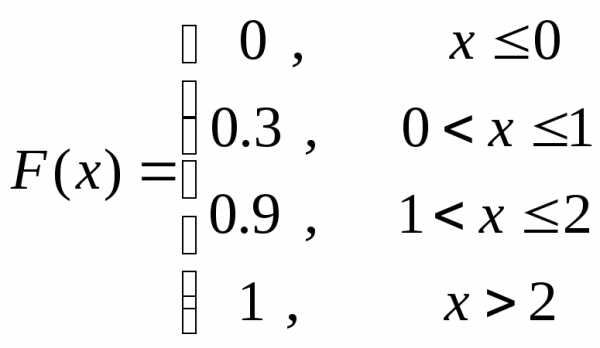
Строим график полученной функции:

Пример. Монета подбрасывается 3 раза. Найти выражение для функции распределения с.в. Х – числа выпавших орлов. Построить ее график.

Пример. Первый стрелок попадает в мишень с вероятностью 0.6, а второй 0.8 . Оба сделали по выстрелу. Найти функцию распределения с.в. Х – числа попаданий в мишень.

После введения понятия функции распределения можно дать более строгое определение для непрерывной случайной величины. Случайная величина называется непрерывной, если ее функция распределения непрерывна на всей числовой прямой, кроме, быть может, отдельных изолированных точек.

Перейдем теперь к свойствам функции распределения, которые лежат в основе применения этих функций.

1. Значения функции распределения заключены между 0 и 1: 0≤F(x)≤1 . Это следует их определения этой функции как значения вероятности некоторого события. Вероятность любого события, как известно, заключена между 0 и 1.

2. Функция распределения возрастает на всей числовой прямой: F(x)↑(0,+∞). Это свойство легко выводится из определения этой функции.

3. Если значения с.в. Х не выходят из отрезка [a,b], то F(x)=0 для всех x≤a и F(x)=1 для всех x>b.

4. Если с.в. может принимать значения на всей числовой прямой, то ,.

5. С помощью функции распределения можно вычислить вероятность попадания значения случайной величины в любой полуинтервал [a,b) : P(a ≤ X <b) = F(b) − F(a)

6. Если с.в. Х непрерывна, то для любого заранее фиксированного числа х₀ вероятность того, что в результате испытания она примет именно это значение, равна 0: Р(Х=х₀) = 0. Этот результат можно вывести из очевидного неравенства 0 ≤ Р(Х=х₀) ≤ Р(х₀ ≤ Х < х₀+ε) = F(х₀+ε) − F(х₀) для любого положительного числа ε. Осталось в этом неравенстве перейти к пределу при ε→0 и воспользоваться непрерывностью функции распределения для непрерывных случайных величин. Вот такое удивительное свойство непрерывных случайных величин: событие (Х=х₀) не является невозможным событием, но вероятность его равна 0.

7. Последнее свойство позволяет следующим образом обобщить предпоследнее свойство, но только для непрерывных случайных величин: P(a ≤ X <b) = P(a < X ≤b)= P(a ≤ X≤ b)= P(a < X <b) = F(b) − F(a).

Пример. Вероятностный прогноз для с.в. Х – процентное увеличение стоимости акций в течение года имеет следующий вид:

Х	5	10	15	20	25	30
Р	0.1	0.1	0.2	0.3	0.2	0.1

Что выгоднее – покупка акций или размещение денег в банке, который гарантирует 18% годовых? А в случае ежемесячной капитализации вклада в банке?

Пример. Дана функция распределения с.в. Х: 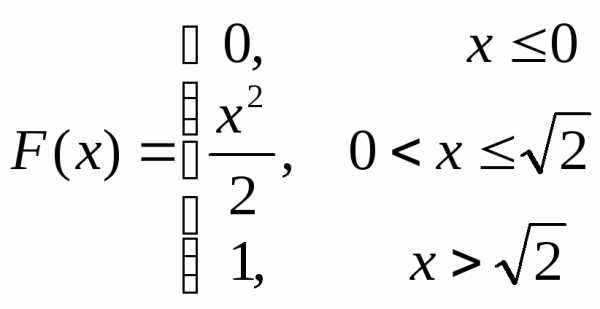. Найти вероятность того, что при испытании случайная величина примет значение из интервала (0,1). Найти вероятность, что при четырех испытаниях этой с.в. она примет значение из интервала (0,1) ровно 3 раза (вспомните формулу Бернулли).

Пример. Автомобиль едет по улице, на которой расположены 3 светофора. Светофоры работают независимо друг от друга и на каждом из них время горения зеленого цвета равно совокупному времени горения желтого и красного цветов. Для с.в. Х – числа остановок автомобиля на этой улице – найти: а) закон распределения этой с.в.; б) интегральную функцию распределения; в) вероятность того, что число остановок будет меньше 2.

studfiles.net
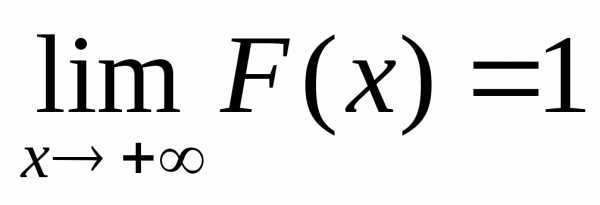