Синус, косинус, тангенс и котангенс острого угла прямоугольного треугольника – онлайн-тренажер для подготовки к ЕНТ, итоговой аттестации и ВОУД
Запомнить
Восстановить пароль
Регистрация
Конспект
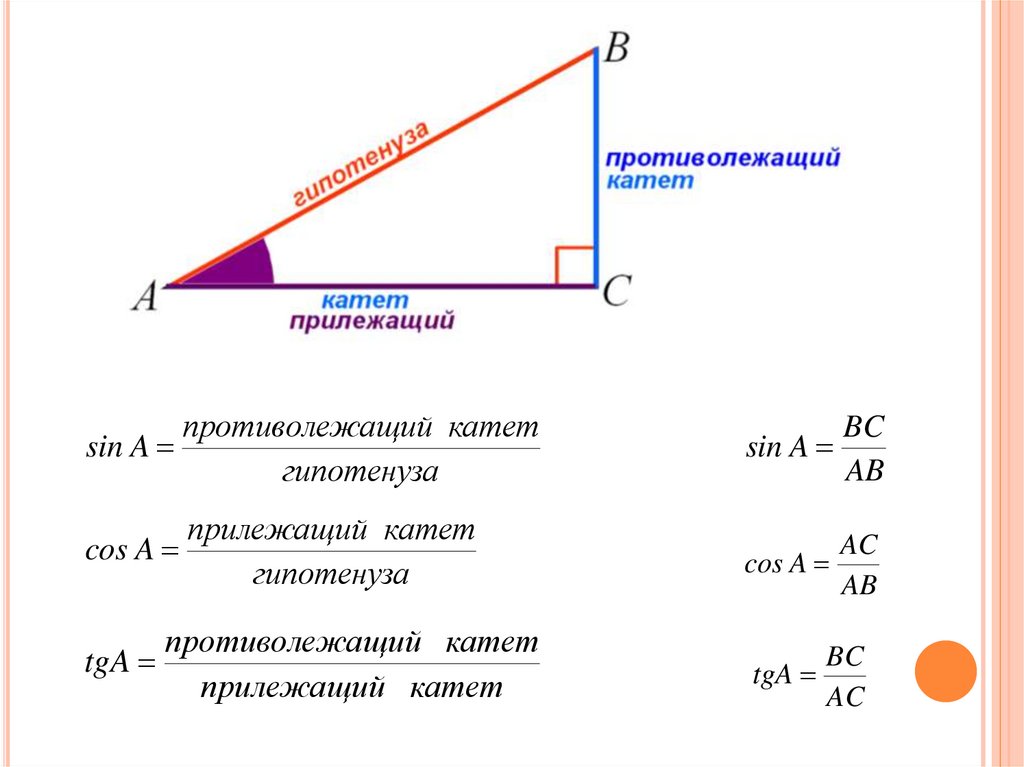
Гипотенуза прямоугольного треугольника – это сторона, лежащая напротив прямого угла.
Катеты – стороны, лежащие напротив острых углов. Катет \(a\), лежащий напротив угла \(\alpha\), называется противолежащим (по отношению к углу \(\alpha\)). Другой катет \(b\), который лежит на одной из сторон угла \(\alpha\), называется прилежащим.
Синус острого угла в прямоугольном треугольнике равен отношению противоположного катета к гипотенузе: \(sin∠A=\frac{a}{c} \).
Косинус острого угла в прямоугольном треугольнике равен отношению прилежащего катета к гипотенузе: \(cos∠A=\frac{b}{c} \).
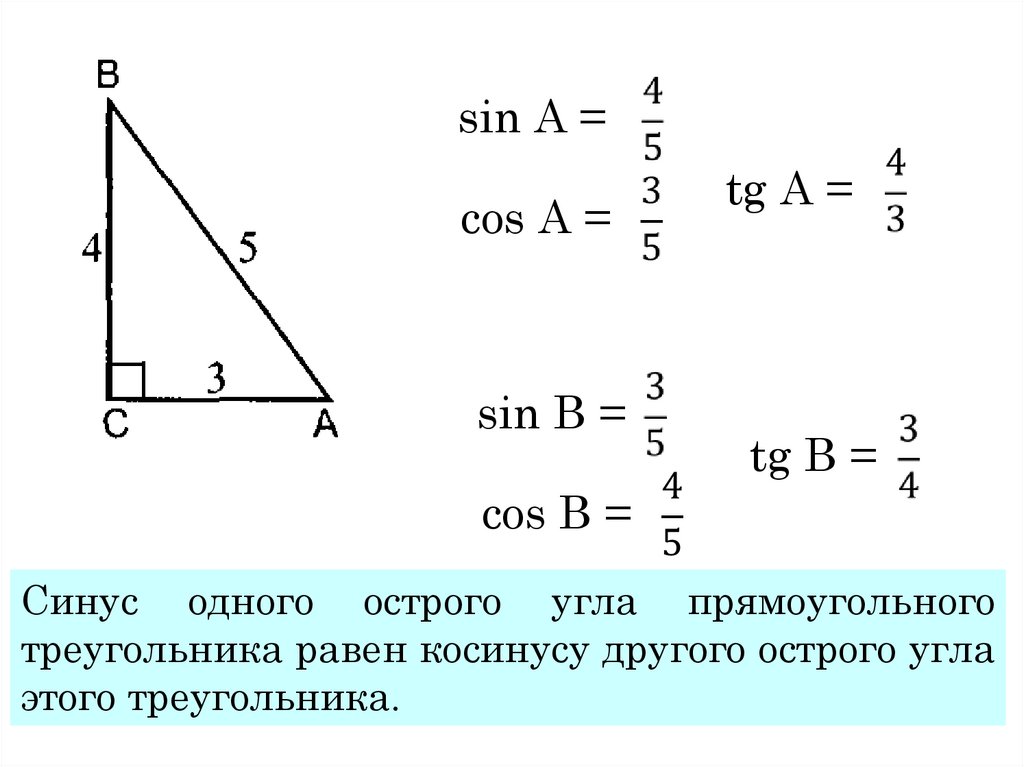
В прямоугольном треугольнике синус одного острого угла равен косинусу другого, и наоборот:
\(sin∠A=cos∠B;\ \sin \angle A=\cos \angle B; \ sin∠A=cos∠B\; \\ sin∠B=cos∠A; \ \sin \angle B=\cos \angle A; \ sin∠B=cos∠A.\)
Тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему: \(tg ∠A=\frac{a}{b} \).
Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу: \(tg\angle A=\frac{sin\angle A}{cos\angle A}\).
Котангенс острого угла в прямоугольном треугольнике равен отношению прилежащего катета к противолежащему: \(ctg ∠A=\frac{b}{a} \).
Котангенсом острого угла называется отношение косинуса к синусу: \(ctg\angle A=\frac{cos\angle A}{sin\angle A}\).
Таблица значений синуса, косинуса, тангенса и котангенса:
| \(\varphi\) | \(0^{\circ}\) | \(30^{\circ}\) | \(45^{\circ}\) | \(60^{\circ}\) | \(90^{\circ}\) |
|---|---|---|---|---|---|
| \(\sin \varphi\) | \(0\) | \(\begin{aligned} \frac{1}{2} \end{aligned}\) | \(\begin{aligned} \frac{\sqrt 2}{2} \end{aligned}\) | \(\begin{aligned} \frac{\sqrt 3}{2} \end{aligned}\) |
\(1\) |
|
\(\cos \varphi\) |
\(1\) | \(\begin{aligned} \frac{\sqrt 3}{2} \end{aligned}\) | \(\begin{aligned} \frac{\sqrt 2}{2} \end{aligned}\) | \(\begin{aligned} \frac{1}{2} \end{aligned}\) |
\(0\) |
| \(\rm tg\ \varphi\) | \(0\) | \(\begin{aligned} \frac{1}{\sqrt 3} \end{aligned}\) | \(1\) | \(\begin{aligned} \sqrt 3 \end{aligned}\) |
\(\color{red}-\) |
| \(\rm ctg\ \varphi\) | \(\color{red}-\) | \(\begin{aligned} \sqrt 3 \end{aligned}\) | \(1\) | \(\begin{aligned} \frac{1}{\sqrt 3} \end{aligned}\) |
\(0\) |
Вопросы
В прямоугольном треугольнике один из катетов равен 3, а котангенс прилежащего угла равен 0,75.
 \circ\). Найдите боковые стороны.
\circ\). Найдите боковые стороны.
Сообщить об ошибке
Обязательные
Математическая грамотность
Грамотность чтения
История Казахстана
Предметы по профилю
Биология
Химия
Английский язык
Французский язык
География
Немецкий язык
Информатика
Основы права
Русская литература
Математика
Физика
Русский язык
Всемирная история
Укажите предмет *
Скопируйте и вставьте вопрос задания *
Опишите подробнее найденную ошибку в задании *
Прикрепите скриншот
Объем файла не должен превышать 1МБ
Казахский
Русский
Обратите внимание! По выбранным Вами предметам ГРАНТЫ не предоставлены.
1. Скачайте приложение iTest, используя QR-код или строку поиска в AppStore или Play Market
2. Авторизуйтесь в приложении и готовьтесь к экзаменам вместе с нами
Определение синуса, косинуса, тангенса и котангенса
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения Подготовка к ЕГЭ по математике.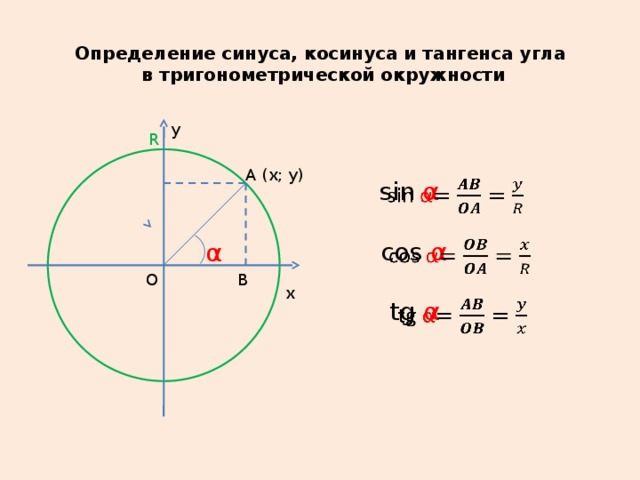 Базовый уровень Сложные задачи
Базовый уровень Сложные задачи
1. Информационно-проектный урок
Информационнопроектный урок2. Тема: Определение синуса, косинуса, тангенса и котангенса.
3. Цели урока:
• 1.Знать определение синуса,косинуса, тангенса и котангенса.
• 2.Уметь применять эти
определения к решению
примеров и задач.
• 3.Привитие творческой
активности и самостоятельности
4. План урока
• История развитиятригонометрии.
• Повторение курса
геометрии.
• Изучение нового
материала.
• Закрепление
5. Историческая справка
тригононТригонометрия
метрио
(измерение треугольника)
Древний
Вавилон-умели предсказывать
солнечные и лунные затмения.
Древнегреческие
учёные-составили
таблицы хорд(первые
тригонометрические таблицы)
Учёные
Индии и Ближнего Востокаположили начало радианной мере угла.
7. Большой вклад в развитие тригонометрии внесли:
• Гиппарх• Птолемей
• Франсуа Виет
• Эйлер
• Бернулли
8.
 ПовторениеА
ПовторениеАsinC=
COS C=
tg C=
?
В
С
9. Повторение
Для единичной полуокружностиy
у
SIN A =
= Y
R
X
1
COS A=
=X
R
В
-1
А
1
х
0 ≤SIN A≤ 1
-1 ≤ COS A ≤1
10. Повторение
Основноетригонометрическое
тождество:
2
SIN
2
X+COS
Х=1
у
А
О
х
12. Угол поворота против часовой стрелки- положительный
Угол поворота против часовой стрелкиположительный УВ
А
О
Х
13. Угол поворота по часовой стрелке — отрицательный
Угол поворота по часовой стрелке отрицательныйУ
А
х
О
В
14. Угол поворота
ПоложительныйОтрицательный
У
У
В
o
700
А
Х
O
А Х
-700
В
15. Из курса геометрии известно:
Мера угла в градусахвыражается числом
от
0
0
до
0
180
16. Ответь на вопрос:
Каким числомможет выражаться
в градусах угол
поворота?
17.
 В Ы В О Д: Угол поворота может выражаться в градусах каким угодно действительным числом от -∞ до +∞
В Ы В О Д: Угол поворота может выражаться в градусах каким угодно действительным числом от -∞ до +∞18. Рассмотрим примеры
УУ
В
1350
О
Х
А
В
1350+3600n
, n=0,1,-1,2,-2…..
О
Х
-1350
А
19. В Ы В О Д Существует бесконечно много углов поворота, при которых начальный радиус ОА переходит в радиус ОВ.
ВЫВОДСуществует бесконечно много углов
поворота, при которых начальный
радиус ОА переходит в радиус ОВ.
В зависимости от того, в какой
координатной четверти
окажется радиус ОВ, угол α
называют углом этой
четверти.
20. З А П О М Н И
ЗАПОМНИ00<α<900 ,то α -угол 1 четверти.
900<α<1800 ,то α – угол 2 четверти.
1800<α<2700 ,то α – угол 3 четверти.
2700<α<3600 ,то α- угол 4 четверти.
21. В ы в о д: Эти углы не относятся ни к какой четверти.
00
±
,±
0
90
0
270
,±
,±
0
180
,
0
360 .
 …
…22. Углом какой четверти является угол β,если:
0β=167
0
β=287
0
β=-65
23. Стр.153.- определение.
ySinα=
X
Cos=
R
y
tgα=
R
X
ctgα=
X
y
24. Лабораторная работа
25. В Ы В О Д: Синус, косинус, тангенс и котангенс не зависят от радиуса.
1.2.
3.
4.
5.
6.
Вычертите три окружности произвольного
радиуса с центром в начале координат.
Постройте начальный радиус ОА.
Поверните начальный радиус на угол α=450
В каждом из случаев найдите SIN 450.
(смотри пример 1. стр.154.)
Какой получился результат? Сделай вывод..
26. Запомни
Sinα, Cosαопределеныпри любом α.
Почему?
27. Стр.154
Прикаком α tgα
не определён?
Почему?
sinα
, cosα ,
tgα , ctgα
–называют
тригонометрическими
функциями.
29. Для единичной окружности:
• Область значениясинуса и косинуса
есть промежуток
[-1;1]
• Область значения
тангенса и
котангенса есть
множество всех
действительных
чисел.

30. Найти синус, косинус,тангенс и котангенс
0270
Проверьте решение на стр.156
•№ 699
•№701
32. Письменно
№705Используй
таблицу стр.155
English Русский Правила
Синусоидальная функция — Графическое упражнение
Синусоидальная функция — Графическое упражнениеПоказать рекламу
Скрыть рекламу
О рекламе
Синусоидальная функция дает очень красивую кривую,
но не верьте нам на слово, сделайте свою!
Синусоидальная функция
Сначала прочтите страницу о синусе, косинусе и тангенсе.
Теперь вы знаете, что синус любого угла равен длине дальней стороны треугольника («противоположная») разделить на длинную сторону («гипотенуза»):
Синус θ = Противоположный / Гипотенуза
Нарисовать треугольники
Чтобы построить график, нам нужно вычислить синус для разных углов, затем нанести эти точки на график и
затем «соединить точки».
Шаг 1. Начертите линии под углом
Поставьте отметку в центре листа бумаги, затем с помощью транспортира отметьте каждые 15 градусов от 0° на 180° по полукругу. Затем поверните транспортир и снова отметьте от 180° до начала. Затем нарисуйте линии, расходящиеся от центра к каждой из ваших меток, чтобы в итоге у вас получилась такая иллюстрация:
Линии под углом 15° (щелкните, чтобы увеличить)
Или вы можете щелкнуть на изображении выше, а затем распечатать результат.
Шаг 2. Начертите и измерьте треугольники
Теперь мы можем превратить каждую из этих линий в треугольник, например:
Измерение треугольников
Когда вы закончите каждый треугольник, останется просто измерить линии . Помните, что синус длина прямой, противоположной углу разделить на гипотенузу (что должно все быть одинаковой длины, если хорошо нарисовали)
Запишите все свои мерки в таблицу. Вот что у меня получилось, но ваши размеры могут отличаться:
Вот что у меня получилось, но ваши размеры могут отличаться:
Уголок | Напротив | Гипотенуза | Противоположный / гипотенуза |
0° | 0 мм | 86 мм | 0,00 |
15° | 22 мм | 86 мм | 0,26 |
30° | 43 мм | 86 мм | 0,50 |
и т. | |||
Здесь можно распечатать готовую для заполнения таблицу.
Важно: когда «противоположная» линия идет вниз, она отрицательна.
Совет: если вы хорошо нарисовали, вы можете воспользоваться симметрией 0-90, 90-180, 180-270 и 270-360.
График результатов
Возьмите миллиметровку и подготовьте ее, уменьшив масштаб от 0 до 360 с шагом 15 по оси x и масштабируя от -1 до +1 по оси Y. Вы можете использовать свою миллиметровую бумагу или распечатать этот график. paper
Теперь нанесите каждую точку из таблицы на график.
Затем соедините точки как можно аккуратнее.
Результат
Результат должен выглядеть примерно так, как показано на графике вверху.
Но вы сделали гораздо больше, чем просто нарисовали красивую кривую. Вы:
- узнали об одной из самых важных функций в математике
- узнал, что вам не обязательно верить тому, что говорят люди — вы можете попробовать это сами.

- имел опыт построения графиков
- узнал, как симметрия может сэкономить усилия
Надеюсь, вам понравилось!
Copyright © 2017 MathsIsFun.com
Синус, косинус и тангенс — объяснение, таблица, примеры решений и часто задаваемые вопросы
Что такое синус, косинус и тангенс?
Дата последнего обновления: 17 апреля 2023 г.
•
Всего просмотров: 243 тыс. тригонометрические функции, связывающие угол прямоугольного треугольника с отношением длин двух сторон. Обратными величинами синуса, косинуса и тангенса являются секанс, косеканс и котангенс соответственно. Каждая из шести тригонометрических функций имеет соответствующие обратные функции (также известные как обратные тригонометрические функции). Тригонометрические функции, также известные как круговые функции, угловые функции или гониометрические функции, широко используются во всех областях науки, связанных с геометрией, таких как навигация, небесная механика, механика твердого тела и т.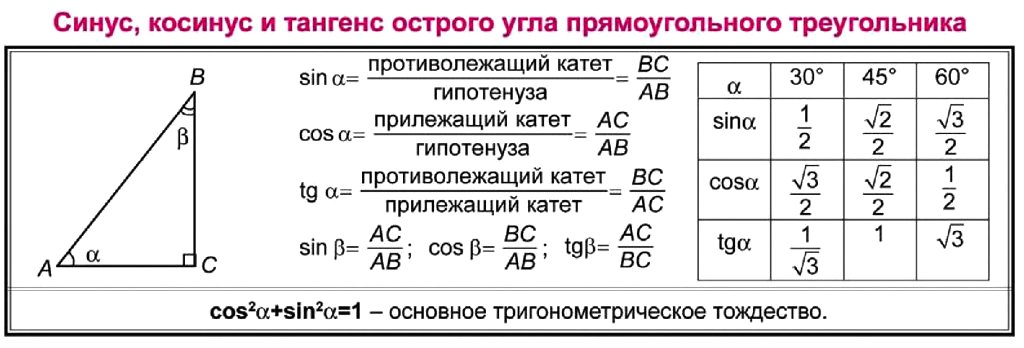 д.
д.
Прочтите ниже, чтобы узнать, что такое функция синуса, функция косинуса и функция тангенса.
Синус Косинус Тангенс Определение
Прямоугольный треугольник включает один угол в 90 градусов и два острых угла. Каждый острый угол прямоугольного треугольника сохраняет свойство синуса косинуса тангенса. Синус, косинус и тангенс острого угла прямоугольного треугольника определяются как отношение двух из трех сторон прямоугольного треугольника.
Как мы знаем, синус, косинус и тангенс основаны на прямоугольном треугольнике, было бы полезно дать имена каждому из треугольников, чтобы избежать путаницы.
(Изображение будет загружено в ближайшее время)
«Сторона гипотенузы» — самая длинная сторона.
«Смежная сторона» — это сторона, следующая за углом θ.
«Противоположная сторона» — сторона, противоположная углу θ.

Соответственно,
Sin θ = Противоположная сторона/Гипотенуза
Cos θ = Прилегающая/Гипотенуза
Tan θ = Противоположная/Прилегающая
Что такое функция синуса?
В прямоугольном треугольнике функция синуса определяется как отношение длины противоположной стороны к длине стороны гипотенузы.
Sin θ = противолежащая сторона/сторона гипотенузы.
(Изображение будет загружено в ближайшее время)
Например, функция синуса треугольника ABC с углом θ выражается как:
Sin θ = a/c
Что такое функция косинуса?
В прямоугольном треугольнике функция косинуса определяется как отношение длины прилежащей стороны к длине стороны гипотенузы.
Cos θ = смежная сторона/сторона гипотенузы
Пример:
Учитывая рисунок, приведенный выше, функция косинуса треугольника ABC с углом θ выражается как:
Cos θ = b/c
Что такое функция касательной?
В прямоугольном треугольнике функция касательной определяется как отношение длины противоположной стороны к длине прилежащей стороны.
Tan θ = Противоположная сторона/Смежная сторона
Пример:
Учитывая рисунок, приведенный выше, функция косинуса треугольника ABC с углом θ выражается как:
Tan θ = a/b
Синус Косинус Тангенс Таблица
Значения тригонометрических соотношений, таких как синус, косинус и тангенс, для некоторых стандартных углов, таких как 0°, 30°, 45°, 60° и 90 ° можно легко определить с помощью таблицы синус-косинус-тангенса, приведенной ниже. Эти значения очень важны для решения тригонометрических задач. Следовательно, важно знать значения тригонометрических отношений этих стандартных углов.
Приведенная ниже таблица синусов, косинусов и тангенсов включает значения стандартных углов, таких как 0°, 30°, 45°, 60° и 90°.
Таблица синусов, косинусов и тангенсов
Углы в градусах | 0° | 30° | 45° 1 90 61 | 90° | ||
Sin | 0 | 1/2 | 1/√2 | √3/2 | 1 | 1 | √3/2 | 1/√2 | 1/2 | 0 |
Желто-коричневый 003 | 1/√3 | 1 | √3 | Не определено |
Знаете ли вы?
Синус и косинус были введены Арьябхаттой, тогда как функция тангенса была введена Мухаммадом ибн Мусой аль-Хорезми (782 г.
 н.э. — 850 г. н.э.).
н.э. — 850 г. н.э.).Формулы синуса, косинуса и тангенса можно легко выучить с помощью SOHCATOA. Поскольку синус — это сторона, противоположная стороне гипотенузы, косинус — сторона, примыкающая к стороне гипотенузы, а тангенс — сторона, противоположная стороне, примыкающей к стороне.
Решенные примеры:
1. Найдите Cos θ относительно следующего треугольника.
Ответ: Чтобы найти Cos θ, нам нужны и прилежащая сторона, и гипотенуза.
(Изображение будет загружено в ближайшее время)
Прилегающая сторона в приведенном выше треугольнике равна BC = 8 см
Но сторона гипотенузы, т.е. AC, не указана.
Чтобы найти сторону гипотенузы, воспользуемся теоремой Пифагора
AC² = AB² + BC² = 6² + 8² = 100
= 4/5
Следовательно, Cos θ = 4/5
2.

 \circ\). Найдите боковые стороны.
\circ\). Найдите боковые стороны.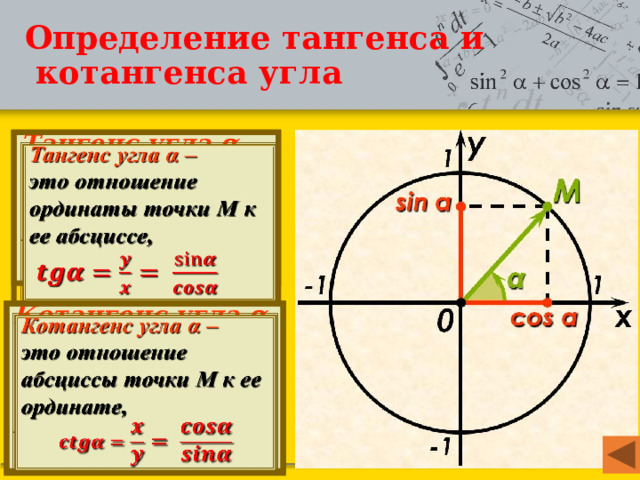 д. …
д. …

 н.э. — 850 г. н.э.).
н.э. — 850 г. н.э.).