Определение параллелограмма и его свойства: Параллелограмм — урок. Геометрия, 8 класс.

\circ}\)

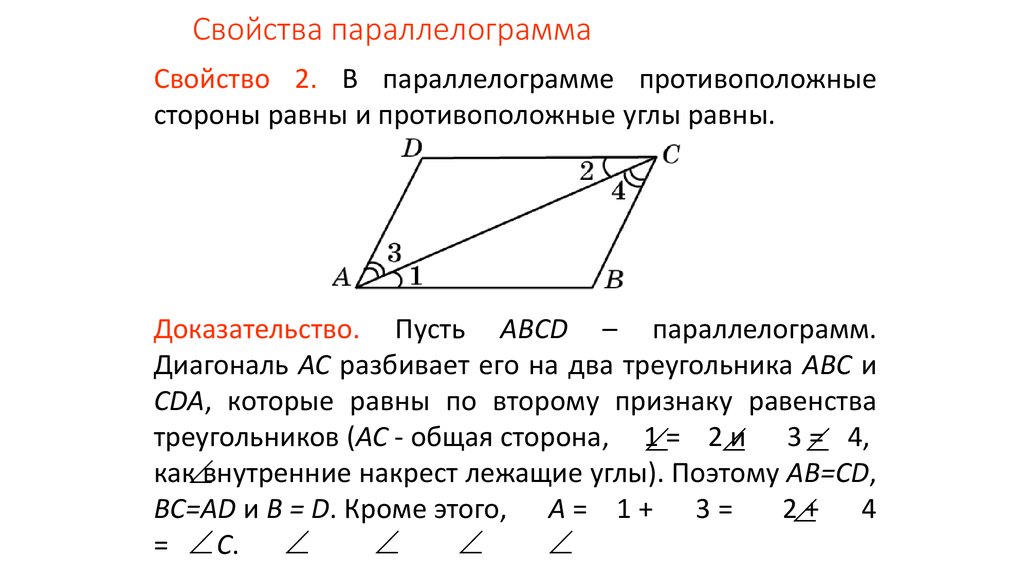
4. Из параллельности сторон вытекает равенство частей углов. Например:

\(\angle DAC = \angle BCA\)

\(\angle CBD = \angle BDA\)

5. Две диагонали делят параллелограмм на две пары равных (по стороне и двум углам) треугольников:

\(\mathrm{\Delta}ABC = \mathrm{\Delta}BCD\)

\(\mathrm{\Delta}ABD = \mathrm{\Delta}ACD\)

6. Диагонали параллелограмма точкой пересечения делятся пополам:

\(AO = OC\)

\(BO = OD\)

Также параллелограмм обладает необычными свойствами, связанные с биссектрисами:

Пусть AL и СК – биссектрисы противоположных углов, а ВМ – биссектриса смежного с ними угла.

Тогда:

1. Биссектрисы противоположных углов параллельны:

\(AL\ ||\ CK\)

2. Биссектрисы смежных углов перпендикулярны:

\(AL,\ CK\bot BM\)

3. Биссектриса параллелограмма отсекает от него два равных угла. Например:

\(\mathrm{\Delta}ABL\ — \ равнобедренный,\ т.к.\ \angle BAL = \angle BLA\)

\(\mathrm{\Delta}ABM\ — \ равнобедренный,\ т. к.\ \angle ABM = \angle AMB\)

ПРИЗНАКИ ПАРАЛЛЕЛОГРАММА:

Для того, чтобы доказать, что фигура действительно является параллелограммом, нужно знать, какими свойствами мы можем пользоваться. Четырехугольник ABCD будет параллелограммом, если выполняется хотя бы одно из следующих условий:

1. Четырехугольник имеет две пары параллельных сторон:

\(AB\ ||\ CD\)

\(BC\ ||\ AD\)

2. Четырехугольник имеет пару параллельных и равных сторон:

\(AB\ ||\ CD,\ AB = CD\)

\(или\)

\(BC\ ||\ AD,\ BC = AD\)

3. В четырехугольнике противоположные стороны попарно равны:

\(AB = CD\)

\(BC = AD\)

4. В четырехугольнике противоположные углы попарно равны:

\(\angle DAB = \angle BCD\)

\(\angle ABC = \angle CDA\)

5. В четырехугольнике диагонали точкой пересечения делятся пополам:

\(AO = OC\)

\(BO = OD\)

6. Сумма углов четырехугольника, прилегающих к любой стороне, равна 180°:

\(\angle ABC + \angle BCD = \angle BCD + \angle CDA = \angle CDA + \angle DAB = \angle DAB + \angle ABC = 180{^\circ}\)

ПЛОЩАДЬ ПАРАЛЕЛОГРАММА:

1.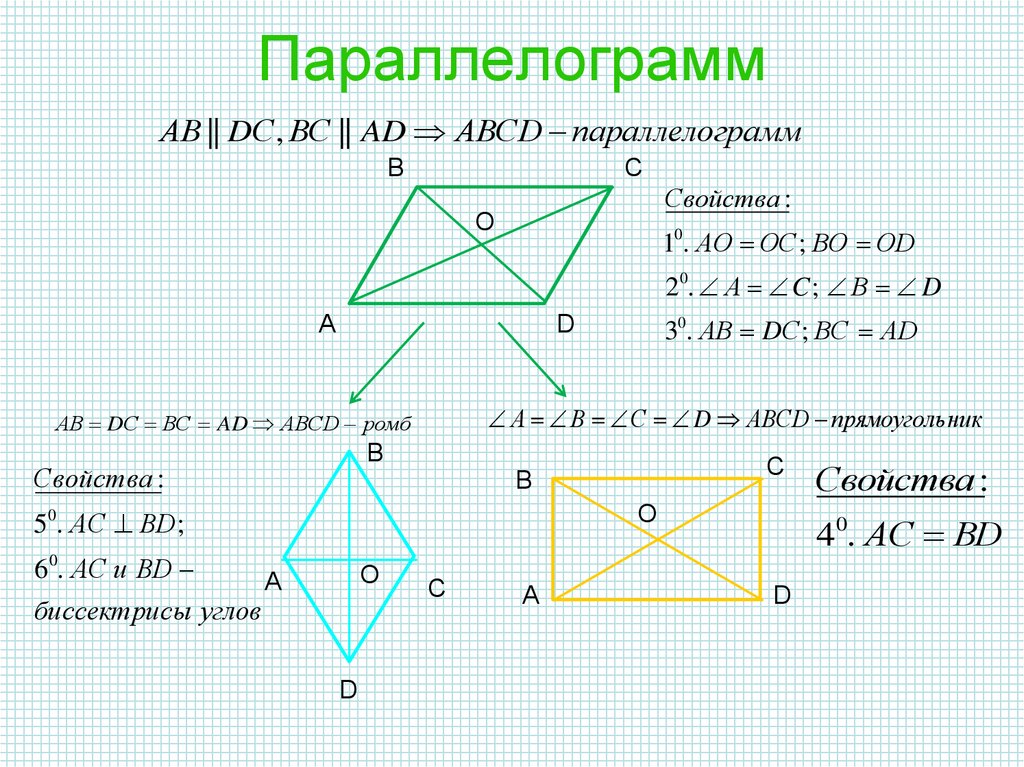 Через высоту и сторону

Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне.

\(S = ah_{1} = bh_{2}\)

2. Через две стороны и угол между ними

Площадь параллелограмма равна произведению его сторон на синус угла между ними.

\(S = ab \bullet \sin\alpha\)

3. Через диагонали и угол между ними

Площадь параллелограмма равна половине произведения его диагоналей на синус угла между ними.

\(S = \frac{1}{2}d_{1}d_{2} \bullet \sin\gamma\)

Какие свойства параллелограмма включены в его определение. Исследовательский проект «параллелограмм и его свойства»

Для того, чтобы определить является ли данная фигура параллелограммом существует ряд признаков. Рассмотрим три основных признака параллелограмма.

1 признак параллелограмма

Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник будет являться параллелограммом.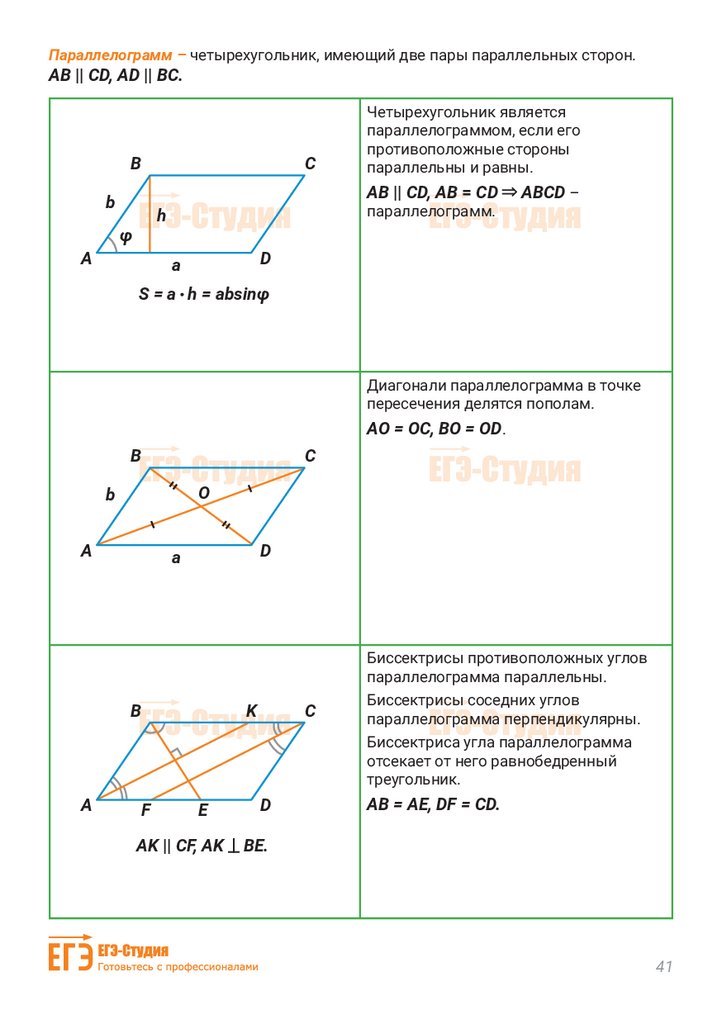

Доказательство:

Рассмотрим четырехугольник ABCD. Пусть в нем стороны AB и СD параллельны. И пусть AB=CD. Проведем в нем диагональ BD. Она разделит данный четырехугольник на два равных треугольника: ABD и CBD.

Эти треугольники равны между собой по двум сторонам и углу между ними (BD — общая сторона, AB = CD по условию, угол1 = угол2 как накрест лежащие углы при секущей BD параллельных прямых AB и CD.), а следовательно угол3 = угол4.

А эти углы будут являться накрест лежащими при пересечении прямых BC и AD секущей BD. Из этого следует что BC и AD параллельны между собой. Имеем, что в четырехугольнике ABCD противоположные стороны попарно параллельны, и, значит, четырехугольник ABCD является параллелограммом.

2 признак параллелограмма

Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник будет параллелограммом.

Доказательство:

Рассмотрим четырехугольник ABCD. Проведем в нем диагональ BD. Она разделит данный четырехугольник на два равных треугольника: ABD и CBD.

Эти два треугольника буду равны между собой по трем сторонам (BD — общая сторона, AB = CD и BC = AD по условию). Из этого можно сделать вывод, что угол1 = угол2. Отсюда следует, что AB параллельна CD. А так как AB = CD и AB параллельна CD, то по первому признаку параллелограмма, четырехугольник ABCD будет являться параллелограммом.

3 признак параллелограмма

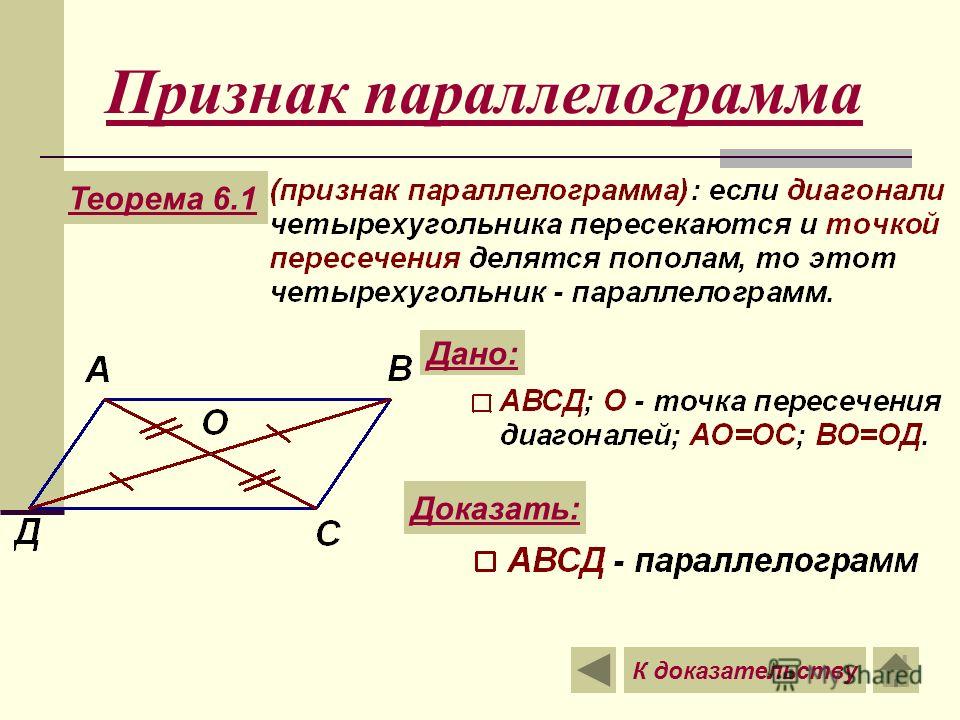
Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник будет являться параллелограммом.

Рассмотрим четырехугольник ABCD. Проведем в нем две диагонали AC и BD, которые будут пересекаться в точке О и делятся этой точкой пополам.

Треугольники AOB и COD будут равны между собой, по первому признаку равенства треугольников. (AO = OC, BO = OD по условию, угол AOB = угол COD как вертикальные углы.) Следовательно, AB = CD и угол1 = угол 2. Из равенства углов 1 и 2 имеем, что AB параллельна CD. Тогда имеем, что в четырехугольнике ABCD стороны AB равны CD и параллельны, и по первому признаку параллелограмма четырехугольник ABCD будет являться параллелограммом.

Конспект урока.

Алгебра 8 класс

Учитель Сысой А.К.

Школа 1828

Тема урока: «Параллелограмм и его свойства»

Тип урока: комбинированный

Цели урока:

1) Обеспечить усвоение нового понятия – параллелограмм и его свойств

2) Продолжить развитие навыков и умений решения геометрических задач;

3) Развитие культуры математической речи

План урока:

1. Организационный момент

(Слайд 1)

На слайде демонстрируется высказывание Льюиса Кэрролла. Ученикам сообщается о цели урока. Проверяется готовность учеников к уроку.

2. Актуализация знаний

(Слайд 2)

На доске задачи для устной работы. Учитель предлагает ученикам подумать над этими задачами и поднять руку тем, кто понял, как задачу решать. После решения двух задач, на доказательство теоремы о сумме углов вызывается к доске ученик, который самостоятельно делает дополнительные построения на чертеже и доказывает устно теорему.

Учениками используется формула суммы углов многоугольника:

3. Основная часть

(Слайд 3)

На доске определение параллелограмма. Учитель говорит о новой фигуре и формулирует определение, делая с помощью чертежа необходимые пояснения. Затем на клетчатой части презентации, с помощью маркера и линейки, показывает, как можно рисовать параллелограмм (возможно несколько случаев)

(Слайд 4)

Учитель формулирует первое свойство параллелограмма. Предлагает ученикам сказать, по рисунку, что дано и что необходимо доказать. После этого на доске появляется дано задачи. Ученики догадываются (может быть при помощи учителя) что искомые равенства надо доказать через равенства треугольников, которые можно получить проведя диагональ (на доске появляется диагональ).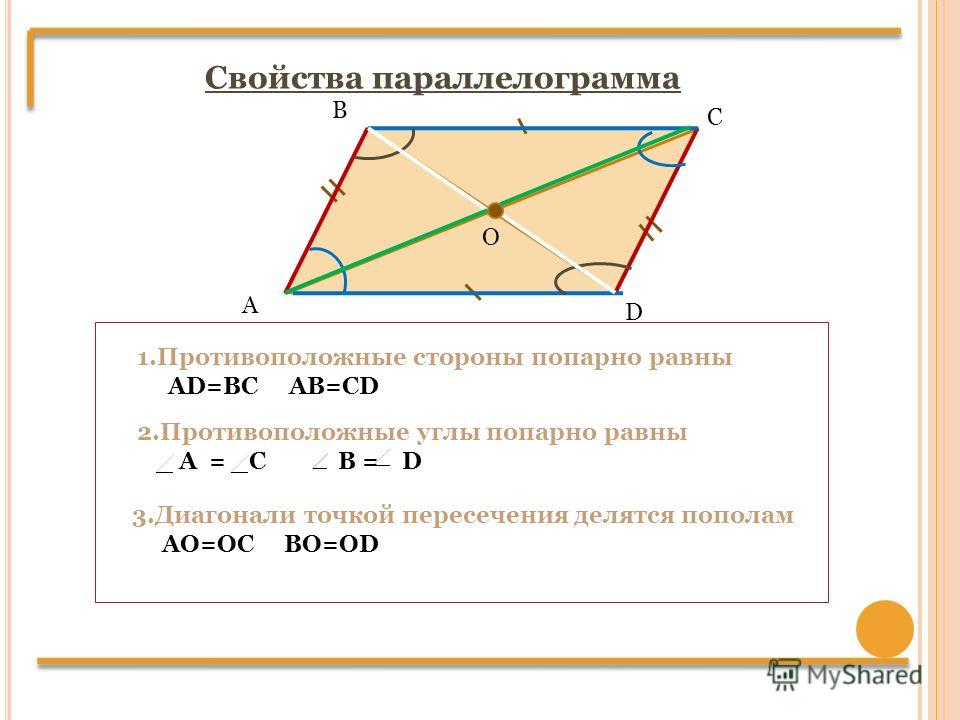 Далее ученики догадываются почему треугольники равны и называют признак равенства треугольников (появляется соответствующая форма). Устно сообщают факты, которые необходимы для равенства треугольников (по мере того как они их называют, появляется соответствующая визуализация). Далее ученики формулируют свойство равных треугольников, оно появляется в виде пункта 3 доказательства и затем самостоятельно завершают доказательство теоремы устно.

(Слайд 5)

Учитель формулирует второе свойство параллелограмма. На доске появляется рисунок параллелограмма. Учитель предлагает по рисунку сказать что дано, что необходимо доказать. После того как ученики правильно сообщают о том, что дано и что необходимо доказать, появляется условие теоремы. Ученики догадываются, что равенство частей диагоналей можно доказать через равенство треугольников AOB и COD . С помощью предыдущего свойства параллелограмма догадываются о равенстве сторон AB и CD . Затем понимают, что надо найти равные углы и с помощью свойств параллельных прямых доказывают равенство прилежащих к равным сторонам углов. Данные этапы визуализируются на слайде. Из равенства треугольников следует и истинность теоремы – проговаривают ученики на слайде появляется соответствующая визуализация.

(Слайд 6)

Учитель формулирует третье свойство параллелограмма. В зависимости от времени, которое остаётся до конца урока, учитель может дать возможность ученикам самостоятельно доказать это свойство, или ограничится его формулировкой, а само доказательство оставить ученикам в качестве домашней работы. Доказательство может опираться на сумму углов вписанного многоугольника, которая повторялась в начале урока, или на сумму внутренних односторонних углов при двух параллельных прямых AD и BC , и секущей, например AB .

4. Закрепление материала

На этом этапе учащиеся, используя ранее изученные теоремы, решают задачи. Идеи к решению задачи подбирают ученики самостоятельно. Так как возможных вариантов оформления немало и все они зависят от того каким образом ученики будут искать решение задачи, визуализации решения задач нет, а ученики самостоятельно оформляют каждый этап решения на отдельной доске с записью решения в тетрадь.

(Слайд 7)

Появляется условие задачи. Учитель предлагает по условию сформулировать «Дано». После того, как ученики, верно составят краткую запись условия на доске появляется «Дано». Ход решения задачи может выглядеть следующим образом:

Проведём высоту BH (визуализировано)

Треугольник AHB – прямоугольный. Угол A равен углу C и равен 30 0 (по свойству о противоположных углах в параллелограмме). 2BH =AB (по свойству катета, лежащего напротив угла в 30 0 в прямоугольном треугольнике). Значит AB = 13 см.

AB = CD , BC = AD (по свойству противоположных сторон в параллелограмме) Значит AB =CD =13см. Так как периметр параллелограмма равен 50 см, то BC =AD =(50 – 26):2=12см.

Ответ: AB = CD = 13 см, BC = AD = 12 см.

(Слайд 8)

Появляется условие задачи. Учитель предлагает по условию сформулировать «Дано». После появляется «Дано» на экране. С помощью красных линий выделяется четырёхугольник, про который нужно доказать, что он параллелограмм.

Ход решения задачи может выглядеть следующим образом:

Т.к. BK и MD перпендикуляры к одной прямой, то прямы BK и MD параллельны.

Через смежные углы можно показать, что сумма внутренних односторонних углов при прямых BM и KD и секущей MD равна 180 0 . Поэтому данные прямые параллельны.

Так как у четырехугольника BMDK противоположные стороны попарно параллельны, то данный четырехугольник параллелограмм.

5. Окончание урока. Поведение итогов.

(Слайд 8)

На слайде появляются вопросы по новой теме, на которые ученики отвечают.

Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны. На следующем рисунке представлен параллелограмм ABCD. У него сторона AB параллельна стороне CD, а сторона BC параллельна стороне AD.

Как вы уже успели догадаться, параллелограмм является выпуклым четырехугольником. Рассмотрим основные свойства параллелограмма.

Свойства параллелограмма

1. В параллелограмме противоположные углы и противоположные стороны равны. Докажем это свойство — рассмотрим параллелограмм, представленный на следующем рисунке.

Диагональ BD разделяет его на два равных треугольника: ABD и CBD. Они равны по стороне BD и двум прилежащим к ней углам, так как углы накрест лежащие при секущей BD параллельных прямых BC и AD и AB и CD соответственно. Следовательно, AB = CD и
BC = AD. А из равенства углов 1, 2 ,3 и 4 следует, что угол A = угол1 +угол3 = угол2 + угол4 = угол С.

2. Диагонали параллелограмма точкой пересечения делятся пополам. Пусть точка О есть точка пересечения диагоналей AC и BD параллелограмма ABCD.

Тогда треугольник AOB и треугольник COD равны между собой, по стороне и двум прилежащим к ней углам. (AB=CD так как это противоположные стороны параллелограмма. А угол1 = угол2 и угол3 = угол4 как накрест лежащие углы при пересечении прямых AB и CD секущими AC и BD соответственно.) Из этого следует, что AO = OC и OB = OD, что и требовалось доказать.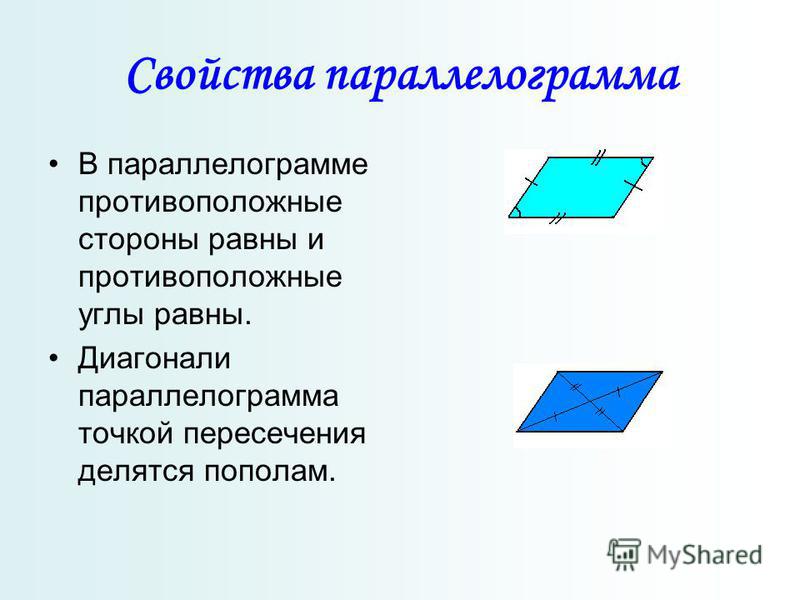

Все основные свойства проиллюстрированы на следующих трех рисунках.

Как в евклидовой геометрии точка и прямая — главные элементы теории плоскостей, так и параллелограмм является одной из ключевых фигур выпуклых четырехугольников. Из него, как нитки из клубка, втекают понятия «прямоугольника», «квадрата», «ромба» и других геометрических величин.

Вконтакте

Определение параллелограмма

Выпуклый четырехугольник, состоящий из отрезков, каждая пара из которых параллельна, известен в геометрии как параллелограмм.

Как выглядит классический параллелограмм изображает четырехугольник ABCD. Стороны называются основаниями (AB, BC, CD и AD), перпендикуляр, проведенный из любой вершины на противоположную этой вершине сторону, — высотой (BE и BF), линии AC и BD — диагоналями.

Внимание! Квадрат, ромб и прямоугольник — это частные случаи параллелограмма.

Стороны и углы: особенности соотношения

Ключевые свойства, по большому счету, предопределены самим обозначением , их доказывает теорема.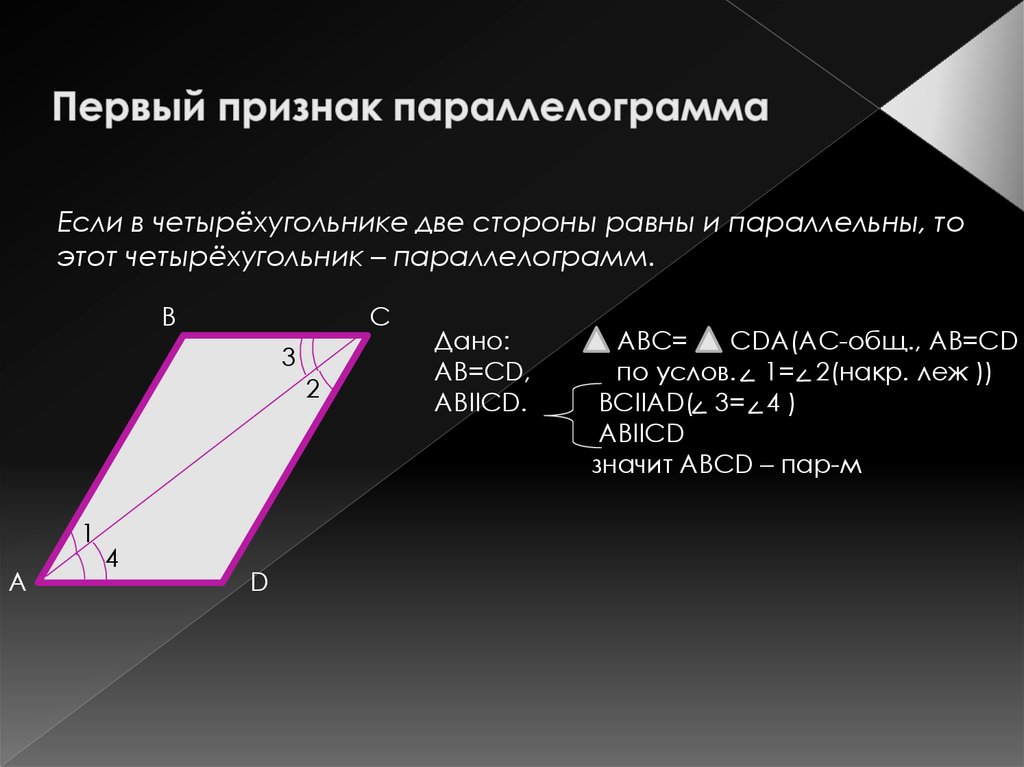 Эти характеристики следующие:

1. Стороны, которые являются противоположными, — попарно одинаковые.
2. Углы, расположенные противоположно друг другу — попарно равны.

Доказательство: рассмотрим ∆ABC и ∆ADC, которые получаются вследствие разделения четырехугольника ABCD прямой AC. ∠BCA=∠CAD и ∠BAC=∠ACD, поскольку AC для них общая (вертикальные углы для BC||AD и AB||CD, соответственно). Из этого следует: ∆ABC = ∆ADC (второй признак равенства треугольников).

Отрезки AB и BC в ∆ABC попарно соответствуют линиям CD и AD в ∆ADC, что означает их тождество: AB = CD, BC = AD. Таким образом, ∠B соответствует ∠D и они равны. Так как ∠A=∠BAC+∠CAD, ∠C=∠BCA+∠ACD, которые так же попарно одинаковые, то ∠A = ∠C. Свойство доказано.

Характеристики диагоналей фигуры

Основной признак этих линий параллелограмма: точка пересечения разделяет их пополам.

Доказательство: пусть т. Е — это точка пересечения диагоналей AC и BD фигуры ABCD. Они образуют два соизмеримых треугольника — ∆ABE и ∆CDE.

AB=CD, так как они противоположные. Согласно прямых и секущей, ∠ABE = ∠CDE и ∠BAE = ∠DCE.

По второму признаку равенства ∆ABE = ∆CDE. Это означает, что элементы ∆ABE и ∆CDE: AE = CE, BE = DE и при этом они соразмерные части AC и BD. Свойство доказано.

Особенности смежных углов

У смежных сторон сумма углов равна 180° , поскольку они лежат по одну сторону параллельных линий и секущей. Для четырехугольника ABCD:

∠A+∠B=∠C+∠D=∠A+∠D=∠B+∠C=180º

Свойства биссектрисы:

1. , опущенные на одну сторону, являются перпендикулярными;
2. противолежащие вершины имеют параллельные биссектрисы;
3. треугольник, полученный проведением биссектрисы, будет равнобедренным.

Определение характерных черт параллелограмма по теореме

Признаки этой фигуры вытекают из ее основной теоремы, которая гласит следующее: четырехугольник считается параллелограммом в том случае, если его диагонали пересекаются, а эта точка разделяет их на равные отрезки.

Доказательство: пусть в т. Е прямые AC и BD четырехугольника ABCD пересекаются. Так как ∠AED = ∠BEC, а AE+CE=AC BE+DE=BD, то ∆AED = ∆BEC (по первому признаку равенства треугольников). То есть ∠EAD = ∠ECB. Они также являются внутренними перекрестными углами секущей AC для прямых AD и BC. Таким образом, по определению параллельности — AD || BC. Аналогичное свойство линий BC и CD выводится также. Теорема доказана.

Вычисление площади фигуры

Площадь этой фигуры находится несколькими методами, одним из самых простых: умножения высоты и основания, к которому она проведена.

Доказательство: проведем перпендикуляры BE и CF из вершин B и C. ∆ABE и ∆DCF — равные, поскольку AB = CD и BE = CF. ABCD — равновеликий с прямоугольником EBCF, так как они состоят и соразмерных фигур: S ABE и S EBCD , а также S DCF и S EBCD . Из этого следует, что площадь этой геометрической фигуры находится так же как и прямоугольника:

S ABCD = S EBCF = BE×BC=BE×AD.

Для определения общей формулы площади параллелограмма обозначим высоту как hb , а сторону — b .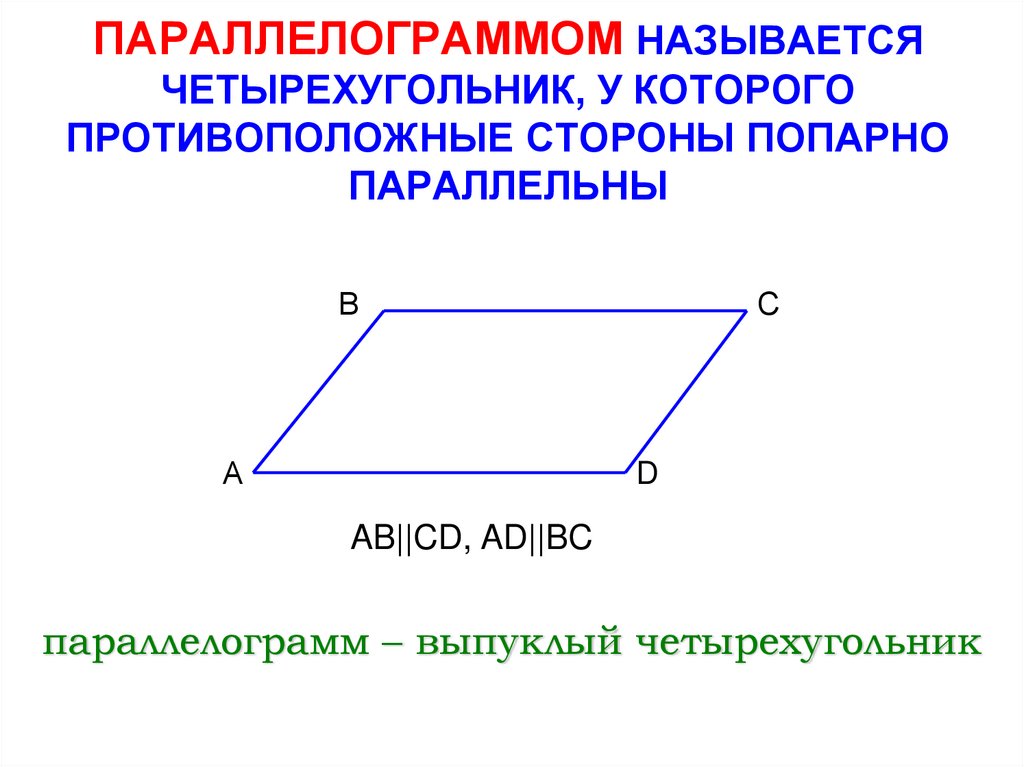 Соответственно:

Другие способы нахождения площади

Вычисления площади через стороны параллелограмма и угол , который они образуют, — второй известный метод.

,

Sпр-ма — площадь;

a и b — его стороны

α — угол между отрезками a и b.

Этот способ практически основывается на первом, но в случае, если неизвестна. всегда отрезает прямоугольный треугольник, параметры которого находятся тригонометрическими тождествами, то есть . Преобразуя соотношение, получаем . В уравнении первого способа заменяем высоту этим произведением и получаем доказательство справедливости этой формулы.

Через диагонали параллелограмма и угол, который они создают при пересечении, также можно найти площадь.

Доказательство: AC и BD пересекаясь, образуют четыре треугольника: ABE, BEC, CDE и AED. Их сумма равна площади этого четырехугольника.

Площадь каждого из этих ∆ можно найти за выражением , где a=BE, b=AE, ∠γ =∠AEB. Поскольку , то в расчетах используется единое значение синуса.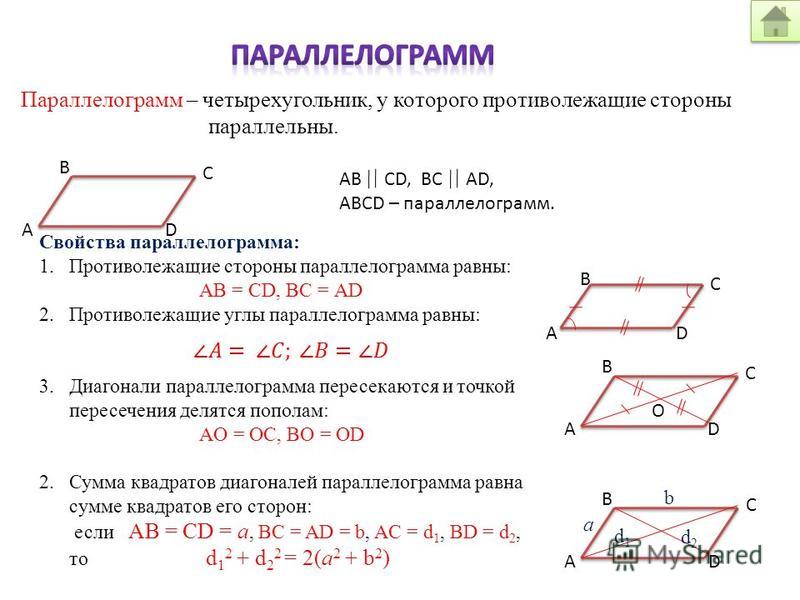 То есть . Поскольку AE+CE=AC= d 1 и BE+DE=BD= d 2 , формула площади сводится до:

.

Применение в векторной алгебре

Особенности составляющих частей этого четырехугольника нашли применение в векторной алгебре, а именно: сложении двух векторов. Правило параллелограмма утверждает, что если заданные векторы и не коллинеарны, то их сумма будет равна диагонали этой фигуры, основания которой соответствуют этим векторам.

Доказательство: из произвольно выбранного начала — т. о. — строим векторы и . Далее строим параллелограмм ОАСВ, где отрезки OA и OB — стороны. Таким образом, ОС лежит на векторе или сумме .

Формулы для вычисления параметров параллелограмма

Тождества приведены при следующих условиях:

1. a и b, α — стороны и угол между ними;
2. d 1 и d 2 , γ — диагонали и в точке их пересечения;
3. h a и h b — высоты, опущенные на стороны a и b;

Параметр	Формула
Нахождение сторон
по диагоналям и косинусу угла между ними
по диагоналям и стороне
через высоту и противоположную вершину
Нахождение длины диагоналей
по сторонам и величине вершины между ними

Это четырёхугольник, противоположные стороны которого попарно параллельны.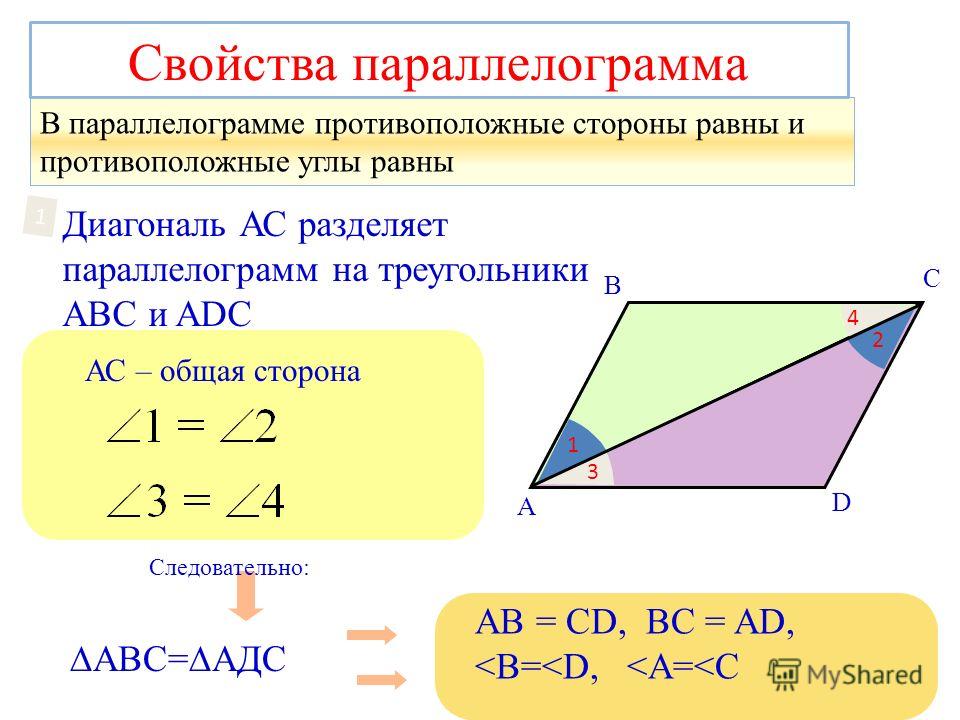

Свойство 1 . Любая диагональ параллелограмма делит его на два равных треугольника.

Доказательство . По II признаку (накрест лежащие углы и общая сторона).

Теорема доказана .

Свойство 2 . В параллелограмме противолежащие стороны равны, противолежащие углы равны.

Доказательство .
Аналогично,

Теорема доказана .

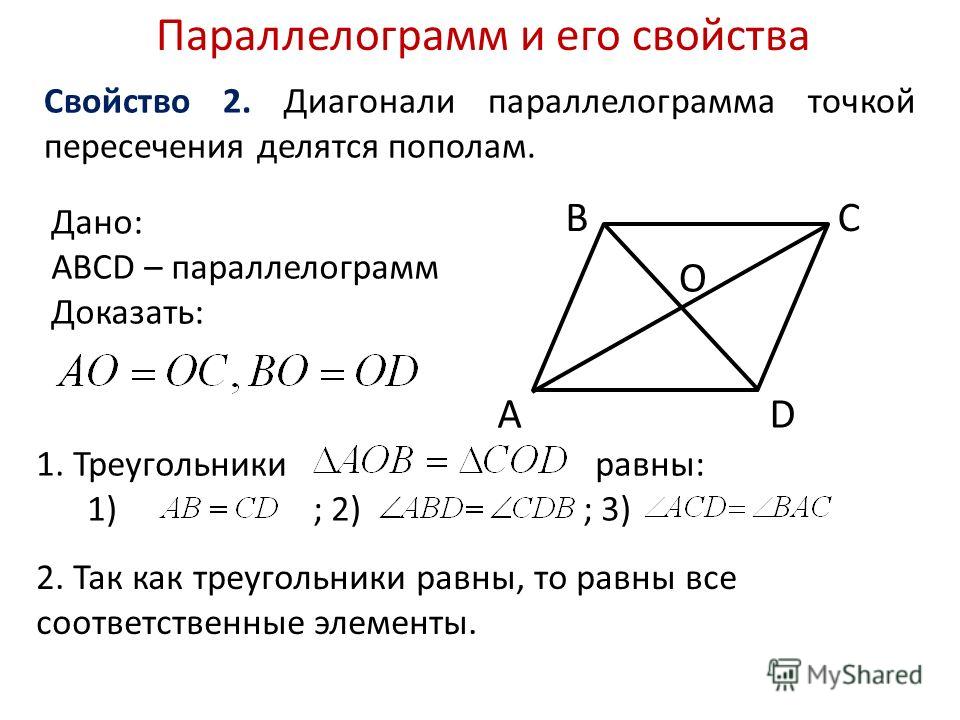
Свойство 3. В параллелограмме диагонали точкой пересечения делятся пополам.

Доказательство .

Теорема доказана .

Свойство 4 . Биссектриса угла параллелограмма, пересекая противоположную сторону, делит его на равнобедренный треугольник и трапецию. (Ч. сл. — вершину — два равнобедренных?-ка).

Доказательство .

Теорема доказана .

Свойство 5 . В параллелограмме отрезок с концами на противоположных сторонах, проходящий через точку пересечения диагоналей, делится этой точкой пополам.

Доказательство .

Теорема доказана .

Свойство 6 . Угол между высотами, опущенными из вершины тупого угла параллелограмма, равен острому углу параллелограмма.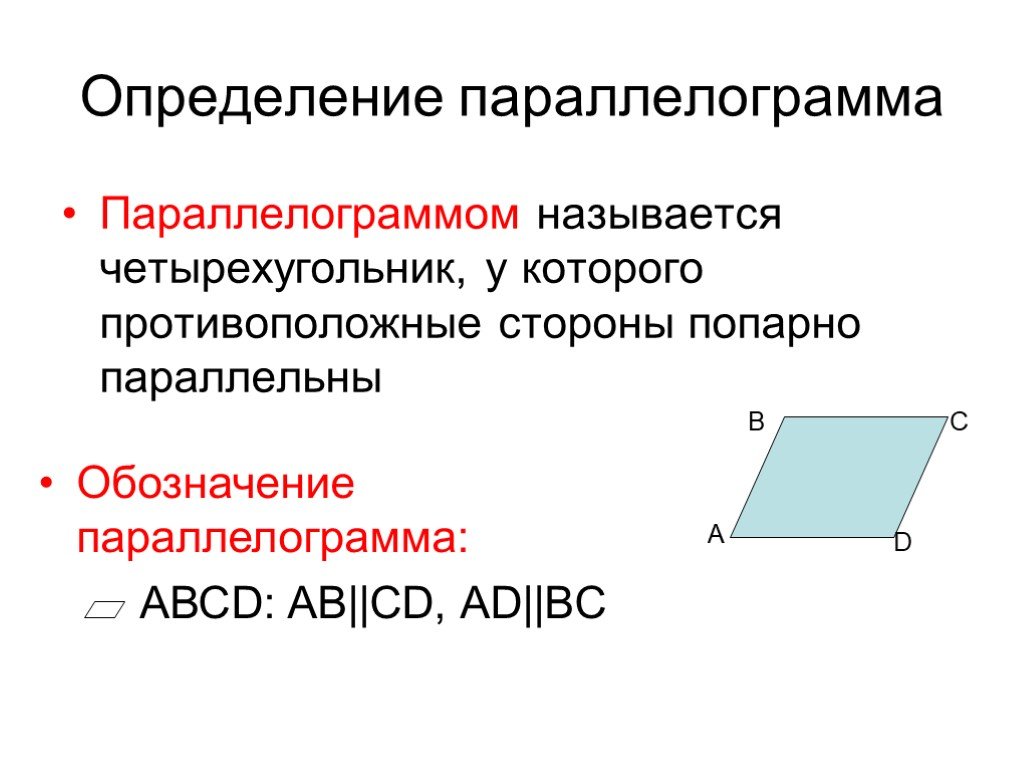

Доказательство .

Теорема доказана .

Свойство 7 . Сумма углов параллелограмма, прилежащих к одной стороне, равна 180°.

Доказательство .

Теорема доказана .

Построение биссектрисы угла. Свойства биссектрисы угла треугольника.

1) Построить произвольный луч DE.

2) На данном луче построить произвольную окружность с центром в вершине и такую же
с центром в начале построенного луча.

3) F и G — точки пересечения окружности со сторонами данного угла, H — точка пересечения окружности с построенным лучом

Построить окружность с центром в точке H и радиусом, равным FG.

5) I — точка пересечения окружностей построенного луча.

6) Провести прямую через вершину и I.

IDH — требуемый угол.
)

Свойство 1 . Биссектриса угла треугольника разбивает противоположную сторону пропорционально прилежащим сторонам.

Доказательство . Пусть x, y-отрезки стороны c. Продолжим луч BC. На луче BC отложим от C отрезок CK, равный AC.

6 Свойства параллелограмма | Что такое параллелограмм

Содержание

Этот пост также доступен в: हिन्दी (хинди)

Слово «параллелограмм» происходит от греческого слова « parallelogrammon », что означает «ограниченный параллельными линиями». Параллелограмм – это четырехугольник, ограниченный параллельными прямыми. Это двумерная фигура, в которой противоположные стороны параллельны и равны.

Существует три типа параллелограммов – квадрат, прямоугольник и ромб, и каждый из них имеет свои уникальные свойства.

Давайте разберемся, что такое параллелограмм и свойства параллелограмма.

Что такое параллелограмм?

Параллелограмм — это особый тип четырехугольника, образованный параллельными прямыми. В параллелограмме обе пары противоположных сторон параллельны и равны. Следовательно, параллелограмм определяется как четырехугольник, в котором обе пары противоположных сторон параллельны и равны.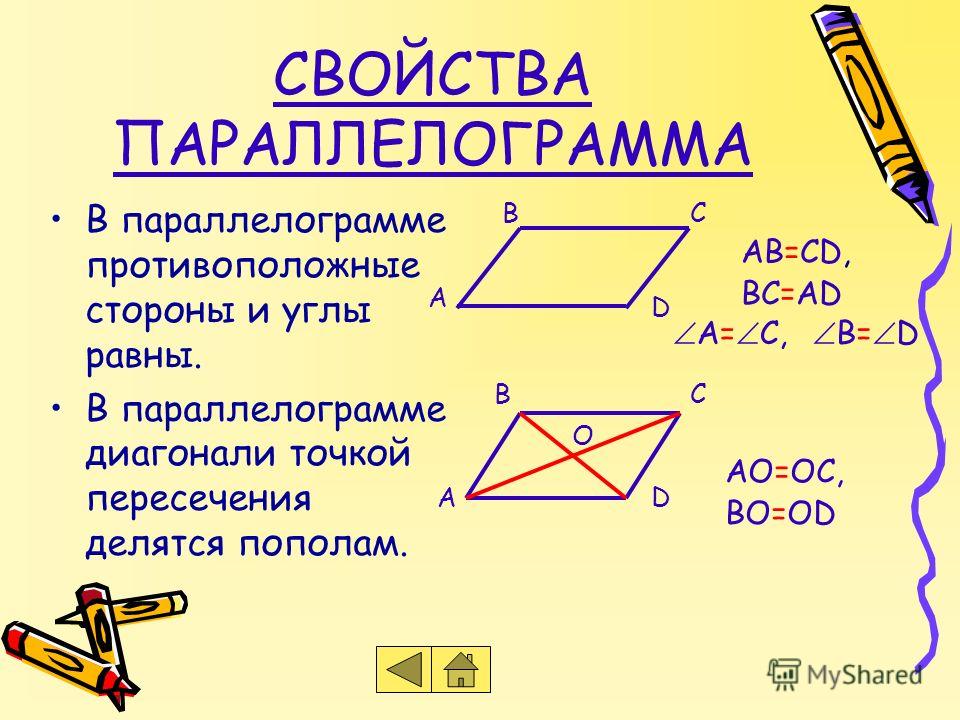

На приведенном выше рисунке показаны три типа параллелограммов.

• Прямоугольник
• Квадрат
• Ромб

Свойства параллелограмма

Ниже приведены основные свойства параллелограммов, которые помогут вам их идентифицировать.

• Противоположные стороны параллелограмма параллельны. Здесь $\text{AB} ‖ \text{CD}$ и $\text{BC} ‖ \text{DA}$.
• Противоположные стороны параллелограмма равны. На приведенном выше рисунке $\text{AB} = \text{CD}$ и $\text{BC} = \text{DA}$.
• Противоположные углы параллелограмма равны. Здесь $\angle \text{A} = \angle \text{C}$ и $\angle \text{B} = \angle \text{D}$ 9{\circ}$.
• Диагонали делят параллелограмм на два равных треугольника. Здесь $\triangle \text{ABD} \cong \triangle \text{BCD}$ и $\triangle \text{ABC} \cong \triangle \text{ACD}$.

СКАЧАТЬ БЕСПЛАТНО КАРТОЧКИ ПО МАТЕМАТИКЕ:

Красиво оформленные карточки для печати, которые помогут вам запомнить все важные математические понятия и формулы.

Диагонали параллелограмма равны

Диагонали параллелограмма делят его на два конгруэнтных треугольника, т. е. в параллелограмме $\text{ABCD}$ $\triangle \text{ABD} \cong \triangle \text{ BCD}$ и $\triangle \text{ABC} \cong \triangle \text{ACD}$.

Давайте посмотрим, как доказать приведенное выше утверждение.

Поскольку $\text{ABCD}$ — параллелограмм, противоположные стороны равны.

Следовательно, $\text{AB} = \text{CD}$ и $\text{BC} = \text{DA}$.

Теперь в $\triangle \text{ABD}$ и $\triangle \text{CBD}$

$\text{AB} = \text{CD}$ (противоположные стороны параллелограмма)

$\ text{DA} = \text{BC}$ (Противоположные стороны параллелограмма)

$\text{BD} = \text{BD}$ (общий)

Таким образом, $\triangle \text{ABD} \cong \triangle \text{CBD}$ (критерий конгруэнтности SSS).

Следовательно, можно сказать, что диагональ параллелограмма делит его на два равных треугольника.

Противоположные стороны параллелограмма равны

Противоположные стороны параллелограмма равны, т.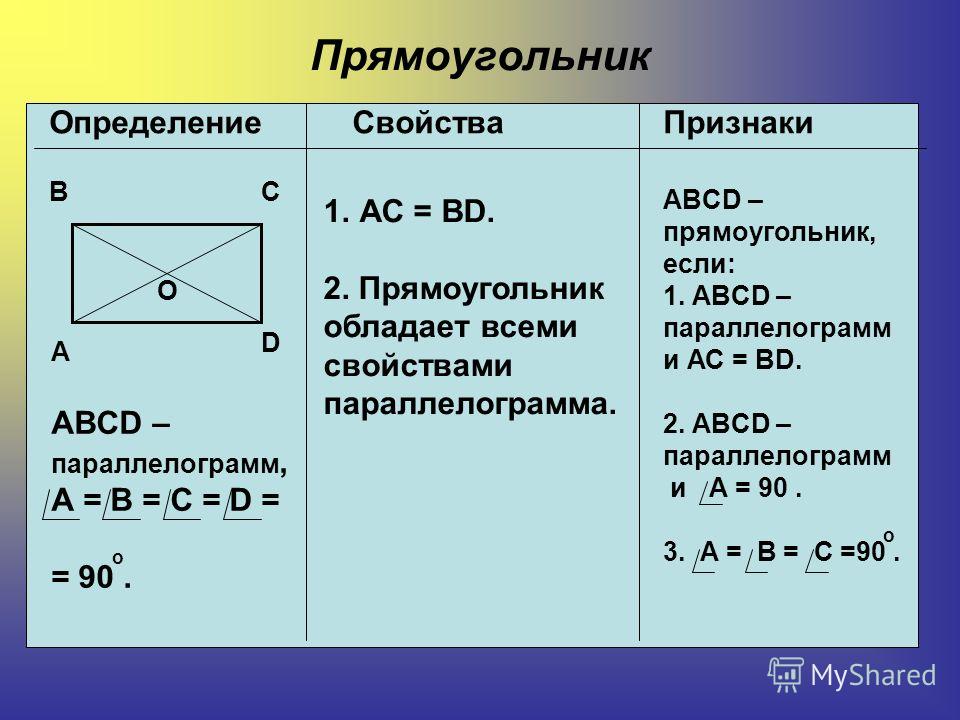 е. в параллелограмме $text{ABCD}$ $\text{AB} = \text{CD}$ и $\text {BC} = \text{DA}$.

Давайте посмотрим, как доказать приведенное выше утверждение.

На приведенном выше рисунке $\text{ABCD}$ — параллелограмм, а $\text{AC}$ — одна из диагоналей.

Диагональ $\text{AC}$ делит параллелограмм $\text{ABCD}$ на два треугольника: $\triangle \text{ABC}$ и $\triangle \text{ABC}$.

Чтобы доказать, что противоположные стороны равны, т. е. $\text{AB} = \text{CD}$ и $\text{BC} = \text{DA}$, нам нужно сначала доказать, что $\ треугольник \text{ABC}  \cong \triangle \text{ABC}$ 

В $\triangle \text{ABC}$ и $\triangle \text{CDA}$ $\text{BC} || \text{DA}$ и $\text{AC}$ — трансверсаль.

Итак, $\angle \text{BCA} = \angle \text{DAC}$ (пара альтернативных углов)

И $\text{AC} = \text{CA}$ (общий)

Таким образом, $\triangle \text{ABC} \cong \triangle \text{CDA}$ (правило ASA).

Следовательно, соответствующие части $\text{AB} = \text{CD}$ и $\text{DA}= \text{BC}$.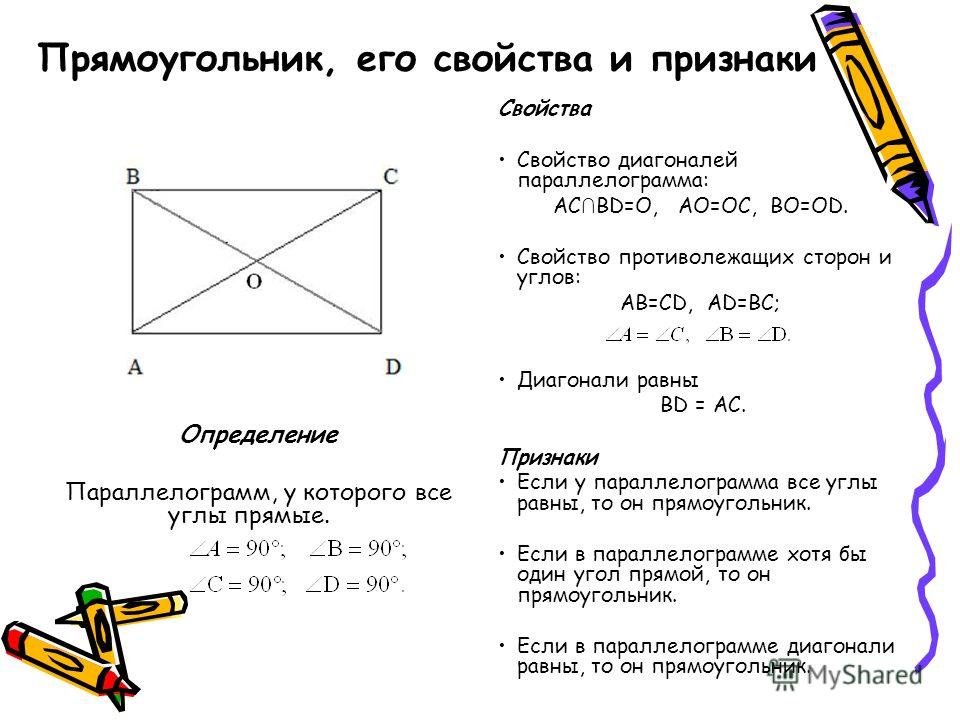

Противоположные углы параллелограмма равны

В параллелограмме противоположные углы равны.

Посмотрим, как доказать приведенное выше утверждение, т.е. в параллелограмме $\text{ABCD}$ $\angle \text{A} = \angle \text{C}$ и $\angle \text{B } = \угол \text{D}$.

На приведенном выше рисунке в параллелограмме $\text{ABCD}$ $\text{AB} || \text{CD}$ и $\text{AD} || \text{БК}$.

Рассмотрим $\triangle \text{ABC}$ и $\triangle \text{ADC}$

$\text{AC} = \text{AC}$ (общая сторона)

Мы знаем, что альтернативные внутренние углы равны равный.

$\angle \text{BAC} = \angle \text{ACD}$

$\angle \text{BCA} = \angle \text{CAD}$

Следовательно, $\triangle \text{ABC} \cong \triangle \text{ADC}$

Следовательно, $\angle \text{A} = \angle \text{C}$, а $\angle \text{B} = \angle \text{D}$ . (соответствующие части конгруэнтных треугольников). 9{\circ}$.

Величайшие математические открытия

Практические задачи

1. Дать определение параллелограмма.
2. Состояние True или False
   • Смежные стороны параллелограмма равны
   • Смежные стороны параллелограмма параллельны
   • Противоположные стороны параллелограмма равны
   • Противоположные стороны параллелограмма параллельны
   • Смежные углы параллелограмма равны
   • Смежные углы параллелограмма смежные
   • Противоположные углы параллелограмма равны
   • Противоположные углы параллелограмма являются дополнительными

Часто задаваемые вопросы

Что такое параллелограмм в геометрии?

В геометрии параллелограмм — это четырехугольник (четырехсторонняя двумерная фигура), у которого противоположные стороны параллельны и равны по длине.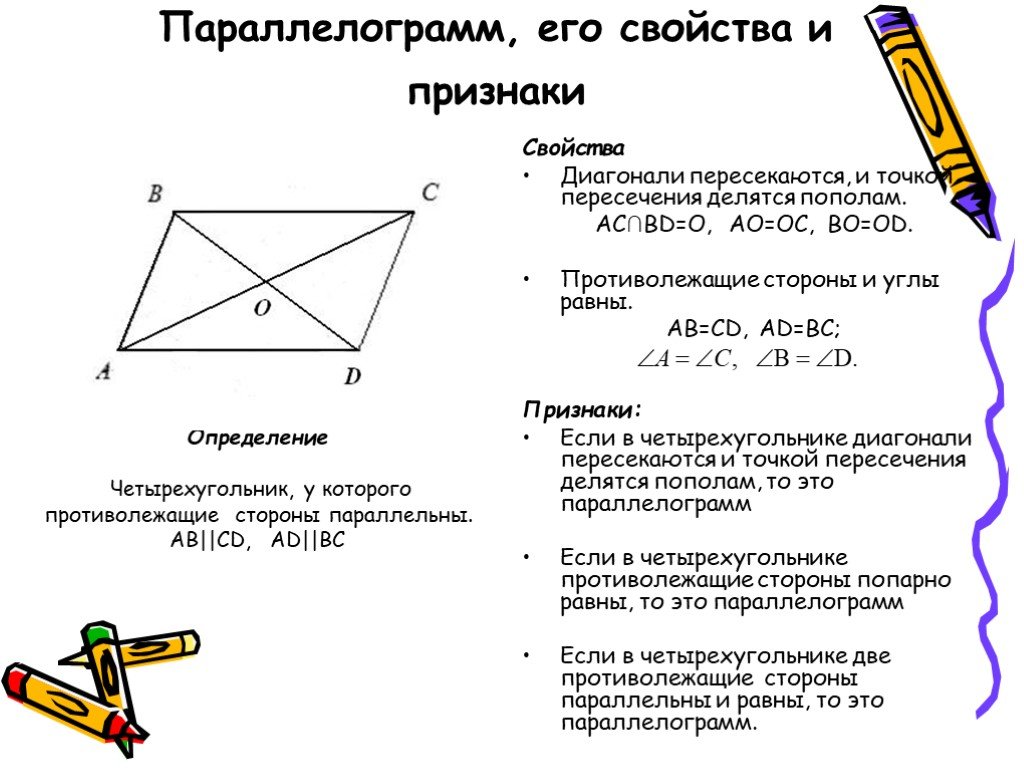 {\circ}$.

Чем параллелограмм отличается от четырехугольника?

Все параллелограммы являются четырехугольниками, но не все четырехугольники обязательно являются параллелограммами. Например, трапеция — это четырехугольник, а не параллелограмм. Чтобы четырехугольник был параллелограммом, все противоположные стороны должны быть параллельны и равны друг другу.

Является ли ромб параллелограммом?

Да, ромб — это параллелограмм, у которого противоположные стороны параллельны, а противоположные углы равны. Кроме того, все стороны ромба равны, а диагонали делят друг друга пополам под прямым углом.

Является ли трапеция параллелограммом?

Нет, трапеция не является параллелограммом, так как все противоположные стороны трапеции не параллельны друг другу. У трапеции только одна пара противоположных сторон параллельна друг другу. Кроме того, трапеция не имеет противоположных сторон, равных друг другу. Следовательно, это четырехугольник, а не параллелограмм.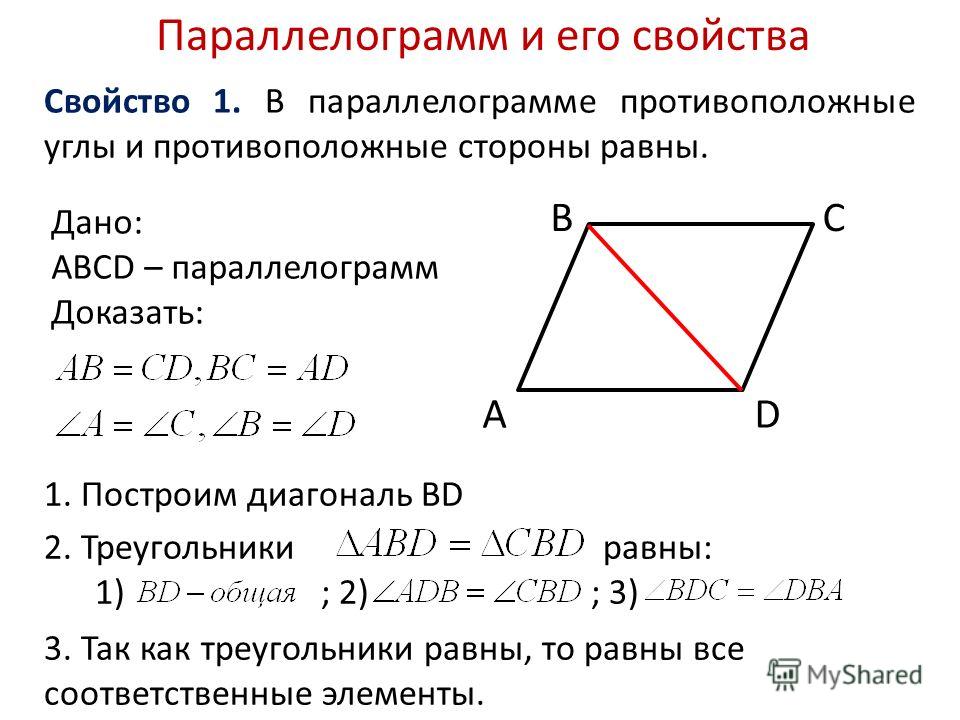

Заключение

Параллелограмм – это особый тип четырехугольника, образованный параллельными прямыми. В параллелограмме обе пары противоположных сторон параллельны и равны. Параллелограмм обладает некоторыми уникальными свойствами, которые отличают его от других четырехугольников. Три типа параллелограммов квадрат, прямоугольник и ромб.

Рекомендуемая литература

• Как построить треугольник (с шагами, диаграммами и примерами)
• Медиана треугольника (определение и свойства)
• Высота треугольника (определение и свойства)
• Критерии конгруэнтности треугольников — SSS , SAS, ASA, RHS
• Критерии подобия треугольников – SSS, SAS, AA
• Биссектриса угла треугольника – определение, свойства и примеры
• Что такое четырехугольник в математике (определение, форма и примеры)
• Свойства треугольника – теоремы и примеры
• Как построить треугольник (с шагами, диаграммами и примерами)
• Медиана треугольника (определение и свойства)
• Высота треугольника (определение и свойства)
• Конгруэнтность Критерии треугольников — SSS, SAS, ASA, RHS
• Критерии подобия треугольников — SSS, SAS, AA
• Типы треугольников — определение и примеры
• Что такое треугольник в геометрии — определение, формы и примеры
• Пара углов – определение, диаграммы, типы и примеры
• Построение углов (с помощью транспортира и компаса)
• Типы углов в математике (острый, прямой, тупой, прямой и обратный)
• Что такое угол в Геометрия – определение, свойства и измерения
• Как построить касательную к окружности (с шагами и изображениями)
• Касательная к окружности – значение, свойства, примеры
• Углы в окружности – значение, свойства и примеры
• Хорда круга – определение, свойства и примеры
• Как нарисовать круг (с шагами и картинками)
• Что такое круг – части, свойства и примеры
• Как построить перпендикулярную линию (с шагами и примерами) )
• Как построить параллельные линии (с шагами и примерами)
• Как построить отрезок линии (с шагами и примерами)
• Что такое коллинеарные точки в геометрии – определение, свойства и примеры
• Что такое поперечная линия в геометрии – определение, свойства и примеры
• Что такое параллельные линии в геометрии – определение, свойства и примеры
• Что такое параллельные линии в геометрии – определение, условия и примеры
• Что такое полупрямая в геометрии Геометрия – определение, свойства и примеры
• Что такое перпендикулярная линия в геометрии – определение, свойства и примеры
• Линии в геометрии (определение, типы и примеры)

Вам также может понравиться

Как решать линейные уравнения с помощью матриц (с методом и примерами)

Содержание Как решать линейные уравнения с помощью матрицУсловие непротиворечивости

Читать далее

Правило Крамера – определение, формулы и примеры

Содержание Что такое правило Крамера?Формула правила КрамераПравило Крамера 2 x

Читать далее

Карточки по математике для печати бесплатно – скачать PDF

Этот пост также доступен на: हिन्दी (хинди) Математические карточки

Читать далее

Вот все, что вам нужно знать о параллелограмме

Параллелограмм — это тип геометрической фигуры, которая существует только в двух измерениях и имеет стороны, перпендикулярные друг другу.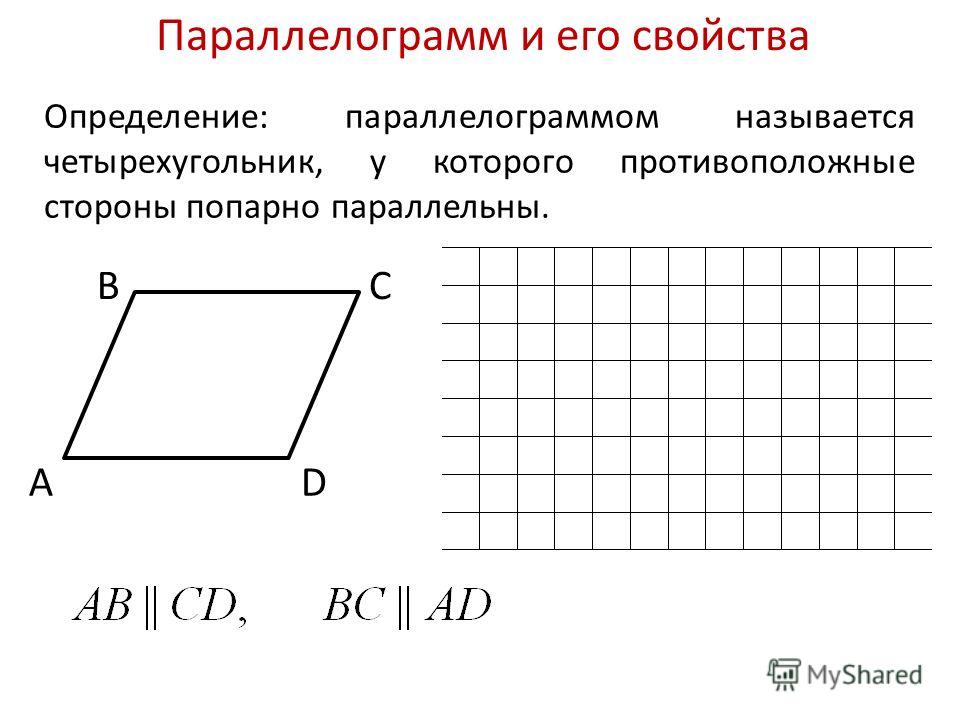 Это своего рода многоугольник, который имеет четыре стороны и также называется четырехугольником, а длины пар сторон, которые параллельны друг другу, одинаковы. Параллелограмм имеет смежные углы, которые в сумме дают 180 градусов, если их сложить. Вы должны были узнать о различных двумерных формах и размерах в геометрии, таких как круги, квадраты, прямоугольники, ромбы и другие подобные формы. Каждая из этих многочисленных форм имеет свой уникальный набор характеристик. Кроме того, формулы площади и периметра для каждой из этих форм отличаются друг от друга и могут применяться для решения самых разных задач.

Определение параллелограмма: 

Четырехугольник, две пары сторон которого параллельны друг другу, называется параллелограммом. Длины противоположных сторон параллелограмма равны друг другу, а противоположные углы имеют одинаковую степень измерения. Кроме того, дополнительными считаются внутренние углы, лежащие по одну сторону от секущей. Общая сумма внутренних углов составляет полные 360 градусов.

Параллелепипед — это термин, используемый для описания трехмерной фигуры, грани которой имеют форму параллелограмма. Площадь параллелограмма определяется как его основанием, которое является одной из его параллельных сторон, так и его высотой, которая представляет собой высоту, измеренную от вершины до низа. Длина каждой из сторон параллелограмма определяет длину периметра фигуры.

И квадрат, и прямоугольник являются примерами форм, которые имеют многие общие характеристики с параллелограммом.

Ромб определяется как параллелограмм, в котором все стороны конгруэнтны друг другу или равны друг другу.

Трапецию можно узнать по тому, что она имеет одну параллельную сторону и две другие стороны, не параллельные друг другу.

На рисунке выше ABCD — параллелограмм, где AB || CD и AD || ДО Н.Э.

Кроме того, AB = CD и AD = BC

И, ∠A = ∠C и ∠B = ∠D

Кроме того, A и D считаются дополнительными углами, поскольку они расположены на той же стороне поперечной, что другие внутренние углы.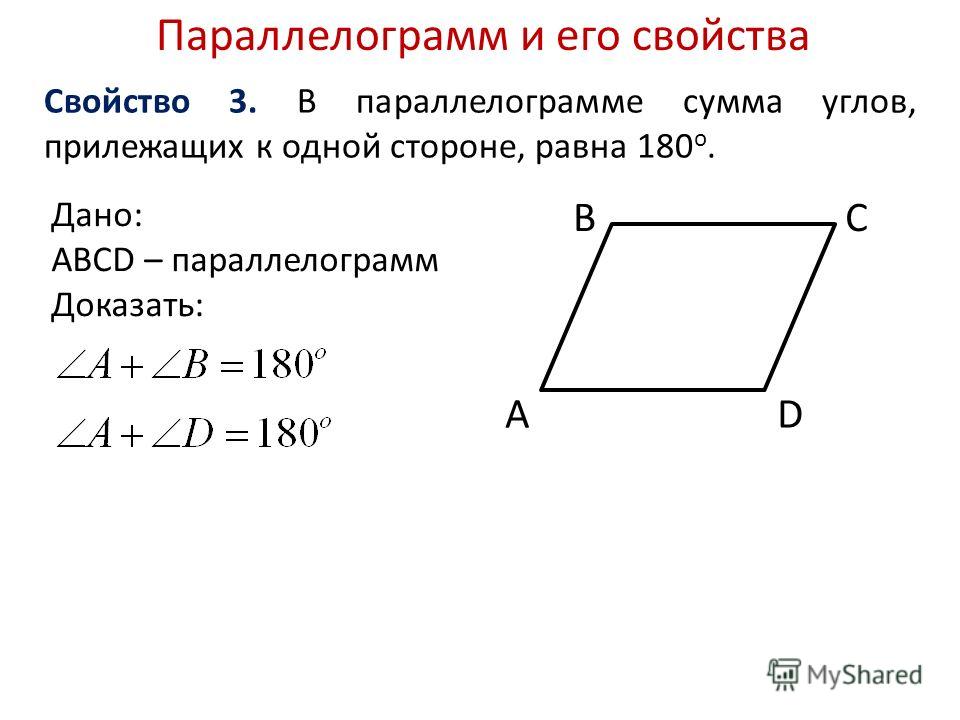 Точно так же ∠B и ∠C считаются дополнительными углами.

Следовательно,

∠A + ∠D = 180

∠B + ∠C = 180 

Форма параллелограмма: 

Параллелограмм — это форма, которая существует только в двух измерениях. Всего у него четыре стороны, две пары из которых параллельны друг другу. Кроме того, длины параллельных сторон одинаковы. Рассматриваемая форма не является параллелограммом, если длины сторон, идущих параллельно друг другу, не равны. Точно так же оба внутренних угла параллелограмма, которые противоположны друг другу, всегда должны быть равны. В таком случае мы не можем назвать его параллелограммом.

Свойства параллелограмма: 

Уникальный тип многоугольника, известный как параллелограмм, образуется, когда четырехугольник имеет пару параллельных противоположных сторон. Ниже приводится список характеристик параллелограмма:

1. Противоположные стороны параллельны и конгруэнтны

2. Углы на противоположных сторонах равны.

3. Углы, следующие друг за другом, дополняют друг друга.

4. В том случае, если хотя бы один из углов будет прямым, то и остальные углы будут также прямыми.

5. Обе диагонали пересекаются и делят друг друга пополам.

6. Каждая диагональ делит параллелограмм пополам, образуя два конгруэнтных друг другу треугольника.

7. Параллелограмм обладает тем свойством, что сумма квадратов всех его сторон равна сумме квадратов его диагоналей. Он также известен как закон параллелограмма.

Типы параллелограмма: 

Из-за множества различных соображений параллелограммы обычно можно разделить на четыре отдельные категории. Углы, стороны и другие характеристики, такие как эти, отличают каждый из этих различных вариантов параллелограмма друг от друга.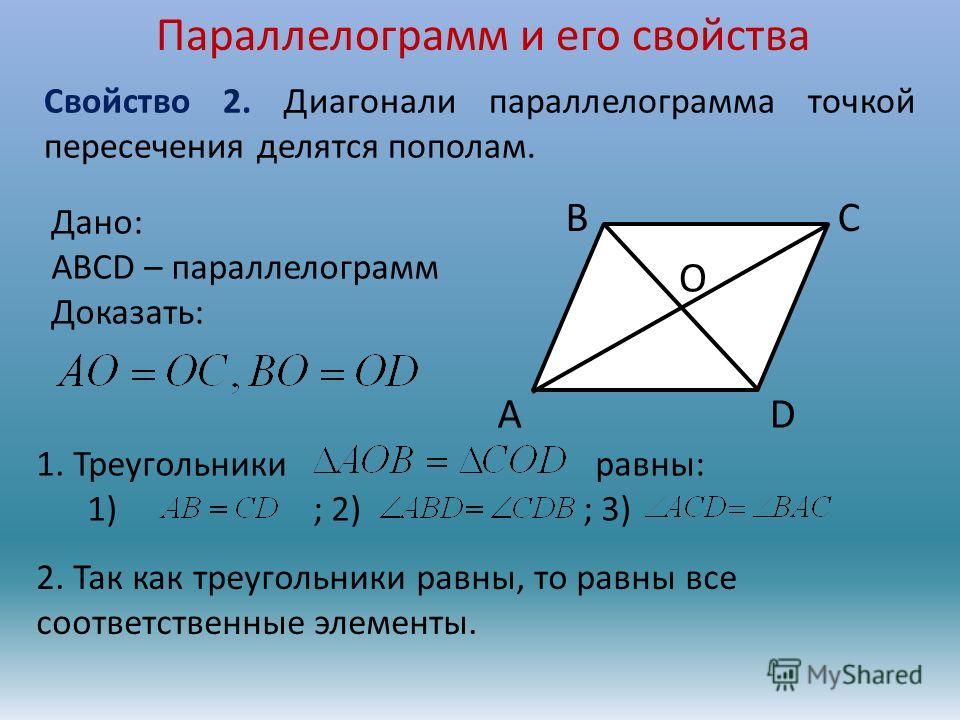

1. In a parallelogram, say PQRS 

2. The other two special types of a parallelogram are:

• Rectangle

• Square 

Angles of parallelogram: 

A parallelogram это тип двумерной формы, которая является плоской и имеет четыре угла. Равное обращение предоставляется противоположным внутренним углам. Углы, которые расположены по одну сторону от секущей, являются дополнительными, что указывает на то, что их сумма равна 180 градусам. Следовательно, общее количество углов, содержащихся в параллелограмме, равно 360 градусам.

Специальные параллелограммы: 

Квадрат и прямоугольник: 

Как квадрат, так и прямоугольник являются примерами фигур, которые во многом схожи с параллелограммом. Обе их противоположные стороны имеют одинаковую длину и идут параллельно друг другу.