| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | ||
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |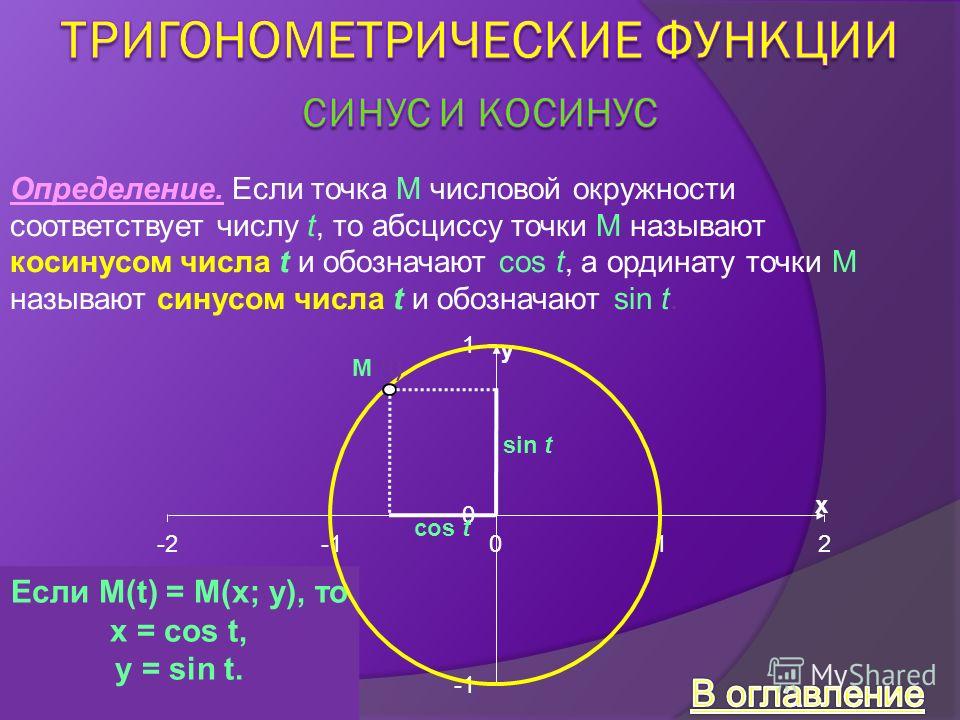
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) | |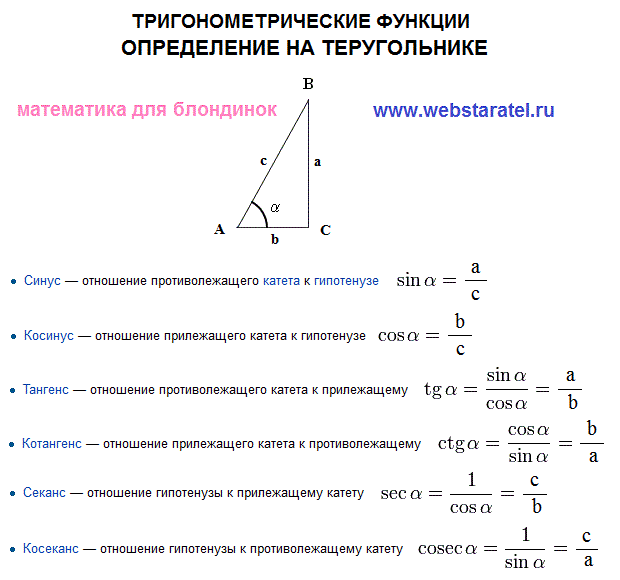
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | cos(150 град. ) | ||
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |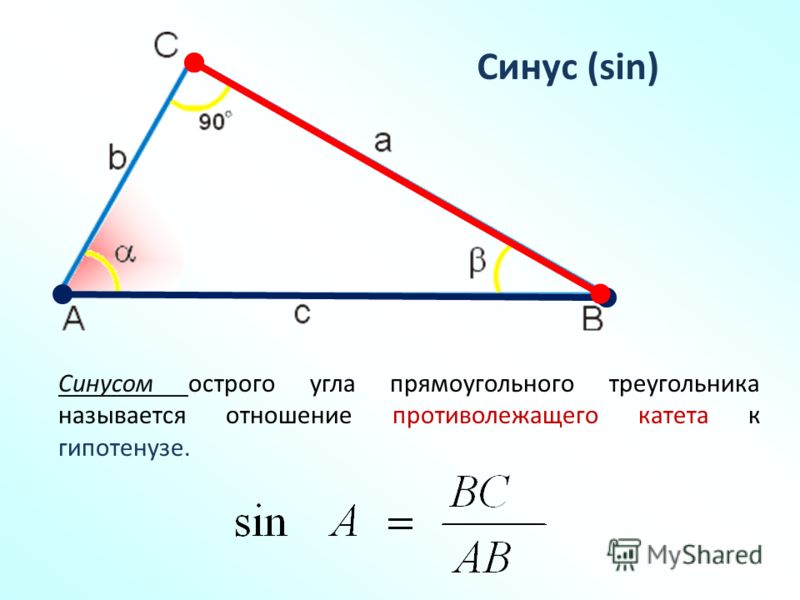
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) | |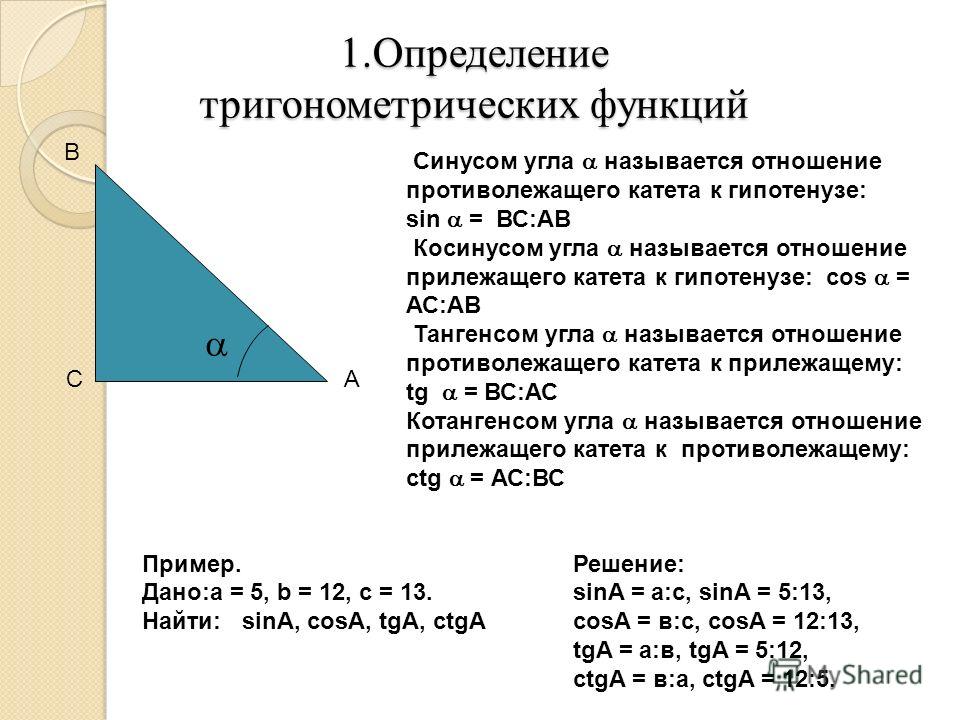
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | ||
| 95 | Найти точное значение | sin(120 град. ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Синус и косинус 10 класс онлайн-подготовка на Ростелеком Лицей
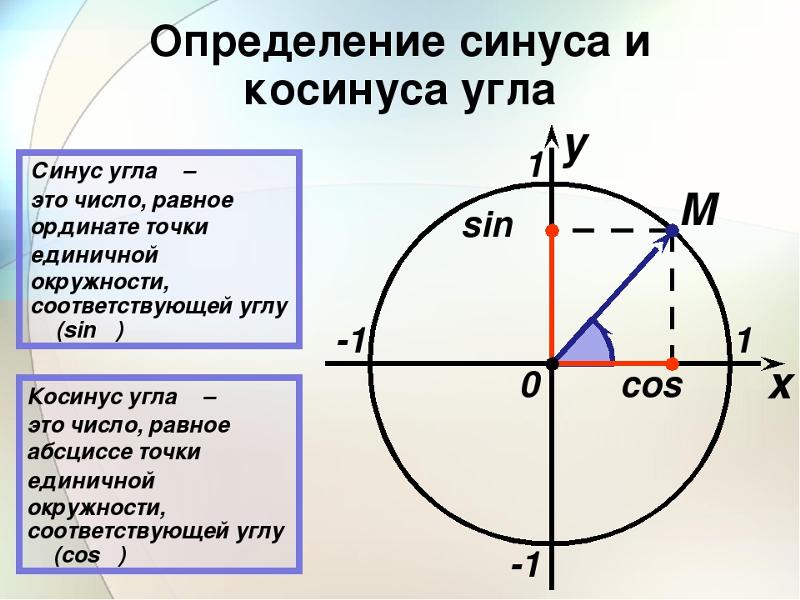
Определение синуса и косинуса
Поместим числовую окружность (окружность с радиусом, равным 1) в координатную плоскость (см.
Рис. 1). Точки , , , – это точки пересечения числовой окружности с осями координат.
Рис. 1. Числовая окружность в координатной плоскости
Числу соответствует единственная точка с координатами . Первая координата – это косинус числа , вторая координата – это синус числа .
Если точка на числовой окружности соответствует числу , то абсциссу точки называют косинусом числа
, а ординату точки называют синусом числа .
– это линия синусов. Синус любого числа лежит в пределах от до .
– это линия косинусов. Косинус любого числа лежит в пределах от до .
Задача 1
Дано: .
Найти: ; .
Решение
Решим данную задачу двумя способами:
1 способ (см. Рис. 2)
Рис. 2. Иллюстрация к задаче
1. Отметим на единичной окружности точку , которая соответствует заданному числу :
Число можно представить в виде . Точка на числовой окружности соответствует числу , следовательно, точка будет лежать на числовой окружности в третьем координатном углу.
2. Опускаем перпендикуляры из точки на оси координат:
— точка – это точка пересечения перпендикуляра с осью , координаты этой точки .
— точка – это точка пересечения перпендикуляра с осью , координаты этой точки .
3.
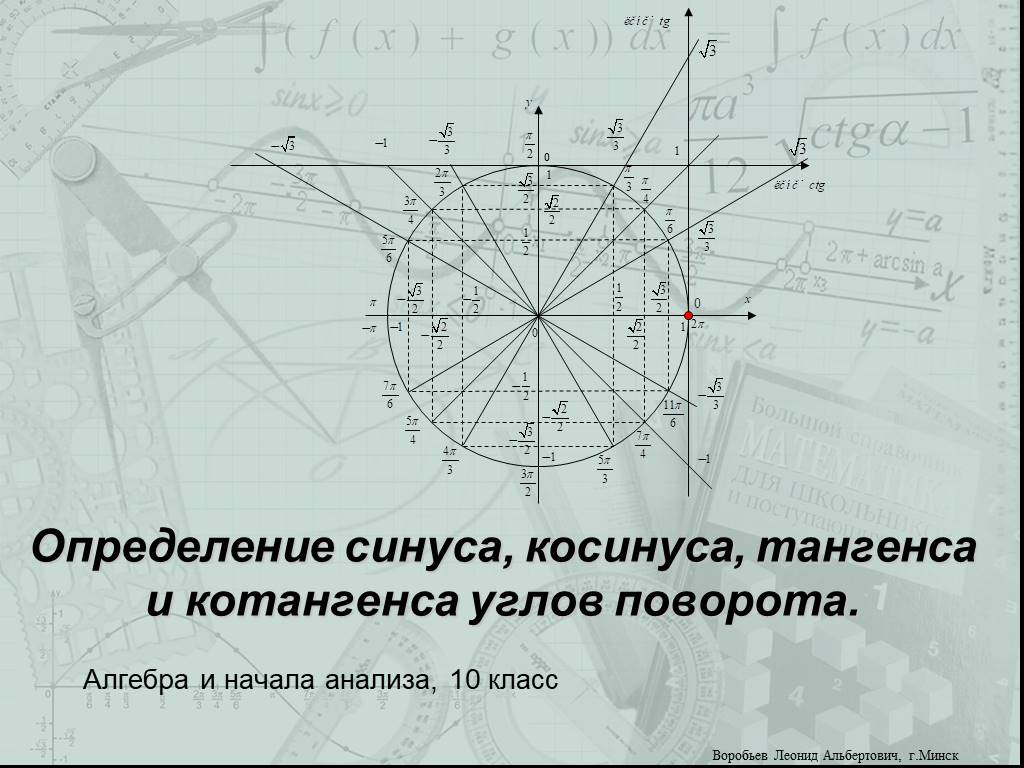Рассмотрим :
— гипотенуза .
— угол равен угловому измерению дуги , то есть .
— катет равен произведению гипотенузы на косинус прилежащего угла, то есть:
— этот прямоугольный треугольник является равнобедренным, так как один из его углов равен , следовательно:
Так как , то .
Значит, , (в обоих случаях знак минус, так как точка лежит на числовой окружности в третьем координатном углу, где значения координаты и отрицательны).
2 способ
Воспользуемся следующими свойствами:
Согласно этим свойствам получаем:
Ответ: ; .
Задача 2
Решить уравнение:
1.
Решение
Синус числа – это ордината точки, находящейся на числовой окружности (см.
Рис. 3). Поэтому чтобы определить, где , нам надо найти, где на единичной окружности . Двигаясь вверх по оси , попадаем в точку , которая соответствует числу .
Рис. 3. Иллюстрация к задаче
Это только одна из точек, в которых синус равен 1. Через полный оборот окружности мы снова попадем в эту точку, через два, три и так далее – тоже. Чтобы учесть все точки, в которых , необходимо к прибавить , где – целое число, то есть .
Ответ: , где .
2.
Решение
Отрезок – это линия синусов (см. Рис. 3). При этом значение синус принимает в точке , которая соответствует числу . Через полный оборот окружности мы снова попадем в эту точку, через два, три и так далее – тоже. Чтобы учесть все точки, в которых , необходимо к прибавить , где – целое число, то есть .
Ответ: , где .
3.
Решение
Отрезок – это линия косинусов (см.
Рис. 4). Обозначим на этой линии точку с координатами . Эта точка будет лежать посередине отрезка , так как .
Рис. 4. Иллюстрация к задаче
Проведем через точку перпендикуляр к оси . Мы получили две точки на пересечении перпендикуляра и числовой окружности – и (только эти точки проектируются на линию косинусов в точку ).
Необходимо определить длину дуги . Данная дуга состоит из дуги , длина которой равна , и дуги :
Для того чтобы определить длину дуги , рассмотрим треугольник . Этот треугольник прямоугольный, катет равен половине гипотенузы , следовательно, угол . Так как углы и – это накрест лежащие углы, то . Отсюда следует, что .
Таким образом:
Следовательно, точке соответствуют числа , где – целое число. Аналогично точке соответствуют числа , где – целое число.
Ответ: , где .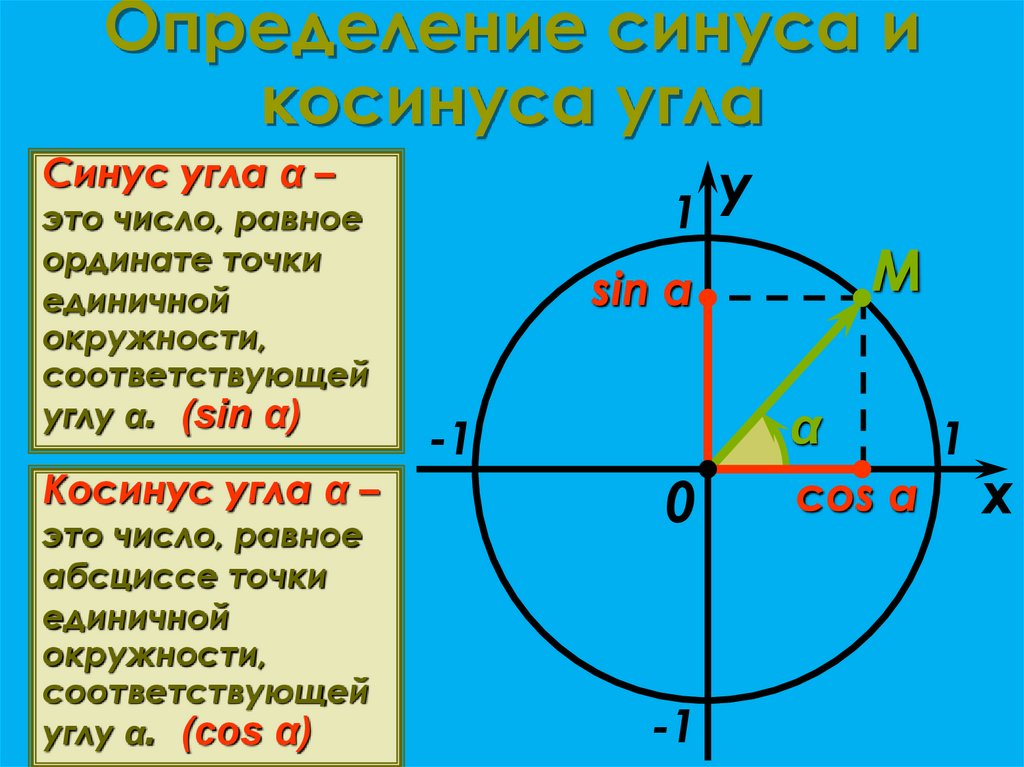
Список литературы
1. Мордкович А.Г., Семенов П.В. Алгебра и начала математического анализа, 10 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений. – М.: Мнемозина, 2009.
2. Мордкович А.Г. Алгебра и начала математического анализа, 10 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений. – М.: Мнемозина, 2009.
3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики). – М.: Просвещение, 1996.
4. Колягин Ю.М., Сидоров Ю.В., Ткачева М.В., Федорова М.В., Шабунин М.И. Алгебра и начала математического анализа, 10 класс. Учебник для учащихся общеобразовательных учреждений (профильный уровень). – М.: Мнемозина, 2009.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1.
Интернет-сайт kursoteka.ru (Источник)
2. Интернет-сайт hijos.ru (Источник)
3. Интернет-сайт YouTube (Источник)
4. Интернет-сайт YouTube (Источник)
Домашнее задание
1. Задание 13.2, 13.28 (стр. 77–80) – Мордкович А.Г. Алгебра и начала математического анализа, 10 класс. В 2 ч. Ч. 2. Задачник (Источник)
2. Решите уравнение .
3. Найдите значение выражения , если .
обыкновенных дифференциальных уравнений. Должны ли мы переопределить синус?
Синус обычно определяется как отношение противолежащего катета к углу к гипотенузе в прямоугольном треугольнике . Другое распространенное определение основано на единичном круге. Однако я думаю, что эти геометрические определения могут привести к путанице и неправильному пониманию. Я некоторое время задавался этим вопросом, поэтому теперь я привожу некоторые причины для этого спора и хочу знать, правильно ли это учение или нет.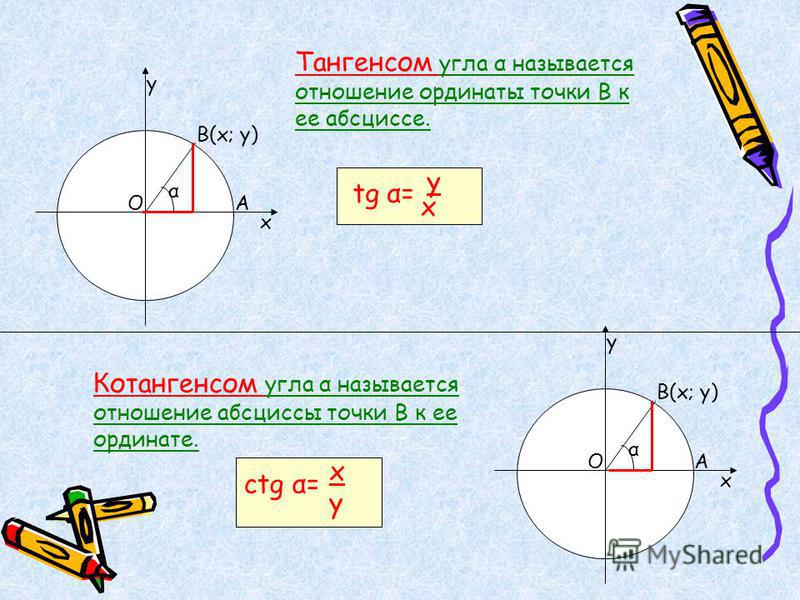
Тогда решение для этого записывается как $y=A\sin(\sqrt{k}x+\phi)$ и начинают возникать вопросы: «Откуда взялся этот синус?! ». Типичный ответ будет таким: «Видишь, если взять вторую производную и подставить ее, она удовлетворяет уравнению». «Да, это правда, но… где круг? Где угол? Там просто объект, соединенный с пружиной». И так далее, у многих студентов есть проблемы.
Эта путаница возникает из-за того, что когда вы впервые определили для них функцию синуса, была окружность, а аргументом был угол и так далее. Неудивительно, если менее любознательные студенты принимают это явление (то, что объект, соединенный с пружиной, движется как функция синуса) как случайность или что-то в этом роде и проходят мимо.
Чтобы решить эту проблему, я предлагаю новое определение. Мы можем определить синус как Ответ на $y’’+ay=0$, учитывая $y(0)=0$ и $y’(0)=1$. Можно доказать (с небольшими усилиями), что отношение противолежащего положения к гипотенузе также подчиняется тому же дифференциальному уравнению, поэтому по [новому] определению это отношение будет равно синусу угла.
Это должно решить проблемы, рассмотренные выше.
Еще одна интересная тема — число пи, связанное с этим обсуждением. Думаю, я смогу убедить вас, что число пи может быть довольно запутанным:
.Однажды, просматривая формулы в какой-то книге, я обнаружил Формула частоты резонансного контура. Была загадка об этом номере, который я не понимал в юности, но это был отличная вещь, и результат как то я искал пи везде.
[??Здесь чего-то не хватает], что было f = 1/2 pi LC, где L — это индуктивность и C [это] емкость [конденсатора, и было также пи. Но где] круг? Вы смеетесь, но я был очень серьезен затем. Пи было штукой с кругами, и вот число Пи выходит из электрическая цепь. Где был круг? Те из вас, кто смеялся знаете, как это происходит? Я должен любить это дело. я должен посмотреть для этого. Я должен подумать об этом. И тут я понял, конечно, что катушки сделаны в кругах. Примерно через пол года я нашел другая книга, в которой дана индуктивность круглых катушек и квадратных катушки, и в этих формулах были другие пи.
я начал думать снова об этом, и я понял, что число пи пришло не из круговые катушки. Теперь я понимаю это лучше; но в душе я до сих пор не знаю, где этот круг, откуда взялось это число Пи.
Ричард Фейнман – «Что такое наука?»
я начал думать
снова об этом, и я понял, что число пи пришло не из
круговые катушки. Теперь я понимаю это лучше; но в душе я до сих пор
не знаю, где этот круг, откуда взялось это число Пи.Другой пример из известной статьи:
ЕСТЬ история о двух друзьях, которые были одноклассниками в старших классах. школе, рассказывают о своей работе. Один из них стал статистиком и работал над демографическими тенденциями. Он показал репринт своему бывший одноклассник. Перепечатка началась, как обычно, с гауссовой распределение и статистик объяснил своему бывшему однокласснику значение символов для реальной численности населения, для средней населения и так далее. Его одноклассник был немного недоверчив и не был вполне уверен, что статистик дурачился. «Как ты можешь знаете это? — был его вопрос. — А что это за символ здесь? — О, — сказал статистик, «это пи.» «Что это такое?» «Соотношение окружности круга к его диаметру».
Естественно, мы склонны улыбаться простоте подход одноклассника. Тем не менее, когда я услышал эту историю, мне пришлось признаться в жутком чувстве, потому что, конечно, реакция одноклассник предал только простой здравый смысл. я еще больше запуталась когда несколько дней спустя кто-то подошел ко мне и высказал свое недоумение [1 Цитируемое замечание было сделано Ф. Вернером, когда он был студентом в Принстоне.] с тем, что мы делаем довольно узкий отбор при выборе данных, на которых мы проверяем наши теории. «Откуда мы это знаем, если мы создали теорию, которая фокусирует внимание на явлениях мы пренебрегаем и пренебрегаем некоторыми явлениями теперь обращая наше внимание на то, что мы не можем построить другую теорию, которая имеет мало общего с настоящим, но который, тем не менее, объясняет столько же явлений, сколько и современная теория?» признал, что у нас нет определенных доказательств того, что такого теория.
Юджин Вигнер – «Необоснованная эффективность математики в Естественные науки»
«Ну, теперь вы
ты слишком далеко зашел в своей шутке, — сказал одноклассник, — наверняка население
не имеет ничего общего с длиной окружности».0005
Предыдущие две истории иллюстрируют два основных момента, которые
являются предметом настоящего дискурса. Первый момент заключается в том, что
математические понятия появляются в совершенно неожиданных связях.
Более того, они часто позволяют неожиданно близко и точно
описание явлений в этих соединениях. Во-вторых, …Итак, после всех этих историй от больших умов мы видим, что пытливые умы с трудом связывают число пи с уравнениями, которые даже не включают окружность. Но если вместо этого мы определим число пи как половину периода синусоидальной функции (вновь определенного), то использование числа пи при отсутствии кругов и треугольников не будет сюрпризом.
В конце этого длинного поста я хочу спросить мнения. Интересно, все, что я сказал выше, имеет смысл или нет? Математика — это точная область, а определения — это все, поэтому я думаю, что то, что я здесь задаю, — важный вопрос.
Редактировать: Несколько друзей отметили это как «Основываясь на мнении». Спасибо, что прочитали мой вопрос, но я действительно не понимаю, как определение может быть «основанным на мнении» в такой точной области, как математика. Таким образом, единственный способ, которым я могу представить, — это то, что они будут «эквивалентны», что я каким-то образом делаю из ответов, но все еще ищу четкое доказательство для этого пункта, которого я здесь не вижу.
синус – определение и значение
- Определение
- Связать
- Список
- Обсудить
- См.
- Услышать
- и Любовь
Определения
из Словаря английского языка American Heritage®, 5-е издание.
- сущ. Ордината конечной точки дуги единичной окружности с центром в начале декартовой системы координат, дуга имеет длину x и измеряется против часовой стрелки от точки (1, 0), если x является положительным или по часовой стрелке, если x является отрицательным.
- сущ. В прямоугольном треугольнике отношение длины стороны, противолежащей острому углу, к длине гипотенузы.
из словаря века.
- После этого; потом: то же, что и с, 1.
- Раньше; назад: то же, что и с, 3: как, lang syne , давным-давно, также используется как существительное, особенно во фразе auld langsyne , старые времена (см. langsyne).
- После; с: так же, как с тех пор.
- сущ. Пропасть.
- сущ. В тригонометрия , прежде по отношению к любой дуге окружности, линия, проведенная от одного конца дуги под прямым углом к диаметру, проходящему через другой ее конец; теперь обычно, в отношении не к дуге, а к углу, который она образует в центре круга, отношение вышеупомянутой линии к радиусу круга.
- существительное функция, выраженная рядом Эти функции были изобретены Вронским.
- Процедить.
- Прекратить доить корову.
- Латинский предлог, означающий «без». См. sine die, sine qua non.
из версии GNU Collaborative International Dictionary of English.
- сущ. Длина перпендикуляра, проведенного от одного конца дуги окружности к диаметру, проведенному через другой конец.
- сущ. Сам перпендикуляр. См. Синус угла ниже.
- сущ. логарифмы натуральных синусов или логарифмические синусы.
- сущ. См. Синусоида.
- существительное десятичные дроби, выражающие значения синусов, радиус которых равен единице.
- сущ. в круге, радиус которого равен единице, синус дуги, измеряющей угол; в прямоугольном треугольнике сторона, противолежащая данному углу, делится на гипотенузу. См. раздел «Тригонометрическая функция» в разделе «Функция».
- сущ. часть диаметра между синусом и дугой.
- предлог Без.
- сущ. тригонометрия, математика В прямоугольном треугольнике отношение длины стороны, противоположной углу, к длине гипотенузы.
из WordNet 3.0 Copyright 2006 Принстонского университета. Все права защищены.
- сущ. отношение длины стороны, противолежащей данному углу, к длине гипотенузы прямоугольного треугольника
Etymologies
from The American Heritage® Dictionary of the English Language, 4th Edition
[средневековая латынь sinus (неправильный перевод арабского jayb , sine, как будто jayb ), от латинской одежды fold in a , кривая, сгиб.
]
От латинского sinus , первоначально путем неправильного перевода арабского جب (jubb). В конечном итоге с санскрита.
Поддержка
Помогите поддержать Wordnik (и сделайте эту страницу свободной от рекламы), приняв слово sine.
Примеры
Адвокат защиты Пауль Рейхлер подробно резюмировал, почему защита подала ходатайство о принуждении правительства к выполнению того, что он назвал sine qua non — существенным условием — досудебного соглашения.
Права человека превыше всего: слушания в военной комиссии Аль-Коси приносят то же самое
И это прекрасно симметричная, простая волна, которую мы называем синусоидальной волной .
«Вечер трудного дня»: таинственный тур по математике
Они также могут оставить открытой возможность оставить сессию до 18-го числа открытой до этого момента, прежде чем они объявят sine die, что будет окончательным отложением, просто чтобы убедиться, что не возникнет никаких проблем.
Стенограмма CNN — Экстренные новости: Выборы 2000: Гор приказывает, чтобы пересчет голосов во Флориде был приостановлен, сегодня вечером он обратится к нации; Чейни на холме, чтобы наметить цели для новой администрации — 13 декабря 2000 г.
— Ну, — сказал Дейд, — я слышал, как они говорят здесь о месте, которое они называют синус -ку-ри — большая плата и никакой работы — и если хоть один из них остался и валяется на свободе, я думаю Я мог бы заполнить его до буквы Т».
Марс Анри: автобиография,
— Ну, — сказал Дейд, — я слышал, как они говорили здесь о месте, которое они называют синус — кю-ри — большая плата и никакой работы — и если хоть один из них остался и валяется на свободе Думаю, я мог бы заполнить его до тройки».
Марс Анри (Том 1) Автобиография
«Ну, — сказал Дейд, — я слышал, как они говорят здесь о месте, которое они называют sine -cu-ree — большая зарплата и никакой работы — и если один из них остался и валяется на свободе, я думаю, я мог бы заполнить его до Т.
