Зависимые и независимые события. Условная вероятность
Определения вероятности
Классическое определение
Классическое «определение» вероятности исходит из понятия равновозможности как объективного свойства изучаемых явлений. Равновозможность является неопределяемым понятием и устанавливается из общих соображений симметрии изучаемых явлений. Например, при подбрасывании монетки исходят из того, что в силу предполагаемой симметрии монетки, однородности материала и случайности (непредвзятости) подбрасывания нет никаких оснований для предпочтения «решки» перед «орлом» или наоборот, то есть выпадение этих сторон можно считать равновозможными (равновероятными).
Наряду
с понятием равновозможности в общем
случае для классического определения
необходимо также понятие элементарного
события (исхода), благоприятствующего
или нет изучаемому событию A. Речь идет
об исходах, наступление которых исключает
возможность наступления иных исходов.
Это несовместимые элементарные события.
Классическое определение вероятности можно сформулировать следующим образом:
Вероятностью случайного события A называется отношение числа n несовместимых равновероятных элементарных событий, составляющих событие A, к числу всех возможных элементарных событий N:
Например, пусть подбрасываются две кости. Общее количество равновозможных исходов (элементарных событий) равно очевидно 36 (6 возможностей на каждой кости). Оценим вероятность выпадения 7 очков. Получение 7 очков возможно следующими способами: 1+6, 2+5, 3+4, 4+3, 5+2, 6+1. То есть всего 6 равновозможных исходов, благоприятствующих событию A — получению 7 очков. Следовательно, вероятность будет равна 6/36=1/6. Для сравнения вероятность получения 12 очков или 2 очков равна всего 1/36 — в 6 раз меньше.
Геометрическое определение
Несмотря
на то, что классическое определение
является интуитивно понятным и выведенным
из практики, оно, как минимум не может
быть непосредственно применено в случае,
если количество равновозможных исходов
бесконечно.
В
виду равновозможности вероятность эта
не зависит от формы области g, она зависит
только от ее площади. Данное определение
естественно можно обобщить и на
пространство любой размерности, где
вместо площади использовать понятие
«объема». Более того, именно такое
определение приводит к современному
аксиоматическому определению вероятности.
Понятие объема обобщается до понятия
«меры» некоторого абстрактного
множества, к которой предъявляются
требования, которыми обладает и «объем»
в геометрической интерпретации — в
первую очередь, это неотрицательность
и аддитивность.
Частотное (статистическое) определение
Классическое определение при рассмотрении сложных проблем наталкивается на трудности непреодолимого характера. В частности, в некоторых случаях выявить равновозможные случаи может быть невозможно. Даже в случае с монеткой, как известно существует явно не равновероятная возможность выпадения «ребра», которую из теоретических соображений оценить невозможно (можно только сказать, что оно маловероятно и то это соображение скорее практическое). Поэтому еще на заре становления теории вероятностей было предложено альтернативное «частотное» определение вероятности. А именно, формально вероятность можно определить как предел частоты наблюдений события A, предполагая однородность наблюдений (то есть одинаковость всех условий наблюдения) и их независимость друг от друга:
где — количество наблюдений, а — количество наступлений события .
Несмотря
на то, что данное определение скорее
указывает на способ оценки неизвестной
вероятности — путем большого количества
однородных и независимых наблюдений —
тем не менее в таком определении отражено
содержание понятия вероятности. А
именно, если событию приписывается
некоторая вероятность, как объективная
мера его возможности, то это означает,
что при фиксированных условиях и
многократном повторении мы должны
получить частоту его появления, близкую
к (тем
более близкую, чем больше наблюдений).
Собственно, в этом заключается исходный
смысл понятия вероятности. В основе
лежит объективистский взгляд на явления
природы. Ниже будут рассмотрены так
называемые законы больших чисел, которые
дают теоретическую основу (в рамках
излагаемого ниже современного
аксиоматического подхода) в том числе
для частотной оценки вероятности.
А
именно, если событию приписывается
некоторая вероятность, как объективная
мера его возможности, то это означает,
что при фиксированных условиях и
многократном повторении мы должны
получить частоту его появления, близкую
к (тем
более близкую, чем больше наблюдений).
Собственно, в этом заключается исходный
смысл понятия вероятности. В основе
лежит объективистский взгляд на явления
природы. Ниже будут рассмотрены так
называемые законы больших чисел, которые
дают теоретическую основу (в рамках
излагаемого ниже современного
аксиоматического подхода) в том числе
для частотной оценки вероятности.
Аксиоматическое определение
В
современном математическом подходе
вероятность задаётся аксиоматикой
Колмогорова.
Предполагается, что задано
некоторое пространство
элементарных событий .
Подмножества этого пространства
интерпретируются как случайные
события.
Объединение (сумма) некоторых подмножеств
(событий) интерпретируется как событие,
заключающееся в наступлении хотя
бы одного из
этих событий. Пересечение (произведение)
подмножеств (событий) интерпретируется
как событие, заключающееся в
наступлении всех этих
событий. Непересекающиеся множества
интерпретируются как несовместные события
(их совместное наступление невозможно).
Соответственно, пустое множество
означает невозможноесобытие.
Пересечение (произведение)
подмножеств (событий) интерпретируется
как событие, заключающееся в
наступлении всех этих
событий. Непересекающиеся множества
интерпретируются как несовместные события
(их совместное наступление невозможно).
Соответственно, пустое множество
означает невозможноесобытие.
Вероятностью (вероятностной мерой) называется мера (числовая функция) , заданная на множестве событий, обладющая следующими свойствами:
В
случае если пространство элементарных
событий X конечно,
то достаточно указанного условия
аддитивности для произвольных двух
несовместных событий, из которого будет
следовать аддитивность для
любого конечного количества
несовместных событий. Однако, в случае
бесконечного (счетного или несчетного)
пространства элементарных событий
этого условия оказывается недостаточно.
Требуется так называемая счетная
или сигма- аддитивность,
то есть выполнение свойства аддитивности
для любого не
более чем счетногосемейства
попарно несовместных событий.
Вероятностная мера может быть определена не для всех подмножеств множества . Предполагается, что она определена на некоторой сигма-алгебре подмножеств [6]. Эти подмножества называются измеримыми по данной вероятностной мере и именно они являются случайными событиями. Совокупность — то есть множество элементарных событий, сигма-алгебра его подмножеств и вероятностная мера — называется вероятностным пространством.
Непрерывные случайные величины.
Кроме
дискретных случайных величин, возможные
значения которых образуют конечную или
бесконечную последовательность чисел,
не заполняющих сплошь никакого интервала,
часто встречаются случайные величины,
возможные значения которых образуют
некоторый интервал. Примером такой
случайной величины может служить
отклонение от номинала некоторого
размера детали при правильно налаженном
технологическом процессе. Такого рода,
случайные величины не могут быть заданы
с помощью закона распределения
вероятностей р(х). Однако их можно задать с помощью функции
распределения вероятностей F(х).
Эта функция определяется точно так же,
как и в случае дискретной случайной
величины:
Однако их можно задать с помощью функции
распределения вероятностей F(х).
Эта функция определяется точно так же,
как и в случае дискретной случайной
величины:
Таким образом, и здесь функция F(х) определена на всей числовой оси, и ее значение в точке х равно вероятности того, что случайная величина примет значение, меньшее чем х. Формула (19) и свойства 1° и 2° справедливы для функции распределения любой случайной величины. Доказательство проводится аналогично случаю дискретной величины. Случайная величина называется непрерывной, если для нее существует неотрицательная кусочно-непрерывная функция* , удовлетворяющая для любых значений
(22) |
Функция называется плотностью
распределения вероятностей,
или кратко, плотностью
распределения. Если x1<x2,
то на основании формул (20)
и (22)
имеем
Если x1<x2,
то на основании формул (20)
и (22)
имеем
(23) |
Исходя из геометрического смысла интеграла как площади, можно сказать, что вероятность выполнения неравенств равна площади криволинейной трапеции с основанием[x1,x2], ограниченной сверху кривой (рис. 6).
Так как , а на основании формулы (22)
, то
(24) |
Пользуясь формулой (22), найдем как производную интеграла по переменной верхней границе, считая плотность распределения непрерывной**:
(25) |
Заметим,
что для непрерывной случайной величины
функция распределения F(х) непрерывна
в любой точке х,
где функция непрерывна. Это следует из того, что F(х) в
этих точках дифференцируема.
На
основании формулы (23),
полагая x1=x, ,
имеем
Это следует из того, что F(х) в
этих точках дифференцируема.
На
основании формулы (23),
полагая x1=x, ,
имеем
В силу непрерывности функции F(х) получим, что
Следовательно
Таким образом, вероятность того, что непрерывная случайная величина может принять любое отдельное значение х, равна нулю. Отсюда следует, что события, заключающиеся в выполнении каждого из неравенств
, , ,
Имеют одинаковую вероятность, т.е.
В самом деле, например,
так
как
Замечание. Как
мы знаем, если событие невозможно, то
вероятность его наступления равна нулю.
При классическом определении вероятности,
когда число исходов испытания конечно,
имеет место и обратное предложение:
если вероятность события равна нулю,
то событие невозможно, так как в этом
случае ему не благоприятствует ни один
из исходов испытания. В случае непрерывной
случайной величины число возможных ее
значений бесконечно. Вероятность того,
что эта величина примет какое-либо
конкретное значение x1 как
мы видели, равна нулю. Однако отсюда не
следует, что это событие невозможно,
так как в результате испытания случайная
величина может, в частности, принять
значение x1.
Поэтому в случае непрерывной случайной
величины имеет смысл говорить о
вероятности попадания случайной величины
в интервал, а не о вероятности того, что
она примет какое-то конкретное
значение.
Так,
например, при изготовлении валика нас
не интересует вероятность того, что его
диаметр будет равен номиналу. Для нас
важна вероятность того, что диаметр
валика не выходит из поля
допуска.
Пример. Плотность
распределения непрерывной случайной
величины задана следующим образом:
В случае непрерывной
случайной величины число возможных ее
значений бесконечно. Вероятность того,
что эта величина примет какое-либо
конкретное значение x1 как
мы видели, равна нулю. Однако отсюда не
следует, что это событие невозможно,
так как в результате испытания случайная
величина может, в частности, принять
значение x1.
Поэтому в случае непрерывной случайной
величины имеет смысл говорить о
вероятности попадания случайной величины
в интервал, а не о вероятности того, что
она примет какое-то конкретное
значение.
Так,
например, при изготовлении валика нас
не интересует вероятность того, что его
диаметр будет равен номиналу. Для нас
важна вероятность того, что диаметр
валика не выходит из поля
допуска.
Пример. Плотность
распределения непрерывной случайной
величины задана следующим образом:
График
функции представлен
па рис. 7. Определить вероятность того,
что случайная величина примет
значение, удовлетворяющее неравенствам . Найти
функцию распределения заданной случайной
величины. (Решение)
Найти
функцию распределения заданной случайной
величины. (Решение)
Следующие два пункта посвящены часто встречающимся на практике распределениям непрерывных случайных величин — равномерному и нормальному распределениям.
Дальше…
* Функция называется кусочно-непрерывной на всей числовой оси, если она на любом сегменте или непрерывна, или имеет конечное число точек разрыва I рода. ** Правило дифференцирования интеграла с переменной верхней границей, выведенное в случае конечной нижней границы, остается справедливым и для интегралов с бесконечной нижней границей. В самом деле,
Так как интеграл
есть величина постоянная.
Различают
события зависимые и независимые. Два
события называются независимыми, если
появление одного из них не изменяет
вероятность появления другого. Например,
если в цехе работают две автоматические
линии, по условиям производства не
взаимосвязанные, то остановки этих
линий являются независимыми событиями.
Пример 3. Монета брошена два раза. Вероятность появления «герба» в первом испытании (событие ) не зависит от появления или не появления «герба» во втором испытании (событие ). В свою очередь, вероятность появления «герба» во втором испытании не зависит от результата первого испытания. Таким образом, события и независимые.
Несколько событий называются независимыми в совокупности, если любое из них не зависит от любого другого события и от любой комбинации остальных.
События называются зависимыми, если одно из них влияет на вероятность появления другого. Например, две производственные установки связаны единым технологическим циклом. Тогда вероятность выхода из строя одной из них зависит от того, в каком состоянии находится другая. Вероятность одного события , вычисленная в предположении осуществления другого события , называется условной вероятностью события и обозначается .
Условие
независимости события от
события записывают
в виде ,
а условие его зависимости — в виде . Рассмотрим пример вычисления условной
вероятности события.
Рассмотрим пример вычисления условной
вероятности события.
Пример 4. В ящике находятся 5 резцов: два изношенных и три новых. Производится два последовательных извлечения резцов. Определить условную вероятность появления изношенного резца при втором извлечении при условии, что извлеченный в первый раз резец в ящик не возвращается.
Решение. Обозначим извлечение изношенного резца в первом случае, а — извлечение нового. Тогда . Поскольку извлеченный резец в ящик не возвращается, то изменяется соотношение между количествами изношенных и новых резцов. Следовательно, вероятность извлечения изношенного резца во втором случае зависит от того, какое событие осуществилось перед этим.
Обозначим событие, означающее извлечение изношенного резца во втором случае. Вероятности этого события могут быть такими:
Следовательно, вероятность события зависит от того, произошло или нет событие .
Пло́тность
вероя́тности —
один из способов задания вероятностной
меры на евклидовом
пространстве . В случае, когда вероятностная мера
является распределением
случайной величины,
говорят о плотности случайной
величины.
В случае, когда вероятностная мера
является распределением
случайной величины,
говорят о плотности случайной
величины.
Плотность вероятности Пусть является вероятностной мерой на , то есть определено вероятностное пространство , где обозначает борелевскую σ-алгебру на . Пусть обозначает меру Лебега на .
Определение 1. Вероятность называется абсолютно непрерывной (относительно меры Лебега) (), если любое борелевское множество нулевой меры Лебега также имеет вероятность ноль:
Если вероятность абсолютно непрерывна, то согласно теореме Радона-Никодима существует неотрицательная борелевская функция такая, что
,
где использовано общепринятое сокращение , и интеграл понимается в смысле Лебега.
Определение 2. В более общем виде, пусть — произвольное измеримое пространство, а и — две меры на этом пространстве. Если найдется неотрицательная , позволяющая выразить меру через меру в виде
то такую функцию называют плотностью меры по мере , или производной Радона-Никодима меры относительно меры , и обозначают
.
Случайные процессы
Случайные процессы
ОглавлениеПРЕДИСЛОВИЕЗадания для самопроверки ОСНОВНЫЕ ОБОЗНАЧЕНИЯ ВВЕДЕНИЕ 1. ИСХОДНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ 1.1. Случайная функция, случайный процесс и случайная последовательность 1.2. Математическое ожидание и ковариационная функция случайного процесса Вопросы и задачи 2. НЕКОТОРЫЕ ТИПЫ СЛУЧАЙНЫХ ПРОЦЕССОВ 2.1. Стационарные случайные процессы 2.2. Нормальные процессы 2.3. Процессы с независимыми приращениями 2.4. Винеровский процесс 2.5. Марковские процессы 2.6. Пуассоновский процесс Вопросы и задачи 3. ЭЛЕМЕНТЫ СТОХАСТИЧЕСКОГО АНАЛИЗА 3.1. Сходимость в смысле среднего квадратичного (СК-сходимость) 3.2. Непрерывность случайного процесса 3.3. Дифференцируемость случайного процесса 3.4. Интегрируемость случайного процесса 3.  5. Действие линейного оператора на случайный процесс 5. Действие линейного оператора на случайный процесс3.6. Эргодические случайные процессы Вопросы и задачи 4. СПЕКТРАЛЬНАЯ ТЕОРИЯ СТАЦИОНАРНЫХ СЛУЧАЙНЫХ ПРОЦЕССОВ 4.1. Стационарные случайные процессы с дискретным спектром 4.2. Стационарные случайные процессы с непрерывным спектром 4.3. Белый шум 4.4. Преобразование стационарного случайного процесса при его прохождении через линейную динамическую систему Вопросы и задачи 5. МАРКОВСКИЕ ПРОЦЕССЫ С ДИСКРЕТНЫМИ СОСТОЯНИЯМИ И ЦЕПИ МАРКОВА 5.2. Цепи Маркова 5.3. Уравнения Колмогорова для вероятностей состояний 5.4. Процесс гибели — размножения и циклический процесс Вопросы и задачи 6. ЭЛЕМЕНТЫ ТЕОРИИ МАССОВОГО ОБСЛУЖИВАНИЯ 6.1. Процессы массового обслуживания (основные понятия) 6.2. Простейший поток 6.3. Время ожидания и время обслуживания 6.4. Основные принципы построения марковских моделей массового обслуживания 6.5. Системы массового обслуживания с ожиданием 6.6.  Стационарный режим функционирования системы обслуживания (основные понятия и соотношения) Стационарный режим функционирования системы обслуживания (основные понятия и соотношения)6.7. Стационарные режимы функционирования некоторых вариантов систем обслуживания Вопросы и задачи 7. СТОХАСТИЧЕСКИЕ МОДЕЛИ СОСТОЯНИЯ 7.1. Случайные возмущения в динамической системе 7.2. Линейные стохастические дифференциальные уравнения 7.3. Стохастические интегралы и дифференциалы Вопросы и задачи 8. МАРКОВСКИЕ ПРОЦЕССЫ С НЕПРЕРЫВНЫМИ СОСТОЯНИЯМИ 8.1. Общие свойства марковских процессов 8.2. Уравнения Колмогорова 8.3. Стохастические модели состояния и уравнения Колмогорова 8.4. Постановки задач для нахождения условной функции плотности вероятностей 8.5. Три характерные задачи теории марковских случайных процессов с непрерывными состояниями Вопросы и задачи 9. ЭЛЕМЕНТЫ СТАТИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ 9.2. Статистические моменты случайного процесса 9.3. Постановка задачи оценивания параметров случайного процесса 9.4. Эффективные оценки.  Неравенство Рао — Крамера Неравенство Рао — Крамера9.5. Единственность решения задачи оценивания параметров случайного процесса 9.6. Метод максимального правдоподобия 9.7. Метод наименьших квадратов Вопросы и задачи 10. ОЦЕНИВАНИЕ ПАРАМЕТРОВ СТОХАСТИЧЕСКИХ МОДЕЛЕЙ СОСТОЯНИЯ 10.1. Еще раз о стохастической модели состояния 10.2. Единственность решения задачи параметрической идентификации стохастической модели состояния 10.3. Выбор наблюдаемых переменных 10.4. Специфика задачи оценивания при наличии ошибок измерений 10.5. Фильтр Калмана 10.6. Оценивание параметров при наличии ошибок измерений Вопросы и задачи Приложение 1. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ Приложение 2. МАТРИЧНАЯ ЭКСПОНЕНТА СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ |
Определение сигма-алгебры событий вероятностного пространства
Задавать вопрос
спросил
Изменено 6 лет, 4 месяца назад
Просмотрено 842 раза
$\begingroup$
Предположим, у нас есть выборочное пространство результатов.
Как нам определить подходящую $\sigma$-алгебру событий на этом пространстве выборок, чтобы затем мы могли создать хорошую меру вероятности для событий? Существует ли общая процедура для этого?
Пример из моей книги («Первый взгляд на строгую теорию вероятностей» Дж. Розенталя) состоит в том, чтобы сначала определить вероятностную меру $P$ на подходящей алгебре событий $\mathcal{A}$, а затем расширить $P$ до сгенерированная $\sigma$-алгебра $\sigma(\mathcal{A}$), пусть $\sigma(\mathcal{A})$ — множество событий для нашего вероятностного пространства. Но мне интересно, всегда ли можно найти такую алгебру, оставаясь при этом достаточно широкой, чтобы охватить большинство интересующих нас событий. Я имею в виду, можно ли просто взять произвольный набор $S$ событий, которые нам нужны, расширить его до алгебры, если это еще не сделано, затем до $\sigma$-алгебры, а затем определить хорошую меру на том??? (Я знаю о теореме Каратеодори о продолжении, но она отвечает на мой вопрос только в том случае, когда у нас уже есть мера алгебры событий, которую мы хотели бы иметь в нашем пространстве. Она не отвечает на вопрос, можем ли мы просто расширить произвольный набор событий. события в алгебру, или мы обязательно можем найти хорошую меру на этой алгебре.)
Она не отвечает на вопрос, можем ли мы просто расширить произвольный набор событий. события в алгебру, или мы обязательно можем найти хорошую меру на этой алгебре.)
Извините, если этот вопрос несколько несфокусирован, но у меня общее чувство замешательства по этой теме, поэтому любой ответ, который прояснит ситуацию, будет очень признателен.
- теория вероятностей
$\endgroup$
$\begingroup$
Вам может помочь следующий результат.
Теорема. (Durrett, A.1 (1.3), p.439) Пусть $\mathcal{S}$ — полуалгебра, и пусть $\mu$, определенная на $\mathcal{S}$, имеет $\mu(\emptyset ) = 0$. Предположим (i) если $S \in \mathcal{S}$ является конечным непересекающимся объединением множеств $S_i \in \mathcal{S}$, то $\mu(S) = \sum_i \mu(S_i)$, и (ii) если $S_i, S \in \mathcal{S}$ с $S$ счетным несвязным объединением $S_i$, то $\mu(S) \leq \sum_i \mu(S_i)$. Тогда $\mu$ имеет единственное расширение $\bar{\mu}$, являющееся мерой на $\bar{\mathcal{S}}$, алгебре, порожденной $\mathcal{S}$. Более того, если расширение $\sigma$-конечно, то по теореме Каратеодори существует единственное расширение $\nu$, являющееся мерой на $\sigma(\mathcal{\bar{\mathcal{S}}}) $. 9c)_{ds}$ — замыкание $\mathcal M$ относительно дополнения $c$, конечных пересечений $d$ и конечных объединений $s$. По соглашению пустое объединение равно $\emptyset$, а пустое пересечение есть $\Omega$
Тогда $\mu$ имеет единственное расширение $\bar{\mu}$, являющееся мерой на $\bar{\mathcal{S}}$, алгебре, порожденной $\mathcal{S}$. Более того, если расширение $\sigma$-конечно, то по теореме Каратеодори существует единственное расширение $\nu$, являющееся мерой на $\sigma(\mathcal{\bar{\mathcal{S}}}) $. 9c)_{ds}$ — замыкание $\mathcal M$ относительно дополнения $c$, конечных пересечений $d$ и конечных объединений $s$. По соглашению пустое объединение равно $\emptyset$, а пустое пересечение есть $\Omega$
Мера, определенная на $\mathcal M$, может быть расширена на $Alg(\mathcal M)$ с помощью этого конструктивного подхода.
$\sigma$-алгебра, порожденная семейством подмножеств, имеет гораздо более сложную конструкцию, которую я сам до конца не понимаю. $\mathcal M$ многократно замкнут относительно дополнений и счетных объединений $\sigma$: 9c)_\sigma$
Тогда $\sigma$-алгебра, порожденная $\mathcal M$, есть $\bigcup \mathcal M_i$
Но объединение выполняется до первого порядкового номера с несчетным числом предшественников (!) В противном случае эта конструкция не исчерпывает всех элементов $\sigma$-алгебры
Поэтому гораздо сложнее распространить меру на порожденную $\sigma$-алгебру. На самом деле меру Лебега невозможно распространить на все подмножества $\mathbb R$
На самом деле меру Лебега невозможно распространить на все подмножества $\mathbb R$
$\endgroup$
2
Демистификация теоретической теоретической теории вероятности (Часть 1: Пространства вероятности)
13 Минутный чтение
. некоторых основных понятий теории меры — математического изучения объектов с «размером», — которые позволили мне глубже понять основы теории вероятностей.
Введение
Будучи студентом бакалавриата компьютерных наук, я изучал базовую и неполную версию теории вероятностей, в которой дискретные результаты (например, бросок костей) обрабатываются совершенно иначе, чем непрерывные результаты (например, температура снаружи). Например, математическое ожидание дискретной случайной величины $X$ определяется выражением.
\[E(X) := \sum_x xP(X=x)\]тогда как, если $X$ непрерывен, его математическое ожидание задается как
\[E(X) := \int_x x \ f(x) \ дх\], где $f(x)$ — функция плотности $X$.
Мало того, что я нашел это разделение неудовлетворительным, но, поскольку я продолжал изучать статистику и машинное обучение в аспирантуре, я обнаружил, что оно недостаточно для более глубокого понимания работы тем, которые я изучал.
Я узнал, что это разделение на непрерывные и дискретные распределения на самом деле является мостом через более глубокую и полную теорию вероятностей, основанную на теории меры, которая не только объединяет дискретные и непрерывные сценарии, но и расширяет их.
На самом деле, я был удивлен, узнав, что очень формальное определение вероятности требует теории меры! Как будто самый первый шаг в вероятность погружает в расщелину математики. Неудивительно, что учителя строят мост, чтобы пересечь эту расщелину и вообще избежать теории меры. К сожалению, этот мост достигается за счет менее удовлетворительного и более утомительного объяснения вероятности.
Теоретико-мерная основа вероятности
Я введу несколько терминов в свое определение вероятности, и в следующих разделах мы дадим определение и обсудим каждый из них. Во-первых, формальное определение вероятностное пространство :
Во-первых, формальное определение вероятностное пространство :
Определение 1: вероятностное пространство — это пространство меры ($\Omega$, $E$, $P$), где $P(\Omega) = 1$, где
- set $\Omega$, называется пространством образцов .
- $\sigma$-алгебра над $\Omega$, обозначаемая $E$, называется множеством из событий .
- Мера $P$ для измеримого пространства $(\Omega, E)$ есть вероятностная мера .
$\sigma$-алгебра? Измерить пространство? Давайте представим каждую из этих идей, а затем вернемся к этому полному определению, состоящему из трех частей.
$\sigma$-алгебры
Теория меры полностью посвящена абстрагированию идеи «размера». Что мы понимаем под размером? Размер — это число, которое мы приписываем объекту, который подчиняется определенному интуитивному свойству: если мы разобьем объект на части, размеры частей должны составить размер целого.
Есть много явлений, которые следуют этой базовой идее, подобной «размеру», включая такие явления, как масса, длина и объем (и, как мы увидим позже, вероятность). Например, если у нас есть глиняный шар, и мы разделим его на два, то массы двух меньших глиняных шариков в сумме составят массу исходного глиняного шара.
Прежде чем мы сможем обсудить «размеры» объектов и частей объектов, нам нужен математический способ описания объекта. Теория меры использует множество $F$ для обозначения рассматриваемого нами объекта. Например, $F$ может представлять собой глиняный шарик.
Учитывая наш объект/множество $F$, нам нужен способ описать, как $F$ можно разбить на части. Это понятие «разбиения объекта на части» описывается $\sigma$-алгеброй над $F$:
Определение 2: Для множества $F$ и набора подмножеств $\mathcal{F}$ , набор $\mathcal{F}$ называется 9c$ (дополнение к $A$) также является подходящей фигурой. Наконец, третий критерий устанавливает тот факт, что если мы склеим счетное множество частей вместе, то полученная часть также будет частью объекта.
На самом деле из этих трех аксиом определения $\sigma$-алгебры следует, что $\sigma$-алгебра не только замкнута относительно объединения множеств (т.е. аксиома 3), но и пересечения множеств, множества разности и симметричные разности (см. теоремы 1, 2 и 3 в Приложении в конце этой записи в блоге).
Имея в виду эти свойства, другой способ представить себе это — представить $F$ как треснувшую керамическую пластину. $\sigma$-алгебра описывает все способы, которыми пластина может развалиться по своим «трещинам». Это показано на рисунке ниже:
На этом рисунке большой овал вверху представляет собой керамическую пластину с трещинами вдоль ее поверхности. Пусть точками на пластине будет множество $F$. Ниже мы иллюстрируем каждое подмножество $A \subseteq \mathcal{F}$. Вы можете думать о каждом $A$ как о тарелке с некоторой комбинацией удаленных кусков. Нам разрешено удалять кусок только в том случае, если он окружен трещинами. Весь набор конфигураций способов удаления кусков тарелки есть $\sigma$-алгебра $\mathcal{F}$ над $F$.
Измерение пространств
Итак, мы немного подумали о представлении объектов и частей объекта. Теперь, как мы назначаем каждой части «размер»? Здесь вступает в действие мера. Мера — это просто функция, которая присваивает размер каждой части объекта. Как мы обсуждали ранее, сумма размеров двух частей объекта должна равняться размеру целого, именно так и определяется мера:
Определение 3: При заданном множестве $F$ и $\sigma $-алгебра на $F$, обозначаемая $\mathcal{F}$, функция
является мерой , если для $\mu$ выполняются следующие свойства:
- Неотрицательный: $\forall A \in \mathcal{F}, \mu(A) \geq 0$
- Пустое множество имеет нулевую меру:
- Счетная аддитивность: Дано $A, B \ в \mathcal{F}$, где $A \cap B = \emptyset$,
Первая часть определения требует, чтобы «размер» (то есть мера) не мог быть отрицательным. Это интуитивно понятно. Вторая часть говорит о том, что «нулевой кусок» (т.е. ничего) имеет нулевой размер. Наконец, в третьей части говорится, что сумма размеров двух частей предмета должна равняться размеру двух частей, склеенных вместе.
Это интуитивно понятно. Вторая часть говорит о том, что «нулевой кусок» (т.е. ничего) имеет нулевой размер. Наконец, в третьей части говорится, что сумма размеров двух частей предмета должна равняться размеру двух частей, склеенных вместе.
Схематическое изображение пространства меры показано ниже:
Опять же, мы представляем керамическую пластину и $\sigma$-алгебру, индуцированную кусками, образованными трещинами вдоль пластины. Ниже приведены две иллюстрации аксиомы 3 о счетной аддитивности для меры. Интуитивно понятно, что «размер» двух независимых блоков должен быть суммой размеров отдельных блоков.
Теперь пространство мер — это просто комбинация множества (т. е. объекта), $\sigma$-алгебры (т. е. частей объекта) и меры (т. е. способов описания размеров частей) :
Определение 4: Набор $(F, \mathcal{F}, \mu)$, где $F$ — множество, $\mathcal{F}$ — $\sigma$-алгебра на $F$ , а $\mu$ — мера на $F$, а $\mathcal{F}$ — пространство с мерой .
Рассмотрим последнее определение: измеримое пространство — это пара, состоящая из множества (т. е. объекта) и $\sigma$-алгебры (т. е. частей объекта). Слово «измеримый» в измеримом пространстве намекает на то, что оно может быть снабжено мерой. После того, как он оснащен мерой, он образует полное пространство меры.
Определение 5: Набор $(F, \mathcal{F})$, где $F$ — множество, а $\mathcal{F}$ — $\sigma$-алгебра на $F$, является измеримое пространство .
Назад к вероятности
Теперь, когда у нас есть базовая теория меры, давайте вернемся к определению вероятности. Вероятностное пространство — это просто пространство мер, в котором мера, присвоенная всему объекту, равна единице!
Сначала это может показаться несколько неинтуитивным. Что такое «объект», что такое «кусочки» и что мы подразумеваем под «размером»? Здесь все становится немного философским. Мне нравится думать об этом следующим образом:
- «Объект» $\Omega$, называемый образцом пространства, представляет все мыслимые варианты будущего Вселенной.
 Рассмотрим простой подбрасывание монеты. Прежде чем мы подбросим монету, есть множество мыслимых способов, которыми монета вращается в воздухе и оседает на стол. Набор исходов представляет собой теоретическое представление всех возможных мыслимых вариантов будущего, в которых будет разворачиваться этот процесс.
Рассмотрим простой подбрасывание монеты. Прежде чем мы подбросим монету, есть множество мыслимых способов, которыми монета вращается в воздухе и оседает на стол. Набор исходов представляет собой теоретическое представление всех возможных мыслимых вариантов будущего, в которых будет разворачиваться этот процесс. - $\sigma$-алгебра — это просто способ разделить все эти мыслимые варианты будущего. Каждый из этих разделов называется событием. Например, в некотором наборе фьючерсов монета падает орлом — в этом случае мы бы сказали, что произошло событие «орел». В других фьючерсах монета выпадает решкой. Если происходит одно из этих будущих событий, то мы говорим, что произошло событие «решка».
- Вероятностная мера определяет степень уверенности в отношении каждой части мыслимого будущего. В частности, вероятностная мера присваивает каждому событию e ∈ E значение от 0 до 1, которое представляет нашу степень уверенности в том, что наше будущее будет содержаться в e. В частности, 1 представляет полную уверенность в том, что наше будущее будет содержаться в событии e, а 0 представляет полную уверенность в том, что наше будущее не будет содержаться в e.
 Хотя я должен отметить, что философское определение вероятностной меры является глубокой темой (оно лежит в основе дебатов между частотами и байесовцами).
Хотя я должен отметить, что философское определение вероятностной меры является глубокой темой (оно лежит в основе дебатов между частотами и байесовцами).
Все это вызывает вопрос, а зачем нам для всего этого нужна теория меры? Во-первых, мы видим, что теория меры дает естественное описание неопределенности следующими способами:
- $\sigma$-алгебра дает нам способ гарантировать, что, если мы обсуждаем нашу уверенность в наступлении события, мы также можем обсуждать нашу уверенность в том, что событие не произойдет. То есть дополнение любого элемента $\sigma$-алгебры также находится в $\sigma$-алгебре.
- $\sigma$-алгебра гарантирует, что мы можем обсуждать вероятность объединения и пересечения событий. Тот факт, что $P(\emptyset) := 0$, выражает невозможность того, чтобы в пространстве выборки не возникло никакого результата. То есть мы обязательно увидим какое-то мыслимое будущее.
- Тот факт, что $P(\Omega) := 1$, выражает тот факт, что некоторый исход выборочного пространства обязательно произойдет.
 То есть 1 — это значение, которое соответствует максимальной достоверности.
То есть 1 — это значение, которое соответствует максимальной достоверности. - Неопределенность имеет «размер» в следующем смысле: если у нас есть два непересекающихся события, то вероятность возникновения любого из этих событий должна быть суммой вероятностей отдельных событий. Используя пространство мер для моделирования неопределенности, мы гарантируем, что для $A, B \subset \Omega$, где $A \cap B = \emptyset$, следует, что $P(A \cup B) = P(A) + П(В)$.
Во-вторых, как мы увидим в части 2, эта основа теории вероятностей позволит нам объединить как дискретные, так и непрерывные распределения вероятностей.
Приложение: Теоремы для свойств $\sigma$-алгебр
В следующих теоремах мы доказываем, что $\sigma$-алгебры замкнуты относительно пересечений множеств, разностей и симметричных разностей.
Теорема 1: Пусть $F$ — множество и $\mathcal{F}$ — $\sigma$-алгебра на $F$ с $A, B \in \mathcal{F}$. Затем 9c = A \setminus B$, то $A \setminus B \in \mathcal{F}$.

 Н.Э. Баумана.
Н.Э. Баумана.
 Рассмотрим простой подбрасывание монеты. Прежде чем мы подбросим монету, есть множество мыслимых способов, которыми монета вращается в воздухе и оседает на стол. Набор исходов представляет собой теоретическое представление всех возможных мыслимых вариантов будущего, в которых будет разворачиваться этот процесс.
Рассмотрим простой подбрасывание монеты. Прежде чем мы подбросим монету, есть множество мыслимых способов, которыми монета вращается в воздухе и оседает на стол. Набор исходов представляет собой теоретическое представление всех возможных мыслимых вариантов будущего, в которых будет разворачиваться этот процесс. Хотя я должен отметить, что философское определение вероятностной меры является глубокой темой (оно лежит в основе дебатов между частотами и байесовцами).
Хотя я должен отметить, что философское определение вероятностной меры является глубокой темой (оно лежит в основе дебатов между частотами и байесовцами).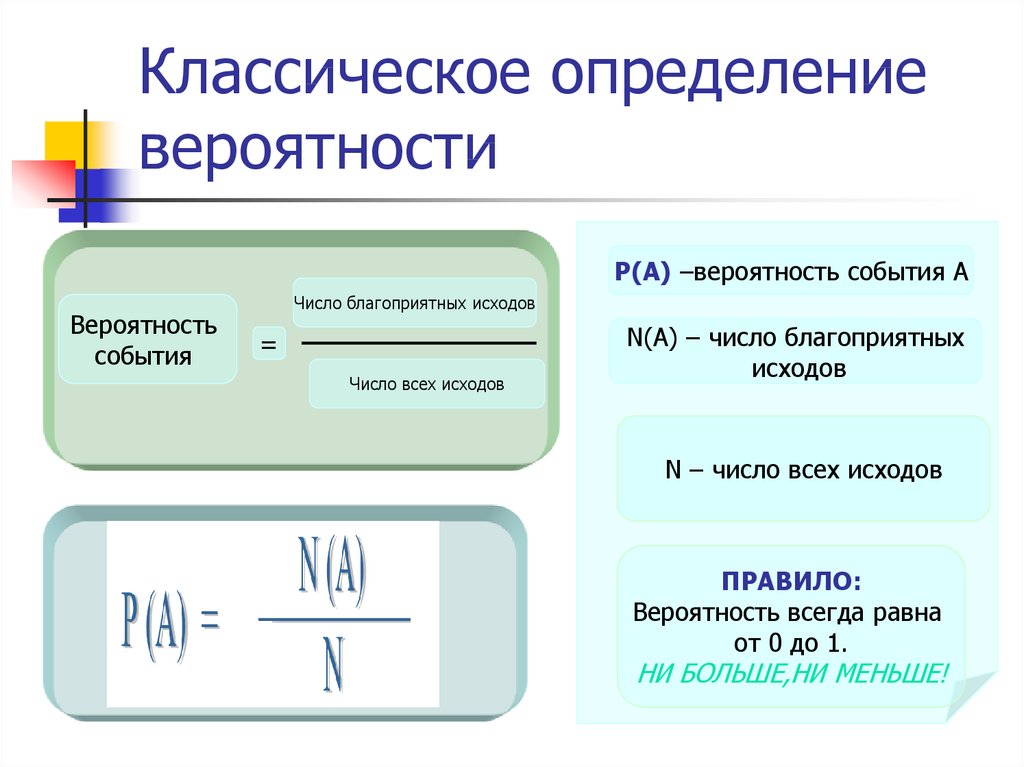 То есть 1 — это значение, которое соответствует максимальной достоверности.
То есть 1 — это значение, которое соответствует максимальной достоверности.