Свойства векторов, свойства скалярного и векторного произведения векторов.
Содержание:
- Действия над векторами
- Свойства операции сложения:
- Свойства умножения вектора на число:
- Свойства скалярного произведения:
- Свойства векторного произведения:
- Свойства смешанного произведения:
В данной теме мы подытожим раздел векторы, опишем все действия, которые можно совершать над векторами и какими свойствами они обладают.
Определение
Вектором называется направленный отрезок $\overline{A B}$ , где точка $A$ — начало, точка $B$ — конец вектора.
Суммой $\overline{a}+\overline{b}$ векторов $\overline{a}$ и
$\overline{b}$ называют такой третий вектор
$\overline{c}$, начало которого совпадает с началом
$\overline{a}$, а конец — с концом
$\overline{b}$ при условии, что конец вектора
$\overline{a}$ и начало вектора
$\overline{b}$ совпадают.
Свойства операции сложения:
1 $\overline{a}+\overline{b}=\overline{b}+\overline{a}$ — коммутативность
2 $(\overline{a}+\overline{b})+\overline{c}=\overline{a}+(\overline{b}+\overline{c})$ — ассоциативность
3 $\overline{a}+\overline{0}=\overline{a}$
4 $\overline{a}+(-\overline{a})=\overline{0}$
Определение
Разностью $\overline{a}-\overline{b}$ векторов $\overline{a}$ и $\overline{b}$ называется вектор $\overline{c}$ такой, что выполняется условие: $\overline{b}+\overline{c}=\overline{a}$.
Произведением $\alpha \overline{a}$ вектора $\overline{a}$ на число $\alpha$ называется вектор $\overline{b}$, удовлетворяющий условиям:
- $\overline{b} \| \overline{a}$
- $|\overline{b}|=|\alpha||\overline{a}|$
- $\overline{a} \uparrow \uparrow \overline{b}$, если
$\alpha>0$,
$\overline{a} \uparrow \downarrow \overline{b}$, если
$\alpha \lt 0$.
Свойства умножения вектора на число:
1 $(\alpha \pm \beta) \overline{a}=\alpha \overline{a} \pm \beta \overline{a}$
2 $\alpha(\overline{a} \pm \overline{b})=\alpha \overline{a} \pm \alpha \overline{b}$
3 $\alpha(\beta \overline{a})=(\alpha \beta) \overline{a}=\beta(\alpha \overline{a})$
4 $1 \cdot \overline{a}=\overline{a}$
5 $-1 \cdot \overline{a}=-\overline{a}$
6 $0 \cdot \overline{a}=\overline{0}$
Определение
Скалярным произведением двух ненулевых векторов $\overline{a}$ и $\overline{b}$ называется число, равное произведению длин этих векторов на косинус угла между ними:
$$\bar{a} \bar{b}=\bar{a} \cdot \bar{b}=(\bar{a}, \bar{b})=|\bar{a}||\bar{b}| \cos (\bar{a}, \bar{b})$$
Свойства скалярного произведения:
1 $(\overline{a}, \overline{b})=(\overline{b}, \overline{a})$ — симметричность.
2 $(\overline{a}, \overline{a})=|\overline{a}|^{2}$.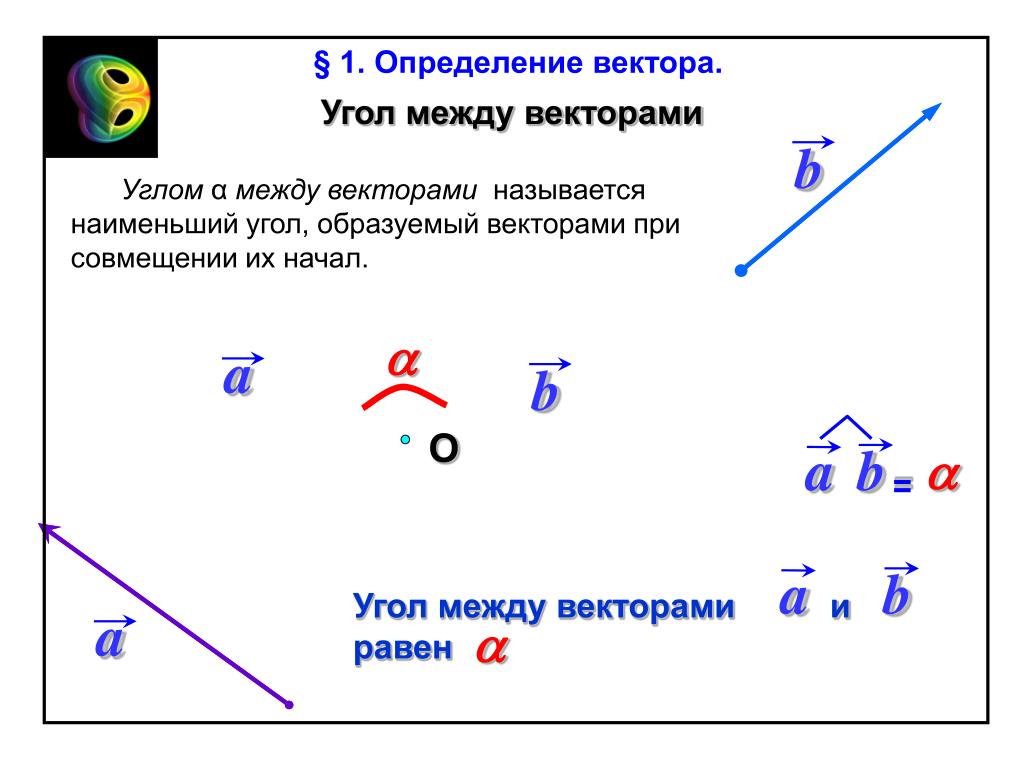
{2}$ и называется скалярный квадрат.
3 Если $\overline{a} \neq \overline{0}$, то $(\bar{a}, \bar{b})=|\bar{a}| \cdot Пр_{\bar{a}} \bar{b}$
4 Если $\overline{a} \neq \overline{0}$ и $\overline{b} \neq \overline{0}$ и $(\overline{a}, \overline{b})=0$, то $\overline{a} \perp \overline{b}$. Верно и обратное утверждение.
5 $(\overline{a}+\overline{b}, \overline{c})=(\overline{a}, \overline{c})+(\overline{b}, \overline{c})$
6 $(\lambda \overline{a}, \overline{b})=\lambda(\overline{a}, \overline{b})$
7 $(\alpha \overline{a}+\beta \overline{b}, \gamma \overline{c}+\delta \overline{d})=\alpha \gamma(\overline{a}, \overline{c})+\alpha \delta(\overline{a}, \overline{d})+\beta \gamma(\overline{b}, \overline{c})+\beta \delta(\overline{b}, \overline{d})$
Определение
Векторным произведением ненулевых векторов $\overline{a}$ и
$\overline{b}$ называется вектор $\overline{c}$,
обозначаемый символом $[\overline{a}, \overline{b}]$ или
$\overline{a} \times \overline{b}$, длина которого
$|\bar{c}|=|\bar{a}||\bar{b}| \sin (\bar{a}, \bar{b})$.
Свойства векторного произведения:
1 $[\overline{a}, \overline{b}]=\overline{0}$, тогда и только тогда, когда $\overline{a} \| \overline{b}$
2 $[\overline{a}, \overline{b}]=-[\overline{b}, \overline{a}]$
3 Модуль векторного произведения $|[\overline{a}, \overline{b}]|$ равен площади параллелограмма, построенного на заданных векторах $\overline{a}$ и $\overline{b}$ (рис. 2), т.е.
$$S=|[\bar{a}, \bar{b}]|=|\bar{a}||\bar{b}| \sin (\bar{a}, \bar{b})$$
4 $[\lambda \overline{a}, \overline{b}]=[\overline{a}, \lambda \overline{b}]=\lambda[\overline{a}, \overline{b}]$
5 $\left[\overline{a}_{1}+\overline{a}_{2}, \overline{b}\right]=\left[\overline{a}_{1}, \overline{b}\right]+\left[\overline{a}_{2}, \overline{b}\right] ;\left[\overline{a}, \overline{b}_{1}+\overline{b}_{2}\right]=\left[\overline{a}, \overline{b}_{1}\right]+\left[\overline{a}, \overline{b}_{2}\right]$
Определение
Смешанным произведением трех векторов $\overline{a}$, $\overline{b}$, $\overline{c}$ называется число, равное скалярному произведению вектора $\overline{a} \times \overline{b}$ на вектор $\overline{c}$: $(\overline{a}, \overline{b}, \overline{c})=([\overline{a}, \overline{b}], \overline{c})$
Свойства смешанного произведения:
1 $(\overline{a}, \overline{b}, \overline{c})=(\overline{a},[\overline{b}, \overline{c}])$
2 $(\overline{a}, \overline{b}, \overline{c})=(\overline{b}, \overline{c}, \overline{a})=(\overline{c}, \overline{a}, \overline{b})=-(\overline{b}, \overline{a}, \overline{c})=-(\overline{c}, \overline{b}, \overline{a})=-(\overline{a}, \overline{c}, \overline{b})$
3 Три вектора компланарны тогда и только тогда, когда $(\overline{a}, \overline{b}, \overline{c})=0$
4 Тройка векторов является правой тогда и только тогда, когда $(\overline{a}, \overline{b}, \overline{c})>0$.
Если же $(\overline{a}, \overline{b}, \overline{c}) \lt 0$, то векторы $\overline{a}$, $\overline{b}$ и $\overline{c}$ образуют левую тройку векторов. \lt /p> \lt p>5 $(\lambda \overline{a}, \overline{b}, \overline{c})=(\overline{a}, \lambda \overline{b}, \overline{c})=(\overline{a}, \overline{b}, \lambda \overline{c})=\lambda(\overline{a}, \overline{b}, \overline{c})$
6 $\left(\overline{a}_{1}+\overline{a}_{2}, \overline{b}, \overline{c}\right)=\left(\overline{a}_{1}, \overline{b}, \overline{c}\right)+\left(\overline{a}_{2}, \overline{b}, \overline{c}\right)$
7 $\left(\overline{a}, \overline{b}_{1}+\overline{b}_{2}, \overline{c}\right)=\left(\overline{a}, \overline{b}_{1}, \overline{c}\right)+\left(\overline{a}, \overline{b}_{2}, \overline{c}\right)$
8 $\left(\overline{a}, \overline{b}, \overline{c}_{1}+\overline{c}_{2}\right)=\left(\overline{a}, \overline{b}, \overline{c}_{1}\right)+\left(\overline{a}, \overline{b}, \overline{c}_{2}\right)$
9 $([\overline{a}, \overline{b}], \overline{c})=\overline{b}(\overline{a}, \overline{c})-\overline{a}(\overline{b}, \overline{c}) ;(\overline{a},[\overline{b}, \overline{c}])=\overline{b}(\overline{a}, \overline{c})-\overline{c}(\overline{a}, \overline{b})$
10 Тождество Якоби: $(\overline{a},[\overline{b}, \overline{c}])+(\overline{b},[\overline{c}, \overline{a}])+(\overline{c},[\overline{a}, \overline{b}])=0$
Читать дальше: примеры решения задач с векторами.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Операции над векторами, формулы и онлайн калькуляторы
Содержание:
- Сложение и вычитание векторов
- Умножение вектора на число
Определение
Линейными операциями над векторами называются операции сложения векторов и умножения вектора на число.
Сложение и вычитание векторов
Определение
Сложение векторов $\overline{a}$ и $\overline{b}$ осуществляется по правилу треугольника.
Суммой $\overline{a}+\overline{b}$ двух векторов $\overline{a}$ и $\overline{b}$ называют такой третий вектор
$\overline{c}$, начало которого совпадает с началом
$\overline{a}$, а конец — с концом
$\overline{b}$ при условии, что конец вектора
$\overline{a}$ и начало вектора
$\overline{b}$ совпадают (рис.
Для сложения векторов применяется также правило параллелограмма.
Определение
Правило параллелограмма — если два неколлинеарных вектора $\overline{a}$ и $\overline{b}$ привести к общему началу, то вектор $\overline{c}=\overline{a}+\overline{b}$ совпадает с диагональю параллелограмма, построенного на векторах $\overline{a}$ и $\overline{b}$ (рис. 2). Причем начало вектора $\overline{c}$ совпадает с началом заданных векторов.
Определение
Вектор $-\overline{a}$ называется противоположным вектором к вектору $\overline{a}$, если он коллинеарен вектору $\overline{a}$, равен ему по длине, но направлен в противоположную сторону вектору $\overline{a}$.
Операция сложения векторов обладает следующими свойствами:
- $\overline{a}+\overline{b}=\overline{b}+\overline{a}$ — коммутативность
- $(\overline{a}+\overline{b})+\overline{c}=\overline{a}+(\overline{b}+\overline{c})$ — ассоциативность
- $\overline{a}+\overline{0}=\overline{a}$
- $\overline{a}+(-\overline{a})=\overline{0}$
Определение
Разностью $\overline{a}-\overline{b}$ векторов $\overline{a}$ и $\overline{b}$ называется вектор $\overline{c}$
такой, что выполняется условие: $\overline{b}+\overline{c}=\overline{a}$ (рис.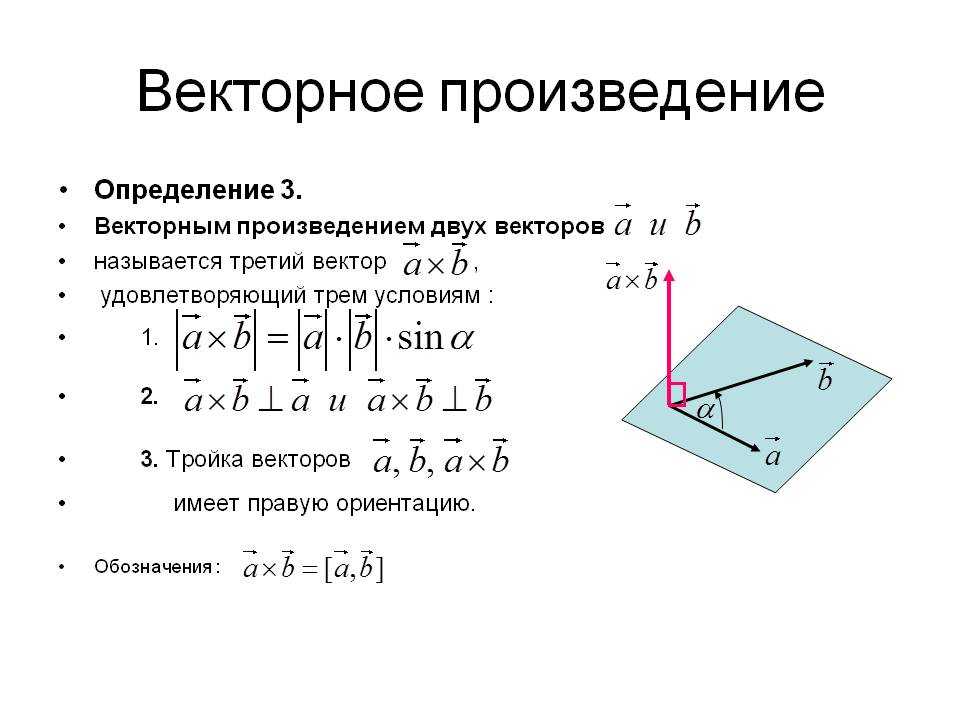
3).
Умножение вектора на число
Определение
Произведением $\alpha \overline{a}$ вектора $\overline{a}$ на число $\alpha$ называется вектор $\overline{b}$, удовлетворяющий условиям:
- $\overline{b}\|\overline{a}$
- $|\overline{b}|=|\alpha||\vec{a}|$
- $\overline{a} \uparrow \uparrow \overline{b}$, если $\alpha>0$, $\overline{a} \uparrow \downarrow \overline{b}$, если $\alpha \lt 0$.
Свойства умножения вектора на число:
- $(\alpha \pm \beta) \overline{a}=\alpha \overline{a} \pm \beta \overline{a}$
- $\alpha(\overline{a} \pm \overline{b})=\alpha \overline{a} \pm \alpha \overline{b}$
- $\alpha(\beta \overline{a})=(\alpha \beta) \overline{a}=\beta(\alpha \overline{a})$
- $1 \cdot \overline{a}=\overline{a}$
- $-1 \cdot \overline{a}=-\overline{a}$
- $0 \cdot \overline{a}=\overline{0}$
Здесь $\overline{a}$ и
$\overline{b}$ — произвольные векторы,
$\alpha$,
$\beta$ — произвольные числа.
Читать дальше: разложение вектора на составляющие.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Определение и значение вектора — Merriam-Webster
1 из 2
вектор ˈvek-tər
1
а
: Величина, которая имеет величину и направление и обычно изображается направленным отрезком, длина которого представляет величину, а ориентация в пространстве представляет направление
широко : элемент векторного пространства
б
: курс или направление по компасу, особенно самолета
2
а
: организм (например, насекомое), который передает патоген от одного организма или источника к другому
Насекомым-переносчиком малярии является комар-анофелин, род, включающий множество видов по всему миру.
Фрэнк Грэм-младший, 9 лет0003
сравнить датчик носителя 5a, датчик резервуара 3
б
: чувство опылителя
3
: агент (такой как плазмида или вирус), который содержит или переносит модифицированный генетический материал (такой как рекомбинантная ДНК) и может быть использован для введения экзогенных генов в геном организма
вектор прилагательное
векторный
век-ˈtȯr-ē-əl
имя прилагательное
векторно
век-ˈtȯr-ē-ə-lē
наречие
вектор
2 из 2
переходный глагол
1
: направлять (что-то или кого-то, например, самолет, его пилота или ракету) в полете с помощью радио вектора
2
: менять направление (тяги реактивного двигателя) для рулевого управления
Примеры предложений
Существительное комар главный переносчик желтой лихорадки
Последние примеры в Интернете
На своем веб-сайте Национальный центр по борьбе с трансмиссивными заболеваниями перечисляет использование этих репеллентов от комаров в качестве одной из нескольких стратегий борьбы с переносчиками .
Моника Мондал, 9 лет0083 ПРОВОДНАЯ , 15 октября 2022 г.
Организации — как государственные, так и частные — должны активно защищать свои атаки номер один вектор : веб-приложения и API-интерфейсы.
Сонали Шах, Forbes , 8 августа 2022 г.
Вместо потокового видео этот сервис просто обслуживал текстовые данные и векторных графических файла NAPLPS.
Бендж Эдвардс, 9 лет0083 Ars Technica , 27 октября 2022 г.
Обычно переносчиком служат насекомые, питающиеся соком (тли, цикадки, трипсы и др.), поскольку вирус или фитоплазма не могут выжить вне растительной ткани.
Мири Талабак, Балтимор, солнце , 28 июля 2022 г.
Российские дипломаты также стали ключевым вектором дезинформации.
Дэвид Клеппер, 9 лет0083 ajc , 19 мая 2022 г.
С появлением социальных сетей как вектора дезинформации неверная информация часто распространяется по нескольким каналам, таким как Facebook, Twitter, Reddit и т. д.
Пранав Десаи, Forbes , 16 мая 2022 г.
В Соединенных Штатах одинокий звездчатый клещ, обитающий преимущественно на юго-востоке, был идентифицирован как вектор 9.0084 . New York Times , 9 мая 2022 г.
На вопрос, как Facebook относится к превращению Китая в вектора российской пропаганды, Facebook привел несколько примеров проверки фактов, применяемых к вводящему в заблуждение пророссийскому контенту китайских государственных СМИ. Washington Post , 8 апреля 2022 г.
Вентиляторы также имеют отдельные закрылки с вектором тяги.
Рохит Джагги, Отчет Робба , 15 августа 2022 г.
Эта способность направлять крутящий момент на тягу должна наделить электромобиль Hummer беспрецедентной способностью продолжать движение вперед даже в самых суровых скользких условиях.
Уэс Силер, Снаружи Онлайн , 21 окт. 2020 г.
В 1998 году во Флориде появилось насекомое под названием азиатская цитрусовая листоблошка (ACP), которое вызвало беспокойство, поскольку было известно, что оно является переносчиком этой болезни, питаясь соком дерева.
Стивен Сэвидж, Forbes , 26 января 2022 г.
Благодаря своим массивным шинам, полному приводу и крутящему моменту , управляемому задним дифференциалом , Urus давал 1,04 g сцепления с тормозной площадкой и останавливался со скорости 70 миль в час на 150 футах, что в основном соответствовало результатам стандартной версии.
Скотт Олдхэм, 9 лет0083 Автомобиль и водитель , 19 марта 2020
В уличной версии передние электродвигатели генерируют векторный эффект крутящего момента, который управляет тягой при повороте.
Эрик Адамс, Wired , 17 февраля 2020 г.
Тестовый автомобиль, полноприводная модель Elite, использует компьютеризированный крутящий момент , векторизируя для передачи до 70% крутящего момента трансмиссии между осями и 100% между колесами для лучшего сцепления при прохождении поворотов.
Служба новостей Трибуна, Кливленд , 25 января 2020 г.
Пакет Sport Chrono, который включает вектора крутящего момента с механическим дифференциалом повышенного трения, также входит в стандартную комплектацию.
Коннор Хоффман, Автомобиль и водитель , 15 января 2020 г.
Оба использовали более широкую разрушительную энергию — от укоренившихся партийных учреждений к более популистской и общенациональной направленности .0084 политика.
Фред Бауэр, National Review , 13 декабря 2019 г.
Узнать больше
Эти примеры предложений автоматически выбираются из различных онлайн-источников новостей, чтобы отразить текущее использование слова «вектор». Мнения, выраженные в примерах, не отражают точку зрения Merriam-Webster или ее редакторов. Отправьте нам отзыв.
История слов
Этимология
Существительное
ранее, сокращение от радиус-вектора, заимствовано из латыни, «перевозчик, конвейер», от vec- , альтернативная основа vehere «перевозить, нести» + -tor , суффикс агента — more at way entry 1
Первое известное употребление
Существительное
1846, в значении, определенном в смысле 1a
Глагол
1941, в значении, определенном в смысле 1
Путешественник во времени
Первое известное использование вектора было
в 1846 г.
Посмотреть другие слова того же года векторограф
вектор
сложение векторов
Посмотреть другие записи поблизости
Процитировать эту запись «Вектор.»
Словарь Merriam-Webster.com , Merriam-Webster, https://www.merriam-webster.com/dictionary/vector. По состоянию на 27 ноября 2022 г.вектор
ˈvek-tər
1
: величина, имеющая величину и направление и обычно изображаемая отрезком линии с заданным направлением и длиной, представляющей величину
2
: организм (как насекомое), который переносит и передает болезнетворный микроб
Медицинское определение
переносчик 1 из 2
вектор ˈvek-tər
1
: величина, которая имеет величину и направление и обычно изображается частью прямой линии с заданным направлением и длиной, представляющей величину
2
: организм (как насекомое), передающее патоген от одного организма или источника к другому
блохи являются переносчиками чумы
сравните смысл переносчика 1a, смысл резервуара 2
3
: агент (в виде плазмиды или вируса), который содержит или несет модифицированный генетический материал (в виде рекомбинантной ДНК) и может быть использован для введения экзогенных генов в геном организма
векторный
век-ˈtōr-ē-əl, -ˈtȯr-
имя прилагательное
вектор
2 из 2
: передавать (патоген или болезнь) от одного организма к другому : действовать как переносчик
болезнь, переносимая мухами
Еще от Merriam-Webster о векторе
Нглиш: перевод вектора для говорящих на испанском языке
Britannica English: Перевод вектора для говорящих на арабском языке Последнее обновление: — Обновлены примеры предложений
Подпишитесь на крупнейший словарь Америки и получите тысячи дополнительных определений и расширенный поиск без рекламы!
Merriam-Webster без сокращений
определение вектора в The Free Dictionary
вектор·тор
(vĕk′tər) сущ.
1. Математика
а. Величина, такая как скорость, полностью заданная величиной и направлением.
б. Одномерный массив.
в. Элемент векторного пространства.
2. Организм, такой как комар или клещ, который переносит болезнетворные микроорганизмы от одного хозяина к другому.
3. Бактериофаг, плазмида или другой агент, переносящий генетический материал из одной клетки в другую.
4. Сила или влияние.
5. Курс или направление самолета.
тр.в. векторный , векторный , векторный
Направлять (например, пилота или самолет) посредством радиосвязи по векторам.
[латиница, перевозчик , от vehere, vect-, до нести ; см. wegh- в индоевропейских корнях.]
vec·to′ri·al (vĕk-tôr′ē-əl) прил.
Словарь английского языка American Heritage®, пятое издание. Авторские права © 2016, издательство Houghton Mifflin Harcourt Publishing Company. Опубликовано издательством Houghton Mifflin Harcourt Publishing Company. Все права защищены.
вектор
(ˈvɛktə)n
1. (Математика) математика Также называется: полярный вектор переменная величина, такая как сила, которая имеет величину и направление и может быть разложена на компоненты, являющиеся нечетными функциями координат. В печати он представлен жирным курсивом: F или ̄F . Сравнить псевдоскаляр, псевдовектор, скаляр 1 , тензор 2
2. (Математика) математика элемент векторного пространства
3. (Патология) патол Также называется: носитель организм, особенно насекомое, которое переносит болезнетворный микроорганизм от одного хозяина к другому либо внутри, либо на поверхности своего тела
4 (Генетика) генетика Также называется: клонирующий вектор агент, такой как бактериофаг или плазмида, с помощью которого фрагмент чужеродной ДНК встраивается в клетку-хозяин для получения генного клона в генной инженерии
5.
(навигация) Направление курса или компас самолета
6. Любое поведенческое влияние, сила, или привод
VB ( TR )
7. (NAVGEGE направлять или направлять (пилота, самолета и т. д.) по направлениям, передаваемым по радио
8. (воздухоплавание) изменять направление (тяги реактивного двигателя) как средство управления самолетом
[C18 : с латыни: носитель, от vehere to convey]
vectorial adj
vecˈtorially adv
Collins English Dictionary – Complete and Unabridged, 12th Edition 2014 © HarperCollins Publishers 1991, 1994, 1998, 2000, 2003, 2006, 2007, 2009, 2011, 2014
вектор
(ˈvɛk tər)н.
1. величина, обладающая как величиной, так и направлением, как сила или скорость. Сравните скаляр (определ. 4).
2. направление или курс чего-либо, например самолета.
3.
а. что-то или кто-то, как человек или насекомое, которое переносит и передает болезнетворный организм.
б. любой агент, как мутировавший вирус, который действует как носитель или переносчик.
в.т.4.
а. , чтобы направлять (самолет) в полете, выдавая соответствующие заголовки.
б. для изменения направления (тяги реактивного или ракетного двигателя) для управления кораблем.
[1695–1705; < латинский: тот, который переносит, производное от vehere переносить]
vec•to′ri•al (-ˈtɔr i əl, -ˈtoʊr-) прил.
век•тори•ал•лы, нар.
Рэндом Хаус Словарь колледжа Кернермана Вебстера, © 2010 K Dictionaries Ltd. Авторские права Random House, Inc., 2005, 1997, 1991. Все права защищены.
вектор
(vĕk′tər) 1. Величина, такая как скорость или изменение положения, которая имеет как величину, так и направление.