Определитель грамма: Недопустимое название | Математика | Fandom

Грама. Определитель Грамма, его геометрический смысл

   Пусть — система векторов в евклидовом (унитарном) пространстве.

   Матрицей Грама данной системы векторов называется матрица вида: .

       Матрице Грама поставим в соответствие ее определитель: .

Свойства определителя Грама:

1. 

2.  — линейно зависимы.

3.  Для,- квадрат длины вектора.

,- квадрат площади.

,- квадрат объема.

,- квадрат объема-мерного параллелепипеда, со сторонами.

    4. Процесс ортогонализации Грама-Шмидта не меняет определитель Грама.

Для доказательства этого установим, что если к одному из векторов прибавить линейную комбинацию остальных, состоящую из одного вектора, то определитель не изменится. 

Умножим первый столбец на и прибавим к-тому столбцу:

 

умножим первую строку на и прибавим к-той строке, получим определитель Грама:

.

Что и требовалось доказать.

Используя это обстоятельство, мы ортогонализируем систему векторов методом Грама-Шмидта: 

, где. Следовательно

  .

 

При этом, для ,- квадрат площади,

для ,- квадрат объема исходного параллелепипеда.

Чтобы найти высоту  , опущенную изна основаниедостаточно вычислить.

Скалярное произведение в произвольном базисе

 

Пусть — базис евклидова пространства,

                       ,

рассмотрим скалярное произведение:

 

=

                                       (*)

Если записать (*) в матричном виде, то получим:

.

Если базис — ортонормированный, то, то

 

.

 

Ортогональное дополнение подпространства m из l

 

Пусть  — евклидово (унитарное) пространство, подпространство. Векторназываетсяортогональным  к  подпространству,  если  для всех.

                    Множество всех  векторов ортогональных  к  подпространству называется ортогональным дополнением и обозначается.

Очевидно,  

М^┴является подпространством пространства, причем для  размерности подпространств   и размерность пространства связаны соотношением

                                   .

Действительно,  выберем базис  подпространства, дополним его до базиса, получим. Ортогонализируем  данный базис методом Грамма-Шмидта, получим:- базис пространства,

 — базис подпространства,- базис  подпространства  ортогонального дополнения.

Говорят, что пространство является прямой ортогональной суммой своих подпространств и  :

Прямая сумма подпространств

Пространство являетсяпрямой суммой подпространств, если

1. любой вектор представляется в виде, где

2. представление единственно.

Обозначается   .

Если пространство

евклидовои выполняется дополнительно условие

3.  при,

то прямая сумма состоит из попарно ортогональных подпространств (ортогональная сумма) и обозначается так

Билет 12+13

Теорема. Пусть — линейный оператор в евклидовом (унитарном) пространстве. Сопоставим ему билинейную (полуторалинейную) функцию,. Это соответствие является биекцией между операторами и билинейными (полуторалинейными) функциями.

Рассмотрим билинейную (полуторалинейную) функцию , заданную формулой. Тогда матрица для функциив ортонормированном базисе— это матрица, т.е.. Будем говорить, что функцияопределяетсопряженный оператор . Более подробно

Определение. Сопряженным оператором к оператору называется такой оператор, который удовлетворяет равенству.

Определение. Оператор называется

самосопряженным или симметричным (эрмитовым), если , т.е.. Операторназываетсякососимметричным ( косоэрмитовым), если , т.е.. Операторназываетсяортогональным (унитарным для ), если.

Теорема. Пусть — ортонормальный базис в евклидовом (унитарном) пространстве, и— линейный оператор. Операторявляется самосопряженным (эрмитовым) тогда и только тогда, когда его матрица в базисесимметрична(эрмитова).

Теорема. Пусть — ортонормальный базис в евклидовом (унитарном) пространстве, и— линейный оператор. Операторявляется кососимметричным (косоэрмитовым) тогда и только тогда, когда его матрица в базисекососимметрична(косоэрмитова).

Лемма. Если — инвариантное подпространство для самосопряженного операторав евклидовом (унитарном) пространстве, тотоже инвариантно относительно.

Лемма. Пусть — самосопряженный оператор на-мерном евклидовом пространстве. Тогда длясуществует собственный вектор.

Теорема. Для всякого самосопряженного оператора в-мерном евклидовом (унитарном) пространствесуществует ортонормальный базис, состоящий из собственных векторов оператора, т.е. в таком базисе матрица оператора диагональна. Матрицаоператораодна и та же во всех таких канонических базисах, с точностью до перестановки диагональных элементов. Верно и обратно.

Замечание. В унитарном пространстве все собственные числа для самосопряженного операторавещественны,.

Если (— евклидово или унитарное пространство) — собственные векторы с разными собственными значениямидля самосопряженного оператора, то, так как.

Следствие. Для всякой (эрмитовой) квадратичной функции в-мерном евклидовом (унитарном) пространствесуществует ортонормальный базис, в котором().

При этом, системане зависит от выбора базиса, с точностью до перестановок.

Пусть — ортогональный (унитарный) оператор в евклидовом (унитарном) пространстве. Тогда, т.е.. Если— собственное значения, то, так как.

Лемма. Ортогональный (унитарный) оператор невырожден.

Теорема.Следующие свойства линейного оператора в-мерном евклидовом (унитарном) пространстве равносильны.

— ортогональный (унитарный) оператор.

В любом ортонормальном базисе матрица оператораортогональна (унитарна, т.е.).

В некотором ортонормальном базисе матрица оператораортогональна (унитарна).

Оператор переводит любой ортонормальный базис в ортонормальный базис.

Оператор переводит некоторый ортонормальный базис в ортонормальный базис.

Лемма. Если — ортогональный (унитарный) оператор в евклидовом (унитарном) пространстве, и— инвариантное дляподпространство в, то ортогональное дополнениетакже является инвариантным подпространством для.

Лемма. Пусть — ортогональный оператор без собственных векторов в-мерном евклидовом пространстве. Тогда в ортонормальном базисе его матрицаимеет вид.

Теорема. Для всякого ортогонального (унитарного) оператора в-мерном евклидовом (унитарном) пространстве существует ортонормальный базис, в котором матрица оператора имеет вид:

для евклидова случая и , где, для унитарного пространства.

Определение. Пусть — самосопряженный оператор в-мерном евклидовом пространстве. Он определяет билинейную функцию, заданную формулой. Операторназываетсяположительно определенным, если — положительно определенная симметрическая функция, т.е.для любого вектора.

Лемма. Для всякого невырожденного оператора в-мерном евклидовом пространствепроизведениеявляется положительно определенным самосопряженным оператором.

Лемма. Самосопряженный оператор в-мерном евклидовом пространствеявляется положительно определенным тогда и только тогда, когда все собственные значения дляположительны.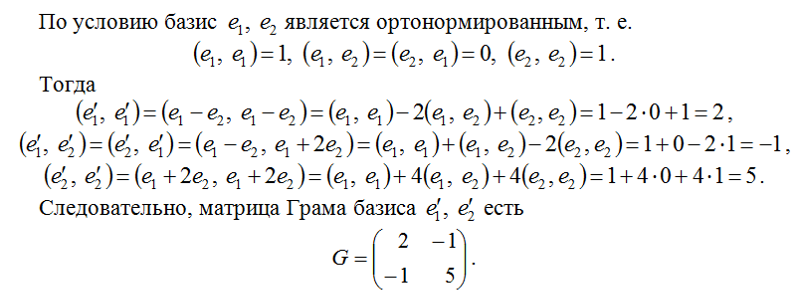

Лемма. Для всякого невырожденного положительно определенного самосопряженного оператора в-мерном евклидовом пространствесуществует такой невырожденный положительно определенный самосопряженный оператор, что.

Теорема.[о полярном разложении] Всякий невырожденный линейный оператор в-мерном евклидовом пространствеможет быть разложен в произведение, где— ортогональный оператор, а— самосопряженный положительно определенный оператор.

Билет 14

Билинейные функции

Определение.Пусть— линейное пространство над полем. Тогда отображениеназываетсябилинейной функцией, если

для любых векторови любых чисел,

для любых векторови любых чисел.

Определение.Матрицейбилинейной функциив базисеназывается матрица, где.

Теорема.Пусть— базис-мерного линейного пространства. Тогда для любой квадратной матрицыпорядкасуществует, причем единственная, билинейная функцияна пространствес матрицейв базисе. При этом значения, гдеи, могут быть найдены по формуле.

Замечание.Билинейные функцииобразуют линейное пространство. Линейная комбинация двух функций— это функция, заданная формулой.

Если зафиксировать базис в пространстве , то мы получаем изоморфизм из пространства билинейных функций в пространствоквадратных матриц порядканад полем.

Лемма.Пустьи— матрицы размераисоответственно. Тогда.

Теорема.Еслии— матрицы билинейной функциив разных базисахипространства, то, гдематрица перехода от базисак, т.е..

Определение.Билинейная функцияназываетсясимметрической, еслидля любых векторов.

Билинейная функция называетсякососимметрической, еслидля любых векторов.

Теорема.Если матрицабилинейной функциив некотором базисе симметрическая (кососимметрическая), т.е.(), то функцияявляется симметрической (кососимметрической) билинейной функцией.

Если билинейная функцияявляется симметрической (кососимметрической), то ее матрицав любом базисе симметрическая (кососимметрическая).

Определение.Пусть— линейное пространство над полем. Функцияназываетсяполуторалинейной, если

для любых векторови любых чисел,

для любых векторови любых чисел.

Для полуторалинейной функции имеем .

Определение.Полуторалинейная функцияназываетсяэрмитовой, если.

Теорема.Если матрицаполуторалинейной функциив некотором базисе эрмитова, т.е., то функцияявляется эрмитовой полуторалинейной функцией.

Если полуторалинейная функцияявляется эрмитовой, то ее матрицав любом базисе эрмитова, т.е..

Определение.Рангомбилинейной функцииназывается рангее матрицыв некотором базисе.

Замечание.При умножении на невырожденную матрицу ранг не меняется, поэтому определение ранга функции корректно. Заметим, чтотогда и только тогда, когда.

Определение.Ядросимметрической билинейной функции— это множестводля любого.

Теорема.Ядро симметрической билинейной функциина-мерном линейном пространствеявляется подпространством размерности.

Теория матриц

Теория матриц

Гантмахер Ф.Р. Теория матриц. – М.: Наука, 1968. — 576 с. Оглавление Предисловие автора к первому изданию Предисловие автора ко второму изданию ЧАСТЬ I. ОСНОВЫ ТЕОРИИ Глава I. Матрицы и действия над ними § 1. Матрицы. Основные обозначения § 2. Сложение и умножение прямоугольных матриц § 3. Квадратные матрицы § 4. Ассоциированные матрицы. Миноры обратной матрицы § 5. Обращение прямоугольных матриц. Псевдообратная матрица Глава II. Алгоритм Гаусса и некоторые его применения § 1. Метод исключения Гаусса § 2. Механическая интерпретация алгоритма Гаусса § 3. Детерминантное тождество Сильвестра § 4. Разложение квадратной матрицы на треугольные множители § 5. Разбиение матрицы на блоки. Техника оперирования с блочными матрицами. Обобщенный алгоритм Гаусса Глава III. Лииейиые операторы в n-мерном векторном пространстве § 1. Векторное пространство § 2. Линейный оператор, отображающий n-мерное пространство в m-мерное § 3. Сложение и умножение линейных операторов § 4. Преобразование координат § 5. Эквивалентные матрицы. Ранг оператора. Неравенства Сильвестра § 6. Линейные операторы, отображающие n-мерное пространство само в себя § 7. Характеристические числа и собственные векторы линейного оператора § 8. Линейные операторы простой структуры Глава IV. Характеристический и минимальный многочлены матрицы § 1. Сложение и умножение матричных многочленов § 2. Правое и левое деление матричных многочленов. Обобщенная теорема Безу § 3. Характеристический многочлен матрицы. Присоединенная матрица § 4. Метод Д. К. Фаддеева одновременного вычисления коэффициентов характеристического многочлена и присоединенной матрицы § 5. Минимальный многочлен матрицы Глава V. Функции от матрицы § 1. Определение функции от матрицы § 2. Интерполяционный многочлен Лагранжа–Сильвестра § 3. Другие формы определения f(A). Компоненты матрицы A § 4. Представление функций от матриц рядами § 5. Некоторые свойства функций от матриц § 6. Применение функций от матрицы к интегрированию системы линейных дифференциальных уравнений с постоянными коэффициентами § 7. Устойчивость движения в случае линейной системы Глава VI. Эквивалентные преобразования многочленных матриц. Аналитическая теория элементарных делителей § 1. Элементарные преобразования многочленной матрицы § 2. Канонический вид матрицы § 3. Инвариантные многочлены и элементарные делители многочленной матрицы § 4. Эквивалентность линейных двучленов § 5. Критерий подобия матриц § 6. Нормальные формы матрицы § 7. Элементарные делители матрицы f(A) § 8. Общий метод построения преобразующей матрицы § 9. Второй метод построения преобразующей матрицы Глава VII. Структура линейного оператора в n-мерном пространстве (геометрическая теория элементарных делителей) § 1. Минимальный многочлен вектора, пространства (относительно заданного линейного оператора) § 2. Расщепление на инвариантные подпространства с взаимно простыми минимальными многочленами § 3. Сравнения. Надпространство § 4. Расщепление пространства на циклические инвариантные подпространства § 5. Нормальная форма матрицы § 6. Инвариантные многочлены. Элементарные делители § 7. Нормальная жорданова форма матрицы § 8. Метод акад. А. Н. Крылова преобразования векового уравнения Глава VIII. Матричные уравнения § 1. Уравнение AX=XB § 2. Частный случай: A=B. Перестановочные матрицы § 3. Уравнение AX-XB=C § 4. Скалярное уравнение f(X)=0 § 5. Матричное многочленное уравнение § 6. Извлечение корня m-й степени из неособенной матрицы § 7. Извлечение корня m-й степени из особенной матрицы § 8. Логарифм матрицы Глава IX. Линейные операторы в унитарном пространстве § 1. Общие соображения § 2. Метризация пространства § 3. Критерий Грама линейной зависимости векторов § 4. Ортогональное проектирование § 5. Геометрический смысл определителя Грама и некоторые неравенства § 6. Ортогонализация ряда векторов § 7. Ортонормированный базис § 8. Сопряженный оператор § 9. Нормальные операторы в унитарном пространстве § 10. Спектр нормальных, эрмитовых, унитарных операторов § 11. Неотрицательные и положительно определенные эрмитовы операторы § 12. Полярное разложение линейного оператора в унитарном пространстве. Формулы Кэли § 13. Линейные операторы в евклидовом пространстве § 14. Полярное разложение оператора и формулы Кэли в евклидовом пространстве § 15. Коммутирующие нормальные операторы § 16. Псевдообратный оператор Глава X. Квадратичные и эрмитовы формы § 1. Преобразование переменных в квадратичной форме § 2. Приведение квадратичной формы к сумме квадратов. Закон инерции § 3. Метод Лагранжа приведения квадратичной формы к сумме квадратов. Формула Якоби § 4. Положительные квадратичные формы § 5. Приведение квадратичной формы к главным осям § 6. Пучок квадратичных форм § 7. Экстремальные свойства характеристических чисел регулярного пучка форм § 8. Малые колебания системы с n степенями свободы § 9. Эрмитовы формы § 10. Ганкелевы формы ЧАСТЬ II. СПЕЦИАЛЬНЫЕ ВОПРОСЫ И ПРИЛОЖЕНИЯ Глава XI. Комплексные симметричные, кососимметрические и ортогональные матрицы § 1. Некоторые формулы для комплексных ортогональных и унитарных матриц § 2. Полярное разложение комплексной матрицы § 3. Нормальная форма комплексной симметрической матрицы § 4. Нормальная форма комплексной кососимметрической матрицы § 5. Нормальная форма комплексной ортогональной матрицы ГЛАВА XII. СИНГУЛЯРНЫЕ ПУЧКИ МАТРИЦ § 1. Введение § 2. Регулярный пучок матриц § 3. Сингулярные пучки. Теорема о приведении § 4. Каноническая форма сингулярного пучка матриц § 5. Минимальные индексы пучка § 6. Сингулярные пучки квадратичных форм § 7. Приложения к дифференциальным уравнениям ГЛАВА XIII. МАТРИЦЫ С НЕОТРИЦАТЕЛЬНЫМИ ЭЛЕМЕНТАМИ § 1. Общие свойства § 2. Спектральные свойства неразложимых неотрицательных матриц § 3. Разложимые матрицы § 4. Нормальная форма разложимой матрицы § 5. Примитивные и импримитивные матрицы § 6. Стохастические матрицы § 7. Предельные вероятности для однородной цепи Маркова с конечным числом состояний § 8. Вполне неотрицательные матрицы § 9. Осцилляционные матрицы Глава XIV. Различные критерии регулярности и локализации собственных значений § 1. Критерий регулярности Адамара и его обобщения § 2. Норма матрицы § 3. Распространение критерия Адамара на блочные матрицы § 4. Критерий регулярности Фидлера § 5. Круги Гершгорина и другие области локализации Глава XV. Приложения теории матриц к исследованию систем линейных дифференциальных уравнений § 1. Системы линейных дифференциальных уравнений с переменными коэффициентами. Общие понятия § 2. Преобразование Ляпунова § 3. Приводимые системы § 4. Каноническая форма приводимой системы. Теорема Еругина § 5. Матрицант § 6. Мультипликативный интеграл. Инфинитезимальное исчисление Вольтерра § 7. Дифференциальные системы в комплексной области. Общие свойства § 8. Мультипликативный интеграл в комплексной области § 9. Изолированная особая точка § 10. Регулярная особая точка § 11. Приводимые аналитические системы § 12. Аналитические функции от многих матриц и их применение к исследованию дифференциальных систем. Работы И. A. Лaппo-Данилевского ГЛАВА XVI. ПРОБЛЕМА РАУСА-ГУРВИЦА И СМЕЖНЫЕ ВОПРОСЫ § 1. Введение § 2. Индексы Коши § 3. Алгоритм Рауса § 4. Особые случаи. Примеры § 5. Теорема Ляпунова § 6. Теорема Рауса-Гурвица § 7. Формула Орландо § 8. Особые случаи в теореме Рауса — Гурвица § 9. Метод квадратичных форм. Определение числа различных вещественных корней многочлена § 10. Бесконечные ганкелевы матрицы конечного ранга § 11. Определение индекса произвольной рациональной дроби через коэффициенты числителя и знаменателя § 12. Второе доказательство теоремы Рауса—Гурвица § 13. Некоторые дополнения к теореме Рауса—Гурвица. Критерий устойчивости Льенара и Шипара § 14. Некоторые свойства многочлена Гурвица. Теорема Стильтьеса. Представление многочленов Гурвица при помощи непрерывных дробей § 15. Область устойчивости. Параметры Маркова § 16. Связь с проблемой моментов § 17. Связь между определителями Гурвица и определителями Маркова § 18. Теоремы Маркова и Чебышева § 19. Обобщенная задача Рауса-Гурвица ДОБАВЛЕНИЕ. НЕРАВЕНСТВА ДЛЯ СОБСТВЕННЫХ И СИНГУЛЯРНЫХ ЧИСЕЛ § 1. Мажорирующие последовательности § 2. Неравенства Неймана-Хорна § 3. Неравенства Вейля § 4. Максимально-минимальные свойства сумм и произведений собственных чисел эрмитовых операторов § 5. Неравенства для собственных и сингулярных чисел сумм и произведений операторов § 6. Другая постановка задачи о спектре суммы и произведения эрмитовых операторов ЛИТЕРАТУРА

Определитель Грамма — Математическая энциклопедия

Определитель вида

$$ \Gamma = \Gamma ( a _ {1} \dots a _ {n} ) = \ \mathop{\rm det} | (а _ {я}, а _ {к}) | ,\\ i, k = 1 \ точек n, $$

где $ a _ {1} \dots a _ {n} $ являются элементами (пред)гильбертова пространства и $(a_{i}, a_{k})$ являются их скалярными произведениями. {2} . $$

В частности, определитель Грама равен нулю, если любой из его главных миноров (который также является определителем Грама) равен нулю.

2) $ \Gamma ( a _ {1} \dots a _ {n} ) \leq \Gamma ( a _ {1} \dots a _ {p} ) \Gamma ( a _ {p + 1 } \ точки a _ {n} ) $, равенство выполняется тогда и только тогда, когда подпространства $ L ( a _ {1} \dots a _ {p} ) $ и $ L ( a _ {p+} 1 \dots a _ {n} ) $ ортогональны или если один из определителей $\Gamma ( a _ {1} \dots a _ {p} ) $, $ \Gamma ( a _ {p+} 1 \dots a _ {n} ) $ равен нулю. Геометрический смысл этого неравенства состоит в том, что объем параллелоэдра не больше произведения объемов дополнительных граней. В частности, 9{2} ,\\ i, j = 1 \ точек n. $$

Детерминанты Грама были введены Дж. П. Грамом [1] и, независимо, К.А. Андреева [2] в связи с проблемами разложения функций в ортогональные ряды и наилучшего квадратичного приближения функций.

Определитель Грама используется во многих задачах линейной алгебры и теории функций: исследованиях линейной зависимости систем векторов или функций, ортогонализации систем функций, построении проекций, а также при исследованиях свойств систем функций. См. также матрицу Грама.

Определитель Грама является частным случаем определителей типа

$$ \Гамма\влево ( \начать{массив}{с} а _ {1} \ точки а _ {п} \\ б _ {1} \ точки б _ {п} \\ \конец{массив} \ справа ) знак равно \ mathop {\ rm det} | ( а _ {я} , б _ {j} ) | ,\\ i, j = 1 \точки n, $$

эрмитовых и билинейных относительно векторов $ a _ {i} $ и $b_{j}$. Если все $ a _ {i} $ относятся к классу $L_{2}(E)$, то справедлива следующая формула:

$$ \ mathop{\ rm det} ( а _ {я} , б _ {j} ) знак равно $$

$$ «=» { \frac{1}{n!} } \int\limits _ {E} \dots \int\limits _ {E} \mathop{\rm det} | а _ {я} ( Икс _ {j} ) | \mathop{\rm det} | \overline{ {b _ {i} }}\; ( Икс _ {j} ) | dx _ {1} \dots dx _ {n} . $$

References

[1]	J.P. Gram, «On Raekkeudviklinger bestemmte ved Hjaelp of de mindste Kvadraters Methode» , Copenhagen (1879)
[2]	K. A. Андреев, , Избранное произведение , Харьков (1955) (на русском языке)
[3]	Ф.Р. [Ф.Р. Гантмахер] Гантмахер, «Теория матриц» , 1 , Челси, переиздание (1977)

Комментарии

Используя определители Грама и их свойства, можно доказать теорему Адамара об определителе (ср. Адамара теорема).

Ссылки

[a1]	П. Дж. Дэвис, «Интерполяция и аппроксимация», Довер, перепечатка (1975) стр. 108–126

Как цитировать эту запись:
Определитель грамм. Математическая энциклопедия. URL: http://encyclopediaofmath.org/index.php?title=Gram_determinant&oldid=47113

Эта статья адаптирована из оригинальной статьи Л. П. Купцова (составитель), опубликованной в Encyclopedia of Mathematics — ISBN 1402006098. См. оригинальную статью

линейная алгебра — Доказательство, когда определитель Грама равен нулю

92,$$

равно квадрату (гипер)объема параллелепипеда, образованного векторами $x_i$; далее векторы $x_1,\cdots,x_n$ линейно независимы тогда и только тогда, когда $\dim_{\,\bf R}\langle x_1,\cdots,x_n\rangle=n$ тогда и только тогда, когда ни один $x_i$ не содержится в подпространстве, натянутом на остальные $x_j$s тогда и только тогда, когда параллелепипед, порожденный $x_i$, имеет ненулевой $n$-мерный объем, независимо от того, какова размерность $m$ относительно $n$.