Способ моментов — Студопедия
Поделись с друзьями:
Применяя этот способ, среднюю арифметическую рассчитывают по формуле:
Эта формула технически упрощает расчеты, особенно в тех случаях, когда варианты состоят из многозначных чисел, а совокупность — из большого числа наблюдений.
Например: Методика расчета средней арифметической величины по способу моментов Таблица 8.
| V кг | p | а | а ×р |
| 64 | 2 | +2 | +4 |
| 63 | 3 | +1 | +3 |
| 62 | 9 | 0 | 0 |
| 61 | 6 | -1 | -6 |
| 60 | 4 | -2 | -8 |
| 59 | -3 | -3 | |
| n =25 | Sа × р = -10 кг |
Этапы расчета М по способу моментов:
1) за условную среднюю Ао рекомендуется принять варианту, чаще других повторяющуюся в вариационном ряду.
В нашем примере: Ао = М = 62 кг., так как 62 кг было у 9 юношей из 25;
2) определяем а — условное отклонение от условной средней. Для этого из каждой варианты вычитаем условную среднюю а = (V — Ао).
В нашем примере: а = 64 — 62 = + 2 и т. д.;
3) умножаем условное отклонение (а) на частоту (р) каждой варианты и получаем произведения
(а × р).
В нашем примере: 2 ×(+2) = 4 и т.д.
4) получаем сумму S а × р
В нашем примере
: — 10кг;5) определяем интервал между группами вариант (I)
В нашем примере: i = 1 кг;
6) момент первой степени
В нашем примере: -10 кг / 25× 1 = — 0,4
7)рассчитываем среднюю арифметическую по способу моментов:
В нашем примере: М = 62 кг – 0,4 = 61,6 кг
Есливариационный ряд предварительно был сгруппирован, то в качестве ряда (V) используются середины групп.
Средняя арифметическая величина обладает тремя свойствами.
1. Средняя занимает серединное положение в вариационном ряду. В строго симметричном ряду: М = Мо = Ме.
2. Средняя является обобщающей величиной и за ней не видны колебания, различия индивидуальных данных.
3. Сумма отклонений всех вариант от средней равна нулю.
Величина того или иного признака неодинакова у всех членов совокупности, несмотря на ее относительную однородность.
Наиболее полную характеристику разнообразию признака в совокупности дает так называемое среднее квадратическое отклонение, обозначаемое греческой буквой «сигма» — s.
Существует два способа расчета среднего квадратического отклонения: среднеарифметический и способ моментов. При среднеарифметическом способе расчета применяют формулу: s =
где d — истинное отклонение вариант от истинной средней (V-М). Эта формула используется при небольшом числе наблюдений (n<30), когда в вариационном ряду все частоты р =1.
При р>1 используют формулу такого вида:
s = ;
При Р>1 и N>30 — s =
Следующая формула предназначена для определения s по способу моментов: s = i×
где а — условное отклонение вариант от условной средней: а =V — А; Sa2×p/n момент второй степени, а (Sa×p/n)2 — момент первой степени, возведённый в квадрат. Этот способ применяется в тех случаях, когда нет вычислительной техники, а вариационный ряд громоздкий как за счет большого числа наблюдений, так и за счет вариант, выраженных многозначными числами. При числе наблюдений, равном 30 и менее, в моменте второй степени n заменяют на (n-1).
Например: Расчет среднего квадратического отклонения по среднеарифметическому способу. Таблица 9.
| Рост мальчиков 12 лет. | Число детей (р) | V • Р | d | d2 | d2 × Р |
| 155 | 1 | 155 | +2 | 4 | 4 |
| 154 | 4 | 616 | +1 | 1 | 4 |
| 153 | 6 | 918 | 0 | 0 | 0 |
| 152 | 4 | 608 | —1 | 1 | 4 |
| 151 | 1 | 151 | —2 | 4 | 4 |
| М = 153 | n = 16 | SV ×p = 1448 | S d2 × Р = 16 |
Последовательность расчета s.
1.Определить М (по среднеарифметическому способу).
В нашем примере: = 153см.
2.Найти истинное отклонение d =(V-M).
В нашем примере: 155-153=+2; 154-153= +1 и т.д.
3.Возвести каждое отклонение в квадрат d2.
4.Найти произведение (d2 × р) по всем строкам ряда.
5.Определить сумму (S d2 ×р).
В нашем примере: 4+4+0+4+4=16
6.Рассчитать s по формуле:
В нашем примере: Ö16/16-1 =1,05 см. =1,05
Например: Расчет среднего квадратического отклоненияпо способу моментов Таблица 10.
| Рост, см (V) | Число детей (р) | а | а×р а×р | a2×р |
| 155 | 1 | +2 | 2 | 4 |
| 154 | 4 | + 1 | 4 | 4 |
| 153 | 6 | 0 | 0 | 0 |
| 152 | 4 | -1 | -4 | 4 |
| 151 | 1 | -2 | -2 | 4 |
| n = 16 | Sар = 0 | Sa2×р = 16 |
Последовательность расчета s по способу моментов.
1.Найти условную среднюю А
В нашем примере: А =153 cм.
2.Определить условное отклонение (а) каждой варианты от условной средней: а =V — А.
3.Получить произведения а × р, а затем их просуммировать.
В нашем примере: = 0.
4.Рассчитать истинную среднюю арифметическую по формуле
=153 см, так как сумма отклонений равна 0, то поэтому М=А.
5.Получить произведения а2×p по всем строкам вариационного ряда и просуммировать их.
В нашем примере:Sa2×p =16.
6. Рассчитать по способу моментов по формуле: s =i×
В нашем примере: s =1× = 1,05
Ошибка репрезентативности (m) является важнейшей статистической величиной, необходимой для оценки достоверности результатов исследования. Эта ошибка возникает в тех случаях, когда требуется по части охарактеризовать явление в целом.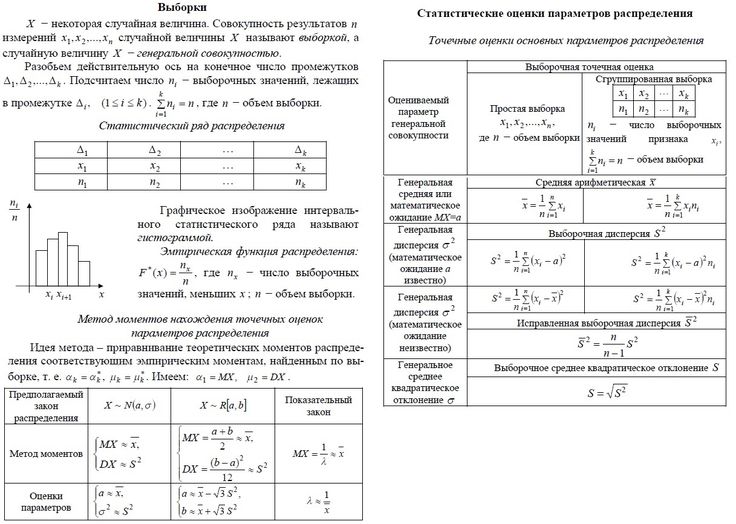
Эти ошибки неизбежны. Они проистекают из сущности выборочного исследования: генеральная совокупность может быть охарактеризована по выборочной совокупности только с некоторой погрешностью, измеряемой ошибкой репрезентативности.
По величине ошибки репрезентативности определяют, насколько результаты, полученные при выборочном наблюдении, отличаются от результатов, которые могли бы быть получены при проведении сплошного исследования всех без исключения элементов генеральной совокупности.
Ошибки репрезентативности можно свести к достаточно малой величине, т. е. к величине допустимой погрешности. Делается это путем привлечения в выборку достаточного количества наблюдений (n):
· – для выборочного исследования, в котором будут рассчитываться относительные величины.
· – для выборочного исследования, в котором будут рассчитываться средние величины.
p – вероятность наступления явления (выбирается по данным аналогичных исследований)
q — вероятность не наступления явления, q =100-p
t — доверительный критерий – таблица 11.
D — предельная ошибка, вытекает из таблицы 6, исходя из выбранного t.
Таблица 11.
| Степень безошибочного прогноза (Р) | Доверительный критерий (t) | Предельная ошибка (D) |
| 68% | — | |
| 95% | 5% | |
| 99% | 1% |
Если аналогичных исследований нет, то p и q принимаются как 50% на 50%.
Ошибки репрезентативности рассчитываются по следующим формулам:
· – для относительных величин;
· – для средних величин.
В медицине и здравоохранении по разности параметров оценивают средние и относительные величины, полученные для разных групп населения по полу, возрасту, а также групп больных и здоровых и т. д. Во всех случаях при сопоставлении двух сравниваемых величин возникает необходимость не только определить их разность, но и оценить ее достоверность. Достоверность разности величин, полученных при выборочных исследованиях, означает, что вывод об их различии может быть перенесен на соответствующие генеральные совокупности.
Формула оценки достоверности разности сравниваемых величин такова:
· — для средних величин;
· — для относительных величин.
Разность величин считается достоверной при значениях, равных или больших 2. Р1 всегда выбирается больше, чем Р2 .
Например: При изучении влияния анаболических гормонов при инфаркте миокарда на белковый обмен были получены следующие данные: общий белок до лечения (Р) составил 7,14% ( m -±0,17%), после лечения (Р) 8,04% ( m -±0,12%).
Последовательность расчёта:
1. Определяем большую величину как Р1 , а меньшую как Р2 .
2.Возводим ошибки репрезентативности в квадраты:
В нашем примере: 0,172=0,0289;0,122= 0,0144.
3.Складываем квадраты и извлекаем квадратный корень.
В нашем примере: Ö0,0289+0,0144=Ö0,0433 = 0,2.
4.Находим разность сравниваемых величин и делим на знаменатель.
В нашем примере: 8,04-7,14=0,9/0,2=4,5.
5.Оцениваем результат.
В нашем примере: 4,5 >2, значит разность величин достоверна, т.е, анаболические гормоны действительно увеличивают уровень общего белка.
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
Среднее значение по способу моментов онлайн
Метод моментов приравнивает моменты теоретического распределения к моментам эмпирического распределения (распределения, построенного по наблюдениям).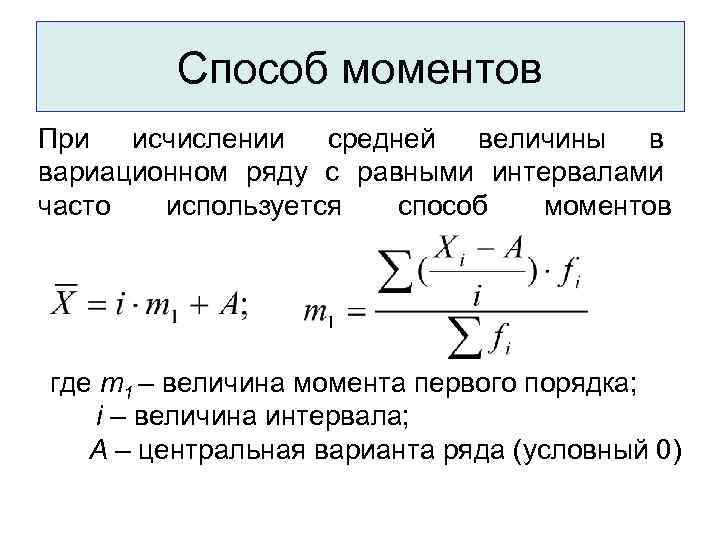
Из полученных уравнений находятся оценки параметров распределения. Например, для распределения с двумя параметрами первые два момента (среднее и дисперсия распределения, соответственно, m и s) будут приравнены первым двум эмпирическим (выборочным) моментам (среднему и дисперсии выборки, соответственно), и затем будет произведено оценивание.
где А – условный нуль, равный варианте с максимальной частотой (середина интервала с максимальной частотой), h – шаг интервала,Назначение сервиса. С помощью онлайн-калькулятора вычисляется среднее значение по способу моментов. Результат решения оформляется в формате Word.
- Шаг №1
- Шаг №2
- Видеоинструкция
Инструкция. Для получения решения необходимо заполнить исходные данные и выбрать параметры отчета для оформления в Word.
Количество строк
- Определяем параметр A.
Вычисляем x*i - Вычисляем x*i*fi
- Находим среднее значение по формуле
Вычисляем x*iПример. Затраты рабочего времени на однородную технологическую операцию распределялись между рабочими следующим образом:
| Затраты времени, мин. | Число рабочих, чел. |
| до 15 | 20 |
| 15-20 | 25 |
| 20-25 | 50 |
| 25-30 | 30 |
| 30-35 | 15 |
| более 35 | 10 |
Таблица для расчета показателей.
| Группы | Середина интервала, xi | Кол-во, fi | xi·fi | Накопленная частота, S | (x-x)2·f |
| 5 — 10 | 7. 5
| 20 | 150 | 20 | 4600.56 |
| 15 — 20 | 17.5 | 25 | 437.5 | 45 | 667.36 |
| 20 — 25 | 22.5 | 50 | 1125 | 95 | 1.39 |
| 25 — 30 | 27.5 | 30 | 825 | 125 | 700.83 |
| 30 — 35 | 32.5 | 15 | 487.5 | 140 | 1450.42 |
| 35 — 40 | 37.5 | 10 | 375 | 150 | 2200.28 |
| 150 | 3400 | 9620.83 |
Мода
где x0 – начало модального интервала; h – величина интервала; f2 –частота, соответствующая модальному интервалу; f1 – предмодальная частота; f3 – послемодальная частота.
Выбираем в качестве начала интервала 20, так как именно на этот интервал приходится наибольшее количество.
Наиболее часто встречающееся значение ряда – 22.78 мин.
Медиана
Медианным является интервал 20 — 25, т.к. в этом интервале накопленная частота S, больше медианного номера (медианным называется первый интервал, накопленная частота S которого превышает половину общей суммы частот).
Таким образом, 50% единиц совокупности будут меньше по величине 23 мин.
Среднее значение изучаемого признака по способу моментов.
где А – условный нуль, равный варианте с максимальной частотой (середина интервала с максимальной частотой), h – шаг интервала.
Находим А = 22.5, шаг интервала h = 5.
Средний квадрат отклонений по способу моментов.
| xц | x*i | x*ifi | [x*i]2fi |
7. 5
| -3 | -60 | 180 |
| 17.5 | -1 | -25 | 25 |
| 22.5 | 0 | 0 | 0 |
| 27.5 | 1 | 30 | 30 |
| 32.5 | 2 | 30 | 60 |
| 37.5 | 3 | 30 | 90 |
| 5 | 385 |
мин.
Среднее квадратическое отклонение.
мин.
Коэффициент вариации — мера относительного разброса значений совокупности: показывает, какую долю среднего значения этой величины составляет ее средний разброс.
Поскольку v>30% ,но v<70%, то вариация умеренная.
Пример
| Группы | x | Кол-во f | x·f | (x-x)2·f |
6. 0 — 8.5
| 7.25 | 26 | 188.5 | 480.74 |
| 8.5 — 11.0 | 9.75 | 112 | 1092 | 362.88 |
| 11.0 — 13.5 | 12.25 | 210 | 2572.5 | 102.9 |
| 13.5 — 16.0 | 14.75 | 52 | 767 | 532.48 |
| 400 | 4620 | 1479 |
Средняя взвешенная
Среднее значение изучаемого признака по способу моментов.
где А – условный нуль, равный варианте с максимальной частотой (середина интервала с максимальной частотой), h – шаг интервала.
Находим А = 12.25.
Шаг интервала h = 2.5.
Средний квадрат отклонений по способу моментов.
| xц | x*i | x*ifi | [x*i]2fi |
| 7.25 | -2 | -52 | 104 |
| 9.75 | -1 | -112 | 112 |
| 12.25 | 0 | 0 | 0 |
| 14.75 | 1 | 52 | 52 |
| -112 | 268 |
Среднеквадратическое отклонение по способу моментов.
Дисперсия — характеризует меру разброса около ее среднего значения (мера рассеивания, т.е. отклонения от среднего).
Формула для средневзвешенного:
Среднеквадратическое отклонение.
Каждое значение ряда отличается от среднего значения 11.55 не более, чем на 1.
92.
Как видим, оценки для среднего значения m и квадрата отклонений s рассчитанные по разным формулам совпадают.
к), \; k=3, 4, \ldots\) до тех пор, пока у вас не будет столько уравнений, сколько у вас есть параметров.Полученные значения называются методом оценки моментов . Кажется разумным, что этот метод дает хорошие оценки, поскольку эмпирическое распределение в некотором смысле сходится к распределению вероятностей. Поэтому соответствующие моменты должны быть примерно равны.
Пусть \(X_1, X_2, \ldots, X_n\) — случайные величины Бернулли с параметром \(p\). Каков метод оценки моментов \(p\)? 92\)
Опять же, для этого примера метод оценок моментов такой же, как и оценки максимального правдоподобия.
В некоторых случаях вместо выборочных моментов относительно начала координат проще использовать выборочные моменты относительно среднего значения. Это дает нам альтернативную форму метода моментов.
2\) 92\)
(которое, как мы знаем из нашей предыдущей работы, необъективно). Этот пример в сочетании со вторым примером иллюстрирует, как две разные формы метода могут потребовать разного объема работы в зависимости от ситуации.
Метод моментов | Реальная статистика с использованием Excel
Основные понятияИмея набор данных, который, по нашему мнению, соответствует определенному распределению, мы хотели бы оценить параметры, которые лучше всего соответствуют этим данным. Опишем теперь один из способов сделать это — метод моментов. В другом месте мы опишем два других таких метода: метод максимального правдоподобия и регрессию.
В методе моментов мы используем факты о взаимосвязи между интересующими параметрами распределения и соответствующими статистическими данными, которые могут быть оценены по выборке (особенно среднее значение и дисперсия). Мы будем использовать выборочное среднее x̄ в качестве нашей оценки для среднего значения генеральной совокупности μ и статистику t 2 определенную как
в качестве оценки дисперсии генеральной совокупности.
о 2 . x̄ и t 2 реализованы в Excel с помощью функций СРЗНАЧ и ДИСП.П соответственно.
Из оценщиков мы знаем, что t 2 является смещенной оценкой, но по мере увеличения размера выборки t 2 90 204 становится (асимптотически) несмещенным и непротиворечивым.
Поскольку часто наши выборки малы, мы склонны использовать выборочную дисперсию s 2 , которая является несмещенной, последовательной оценкой, вместо σ 2 . Технически это не метод моментов, но он часто служит нашим целям. s 2 реализуется в Excel с помощью функции VAR.S. Также обратите внимание, что когда мы используем s 2 в следующих примерах, мы технически должны заменить s 2 на ( n– 1) s 2 902 04 / n чтобы получить т 2 .
- Экспоненциальное распределение
- Распределение Вейбулла
- Бета-версия
- Распределение Парето
- Равномерное распределение
- Логнормальное распределение
- Распределение обобщенных экстремальных значений (GEV)
- Обобщенное распределение Парето (GPD)
- Поддержка реальной статистики
Многие из дистрибутивов, которые мы изучали на этом сайте, могут обрабатываться как экспоненциальное распределение, описанное выше. Например, параметры нормального распределения можно оценить по выборочному среднему и стандартному отклонению. Точно так же параметр лямбда для распределения Пуассона можно оценить по выборочному среднему.
Параметры гамма-распределения можно рассчитать как β = s 2 / x̄ и α = x̄ / β .
Параметр геометрического распределения можно оценить как p = 1/(1– x̄ ).