Определитель матрицы 3х3: Определитель матрицы 3х3 – онлайн калькулятор с подробным решением.

2.1. Определитель матрицы 2х2.

Рассмотрим теперь систему двух линейных уравнений с двумя неизвестными:

(*)

Коэффициенты при неизвестных и для удобства обозначений имеют два индекса, первый из которых указывает, какому уравнению принадлежит коэффициент, а второй – при каком неизвестном он стоит. Таблица

,

составленная из коэффициентов при неизвестных, называется матрицей системы.

Исключим из этой системы неизвестное . Для этого умножим первое уравнение системы на , а второе – на , затем вычтем из первого уравнения второе. Получим

. (**)

Аналогично исключаем : . (***)

Если , то, разделив обе части уравнений (**) и (***) на , получим единственное решение системы (*):

, (****).

Числитель и знаменатель полученных выражений называют определителями или детерминантами второго порядка. Таким образом,

Определение. Назовем определителем или детерминантом 2-го порядка матрицы

число, равное . Обозначения: ==.

Об этом определителе говорят, что он соответствует матрице , и называют определителем системы (*). Числа называют элементами определителя (как и матрицы). Элементы образуют так называемую главную диагональ, а элементы — побочную.

Согласно этому определению формулы (****) принимают следующий вид:

, (*****).

Заметим, что определители и получаются из из определителя системы при помощи замены соответственно его первого и второго столбца столбцом свободных членов системы (*).

Формулы (*****) называтся формулами Крамера.

Таким образом, если определитель (*) системы не равен нулю, то формулы Крамера дают единственное решение этой системы.

Рассмотрим другие случаи. Если определитель , но покрайней мере один из определителей или отличен от нуля, то система (*) не имеет решений (несовместна), так как покрайней мере одно из уравнений (**) или (***) является не возможным. Если , то система (*) имеет бесконечно много решений, так как или , следовательно, уравнения пропорциональны, т.е. .

Поэтому системы следующего вида решаются аналогично, с разницей только количества свободных переменных:

, , — произвольное.

Пример:

.

Свойство 1. Определитель не изменится, если его строки поменять местами с соответствующими столбцами (транспонирование).

Доказательство:

.

Свойство 2. При перестановке двух строк (столбцов) определитель изменит знак на противоположный, сохраняя абсолютную величину.

Доказательство: Например, пусть

.

Свойство 3. Определитель с двумя одинаковыми строками (или столбцами) равен нулю.

Доказательство: Например, пусть и , тогда

.

Свойство 4. Общий множитель всех элементов строки (или столбца) можно выносить за знак определителя.

Доказательство: Например, пусть

.

Свойство 5. Если к элементам какой-либо строки (столбца) определителя прибавит соответствующие элементы другой строки (столбца), умноженное на одно и то же число, то определитель не изменит своей величины.

Доказательство: Например, пусть

Свойство 6. Если все элементы какой-либо строки (столбца) определителя умножеть на одно и то же число , то и значение определителя умножится на это число .

Свойство 7. Определитель, у которого элементы двух строк (столбцов) соответственно пропорциональны, равен нулю.

Доказательство: Например, пусть и , тогда

.

Свойство 8. Пусть каждый элемент некоторой строки (столбца) определителя есть сумма двух слагаемых. Тогда этот определитель равен сумме двух определителей, причем в одном определителе одноименная строка (столбец) состоит из первых слагаемых, а в другом – из вторых слагаемых. Остальные элементы у определителей одинаковы.

Доказательство: Например, пусть

.

Свойство 9. Если все элементы, кроме главной диагонали, равны нулю, то определитель равен произведению элементов, стоящих на главной диагонали.

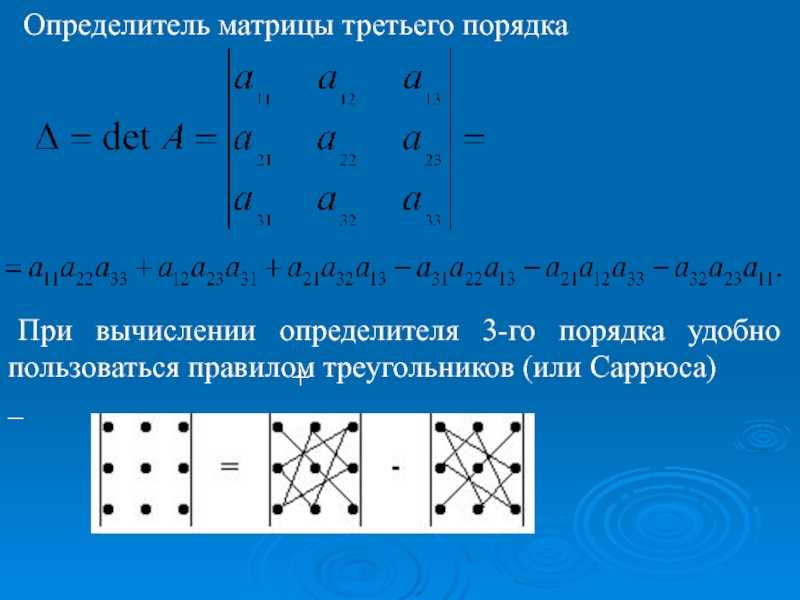
2. Определитель матрицы 3х3. Для квадратной матрицы 3-го порядка определитель или детерминант задается следующим образом:

,

называемое разложением определителя по первой строке.

Раскрывая входящие в это выражение определители второго порядка, получаем:

.

Определение. Минором называется определитель матрицы, получившейся из исходной вычеркиванием -й строки и -го столбца.

Следовательно,

Определение. Число называется алгебраическим дополнением элемента . Тогда формула (**) примет более изящный вид: .

Все свойства определителей второго порядка справедливы и для определителей третьего порядка.

Свойство 10. Теорема. Справедливы разложения определителя третьего порядка как по произвольной строке, так и по произвольному столбцу, т.е. определитель третьего порядка равен сумме парных произведений элементов какой-либо его строки (или столбца) на их алгебраические дополнения.

Это следует из перестоновочности строк и столбцов и транспонирования.

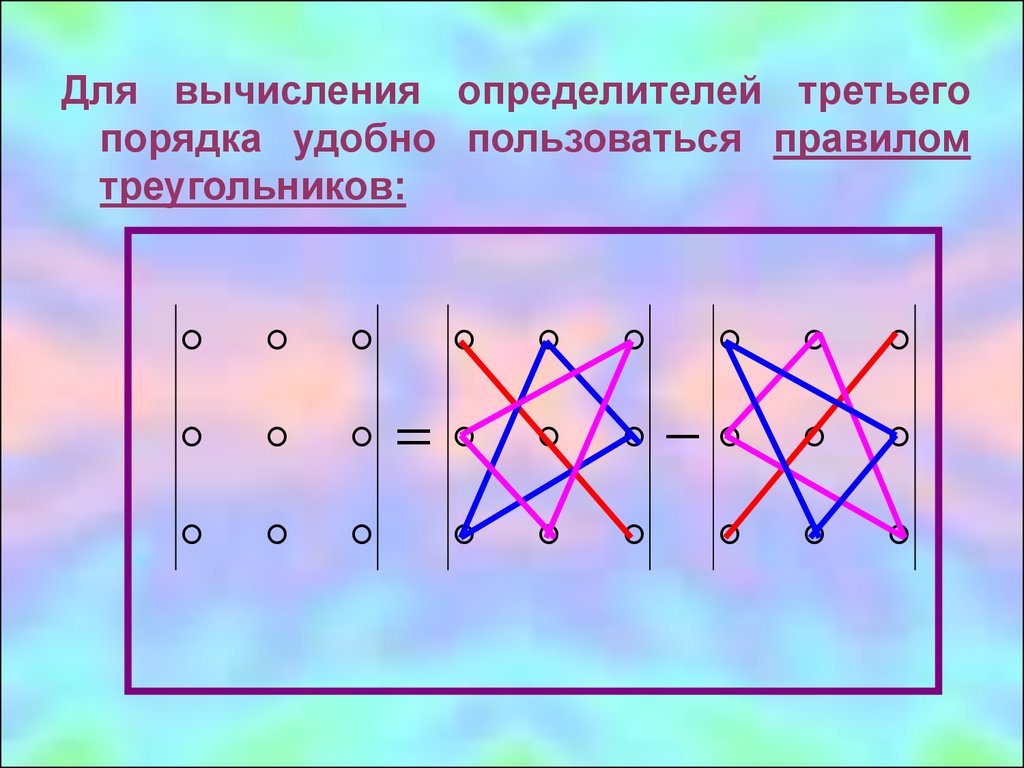
Свойство 11.

Сумма парных произведений элементов какой-либо его строки (или столбца) на алгебраические дополнения соответствующих элементов какой-либо другой строки (или столбца) равна нулю.

Определение. Определителем -го порядка

называется число, равное алгебраической сумме , где — соответствующие алгебраические дополнения, т.е. являются определителями -го порядка, получаемым из исходного вычеркиванием первого столбца и -й строки и умножением полученного определителя на . Все рассмотренные свойства определителей второго и третьего порядков имеют место и для определителей -го порядка.

2.11. Системы линейных уравнений. Основные понятия. Пусть дана система линейных уравнений:

Решением системы линейных уравнений называется набор чисел , при подстановке которых в уравнения вместо соответствующих переменных получаются верные числовые равенства.

Если система имеет хотя бы одно решение, она называется совместной. Если это решение единственное, она называется определенной. Если это решение не единственное, она называется неопределенной.

Если система не имеет решений, она называется несовместной.

Система называется однородной, если все правые части равны нулю: Если хотя бы одно из чисел не равно нулю, система называется неоднородной.

Заметим, что однородная система всегда совместна, т.к. она всегда имеет нулевое решение . Это решение обычно называют тривиальным.

Алгебра: Матрицы. Действия с матрицами. Определитель. Его вычисление и основные свойства

Похожие презентации:

Матрицы. Действия над матрицами. Определители и их свойства

Матрицы. Элементарные преобразования и действия над матрицами

Определители и их свойства. Лекции 9,10

Линейная алгебра. Матрицы и действия над ними

Определитель и его свойства. Обратная матрица

Определители. Свойства определителей

Определители. Свойства определителей и методы их вычисления

Определители. Свойства определителей

Матрицы и их виды. Действия над матрицами. Тема 2

Определители, системы

1. Лекция №1

1
Лекция №1
Алгебра:
Матрицы. Действия с матрицами.
Определитель. Его вычисление и основные
свойства. Система линейных
алгебраических уравнений (СЛАУ). Методы
решения СЛАУ.

2. Матрицы.

2
Матрицы.
Определение: Матрица размерности mxn – это
таблица чисел расположенных в m строках и n
столбцах вида
a11 a12 a13
a21 a22 a23
a
a
a
33
31 32
Матрицы бывают квадратные:
a11 a12
Прямоугольные: a21 a22
a
a
31 32
a11 a12
a21 a22
a11 a12
или
a21 a22
a13
a23

3.

Матрицы.3
Матрицы.
Главная диагональ
Побочная диагональ
0 0 0
O 0 0 0
0 0 0
Нулевая матрица
0 0 0
O 0 0 0
0 0 0
Матрица столбец
b1
b2
b
3
1 0 0
E 0 1 0
0 0 1
Единичная матрица
1 0 0
E 0 1 0
0 0 1
Матрица строка
a1
a2
a3

4. Действия над матрицами.

4
Действия над матрицами.
Сложение матриц:
a11 a12
a21 a22
a13 b11 b12 b13 a11 b11 a12 b12
a23 b21 b22 b23 a21 b21 a22 b22
a13 b13
a23 b23
Вычитание матриц:
a11 a12 a13 b11 b12 b13 a11 b11 a12 b12 a13 b13
a21 a22 a23 b21 b22 b23 a21 b21 a22 b22 a23 b23
Умножение матрицы на число:
a11 a12
a21 a22
a13 a11 a12 a13
a23 a21 a22 a23

5. Действия над матрицами

5
Действия над матрицами
Умножение матриц:
a11 a12
b11 b12 b13
a 21 a 22
b21 b22 b23
a
31 a32
a11 b11 a12 b21 a11 b12 a12 b22
a 21 b11 a 22 b21 a 21 b12 a 22 b22
a b a b
31 11 32 21 a31 b12 a32 b22
a11 b13 a12 b23
a 21 b13 a 22 b23
a31 b13 a32 b23

6.

Пример умножения матриц.6
Пример умножения матриц.
1 0
1 2 0
2 1
1 1 0 1 1
1 1 0 0 1 2 0 ( 1) 1 0 0 1
2 1 1 0 2 2 1 ( 1) 2 0 1 1
1 1 1 0 1 2 1 ( 1) 1 0 1 1
2 0
1
2
3 1
1 3 1

7. Действия над матрицами.

7
Действия над матрицами.
Операции сложения и умножения матриц обладают
следующими свойствами:
Сложения:
1. А+В=В+А (переместительный закон)
2. А+(В+С)=(А+В)+С (сочетательный закон)
3. А+0=А
4. (α·β)·А= α·(β·А)
5. (α+β)·А= α·А+β·А (распределительный
6. (А+В)·α=α·А+α·В
закон)
Умножения:
1. А·В≠В·А
2. А·(В·С)= (А·В)·С
3. А·(В+С)= А·В+А·С
(А+В)·С= А·С+В·С
4. А·Е= Е·А=А

8. Определитель матрицы.

8
Определитель матрицы.
Каждой квадратной матрице ставится в
соответствие число, называемое
определителем матрицы.
Обозначается: det|A| или ||A|| или |A|

9. Вычисление определителя.

9
Вычисление определителя.
Для матрицы размера 2х2, определитель
вычисляется по следующей формуле:
a11
a12
a21 a22
a11 a22 a12 a21
Для вычисления определителя матрицы размера
3х3 (nxn), введем понятие миноров и
алгебраических дополнений.

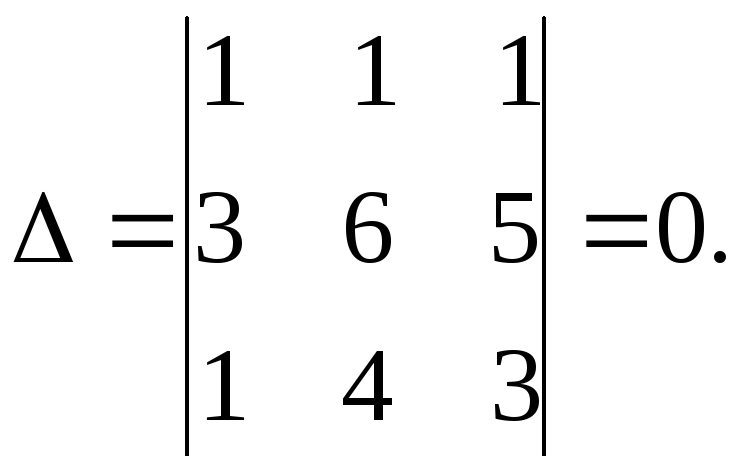
10. Вычисление определителя.

10
Вычисление определителя.
Будем называть минором (Mkl) определитель
матрицы полученной из исходной после
вычеркивания из нее k-ой строки и l-го столбца.
a11 a12 a13
a21 a22 a23
a
a
a
33
31 32
M 11
a22
a23
a32
a33
M 23
a11
a12
M 32
a31 a32
a11
a13
a21 a23
a22 a33 a23 a32
a11 a32 a12 a31
a11 a23 a13 a21

11. Вычисление определителя.

11
Вычисление определителя.
Алгебраическим дополнением элемента
матрицы с индексами k, l называется число ,
полученное умножением минора (Mkl) на (-1)
в степени (k+l).
Akl ( 1)
k l
M kl

12. Вычисление определителя.

12
Вычисление определителя.
Определитель матрицы размера более чем 3х3,
вычисляется путем разложения этой матрицы
по строке или столбцу, следующим образом:
a11
a12
det A a21 a22
a31 a32
a13
a23 a11 A11 a12 A12 a13 A13
a33
a21 A21 a22 A22 a23 A23
a31 A31 a32 A32 a33 A33
a11 A11 a21 A21 a31 A31
a12 A12 a22 A22 a32 A32
a13 A13 a23 A23 a33 A33

13.

Вычисление определителя.13
Вычисление определителя.
Для вычисления определителя матрицы 3х3
можно использовать следующую формулу:
a11 a12 a13
a21 a22 a23
a
31 a32 a33
a11 a12 a13 a11 a12
a21 a22 a23 a21 a22
a
a
a
a
a
33
31
32
31 32
a11 a22 a33 a12 a23 a31 a13 a21 a32
a13 a22 a31 a11 a23 a32 a12 a21 a33

14. Пример вычисление определителя.

14
Пример вычисление
определителя.
1 2
1 3
1 3 2 1 3 2 1

15. Пример вычисление определителя.

15
Пример вычисление
определителя.
1
0 1
1
2
1 1
3 1 2 0 0 3 ( 1) ( 1) 1 1
0
( 1) 2 ( 1) 1 3 1 0 1 0 0 0 1 2 3 0 6
1 0 1 1 0
1 2 3 1 2
1 1 0 1 1

16. Пример вычисление определителя.

16
Пример вычисление
определителя.
1
0 1
1
2
1 1
3 1 ( 3) 0 ( 3) ( 1) 3 3 3 6
0
1 1
A11 ( 1)
1 2
A12 ( 1)
1 3
A13 ( 1)
M 11
2 3
1 0
M 12 1
M 13
1
2 0 3 1 0 3 3
1
3
1 0
2
1 1
1 (1 0 3 ( 1)) 1 (0 3) 3
1 1 2 ( 1) 1 2 3

17.

Свойства определителей.17
Свойства определителей.
Свойство 1. При перестановке двух строк (или столбцов)
определитель меняет знак.
Свойство 2. Общий множитель какой-либо строки или
столбца можно выносить за знак определителя.
Свойство 3. Если в определителе две строки (или два
столбца) пропорциональны (в частности, равны), то
определитель равен нулю.
Свойство 4. При замене всех строк определителя на
столбцы с теми же номерами
величина
его не
изменится.

18. Свойства определителей.

18
Свойства определителей.
Свойство 5. Если все элементы некоторой строки (столбца)
нули, то определитель равен нулю.
Свойство 6. Определитель не изменится, если к элементам
какой-либо строки (столбца) прибавить соответствующие
элементы другой строки (столбца), умноженные на одно и
тоже число.
Свойство 7. Сумма парных произведений элементов какойлибо
строки
(столбца)
на
соответствующие
алгебраические дополнения другой строки (столбца)
равна нулю.

19. Система линейных алгебраических уравнений (СЛАУ)

19
Система линейных
алгебраических уравнений
(СЛАУ)
Система вида:
где
x
y
z
a11 a12
a21 a22
a
31 a32
a13
a23
a33
a11 x a12 y a13 z f1
a21 x a22 y a23 z f 2
a x a y a z f
32
33
3
31
матрица системы,
— вектор неизвестных,
f1
f2
f 3
— вектор правой
части
уравнения,
называется системой линейных алгебраических
уравнений (СЛАУ).

20. Система линейных алгебраических уравнений (СЛАУ)

20
Если обозначим:
a11 a12
A a21 a22
a
31 a32
a13
a23
a33
x
x y
z
f
f1
f2
f 3
То нашу систему можно записать в виде:
Тогда решение будет иметь вид:
где
A
1
A x f
x A 1 f
обратная матрица системы.

21. Система линейных алгебраических уравнений (СЛАУ)

21
Система линейных
алгебраических уравнений
(СЛАУ)
Обратная матрица – это такая матрица при умножении на
которую самой матрицы получается единичная матрица.
A A
1
E

22. Система линейных алгебраических уравнений (СЛАУ)

Геометрически, каждое уравнение нашей системы
22
является уравнением плоскости. Возможны
следующие варианты взаимного расположения трех
плоскостей:
1.Пересечение в одной точке:

23. Система линейных алгебраических уравнений (СЛАУ)

23
Система линейных
алгебраических уравнений
(СЛАУ)
2.Пересечение по прямой: 3.Нет общих точек пересечения:

24. Система линейных алгебраических уравнений (СЛАУ)

24
Система линейных
алгебраических уравнений
(СЛАУ)
В первом случае определитель нашей системы
НЕ равен нулю, а значит решение существует
и единственно.
Найти решение такой системы мы можем двумя
методами: 1. Методом Крамера, 2. Методом
обратной матрицы.
Во втором случае решений системы бесконечно
много, и решить эту системы мы можем при
помощи метода Гаусса.
В третьем случае система не имеет решения,
проверить это можно также методом Гаусса.

25. Метод Крамера.

25
Метод Крамера.
Данный метод сводиться к нахождению четырех
определителей:
f1
a12
a13
a23
D1 f 2
a22
a23
a32
a33
f3
a32
a33
a11
f1
a13
D 2 a21
a11
a12
f1
f2
a23
D3 a21 a22
f2
a31
f3
a33
a31
f3
a11
a12
a13
D a21 a22
a31
a32

26. Метод Крамера.

26
Метод Крамера.
В результате получим решение СЛАУ:
D1
x
D
D2
y
D
D3
z
D

27. Метод Крамера. Пример.

27
Метод Крамера. Пример.
Решить систему уравнений:
x
x
0
y
y
y
1 1 0
A 0 1 2
1 1 1
2 z 4
z
2
0
f 4
2

28. Метод Крамера. Пример.

28
Метод Крамера. Пример.
Вычислим определитель системы:
D A 1 A11 1 A12 0 A13
1 1 0
A 0 1 2
1 3 1 2 5
1 1 1
1 2
1 1
A11 ( 1)
1 2 3
1 1
1 2
A12 ( 1)
0 2
1 1
1 ( 0 2 ) 2

29.

Метод Крамера. Пример.29
Метод Крамера. Пример.
1 1 0
A 0 1 2
1 1 1
0
f 4
2
0 1 0
D1 4 1 2 0 A11 1 A12 0 A13 1 0 0
2 1 1
1 2
A12 ( 1)
4 2
2 1
1 (4 4) 0

30. Метод Крамера. Пример.

30
Метод Крамера. Пример.
0
f 4
2
1 1 0
A 0 1 2
1 1 1
1 0 0
D 2 0 4 2 1 A11 0 A12 0 A13 1 0 0
1 2 1
1 1
A11 ( 1)
4 2
2 1
4 4 0

31. Метод Крамера. Пример.

31
Метод Крамера. Пример.
0
f 4
2
1 1 0
A 0 1 2
1 1 1
1 1 0
D3 0 1 4 1 A11 0 A21 1 A31 1 6 1 4 10
1 1 2
1 4
1 1
A11 ( 1)
2 4 6
1 2
A31 ( 1)
3 1
1 0
1 4
4 0 4

32. Метод Крамера. Пример.

32
Метод Крамера. Пример.
В результате мы получили: D=5, D1=0,
D2=0, D3=10.
D1 0
x
0
D 5
D2 0
y
0
D 5
D3 10
z
2
D
5

33. Метод Крамера. Пример.

33
Метод Крамера. Пример.
x
x
0
y
y
y
0 0
0
0 0
2 z 4
z
2
0
2 2 4
2
2

34. Решение СЛАУ методом обратной матрицы.

34
Решение СЛАУ методом
обратной матрицы.
A x f
x A f
1
A11
1
1
A
A12
A
A13
A21
A22
A23
A31
A32
A33

35. Решение СЛАУ методом обратной матрицы.

35
Решение СЛАУ методом
обратной матрицы.
x
x
0
y
y
2 z 4
y
1 1 0
A 0 1 2
1 1 1
z
2
0
f 4
2

36. Решение СЛАУ методом обратной матрицы.

36
Решение СЛАУ методом
обратной матрицы.
1 1
A11 ( 1)
1 2
A12 ( 1)
1 3
A13 ( 1)
A31 ( 1)
1
1 1
0 2
1 1
0
3 2
1 2 3
1(0 2) 2
1
1 1
3 1
A32 ( 1)
2
1 0
1 0
1 2
0 2
0 1 1
A21 ( 1)
2 1
A22 ( 1)
2 2
A23 ( 1)
2 3
1
0
1(1 0) 1
1 1
1 0
1
1 1
1 1 0
A 0 1 2
1 1 1
(1 0) 1
1
1 1
1( 1 1) 2
2 0 2
1(2 0) 2,
A33 ( 1)
3 3
1 1
0 1
1 0 1

37.

Решение СЛАУ методом обратной матрицы.37
Решение СЛАУ методом
обратной матрицы.
3 1 2
1
1
A 2 1 2
5
1
2
1
3 1 2 0
1
1
x A f 2 1 2 4
5
2
1
2
1
3 0 ( 1) 4 2 2
0 0
1
1
2 0 1 4 ( 2) 2 0 0
5
5
( 1) 0 2 4 1 2
10 2

38. Метод Гаусса

38
Метод Гаусса
Расширенной матрицей системы
A x f
будем называть матрицу вида
a11 a12
A | f a21 a22
a
31 a32
a13
a23
a33
f1
f2
f 3

39. Метод Гаусса

39
Метод Гаусса
Ранг матрицы – это размер наибольшего
ненулевого минора этой матрицы.
Ранг
матрицы
с
ненулевым
определителем равен размеру этой
матрицы.

40. Метод Гаусса

40
Метод Гаусса
Для того, чтобы СЛАУ была совместна ранг матрицы
системы должен быть равен рангу расширенной
матрицы.
Заметим:
1. Если ранг матрицы системы равен размерности
самой матрицы, то система имеет единственное
решение.
2. Если ранг матрицы системы равен рангу
расширенной матрицы, но меньше размерности
самой матрицы системы, то система имеет
бесконечное множество решений.
3. Если ранг матрицы системы меньше ранга
расширенной матрицы, то система несовместна и
решений не существует.

41. Метод Гаусса

41
Метод Гаусса
Сам метод Гаусса состоит в том, чтобы
преобразованием строк получить нули
под главной диагональю расширенной
матрицы системы.

42. Метод Гаусса

42
Метод Гаусса
x
x
0
y
y
2 z 4
y
1 1 0
A 0 1 2
1 1 1
z
2
0
f 4
2

43. Метод Гаусса

43
Метод Гаусса
1 1 0
(A | f ) 0 1 2
1 1 1
1 1 0
0 1 2
0 2 1
0
4
2
1 1 0 0
0 1 2 4
0 0 5 10
0
4
2
Вычитаем из 3 строки
первую строку
Добавим к 3 строке вторую
умноженную на 2

44. Метод Гаусса

44
Метод Гаусса
1 1 0 0
0 1 2 4
0 0 5 10
Теперь из расширенной матрицы
запишем получившуюся систему:
0
x y
y 2z 4
5 z 10

45.

Метод Гаусса45
Метод Гаусса
Осталось только решить нашу систему.
Из последнего уравнения получаем z=2,
подставляем это значение z во второе
уравнение и получаем y=0, теперь
подставляем значение y в первое
уравнение и получаем x=0.

46. Метод Гаусса

46
Метод Гаусса
Исследовать СЛАУ на совместность:
x y z 1
x 4 y 3z 0
3 x 2 y z 2
Запишем расширенную матрицу системы:
1 1 1 1
1 4 3 0
3 2 1 2

47. Метод Гаусса

47
Метод Гаусса
1 1 1 1
1 4 3 0
3 2 1 2
Вычитаем из 2 строки
первую
1 1 1
0 5 4
3 2 1
1
1
2
Вычитаем из 3 строки
первую умноженную на 3
1 1 1
0 5 4
0 5 4
1
1
1
1 1 1
0 5 4
0 0
0
1
1
0
Вычитаем из 3 строки
вторую

48. Метод Гаусса

48
Метод Гаусса
1 1 1
0 5 4
0 0
0
1
1
0
Заметим, что наибольший ненулевой минор имеет
размерность 2, а количество неизвестных системы
равно 3, т. е. ранг системы совпадает с рангом
расширенной матрицы, но он меньше чем количество
неизвестных системы – это означает, что наша
система имеет бесконечное множество решений.

49. Метод Гаусса

49
Метод Гаусса
Исследовать СЛАУ на совместность:
x y z 1
x 4 y 3z 1
3 x 2 y z 2
Запишем расширенную матрицу системы:
1 1 1 1
1 4 3 1
3 2 1 2

50. Метод Гаусса

50
Метод Гаусса
1 1 1 1
1 4 3 1
3 2 1 2
Вычитаем из 2 строки
первую
1 1 1 1
0 5 4 0
3 2 1 2
Вычитаем из 3 строки
первую умноженную на 3
1 1 1
0 5 4
0 5 4
Вычитаем из 3 строки
вторую
1
0
1
1 1 1 1
0 5 4 0
0 0
0
1

51. Метод Гаусса

51
Метод Гаусса
Заметим, что наибольший
ненулевой минор имеет
размерность 3.
Заметим, что ран матрицы
самой системы равен 2 –
это означает, что наша
система
не
имеет
решения,
т.к.
ранг
расширенной
матрицы
больше ранга матрицы
системы.
1 1 1 1
0 5 4 0
0 0
0 1
1 1 1
0 5 0
0 0 1

English     Русский Правила

Определители 3 на 3 | Purplemath

2-на-2

Purplemath

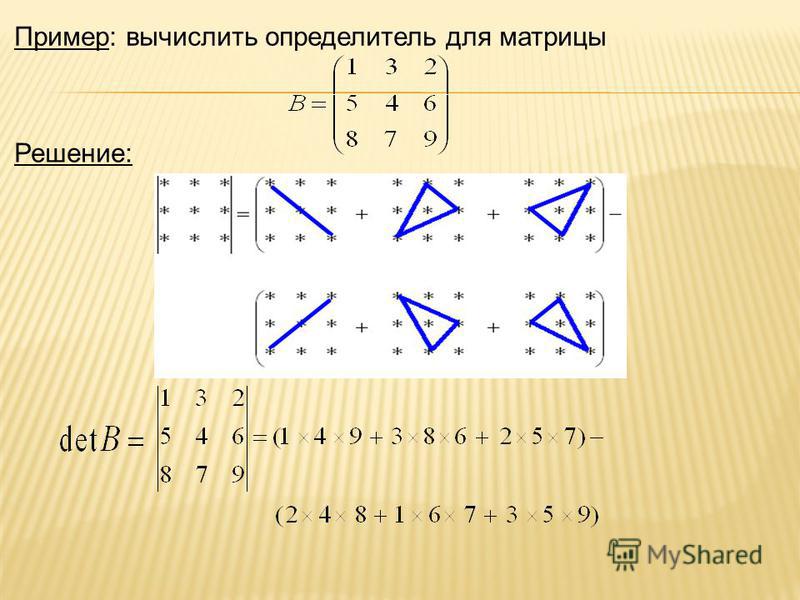
Вычисления для определителей 3×3 сложнее, чем для 2×2. Можно использовать различные методы, но наиболее простым, вероятно, является следующий:

Взять матрицу A :

Содержание продолжается ниже :

Это определитель матрицы 3 на 3. Но чтобы найти значение этого определителя (то есть, когда вы выполняете свои фактические вычисления), удалите эти столбцы и расширьте сетку определителя, переписав первые два столбца чисел после третьего (то есть справа от него). столбец в сетке чисел. У вас должен получиться следующий массив:

Когда мы находили определители матриц 2 на 2, мы умножали по диагонали, а затем вычитали значение «вверх и вправо» из значения «вниз и вправо».

С расширенной сеткой чисел, которую мы создали здесь, мы можем сделать что-то подобное.

Начиная с верхнего левого угла, умножаем по (первым трем) диагоналям вниз:

Затем, начиная с левого нижнего угла, умножаем по (первым трем) диагоналям вверх:

Складываем вниз- диагоналей и вычесть диагонали вверх:

Обратите внимание на скобки выше. Это может помочь отслеживать знаки, особенно если вам нужно вычесть отрицательное число.

Теперь, когда я выполнил умножение и настроил сложение и вычитание, пришло время упростить:

Тогда мой ответ:

det(  A  ) = 1

---

Итак, эти шаги для нахождения определителя матрицы 3 на 3:

1. Удалите квадратные скобки из матрицы
2. Замените эти скобки столбцами абсолютного значения (это определитель)
3. Чтобы выполнить вычисления, повторите первые два столбца после третьего столбца
4. Умножьте значения вдоль каждой из диагоналей слева вверху и справа внизу
5. Умножьте значения вдоль каждой из диагоналей от нижнего левого до верхнего правого угла
6. Сложите вместе значения, найденные на шаге 4
7. Сложите значения, найденные на шаге 5
8. Вычтите значение, найденное на шаге 7, из значения на шаге 6 и упростите

---

• Найдите определитель следующей матрицы:

Сначала я перехожу от матрицы к установке для нахождения ее определителя, удаляя квадратные скобки и добавляя первые два столбца справа от сетки чисел:

Затем я умножаю вниз и вверх шесть диагоналей:

Наконец, я складываю нижние диагонали, вычитаю верхние диагонали и упрощаю для получения окончательного ответа:

Тогда мой вводной ответ:

det( A  ) = 103

---

Существуют и другие методы ручного упрощения определителей, и эти другие методы необходимы при ручном вычислении более крупных определителей, но эти методы, вероятно, можно подождать.

Пока что обратите внимание, что ваш графический калькулятор должен уметь вычислять определитель любой (квадратной) матрицы, которую вы вводите. Например:

Но убедитесь, даже если у вас есть графический калькулятор, что вы можете вычислить определители 2 × 2 и 3 × 3 вручную, потому что вам, вероятно, будут даваться текстовые задачи, где определители содержат переменные, которые ваш калькулятор не может обработать. .

---

URL: https://www.purplemath.com/modules/determs2.htm

Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в нахождении значений определителей 3 на 3. Попробуйте введенное упражнение или введите свое собственное упражнение. Затем нажмите кнопку и выберите «Найти определитель», чтобы сравнить свой ответ с ответом Mathway.

Пожалуйста, примите куки-файлы настроек, чтобы включить этот виджет.

(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления. )

Page 1

3×3 Определитель | Superprof

Введение

Из квадратной матрицы можно вычислить специальное число, известное как определитель . Квадратная матрица — это матрица, имеющая одинаковое количество строк и столбцов. Она может быть любого порядка, например, квадратная матрица порядка 2х2 означает, что в ней две строки и два столбца. Точно так же квадратная матрица 3×3 означает, что в ней три строки и три столбца. У нас также есть квадратные матрицы более высоких порядков, например 4×4, 5×5 и так далее. Мы используем символ вертикальных линий || для обозначения матрицы.

Если нам дана матрица B, то ее определитель обозначается как |B|. Определитель матрицы с неравным количеством строк и столбцов невозможен. Определители матриц полезны при нахождении обратной матрицы и решении системы линейных уравнений. В этой статье мы обсудим, как найти определитель матрицы 3×3.

 

Лучшие репетиторы по математике

Поехали

Определитель матрицы 3×3

Чтобы найти определитель матрицы 3×3, мы разбиваем его на более мелкие составляющие, например определители матриц 2×2, чтобы их было легче вычислять. Рассмотрим следующую матрицу 3×3:

Определитель матрицы B будет рассчитываться как:

Вы можете заметить, что:

• Элементы в первой строке; a, b и c умножаются на соответствующую матрицу 2×2.
• Элементы a умножаются на матрицу 2×2, полученную после удаления строки и столбца, в которых присутствует элемент a.
• То же самое касается других элементов b и c.

Теперь мы решим несколько примеров, в которых будем вычислять определитель матрицы 3×3 вручную.

Пример 1

Вычислите определитель следующей матрицы.

Решение

Мы будем использовать следующую формулу для вычисления определителя приведенной выше матрицы:

Матрица 2х2.

Мы знаем, что формула для нахождения определителя следующей матрицы 2×2:

Мы будем использовать эту формулу для вычисления определителей меньших матриц 2×2.

Следовательно, определитель матрицы A равен -67.

 

Пример 2

Вычислите определитель следующей матрицы.

Раствор

Следующая формула будет использоваться для вычисления определителя матрицы 3×3.

Чтобы разбить эту матрицу на более мелкие матрицы 2×2, нам нужно посмотреть на первую строку и умножить каждый элемент на определитель матрицы 2×2. Матрица 2×2 будет получена после исключения строки и столбца, в которых присутствует элемент.

Мы знаем, что формула для нахождения определителя следующей матрицы 2×2:

Мы будем использовать эту формулу для вычисления определителей меньших матриц 2×2.

Следовательно, определитель матрицы B равен 57.

 

Решение

Следующая формула будет использоваться для вычисления определителя приведенной выше матрицы 3×3.

Мы разобьем эту матрицу на более мелкие матрицы 2×2, взглянув на первую строку и умножив каждый элемент на определитель матрицы 2×2. Матрица 2х2 получится после исключения строки и столбца, в которых элементы 9, 4 и 7 присутствуют,

Мы знаем, что формула для нахождения определителя следующей матрицы 2×2:

Мы будем использовать эту формулу для вычисления определителей меньших матриц 2×2.

Следовательно, определитель матрицы C равен -151.

 

Пример 4

Вычислите определитель следующей матрицы.

Решение

Мы подставим значения из приведенной выше матрицы в следующую формулу для вычисления определителя.

Мы разобьем эту матрицу на более мелкие матрицы 2×2, взглянув на первую строку и умножив каждый элемент на определитель матрицы 2×2. Матрица 2×2 будет получена после исключения строки и столбца, в которых присутствуют элементы 3, 4 и 0,

Мы знаем, что формула для нахождения определителя следующей матрицы 2×2:

Мы будем использовать эту формулу для вычисления определителей меньших матриц 2×2.