Определитель матрицы равен: Определитель матрицы онлайн

Определитель матрицы — Энциклопедия по экономике

My — минор элемента ау — определитель матрицы (л— 1)-го порядка, полученной из матрицы А вычеркиванием /-и строки и j-го столбца.  [c.263]
При перестановке любых строк матрицы меняется только знак определителя матрицы.  [c.263]

За знак определителя матрицы можно выносить общий множитель элементов любой строки (столбца).  [c.263]

Определитель матрицы не изменится, если к элементам любой строки (или столбца) прибавить элементы другой строки (или столбца), умноженные на одно и то же число.  [c.263]

Д, — определитель матрицы AJ, получаемой из матрицы А заменой у -го столбца столбцом свободных членов, т. е. Д= А,.  [c.268]

Тогда определитель матрицы А  [c.275]

Вычислить определители матриц 0123 1012 2101  [c.277]

В соответствии с правилом Крамера 1 1 17] решение находится делением определителя матрицы, полученной заменой в U (г + 1)Л-го столбца вектором свободных членов, на определитель Ц. Вектор свободных членов содержит только две ненулевые компоненты первую и последнюю. Поэтому  [c.230]

Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами.  [c.54]

Чем ближе к 0 определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И наоборот, чем ближе к 1 определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.  [c.54]

Достаточное условие идентификации — определитель матрицы, составленной из коэффициентов при переменных, отсутствующих в исследуемом уравнении, не равен нулю, и ранг этой матрицы не менее числа эндогенных переменных системы без единицы.  [c.107]

Определитель матрицы не равен 0, ранг матрицы равен 2 следовательно, выполняется достаточное условие идентификации, и первое уравнение точно идентифицируемо.  [c.109]

В соответствии с достаточным условием идентификации определитель матрицы коэффициентов при переменных, не входящих в исследуемое уравнение, не должен быть равен нулю, а ранг матрицы должен быть равен числу эндогенных переменных модели минус 1, т.

е. 4-1=3.  [c.119]

Для уравнения у = а + 6, хх + Ь2 х2 +. .. + Ьр хр + е определитель матрицы коэффициентов парной корреляции примет вид  [c.115]

Целесообразность проверки условия идентификации модели через определитель матрицы коэффициентов, отсутствующих в данном уравнении, но присутствующих в других, объясняется тем, что возможна ситуация, когда для каждого уравнения системы выполнено счетное правило, а определитель матрицы названных коэффициентов равен нулю. В этом случае соблюдается лишь необходимое, но недостаточное условие идентификации.  [c.190]

Определитель матрицы межфакторной корреляции (на примере модели  [c.16]

Чем ближе к нулю определитель матрицы межфакторной корреляции,  [c.16]

Применение правила Крамера при D, обозначающей определитель матрицы коэффициентов, дает  [c.29]

Обсуждаемый здесь рынок капитала, без сомнения, является полным, так как мы имеем дело, с одной стороны, с тремя ситуациями, а с другой — с тремя рыночными ценными бумагами, денежные потоки которых линейно независимы.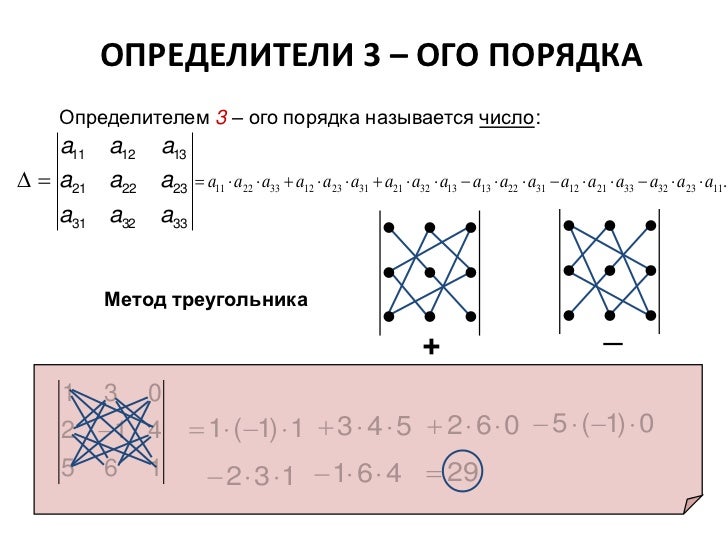 Линейная независимость подтверждена, так как в противном случае определители матрицы денежных потоков в предыдущей части задачи приобрели бы нулевое значение, и мы не были бы в состоянии определить эквивалентный портфель. Но для наличия рынка, свободного от арбитража, нужно большего все цены Эрроу—Дебре должны быть положительными. Имеем ли мы дело с этим случаем или нет, нужно еще исследовать. Для этой цели рассчитаем соответствующие цены из системы уравнений  [c.288]

Если определитель матрицы-коэффициента А не равен 0, то  [c.202]

АУ iJ /г а > гДе Д>- =( 1) +J Мд— алгебраическое дополнение элемента btj матрицы ( — A), Mtj — минор этого элемента, а Е — А = А — определитель матрицы (Е — А).  [c.261]

Определитель матрицы, в которой вычеркнуты произвольная строка (напр. i-я), и произвольный столбец (напр. у -й), называется минором. Он имеет (я — 1)-й порядок, т.е. порядок на 1 меньше, нежели исходный определитель.  [c.242]

Другой подход состоит в исследовании матрицы Х Х. Если определитель матрицы Х Х либо ее минимальное собственное значение A.min близки к нулю (например, одного порядка с накапливающимися ошибками вычислений), то это говорит о наличии мультиколлинеарности. О том же может свидетельствовать и значительное отклонение максимального собственного значения Хтах матрицы Х Х от ее минимального собственного значения Хт-т.  [c.109]

Проверим каждое уравнение системы на необходимое и достаточное условия идентификации. Для первого уравнения Н— 3 (У[, у2,. у3) и Z> = 2 (х3 их4 отсутствуют), т. е. D + 1 = Яи необходимое условие идентификации выдержано, поэтому уравнение точно идентифицируемо. Для проверки на достаточное условие идентификации заполним следующую таблицу коэффициентов при отсутствующих в первом уравнении переменных, в которой определитель матрицы (detA) коэффициентов равен нулю  [c.190]

Уравнение лишь тогда имеет одно решение для 71 и 72 когда матрица выплат является обратимой. Обратимость предполагает отличный от нуля определитель матрицы коэффициентов. Так как это условие здесь соблюдается, то, преобразуя рассматриваемую матрицу в обратную  [c.135]

См. также Блочная матрица, Блоч-но-диагональная матрица, Блочно-треу-голъная матрица, Вырожденная матрица, Диагональная матрица, Единичная матрица, Идемпотентная матрица, Квадратная матрица, Транспонированная матрица, Треугольная матрица, а также Алгебраическое дополнение, Главная диагональ матрицы, Обращение матрицы, Определитель матрицы, Плотность матрицы, Разлоокимость матрицы, Ранг матрицы.  [c.188]

ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ, ДЕТЕРМИНАНТ [determinant]—число, соответствующее квадратной матрице и полученное путем ее преобразования по определенному правилу. Обычное обозначение (для матрицы A) det А. Напр., определитель (второго порядка) матрицы  [c.242]

РАНГ МАТРИЦЫ [rank of matrix] — наивысший из порядков отличных от нуля миноров этой матрицы (см. Определитель матрицы, детерминант). Р.м. неизменен при ее простых преобразованиях.  [c.299]

Численность, математика и статистика — Набор академических навыков

Определитель матрицы

ContentsToggle Главное меню 1 Определение 2 Определитель матрицы $2 imes 2$ 2. 1 Определение 2.2 Рабочие примеры 2.3 Видеопримеры 3 3 $ imes $3 Определители 3.1 Определение3 .2 Примеры работы3.3 Пример видео 4 Рабочая тетрадь 5 Проверьте себя 6 Внешние ресурсы

Определение

Определитель матрицы представляет собой одно числовое значение, которое используется при вычислении обратной или при решении систем линейных уравнений.

Определитель матрицы $\mathbf{A}$ обозначается $\lvert \mathbf{A} \rvert$ или иногда $\det(\mathbf{A})$. Определитель определен только для квадратных матриц.

Матрица называется сингулярной , если ее определитель равен нулю.

Общая формула определителя матриц любого размера очень сложна. Вам будет предложено только вычислить определители матриц $2 \times 2$ или $3 \times 3$ вручную.

Определитель матрицы $2 \times 2$

Определение

Пусть $\mathbf{A} = \begin{pmatrix} a & b\\ c & d \end{pmatrix}$.

Определитель $\mathbf{A}$ равен \[\lvert \mathbf{A} \rvert = ad — bc\]

Примеры работы

Пример 1

Найдите определитель матрицы $\mathbf{ A} = \begin{pmatrix} 4 & 1\\ 0 & 2\end{pmatrix}$.

Решение

\begin{align} \lvert \mathbf{A} \rvert = \begin{vmatrix} 4 & 1 \\ 0 & 2 \end{vmatrix} &= 4 \times 2 — 1 \times 0\ \ &=8 — 0\\ &=8 \end{align}

Пример 2

Найдите определитель матрицы $\mathbf{A} = \begin{pmatrix} -6 & 3\\ -1 & 1\end{pmatrix}$.

Решение

\begin{align} \lvert \mathbf{A} \rvert &= (-6) \times 1 — 3 \times (-1)\\ &=(-6) — (-3)\ \ &=-6+3\\ &=-3 \end{align}

Пример 3

Найдите определитель матрицы $\mathbf{A} = \begin{pmatrix} 5 & -10\\ -2 & 4\end{pmatrix}$.

Решение

\begin{align} \lvert \mathbf{A} \rvert &= 5 \times 4 — (-10) \times (-2)\\ &=20 — 20\\ &=0 \end {выравнивание}

Примечание: Поскольку ее определитель равен нулю, эта матрица не имеет обратной.

Примеры видео

Хейли Бишоп находит определитель матриц $2\times 2$ $\mathbf{A} = \begin{pmatrix}3&-1\\0&4\end{pmatrix}$ и $\mathbf{B} = \begin{pmatrix} -2&10\\-1&5\end{pmatrix}$.

3$\times$3 Определители

Определение

Определитель матрицы $3 x 3$ можно вычислить, разбив ее на более мелкие матрицы $2 x 2$ следующим образом:

\[\begin{vmatrix} а и б и в \\ д & д & ж \\ г и ч и я \end{vmatrix} знак равно а \begin{vmatrix} е & ж \\ Привет \end{vmatrix} — б \begin{vmatrix} д и ж \\ г и я \end{vmatrix} + с \begin{vmatrix} д & е \\ г и ч \end{vmatrix}\]

Или,

\[\begin{vmatrix} а_{11} и а_{12} и а_{13} \\ а_{21} и а_{22} и а_{23} \\ а_{31} и а_{32} и а_{33} \end{vmatrix} знак равно а_{11} \begin{vmatrix} а_{22} и а_{23} \\ а_{32} и а_{33} \end{vmatrix} — а_{12} \begin{vmatrix} а_{21} и а_{23} \\ а_{31} и а_{33} \end{vmatrix} + а_{13} \begin{vmatrix} а_{21} и а_{22} \\ а_{31} и а_{32} \end{vmatrix}\]

Вот один из способов интерпретации формулы: для каждого элемента $a_{1i}$ в верхней строке заблокируйте строку и столбец, которым он принадлежит, и вычислите определитель оставшейся непокрытой матрицы $2 \times 2$, затем умножьте это на $a_{1i}$. Определитель представляет собой сумму этих значений, чередующихся сложением и вычитанием.

Примеры работы

Пример 1

Найдите определитель матрицы $\begin{pmatrix} 1 & 2 & 1\\ 0 & 3 & 4\\ 3 & 1 & 4 \end{pmatrix}$.

Решение

\begin{align} \lvert \mathbf{A} \rvert &= 1\begin{vmatrix} 3 и 4\\ 1 и 4 \end{vmatrix} -2 \begin{vmatrix} 0 и 4 \\ 3 & 4 \end{vmatrix} +1 \begin{vmatrix} 0 & 3\\ 3 & 1 \end{vmatrix}\\\\ &= 1(3\times 4 — 4\times 1) -2 (0\умножить на 4 — 4\умножить на 3) +1(0 \умножить на 1 — 3\умножить на 3)\\ &= 1(12-4) -2(0-12) +1(0-9)\\ &= 8 +24-9\\ &=23 \end{align}

Пример 2

Найдите определитель матрицы $\begin{pmatrix} 1 & 0 & 3\\ -1 & -1 & -3 \\ 0 & 0 & 6 \end{pmatrix}$.

Решение

\begin{align} \lvert \mathbf{A} \rvert &= 1\begin{vmatrix} -1 & -3\\ 0 & 6 \end{vmatrix} -0 \begin{vmatrix} — 1 & -3\\ 0 & 6 \end{vmatrix} +3 \begin{vmatrix} -1 & -1\\ 0 & 0 \end{vmatrix}\\\\ &= 1\bigl((-1) \times 6 — (-3)\times 0\bigr) -0(\,\dotso\,) +3\bigl((-1) \times 0 — (-1)\times 0\bigr)\\ & = 1\bigr((-6)-0\bigl) -0 +3(0-0)\\ &=-6 +0\\ &=-6 \end{align}

Примечание: Был нет необходимости вычислять второй определитель $2 \times 2$, так как он умножается на ноль.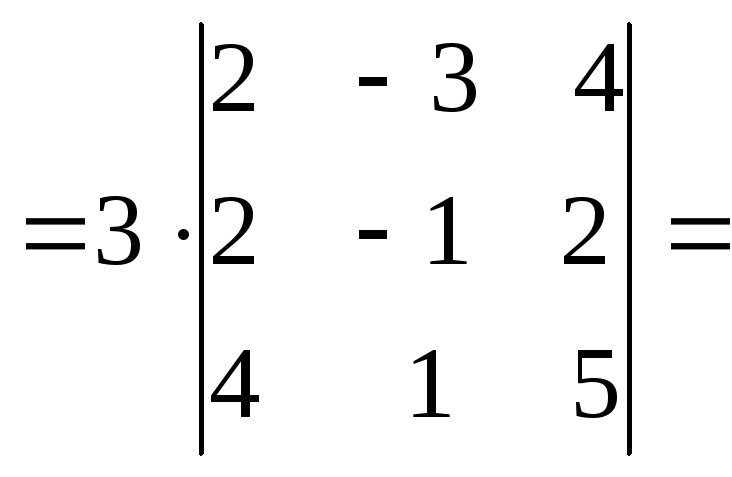

Видеопример

Хейли Бишоп вычисляет определитель матрицы $3\times 3$ $\mathbf{A} = \begin{pmatrix}1&0&2\\3&1&0\\-1&1&4\end{pmatrix}$.

Рабочая тетрадь

Эта рабочая тетрадь, созданная HELM, является хорошим пособием по повторению, содержащим ключевые моменты для исправления и множество рабочих примеров.

• Детерминанты

Проверь себя

Проверь себя: тест Numbas на детерминантах 2×2

Внешние ресурсы

• Буклет с определителями в math center.
• Определитель листовки матрицы $2 \times 2$ в math center.
• Определитель листовки матрицы $3 x 3$ в math center.
• Пример нахождения определителя листовки матрицы $3\times 3$ в математическом центре .

Определитель — Линейная алгебра | Элеври

Линейная алгебра

Определитель

Определитель – это скалярное представление матрицы, определяемое специальным расчетом.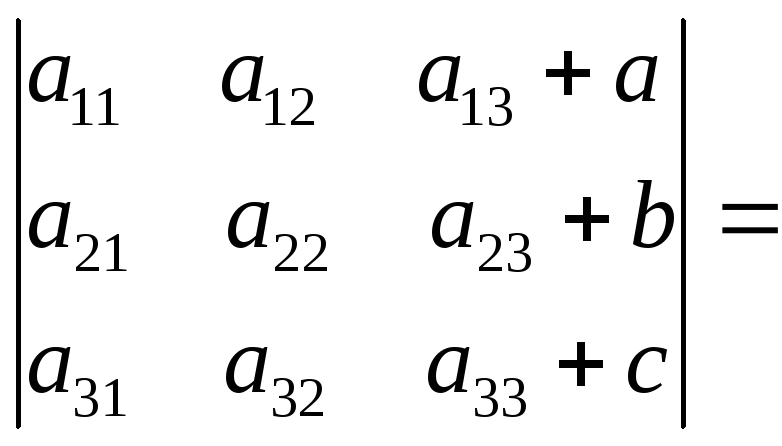 Геометрическая интерпретация заключается в том, что это масштабный коэффициент для линейного преобразования, которое представляет матрица. Он также говорит о том, имеет ли система линейных уравнений, которую представляет матрица, единственное решение или нет.

Содержание

Почему это правило называется правилом Крамера?

В 1750 году Габриэль Крамер опубликовал статью с изложением знаменитой техники, которая сегодня носит его имя: Правило Крамера . Швейцарский гений понял, что определителя можно использовать для решения систем линейных уравнений.

В возрасте всего 18 лет Крамер получил докторскую степень в Женевском университете. Учебное заведение было настолько впечатлено способностями молодого математика, что для него создали новую должность сопредседателя кафедры математики в университете.

Как оказалось, это был умный ход со стороны Университета, от которого выиграла вся Женева.

Крамер остался в университете до конца своей жизни, где он реформировал систему образования, чтобы математика преподавалась на французском языке, а не только на латыни, таким образом охватив более широкую аудиторию.

Каково определение определителя?

Определитель матрицы представляет собой скалярное значение, обозначаемое или . Чтобы существовать, матрица должна быть квадратной, и если она квадратная, то раскрывает информацию о решениях системы уравнений, которую составляет матрица.

Если определитель равен нулю, то у данной системы либо бесконечно много решений, либо их нет вообще. Все остальные значения означают, что существует единственное решение.

Для матриц, определители которых равны нулю, мы можем быть уверены, что либо существует бесконечное число решений, либо ни одного из них. Более того, ненулевой определитель всегда будет давать единственное решение.

Значение определителя также тесно связано с обратной матрицей. Тогда и только тогда, когда матрица имеет ненулевой определитель, она обратима, и мы можем использовать определитель, чтобы найти обратную матрицу.

Кроме того, определитель дает коэффициент масштабирования линейного преобразования, описываемого матрицей.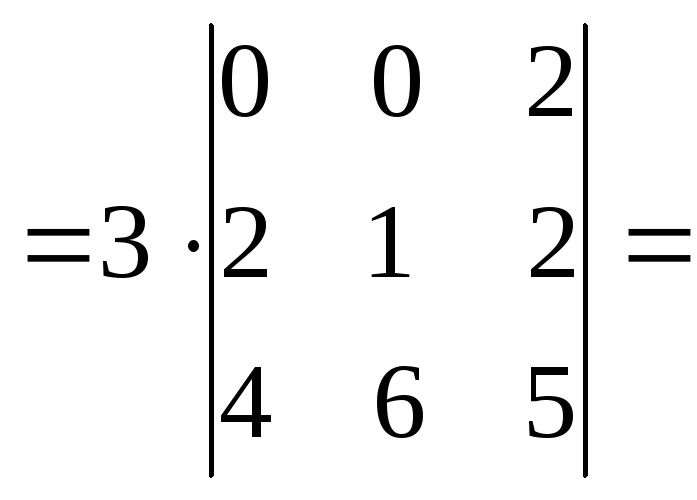

Как найти определитель квадратной матрицы?

Чтобы найти определитель квадратной матрицы (он должен быть квадратным), мы можем использовать такие методы, как формула Лейбница или разложение Лапласа, которые всегда будут работать. Однако есть короткие пути, которые мы можем использовать в определенных случаях.

Если — матрица, ее определитель можно быстро найти по следующей формуле:

В случае, если мы имеем дело с матрицей, используем следующую формулу:

Подробнее об определителе

Введение

Определитель является скаляром и отмечен:

Определитель может быть введен как поздно, так и рано в курсе линейной алгебры. Что касается того, что это такое, студентов традиционно сначала знакомят с тем, как вычисляется определитель, а затем с практической связью и ее геометрической интерпретацией.

Мы делаем наоборот.

Практическая связь

Определитель показывает, имеет ли линейная система уравнений решения. Помните три случая; единственное решение , бесконечно много решений или нет решений .

Если определитель равен нулю, система имеет «бесконечное множество решений» или «нет решений».

Если определитель отличен от нуля, система имеет единственное решение.

Геометрическая интерпретация

Определитель геометрически интерпретируется как масштабный коэффициент для линейного преобразования, с которым, к сожалению, обычно не знаком новичок, когда необходимы вычисления определителя.

Короче говоря, каждое умножение матриц является линейным преобразованием, но с практической точки зрения можно сказать, что линейное преобразование — это матрица, которая умножается на вектор для получения желаемого результата.

Простым примером может быть линейное преобразование, которое поворачивает по часовой стрелке на угол и удваивает свою длину. Тогда масштабный коэффициент, то есть определитель, будет равен .

Определитель 2×2

Определение определителя -матрицы формирует основу для вычисления определителя -матрицы.

Пусть:

откуда определение определителя:

Определитель 3×3

Алгоритм вычисления определителя -матрицы состоит из суммы трех -определителей. Мы получаем их, расширяя одну строку или столбец в определителе (называемый расширением кофактора ).

Пусть:

и тогда применимо, что определитель равен:

где мы сделали разложение первой строки, потому что скаляры каждой -матрицы — это просто элементы из первой строки.

Теперь рассмотрим, как делается расширение. Рассмотрим определитель:

Мы начнем с расширения вдоль первой строки и начнем с первого элемента:

Расширение затем происходит путем выбора строки и столбца текущего элемента для извлечения оставшихся элементов в виде -детерминанта, умноженного на :

Переходим к следующему элементу по первой строке и получаем:

Обратите внимание, что расширение вокруг идет со знаком минус! Мы скоро вернемся к этому.

Теперь мы продолжаем расширять следующий и последний элемент: .

Обратите внимание, что элемент идет со знаком плюс!

Теперь мы закончим вычисление, используя определение -определителя:

Это завершает формулу для -определителя, а также алгоритм, облегчающий запоминание определения вместо того, чтобы заучивать формулу наизусть (что-то, что требуется для продвижения со статусом новичка).

Альтернативная формула

Приведенный выше метод можно легко аналогично распространить на более крупные матрицы, поэтому мы начали с него. Однако существует альтернативный алгоритм, применимый к -определителю, который визуально напоминает определение -определителя:

Если мы расширим этот образ мышления, мы получим метод, который работает, но работает только для вычисления -определителей. Метод называется Правило Сарру .

определитель nxn

Вычисление определителя, вне зависимости от размерности матрицы, производится аналогично -определителю — можно выразить в виде алгоритма для каждого -определителя. Но прежде чем мы это сделаем, мы объясним, почему элемент в вычислении -детерминанта имел знак минус.

Рассмотрим -матрицу . В этом случае каждый извлеченный элемент в своем определителе несет с собой знак плюс или минус в зависимости от его положения в соответствии со следующим «шахматным шаблоном»:

Это означает, что для -определителя скрытый знак для каждого элемента следующим образом:

Например, если бы мы выбрали расширение по второму столбцу, сумма произведений была бы:

Обратите внимание, что знаки плюс и минус, записанные в указанных выше определителях, не должны использоваться ни в каких вычислениях, но теперь они сделано только в образовательных целях.

Общая форма разложения вдоль линии (кофакторное разложение) для определителя -матрицы может быть записана как:

где — каждый элемент в выбранной строке , и — кофактор , который является -детерминантом другие элементы, которые не делят строку или столбец с соответствующим .

Алгоритм для определителя nxn

1. Выберите строку или столбец для разложения в сумму произведения элементов матрицы и -определителей

2. Для каждого элемента в выбранной строке/столбце:
   \begin{enumerate}

3. Извлечь элемент со знаком плюс или минус, который он несет, и умножить на -детерминант элементов, которые не разделяют строку или столбец с выделенным элементом

4. Повторять до тех пор, пока не будут извлечены все элементы в выбранной строке/столбце

\item Повторять вышеуказанные шаги до тех пор, пока последняя сумма произведений не будет содержать только -детерминанты.
\end{enumerate}
Алгоритм показывает, что вычисление определителя может быть чрезвычайно трудоемким, если размерность велика.

Однако обратите внимание на преимущество извлечения строки или столбца, число элементов которых равно нулю! Это означает, что сумма разработанного продукта значительно снижается. Например, как в:

Если определитель, который вы вычисляете, не хватает 0-элементов или их недостаточно, чтобы значительно упростить вычисление, вы можете, как Гаусс-Жордан, сократить строку матрицы определителя без изменения определителя. Эти и другие функции обсуждаются в следующем разделе.

Сопряжение к матрице

Сопряжение к матрице основано на кофакторных разложениях . Это становится интересным в теореме для выражения , если обратное существует. Наше определение сопряженной матрицы:

Если -матрица и является кофактором , то отсюда следует, что матрица:

называется кофакторной матрицей матрицы A. Транспонирование этой матрицы называется примыкает к матрице и обозначается как .

Используя сопряженную матрицу , мы можем очень легко выразить, существует ли обратная, используя следующую теорему, которую мы оставляем недоказанной.

Если матрица обратима, то:

Сейчас мы покажем все это на примерах. Пусть следующая обратимая матрица:

, кофакторы которой становятся:

и, таким образом, матрица кофакторов и сопряженная матрица становятся следующими:

Определяющие свойства

детерминантную матрицу перед расширением строки, чтобы максимизировать количество 0-элементов.

Для каждой -матрицы применяется следующее:

• Если матрица является результатом умножения скаляра на строку или столбец матрицы , то:

• Если матрица является результатом двух строк или столбцов, поменявшихся местами в , применяется следующее:

• Если матрица является результатом умножения строки или столбца матрицы на другую строку или столбец, то:

Доказательство первого и третьего пункта — хорошее упражнение для новичка, прямого доказательства -детерминанта и -детерминанта достаточно, чтобы убедиться. Чтобы создать устойчивое математическое доказательство, рекомендуется доказательство по индукции.

Второй пункт следует из определения определителя с «шахматной» схемой символов в предыдущем разделе.

С помощью предыдущего утверждения мы можем получить следующее утверждение:

Пусть — -матрица.

• Если две строки или столбца равны, то:

• Если строку или столбец можно уменьшить до 0, то:

• Если скаляр, то:

2 Теперь мы готовы к самой запоминающейся теореме для студентов, которая основана на последних теоремах и доказательствах, которые мы представили для того, как обратимая матрица может быть уменьшена по строкам до:

Квадратная матрица обратима тогда и только тогда, когда .

Предположим, что можно свести к , тогда:

Предположим противное, что нельзя свести к , а к . Это означает, что необратимо, потому что по крайней мере две строки в линейно зависимы, и мы получаем по крайней мере одну нулевую строку в . Одна нулевая строка дает:

Другая полезная теорема для арифметики:

Если и — квадратные матрицы одинаковой размерности, то:

Следующее утверждение применимо к обратному:

Если матрица обратима, то применяется:

Помните, что . Тогда у нас есть:

Поскольку , у нас есть:

Мы заканчиваем этот раздел, связывая теорему, которая вводится с обратными и линейными системами уравнений, а также наши идеи с определителем.

Пусть -матрица. Тогда применяются следующие утверждения:

• Сокращенная ступенчатая форма строки для is

• может быть выражена как произведение элементарных матриц

• IS Invertible

• имеет только тривиальное решение

• для каждого вектора в

• имеет ровно одно решение для каждого вектора

• .

• Векторы-строки линейно независимы. Правило Крамера — это утверждение, которое, прежде всего, облегчает выражение решения, так как у нас нет чисел в матрице.

  Правило Крамера Если это линейная система уравнений с уравнениями и переменными, то система имеет единственное решение тогда и только тогда, когда , после чего решение может быть выражено как:

  где матрица где столбец в заменено на .

  No related posts.