Определитель в матрице это: Определитель матрицы | это… Что такое Определитель матрицы?

Содержание

Определитель матрицы.

Определение Это число, которое ставится в соответствие каждой квадратной матрице по некоторому правилу.

Определителем N-ного порядка(если матрица такого же порядка) является

Прямоугольные матрицы не имеют определителя.

Определение Численной характеристикой матрицы первого порядка, то есть определителем первого порядка, называется величина ее элемента .

Обозначается определитель одним из символов .

Определение Определителем второго порядка, соответствующим матрице второго порядка, называется число, равное .

Обозначается определитель одним из символов

Очевидно, что для составления определителя второго порядка, необходимо найти разность произведения элементов, стоящих на главной диагонали матрицы, и произведения элементов, стоящих на побочной диагонали этой матрицы.

Правило Сарруса для квадратных матриц 3 порядка.

Определителем матрицы третьего порядка, или определителем третьего порядка,

называется число, которое вычисляется по формуле:

Это число представляет алгебраическую сумму, состоящую из шести слагаемых. В каждое слагаемое входит ровно по одному элементу из каждой строки и каждого столбца матрицы. Каждое слагаемое состоит из произведения трех сомножителей.

Знаки, с которыми члены определителя входят в формулу нахождения определителя третьего порядка можно определить, пользуясь приведенной схемой, которая называется правилом треугольников или правилом Сарруса. Первые три слагаемые берутся со знаком плюс и определяются из левого рисунка, а последующие три слагаемые берутся со знаком минус и определяются из правого рисунка.

Пример. Вычислить определитель третьего порядка:

Решение.

{1,2,3…n}

Произвольная запись слева на право в определённом порядке данных n символов называется перестановкой

Р-число перестановок из n символов

Пара i, j образует инверсию, если большее стоит впереди меньшего(i>j)

Теорема: Все перестановки из n символов можно расположить

с лева на право последовательно так, что чётности соседних будут различны.

Доказывается с помощью леммы.

Лемма: Всякая перемена местами двух символов перестановки меняет её четность на противоположную.

Всякая транспозиция меняет четность перестановки на противоположную.

Чётные перестановки = нечётные перестановки =

Подстановка из n символов.

Всякая подстановка записывается как двустрочная матрица, каждая строка является перестановкой из n символов.

Сумма чисел инверсий в обеих перестановках называется числом инверсий подстановки.

Если сумма чисел инверсий в двух строках чётно, то число инверсий подстановки чётно, а если нет, то нечётно.

Л юбую подстановку можно записать в стандартном виде.

34, 1  2, 2  1, 4  3

Детерминант порядка n – определитель.

Пусть дана матрица порядка n

(*)

Определение:

Определителем порядка n называется число, равное алгебраической сумме n! слагаемых, каждое слагаемое которой представляет из себя произведение n элементов определителя матрицы, взятых по одному и только по одному из каждой строки и каждого столбца определителя.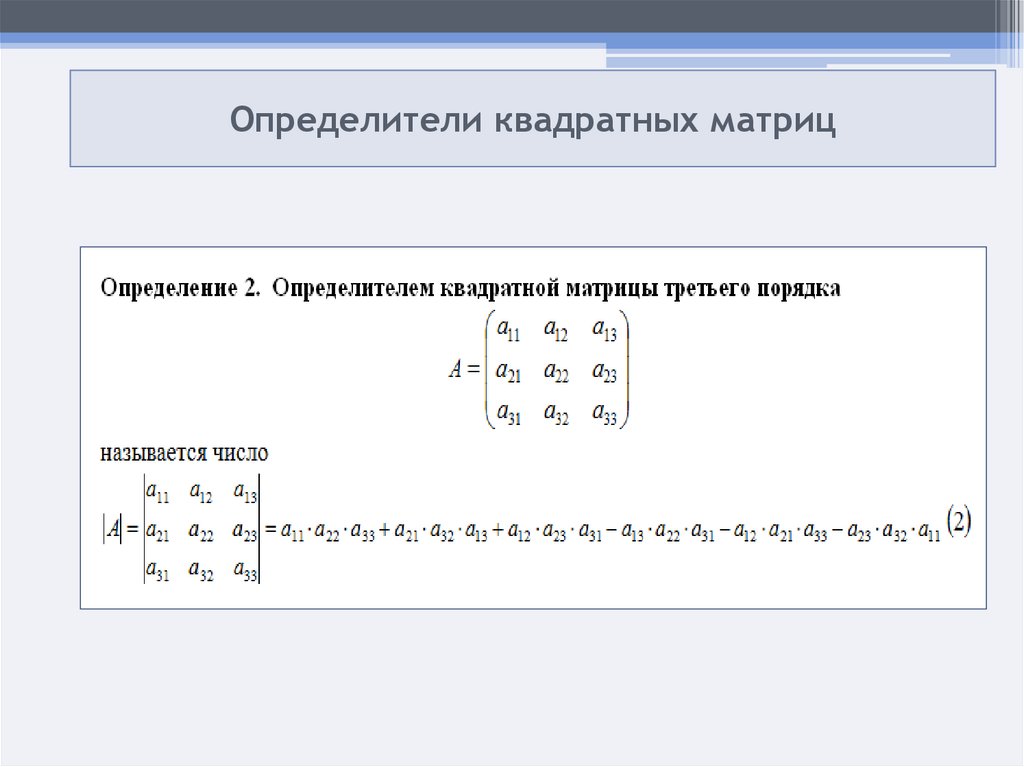 При этом слагаемое берется со знаком “+”, если перестановка, составленная из номеров строк и номеров столбцов, входящих в это произведение – чётное и со знаком “-”, если она не четная.

(*) =

Разложение определителя 3-го порядка по строке и столбцу

Свойства определителя:

Определитель не меняется при транспонирование.

Следствие: всякое свойство, справедливое для строк, справедливо и для столбцов.

Если в определители есть строка, состоящая из 0, то определитель равен 0.
При перемене местами двух строк, определитель меняет знак.
Если в определители есть одинаковые строки, то он равен 0.
Общий множитель элементов любой строки можно выносить за знак определителя.
Если в определителе имеются пропорциональные строки, то определитель равен 0.
Если какая-то строка определителя представленна в виде суммы двух слагаемых(матричных строк) то определитель равен сумме двух определителей у которых все строки, кроме данной такие же как и в исходном определителе.
А данная строка в первом слагаемом заменяется на первое слагаемое матричной строки, а во втором на вторую.
Если одна из строк определителя есть линейная комбинация его других строк, то определитель равен 0.
Определитель не изменится, если к одной из его строк прибавить другую, его же, строку, предварительно умножив на любое число.

Миноры и алгебраические дополнения.

Определитель порядка k называется минором

1 k min

m=n A-квадратная матрица

Вычёркиваем выбранные k строк и k столбцов, остается (m-k) строк и столбцовю

M’- минор, оставшийся после отбрасывания выбрранных строк и столбцов.

M’ – дополнительный минор для M минора.

M’ – алгебраическое дополнение.

Теорема. Произведение любого минора |

M| k-го порядка на его

алгебраическое дополнение в определителе является алгебраической суммой, слагаемые которой, получающиеся от умножения членов минора |М| на взятые со знаком (-1) Sm члены дополнительного минора |М’|, будут некоторыми членами определителя , причем их знаки в этой сумме совпадают с теми знаками, с какими они входят в состав определителя.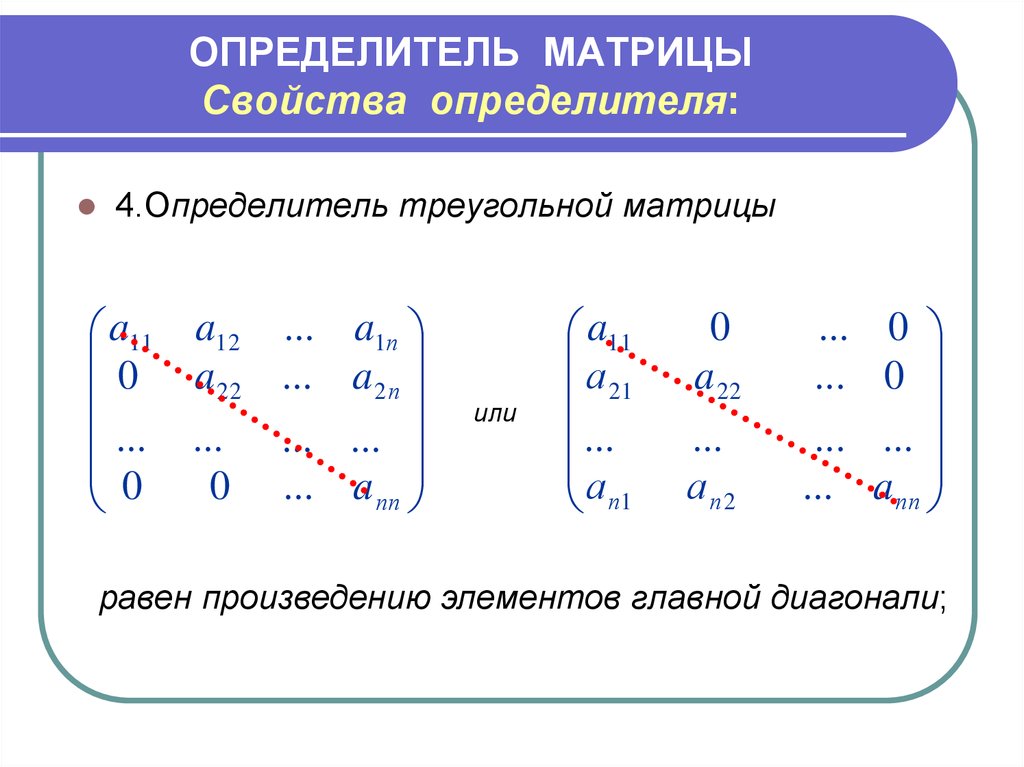

Доказательство. Доказательство этой теоремы начнем со случая, когда

минор |M| расположен в левом верхнем углу определителя:

т. е. в строках с номерами 1,2, …,k и в столбцах с такими же номерами.

Тогда минор |M‘| будет занимать правый нижний угол определителя. Число SM в этом случае будет четным:

SM =1+2+…+k+1+2+…+k=2(1+2+…k),

поэтому алгебраическим дополнением для |M| служит сам минор |M‘|.

Берем произвольный член

(1)

минора |M|; его знак в |M| будет , если l есть число инверсий в

подстановке

(2)

Произвольный член

(3)

минора |M‘| имеет в этом миноре знак , где l‘ есть число инверсий в подстановке

Перемножая члены (1) и (3), мы получим произведение n элементов

(4)

расположенных в разных строках и разных столбцах определителя; оно будет, следовательно, членом определителя . Знак члена (4) в

произведении |M||M‘| будет произведением знаков членов (1) и (3), т.е. . Такой же знак имеет, однако, член (4) и в определителе .

Действительно, нижняя строка подстановки

составленной из индексов этого члена, содержит лишь l+ l‘ инверсий, так как никакое  ни с одним не может составить инверсию: все не больше k, все не меньше k+1.

37. Определитель матрицы

Далее будем рассматривать только квадратные матрицы. Каждой квадратной матрице ставится в соответствие действительное число, называемое Определителем матрицы и вычисляемое по определенному правилу.

Определитель матрицы естественно возникает при решении систем линейных уравнений, или в свернутой форме , или в свернутой форме . Предыдущая формула получается разложением определителя по первой строке.

Возьмем теперь квадратную матрицу -го порядка

(9. 2)

Для записи определителя -го порядка матрицы будем применять обозначения . При матрица состоит из одного элемента и ее определитель равен этому элементу. При получаем определитель .

Минором элемента матрицы называют определитель матрицы -го порядка, получаемого из матрицы вычеркиванием -той строки и -го столбца.

Пример 7. Найти минор матрицы:

По определению, минор элемента есть определитель матрицы, получаемой из матрицы вычеркиванием первой строки и второго столбца. Следовательно, .

Алгебраическим дополнением элемента матрицы называется минор , взятый со знаком . Алгебраическое дополнение элемента обозначается , следовательно, .

Пример 8. Найти алгебраическое дополнение элемента матрицы из примера 7.

Определителем квадратной матрицы -го порядка называется число:

(9.3)

Где ‑ элементы первой строки матрицы (9.

2), а их алгебраические дополнения.

Запись по формуле (9.3) называется Разложением определителя по первой строке.

Рассмотрим свойства определителей.

Свойство 1. При транспонировании матрицы ее определитель не меняется.

Это свойство устанавливает равноправность строк и столбцов определителя, поэтому определение определителя можно сформулировать так:

Определителем квадратной матрицы -го порядка называется число:

(9.4)

Где ‑ элементы первого столбца матрицы (9.2), а их алгебраические дополнения.

Свойство 2. Если поменять местами две строки или два столбца матрицы , то ее определитель изменит знак на противоположный.

Свойства 1 и 2 позволяют обобщить формулы (9.3) и (9.4) следующим образом:

Определитель квадратной матрицы -го порядка (будем в дальнейшем говорить определитель -го порядка) равен сумме попарных произведений любой строки (столбца) на их алгебраические дополнения.

, или .

Свойство 3. Определитель, у которого две строки или два столбца одинаковы, равен нулю.

Действительно, поменяем в определителе две одинаковые сроки местами. Тогда, по свойству 2 получим определитель , но с другой стороны, определитель не изменится, т. е. . Отсюда .

Свойство 4. Если все элементы какой-нибудь строки (столбца) определителя умножить на число , то определитель умножится на .

Умножим элементы -той строки на . Тогда получим определитель:

Следствие 1. Если все элементы какой-нибудь строки (столбца) имеют общий множитель, то его можно вынести за знак определителя.

Следствие 2. Если все элементы какой-нибудь строки (столбца) равны нулю, то определитель равен нулю.

Свойство 5. Определитель, у которого две строки (два столбца) пропорциональны, равен нулю.

Пусть -я строка пропорциональна -ой строке. Вынося коэффициент пропорциональности за знак определителя, получим определитель с двумя одинаковыми строками, который по свойству 3 равен нулю.

Свойство 6. Если каждый элемент строки (столбца) определителя есть сумма двух слагаемых, то определитель равен сумме двух определителей: у одного из них -той строкой (столбцом)служат первые слагаемые, а у другого – вторые.

Разложив определитель по -той строке получим:

Свойство 7. Определитель не изменится, если к элементам какой-нибудь строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число.

Прибавив к элементам -той строки определителя соответствующие элементы -ой строки, умноженные на число , получим определитель . Определитель равен сумме двух определителей: первый есть , а второй равен нулю, так как у него -тая и -тая строки пропорциональны.

Свойство 8. Определитель диагональной матрицы равен произведению элементов, стоящих на главной диагонали, т. е.:

Свойство 9. Сумма произведений элементов какой-нибудь строки (столбца) определителя на алгебраические дополнения элементов другой строки (столбца) равна нулю.

Рассмотрим вспомогательный определитель , который получается из данного определителя заменой -той строки -той строкой. Определитель равен нулю, так как у него две одинаковые строки. Разложив его по -той строке получим:

Большое значение имеет следующий критерий равенства определителя нулю. Определитель квадратной матрицы равен нулю тогда и только тогда когда его строки (столбцы) линейно зависимы.

Строки (столбцы) матрицы называются линейно зависимыми, если одна (один) из них является линейной комбинацией с действительными коэффициентами остальных.

Теорема об определителе произведения двух квадратных матриц. Определитель произведения двух квадратных матриц равен произведению определителей этих квадратных матриц, т. е. .

< Предыдущая		Следующая >

Понимание свойств определителей | Колледж Алгебра |

Существует много свойств определителей . Здесь перечислены некоторые свойства, которые могут быть полезны при вычислении определителя матрицы.

A Общее примечание: Свойства определителей

Если матрица имеет форму верхнего треугольника, определитель равен произведению элементов по главной диагонали.
При перестановке двух строк определитель меняет знак. 9{-1}A−1
является обратной величиной определителя матрицы
AAA
.
Если какая-либо строка или столбец умножается на константу, определитель умножается на тот же коэффициент.

Пример 7: Иллюстрация свойств определителей

Проиллюстрируйте каждое из свойств определителей.

Раствор

Свойство 1 гласит, что если матрица имеет форму верхнего треугольника, определитель равен произведению элементов по главной диагонали.

A=[12302100−1]A=\left[\begin{array}{rrr}\qquad 1& \qquad 2& \qquad 3\\ \qquad 0& \qquad 2& \qquad 1\\ \qquad 0& \qquad 0& \qquad -1\end{массив}\right]A=⎣

⎡10022031−1⎦

⎤

Дополните

AAA

первыми двумя столбцами.

A=[12302100−1∣100220]A=\left[\begin{array}{ccc}1& 2& 3\\ 0& 2& 1\\ 0& 0& -1\end{массив}|\begin{массив}{ c}1\\ 0\\ 0\end{массив}\begin{массив}{c}2\\ 2\\ 0\end{массив}\right]A=⎣

⎡10022031−1∣100220⎦

⎤

Тогда

det(A)=1(2)(−1)+2(1)(0)+3(0)(0)−0(2)(3)−0(1)(1)+1 (0)(2)=-2\begin{array}{l}\mathrm{det}\left(A\right)=1\left(2\right)\left(-1\right)+2\left (1\правый)\левый(0\правый)+3\левый(0\правый)\левый(0\правый)-0\левый(2\правый)\левый(3\правый)-0\левый(1 \вправо)\влево(1\вправо)+1\влево(0\вправо)\влево(2\вправо)\qquad \\ =-2\qquad \end{массив}det(A)=1(2)( −1)+2(1)(0)+3(0)(0)−0(2)(3)−0(1)(1)+1(0)(2)=−2

Свойство 2 утверждает, что перестановка строк меняет знак. Учитывая

A=[−154−3],det(A)=(−1)(−3)−(4)(5)=3−20=−17B=[4−3−15],det(B )=(4)(5)−(−1)(−3)=20−3=17\begin{массив}{l}\begin{массив}{l}\\ A=\left[\begin{массив }{cc}-1& 5\\ 4& -3\end{массив}\right],\mathrm{det}\left(A\right)=\left(-1\right)\left(-3\right) -\left(4\right)\left(5\right)=3 — 20=-17\end{массив}\qquad \\ \qquad \\ B=\left[\begin{array}{cc}4& — 3\\ -1& 5\end{массив}\right],\mathrm{det}\left(B\right)=\left(4\right)\left(5\right)-\left(-1\right) )\left(-3\right)=20 — 3=17\qquad \end{массив}A=[−145−3],det(A)=(−1)(−3)−(4 )(5)=3−20=−17B=[4−1−35],det(B)=(4)(5)−(−1)(−3)=20−3=17

Свойство 3 гласит, что если две строки или два столбца идентичны, определитель равен нулю.

A=[122222−122∣12−1222]det(A)=1(2)(2)+2(2)(−1)+2(2)(2)+1(2)(2) −2(2)(1)−2(2)(2)=4−4+8+4−4−8=0\begin{массив}{l}A=\left[\begin{массив}{ccc }1& 2& 2\\ 2& 2& 2\\ -1& 2& 2\end{массив}\text{ }|\text{ }\begin{массив}{c}1\\ 2\\ -1\end{массив} \begin{array}{c}2\\ 2\\ 2\end{массив}\right]\qquad \\ \qquad \\ \mathrm{det}\left(A\right)=1\left(2\ вправо)\влево(2\вправо)+2\влево(2\вправо)\влево(-1\вправо)+2\влево(2\вправо)\влево(2\вправо)+1\влево(2\вправо) )\влево(2\вправо)-2\влево(2\вправо)\влево(1\вправо)-2\влево(2\вправо)\влево(2\вправо)\qquad \\ =4 — 4+8 +4 — 4-8=0\qquad \end{массив}A=⎣

⎡12−1222222 ∣ 12−1222⎦

⎤det(A)=1(2)(2)+2(2)(−1)+2(2) (2)+1(2)(2)−2(2)(1)−2(2)(2)=4−4+8+4−4−8=0

Свойство 4 гласит, что если строка или столбец равны нулю, определитель равен нулю. Таким образом,

A=[1200],det(A)=1(0)−2(0)=0A=\left[\begin{array}{cc}1& 2\\ 0& 0\end{array}\ вправо],\mathrm{det}\left(A\right)=1\left(0\right)-2\left(0\right)=0A=[1020],det(A)=1( 0)−2(0)=0

Свойство 5 утверждает, что определитель обратной матрицы

9{-1}\right)=-2\left(-\frac{1}{2}\right)-\left(\frac{3}{2}\right)\left(1\right)=-\ frac{1}{2}\qquad \end{array}A=[1324],det(A)=1(4)−3(2)=−2A−1=[−2231− 21],det(A−1)=−2(−21)−(23)(1)=−21

Свойство 6 гласит, что если любую строку или столбец матрицы умножить на константу, определитель умножается на тот же коэффициент. Таким образом,

A=[1234],det(A)=1(4)−2(3)=−2B=[2(1)2(2)34],det(B)=2(4)− 3(4)=−4\begin{массив}{l}A=\left[\begin{массив}{cc}1& 2\\ 3& 4\end{массив}\right],\mathrm{det}\left (A\right)=1\left(4\right)-2\left(3\right)=-2\qquad \\ \qquad \\ B=\left[\begin{array}{cc}2\left (1\правый)& 2\левый(2\правый)\\ 3&4\конец{массив}\правый],\mathrm{det}\левый(B\правый)=2\левый(4\правый)-3 \left(4\right)=-4\qquad \end{array}A=[1324],det(A)=1(4)−2(3)=−2B=[2(1)3 2(2)4],det(B)=2(4)−3(4)=−4

Пример 8. Использование правила Крамера и свойств определителя для решения системы

Найдите решение данной системы 3 × 3.

2x+4y+4z=2(1)3x+7y+7z=−5(2) x+2y+2z=4(3)\begin{массив}{ll}2x+4y+4z=2\qquad & \left(1\right)\qquad \\ 3x+7y+7z=-5\qquad & \left(2\right)\qquad \\ \text{ }x+2y+2z=4\qquad & \left (3\right)\qquad \end{array}2x+4y+4z=23x+7y+7z=−5 x+2y+2z=4(1)(2)(3)

Решение

Используя Правило Крамера , мы имеем

D=∣244377122∣D=|\begin{массив}{ccc}2& 4& 4\\ 3& 7& 7\\ 1& 2& 2\end{массив}|D=∣231472472∣

Обратите внимание, что второй и третий столбцы идентичны. Согласно свойству 3 определитель будет равен нулю, поэтому решения либо нет, либо решений бесконечное множество. Мы должны выполнить исключение, чтобы узнать.

Умножьте уравнение (3) на –2 и добавьте результат к уравнению (1).
−2x−4y−4x=−8 2x+4y+4z=20=−6\frac{\begin{array}{l}-2x — 4y — 4x=-8\qquad \\ \text{ }2x+ 4y+4z=2\qquad \end{array}}{0=-6}0=−6−2x−4y−4x=−8 2x+4y+4z=2

Получение утверждения, являющегося противоречием, означает, что система не имеет решения.

Математика -детерминант — Мартин Бейкер

Мы часто знакомимся с определителями как конструкциями матриц, но детерминанты имеют геометрическую интерпретацию, как обсуждается здесь.

Независимость векторов (ортогональный базис)

Представьте, что у нас есть 3 вектора в трехмерном пространстве, затем мы нормализуем эти векторы и поместим их в матрицу 3×3:

х1	x2	х3
у1	у2	у3
z1	z2	z3

Если все эти векторы лежат в одной плоскости, то определитель матрицы будет равен нулю:

Если эти векторы взаимно перпендикулярны, то определитель матрицы будет равен единице (или минус единице):

, поэтому определитель позволяет нам определить, являются ли векторы независимыми, чтобы они могли охватывать пространство.

Здесь мы определяем набор базисных векторов в терминах другого. Другими словами, определение одной системы координат через другую систему координат. Это то же самое, что и представление преобразования, как описано здесь.

Если |М| =1, то преобразование представляет собой поворот (или четное число отражений) от исходной системы координат.

Если |М| = -1, то преобразование представляет собой нечетное число отражений от исходной системы координат.

Если |М| положительно, то новые базисные векторы будут иметь одинаковую ориентацию, например, если абсолютная система координат правая, то базисные векторы также будут формировать правую систему координат.

Если |М| отрицательно, то новые базисные векторы будут иметь противоположную направленность, например, если абсолютная система координат правосторонняя, то базисные векторы будут формировать левостороннюю систему координат.

Объем, окруженный векторами

|M| — это объем, заключенный между векторами. Однако знак значим, он может быть отрицательным, если инвертировано нечетное количество координат, «объем» будет отрицательным.

Это то же самое, что и тривектор трехмерной алгебры Клиффорда.

Двумерный определитель

Если мы возьмем два двумерных вектора (показаны здесь красным и синим) и возьмем площадь, образованную параллелограммом между ними. Затем мы обрезаем части этого параллелограмма и переставляем его так, чтобы получилось:

, что дает площадь, которую можно рассчитать как:

Ay*Bx — Ax*By

, что в терминах матрицы:

det

Бх	Топор
По	Ай

определитель матрицы образованной из векторов, обратите внимание как здесь важен порядок векторов иначе мы получим отрицательную площадь.

Трехмерный определитель

Это сложнее сделать графически, но мы получаем

Ax By Cz + Ay Bz Cx + Az Bx Cy — Ax Bz Cy — Ay Bx Cz — Az By Cx