Фейнмановские лекции по физике: Т.2 Пространство. Время. Движение
Фейнмановские лекции по физике: Т.2 Пространство. Время. Движение
ОглавлениеГлава 15. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ§ 1. Принцип относительности § 2. Преобразование Лоренца § 3. Опыт Майкельсона-Морли § 4. Преобразование времени § 5. Лоренцево сокращение § 6. Одновременность § 7. Четырехвекторы § 8. Релятивистская динамика § 9. Связь массы и энергии Глава 16. РЕЛЯТИВИСТСКАЯ ЭНЕРГИЯ И РЕЛЯТИВИСТСКИЙ ИМПУЛЬС § 1. Относительность и «философы» § 2. Парадокс близнецов § 3.  Преобразование скоростей Преобразование скоростей§ 4. Релятивистская масса § 5. Релятивистская энергия Глава 17. ПРОСТРАНСТВО-ВРЕМЯ § 1. Геометрия пространства-времени § 2. Пространственно-временные интервалы § 3. Прошедшее, настоящее, будущее § 4. Еще о четырехвекторах § 5. Алгебра четырехвекторов Глава 18. ДВУМЕРНЫЕ ВРАЩЕНИЯ § 1. Центр масс § 2. Вращение твердого тела § 3. Момент количества движения § 4. Закон сохранения момента количества движения Глава 19. ЦЕНТР МАСС; МОМЕНТ ИНЕРЦИИ § 1. Свойства центра масс § 2. Положение центра масс § 3. Вычисление момента инерции § 4. Кинетическая энергия вращения Глава 20. ВРАЩЕНИЕ В ПРОСТРАНСТВЕ § 1. Моменты сил в трехмерном пространстве § 2. Уравнения вращения в векторном виде § 4. Момент количества движения твердого тела Глава 21. ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР § 1. Линейные дифференциальные уравнения § 2. Гармонический осциллятор § 3. Гармоническое движение и движение по окружности § 4.  Начальные условия Начальные условия§ 5. Колебания под действием внешней силы Глава 22. АЛГЕБРА § 1. Сложение и умножение § 2. Обратные операции § 3. Шаг в сторону и обобщение § 4. Приближенное вычисление иррациональных чисел § 5. Комплексные числа § 6. Мнимые экспоненты Глава 23. РЕЗОНАНС § 1. Комплексные числа и гармоническое движение § 2. Вынужденные колебания с торможением § 3. Электрический резонанс § 4. Резонанс в природе Главa 24. ПЕРЕХОДНЫЕ РЕШЕНИЯ § 1. Энергия осциллятора § 2. Затухающие колебания § 3. Переходные колебания в электрических цепях Глава 25. ЛИНЕЙНЫЕ СИСТЕМЫ И ОБЗОР § 1. Линейные дифференциальные уравнения § 2. Суперпозиция решений § 3. Колебания в линейных системах § 4. Аналогии в физике § 5. Последовательные и параллельные сопротивления |
Трансформировать поля (Управление данными)—ArcGIS Pro
В этом разделе
- Краткая информация
- Иллюстрация
- Использование
- Параметры
- Параметры среды
- Информация о лицензиях
Краткая информация
Трансформирует непрерывные значения в одно или несколько полей, путем применения математических функций к каждому значению и изменению формы распределения. Методы трансформирования в инструменте включают логарифм, квадратный корень, Box-Cox, множественную инверсию, квадрат, экспоненты и обратный Box-Cox.
Методы трансформирования в инструменте включают логарифм, квадратный корень, Box-Cox, множественную инверсию, квадрат, экспоненты и обратный Box-Cox.
Трансформирование можно применить для сокращения перекосов в распределении и приближении его к нормальному (Гауссову) распределению.
Иллюстрация
Исходные значения трансформируются таким образом, чтобы они стали ближе к нормальному распределению.Использование
Этот инструмент принимает на вход классы объектов или представление таблицы.
В параметре Методы трансформирования доступно 7 вариантов.
- Логарифм—применяет естественную функцию логарифма, log(x) с исходному значению (x) в выбранных полях.
- Преобразование по типу логарифма можно применить только к положительным значениям. Если у вас есть отрицательные или нулевые значения в выбранных полях, по умолчанию к данным перед трансформированием добавляется «сдвиг» log(x+shift), чтобы значения стали положительными.
 По умолчанию значение «сдвига» равно максимальному абсолютному отрицательному значению в полях плюс небольшая положительная величина (~10-6). Например, если максимальное отрицательное число в выбранном поле равно -25, то все значения будут сдвинуты на 25.000001, чтобы они стали положительными.
По умолчанию значение «сдвига» равно максимальному абсолютному отрицательному значению в полях плюс небольшая положительная величина (~10-6). Например, если максимальное отрицательное число в выбранном поле равно -25, то все значения будут сдвинуты на 25.000001, чтобы они стали положительными.
- Преобразование по типу логарифма можно применить только к положительным значениям. Если у вас есть отрицательные или нулевые значения в выбранных полях, по умолчанию к данным перед трансформированием добавляется «сдвиг» log(x+shift), чтобы значения стали положительными.
- Квадратный корень—берет квадратный корень из каждого значения в выбранных полях.
- Трансформирование методом квадратного корня нельзя применить к отрицательным значениям. Если у вас есть отрицательные значения в выбранных полях, по умолчанию к данным перед трансформированием добавляется «сдвиг», чтобы значения стали положительными. По умолчанию значение «сдвига» равно максимальному абсолютному отрицательному значению в полях.
- Box-Cox—применяет следующую степенную функцию для нормального распределения данных в выбранных полях:
где x’ — это трансформированное значение, x — исходное значение, λ1 — параметр степени (экспоненты), а λ2 — параметр сдвига.

- Преобразование по типу Box-Cox можно применить только к положительным значениям. Если у вас есть отрицательные или нулевые значения в выбранных полях, по умолчанию к данным перед трансформированием добавляется «сдвиг», чтобы значения стали положительными. По умолчанию значение «сдвига» равно максимальному абсолютному отрицательному значению в полях плюс небольшое значение (~10-6), чтобы полученные значения были ненулевыми. Параметр Степень можно использовать для настройки значения степени, которая может быть от -5 до 5. Если значение не указано, будет использоваться наилучшее приближение кривой нормального распределения и оно же будет отображаться в сообщениях геообработки.
- Множественная инверсия—принимает обратную величину (1 / x) каждого значения (x) в выбранных полях.
- Трансформирование методом множественной инверсии нельзя применить к нулевым значениям. Если в выбранных полях есть нулевые значения, в трансформированном поле они будут идти как null.
 Сдвиги в этом методе не используются.
Сдвиги в этом методе не используются.
- Трансформирование методом множественной инверсии нельзя применить к нулевым значениям. Если в выбранных полях есть нулевые значения, в трансформированном поле они будут идти как null.
- Экспонента—применяет функцию экспоненты (ex) с исходному значению (x) в выбранных полях. Трансформирование методом экспоненты по сути является обратным вычислением для метода логарифма, а это значит, что применение экспоненциальной трансформации и к полю, трансформированному методом логарифма, приведет к вычислению исходных значений данных.
- По умолчанию к выбранному полю сдвиг не применяется. Чтобы вернуться к исходным значениям для трансформированных методом логарифма полей, укажите то же значение сдвига, которое использовали для создания логарифмических полей. Этот сдвиг будет вычитаться после того, как будет применена трансформация методов экспоненты: ex — сдвиг.
- Квадратный—применяет функцию квадрата к каждому значению в выбранных полях. Трансформирование методом квадрата по сути является обратным вычислением для метода квадратного корня, а это значит, что применение трансформации квадратом к полю, трансформированному методом квадратного корня, приведет к вычислению исходных значений данных.

- По умолчанию к выбранному полю сдвиг не применяется. Чтобы вернуться к исходным значениям для трансформированных методом квадрата полей, укажите то же значение сдвига, которое использовали для создания полей методом квадратного корня. Этот сдвиг будет вычитаться после того, как будет применена трансформация методов квадрата: x2 — сдвиг.
- Обратный Box-Cox — применяет обратную трансформацию Box-Cox, а это значит, что применение трансформации методом обратного Box-Cox к полю, трансформированному методом Box-Cox, приведет к вычислению исходных значений данных. Функция степени обратного Box-Cox вычисляется по формуле:
где x’ — это трансформированное значение, x — исходное значение, λ1 — параметр степени (экспоненты), а λ2 — параметр сдвига.
- По умолчанию к выбранному полю сдвиг или степень не применяется. Чтобы вернуться к исходным значениям для трансформированных методом Box-Cox, укажите те же значения сдвига и степени, которые использовали для создания полей Box-Cox.

- По умолчанию к выбранному полю сдвиг или степень не применяется. Чтобы вернуться к исходным значениям для трансформированных методом Box-Cox, укажите те же значения сдвига и степени, которые использовали для создания полей Box-Cox.
- Логарифм—применяет естественную функцию логарифма, log(x) с исходному значению (x) в выбранных полях.
Если вы не хотите, чтобы в методах логарифма, квадратного корня и Box-Cox использовался сдвиг по умолчанию, вы можете указать значение 0 в параметре Сдвиг, тогда он не будет применяться.
Если в запуске инструмента используется несколько полей, то выбранный метод трансформации будет применен к каждому из них. Если не указано значение сдвига или степени, то одни и те же значения будут применены ко всем выбранным полям. Если для параметров Сдвиг и Степень значения не указаны, то значения по умолчанию вычисляются независимо для каждого выбранного поля на основе выбранного метода трансформирования.
Инструмент изменяет входные данные и присоединяет новые созданные поля трансформирования к входной таблице или классу объектов.
В параметре Поле для трансформирования можно задать имена для входного и выходного поля.
 Если имя выходного поля уже существует в данных, инструмент перезапишет значения в этом поле.
Если имя выходного поля уже существует в данных, инструмент перезапишет значения в этом поле.Для каждого трансформированного поля и для поля-источника в сообщениях результатов геообработки приводится суммарная статистика. В эту статистику входят: минимум, максимум, сумма, среднее, стандартное отклонение, медиана, асимметрия и эксцесс.
Также в сообщениях геообработки будут показаны значения параметров Степень и Сдвиг, вычисленные инструментом. Эти значения можно использовать для получения исходных значений данных с использованием обратных методов трансформирования.
Инструмент создает гистограмму для каждого нового созданного трансформированного поля для визуализации распределения.
Параметры
| Подпись | Описание | Тип данных |
Входная таблица | Входная таблица или класс пространственных объектов, содержащее поля, которые нужно трансформировать. | Table View; Raster Layer; Mosaic Layer |
Поля, которые нужно трансформировать | Поля, содержащие значения, которые будут трансформированы. Для каждого поля можно указать имя выходного поля. Если имя выходного поля не указано, инструмент создает выходное поле с именем, созданным на основе имени входного поля и метода трансформирования. | Value Table |
Методы трансформирования (Дополнительный) | Определяет метод, который используется для преобразования значений, содержащихся в выбранных полях.
| String |
Степень (Дополнительный) | Параметр степени ( λ1) для трансформации Box-Cox. | Double |
Сдвиг (Дополнительный) | Значение, на которое смещаются все данные (добавление постоянного значения). Если указано 0, ничего не добавляется. Для трансформаций логарифма, Box-Cox и квадратного корня перед преобразованием добавляется значение сдвига по умолчанию, если в данных нет отрицательных или нулевых значений. Для трансформаций методами экспоненты (обратный логарифм), обратный Box-Cox и квадрат (обратный квадратный корень) по умолчанию сдвиг не применяется. Если задано значение сдвига, то это значение вычитается после того, как применен метод трансформирования. Это позволяет использовать то же значение сдвига для преобразований и связанных с ними обратных преобразований. | Double |
Производные выходные данные
| Подпись | Описание | Тип данных |
| Обновленная входная таблица | Обновленная таблица, содержащая преобразованные поля. | Представление таблицы |
arcpy.management.TransformField(in_table, fields, {method}, {power}, {shift})| Имя | Описание | Тип данных |
in_table | Входная таблица или класс пространственных объектов, содержащее поля, которые нужно трансформировать. Новые трансформированные поля добавляются к входной таблице. | Table View; Raster Layer; Mosaic Layer |
fields [[input_field, output_field_name],…] | Поля, содержащие значения, которые будут трансформированы. Для каждого поля можно указать имя выходного поля. Если имя выходного поля не указано, инструмент создает выходное поле с именем, созданным на основе имени входного поля и метода трансформирования. | Value Table |
method (Дополнительный) | Определяет метод, который используется для преобразования значений, содержащихся в выбранных полях.
| String |
power (Дополнительный) | Параметр степени ( λ1) для трансформации Box-Cox. Если значение не указано, будет определено оптимальное значение с использованием оценки максимального правдоподобия (MLE). | Double |
shift (Дополнительный) | Значение, на которое смещаются все данные (добавление постоянного значения). Если указано 0, ничего не добавляется. Для трансформаций логарифма, Box-Cox и квадратного корня перед преобразованием добавляется значение сдвига по умолчанию, если в данных нет отрицательных или нулевых значений. Для трансформаций методами экспоненты (обратный логарифм), обратный Box-Cox и квадрат (обратный квадратный корень) по умолчанию сдвиг не применяется. Если задано значение сдвига, то это значение вычитается после того, как применен метод трансформирования. Это позволяет использовать то же значение сдвига для преобразований и связанных с ними обратных преобразований. | Double |
Производные выходные данные
| Имя | Описание | Тип данных |
| updated_table | Обновленная таблица, содержащая преобразованные поля. | Представление таблицы |
Пример кода
TransformField пример 1 (окно Python)В следующем скрипте окна Python показано, как используется инструмент TransformField.
import arcpy
arcpy.management.TransformField("County_Data", "Income", "LOG")TransformField пример 2 (автономный скрипт)Следующий автономный скрипт Python демонстрирует, как использовать инструмент TransformField.
# Import system modules.
import arcpy
try:
# Set the workspace and input features.
arcpy.env.workspace = r"C:\\Transform\\MyData.gdb"
inputFeatures = "County_Data"
# Set the input fields that will be standardized
fields = "population_total;unemployment_rate;income"
# Set the standardization method.
method = "BOX-COX"
# Run the Transform Field tool
arcpy.management.TransformField(inputFeatures, fields, method)
except arcpy.ExecuteError:
# If an error occurred when running the tool, print the error message.
print(arcpy.GetMessages())
Параметры среды
Экстент
Информация о лицензиях
- Basic: Да
- Standard: Да
- Advanced: Да
Связанные разделы
Отзыв по этому разделу?
математических слов: степень термина
математических слов: степень термина
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Многочлены многочлен — одночлен или два или более одночлена, объединенные путем сложения или вычитания | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Обратите внимание, что каждый одночлен, двучлен и трехчлен также является полиномом. {2}-7x — 9{3}[/латекс]
{2}-7x — 9{3}[/латекс]
попробуйте
Определение степени полиномов
В этом разделе мы будем работать с полиномами, каждый член которых содержит только одну переменную. Степень полинома и степени его членов определяются показателями переменной.
Одночлен, у которого нет переменной, а есть только константа, является особым случаем. Степень константы равна [latex]0[/latex] — она не имеет переменной.
Степень многочлена
Степень члена — это показатель степени его переменной.
Степень константы равна [latex]0[/latex].
Степень многочлена — это наивысшая степень всех его членов.
Давайте посмотрим, как это работает, взглянув на несколько многочленов. Мы будем делать это шаг за шагом, начиная с одночленов, а затем переходя к полиномам с большим количеством членов.


 По умолчанию значение «сдвига» равно максимальному абсолютному отрицательному значению в полях плюс небольшая положительная величина (~10-6). Например, если максимальное отрицательное число в выбранном поле равно -25, то все значения будут сдвинуты на 25.000001, чтобы они стали положительными.
По умолчанию значение «сдвига» равно максимальному абсолютному отрицательному значению в полях плюс небольшая положительная величина (~10-6). Например, если максимальное отрицательное число в выбранном поле равно -25, то все значения будут сдвинуты на 25.000001, чтобы они стали положительными.
 Сдвиги в этом методе не используются.
Сдвиги в этом методе не используются.
 Если имя выходного поля уже существует в данных, инструмент перезапишет значения в этом поле.
Если имя выходного поля уже существует в данных, инструмент перезапишет значения в этом поле. Новые трансформированные поля добавляются к входной таблице.
Новые трансформированные поля добавляются к входной таблице.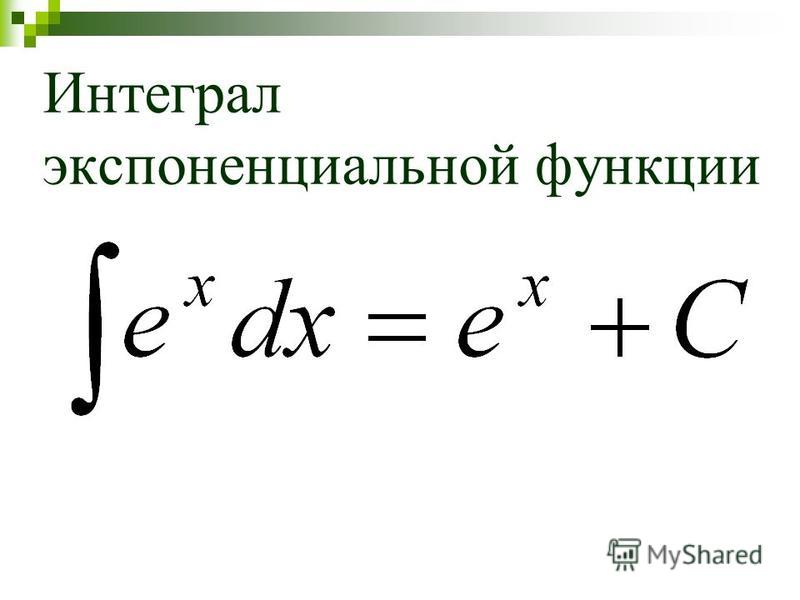
 Если значение не указано, будет определено оптимальное значение с использованием оценки максимального правдоподобия (MLE).
Если значение не указано, будет определено оптимальное значение с использованием оценки максимального правдоподобия (MLE).