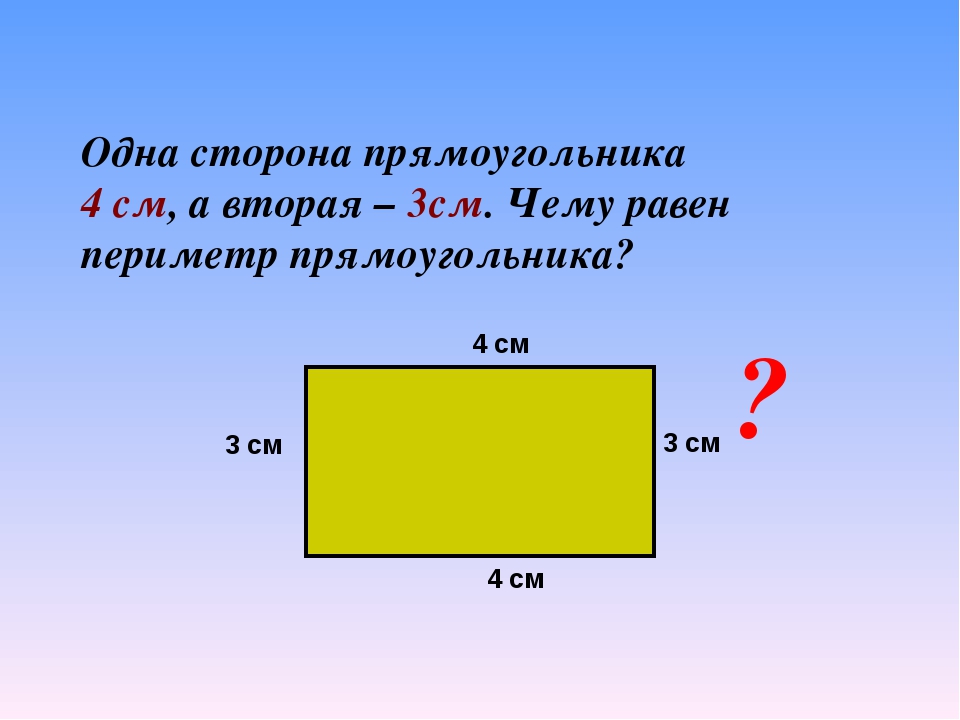
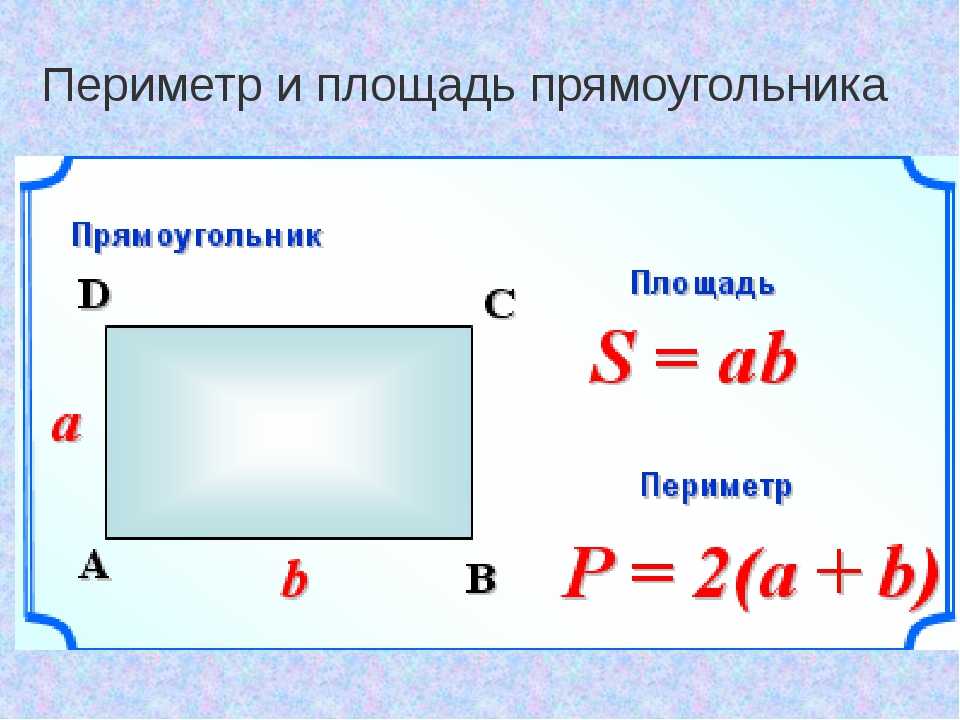
Периметр Прямоугольная зона Трапеция Параллелограмм, цилиндр, угол, текст, прямоугольник png
Периметр Прямоугольная зона Трапеция Параллелограмм, цилиндр, угол, текст, прямоугольник pngтеги
- угол,
- текст,
- прямоугольник,
- треугольник,
- геометрическая форма,
- ромб,
- параллель,
- диагональ,
- трапеция,
- площадь,
- квадрат,
- геометрия,
- линия,
- точка,
- зеленый,
- параллелограмм,
- диаграмма,
- математика,
- периметр,
- png,
- прозрачный,
- бесплатная загрузка
Об этом PNG
- Размер изображения
- 1200x724px
- Размер файла
- 30.15KB
- MIME тип
- Image/png
изменить размер PNG
ширина(px)
высота(px)
Лицензия
Некоммерческое использование, DMCA Contact Us
org/ImageObject»> Геометрия Евклидова абстракция, Геометрическая абстракция, синий, серый и зеленый иллюстрации, угол, прямоугольник, треугольник png
386x849px
27.24KB
79KB
4KB
25KB
62KB
org/ImageObject»> Рисунок Геометрическая форма Геометрия, геометрические фигуры, разное, текст, прямоугольник png
500x500px
61.78KB
2KB
53KB
04KBОпределение, признаки и свойства произвольной, равнобедренной и прямоугольной трапеции
Математика
12.11.21
8 мин.
В курсе геометрии за 8-й класс подразумевается изучение свойств и признаков выпуклых четырёхугольников. К ним относятся параллелограммы, частными случаями которых являются квадраты, прямоугольники и ромбы, и трапеции. И если решение задач на различные вариации параллелограмма чаще всего не вызывает сильных затруднений, то разобраться, какой четырёхугольник называется трапецией, несколько сложнее.
Оглавление:
- Основные свойства элементов
- Вычисление периметра и площади
- Вписанная и описанная окружность
- Частные случаи
Определение и виды
В отличие от других четырёхугольников, изучаемых в школьной программе, трапецией принято называть такую фигуру, две противоположные стороны которой параллельны друг другу, а две другие — нет. Существует и другое определение: это четырёхугольник с парой сторон, которые не равны между собой и параллельны.
Различные виды указаны на рисунке ниже.
На изображении под номером 1 изображена произвольная трапеция. Номером 2 обозначен частный случай — прямоугольная трапеция, одна из сторон которой перпендикулярна её основаниям. Последняя фигура — тоже особый случай: это равнобедренная (равнобокая) трапеция, т. е. четырёхугольник с равными боковыми сторонами.
youtube.com/embed/gpFCuFPgiNk» allowfullscreen=»allowfullscreen»> Важнейшие свойства и формулы
Для описания свойств четырёхугольника принято выделять определённые элементы. В качестве примера можно рассмотреть произвольную трапецию ABCD.
В её состав входят:
- основания BC и AD — две стороны, параллельные по отношению друг к другу;
- боковые стороны AB и CD — два непараллельных элемента;
- диагонали AC и BD — отрезки, соединяющие противоположные вершины фигуры;
- высота трапеции CH — перпендикулярный основаниям отрезок;
- средняя линия EF — линия, соединяющая середины боковых сторон.
Основные свойства элементов
Чтобы решить задачи по геометрии или доказать какие-либо утверждения, наиболее часто используют свойства, которые связывают различные элементы четырёхугольника.
Они формулируются следующим образом:
- Средняя линия всегда проходит параллельно обоим основаниям фигуры и численно равна их полусумме: EF = (BC + AD)/2.
- Точка пересечения диагоналей фигуры разделяет их с таким же соотношением длины, с каким относятся основания трапеции: AD : BC = AO : CO = DO : BO.
- Основание можно вычислить, зная длину второго основания и средней линии: BC = 2 · EF — AD, AD = 2 · EF — BC.
- Боковые стороны вычисляются, если известна высота фигуры и синус угла при основании: AB = CH / sinA, CD = CH / sinD.
- Для расчёта высоты необходимо знать, чему равна боковая сторона и прилегающий угол: CH = AB · sinA = CD · sinD.
Кроме того, часто полезно знать и применять следующие утверждения:
- Биссектриса, проведённая из произвольного угла, отделяет на основании отрезок, длина которого равна боковой стороне фигуры.
- При проведении диагоналей образуются 4 треугольника; из них 2 треугольника, образованных основаниями и отрезками диагоналей, обладают подобием, а оставшаяся пара имеет одинаковую площадь.
- Через точку пересечения диагоналей O, середины оснований, а также точку, в которой пересекаются продолжения боковых сторон, можно провести прямую.
Вычисление периметра и площади
Периметр рассчитывается как сумма длин всех четырёх сторон (аналогично любой другой геометрической фигуре):
P = AD + BC + AB + CD.
Есть несколько способов, как можно рассчитать площадь трапеции по формуле. Следует выбрать из них наиболее подходящий вариант, опираясь на то, какие данные известны по условию задачи.
Вписанная и описанная окружность
Окружность возможно описать около трапеции только в том случае, когда боковые стороны четырёхугольника равны.
Чтобы вычислить радиус описанной окружности, необходимо знать длины диагонали, боковой стороны и большего основания.
Величина p, используемая в формуле, рассчитывается как полусумма всех вышеперечисленных элементов: p = (a + c + d)/2.
Для вписанной окружности условие будет следующим: сумма оснований должна совпадать с суммой боковых сторон фигуры. Радиус её можно найти через высоту, и он будет равен r = h/2.
Частные случаи
Рассмотрим часто встречаемый случай — равнобокую (равностороннюю) трапецию. Её признаки — равенство боковых сторон или равенство противолежащих углов. К ней применимы все утверждения, которые характерны для произвольной трапеции. Другие свойства равнобедренной трапеции:
- Прямая, которая проходит через середины оснований фигуры, пересекает их под углом 90 градусов.
- Углы, лежащие при любых основаниях, попарно равны.
- Длины диагоналей совпадают.
- Высота будет равна средней линии, если диагонали проходят перпендикулярно друг к другу.
- Высота, опущенная из вершины к основанию, делит его на 2 отрезка, длина большего вычисляется как половина суммы оснований, а длина меньшего — как половина разности.
Прямоугольная трапеция встречается в задачах не так часто. Её признаки — наличие двух смежных углов, равных 90 градусов, и наличие боковой стороны, перпендикулярной основаниям. Высота в таком четырёхугольнике одновременно является одной из его сторон.
Все рассмотренные свойства и формулы обычно используются для решения планиметрических задач. Однако также их приходится применять в некоторых задачах из курса стереометрии, например, при определении площади поверхности усечённой пирамиды, внешне напоминающей объёмную трапецию.
Периметр прямоугольников — Xcelerate Math
«Пери» означает «около» , а «метр» означает «мера» .
При расчете длины забора вокруг фермы, длины рамы вокруг картины или длины карниза вокруг потолка комнаты отрабатывается именно периметр.
Действительно, чтобы найти периметр, все, что вам нужно сделать, это сложить все стороны фигуры. Однако для некоторых форм существуют такие правила, как:
- Периметр прямоугольника = (Д + Ш) × 2
- Периметр квадрата = S × 4
Часто нам приходится конвертировать единицы длины. Например, плотники измеряют в миллиметрах для точности, а затем эти измерения часто конвертируют в метры при расчете стоимости таких материалов, как древесина.
| ДЛИНА ПРАВИЛ | ПЕРЕВОД ЕДИНИЦ ДЛИНЫ |
| 10 миллиметров = 1 сантиметр 1000 миллиметров = 1 метр 100 сантиметров = 1 метр 1000 метров = 1 километр | При преобразовании из большой единицы в малую единицу вы умножаете . При преобразовании из маленькой единицы в большую единицу вы делите . |
com/embed/wSGo2FwAfzM?list=PLG1wXdfLSA80Cvs9G24SDMnmpCb9b8wi9″ frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»> Пример 1 — Фрираннинг
Фрираннинг (ранее называвшийся « par cours ») — это уличный вид спорта, в котором спортсмены находят кратчайший маршрут по кругу. препятствия в городских пейзажах. Рассчитайте общую длину трассы ниже.
(Не забудьте перевести все измерения в одни и те же единицы, например, в метры.)
- Старт до А — 320 метров
- от А до В — 350 метров
- B — C — 1,1 км
- C до D — 1,3 км
- D-E-F-G (через мост через арку) — 1430 метров
- D — G (по мосту через дорогу) — 1100 метров
Ответ:
Периметр поля
= 320 + 350 + 1100 + 1300 + 1430 + 1100 + 1300 + 1100 + 350 + 320
= 3060 м или 3,06 км
Пример второй.
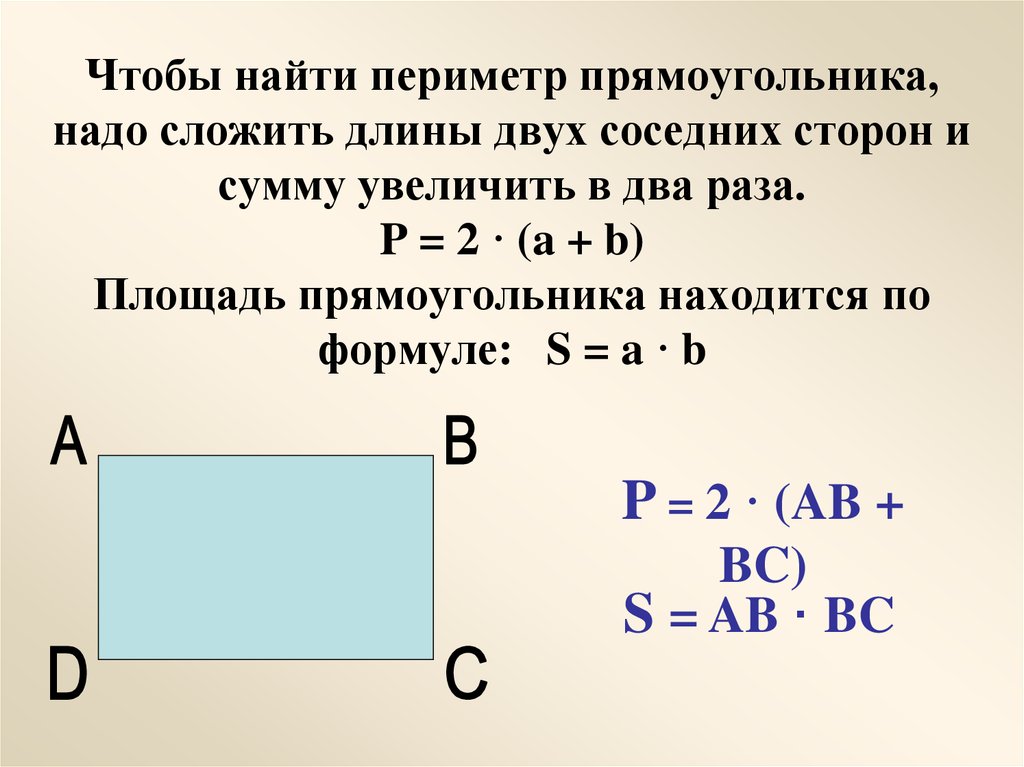Длина забораНайдите длину забора вокруг прямоугольной фермы длиной 2 км и шириной 500 метров .
(Проверьте, чтобы размеры были в одних и тех же единицах измерения. Нарисуйте схему. Запишите правило и единицу измерения.)
Ответ:
Периметр прямоугольника
= (Д + Ш) × 2
= (2000 + 500) × 2
= 2500 × 2
= 5000 м или 5 км
Пример 3. Рамка вокруг картины
Какой длины требуется рамка для квадратной картины со стороной 20 см ?
Ответ:
Периметр квадрата
= С × 4
= 20 × 4
= 80 см
Вопрос
Периметр прямоугольника 336 см, а ширина 68 метров. Как долго это?
Ответить
100 м
Знаете ли вы, что…?
При касании электрический забор и получите удар током, потому что вы замкнули электрическую цепь с землей.
Если вы носите обувь с утепленной резиновой подошвой, цепь с землей не замкнется и вас не ударит током.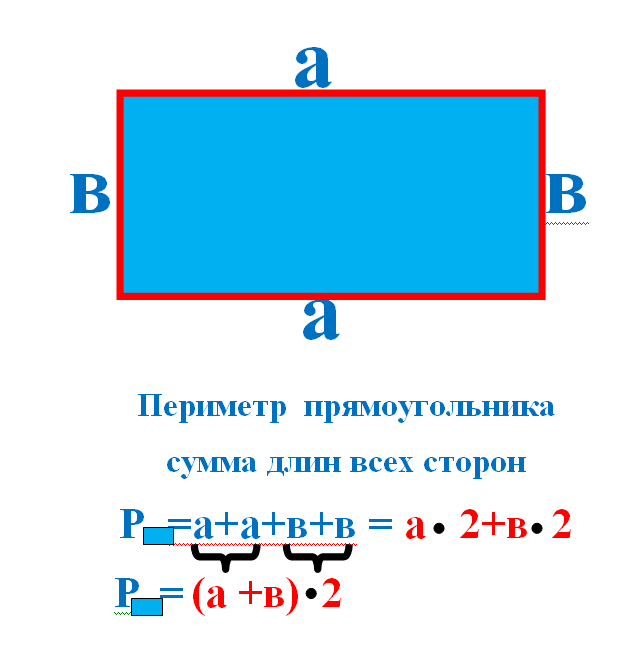
Внимание! Не пытайтесь это сделать! Забор может быть под высоким напряжением или у вас может быть неправильная обувь.
Программа Python для нахождения периметра прямоугольника
Питон Джава С С++ HTML CSS JavaScript PHP SQL Контрольный опрос
В этой статье мы создали несколько программ на Python для поиска и печати периметра прямоугольника на основе длина и ширина, введенные пользователем во время выполнения. Вот список подходов, используемых для решения задачи:
- Найти периметр прямоугольника без использования функции
- Использование пользовательской функции
- Использование класса и объекта
Прежде чем создавать эти программы, напомню об используемой здесь формуле.
Формула для нахождения периметра прямоугольника
Чтобы найти значение периметра прямоугольника, используйте следующую формулу:
per = len+bre+len+bre
= (2*длина)+(2*ширина)
= 2*(len+bre) Здесь per указывает на периметр , len указывает на длину и bre указывает на
ширина прямоугольника.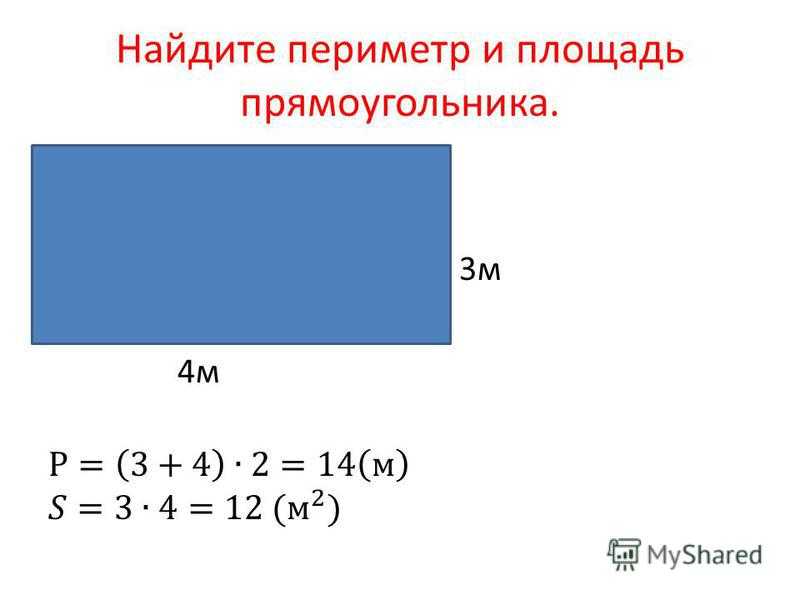
Вы можете использовать любую из этих трех формул. Третью лучше брать.
Найти периметр прямоугольника без функции
Чтобы вычислить периметр прямоугольника в Python, вы должны попросить пользователя ввести значение длины и ширины прямоугольника, периметр которого вы хотите узнать. Вопрос в том, написать программу Python, чтобы найти периметр прямоугольник. Вот его ответ:
print("Введите длину прямоугольника:")
л = интервал (ввод ())
print("Введите ширину прямоугольника:")
б = интервал (ввод ())
р = 2*(л+б)
print("\nPerimeter = ", p) Вот начальный вывод этой программы Python:
Теперь введите 6 как длину и 2 как ширину, нажмите ENTER чтобы найти и распечатать
периметр, как показано на снимке ниже:
Модифицированная версия предыдущей программы
Эта программа использует end= для пропуска автоматической печати новой строки с помощью print() . {:.2f} используется для печати значения внутри метода format() только до двух знаков после запятой.
print("Введите длину и ширину прямоугольника: ", end="")
л = с плавающей запятой (ввод ())
б = с плавающей запятой (ввод ())
print("\nPerimeter = {:.2f}".format(2*(l+b))) Вот пример запуска с пользовательским вводом, 12.2 как длина и 6.4 как ширина прямоугольника:
Найти периметр прямоугольника с помощью функции
выполните ту же задачу, что и в предыдущей программе. Функция принимает два аргумента. Первый аргумент относится к длине, а второй — к ширине прямоугольника. Функция возвращает значение периметра. Следовательно, значение периметра инициализируется равным 9.0003 res и значение он печатается как периметр прямоугольника. Вот и все.
по определению findPeri(a, b):
р = 2*(а+б)
вернуть р
print("Введите длину и ширину прямоугольника: ", end="")
л = с плавающей запятой (ввод ())
б = с плавающей запятой (ввод ())
res = найтиPeri(l, b)
print("\nPerimeter = {:.2f}".format(res)) Эта программа выводит точно такой же результат, как и предыдущая программа.