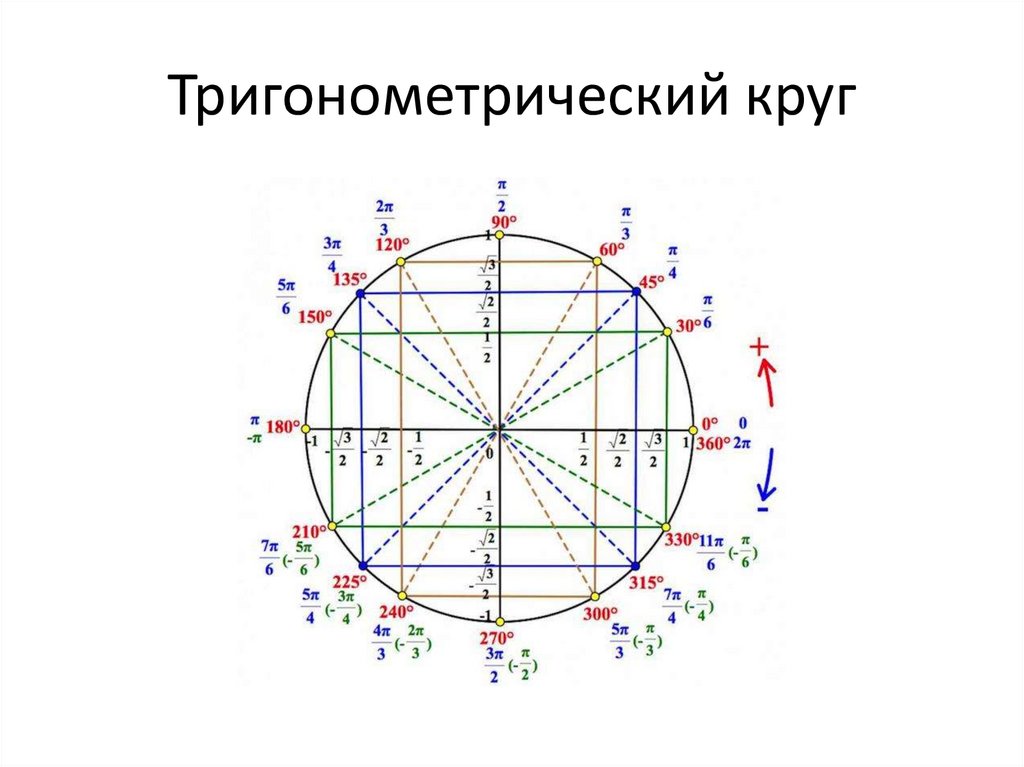
Ось синусов и косинусов. Тригонометрический круг
Зеркально отражаются, но это не так. Если вопрос изучить более внимательно, можно заметить их асимметрию. При измерении размеров мозга оказывается, что левое полушарие всегда немного больше, чем правое. Но это не единственная разница. Правое полушарие содержит длинные соединяющие отдаленные участки мозга, а левое имеет короткие волокна, образующие связи на ограниченном участке.
Медицинские наблюдения
Исследуя мозг пациента, который страдал потерей речи, Поль Брока, французский врач, в 1861 году обратил внимание на то, что в левом полушарии поврежден участок лобной доли, которая ответственна за порождение речи.
И только совсем недавно ученые смогли определить, за что же еще отвечает каждое полушарие в отдельности. Дело в том, что при нормальном функционировании наш мозг работает как единая слаженная система, и информация моментально передается от полушария к полушарию по широкому пучку нервных волокон, соединяющих их. Эти волокна называются
Эти волокна называются
При эпилепсии этот связующий мост может вызвать проблемы и повредить мозг. Стремясь предотвратить подобный исход, нейрохирурги в некоторых случаях рассекают мозолистое тело.
Такие пациенты живут обычной жизнью, а ученые могут тщательно исследовать работу полушарий по отдельности. И вот что было определено.
Способно выражать себя речью, выполнять сложные расчеты и логические операции. Правое полушарие реагирует только на простую легкую речь.
Зато правое полушарие великолепно осознает пространство и структуру, поэтому оно лучше левого создает геометрические рисунки и рисунки с перспективой. Левым полушарием контролируется правая сторона тела, а правым — левая.
При повреждении правого полушария у человека происходят нарушения в узнавании лиц или восприятии информации, глубины и пространства. Дополнительные сведения относительного специализации правого полушария ученые получили, наблюдая за больными, у которых нарушена речь, но способность к пению сохраняется.
Отличия полушарий
Асимметрия бывает психической, сенсорной и моторной межполушарной.
При изучении психофизиологических функций было выяснено, что контроль за словесным информационным каналом в речи осуществляет левое полушарие, а за несловесным каналом, т.е. голосом и интонацией, следит правое. в левом полушарии производится аналитически, последовательно, по принципу индукции. Правое полушарие обрабатывает поступившую информацию одновременно, синтезируя ее, по принципу дедукции.
Левое полушарие представляет чаще всего положительные эмоции и подавляет проявление слабых эмоций. Правое полушарие более «эмоционально» и представляет в основном отрицательные эмоции, контролируя проявления сильных.
В сенсорной сфере правое и левое полушарие отличаются способностью к зрительному восприятию. Правое полушарие мозга воспринимает целостно зрительный образ и легче справляется с задачей различения предметов и визуализации.
Моторная асимметрия полушарий выражается в право-лево-рукости, которая управляется моторной корой мозга противоположного полушария.
Развитие правого полушария
Чтобы развить интуицию, надо научиться активизировать правое полушарие. Как же достичь этого? Самым простым и естественным путем является занятие теми видами деятельности, при которых «включается» правая часть мозга. Это все виды творчества: рисование, пение, танцы, а также прослушивание музыки, восприятие запахов, оперирование символами, образами.
Человеческий мозг нуждается в постоянном развитии, но каждому его полушарию необходим особый подход. Левое и правое полушарие ответственны за разные умения, навыки и чувства. Помимо этого, каждое из них обслуживает противоположную сторону тела человека: правое – левую, а левое – правую.
Развитие той или иной части мозга предопределяет ваши навыки. Например, чрезмерная чувствительность говорит о доминировании правого полушария мозга, а логика – левого. Возможно, ли развить правое полушарие мозга специально, прибегая к тренировкам и упражнениям? Конечно да.
Например, чрезмерная чувствительность говорит о доминировании правого полушария мозга, а логика – левого. Возможно, ли развить правое полушарие мозга специально, прибегая к тренировкам и упражнениям? Конечно да.
Правое полушарие мозга — особенности
Перед тем, как заниматься развитием правого полушария необходимо разобраться за что оно отвечает. Следует знать, что это, прежде всего — эмоции, интуиция и творчество человеческого мышления.
При активном развитии правого полушария, люди способны видеть мир целостно, не дробя картину на элементы. Так происходит улучшенное восприятие образов и символики, нежели цифро-буквенные значения. Пожалуй, главным преимуществом является возможность делать несколько дел одновременно и думать о каждом из них в равной мере, не игнорируя деталей. Если обобщить функционал правого полушария человеческого мозга, то можно назвать его одним словом – творческое.
Как можно развить правое полушарие?
На сегодняшний день упражнений для развития правого полушария, в т.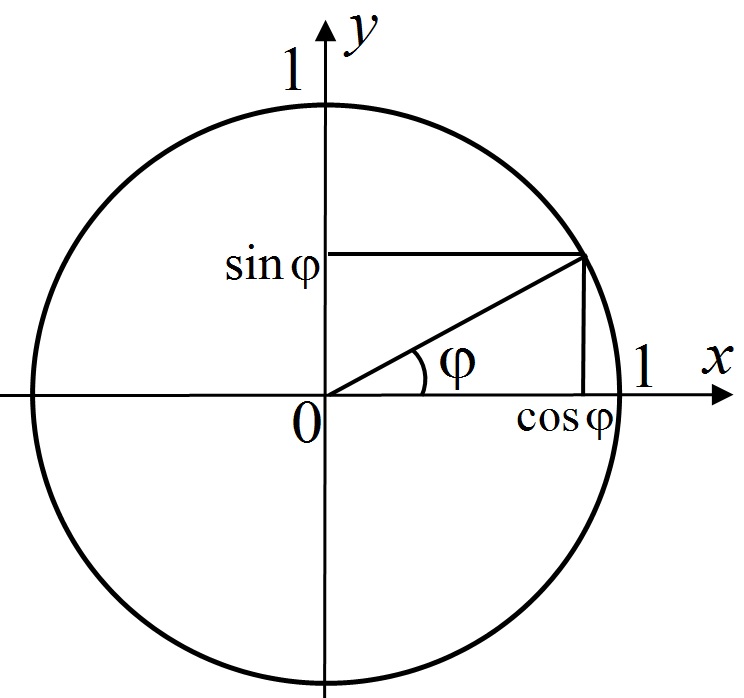 ч. игр великое множество. Отметим, что это не столько физические нагрузки, сколько техники на моторику, восприятие и темп. При использовании некоторых упражнений может понадобиться инструментарий.
ч. игр великое множество. Отметим, что это не столько физические нагрузки, сколько техники на моторику, восприятие и темп. При использовании некоторых упражнений может понадобиться инструментарий.
Каждое из приведенных в статье упражнений, помогут развить правое полушарие человеческого мозга. Их можно применять как по отдельности, так и в комплексе. Необходимо выбрать одно или несколько наиболее подходящее для Вашего образа жизни, которое не будет мешать в повседневных делах. Однако, невзирая на упражнение, существует важное правило – эффективное развитие правого полушария мозга возможно лишь при условии систематического выполнения упражнений.
Мозг можно сравнить с мышцами, чем больше тренируешь, тем быстрее растут их способности. Как только забываешь об их потребностях, они ослабевают и даже атрофируются.
Презентация: «Содружество полушарий мозга человека»
Первые шаги в развитии мозга
При возникновении трудностей с выбором такой деятельности, советует посетить культурно-массовые мероприятия.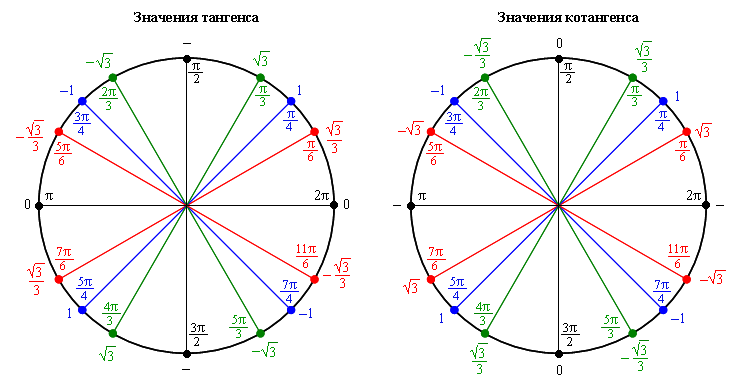 К примеру, художественные выставки, ярмарки народного творчества, музеи и иное. Такие места вызывают различные ассоциации. Так можно выбрать рисование или написание небольших рассказов и миниатюр.
К примеру, художественные выставки, ярмарки народного творчества, музеи и иное. Такие места вызывают различные ассоциации. Так можно выбрать рисование или написание небольших рассказов и миниатюр.
Следует понимать, что тело и мозг тесно взаимосвязаны, ввиду этого наиболее эффективным будет через тело воздействовать на мозг. Помните, что правое полушарие воздействует на левую часть организма и тела.
В том случае, если Вы привыкли писать правой рукой, то следует развивать левую. К примеру, при игре на музыкальном инструменте используйте левую часть в музицировании простой мелодии. Также будет эффективным замена рук при повседневных занятиях. Так можно при размешивании сахара сменить руку с левой в правую и наоборот. Необходимо довести эти упражнения до автоматизма. Безусловно, поначалу будет нелегко, однако и писать в первом классе, вы начали не сразу, как впрочем, и ходить. Если каждый день так практиковаться, то результат не заставит себя ждать.
Визуализация – начало
Данное упражнение для развития правого полушария не только полезно, но и увлекательно.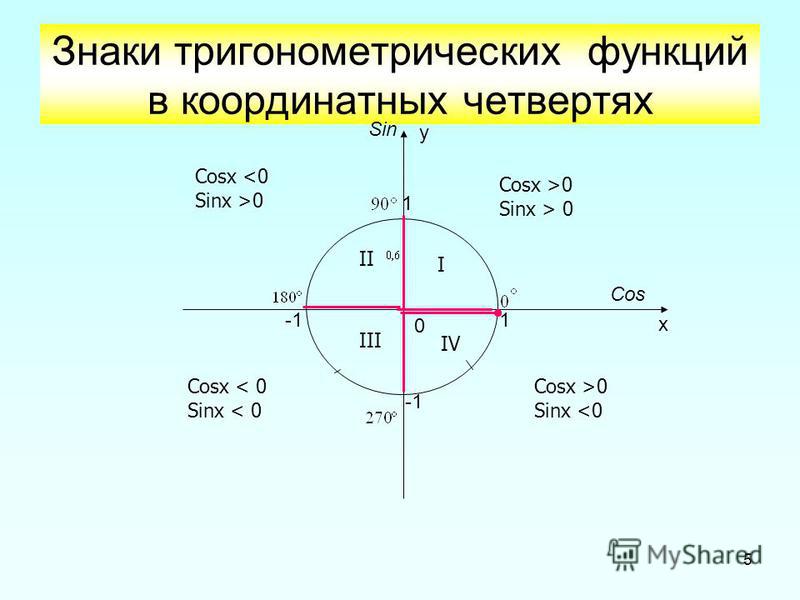
Интересно будет любому поколению, ведь мы фантазируем и мечтаем независимо от возраста.
- Визуализация – прикройте глаза и вообразите белый лист бумаги или фон. Мысленно выведите на нем свое имя. Представьте, что цвет букв зеленый, затем синий, а после красный. Можно попробовать изменять и цвет фона. Чем ярче будут краски, тем эффективнее.
- Аудиальные фантазии. Чтобы полноценно развивать правое полушарие, необходимо работать и со звуком. Представьте, что вас кто-то зовет. Сконцентрируйтесь, чтобы такое «виденье» стало четким. Попробуйте идентифицировать, кому принадлежит этот голос. Возможно, это бабушка или мама. Следующим этапом будет воспроизведение в голове музыки. Самое действенное это вспомнить любимую песню.
- Тактильные ощущения. Довольно интересное упражнение на ощущение слов. Примите удобное положение тела, прикройте глаза и попробуйте представить своё имя. Какое оно? Холод и твердость, словно камень или ласковое и теплое, как любимая кошка.
 Аналогично можно экспериментировать со вкусовыми ощущениями и запахом. Важно пытаться представить все визуализированные вещи так, что вы сможете ощущать их органами чувств.
Аналогично можно экспериментировать со вкусовыми ощущениями и запахом. Важно пытаться представить все визуализированные вещи так, что вы сможете ощущать их органами чувств.
Зеркальное рисование для развития мозга
Отличное упражнение, которое улучшает эффективность работы обоих полушарий мозга. Рисование, таким образом, задействует оба полушария фактически «подтягивая» одно из них, отстающее в развитии. Вам понадобится бумага и два карандаша. Пытайтесь рисовать одинаковые формы обеими руками одновременно. Это могут быть колечки, сердечки, квадраты, все что угодно. Главное, и правая, и левая рука должны выполнять одновременно одно и то же задание.
Игра на музыкальных инструментах отлично сказывается на развитии мозга, так как задействованы оба полушария. Это отличная тренировка, способствующая быстрому развитию.
Развитие с помощью этих упражнений очень эффективно и результаты не заставляют себя долго ждать. Единственное правило – систематичность. Следуя этим советам, вам наверняка гарантировано развитое, продуктивное правое полушарие.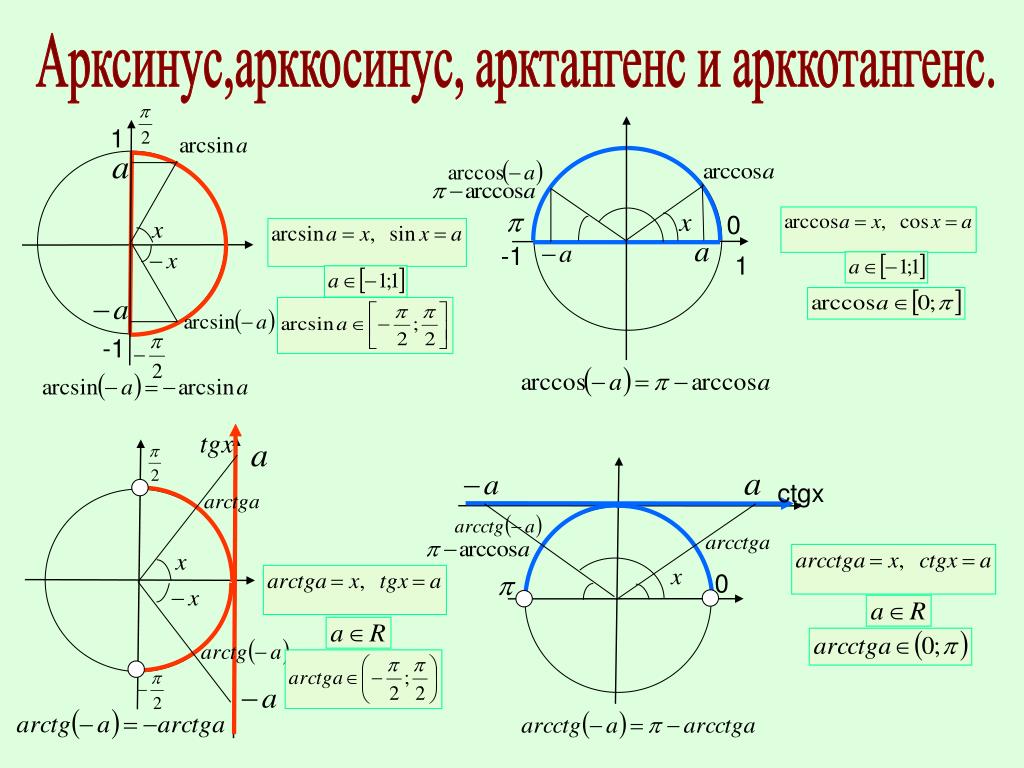
Как мандала влияет на мозг
Мандала является священным узором Тибета и индуской религии. Созерцание этого рисунка можно назвать первым шагом с работой правого полушария. Мандалу можно нарисовать или найти в Internet готовую.
Расслабьте тело, начиная от кончиков пальцев ног и заканчивая мышцами лица. Сконцентрируйте внимание на центре узора (3 минуты). Спустя время Вы заметите, что рисунок стал «играть», как в калейдоскопе.
Кстати, в Тибете монахи используют рисование мандалы, как одну из сложнейших практик. Они собирают узоры из цветных зернышек. Такое занятие может длиться не день и не два, порой доходя до несколько месяцев. По окончании рисования, узор стирают одним взмахом руки.
В 1975 году в штате Калифорния была вручена премия за выдающиеся исследования Полу Деннисону. Ученый предложил через различные упражнения задействовать те участки мозга, которые менее активны.
В процессе тестирования были выявлены следующие результаты:
- Улучшилась концентрация, и способность запоминать больше данных за небольшой промежуток времени.

- Увеличилась стрессоустойчивость.
- Адаптация к новым условиям происходила легче и быстрее.
- Контроль за эмоциональным состоянием.
- После различных нагрузок организм быстрее восстанавливался.
- Развитие творческого потенциала.
Упражнения с такими результатами актуальны не только для младшего поколения, но и для взрослых.
Занятий по методу «brain gym» достаточно много, рассмотрим самые популярные.
Симметричные упражнения
- Движения в параллели
Когда Вы ходите, то дотрагивайтесь левой рукой до колена левой ноги, а правой – правого колена. Сделать необходимо 12 шагов. Необходимо следить, что бы руки касались колен поочередно, не сбиваясь с ритмом. При этом необходимо смотреть на рисунок с двумя параллельными линиями, который должен находиться на уровне глаз.
- Бесконечность
Прижмите ухо к левому плечу, а левую руку вытяните вперед. Сконцентрируйтесь на указательном пальце и нарисуйте горизонтальный знак «восьмерки».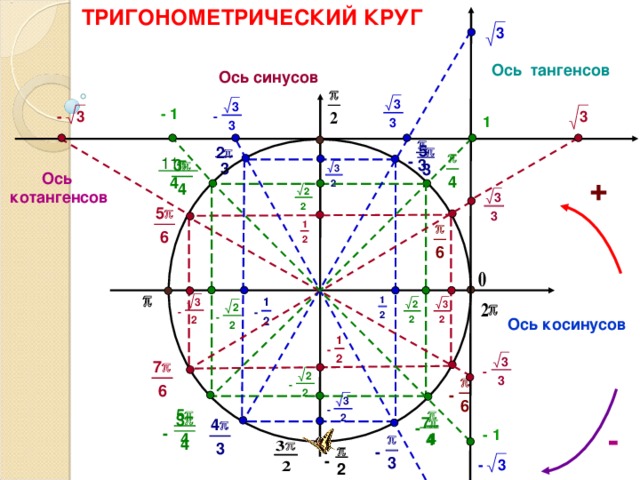 Рисовать следует от центральной точки вверх и лево. Сделайте такое упражнение восемь раз, а затем повторите с правой стороной тела.
Рисовать следует от центральной точки вверх и лево. Сделайте такое упражнение восемь раз, а затем повторите с правой стороной тела.
- Симметричный рисунок
Примите удобное положение тела стоя или сидя. Одновременно руками нарисуйте одинаковые, но с зеркальным отражением рисунки. Их можно рисовать как на бумаге, так и в воздухе.
Несимметричные упражнения
- Перекресток
Упражнение выполняется аналогично симметричному заданию. Разница в том, что ладонями нужно касаться противоположного колена, т.е. левой ладонью – правого колена, и наоборот. Рисунок для визуального сопровождение – X.
- Гимнастика для пальцев
Обе руки сожмите в кулак. Одним движением выпрямите указательный палец правой руки и большой палец на другой. Затем зеркально распрямите указательный палец на левой руке и большой на правой. Верните в исходное положение. Просто? Увеличьте темп.
Ещё один вариант этого упражнение – одновременно выбросьте другие пальцы на руках. Например: на левой руке – мизинец, а на правой – средний. Затем указательный плюс безымянный.
Например: на левой руке – мизинец, а на правой – средний. Затем указательный плюс безымянный.
Чтобы усложнить задачу, можно к чередованию пальцев добавить круговое или иное движение.
Планиметрия — Фонд развития Физтех-школ
Геометрия, 10 класс | Степень точки относительно окружности. Радикальная ось. Часть 1
Геометрия, 10 класс | Степень точки относительно окружности. Радикальная ось. Часть 2
Геометрия, 10 класс | Степень точки относительно окружности. Радикальная ось. Часть 3
Геометрия, 10 класс | Степень точки относительно окружности. Радикальная ось. Часть 4
Геометрия, 10 класс | Площадь многоугольника.
Геометрия, 10 класс | Площадь параллелограмма и треугольника
Геометрия, 10 класс | Площади треугольников и четырехугольников. Часть 2.
Геометрия, 10 класс | Теорема синусов. Часть 1Геометрия, 10 класс | Теорема синусов. Часть 1
Геометрия, 10 класс | Теорема синусов. Часть 2
Часть 2
Геометрия, 10 класс | Теорема синусов. Часть 3
Геометрия, 10 класс | Теорема синусов. Часть 4
Геометрия, 10 класс | Теорема косинусов.
Геометрия, 10 класс | Теорема косинусов и синусов. Часть 1
Геометрия, 10 класс | Теорема косинусов и синусов. Часть 2
Геометрия, 10 класс | Теорема косинусов и синусов. Часть 3
Геометрия, 10 класс | Теорема Чевы. Часть 1
Геометрия, 10 класс | Теорема Чевы. Часть 2
Геометрия, 10 класс | Теорема Чевы. Часть 3
Геометрия, 10 класс | Теорема Менелая. Часть 1
Геометрия, 10 класс | Теорема Менелая. Часть 2
Геометрия, 10 класс | Векторы. Часть 1
Геометрия, 10 класс | Векторы. Часть 2
Геометрия, 10 класс | Векторы. Часть 3
Геометрия, 10 класс | Векторы. Часть 4
Геометрия, 10 класс | Скалярное произведение векторов.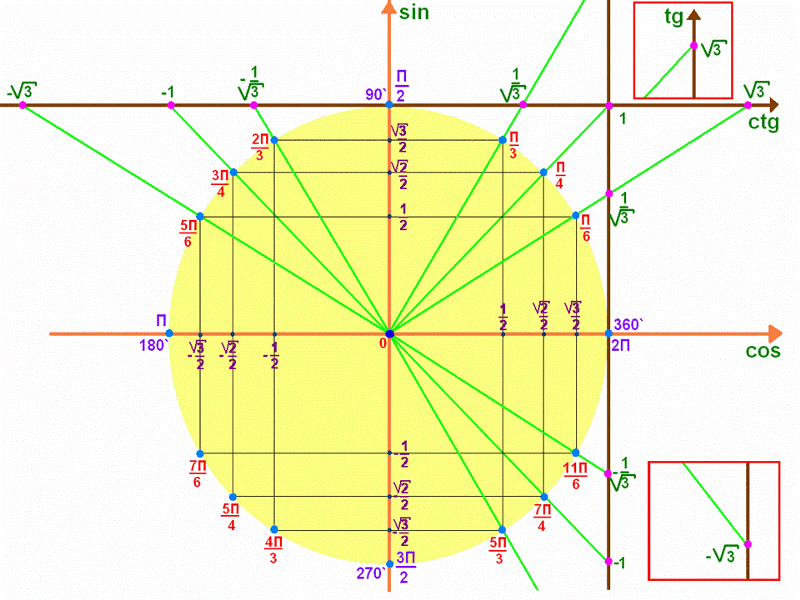 Часть 1
Часть 1
Геометрия, 10 класс | Скалярное произведение векторов. Часть 2
Геометрия, 10 класс | Скалярное произведение векторов. Часть 3
Геометрия, 10 класс | Элементы метода координат. Часть 1
Геометрия, 10 класс | Элементы метода координат. Часть 2
Геометрия, 10 класс | Элементы метода координат. Часть 3
Геометрия, 10 класс | Элементы метода координат. Часть 4
Геометрия, 10 класс | Элементы метода координат. Часть 5
Геометрия, 10 класс | Элементы метода координат. Часть 6
Геометрия, 10 класс | Треугольники с углами 60 и 120 градусов. Часть 1
Геометрия, 10 класс | Треугольники с углами 60 и 120 градусов. Часть 2
Геометрия, 10 класс | Треугольники с углами 60 и 120 градусов. Часть 3
Геометрия, 10 класс | Подобные треугольники. Часть 1
Геометрия, 10 класс | Подобные треугольники. Часть 2
Геометрия, 10 класс | Подобные треугольники.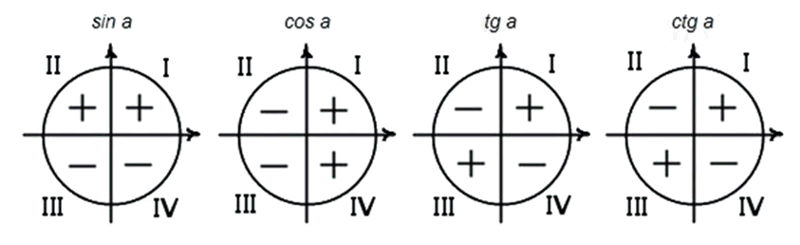 Часть 3
Часть 3
Геометрия, 10 класс | Подобные треугольники. Часть 4
Геометрия, 10 класс | Подобные треугольники. Часть 5
Геометрия, 10 класс | Вписанный угол и вписанный четырехугольник. Часть 1
Геометрия, 10 класс | Вписанный угол и вписанный четырехугольник. Часть 2
Геометрия, 10 класс | Вписанный угол и вписанный четырехугольник. Часть 3
Геометрия, 10 класс | Вписанный угол и вписанный четырехугольник. Часть 4
Геометрия, 10 класс | Вписанный угол и вписанный четырехугольник. Часть 5
Геометрия, 10 класс | Вписанный угол и вписанный четырехугольник. Часть 6
Геометрия, 10 класс | Вписанный угол и вписанный четырехугольник. Часть 7
Геометрия, 10 класс | Описанный четырехугольник. Часть 1
Геометрия, 10 класс | Описанный четырехугольник. Часть 2
Геометрия, 10 класс | Описанный четырехугольник. Часть 3
Геометрия, 10 класс | Преобразования плоскости. Основные определения
Основные определения
Геометрия, 10 класс | Преобразования плоскости. Движение. Часть 1
Геометрия, 10 класс | Преобразования плоскости. Движение. Часть 2
Геометрия, 10 класс | Преобразования плоскости. Движение. Часть 3
Геометрия, 10 класс | Преобразования плоскости. Движение. Часть 4
Геометрия, 10 класс | Преобразования плоскости. Движение. Часть 5
Геометрия, 10 класс | Преобразования плоскости. Движение. Часть 6
Геометрия, 10 класс | Преобразования плоскости. Движение. Часть 7
Геометрия, 10 класс | Преобразования плоскости. Движение. Часть 8
Геометрия, 10 класс | Преобразования плоскости. Движение. Часть 9
Геометрия, 10 класс | Преобразования плоскости. Движение. Часть 10
Геометрия, 10 класс | Преобразования плоскости. Движение. Часть 11
Геометрия, 10 класс | Преобразования плоскости. Движение. Часть 12
Геометрия, 10 класс | Преобразования плоскости.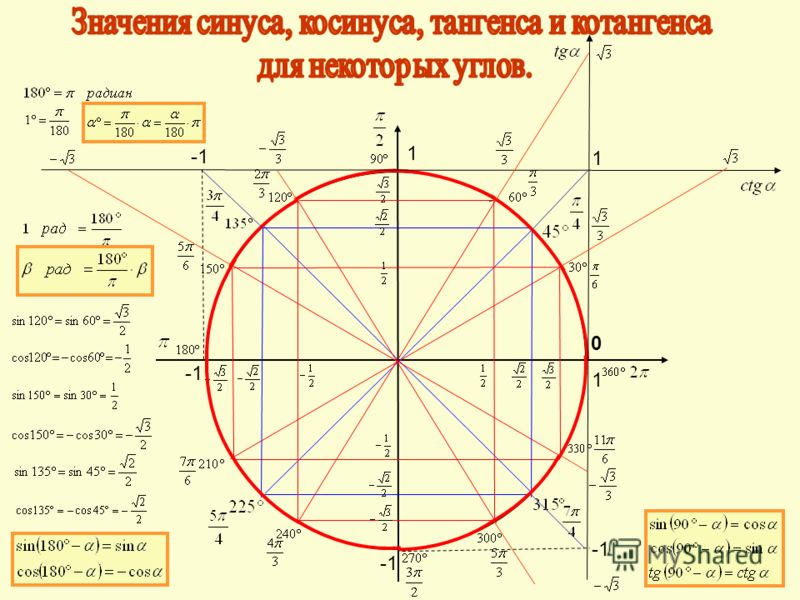 Движение. Часть 13
Движение. Часть 13
Геометрия, 10 класс | Преобразования плоскости. Гомотетия. Часть 1
Геометрия, 10 класс | Преобразования плоскости. Гомотетия. Часть 2
Геометрия, 10 класс | Преобразования плоскости. Гомотетия. Часть 3
Геометрия, 10 класс | Преобразования плоскости. Гомотетия. Часть 4
Геометрия, 10 класс | Преобразования плоскости. Гомотетия. Часть 5
Геометрия, 10 класс | Преобразования плоскости. Гомотетия. Часть 6
Геометрия, 10 класс | Лемма о трезубце. Часть 1
Геометрия, 10 класс | Лемма о трезубце. Часть 2
Геометрия, 10 класс | Лемма о трезубце. Часть 3
Геометрия, 10 класс | Принцип Кавальери и его обращения. Часть 1
Геометрия, 10 класс | Принцип Кавальери и его обращения. Часть 2
Геометрия, 10 класс | Краткая апология стереометрии. Часть 1
Геометрия, 10 класс | Краткая апология стереометрии. Часть 2
Часть 2
Аналитическая тригонометрия Симметрия
Мы склонны думать о симметрии с точки зрения геометрии больше, чем что-либо еще. Это понятно; легко сложить фигуры пополам разными способами, чтобы посмотреть, совпадают ли они. Что ж, функции тоже могут иметь симметрию, а триггерные функции подобны чемпионам по симметрии сумо.
Есть два типа симметрии, когда мы рассматриваем триггерные функции. Давайте начнем с рассмотрения y = cos x .
Имеет симметрию над и -ось. Мы могли бы свернуть весь график на x = 0, и все совпало бы с другой стороны. Любая функция, симметричная относительно оси y , является функцией даже .
Нам не нужно смотреть на график, чтобы показать, что функция четна. Наденьте на нас повязку, нам все равно. Вместо этого мы можем увидеть, соответствует ли функция следующему уравнению:
f (- x ) = f ( x )
Снимите повязку с глаз и еще раз посмотрите на график.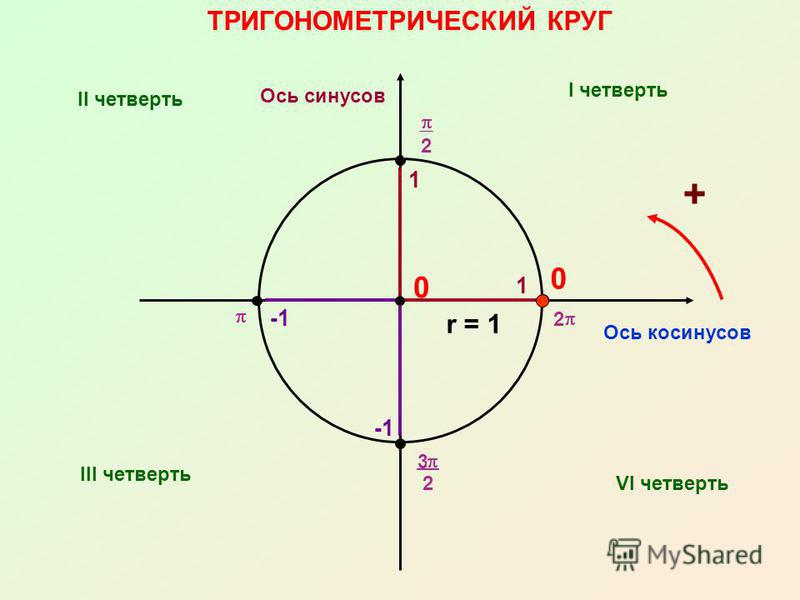 Сравнить каждые — 9от 0005 x до x : они имеют одинаковое значение y . Это симметрия четной функции, и это именно то, что говорит уравнение. Это и «Накорми меня, Сеймур», но мы не слушаем эту старую песню и танец.
Сравнить каждые — 9от 0005 x до x : они имеют одинаковое значение y . Это симметрия четной функции, и это именно то, что говорит уравнение. Это и «Накорми меня, Сеймур», но мы не слушаем эту старую песню и танец.
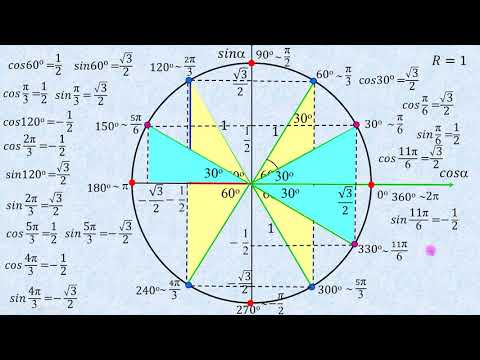
Мы можем проверить соответствие косинуса уравнению, взглянув на единичный круг. Для этого запоминаем запоминающее устройство, ASTC. Некоторые люди говорят, что все студенты изучают математику, но нам нравится думать об этом как о маленьком запутанном коте. Там столько пряжи, как ты выберешься, кот? О, это также говорит нам, какие функции положительны в каждом квадранте:
A(ll) S(ine) T(angent) C(osine). Вот знаки косинуса (и секанса) углов , и —, :
,,
,
. имеют одинаковый опорный угол. Кроме того, квадранты I и IV положительны для косинуса. Это переводится как cos a = cos (- a ). Это именно то, что мы хотели, и мы это получили.
Нам это кажется странным
Если существует что-то, называемое «четными» функциями, разве не удивительно, что есть нечетных функций? Поднимите челюсть с пола; это испачкает ваш подбородок.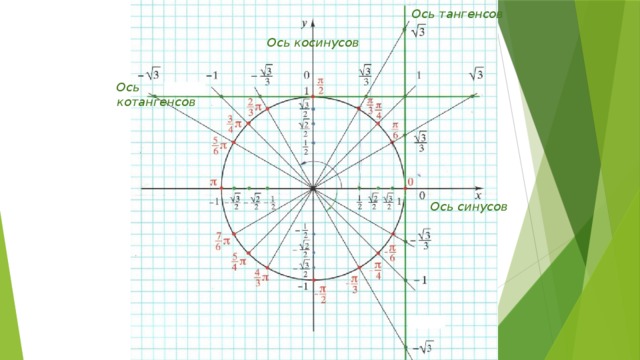 Нечетные функции симметричны относительно начала координат.
Нечетные функции симметричны относительно начала координат.
Оказывается, что y = sin x — нечетная функция. Шок и удивление продолжаются.
Если мы возьмем этот график и свернем его по оси y , мы увидим, что он не совпадает, так что это не симметричен относительно оси y ; это не четная функция. Однако, если мы сравним любые х и — х , их значения y противоположны: y и — y . Это симметрия относительно начала координат, когда мы переворачиваем оси x и y . У него также есть удобная формула:
f (- x ) = — f ( x )
Для синуса (и его обратного косеканса) мы имеем следующую разбивку знаков:
Мы видим, что угол a находится на положительной территории. В обратном направлении — и находятся в отрицательной зоне. Они охватили все территории.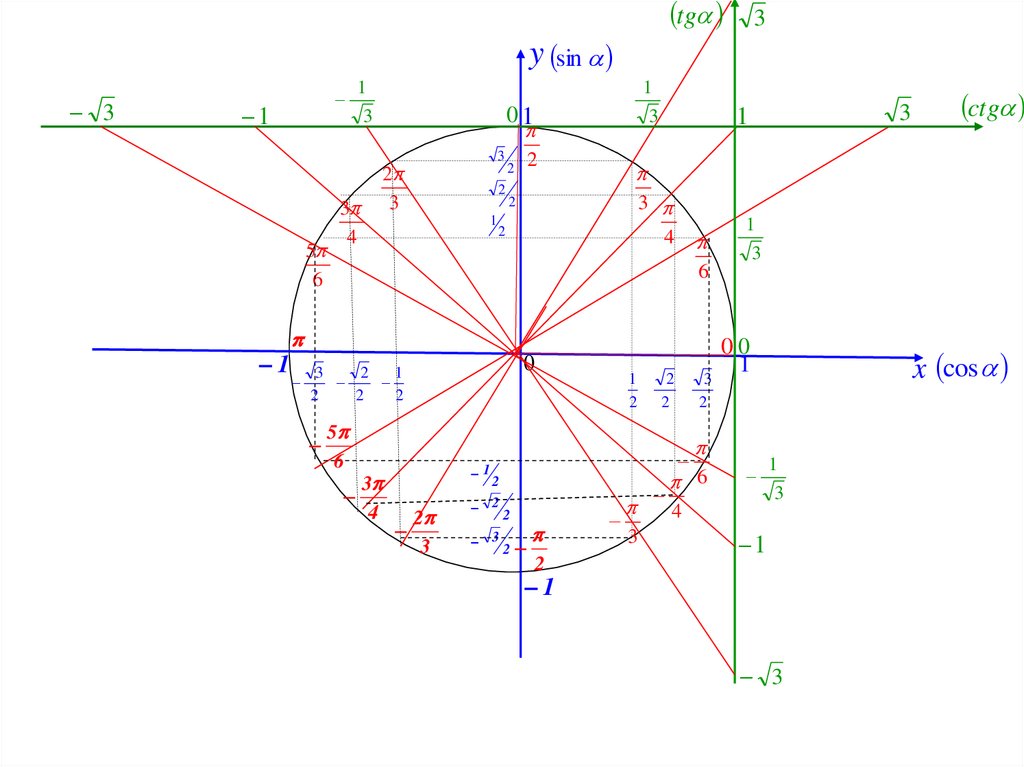 Зная это, мы можем видеть, что sin(- a ) = -sin a , что точно так же, как f ( -x ) = -f ( x ) нечетной функции.
Зная это, мы можем видеть, что sin(- a ) = -sin a , что точно так же, как f ( -x ) = -f ( x ) нечетной функции.
Да, кстати…
Мы находимся на другой касательной для касательной (и котангенса). Он имеет другое распределение знаков, чем синус или косинус.
Однако, проверяя значения функции для и и — и , мы видим, что это работает так же, как синус. tan (- a ) = -tan a , так что это нечетная функция. Мы всегда знали, что тангенс нечетен, но теперь у нас есть доказательство.
Вещи, которые вы могли попробовать | Можете ли вы найти… издание по тригонометрии | Тригонометрия: треугольники к функциям
Выйти из полноэкранного режима
Обратите внимание, что в этом обсуждении мы использовали радианы, но могли бы использовать и градусы. Мышление и идеи будут одинаковыми в обоих случаях, поэтому постарайтесь прочитать это, даже если вы использовали степени.
Можете ли вы найти …
- … два графика синусов, которые пересекаются только на оси \(x\)?
Учитывая, что \(y=\sin x\) пересекает ось \(x\), какие простейшие преобразования можно применить к ней, чтобы получить другой синусоидальный график, который пересекает ось \(x\) в точке одинаковые точки?
Одним из вариантов может быть отражение \(y=\sin x\) по оси \(x\), чтобы получить два синусоидальных графика. Другим было бы растянуть его параллельно оси \(y\).
- … график синусоиды, график косинуса и график касательной, которые пересекаются в определенных точках? Что, если все три графа должны встретиться в начале координат?
Один из подходов может состоять в том, чтобы посмотреть, где встречаются два из \(y=\sin x\), \(y=\cos x\) и \(y=\tan x\), а затем преобразовать третий график так, чтобы он также проходит через эти точки.
Например, мы можем заметить, что \(y=\sin x\) и \(y=\cos x\) встречаются в точках \(\big(\tfrac{\pi}{4}, \tfrac{\sqrt {2}}{2}\big)\), но \(\tan \tfrac{\pi}{4} = 1\), поэтому мы могли масштабировать \(y=\tan x\), чтобы получить наш третий график .
Если бы мы хотели удостовериться, что все графы пересекаются в начале координат, мы могли бы заметить, что \(y=\sin x\) и \(y=\tan x\) встречаются в целых числах, кратных \(\pi\) , поэтому оба проходят через начало координат. Поскольку \(y=\cos x\) проходит через \((0,1)\), мы можем перевести этот граф, чтобы убедиться, что он также проходит через начало координат. Мы могли бы подумать об использовании \(y= \cos ( x \pm \tfrac{\pi}{2})\), но как будут выглядеть графики в каждом случае?
- … график синусоиды и график косинуса, которые не пересекаются? Что, если графики должны лежать между \(y=1\) и \(y=-1\)?
Здесь следует задуматься о том, что значит «не пересекаться». Если мы рассмотрим \(y=\cos x\) и \(y=\sin\left(x+ \tfrac{\pi}{2}\right)\), или \(y=\sin x\) и \ (y=2-\sin x\), то пары графиков не пересекаются, но имеют много общих точек. Попробуем найти графы, не имеющие общих точек. Если нам не удастся найти графы, которые будут работать, то мы можем разрешить графам встречаться, но не пересекаться.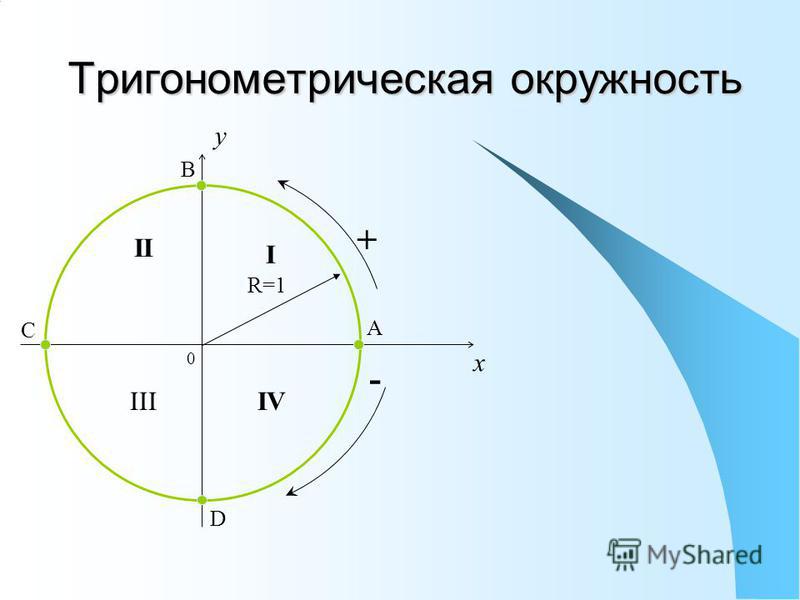
Графики \(y=\sin x\) и \(y=\cos x\) принимают значения между \(-1\) и \(1\). Один из вариантов — сдвинуть один или оба графика параллельно оси \(y\), чтобы их значения вообще не перекрывались.
Чтобы решить вторую часть проблемы, мы могли бы масштабировать графики так, чтобы их можно было раздвинуть и по-прежнему помещать между линиями \(y=1\) и \(y=-1\). Мы также можем комбинировать это со сдвигами, параллельными осям \(x\) или \(y\), чтобы диапазоны функций перекрывались, но графики на самом деле не пересекались. Вот одно из возможных решений, чтобы проиллюстрировать это.
- … график косинуса и график тангенса, которые встречаются с осью \(x\) одинаковое количество раз между \(x=-4\) и \(x=4\)? Что, если эти точки должны быть одинаковыми для обоих графиков?
График \(y=\tan x\) трижды пересекает ось \(x\) между \(x=-4\) и \(x=4\), тогда как \(y=\cos х\) пересекает ось \(х\) только дважды на этом интервале. Одним из вариантов было бы перевести график \(y=\cos x\) так, чтобы он пересекал ось \(x\) три раза вместо двух.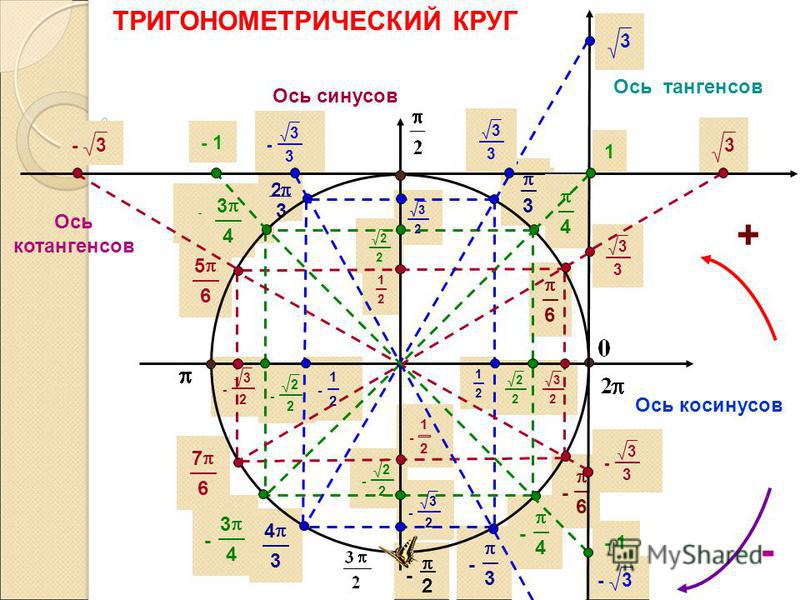

 Аналогично можно экспериментировать со вкусовыми ощущениями и запахом. Важно пытаться представить все визуализированные вещи так, что вы сможете ощущать их органами чувств.
Аналогично можно экспериментировать со вкусовыми ощущениями и запахом. Важно пытаться представить все визуализированные вещи так, что вы сможете ощущать их органами чувств.