| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град.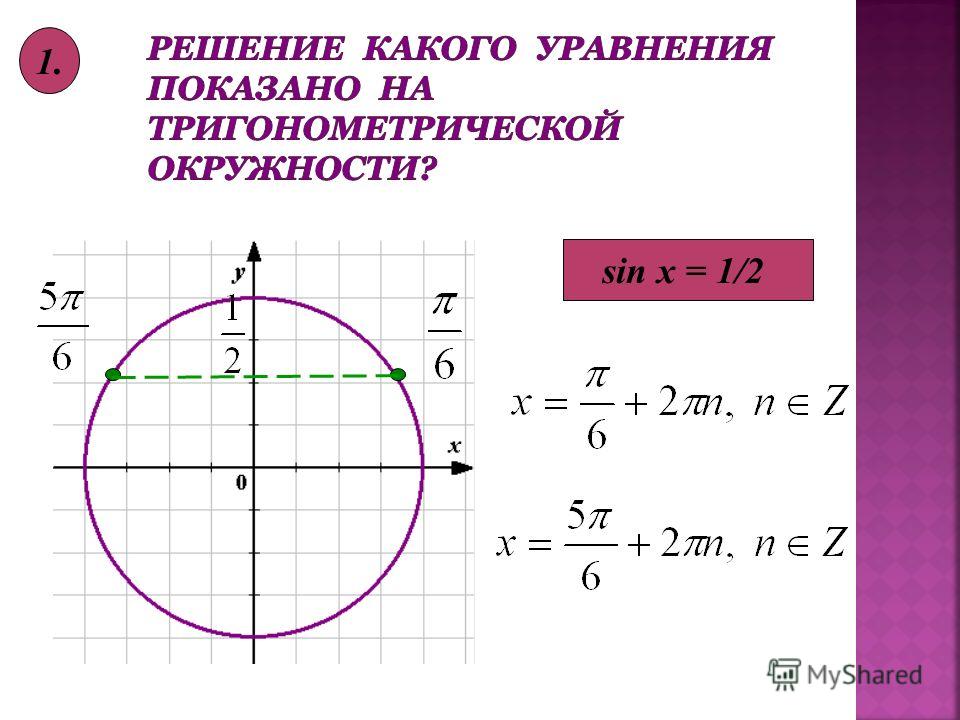 2 2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град.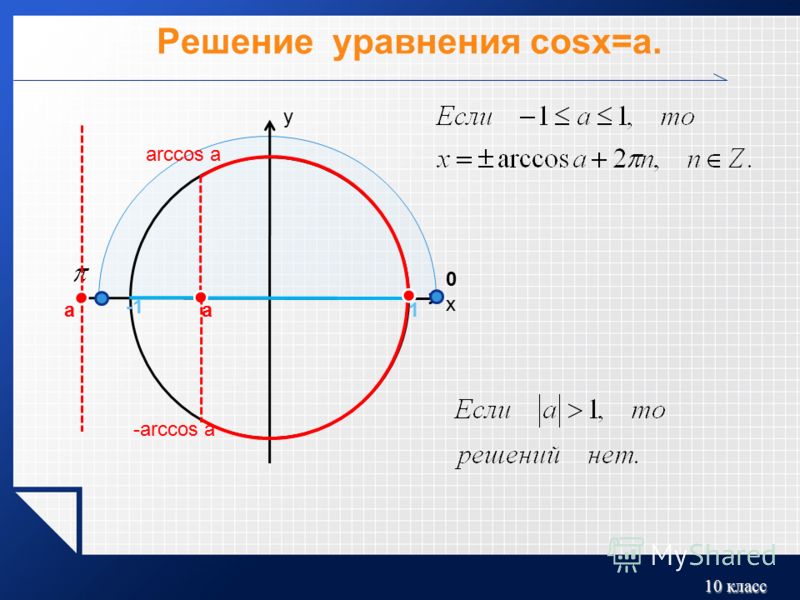 ) ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град.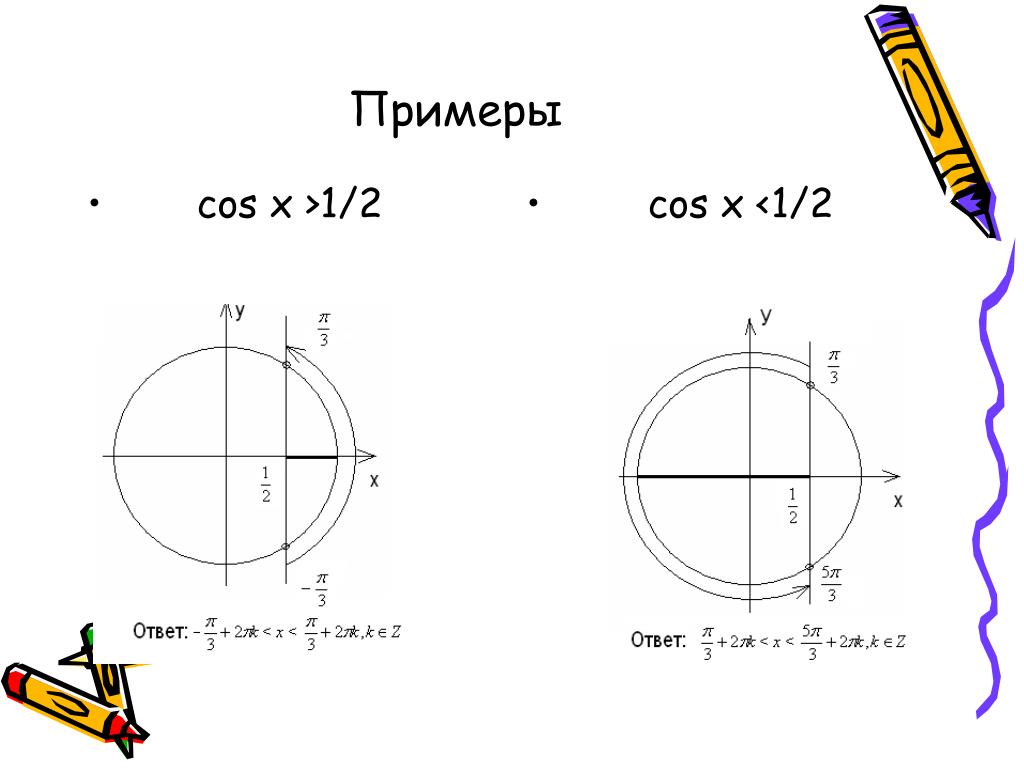 ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град.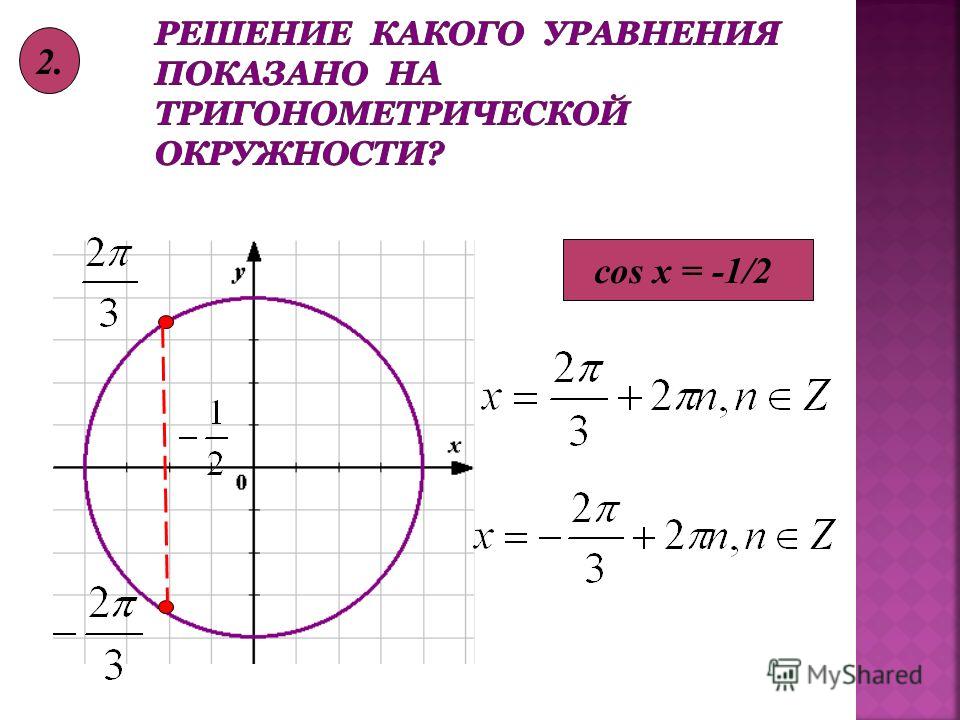 |
тригонометрических тождеств | Purplemath
Purplemath
В математике «тождество» — это уравнение, которое всегда верно. Они могут быть «тривиально» истинными, например, « x = x », или полезными истинами, такими как теорема Пифагора: прямоугольные треугольники. Существует множество тригонометрических тождеств, но ниже приведены те, которые вы, скорее всего, увидите и будете использовать.
Базовый и Пифагорейский, Сумма углов и разность, Двойной угол, Половина угла, Сумма, Произведение
Содержание продолжается ниже
MathHelp.com
Нужен индивидуальный курс математики?
К12 | Колледж | Подготовка к экзамену
Основные и пифагорейские тождества
Обратите внимание, что триггерный коэффициент «со-(что-то)» всегда является обратным коэффициенту «не-со». Вы можете использовать этот факт, чтобы понять, что косеканс идет с синусом, а секанс идет с косинусом.
Следующие (в частности, первая из трех ниже) называются «пифагорейскими» тождествами.
SIN 2 ( T ) + COS 2 ( T ) = 1
TAN 2 ( T ) + 1 = SEC 2 ( T )
1 + 10011 2 ( T )
1 + 1 +. cot 2 ( t ) = csc 2 ( t )
Обратите внимание, что три тождества, прежде всего, включают в себя квадрат и число 1. Вы можете ясно увидеть связь Пифагора и Теома, если рассмотрите единичный круг , где угол равен t , «противоположная» сторона равна sin(
У нас есть дополнительные тождества связанные с функциональным состоянием триггерных соотношений:
sin( −t ) = − sin( t )
cos( −t ) = cos( 0 0 0 tg
) 1 −t
) = − tan( t )
Обратите внимание, в частности, что синус и тангенс являются нечетными функциями, будучи симметричными относительно начала координат, в то время как косинус является четной функцией, будучи симметричным относительно начала координат. 0005 и -ось. Тот факт, что вы можете вынести знак «минус» аргумента за пределы (для синуса и тангенса) или полностью исключить его (для косинуса), может быть полезен при работе со сложными выражениями.
0005 и -ось. Тот факт, что вы можете вынести знак «минус» аргумента за пределы (для синуса и тангенса) или полностью исключить его (для косинуса), может быть полезен при работе со сложными выражениями.
Тождества суммы углов и разностей
sin(α + β) = sin(α) cos(β) + cos(α) sin(β)
sin(α − β) = sin(α ) cos(β) − cos(α) sin(β)
cos(α + β) = cos(α) cos(β) − sin(α) sin(β)
cos(α − β) = cos (α) cos(β) + sin(α) sin(β)
Кстати, в приведенных тождествах углы обозначены греческими буквами. Буква а-типа «α» называется «альфа», что произносится как «AL-fuh». Буква b-типа, «β», называется «бета», что произносится как «БАЙ-тух».
Двойной угла идентификации
SIN (2 x ) = 2 SIN ( x ) COS ( x )
COS (2 x ) = COS 2 ( x (2 x ) = COS 2 ( x 6. ) − грех 2 ( x ) = 1 − 2 sin 2 ( x ) = 2 cos 2 ( x ) − 1
Half-Angle Identities
The above identities можно переформулировать, возведя в квадрат каждую сторону и удвоив все угловые меры. Результаты следующие:
Результаты следующие:
sin 2 ( x ) = ½[1 − cos(2 x )]
cos 2 ( x ) = ½[1 + cos(2 х )]
Идентичности суммы
Идентичности произведения
Вы будете использовать все эти тождества или почти все для доказательства других триггерных уравнений и для решения триггерных уравнений. Однако, если вы собираетесь изучать исчисление, обратите особое внимание на переформулированные тождества половин углов синусов и косинусов, потому что вы будете использовать их в интегральном исчислении. 93
92-4

