Основные формулы комбинаторики: 2.03. Основные формулы комбинаторики

Основные формулы комбинаторики — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Основные формулы комбинаторики

• Комбинаторика изучает количества
комбинаций, подчиненных
определенным условиям, которые
можно составить из элементов,
безразлично какой природы, заданного
конечного множества.
Размещения с повторениями.
Кортеж-множество где каждый элемент стоит на своем месте и не повторяется.
Кортежи длины k, составленные из элементов m – элементного множества х,
называют размещениями с повторениями из m элементов по k. Число этих
кортежей обозначают Ākm. Рассчитывают по формуле:
Ākm =mk.
Задача:
Сколько пятизначных номеров можно составить из девяти цифр
1,2,3,4,5,6,7,8,9?
Решение:
Такие номера являются кортежами длины 5, составляем из этих элементов
множества X={ 1,2,3,4,5,6,7,8,9}. По формуле
Аkm=mk рассчитываем:
А59=95=6561.
Размещения без повторений.
Упорядоченное множество длины k, составленное из элементов m – элементного
множества X, называют размещениями без повторений из m элементов множества
Х по k. Рассчитывают по формуле:
N!=1*2*3*…*n, где 0!=1.
m!
k
Аm=
(m k )!
Задача:
Сколькими способами можно выбрать из класса, насчитывающего 40 учеников,
старосту, комсорга и физорга.
Решение:
Любой такой выбор является размещением без повторений из 40 элементов по
3 (он задается кортежем длины 3 без повторений, составленным из элементов
множества учеников). Значит, число способов выбора равно
А340=40! / 37! = 59280.
Ответ:59280.
Перестановки с повторениями.
Перестановки с повторениями состава (k1,…,km) из букв (a1,…,am) называют
любой кортеж длины k= k1+k2+…+km, в которой буква a1 входит в k1 раз, …, буква
am – km раз. Число таких перестановок обозначается P(k1,…,km). Рассчитывается
по формуле:
(k1 k 2 …kn)!
P(k1,…,km) =
k1!k 2!..kn!
Задача:
Сколько слов можно получить, переставляя буквы в слове «математика»?
Решение:
Слово «математика» является кортежем длины 10, имеющим состав (2, 3, 2, 1,
1, 1) (буква «м» входит 2 раза, буква «а» — раза, буква «т» — 2 раза, буквы «е»,
«и», «к» — по одному разу).
10!
P (2, 3, 2, 1, 1, 1) =
= 151200.
2!3!2!1!1!1!
Ответ: 151200
Перестановка без повторений.
Перестановка без повторений из m – элементов называют размещением без
повторений из этих элементов по m. Число перестановок обозначают Рm.
Рассчитывают по формуле:
Pm = m!
Задача:
Сколькими способами 6 человек могут сесть в 6 машин?
Решение:
Пронумеруем машины числами 1, 2, 3, 4, 5, 6 и обозначим человека, севшего в k
–тую машину через Xk. 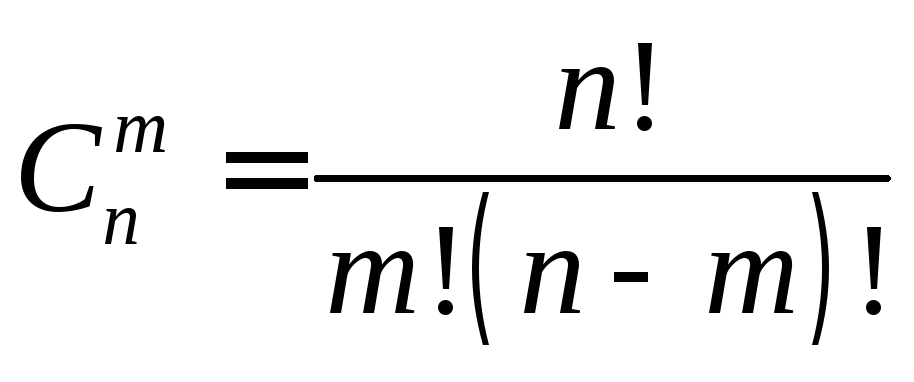Тогда (х1,…,х6) – перестановка из имен этих шести
людей, причем каждой такой перестановке соответствует один и только один
способ размещения в машинах, следовательно:
Р6 = 6!=720
Ответ: 720.
5
2
4
1
3
6
Сочетание с повторениями.
Имеются предметы m видов и из них составляется набор, содержащие k элементов. Два
таких набора считаются одинаковыми в том и только в том случае, когда они имеют
одинаковый состав. Такие наборы называются сочетаниями с повторениями из m
элементов по k. Рассчитываются по формуле:
Сkm = Ckk+m-1
Задача:
Сколько наборов из 7 пирожных можно составить, если в продаже имеются 4
сорта пирожных?
Решение:
Искомое число равно: С74 т.е. C77+4-1 следовательно:
С710 = C310 = (10*9*8) / (1*2*3)=120
Ответ: 120.
Сочетания без повторений.
K – элементные подмножества m-элементного множества x называют
сочетаниями без повторений из элементов этого множества по K. Их число
обозначают Ckm. Рассчитывают по формуле:
m!
Ckm =
k!(m k )!
Задача:
Сколькими способами можно выбрать один цветок из 5 роз и 3 водяных
лилий?
5!
С = 1!4! =5
3!
1
С 3= 1!2! =3
1
5
Решение:
С13+С15=3+5=8 способов
Ответ: 8 способов.
Бином Ньютона.
Формула: (x-a)n=xn-naxn-1+C2na2xn-2-C3na3xn-3+…+(-1)kCkrakxn-k+…+(-1)nan.
Пример: Найдите разложения: а) (2y2-3y) 5 ; б) (1- 2)6
Решение: а) y5(2y – 3)5 = y5(32y5 – 16y4*5*3 + 8y3*10*9 – 4y2*10*27 + 2y*5*81 –
— 243) = 32y10 — 240y9 + 720y8 — 1080y7 + 810y6 – 243y5;
б) 1 — 6 2 + 15*2 – 20*2 2 +15*4 – 6*4 2 + 8 = 99 — 70 2.
Для нахождения коэффициентов в биноме Ньютона удобно использовать
треугольник Паскаля.
0-я степень
1
1
1
1
1
1
1
2
3
3
4
5
1
6
10
1
4
10
1
5
1
5-я степень
Коэффициент в разложении многочлена легко искать с
помощью треугольника Паскаля.
(х-а)3=х3-3х2а+3а2х-а3
1
1
1
1
1
1
2
3
4
1
3
6
1
4
1

English     Русский Правила

Ошибка

Перейти к основному содержанию

Вся размещенная на ресурсе информационная продукция предназначена для детей, достигших возраста шестнадцати лет (16+)

Извините, не удалось найти запрашиваемый Вами файл

Подробнее об этой ошибке

Перейти на. .. Перейти на…Новостной форумКомплексные числа (с приложениями к задачам электротехники)Лекционный материал по теме «Комплексные числа»Разбор типовых задач задач по теме «Комплексные числа»Примеры решения задач по теме «Комплексные числа»КОМПЛЕКСНЫЕ ЧИСЛАКомплексные числа. Основы линейной алгебры. Системы линейных уравненийТеория функций комплексного переменного. Операционное исчислениеПрезентация по теме «Комплексные числа»Дополнительный материал к темеОсновы линейной алгебры с приложениями в других разделах математикиЛекционный материал по теме «Матрицы. Определители»Лекционный материал по теме «Системы линейных алгебраических уравнений (СЛАУ). Применение СЛАУ в экономике»Лекционный материал по теме «Линейные операторы»Примеры решения по теме «Системы линейных алгебраических уравнений»ЛИНЕЙНАЯ АЛГЕБРАКомплексные числа. Основы линейной алгебры. Системы линейных уравненийЛинейная алгебра для экономистовМатрицы. ОпределителиВекторная алгебра.Аналитическая геометрияЛекционный материал по теме «Векторная алгебра.

Линейные операции над векторами»Лекционный материал по теме «Скалярное, векторное и смешанное произведения векторов»Примеры решения задач по теме «Векторная алгебра. Линейные операции над векторами»Примеры решения задач по теме «Скалярное, векторное и смешанное произведения векторов»ВЕКТОРНАЯ АЛГЕБРАВекторная алгебра и аналитическая геометрияПрезентация по теме «Векторная алгебра»Векторная алгебра.Аналитическая геометрияТеоретический материал по теме «Метод координат на плоскости и в пространстве»Лекционный материал по теме «Прямая на плоскости»Лекционный материал по теме «Кривые второго порядка»Лекционный материал по теме «Прямая в пространстве»Лекционный материал по теме «Плоскость в пространстве»Лекционный материал по теме «Поверхности второго порядка»Примеры решения задач по теме «Прямая на плоскости»Примеры решения задач по теме «Кривые второго порядка»Примеры решения задач по темам «Прямая и плоскость в пространстве»АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯВекторная алгебра и аналитическая геометрияСправочный материал «Прямая на плоскости»Справочный материал «Кривые второго порядка»Справочный материал «Прямая и плоскость в пространстве»Линейная алгебра для экономистовПрезентация по теме «Прямая на плоскости»Презентация по теме «Уравнения плоскости и прямой в пространстве»▶ Виртуальный тренажер «Прямая на плоскости» 👨‍🎓Введение в анализНачала анализаЛекционный материал по теме «Множества, функции, основные характеристики функций. Основные элементарные функции»Лекционный материал по теме «Предел функции, основные теоремы о пределах.Замечательные пределы. Бесконечно малые функции»Лекционный материал по теме «Непрерывность функции»Примеры решения задач по теме «Множества, функции, основные характеристики функций. Основные элементарные функции»Примеры решения задач по теме «Предел функции. Раскрытие математических неопределенностей»Примеры решения задач по теме «Непрерывность функции»ВВЕДЕНИЕ В АНАЛИЗУпражнения для самостоятельного решения Тест «Введение в анализ»Презентация по теме «Введение в анализ»1. Понятие функцииПрименение функций в экономической теории и практикеПрименение пределов в экономических расчетахПриложение понятия непрерывности функций в экономике▶ Виртуальная справочная «Тригонометрические функции» 👨‍🎓Дифференциальное исчисление функций одной переменнойПриложения дифференциального исчисления функции одной переменнойЛекционный материал по теме «Дифференциальное исчисление функции одной переменной»Лекционный материал по теме «Основные теоремы дифференциального исчисления. Правила Лопиталя»Лекционный материал по теме «Формулы Тейлора и Маклорена»Лекционный материал по теме «Приложения дифференциального исчисления»Примеры решения задач по теме «Дифференциальное исчисление функций одной переменной»ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙТест «Основные правила и формулы дифференцирования»Тест «Дифференциальное исчисление функций одной переменной»Основы дифференцирования. Часть 1Основы дифференцирования. Часть 2Основы дифференцирования. Часть 3Приложения производной Исследование функций, Примеры решения задачПрименение производных при решении экономических задачИнтегральное исчисление функции одной переменнойЛекционный материал по теме «Неопределенный интеграл»Лекционный материал по теме «Определенный интеграл»Практическое занятие 1. Непосредственное интегрирование (неопределённый интеграл)Практическое занятие 2. Интегрирование заменой переменной (неопределённый интеграл)Практическое занятие 3. Интегрирование по частям. Интегрирование выражений, содержащих квадратный многочлен (неопределённый интеграл)Практическое занятие 4. Интегрирование рациональных дробей (неопределенный интеграл)Практическое занятие 5. Определенный интегралПримеры решения задач по теме «Неопределенный интеграл»Примеры решения задач по теме «Определенный интеграл»ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙТест «Таблица основных неопределенных интегралов»Тест «Интегрирование функций одной переменной»1. Неопределенный интеграл. Основы интегрирования2. Интегрирование иррациональных выражений 3. Интегрирование тригонометрических выражений 4. Определенный интегралДифференциальное исчисление функций нескольких переменныхЛекционный материал по теме «Функции нескольких переменных»Примеры решения задач по теме «Функции нескольких переменных»ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХТест «Дифференциальное исчисление функций нескольких переменных»1. Функции нескольких переменныхПрименение функций нескольких переменных в экономикеОбыкновенные дифференциальные уравненияОбыкновенные дифференциальные уравнения и их приложенияДифференциальные уравнения первого порядкаДифференциальные уравнения высших порядковСистемы дифференциальных уравнений и устойчивость их решенийЛекционный материал по теме «Дифференциальные уравнения 1-го порядка»Лекционный материал по теме «Дифференциальные уравнения высших порядков»Примеры решения задач по теме «Дифференциальные уравнения»ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯТест «Обыкновенные дифференциальные уравнения»1. Дифференциальные уравнения 1-го порядка2. Дифференциальные уравнения высших порядковСпециальные разделы высшей математикиСпециальные разделы высшей математики: практикум Кратные, криволинейные и поверхностные интегралы. Элементы теории поляПоверхностные интегралы. Векторный анализЛекционный материал по теме «Двойные интегралы»Примеры решения задач по теме «Двойные интегралы»КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ2. Двойные интегралыРядыЛекционный материал по теме «Числовые ряды»Лекционный материал по теме «Функциональные ряды»Примеры решения задач по теме «Ряды»1. Числовые ряды2. Функциональные ряды3. Разложение функций в степенные рядыТеория функций комплексного переменного. Операционное исчисление.Основы теории функций комплексного переменногоОперационное исчисление.Теория функций комплексного переменного. Операционное исчислениеТеория вероятностей Теория вероятностей (случайные события)Вероятность, случайные процессы, математическая статистикаТеория вероятностей. Случайные процессы: практикумЛекционный материал по теме «Основные подходы к определению вероятности»Лекционный материал по теме «Алгебра событий. Основные теоремы о вероятности»Лекционный материал по теме «Дискретные случайные величины»Лекционный материал по теме «Непрерывные случайные величины»Лекционный материал по теме «Числовые характеристики случайных величин»Лекционный материал по теме «Моменты и другие характеристики распределений»Лекционный материал по теме «Нормальное распределение»Практическое занятие 1. КомбинаторикаПрактическое занятие 2. Действия над событиями. Вероятность событияПрактическое занятие 3. Теоремы умножения и сложения вероятностей событийПрактическое занятие 4. Формула полной вероятности Практическое занятие 5. Схема Бернулли. Локальная и интегральная теоремы ЛапласаПрактическое занятие 6. Дискретные случайные величины. Числовые характеристикиПрактическое занятие 7. Непрерывные случайные величины. Классические законы распределения НСВПримеры решения задач по теме «Классическое определение вероятности»Примеры решения задач по теме «Теоремы сложения и умножения»Примеры решения задач по теме «Формула полной вероятности. Формулы Байеса»Примеры решения задач по теме «Схема независимых испытаний Бернулли»Примеры решения задач по теме «Дискретные случайные величины»Примеры решения задач по теме «Основные числовые характеристики дискретных случайных величин»Примеры решения задач по теме «Непрерывные случайные величины»Примеры решения задач по теме «Основные числовые характеристики непрерывных случайных величин»Примеры решения задач по теме «Классические законы распределения дискретных случайных величин»Примеры решения задач по теме «Классические законы распределения непрерывных случайных величин»Таблица значений функции ЛапласаТЕОРИЯ ВЕРОЯТНОСТЕЙТест по разделу «Случайные события»Тест по теме «Числовые характеристики случайных величин»Тест по теме «Дискретные случайные величины»Тест по теме «Непрерывные случайные величины»Основные подходы к определению вероятностиАлгебра событий. Основные теоремы о вероятностиТеория вероятностей (Лыткина Е.М.,Чихачев А.С., 2013)Математическая статистикаОсновы математической статистикиМатематическая статистика: практикумПримеры решения задач по математической статистикиМАТЕМАТИЧЕСКАЯ СТАТИСТИКАТест по разделу «Математическая статистика». Тема «Статистическое распределение. Точечные и интервальные оценки параметров распределения»Тест по разделу «Математическая статистика». Тема «Статистические гипотезы. Корреляционный и регрессионный анализ»Вероятность, случайные процессы, математическая статистикаСтатистический метод и основы его примененияВероятностно-статистические методы на примере задач исследования работы железнодорожного транспорта Марковские процессы и СМО. Учебное пособиеЛекционный материал по теме «Марковский процесс с дискретным временем»Лекционный материал по теме «Марковский процесс с непрерывным временем»Лекционный материал по теме «Системы массового обслуживания»Примеры решения задач по теме «Марковские процессы»СЛУЧАЙНЫЕ ПРОЦЕССЫЛабораторные работы Вероятность, случайные процессы, математическая статистикаТеория вероятностей. Случайные процессы. ПрактикумЛекция «Марковские процессы»Цепи МарковаСистемы массового обслуживания (СМО)СМОВыбор группы*Тест «Таблица основных неопределенных интегралов»*Тест «Интегрирование функций одной переменной»*Тест «Дифференциальное исчисление функций нескольких переменных»*Тест «Обыкновенные дифференциальные уравнения»*Тест по разделу «Случайные события»*Тест по теме «Дискретные случайные величины»*Тест по теме «Непрерывные случайные величины»*Тест по теме «Числовые характеристики случайных величин»*Тест «Введение в анализ»*Тест «Основные правила и формулы дифференцирования»*Тест «Дифференциальное исчисление функций одной переменной»*Экзаменационный тест «Таблица основных неопределенных интегралов»*Экзаменационный тест «Интегрирование функций одной переменной»*Экзаменационный тест «Дифференциальное исчисление функций нескольких переменных»*Экзаменационный тест «Обыкновенные дифференциальные уравнения»Контрольная работа.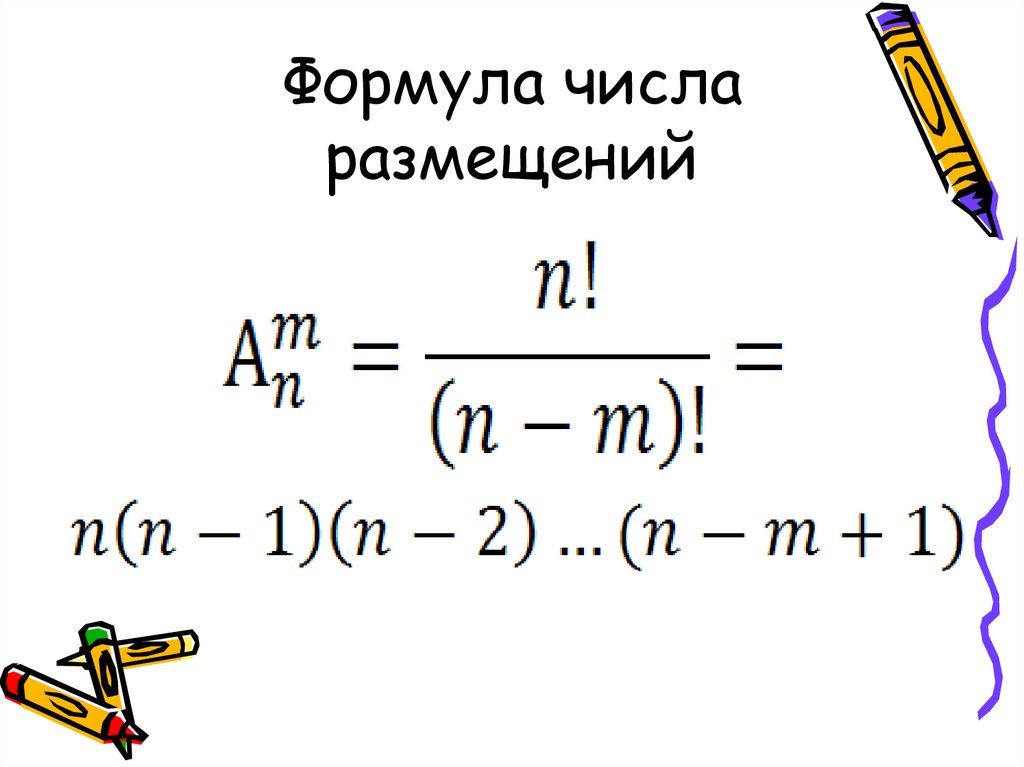 Дифференциальное исчисление функций нескольких переменныхКонтрольная работа. Неопределенный интеграл (методы интегрирования)Контрольная работа. Неопределенный интеграл (интегрирование рациональных дробей)Контрольная работа. Определенный интегралКонтрольная работа. Обыкновенные дифференциальные уравненияКонтрольная работа 1. Теория вероятностей (случайные события)Контрольная работа 2. Теория вероятностей (характеристики дискретной случайной величины)Контрольная работа 3. Теория вероятностей (характеристики непрерывной случайной величины)Контрольная работа 4. Теория вероятностей (классические законы распределения дискретной случайной величины)Контрольная работа 5. Теория вероятностей (классические законы распределения непрерывной случайной величины)Экзамен Математика (2 семестр). СОД.1,2,3-19-1 (И,З)ЭКЗАМЕН. Математика (3 семестр)_СОД.1,2,3-19 (з)

Комбинаторика: правила, методы и приложения

Помните формулу полной вероятности? Он гласит, что вероятность того, что что-то произойдет, равна количеству способов, которыми это может произойти, деленному на общее количество исходов. Но как найти количество способов, которыми что-то может произойти?

Здесь на помощь приходит комбинаторика. Если вы пытаетесь ответить на вопрос, начинающийся со слов «Сколько способов\(\точек\)», комбинаторика может вам помочь!

Определение комбинаторики

Комбинаторика происходит от слова «сочетать» и буквально означает изучение «комбинаций» вещей, таких как объекты или результаты. Он используется для определения количества возможных исходов конкретного события.

Комбинаторика — это раздел математики, изучающий комбинации результатов или объектов.

Давайте рассмотрим некоторые полезные правила и принципы комбинаторики.

Правило произведения в комбинаторике

Правило произведения (иногда называемое принципом умножения или мультипликативным принципом подсчета ) утверждает, что количество результатов для нескольких событий является произведением количества результатов для каждого отдельного события.

Если события \(A, B, C, \dots\) могут происходить \(x, y, z, \dots\) по-разному, то существуют \(x \cdot y \cdot z\cdot \dots \) способы возникновения этих событий.

Это можно легко представить с помощью древовидной диаграммы.

Представление правила продукта в виде древовидной диаграммы

Допустим, пароль состоит из \(3\) символов, которые могут быть либо буквами (прописными или строчными), либо цифрами (от \(0\) до \(9\)). Пароль должен начинаться с буквы. Сколько существует возможных паролей?

Решение

В алфавите \(26\) букв и, следовательно, \(52\) букв, которые либо прописные, либо строчные. Есть \(10\) цифр от \(0\) до \(9\).

Так как вы должны начинать с буквы, есть варианты \(52\) для первого символа в пароле. Всего для последующих символов доступно \(62\) вариантов. Следовательно, количество возможных паролей:

\[52 \cdot 62 \cdot 62=199{,}888.\]

Арифметика в комбинаторике

Арифметика (т.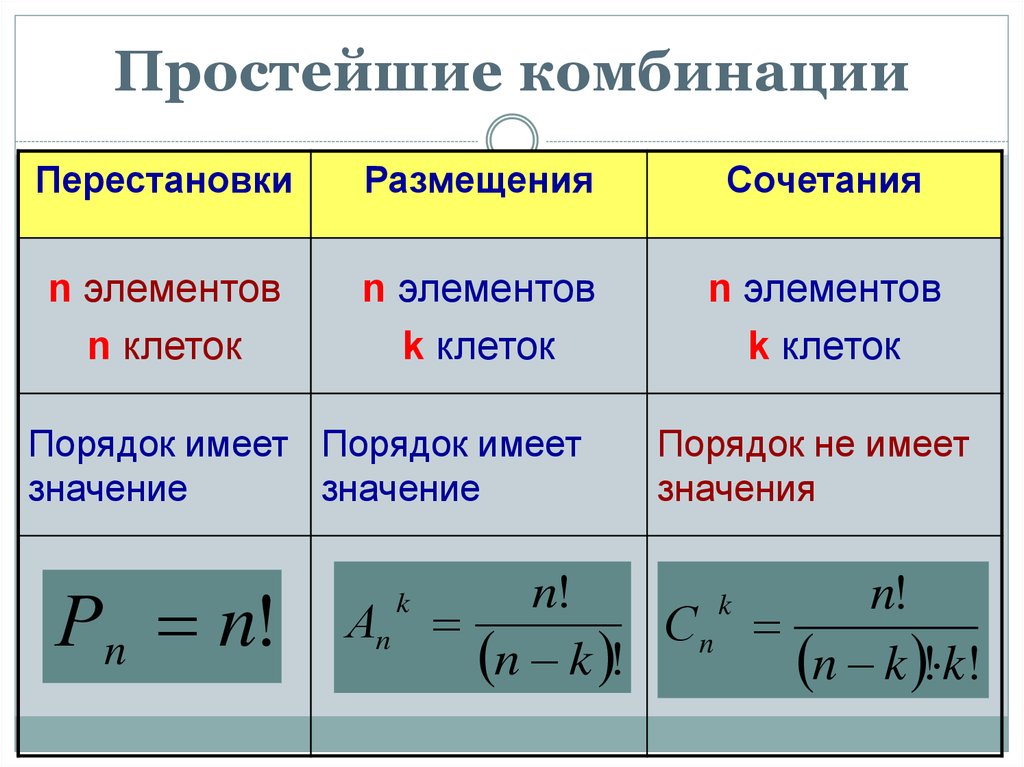 е. сложение и вычитание) используется в комбинаторике для событий, которые менее прямолинейны, чем в приведенном примере выше.

Сложение и вычитание основных элементов

Если существуют дополнительные ограничения на количество результатов, которые вы пытаетесь найти, вы можете просто вычесть количество нежелательных результатов. Это также иногда называют правилом дополнения .

Если есть дополнительные ограничения при попытке найти количество способов, которыми что-то может произойти, просто вычтите количество способов, которыми могут произойти эти ограничения.

Давайте рассмотрим пример с использованием правила дополнения.

Сколько целых положительных чисел меньше \(1000\) содержат цифру \(4\) хотя бы один раз?

Решение

Наше первое ограничение — «целые положительные числа меньше \(1000\)», из которых \(999\) (\(1\) до \(999\)).

Каждая из трех цифр имеет \(10\) результатов, от \(0\) до \(9\), за исключением того, что вы хотите исключить сценарий, в котором есть три нуля.

Хороший способ решить эту задачу — найти дополнение (т. е. сколько чисел не содержит \(4\)) и вычесть его из общего количества положительных целых чисел.

Чтобы найти количество чисел без цифры \(4\), у вас осталось \(9\) цифр на цифру. Нужно убрать вариант с тремя нулями. Следовательно, существует \(93-1=728\).

Количество натуральных чисел меньше \(1000\), содержащих четверку: \(999-728=271\).

Расстановка объектов

Вы также можете столкнуться с вопросами о различных способах «расстановки объектов».

Выстраивание \(n\) объектов в ряд

Представьте, что вы выстраиваете \(5\) объектов в ряд. Сколькими способами их можно расположить?

Назовем \(5\) объекты \(A, B, C, D\) и \(E\). Необходимо заполнить \(5\) пробелов. Для первого места есть выбор между всеми \(5\) объектами. Чтобы заполнить второе пространство, есть выбор между оставшимися \(4\) объектами. Чтобы заполнить третье место, есть выбор между оставшимися \(3\) и так далее.

Следовательно, используя правило произведения, будет

\[5\cdot 4\cdot 3\cdot 2\cdot 1=120\]

способов расположить \(5\) объектов.

Вкратце это выглядит следующим образом.

Существует \(n!=n(n-1)(n-2)\dots (2)(1) \) способов расположить \(n\) объектов в линию.

Давайте рассмотрим пример расстановки букв.

Сколькими способами можно расставить буквы QWERTY?

Решение

Так как букв 6, будет \(6\!=720\) способов расположить буквы.

Расстановка \(n\) предметов по кругу

Вместо этого представьте, что вы расставляете 5 предметов по кругу.

Круг из \(5\) объектов

Для каждого круга, который вы можете сделать, есть 5 линий, которые вы можете сделать, «разрезав» круг в разных местах.

«Вырезать» круги

Все \(5\) линий выше образуют один и тот же круг. Это относится к каждому кругу, который вы можете сделать. Следовательно, количество способов, которыми вы можете расположить \(5\) объектов по кругу, равно 9.0003

\[\frac{5!}{5}=4!=24.\]

Количество способов, которыми вы можете расположить \(n\) объектов по кругу, равно \((n-1)!\ ).

Что делать, если у вас есть \(10\) разных бусин?

У вас есть \(10\) разных бусин. Поскольку вы делаете браслет, расположение по часовой стрелке и против часовой стрелки одинаково. Сколько разных браслетов можно сделать?

Решение

Есть

\[ \begin{align} (10-1)! &=9! \\ &=362{,}880\конец{выравнивание} \]

способа расположить \(10\) объектов по кругу.

Поскольку в этом случае расположение по часовой и против часовой стрелки одинаково, вам нужно разделить на \(2\). Следовательно, есть

\[\begin{align} \frac{9!}{2} &=\frac{362{,}880}{2}\\ &=181{,}440 \end{align} \]

различных браслета.

Комбинации и перестановки

Комбинации и перестановки похожи, но есть одно ключевое отличие: комбинация объектов — это то, где порядок не имеет значения. А перестановка там, где порядок имеет значение .

Допустим, у вас есть буквы \(A\), \(B\) и \(C\). Затем вы выбираете \(2\) из букв. Сколько у вас комбинаций? Сколько у вас перестановок?

Ответ:

Сочетания и перестановки следующие: Б, В)\) Перестановки 93P_2=6\)).

Комбинации

Допустим, у вас есть \(n\) разных объектов и выберите \(r\).

Комбинация является одним из возможных результатов выбора \(r\) объектов из \(n\). Важно помнить, что порядок не имеет значения .

Есть два способа представления комбинаций с помощью обозначений. Во-первых, у нас есть запись «\(\binom{n}{r}\)» (которую вы можете прочитать как «\(n\) выбрать \(r\)»). Во втором обозначении используется «\(C\)», как показано в определении ниже. 9nC_r=\frac{n!}{r!(n-r)!} .\]

Давайте рассмотрим пример вечеринки!

На вечеринке \(50\) человек. Все пожимают друг другу руки ровно один раз. Сколько всего рукопожатий?

Решение

Если все пожали друг другу руки, нужно найти количество пар на вечеринке. Это эквивалентно вопросу «сколько групп \(2\) можно составить из группы \(50\)»?

Так как порядок или пары не имеют значения, вы можете использовать комбинации. Поэтому ответ 9{16}C_3=560.\]

Приложения комбинаторики

Наиболее распространенное применение комбинаторики — теория вероятностей. Чтобы узнать вероятность того, что что-то произойдет, вам также нужно знать, сколько способов что-то может произойти.

Вероятностные методы в комбинаторике

Главное применение комбинаторики — теория вероятностей. Если вы можете найти общее количество способов, которыми что-то может произойти, то вы можете найти вероятность того, что что-то произойдет, используя 92(51\cdot 52\cdot 53)}{(1\cdot 2\cdot 3) (54\cdot 55\cdot 56\cdot 57 \cdot 58\cdot 59)} \\\\&= 0,0104 \text{ до 3 s. f.} \end{align}\]

Комбинаторика — Ключевые выводы

• Комбинаторика — это раздел математики, изучающий комбинации результатов или объектов.
• Правило продукта гласит, что количество результатов для нескольких событий равно произведению количества результатов для каждого отдельного события.
• Существует \(n!=n(n-1)(n-2)\dots(2)(1)\) способов расположить \(n\) объектов в линию. 9nP_r=\frac{n!}{(n-r)!}\]

Комбинаторика — Calcworkshop

1 час 17 минут 15 примеров

• Что такое правило умножения? (Примеры №1-5)
• Обзор правила сумм и принципа включения-исключения? (Примеры №6-7)
• Определить количество подмножеств (примеры №8-9)
• Сколько трехзначных или четырехзначных целых чисел заканчиваются нулем (Пример №10)
• Используйте правило умножения и правило суммы, чтобы найти количество аранжировок (примеры №11-12)
• Сколько четырехбуквенных сочетаний можно составить, если повторение не разрешено (Пример №13)
• Сколько вариантов ответов может дать учащийся в тесте с несколькими вариантами ответов? (Пример №14)
• Найдите количество последовательностей из четырех карт в стандартной колоде (пример 15a-e)

1 час 16 минут 13 примеров

• Формулы перестановок: с повторением или без него (примеры №1-3)
• Сколько различимых перестановок? (Пример № 4а-б)
• Круговое правило для перестановок (примеры № 5-6)
• Определить номер функции, если f инъективна (пример 7a-b)
• Сколько способов расположить людей вокруг двух круглых столов (Пример №8)
• Устроить рыцарей за круглым столом, если две ночи отказываются сидеть рядом друг с другом (Пример №9)
• Сколько теннисных матчей можно устроить? (Пример №10)
• Используйте перестановки, чтобы найти количество аранжировок (примеры № 11-13)

1 час 18 минут 12 примеров

• Комбинации без повторения (примеры #1-4)
• Комбинации с повторением (Примеры №5-6)
• Определить количество раздач в бридж из стандартной колоды (пример № 7a-b)
• Каково минимальное значение n для подмножества (пример 8a-b)
• Комбинации с использованием слов «не более» и «не менее» (примеры № 9–10)
• Сколько комбинаций в покере можно составить хотя бы с одной картой каждой масти (пример 12-a-b)
• Сколько покерных комбинаций содержит ровно одну пару или тройку (пример 12c-d)
• Сколько покерных комбинаций содержит фулл-хаус (Пример №12e)

48 мин. 11 примеров

• Что такое принцип классификации? (Примеры №1-4)
• Обобщенная формула для принципа классификации (примеры № 5–8)
• Сколько карт нужно выбрать, чтобы гарантировать не менее трех червей (пример № 9a-b)
• Докажите, что в игре TENZI есть как минимум 7 кубиков с одинаковыми номерами (Пример №10)
• Показать, что есть как минимум два с одинаковым остатком (Пример №11)

1 час 34 мин 10 примеров

• Как использовать биномиальную теорему (пример №1)
• Треугольник Паскаля для нахождения биномиальных коэффициентов (примеры 2–3)
• Найдите указанный коэффициент для биномиального разложения (Примеры №4-5)
• Найдите постоянный член разложения (Примеры №6-7)
• Биномиальная теорема для нахождения коэффициентов произведения трехчлена и двучлена (примеры № 8–9).2 (Пример № 10c-d)

1 час 49 минут 25 примеров

• Сможете ли вы угадать закономерность и определить следующий член последовательности? (Примеры №1-7)
• Что такое рекурсивное определение и явная формула?
• Найдите первые пять членов последовательности (примеры 8-10)
• Рекурсивная формула и замкнутая формула для арифметических и геометрических последовательностей
• Треугольная — Квадратная — Кубическая — Экспоненциальная — Факториальная — Последовательности Фибоначчи
• Найдите рекурсивное определение для каждой последовательности (примеры №11-14)
• Использование известных последовательностей для поиска замкнутой формулы (примеры №15–20)
• Использование метода реверсивного добавления в арифметических последовательностях (примеры № 21–22)
• Суммирование геометрических последовательностей с использованием метода умножения-сдвига-вычитания (примеры № 23–34)
• Суммирование и обозначение произведения (пример № 25a-d)

1 час 36 мин 8 Примеры

• Обзор решения рекуррентного соотношения с использованием итераций с возвратом
• Использование итерации для решения явной формулы (примеры № 1-2)
• Использование обратной замены для решения рекуррентного соотношения (примеры № 3-4)
• Решить рекуррентное соотношение, используя итерацию и известные суммы (примеры № 5-6)
• Найдите замкнутую формулу (Примеры №7-8)

1 час 39 минут 8 примеров

• Определение линейного однородного рекуррентного соотношения и его степени (пример 1a-i)
• Каков метод характеристического корня и формулы для различных-повторяющихся-комплексных корней?
• Решить рекуррентное соотношение степени 1 (Пример №2)
• Определите замкнутую формулу с различными корнями (примеры № 3-5))
• Найдите замкнутую форму с повторяющимися корнями (Примеры №6-7)
• Раскройте явную формулу с комплексными корнями (Пример №8)

1 час 0 мин 13 практических задач

• Использование принципа счета (задачи №1-2)
• Используйте комбинации без повторений (задача №3)
• Используйте комбинации с повторением (задача №4)
• Использование перестановок (задача № 5)
• Сколькими способами можно выбрать комитет с равными членами (задача № 6а)
• .

  No related posts.