Отношение гипотенузы к катету: «Соотношения между сторонами и углами прямоугольного треугольника» Некрасова А.С., Магистратура, 1 курс, ПМИ

Содержание

Соотношения между сторонами и углами прямоугольного треугольника

Свойство. Сумма двух острых углов прямоугольного треугольника равна 90 0

Свойство. Катет прямоугольного треугольника, лежащий против угла в 300, равен половине гипотенузы.

АС= (1/2)ВС

Признаки равенства:

Теорема. Два прямоугольных треугольника равны, если катеты одного равны катетам другого.

Теорема. Два прямоугольных треугольника равны, если гипотенуза и катет одного равны гипотенузе и катету другого.

Теорема. Два прямоугольных треугольника равны, если острый угол и сторона одного равны острому углу и стороне другого.

Теорема Пифагора

Теорема. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Теорема, обратная теореме Пифагора. Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный.

Раньше при изучении теоремы Пифагора было популярно следующее выражение: «Пифагоровы штаны на все стороны равны». Смешно, пожалуй? Но зато все сразу становится понятным. Посмотрите на следующий рисунок, на котором эти «штаны» изображены.

Соотношение углов и сторон прямоугольного треугольника

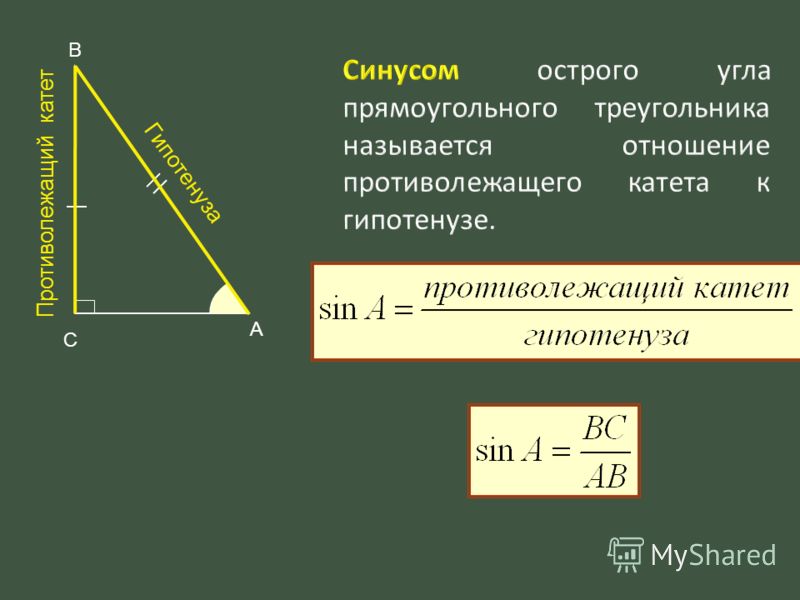
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

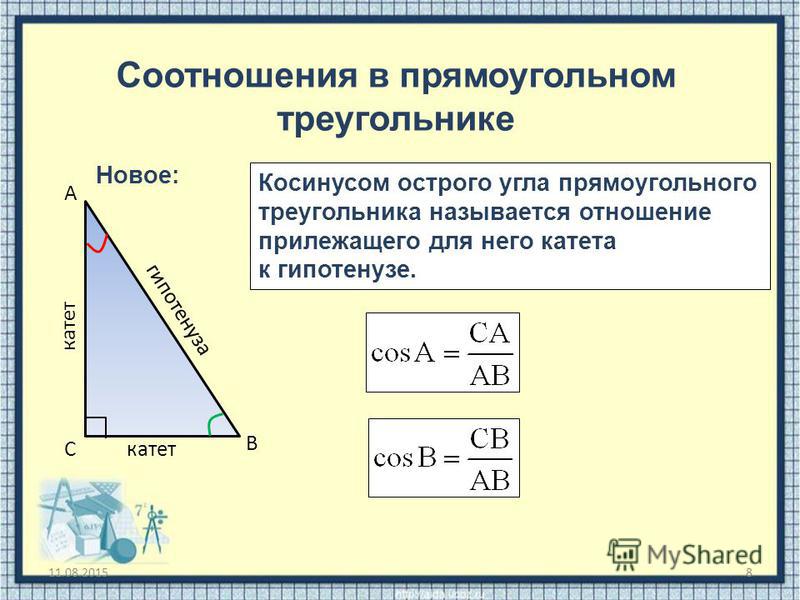
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

Соотношения между сторонами и углами прямоугольного треугольника

Треугольник – геометрическая фигура, образованная тремя отрезками, которые попарно пересекаются в трех точках, называемых вершинами треугольника.

Стороны треугольника образуют в вершинах треугольника три угла.

В треугольнике большая сторона лежит против большего угла.

Стороны и углы треугольника связаны следующими соотношениями.

Прямоугольный треугольник — это треугольник, у которого один угол прямой (равен 90 градусов).

Катетами называются две стороны треугольника, которые образуют прямой угол.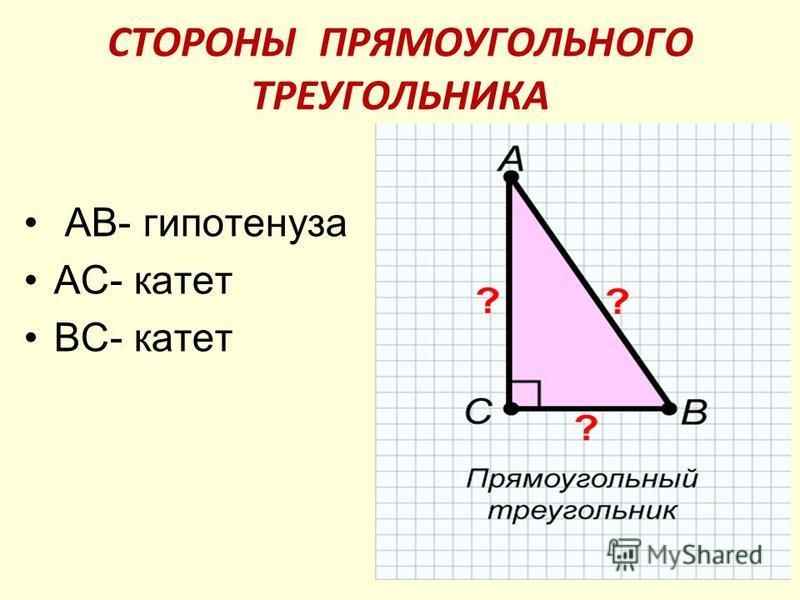 Гипотенузой называется сторона, лежащая напротив прямого угла.

Соотношение между сторонами и углами треугольника

Некоторые свойства прямоугольного треугольника:

Сумма острых углов в прямоугольном треугольнике равна 90 градусов.
Если в прямоугольном треугольнике один из острых углов равен 45 градусов, то этот треугольник равнобедренный.
Катет прямоугольного треугольника, лежащий напротив угла в 30 градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)
Катет прямоугольного треугольника, лежащий напротив угла в 60 градусов, равен малому катету этого треугольника, умноженному на √3.
В равнобедренном прямоугольном треугольнике гипотенуза равна катету, умноженному на √2.
Медиана прямоугольного треугольника, проведенная к его гипотенузе, равна ее половине и радиусу описанной окружности (R)
Медиана прямоугольного треугольника, проведенная к его гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями, которых являются катеты данного треугольника.

Соотношение между сторонами и углами в прямоугольном треугольнике:

В прямоугольном треугольнике АВС, с прямым углом С

Для острого угла В: АС — противолежащий катет; ВС — прилежащий катет.

Для острого угла А: ВС — противолежащий катет; АС — прилежащий катет.

Синусом (sin) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Косинусом (cos) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Тангенсом (tg) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
Котангенсом (ctg) острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.

В прямоугольном треугольнике АВС для острого угла В:

sin⁡B=AC/AB;

cos⁡B=BC/AB;

tgB=AC/BC;

ctgB=BC/AC.

В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.

sinBOA=sinBOC;

cosBOA=−cosBOC;

tgBOA=−tgBOC;

ctgBOA=−ctgBOC.

Значения тригонометрических функций некоторых углов:

Площадь прямоугольного треугольника равна половине произведения его катетов

S=(AC∙BC)/2

Пример:

В треугольнике АВС угол С равен 90 градусов, sin⁡A=4/5,AC=9. Найдите АВ.

Решение:

Распишем синус угла А по определению:

sin⁡A=ВС/АВ=4/5

Так как мы знаем длину катета АС и он не участвует в записи синуса угла А, то можем ВС и АВ взять за части 4х и 5х соответственно.

Применим теорему Пифагора, чтобы отыскать «х»

АС2+ВС2=АВ2

92+(4х)2=(5х)2

81+16х2=25х2

81=25х2−16х2

81=9х2

9=х2

х=3

Так как длина АВ составляет пять частей, то 3∙5=15

Ответ: 15

В прямоугольном треугольнике с прямым углом С и высотой СD:

Квадрат высоты, проведенной к гипотенузе, равен произведению отрезков, на которые высота поделила гипотенузу.

CD2=DB∙AD

В прямоугольном треугольнике: квадрат катета равен произведению гипотенузы на проекцию этого катета на гипотенузу.

CB2=AB∙DB

AC2=AB∙AD

Произведение катетов прямоугольного треугольника равно произведению его гипотенузы на высоту, проведенную к гипотенузе.

AC∙CB=AB∙CD

Для закрепления материала предлагаю разбиться на пары и задать друг другу 3-4 вопроса по изученной теме.

Поделиться статьей в соцсетях

Остались вопросы?
Наши репетиторы помогут

Остались вопросы?

Определение гипотенузы по катету и углу. Как найти гипотенузу, зная катет и угол

Инструкция

Треугольник называется прямоугольным, если один из его углов равен 90 градусов. Он состоит из двух катетов и гипотенузы. Гипотенузой называют большую сторону этого треугольника. Она лежит против прямого угла. Катетами, соответственно, называют меньшие его стороны. Они могут быть как равны между собой, так и иметь разную величину. Равенство катетов , что вы работаете с прямоугольным треугольником. Прелесть его в том, что он объединяет в себе двух фигур: прямоугольного и равнобедренного треугольника. Если катеты не равны, то треугольник произвольный и основному закону: чем больше угол, тем больше лежащий напротив него катит.

Существует несколько способов нахождения гипотенузы по и углу. Но прежде чем воспользоваться одним из них, следует определить, какой и угол известны. Если дан угол и прилежащий к нему катет, то гипотенузу легче все найти по косинусу угла. Косинусом острого угла (cos a) в прямоугольном треугольнике называют отношение прилежащего катета к гипотенузе. Отсюда вытекает, что гипотенуза (с) будет равна отношению прилежащего катета (b) к косинуса угла a (cos a). Это можно записать так: cos a=b/c => c=b/cos a.

Если дан угол и противолежащий катет, то следует работать . Синус острого угла (sin a) в прямоугольном треугольнике есть отношение противолежащего катета (a) к гипотенузе (c). Здесь принцип, что и в предыдущем примере, только вместо функции косинуса берется синус.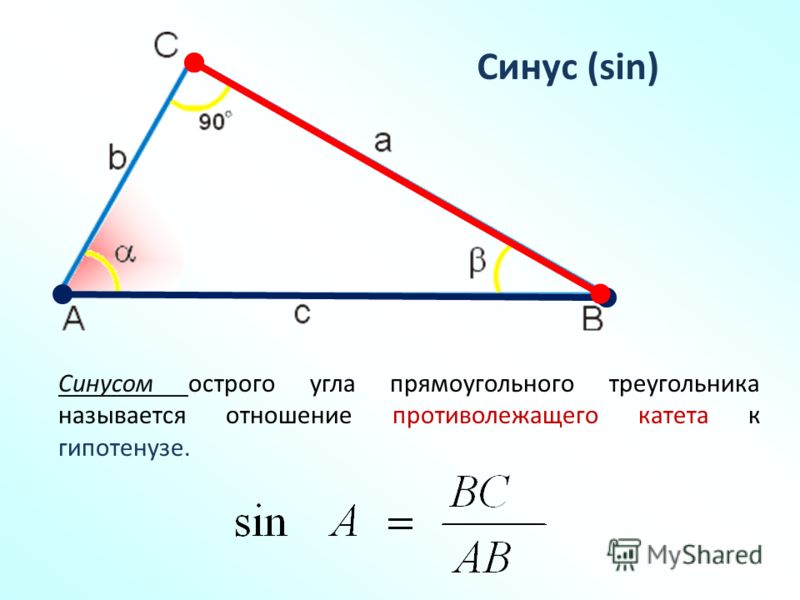 sin a=a/c => c=a/sin a.

Также можно воспользоваться такой тригонометрической функцией, как . Но нахождение искомой величины слегка усложнится. Тангенсом острого угла (tg a) в прямоугольном треугольнике называют отношение противолежащего катета (а) к прилежащему (b). Найдя оба катета, примените теорему Пифагора (квадрат гипотенузы равен сумме квадратов катетов) и большая будет найдена.

Обратите внимание

Работая с теоремой Пифагора, не забывайте, что вы имеете дело со степенью. Найдя сумму квадратов катетов, для получения окончательного ответа следует извлечь квадратный корень.

Источники:

как найти катет и гипотенузу

Гипотенузой называется сторона в прямоугольном треугольнике, которая находится напротив угла в 90 градусов. Для того, чтобы рассчитать его длину, достаточно знать длину одного из катетов и величину одного из острых углов треугольника.

Инструкция

При известном и остром угле прямоугольного , то размер гипотенузы быть отношению катета к / этого угла, если данный угол является ему противолежащим/прилежащим:

h = C1(или C2)/sinα;

h = С1(или С2)/cosα.

Пример: Пусть дан ABC с гипотенузой AB и C. Пусть угол B равен 60 градусам, а угол A 30 градусам Длина катета BC 8 см. Надо длину гипотенузы AB. Для этого можно воспользоваться любым из предложенных выше способов:

AB = BC/cos60 = 8 см.

AB = BC/sin30 = 8 см.

Слово «катет » происходит от греческих слов «перпендикуляр» или «отвесный» — это объясняет, почему именно так назвали обе стороны прямоугольного треугольника, составляющие его девяностоградусный угол. Найти длину любого из катет ов нетрудно, если известна величина прилегающего к нему угла и еще какой-либо из параметров, так как в этом случае фактически станут известны величины всех трех углов.

Инструкция

Если кроме величины прилегающего угла (β) известна длина второго катет а (b), то длину катет а (a) можно определить как частное от деления длины известного

катет а на известного угла: a=b/tg(β). Это вытекает из определения этой тригонометрической . Можно обойтись без тангенса, если воспользоваться теоремой .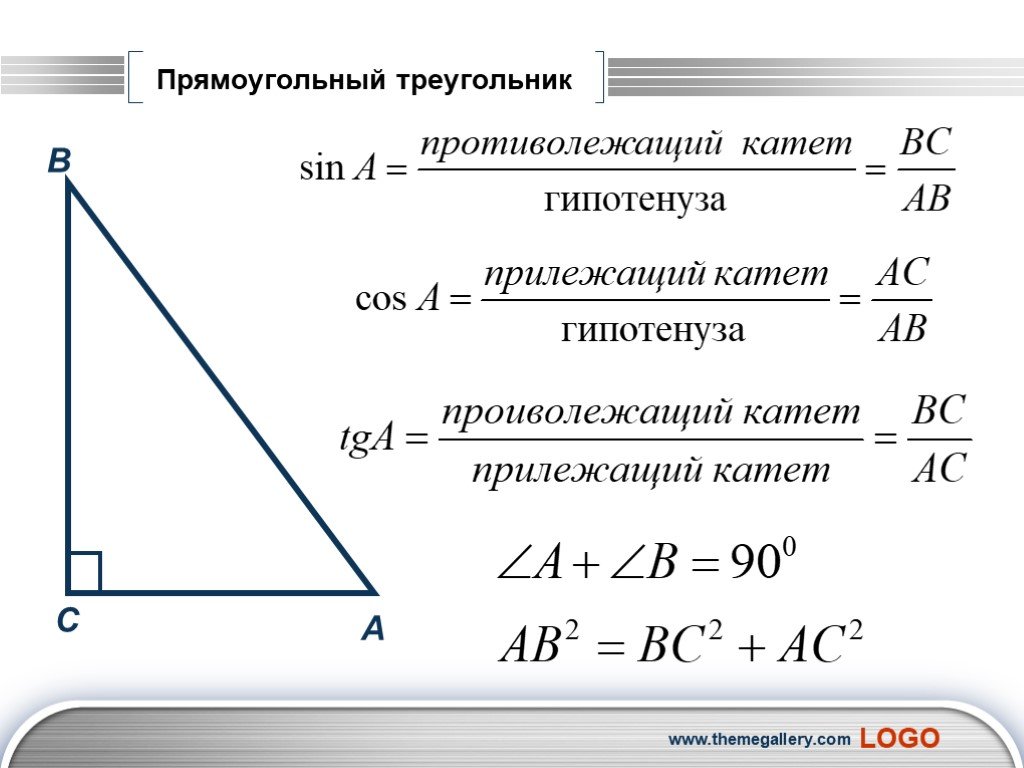

Из нее следует, что длины искомой к синусу противолежащего угла отношению длины известного катет а к синусу известного угла. Противолежащий искомому катет у острый угол можно выразить через известный угол как 180°-90°-β = 90°-β, так как сумма всех углов любого треугольника должна составлять 180°, а один из его углов равен 90°. Значит, искомую длину катет а можно вычислить по формуле a=sin(90°-β)∗b/sin(β).

Если известны величина прилегающего угла (β) и длина гипотенузы (c), то длину катет а (a) можно вычислить как произведение длины гипотенузы на косинус известного угла: a=c∗cos(β). Это вытекает из определения косинуса, как тригонометрической функции. Но можно воспользоваться, как и в предыдущем шаге, теоремой синусов и тогда длина искомого

катет а будет равняться произведению синуса между 90° и известным углом на отношение длины гипотенузы к синусу прямого угла. А поскольку синус 90° равен единице, то можно записать так: a=sin(90°-β)∗c.

Практические вычисления можно производить, например, при помощи имеющегося в составе ОС Windows программного калькулятора.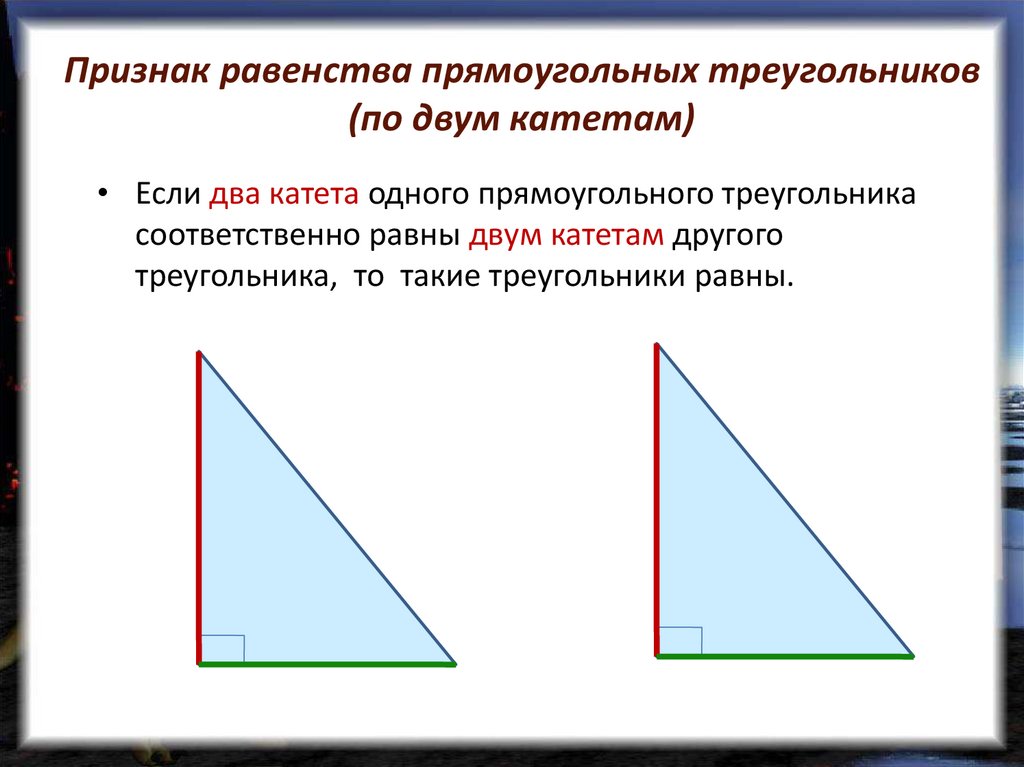 Для его запуска можно в главном меню на кнопке «Пуск» выбрать пункт «Выполнить», набрать команду calc и нажать кнопку «OK». В открывающемся по умолчанию простейшем варианте интерфейса этой программы тригонометрические функции не предусмотрены, поэтому после его запуска надо щелкнуть в меню раздел «Вид» и выбрать строку «Научный» или «Инженерный» (зависит от используемой версии операционной системы).

Видео по теме

Слово «катет» пришло в русский язык из греческого. В точном переводе оно означает отвес, то есть перпендикуляр к поверхности земли. В математике катетами называются стороны, образующие прямой угол прямоугольного треугольника. Противолежащая этому углу сторона называется гипотенузой. Термин «катет» применяется также в архитектуре и технологии сварочных работ.

Начертите прямоугольный треугольник АСВ. Обозначьте его катеты как а и b, а гипотенузу — как с. Все стороны и углы прямоугольного треугольника между собой определенными . Отношение катета, противолежащего одному из острых углов, к гипотенузе называется синусом данного угла. В данном треугольнике sinCAB=a/c. Косинус — это отношение к гипотенузе прилежащего катета, то есть cosCAB=b/c. Обратные отношения называются секансом и косекансом.

Косеканс равен частному от деления гипотенузы на противолежащий катет и это величина, обратная синусу. Она может быть рассчитана по формуле cosecCAB=1/sinCAB

Оба катета связаны между собой и котангенсом. В данном случае тангенсом будет отношение стороны a к стороне b, то есть противолежащего катета к прилежащему. Это отношение может быть выражено формулой tgCAB=a/b. Соответственно, обратным отношением будет котангенс: ctgCAB=b/a.

Соотношение между размерами гипотенузы и обоих катетов определил еще древнегреческий Пифагор. Теоремой, его именем, люди пользуются до сих пор. Она гласит, что квадрат гипотенузы равен сумме квадратов катетов, то есть с2=a2+b2. Соответственно, каждый катет будет равняться квадратному корню из разности квадратов гипотенузы и другого катета. Эту формулу можно записать как b=√(с2-а2).

Длину катета можно выразить и через известные вам соотношения. Согласно теоремам синусов и косинусов, катет равен произведению гипотенузы на одну из этих функций. Можно его выразить и или котангенс. Катет а можно найти, например, по формуле a = b*tan CAB. Точно таким же образом, в зависимости от заданных тангенса или , определяется и второй катет.

В архитектуре также используется термин «катет». Он применяется по отношению к ионической капители и отвес через середину ее задка. То есть и в этом случае этим термином перпендикуляр к заданной линии.

В технологии сварочных работ есть «катет углового шва». Как и в других случаях, это самое короткое расстояние. Здесь речь идет о промежутке между одной из свариваемых деталей до границы шва, находящегося на поверхности другой детали.

Видео по теме

Источники:

что такое катет и гипотенуза в 2019

Геометрия — не простая наука. Она требует к себе особого внимания и знания точных формул. Эта разновидность математики пришла к нам из Древней Греции и даже по прошествии нескольких тысяч лет она не теряет свою актуальность. Не стоит напрасно думать, что это бесполезный предмет, забивающий голову студентов и школьников. На самом деле геометрия применима во многих сферах жизни. Без нее знаний по геометрии не строится ни одно архитектурное сооружение, не создаются автомобили, космические корабли и самолеты. Сложные и не очень развязки дорог и колей — это все нуждается в геометрических расчетах. Да даже порой ремонт в своей комнате вы не сможете сделать без знания элементарных формул. Так что не стоит недооценивать всю важность этого предмета. Наиболее частые формулы, которые приходится использовать во многих решениях, мы изучаем еще в школе. Одна из них это нахождение гипотенузы в прямоугольном треугольнике. Чтобы разобраться в этом, читайте ниже.

Прежде чем приступить к практике, давайте начнем с основ и определим, что такое гипотенуза в прямоугольном треугольнике.

Гипотенуза — одна из сторон в прямоугольном треугольнике, которая находится напротив угла в 90 градусов (прямой угол) и всегда является самой длинной.

Существует несколько способов, как найти длину искомой гипотенузы в заданном прямоугольном треугольнике.

В случае, когда катеты нам уже известны- мы используем теорему Пифагора, где мы складываем сумму из квадратов двух катетов, что и будет равняться квадрату гипотенузы.

а и b -катеты, c- гипотенуза.

В нашем случае, для прямоугольного треугольника, соответственно, формула будет следующей:

Если подставить известные числа катетов а и b, пусть это будет а=3 а b=4, то с=√32+42 , то получим с=√25, с=5

Когда у нас известна длина лишь одного катета, то формулу можно преобразовать, чтобы найти длину второго. Выглядит это следующим образом:

В том случае, когда по условиям задачи у нас известен катет А и гипотенуза С, то можно рассчитать прямой угол треугольника, назовем его α.

Для этого воспользуемся формулой:

Пусть второй угол, который нам необходимо вычислить, будет β.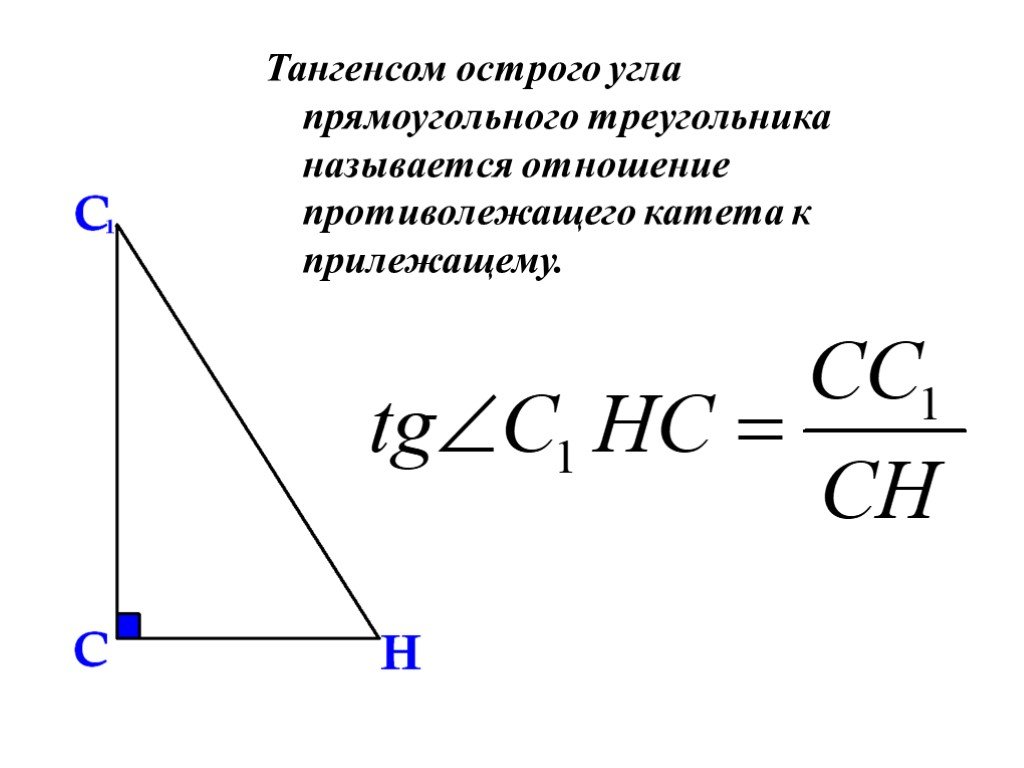 Учитывая, что мы знаем сумма углов треугольника, которая составляет 180°, то: β= 180°-90°-α

В том случае, когда нам известны значения катетов, можно по формуле найти значение острого угла треугольника:

В зависимости от известных общепринятых значений, стороны прямоугольника можно найти по множеству разных формул. Приведем некоторые из них:

При решении задач с нахождением неизвестных в прямоугольном треугольнике, очень важно акцентировать внимание на уже известные вам значения и, исходя из этого, подставлять их в нужную формулу. Сразу запомнить их будет трудно, поэтому советуем вам сделать небольшую рукописную подсказку и вклеить в тетрадь.

Как видите, если вникнуть во все тонкости этой формулы, то можно без труда разобраться в этом. Рекомендуем попробовать решить несколько задач, основанных на данной формуле. После того, как увидите свой результат, вам станет ясно, поняли вы эту тему или нет. Постарайтесь не заучивать, а вникнуть в материал, это будет куда полезнее. Зазубренный материал забывается уже после первой контрольной, а эта формула вам будет встречаться достаточно часто, поэтому сначала поймите ее, а после заучивайте на память. Если эти рекомендации не дали положительного эффекта, то есть смысл в дополнительных занятиях этой темы. И помните: ученье свет, а не ученье тьма!

Теорема Пифагора является фундаментальной для каждой математики. Она устанавливает соотношение между сторонами прямоугольного треугольника. Теперь зафиксировано 367 доказательств этой теоремы.

Инструкция

1. Классическая школьная формулировка теоремы Пифагора звучит так: квадрат гипотенузы равен сумме квадратов катетов. Таким образом, дабы обнаружить гипотенузу прямоугольного треугольника по двум катетам, нужно поочередно построить в квадрат длины катетов, сложить их и извлечь квадратный корень из итога. В первоначальной своей формулировке теорема утверждала, что площадь квадрата, построенного на гипотенузе, равна сумме площадей 2-х квадратов, построенных на катетах.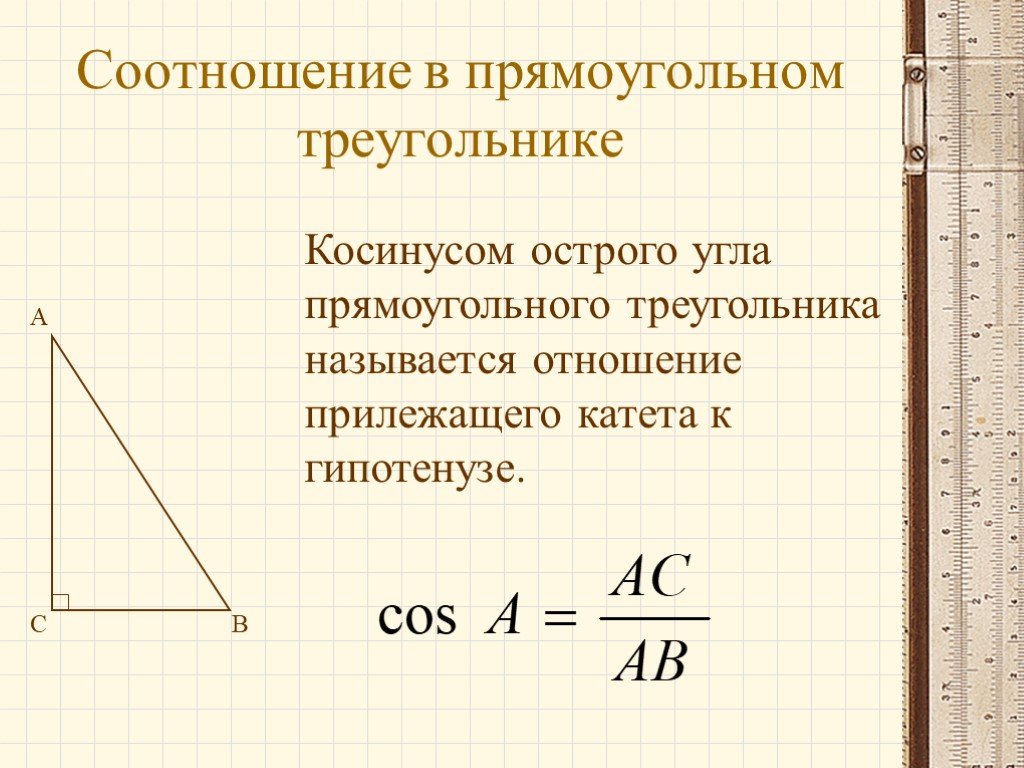 Впрочем современная алгебраическая формулировка не требует вводить представление площади.

2. Пускай, скажем, дан прямоугольный треугольник, катеты которого равны 7 см и 8 см. Тогда, согласно теореме Пифагора, квадрат гипотенузы равен 7?+8?=49+64=113 см?. Сама гипотенуза равна корню квадратному из числа 113. Получилось иррациональное число, которое идет в результат.

3. Если катеты треугольника равны 3 и 4, тогда гипотенуза равна?25=5. При извлечении квадратного корня получилось естественное число. Числа 3, 4, 5 составляют пифагорову тройку, так как они удовлетворяют соотношению x?+y?=z?, будучи все естественными. Другие примеры пифагоровой тройки: 6, 8, 10; 5, 12, 13; 15, 20, 25; 9, 40, 41.

4. В том случае если катеты равны между собой, тогда теорема Пифагора переходит в больше примитивное уравнение. Пускай, к примеру, оба катета равны числу A, а гипотенуза обозначена за C. Тогда C?=A?+A?, C?=2A?, C=A?2. В этом случае не надобно возводить в квадрат число A.

5. Теорема Пифагора – частный случай больше всеобщей теоремы косинусов, которая устанавливает соотношение между тремя сторонами треугольника для произвольного угла между какими-нибудь двумя из них.

Гипотенузой именуется сторона в прямоугольном треугольнике, которая находится наоборот угла в 90 градусов. Для того, дабы рассчитать его длину, довольно знать длину одного из катетов и величину одного из острых углов треугольника.

Инструкция

1. При знаменитом катете и остром угле прямоугольного треугольника, то размер гипотенузы может быть равен отношению катета к косинусу/синусу этого угла, если данный угол является ему противолежащим/прилежащим:h = C1(либо C2)/sin?;h = С1(либо С2)/cos?.Пример: Пускай дан прямоугольный треугольник ABC с гипотенузой AB и прямым углом C. Пускай угол B равен 60 градусам, а угол A 30 градусам Длина катета BC 8 см. Нужно обнаружить длину гипотенузы AB. Для этого дозволено воспользоваться любым из предложенных выше методов:AB = BC/cos60 = 8 см.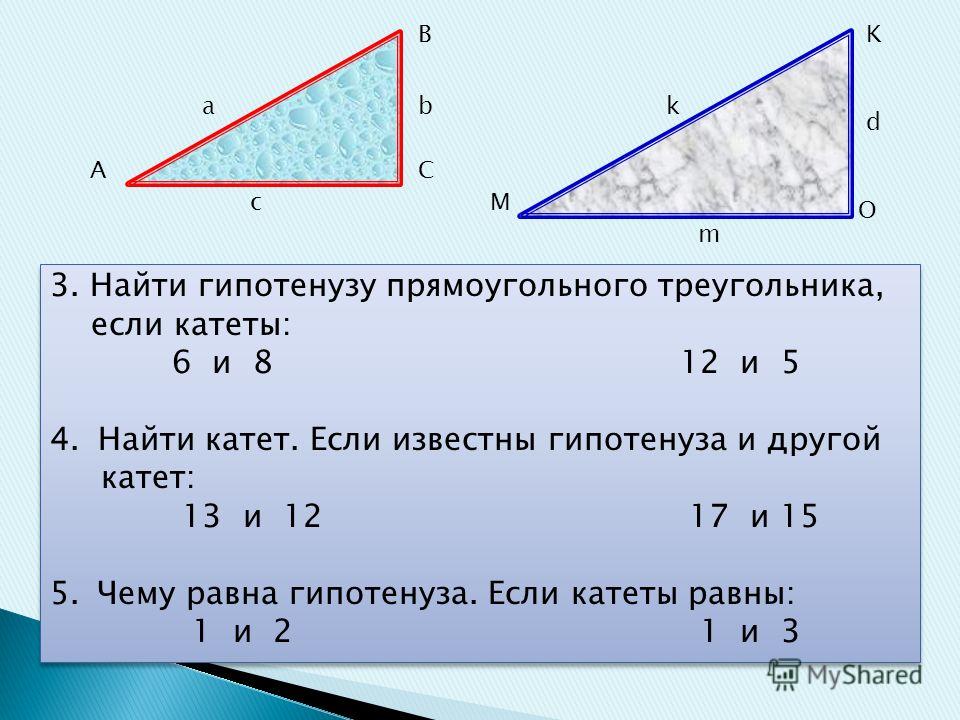 AB = BC/sin30 = 8 см.

Гипотенуза – самая длинная сторона прямоугольного треугольника . Она расположена противоположно прямому углу. Метод нахождения гипотенузы прямоугольного треугольника зависит от того, какими начальными данными вы владеете.

Инструкция

1. Если вестимы катеты прямоугольного треугольника , то длина гипотенузы прямоугольного треугольника может быть обнаружена с поддержкой теоремы Пифагора – квадрат длины гипотенузы равен сумме квадратов длин катетов:с2 = а2 + b2, где а и b – длины катетов прямоугольного треугольника .

2. Если знаменит один из катетов и острый угол, то формула для нахождения гипотенузы будет зависеть от того, какой данный угол по отношению к знаменитому катету – прилежащий (расположенный вблизи катета) либо противолежащий (расположенный наоборот него.В случае прилежащего угла, гипотенуза равна отношению катета на косинус этого угла: с = a/cos?;E угол противолежащий, гипотенуза равна отношению катета на синус угла: с = a/sin?.

Видео по теме

Полезный совет
Прямоугольный треугольник, стороны которого соотносятся как 3:4:5, назван египетским треугольником, от того что именно такие фигуры энергично применялись архитекторами Старинного Египта. Он является также простейшим примером Героновых треугольников, в которых стороны и площадь представлены целыми числами.

Гипотенузой называют сторону прямоугольного треугольника, лежащую напротив прямого угла. Она является наибольшей стороной прямоугольного треугольника. Рассчитать ее можно по теореме Пифагора или с помощью формул тригонометрических функций.

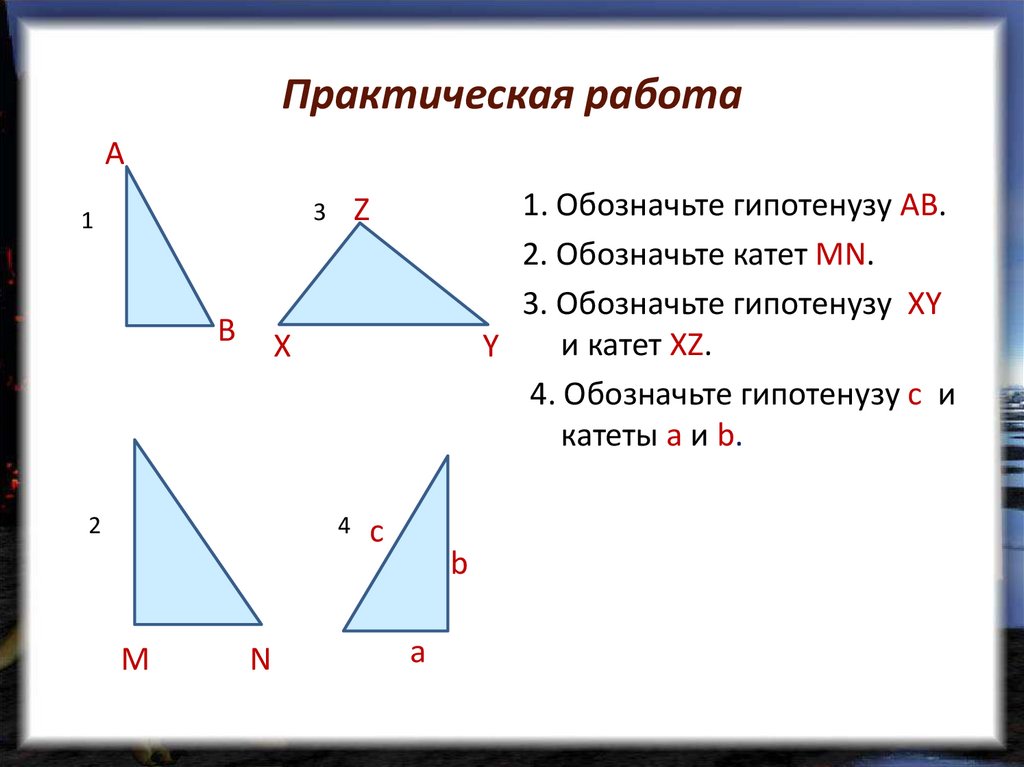
Катетами называют стороны прямоугольного треугольника, прилежащие к прямому углу. На рисунке катеты обозначены как AB и BC. Пусть заданы длины обоих катетов. Обозначим их как |AB| и |BC|. Для того, чтобы найти длину гипотенузы |AC|, воспользуемся теоремой Пифагора. Согласно данной теореме сумма квадратов катетов равна квадрату гипотенузы, т.е. в обозначениях нашего рисунка |AB|^2 + |BC|^2 = |AC|^2. 2 = 169 + 441 = 610. Для того, чтобы получить длину гипотенузы, необходимо извлечь квадратный корень из суммы квадратов катетов, т.е. из числа 610: |AC| = √610. Воспользовавшись таблицей квадратов целых чисел, выясняем, что число 610 не является полным квадратом какого-либо целого числа. Для того, чтобы получить окончательное значение длины гипотенузы, попробуем вынести полный квадрат из под знака корня. Для этого разложим число 610 на множители. 610 = 2 * 5 * 61. По таблице простых чисел смотрим, что 61 – число простое. Поэтому дальнейшее приведение числа √610 невозможно. Получаем окончательный ответ |AC| = √610.
Если бы квадрат гипотенузы был равен, к примеру, 675, тогда √675 = √(3 * 25 * 9) = 5 * 3 * √3 = 15 * √3. В случае, если подобное приведение возможно, выполняйте обратную проверку — возведите результат в квадрат и сравните с исходным значением.
Пусть нам известен один из катетов и прилежащий к нему угол. Для определенности пусть это будут катет |AB| и угол α. Тогда мы можем воспользоваться формулой для тригонометрической функции косинус – косинус угла равен отношению прилежащего катета к гипотенузе. 2 => 225 + 675 = 900. Проверка выполнена.

Инструкция

Видео по теме

Обратите внимание

При расчете сторон прямоугольного треугольника может сыграть знание его признаков:
1) Если катет прямого угла лежит напротив угла в 30 градусов, то он равен половине гипотенузы;
2) Гипотенуза всегда длиннее любого из катетов;
3) Если вокруг прямоугольного треугольника описана окружность, то ее центр должен лежать в середине гипотенузы.

Инструкция

Пусть нам известен один из катетов и прилежащий к нему угол. Для определенности пусть это будут катет |AB| и угол α. Тогда мы можем воспользоваться формулой для тригонометрической косинус – косинус отношению прилежащего катета к . Т.е. в наших обозначениях cos α = |AB| / |AC|. 2 => 225 + 675 = 900. Проверка выполнена.

Полезный совет

Рассчитав гипотенузу, выполняйте проверку — удовлетворяет ли полученное значение теореме Пифагора.

Источники:

Таблица простых чисел от 1 до 10000

Катетами называют две короткие стороны прямоугольного треугольника, составляющие ту его вершину, величина которой равна 90°. Третью сторону в таком треугольнике называют гипотенузой. Все эти стороны и углы треугольника связаны между собой определенными соотношениями, которые позволяют вычислить длину катета, если известны несколько других параметров.

Инструкция

Используйте теорему Пифагора для катета (A), если известна длина двух других сторон (B и C) прямоугольного треугольника. Эта теорема утверждает, что сумма возведенных в квадрат длин катетов равна квадрату гипотенузы. Из этого вытекает, что длина каждого из катетов равна квадратному корню из длин гипотенузы и второго катета: A=√(C²-B²).

Воспользуйтесь определением прямой тригонометрической функции «синус» для острого угла, если известна величина угла (α), лежащего напротив вычисляемого катета, и длина гипотенузы (C). Это утверждает, что синус этого известного отношению длины искомого катета к длине гипотенузы. Это , что длина искомого катета равна произведению длины гипотенузы на синус известного угла: A=C∗sin(α). Для этих же известных величин можно использовать и косеканс и рассчитать нужную длину, разделив длину гипотенузы на косеканс известного угла A=C/cosec(α).

Задействуйте определение прямой тригонометрической функции косинус, если кроме длины гипотенузы (C) известна и величина острого угла (β), прилегающего к искомому . Косинус этого угла как соотношение длин искомого катета и гипотенузы, а из этого можно вывод, что длина катета равна произведению длины гипотенузы на косинус известного угла: A=C∗cos(β). Можно воспользоваться определением функции секанс и вычислить нужное значение, разделив длину гипотенузы на секанс известного угла A=C/sec(β).

Выведите нужную формулу из аналогичного определения для производной тригонометрической функции тангенс, если кроме величины острого угла (α), лежащего напротив искомого катета (A), известна длина второго катета (B). Тангенсом противолежащего искомому катету угла отношение длины этого катета к длине второго катета. Значит, искомая величина будет равна произведению длины известного катета на тангенс известного угла: A=B∗tg(α). Из этих же известных величин можно вывести и другую формулу, если воспользоваться определением функции котангенс. В этом случае для вычисления длины катета надо будет найти соотношение длины известного катета к котангенсу известного угла: A=B/ctg(α).

Видео по теме

Секанс данного угла получается при делении гипотенузы на прилежащий катет, то есть secCAB=c/b. Получается величина, обратная косинусу, то есть выразить ее можно по формуле secCAB=1/cosSAB.
Косеканс равен частному от деления гипотенузы на противолежащий катет и это величина, обратная синусу. Она может быть рассчитана по формуле cosecCAB=1/sinCAB

Видео по теме

Источники:

что такое катет и гипотенуза в 2019

геометрия — Соотношение сторон в треугольниках 15, 75, 90

спросил 6 лет, 1 месяц назад

Изменено 8 месяцев назад

Просмотрено 18 тысяч раз

$\begingroup$

$\text{Какое отношение катетов прямоугольного треугольника с углами 15, 75 и 90?}$ Я знаю отношение катетов треугольника со сторонами $30, 60, 90$, то есть длины $1$, $\sqrt{3}$ и $2$ соответственно. Это то, что я получил до сих пор: Использование соотношения 30-60-90

Как мне сделать еще один шаг и найти ответ? Заранее спасибо.

геометрия
треугольники

$\endgroup$

$\begingroup$ 9\ обр. $$ (Это довольно легко вывести из определения функции $\tan$.)

Вы также можете представить отношение, используя радикалы: $$ r = 2 — \sqrt{3} \приблизительно 0,267949 $$

Если мы вообще не хотим использовать $\tan$, то получаем тот же ответ, просто рассуждая из вашей картинки: $$ г = {1\over2+\sqrt{3}}= 2 — \sqrt{3}. $$

(В этом отношении числитель $1$ — это вертикальная часть изображения, а знаменатель $2+\sqrt{3}$ — горизонтальная.)

$\endgroup$ 9\circ)$$

$\endgroup$

$\begingroup$

См. ссылку здесь, она дает объяснение соотношений и другие ресурсы по соотношениям треугольников:

The 15-75-90 Triangle

Краткий обзор: треугольник

15-75-90 основан на правильном двенадцатиугольнике, используя эту диаграмму:

Используя теорему Пифагора и другие методы, мы получаем отношение короткого катета: длинного катета: гипотенузы в виде 15-75-90 как $2-\sqrt{3}:1:2\sqrt{2 — \sqrt{3}}. $ Вложенный радикал в конечном итоге упрощается до $\sqrt{6} — \sqrt{2},$, поэтому упрощенный соотношение $2 — \sqrt{3}:1:\sqrt{6} — \sqrt{2}.$

$\endgroup$

геометрия — Почему правила подобия сторона-угол-сторона и гипотенуза-ног для треугольников верны?

Задавать вопрос

спросил 3 года 3 месяца назад

Изменено 3 года, 3 месяца назад

Просмотрено 233 раза

$\begingroup$

Мой учебник по математике говорит мне, что два треугольника подобны, если все углы равны друг другу («Подобие угол-угол-угол (ААА)»). Есть 4 правила, суммированные на сходство, я их суммировал:

Угол-угол (AA) Сходство. 2 пары углов равны, поэтому равна и третья пара.
Сторона-сторона-сторона (SSS) Сходство. Отношение между всеми соответствующими сторонами постоянно.

А теперь два последних, из которых я хочу узнать, почему эти правила верны. Два вышеприведенных для меня очевидны, а эти нет.

Сторона-угол-сторона (SAS) Сходство. Один угол в обоих треугольниках одинаков, и отношение между сторонами вокруг угла одинаково.
Катет гипотенузы (HL) Сходство. В прямоугольном треугольнике отношения между гипотенузами и между двумя другими равны.

Кто-нибудь может объяснить 3 и 4?

Наконец, если у вас есть 2 прямоугольных треугольника, и отношение сторон вокруг прямого угла одинаковое, они должны быть одинаковыми, верно? Потому что на это действует третье правило.

геометрия

$\endgroup$

$\begingroup$

3 и 4 — это просто SAS и HL, за исключением того, что соответствующие стороны должны быть пропорциональны, а не конгруэнтны. Вы уже приняли аналогичную версию SSS, а AAS и ASA не включены в список, поскольку на них распространяется действие AA.

$\endgroup$

$\begingroup$

Для (3) вы можете использовать правило синусов для двух треугольников, чтобы показать, что два других угла соответственно равны. Таким образом, они похожи.

Как вы указали, (4) происходит от (3).

$\endgroup$

$\begingroup$

Чтобы понять, почему (3) верно, заметим, что две стороны и угол между ними определяют треугольник с точностью до конгруэнтности. Таким образом, если в двух треугольниках углы равны и стороны вокруг равного угла по отдельности имеют одинаковое отношение друг к другу, то это означает, что вы увеличили один треугольник на какой-то постоянный коэффициент, чтобы получить другой. Поскольку эти три элемента определяют треугольник, отсюда следует, что и третьи стороны должны иметь такое же отношение друг к другу и, следовательно, быть подобными.

Соотношения между сторонами и углами прямоугольного треугольника

Определение гипотенузы по катету и углу. Как найти гипотенузу, зная катет и угол

Инструкция

Инструкция

Инструкция

геометрия — Соотношение сторон в треугольниках 15, 75, 90

геометрия — Почему правила подобия сторона-угол-сторона и гипотенуза-ног для треугольников верны?

Добавить комментарий Отменить ответ