Математический анализ. (Виленкин)
Математический анализ. (Виленкин)
ОглавлениеПРЕДИСЛОВИЕ ДЛЯ УЧИТЕЛЯВВЕДЕНИЕ 2. Числовые множества. 3. Пустое множество. 4. Подмножество. 5. Пересечение множеств. 6. Сложение множеств. 7. Разбиение множеств.  8. Вычитание множеств. 9. Отображение множеств. 10. Краткие исторические сведения. Глава I. МНОГОЧЛЕНЫ ОТ ОДНОГО ПЕРЕМЕННОГО § 1. Тождественные преобразования многочленов 2. Целые рациональные выражения и функции. 3. Степень с натуральным показателем и ее свойства. 4. Многочлены. 5. Умножение многочленов. 6. Числовые кольца и поля. 7. Кольцо многочленов над данным числовым полем. 8. Бином Ньютона. § 2. Деление многочленов. Корни многочленов 2. Теорема Безу. Схема Горнера. 3. Корни многочлена. 4. Интерполяционные формулы. 5. Кратные корни. 6. Многочлены второй степени. 7. Многочлены с целыми коэффициентами. 8. Краткие исторические сведения. Глава II. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА § 1. Общая теория уравнений 2. Область допустимых значений. 3. Уравнения. 4. Совокупности уравнений. 5. Преобразования уравнений. 6. Теоремы о равносильности уравнений. § 2. Уравнения с одним неизвестным 2.  Метод разложения на множители. Метод разложения на множители.3. Метод введения нового неизвестного. 4. Биквадратные уравнения. 5. Возвратные уравнения 3-й и 4-й степеней. § 3. Функциональные неравенства 2. Равносильные неравенства. 3. Доказательство неравенств. 4. Линейные неравенства. 5. Решение неравенств второй степени. 6. Решение алгебраических неравенств высших степеней. 7. Краткие исторические сведения. Глава III. ОБОБЩЕНИЕ ПОНЯТИЯ СТЕПЕНИ. ИРРАЦИОНАЛЬНЫЕ ВЫРАЖЕНИЯ § 1. Степени с целым показателем 2. Степень с нулевым показателем. 3. Степень с целым отрицательным показателем. § 2. Корни. Степени с рациональными показателями 2. Степени с рациональными показателями. 3. Свойства степеней с рациональными показателями. § 3. Иррациональные алгебраические выражения 2. Одночленные иррациональные выражения. 3. Сокращение показателей и приведение корней к общему показателю. 5. Вынесение алгебраических выражений из-под корня и внесение их под корень.  6. Возведение корня в степень. 7. Извлечение корня из корня. 8. Подобные корни. 9. Сложение и вычитание корней. 10. Уничтожение иррациональности в знаменателе или в числителе алгебраической дроби. 11. Преобразование выражений вида … 12. Смешанные задачи на преобразование иррациональных выражений. § 4. Иррациональные уравнения и неравенства 2. Сведение иррациональных уравнений к рациональным. 3. Уединение радикала. 4. Введение нового неизвестного. 5. Особые случаи решения иррациональных уравнений. 6. Иррациональные неравенства. 7. Краткие историчесие сведения. Глава IV. МНОГОЧЛЕНЫ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. СИСТЕМЫ УРАВНЕНИЙ И НЕРАВЕНСТВ § 1. Системы алгебраических уравнений 2. Системы уравнений. 3. Геометрический смысл решений уравнений и систем уравнений с двумя неизвестными. 4. Совокупность уравнений. 5. Равносильные системы уравнений. 6. Метод подстановки. 7. Метод алгебраического сложения уравнений.  8. Метод введения новых неизвестных. 9. Системы однородных уравнений. 10. Геометрическая интерпретация решения систем двух уравнений с двумя неизвестными. § 2. Системы линейных уравнений 2. Теоремы о равносильности систем линейных уравнений. 3. Пример решения системы линейных уравнений методом Гаусса. 4. Метод Гаусса (приведение системы к обобщенно-треугольному виду). 5. Решение обобщенно-треугольной системы линейных уравнений. 6. Системы однородных линейных уравнений. § 3. Симметрические многочлены и их приложения к решению систем уравнений 3. Основная теорема о симметрических многочленах от двух переменных. 4. Системы симметрических алгебраических уравнений. 5. Применение симметрических многочленов к решению иррациональных уравнений. § 4. Неравенства с многими переменными 2. Среднее арифметическое и среднее геометрическое трех чисел. 3. Неравенство Коши (двумерный вариант). 4. Задачи на наибольшие и наименьшие значения.  § 5. Решение неравенств 2. Неравенства с двумя переменными. 3. Задание областей неравенствами и системами неравенств. 4. Понятие о линейном программировании. 5. Краткие исторические сведения. Глава V. КОМПЛЕКСНЫЕ ЧИСЛА § 1. Комплексные числа в алгебраической форме 2. Комплексные числа. 3. Сложение комплексных чисел; умножение на действительные числа. 4. Умножение комплексных чисел. 5. Квадратные уравнения с действительными коэффициентами. 6. Деление комплексных чисел. 7. Сопряженные комплексные числа. 8. Извлечение квадратных корней из комплексных чисел. § 2. Тригонометрическая форма комплексных чисел 2. Полярная система координат. 3. Тригонометрическая форма комплексного числа. 4. Умножение и деление комплексных чисел в тригонометрической форме. 5. Возведение комплексных чисел в степень. Формула Муавра. 6. Извлечение корня из комплексного числа. 7. Функции комплексного переменного и преобразования комплексной плоскости.  § 3. Некоторые виды алгебраических уравнений 2. Двучленные уравнения. 3. Корни из единицы и построение правильных многоугольников. 4. Трехчленные уравнения. § 4. Основная теорема алгебры многочленов и ее следствия 2. Многочлены с действительными коэффициентами. 4. Краткие исторические сведения. Глава VI. ЦЕПНЫЕ ДРОБИ § 1. Конечные цепные дроби 2. Пример цепной дроби. 3. Определение цепной дроби. 4. Представление рациональных чисел в виде конечной цепной дроби. 5. Подходящие дроби. 6. Свойства подходящих дробей. 8. Подходящие дроби и календарь. 9. Приближение цепной дроби подходящими дробями. § 2. Бесконечные цепные дроби 2. Подходящие дроби и наилучшие приближения иррациональных чисел рациональными. 3. Цепные дроби как вычислительный инструмент. 4. Краткие исторические сведения. Глава VII. КОМБИНАТОРИКА § 1. Комбинаторные задачи § 2.  Комбинаторные задачи. Продолжение Комбинаторные задачи. Продолжение§ 3. Определения и формулы § 4. Соединения с повторениями § 5. Комбинаторные задачи. Окончание § 6. Бином Ньютона и его обобщения § 7. Краткие исторические сведения Глава VIII. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ § 2. Сложные вероятности. Теоремы сложения и умножения. Условные вероятности § 3. Примеры вычисления вероятностей § 4. Полная вероятность. Формула Байеса § 5. Повторение испытаний § 6. Примеры вычисления вероятностей. Окончание § 7. Краткие исторические сведения |
Конспект урока на тему: «Отображение множеств» 2 класс | План-конспект урока по информатике (2 класс) по теме:
Тема: «Отображение множеств»
Тип урока: изучение нового материала.
Цель урока: Ввести понятие “отображение множеств” в практической деятельности.
Планируемые результаты:
Личностные: стремиться к получению новых знаний, совершенствовать свои умения, прилагать волевые усилия в ходе решения учебной задачи; контролировать и оценивать свою работу и её результат.
Предметные: Учить устанавливать соответствие между элементами двух множеств: Развивать интеллектуальные способности учащихся.
Оборудование: Учебник «Информатика в играх и задачах», 4 класс, часть 2, автор Горячев А.В.; мультимедийный проектор, интерактивная доска, презентация.
№ | Этапы урока методы и приемы | Содержание урока | Деятельность учащихся | УУД |
1. | Орг. момент словесный метод | Здравствуйте. Меня зовут Арина Игоревна. И сегодня я проведу у вас урок информатики. В жизни много интересного, Но пока нам неизвестного. Будем думать и решать! И о многом узнавать. — Ребята, а как вы понимаете, данное высказывание? (Ответы детей. — Ребята, в жизни есть много чего интересного, но неизвестного для нас, и мы постепенно начинаем узнавать, запоминать, ведь в будущем это все нам пригодиться. И даже самые великие открытия начинаются с самых маленьких знаний. -Поэтому мы сегодня с вами должны хорошо постараться и для себя узнать что-то новое. | Настраивать себя на работу | Л: воспринимать речь учителя непосредственно обращенную к учащимся; формирование желания выполнять учебные действия |
2. | Актуализация знаний метод: репродуктивный; проверка д/з. | — Ребята, а какая у вас была тема на прошлом уроке? — Вспомните, что называется множеством? (Объединение предметов (элементов) на основе каких-то общих свойств или признаков.) (элементы, связанные одними признаками) -Как называются предметы, которые входят, в какое- либо множество? (Элементы множеств. — Что нужно сделать, чтобы задать множество? (Перечислить его элементы). — Кто мне скажет какое Д/З вам было задано. Правильно №30 на стр.13. — Начинаем проверять, кто как сделал. Что от вас требовалось в данном задании? (Нарисовать множество из 3 овощей и рядом нарисовать равное ему множество.) — Кто желает выйти и показать, как он справился с заданием? — Молодцы справились с домашним заданием! — А сейчас внимательно послушайте загадку. Бела баба успевает Весь свет одевает. (Зима) — Ребята, а какие слова у вас ассоциируются с отгадкой? (Снег, метель, горка и т.д.) — В какие игры играют зимой? (Хоккей, снежки и т.д.) — А сейчас давайте возьмём санки и отправимся на прогулку. — Давайте откроем тетради с.14 и найдем № 31. — Давайте прочитаем задание (Спрашиваю 1-го) — Что от нас требуется в задание? (Ответы детей.) -Попробуйте раздать детям санки. (Раздать детям санки.) — Что для этого будите делать? (Дорисовать верёвочки от санок к детям). — Ребята, посмотрите, как выполнено задание на доске. Вы согласны? — Ребята то, что мы сейчас с вами выполняли практически, можно отобразить в схеме. — Рассмотрите схему. (На слайде вывешивается схема).
— Что обозначают точки в кружочке слева? (Кол-во санок.) — Почему справа тоже 3 точки? (Потому что детей 3.) — Что обозначают данные стрелки? — Какое множество больше санок или детей? (Одинаково.) -А мы можем по схеме сказать какие санки у детей? (со пинкой, простые.) -А что мы по схеме может сказать? Какой мы можем сделать вывод: Каждому элементу одного множества соответствует элемент другого множества. — Как вы думаете, какая тема урока будет? (Отображение множеств.) — Если наша тема отображение множеств значит, какую мы поставим с вами цель? (Научиться отображать множества.) | Повторять материал пройденной ранее темы ; Проверять правильность выполнения задания сверяя с эталоном; | К: высказывать свое мнение при обсуждении задания П: применять базовые знания для решения конкретной проблемы Р: контроль и самоконтроль учебных действий |
3. | Мотивационный этап Постановка учебной задачи фронтальная беседа; | — Как вы думаете, какая тема урока будет? (Отображение множеств.) — Если наша тема отображение множеств значит, какую мы поставим с вами цель? (Научиться отображать множества.) Что значит отобразить множество? 1. Необходимы 2 множества. 2. От одного элемента множества проводим стрелочку к элементу другого множества. 3. Все это удобно сделать на схеме. — Посмотрите на №32, рядом с горкой в лесу живут козлята, которые проголодались, давайте накормим их. — Чтобы легче козлятам было найти свою капусту, давайте нарисуем от каждого козленка дорожку к своей капусте. (Вызывать 1-го ученика.) -А теперь попробуйте отобразить это на схеме самостоятельно. (1 ребенка к доске.) — Ребята, чтобы узнать тему нашего сегодняшнего урока мы должны немного с вами подумать. — А вот рядом с которые еще и проголодались, давайте накормим их. Давайте им поможем. Чтобы легче им было найти свою капуту, нарисуем к каждому — дорожку. (Выслушиваем варианты детей, при необходимости дополняем их вопросами) -А теперь, давайте попробуем отобразить это на схеме. (Одного ученика к доске, все остальные выполняют самостоятельно.) — Сравните свою схему, со схемами на доске. — Что вы можете сказать о соответствии между элементами двух множеств? ВЫВОД: Не каждому элементу одного множества, соответствует элемент другого множества. | Воспринимать информацию сообщаемую учителем; обобщать информацию, | П: понимать заданный вопрос, в соответствии с ним строить ответ в устной форме |
4. | Постановка учебной задачи. Решения частных задач. методы: репродуктивный, беседа, наглядный практический, комментирование у доски | — Посмотрите внимательно на рисунок в № 33. -Давайте внимательно рассмотрим и отобразим на схеме, как расселились вороны. — Кто желает пойти к доске и выполнить задание? Все остальные сами, молча выполняют задание. — Ребята, сравните свою схему со схемой на доске. Что вы можете сказать о соответствии между элементами двух множеств? — Вывод: Не каждому элементу одного множества, соответствует элемент другого множества. — Переходим к №34, прочитайте задание. Что нам нужно сделать? (Ответы детей.) — Правильно, нам нужно раздать детям шарики с помощью схемы. Самостоятельно выполняем задание. — Давайте проверим, сколько шариков получил каждый ребенок? — Какое соответствие между элементами 2-х множеств? — А теперь, после игры с шариками Таня с Сашей отправились в библиотеку.0ни очень любят читать книги. Как говорится в пословице: “Делу время, а потехе — час”. Рассмотрите внимательно рисунок на с. — Отобразите на схеме данные элементы множеств и покажите их соответствие (самостоятельно работают в тетрадях). Таня- 1, Саша-4; Таня-2, Саша-3; Таня-3, Саша-2; Таня-4, Саша-1. — Найдите все №39, прочитайте задание про себя. Что нам нужно сделать в этом задание? (Ответы детей.) | выходить к доске; для выполнения задания; проводить сверку с решением учащихся у доски; отвечать на вопросы; проверять правильность выполнения задания. | Р: контроль и самоконтроль учебных действий П: применять базовые знания для решения конкретной проблемы П: выбор наиболее эффективных способов решения задач в зависимости от конкретных условий Л: строить логическую цепь рассуждений |
5. 6. | Рефлексия теоретической части Физкультминутка | — Давайте подведём с вами итоги. — Какую тему мы сегодня с вами изучали? — Кто может сказать, какую цель мы поставили в начале урока? — Мы достигли ее? — Что такое что такое множество? — Откройте дневники и запишите: д/з стр. 17, №40. Этот пальчик – дедушка, Этот пальчик – бабушка, Этот пальчик – папочка, Этот пальчик – мамочка, Этот пальчик – я, Вот и вся моя семья! (Дети поочерёдно сгибают пальцы, начиная с большого, одновременно на обеих руках. — Элементы, какого множества вы называли? (Семья) — Перечислите эти элементы. (Дедушка, бабушка, папочка, мамочка, я). | Подводить итоги, отвечать на поставленные вопросы учителя. Понимать и записывать д/з. Выполняют упражнения | |
7. | Мотивационный этап Постановка учебной задачи
побуждающий диалог; | — Сегодня мы с вами поработаем в Русландии. — Рассаживайтесь за компьютеры. Откройте программу 2 год обучения. Дальше идем по стрелки вниз, находим Русландия, -первым вашим заданием будет вставить пропущенную букву в словарные слова. Если все успели, стрелка вернуться «игры со словами». Здесь вам нужно выбрать противоположное слово.
| Слушать инструкцию учителя. | П: применять базовые знания для решения конкретной проблемы П: выбор наиболее эффективных способов решения задач в зависимости от конкретных условий Р: самостоятельно планировать и выполнять свои действия на знакомом учебном материале |
8. | Разминка для глаз | Закройте программу и сядьте за парты. И давайте сделаем гимнастику для глаз. | Выполнять упражнения; | |
9. | Рефлексия деятельности. Выставление оценок. методы анализа; фронтальный опрос. | Чему мы научились работая за компьютером? | Подводить итоги урока, анализировать свою деятельность на предмет достижения целей урока; прощаются с учителем. | Р: анализировать работу; отслеживать цель учебной д-ти П: осознанное и произвольное построение речевого выяснения в устной форме |
элементарная теория множеств — Что такое отображение множеств?
спросил
Изменено 1 год, 10 месяцев назад
Просмотрено 8к раз
$\begingroup$
Короткий вопрос, что такое отображение множества? Мне трудно использовать набор в качестве аргумента. В данный момент я борюсь с теорией меры, и примером является функция 9{-1}(B) = \{s \in S; f(s) \in B \}$ with $B \subset T$
Если бы кто-нибудь мог это объяснить.
Спасибо.
- элементарная теория множеств
$\endgroup$
$\begingroup$
Пусть $S$ и $T$ — множества, а $f:S\to T$ — функция.
У нас есть наборы мощности $\mathcal{P}(S)$ и $\mathcal{P}(T)$.
Функция $f$ индуцирует/определяет функцию $\mathcal{P}(S)\to\mathcal{P}(T)$, которая задается: $$A\mapsto\{f(x)\mid x \in A\}$$ Результат сокращен $f(A)$, поэтому мы имеем: $$A\mapsto f(A)$$ 9{-1}(B)$$
Осторожно: мы , а не имеем дело с любым обратным отображением $f$, как следует из обозначений.
$\endgroup$$\begingroup$
Отображение набора — это отображение между наборами. Это несет на удивление мало информации само по себе.
Функция $f: S \longrightarrow T$ — это способ сопоставить каждому $s$ в $S$ некоторый $t$ в $T$. $t$, связанный с $s$, обычно обозначается как $f(s)$.
С другой стороны, функция $f: S \longrightarrow T$ является частным отношением, т.е. набором упорядоченных пар $(s, t)$ с $s$ в $S$ и $t$ в $T$, с свойство, состоящее в том, что существует ровно одна упорядоченная пара, содержащая $s$ для каждого $s$ в $S$. 9{-1} 0$? И это в точности четные числа.
9{-1} 0$? И это в точности четные числа.
$\endgroup$
1
$\begingroup$
Вместо того, чтобы смотреть на обратную функцию, проще сначала посмотреть на функцию $f$ и разобраться в отображении множеств. Тогда функция набора $B$ представляет собой набор всех элементов, попадающих в поле, когда элементы в $B$ отображаются с помощью $f$, или, другими словами, это диапазон функции, ограниченный конкретным набором. 9{-1}([0,4]) = [-2,2] $, так как все элементы в интервале $[-2,2]$ отображаются в интервале $[0,4]$, а это единственные элементы, которые отображаются там.
$\endgroup$
1
мягкий вопрос — Есть ли разница между отображением и функцией?
спросил
Изменено 3 года, 10 месяцев назад
Просмотрено 58 тысяч раз
$\begingroup$
Интересно, есть ли разница между отображением и функцией? Кто-то сказал мне, что единственная разница в том, что отображение может быть из любого набора в любой набор, но функция должна быть из $\mathbb R$ в $\mathbb R$. Но я не согласен с этим ответом. Мне нужен простой способ объяснить различия между отображением и функцией неспециалисту вместе с некоторой иллюстрацией (если возможно).
Но я не согласен с этим ответом. Мне нужен простой способ объяснить различия между отображением и функцией неспециалисту вместе с некоторой иллюстрацией (если возможно).
Спасибо за любую помощь.
- мягкий вопрос
- терминология
$\endgroup$
1
$\begingroup$
Боюсь, человек, который сказал вам это, был неправ. Нет никакой разницы между отображением и функцией, это просто разные термины, используемые для одного и того же математического объекта. Как правило, я говорю «отображение», когда хочу подчеркнуть, что я говорю о соединении элементов одного набора с элементами другого набора, и «функция», когда я хочу подчеркнуть, что то, о чем я говорю, принимает входные данные и возвращает выходные данные. . Но это всего лишь личное предпочтение, и я не знаю никаких соглашений.
$\endgroup$
6
$\begingroup$
Хотя в большинстве случаев слова «функция» и «отображение» могут использоваться взаимозаменяемо, в некоторых разделах математики акценты различаются, особенно в анализе и дифференциальной геометрии. n$, не будет называться функцией. Это соглашение не всегда соблюдается (иногда вы можете прочитать о «векторнозначных функциях»), но это обычная интерпретация. 9p$ «функции», хотя на самом деле они являются классами эквивалентности отображений. Опять же, идея состоит в том, что функции должны присваивать номера некоторым объектам (например, точкам в некотором пространстве) в подходящем смысле. Таким образом, функции считаются объектами, изучаемыми в анализе, тогда как «отображение» считается термином из теории множеств.
n$, не будет называться функцией. Это соглашение не всегда соблюдается (иногда вы можете прочитать о «векторнозначных функциях»), но это обычная интерпретация. 9p$ «функции», хотя на самом деле они являются классами эквивалентности отображений. Опять же, идея состоит в том, что функции должны присваивать номера некоторым объектам (например, точкам в некотором пространстве) в подходящем смысле. Таким образом, функции считаются объектами, изучаемыми в анализе, тогда как «отображение» считается термином из теории множеств.
$\endgroup$
3
$\begingroup$
Для меня функция и карта означают две совершенно разные вещи. Функция — это просто теоретико-множественная конструкция, нечто, что сопоставляет каждому объекту в наборе какой-то уникальный объект из другого набора. Карта, с другой стороны, является построением из теория категорий , а не теория множеств . Это означает более или менее то же самое, что и морфизм : функция, которая сохраняет структуру в любой категории, с которой мы работаем. Таким образом, карта — это не просто карта, это карта чего-то:
Это означает более или менее то же самое, что и морфизм : функция, которая сохраняет структуру в любой категории, с которой мы работаем. Таким образом, карта — это не просто карта, это карта чего-то:
- Карта групп или кольца является гомоморфизмом
- Карта векторных пространств является линейной функцией
- Карта топологических пространств является непрерывной функцией
- Карта гладких многообразий является гладкой функцией
- Карта измеримых пространств есть измеримая функция
- Карта многообразий является морфизмом
- Картой множеств является любая функция
Обратите внимание, что здесь я намеренно избегаю термина «карта» в предикатах. Это связано с тем, что части «карты» таких терминов, как «непрерывная карта» и «линейная карта», на самом деле избыточны; линейная карта — это просто карта (векторных пространств), а непрерывная карта — это просто карта (топологических пространств). Следовательно, я избегаю многих из этих избыточных терминов и просто говорю: «Пусть $f\colon X\to Y$ будет отображением», когда из контекста ясно, какую категорию я в настоящее время считаю объектами $X$ и $Y$. из. Мне особенно приятно избегать длинного и сложного термина «гомоморфизм». 9p$ классов эквивалентности функций) словом «функция», даже если они измеримы и, следовательно, могут рассматриваться как карты измеримых пространств. Точно так же я бы в основном называл элементы колец многочленов или координатных колец «функциями», если только меня не интересует какая-то структура, которую они сохраняют.
из. Мне особенно приятно избегать длинного и сложного термина «гомоморфизм». 9p$ классов эквивалентности функций) словом «функция», даже если они измеримы и, следовательно, могут рассматриваться как карты измеримых пространств. Точно так же я бы в основном называл элементы колец многочленов или координатных колец «функциями», если только меня не интересует какая-то структура, которую они сохраняют.
Итак, резюмируем: карта — это функция, сохраняющая некоторую структуру, а именно структуру той категории, с которой мы работаем. карта наборов. (Обратите внимание, однако, что я хорошо знаю, что не все люди следуют этому соглашению.)
$\endgroup$
1
$\begingroup$
Не такая уж большая разница в долгосрочной перспективе. Когда я использую слово «функция», я обычно имею в виду, что точка отображается в одну точку. Итак, если точка может отображаться в несколько точек, я не буду использовать это слово, скорее отображение или преобразование.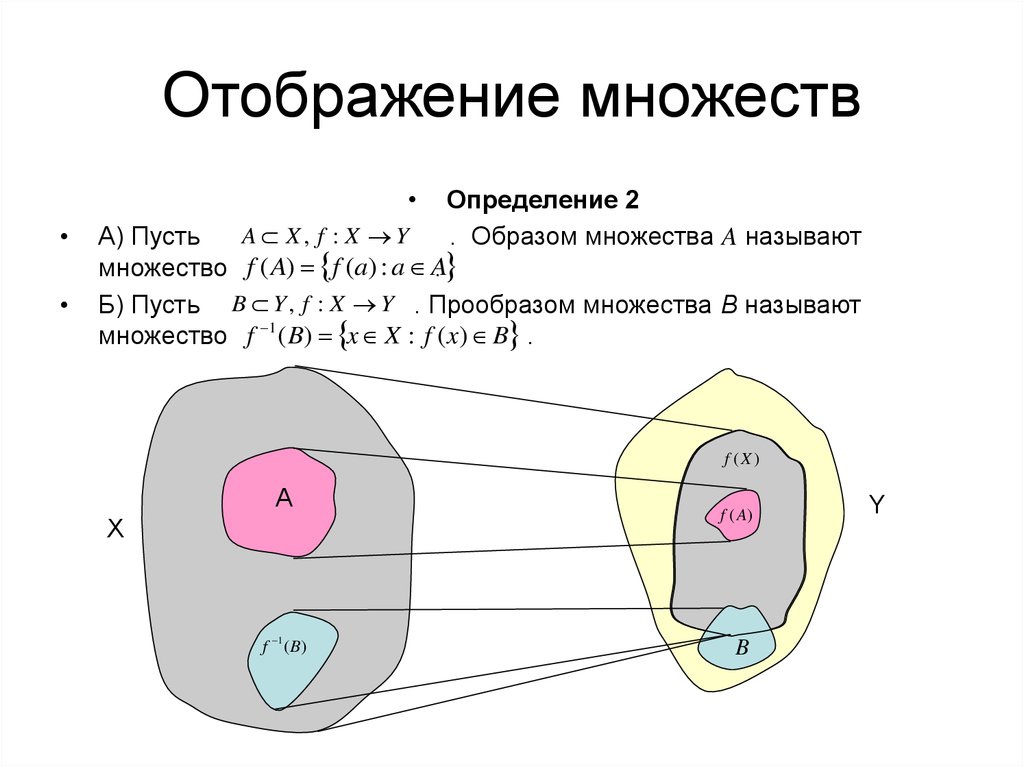 В недавней статье у меня была одна из них, каждая точка шла к нескольким точкам, и каждая точка на изображении, вероятно, имела несколько прообразов, поэтому я подчеркнул, используя традиционную фразу, что отображение было «многие ко многим». » Теперь и праймаж, и образ были классами эквивалентности при более слабой эквивалентности, поэтому отображение действительно индуцировало функцию из «рода» в «род», но не было четко определено на уровне классов изометрии квадратичных форм. 9n$ практически из чего угодно, но с меньшей вероятностью будет использовать функцию для отображения между двумя другими многообразиями. Различные виды отображений в алгебре вряд ли можно назвать функциями.
В недавней статье у меня была одна из них, каждая точка шла к нескольким точкам, и каждая точка на изображении, вероятно, имела несколько прообразов, поэтому я подчеркнул, используя традиционную фразу, что отображение было «многие ко многим». » Теперь и праймаж, и образ были классами эквивалентности при более слабой эквивалентности, поэтому отображение действительно индуцировало функцию из «рода» в «род», но не было четко определено на уровне классов изометрии квадратичных форм. 9n$ практически из чего угодно, но с меньшей вероятностью будет использовать функцию для отображения между двумя другими многообразиями. Различные виды отображений в алгебре вряд ли можно назвать функциями.
$\endgroup$
3
$\begingroup$
Джон М. Ли, Введение в гладкие многообразия, 2002:
Хотя термины функция и отображают технически синонимы, при изучении
гладкие многообразия часто удобно проводить между ними небольшое различие. В этой книге мы обычно оставляем за собой термин 9k$ для некоторого $k > 1$ ( вектор-функция ). Слово карта или отображение может означать карту любого типа, например карту между произвольными многообразиями.
В этой книге мы обычно оставляем за собой термин 9k$ для некоторого $k > 1$ ( вектор-функция ). Слово карта или отображение может означать карту любого типа, например карту между произвольными многообразиями.
$\endgroup$
$\begingroup$
Из P216 Mathematical Proofs by Gary Chartrand:
С помощью функции f из A в B, записанной f : A → B, мы означает отношение от A к B со свойством, что каждый элемент a в A является первым координата ровно одной упорядоченной пары в f. …
Если (a, b) ∈ f , то мы пишем b = f (a) и называем b образом a. Иногда f сказали отображать a в b. В самом деле, само f иногда называют отображением .
$\endgroup$
$\begingroup$
Автор Nii: Насколько я понимаю, отображение — это просто процесс сопоставления элементов одного набора с элементами другого набора.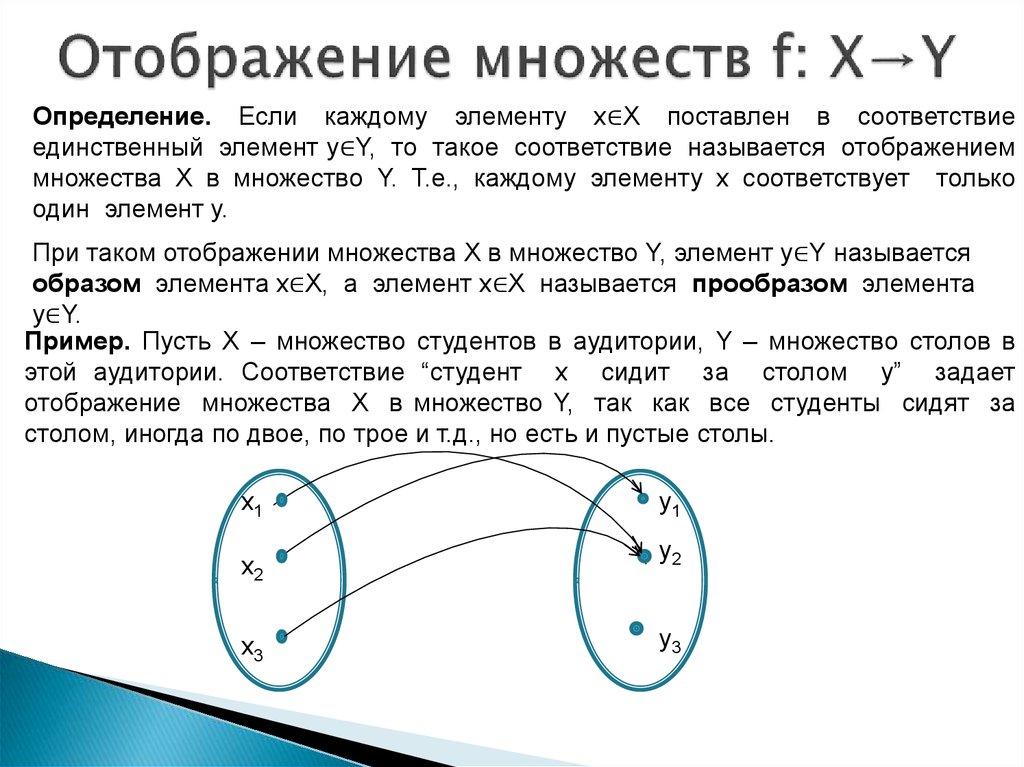

 )
) )
)

 С.14 №32
С.14 №32 Вороны не стали ждать, когда мы их расселим в домики, а сами уже выбрали удобное местечко на деревьях.
Вороны не стали ждать, когда мы их расселим в домики, а сами уже выбрали удобное местечко на деревьях. 16. № 36
16. № 36
 На последней строке – сжимают все пальцы вместе).
На последней строке – сжимают все пальцы вместе).