P прямоугольника: Как найти периметр прямоугольника, формула ⬅️

2

Прямоугольник. Формулы и свойства прямоугольника

Навигация по странице: Определение прямоугольника Основные свойства прямоугольника Стороны прямоугольника (длина и ширина прямоугольника) Диагональ прямоугольника Периметр прямоугольника Площадь прямоугольника Окружность описанная вокруг прямоугольника Угол между стороной и диагональю прямоугольника Угол между диагоналями прямоугольника

Определение.

Прямоугольник — это четырехугольник у которого две противоположные стороны равны и все четыре угла одинаковы.

Прямоугольники отличаются между собой только отношением длинной стороны к короткой, но все четыре угла у них прямые, то есть по 90 градусов.

Длинную сторону прямоугольника называют длиной прямоугольника, а короткую — шириной прямоугольника.

Стороны прямоугольника одновременно является его высотами.

Рис. 1		Рис.2

Основные свойства прямоугольника

Прямоугольником могут быть параллелограмм, квадрат или ромб.

1. Противоположные стороны прямоугольника имеют одинаковую длину, то есть они равны:

AB = CD,   BC = AD

2. Противоположные стороны прямоугольника параллельны:

AB||CD,   BC||AD

3. Прилегающие стороны прямоугольника всегда перпендикулярны:

AB _┴ BC,   BC _┴ CD,   CD _┴ AD,   AD _┴ AB

4. Все четыре угла прямоугольника прямые:

∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°

5. Сумма углов прямоугольника равна 360 градусов:

∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°

6. Диагонали прямоугольника имеют одинаковой длины:

AC = BD

7.

Сумма квадратов диагонали прямоугольника равны сумме квадратов сторон:

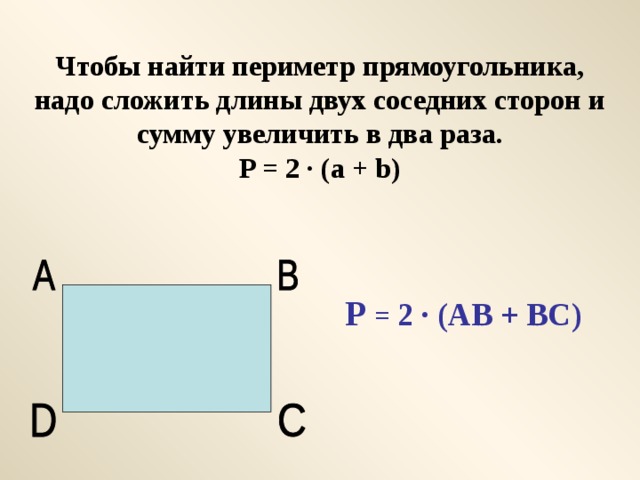
2d² = 2a² + 2b²

8. Каждая диагональ прямоугольника делит прямоугольник на две одинаковые фигуры, а именно на прямоугольные треугольники.

9. Диагонали прямоугольника пересекаются и в точке пересечения делятся пополам:

		AO = BO = CO = DO =	d
			2

10. Точка пересечения диагоналей называется центром прямоугольника и также является центром описанной окружности

11. Диагональ прямоугольника является диаметром описанной окружности

12. Вокруг прямоугольника всегда можно описать окружность, так как сумма противоположных углов равна 180 градусов:

∠ABC = ∠CDA = 180°   ∠BCD = ∠DAB = 180°

13. В прямоугольник, у которого длина не равна ширине, нельзя вписать окружность, так как суммы противоположных сторон не равны между собой (вписать окружность можно только в частный случай прямоугольника — квадрат).

Стороны прямоугольника

Определение.

Длиной прямоугольника называют длину более длинной пары его сторон. Шириной прямоугольника называют длину более короткой пары его сторон.

Формулы определения длин сторон прямоугольника

1. Формула стороны прямоугольника (длины и ширины прямоугольника) через диагональ и другую сторону:

a = √d² — b²

b = √d² — a²

2. Формула стороны прямоугольника (длины и ширины прямоугольника) через площадь и другую сторону:

a =	S
	b

b =	S
	a

3. Формула стороны прямоугольника (длины и ширины прямоугольника) через периметр и другую сторону:

a =	P — 2b
	2

b =	P — 2a
	2

4. Формула стороны прямоугольника (длины и ширины прямоугольника) через диаметр и угол α:

a = d sinα

b = d cosα

5. Формула стороны прямоугольника (длины и ширины прямоугольника) через диаметр и угол β:

a = d sin	β
	2

b = d cos	β
	2

Диагональ прямоугольника

Определение.

Диагональю прямоугольника называется любой отрезок соединяющий две вершины противоположных углов прямоугольника.

Формулы определения длины диагонали прямоугольника

1. Формула диагонали прямоугольника через две стороны прямоугольника (через теорему Пифагора):

d = √a² + b²

2. Формула диагонали прямоугольника через площадь и любую сторону:

d =	√S 2 + a4	=	√S2 + b4
	a		b

3.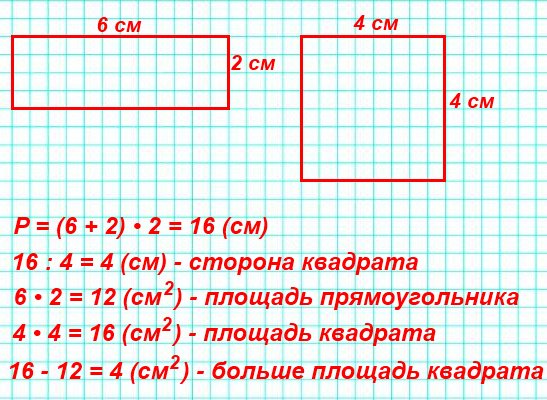 Формула диагонали прямоугольника через периметр и любую сторону:

d =	√P2 — 4Pa + 8a2	=	√P2 — 4Pb + 8b2
	2		2

4. Формула диагонали прямоугольника через радиус описанной окружности:

d = 2R

5. Формула диагонали прямоугольника через диаметр описанной окружности:

d = D_о

6. Формула диагонали прямоугольника через синус угла, прилегающего к диагонали, и длину стороны противоположной этому углу:

d =	a
	sin α

7. Формула диагонали прямоугольника через косинус угла, прилегающего к диагонали, и длину стороны прилегающей к этому углу:

d =	b
	cos α

8.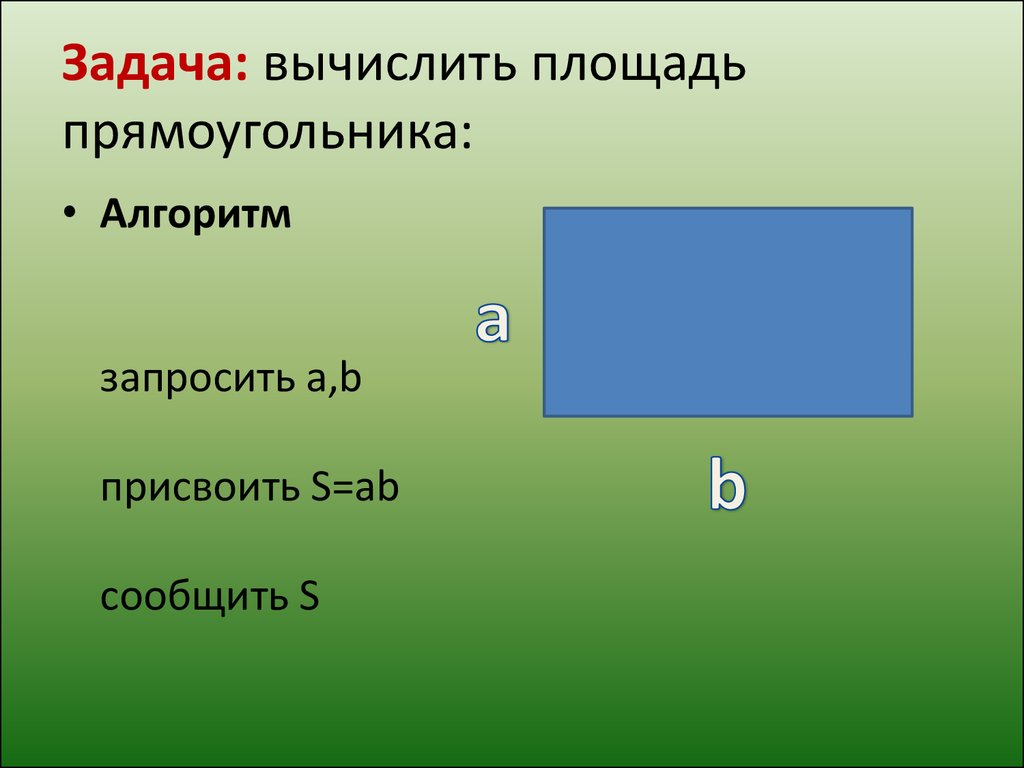 Формула диагонали прямоугольника через синус острого угла между диагоналями и площадью прямоугольника

d = √2S : sin β

Периметр прямоугольника

Определение.

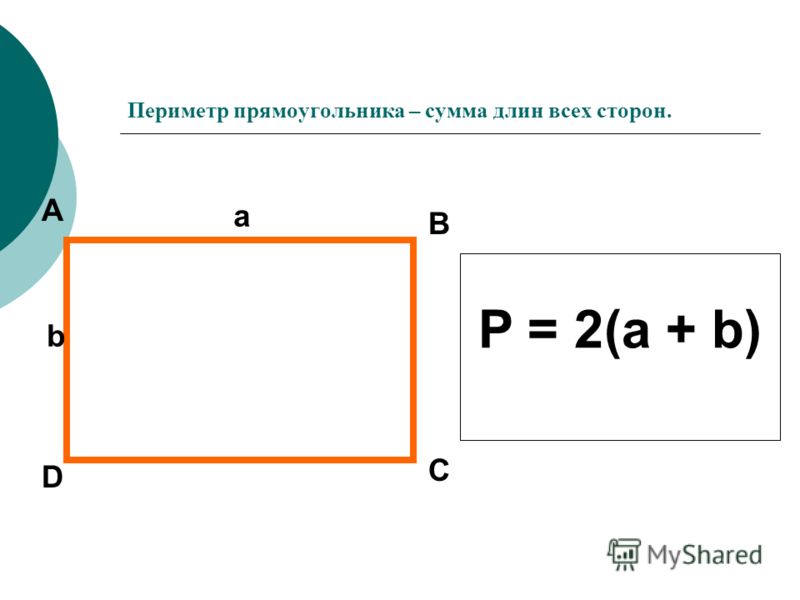
Периметром прямоугольника называется сумма длин всех сторон прямоугольника.

Формулы определения длины периметру прямоугольника

1. Формула периметру прямоугольника через две стороны прямоугольника:

P = 2a + 2b

P = 2(a + b)

2. Формула периметру прямоугольника через площадь и любую сторону:

P =	2S + 2a2	=	2S + 2b2
	a		b

3. Формула периметру прямоугольника через диагональ и любую сторону:

P = 2(a + √d² — a²) = 2(b + √d² — b²)

4. Формула периметру прямоугольника через радиус описанной окружности и любую сторону:

P = 2(a + √4R² — a²) = 2(b + √4R² — b²)

5. Формула периметру прямоугольника через диаметр описанной окружности и любую сторону:

P = 2(a + √D_o² — a²) = 2(b + √D_o² — b²)

Площадь прямоугольника

Определение.

Площадью прямоугольника называется пространство ограниченный сторонами прямоугольника, то есть в пределах периметра прямоугольника.

Формулы определения площади прямоугольника

1. Формула площади прямоугольника через две стороны:

S = a · b

2. Формула площади прямоугольника через периметр и любую сторону:

S =	Pa — 2a2	=	Pb — 2b 2
	2		2

3. Формула площади прямоугольника через диагональ и любую сторону:

S = a√d² — a² = b√d² — b²

4. Формула площади прямоугольника через диагональ и синус острого угла между диагоналями:

S =	d2 · sin β
	2

5. Формула площади прямоугольника через радиус описанной окружности и любую сторону:

S = a√4R² — a² = b√4R² — b²

6. Формула площади прямоугольника через диаметр описанной окружности и любую сторону:

S = a√D_o²

— a² = b√D_o² — b²

Окружность описанная вокруг прямоугольника

Определение.

Окружностью описанной вокруг прямоугольника называется круг проходящий через четыре вершины прямоугольника, центр которого лежит на пересечении диагоналей прямоугольника.

Формулы определения радиуса окружности описанной вокруг прямоугольника

1. Формула радиуса окружности описанной вокруг прямоугольника через две стороны:

R =	√a2 + b2
	2

2. Формула радиуса окружности описанной вокруг прямоугольника через периметр квадрата и любую сторону:

R =	√P2 — 4Pa + 8a2	=	√P2 — 4Pb + 8b2
	4		4

3. Формула радиуса окружности описанной вокруг прямоугольника через площадь квадрата:

R =	√S2 + a4	=	√S2 + b4
	2a		2b

4. Формула радиуса окружности описанной вокруг прямоугольника через диагональ квадрата:

R =	d
	2

5.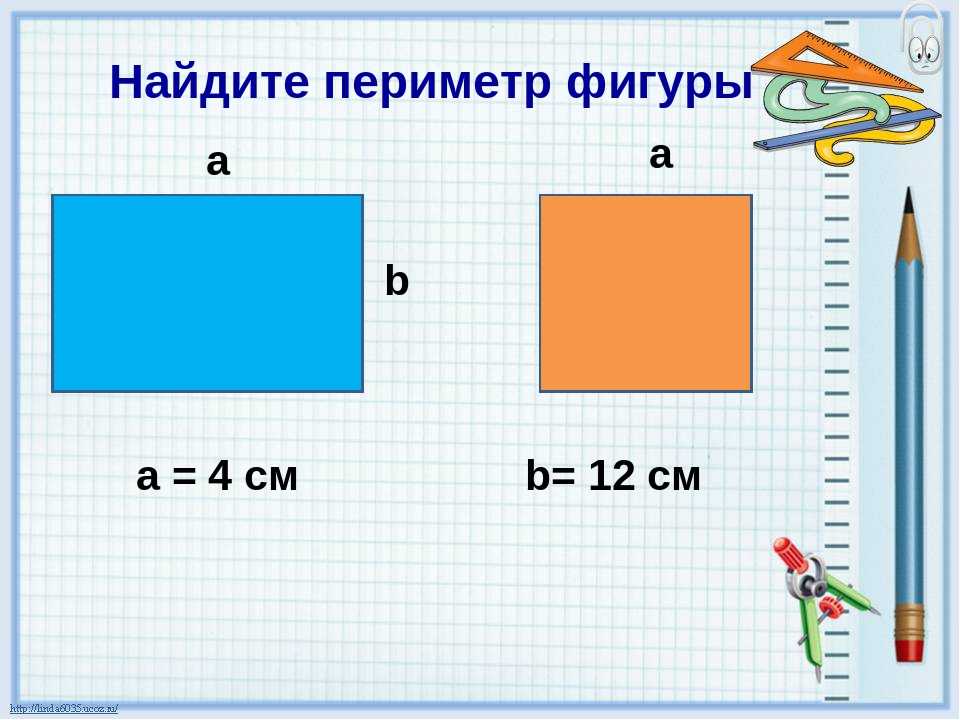 Формула радиуса окружности описанной вокруг прямоугольника через диаметр описанной окружности:

R =	Dо
	2

6. Формула радиуса окружности описанной вокруг прямоугольника через синус угла, прилегающего к диагонали, и длину стороны противоположной этому углу:

R =	a
	2sin α

7. Формула радиуса окружности описанной вокруг прямоугольника через косинус угла, прилегающего к диагонали, и длину стороны прилегающей к этому углу:

R =	b
	2cos α

8. Формула радиуса окружности описанной вокруг прямоугольника через синус острого угла между диагоналями и площадью прямоугольника:

R =	√2S : sin β
	2

Угол между стороной и диагональю прямоугольника

Формулы определения угла между стороной и диагональю

1. Формула определения угла между стороной и диагональю прямоугольника через диагональ и сторону:

sin α =	a
	d

cos α =	b
	d

2. Формула определения угла между стороной и диагональю прямоугольника через угол между диагоналями:

α =	β
	2

Угол между диагоналями прямоугольника

Формулы определения угла между диагоналями прямоугольника

1. Формула определения угла между диагоналями прямоугольника через угол между стороной и диагональю:

β = 2α

2. Формула определения угла между диагоналями прямоугольника через площадь и диагональ:

sin β =	2S
	d2

Формулы по геометрии Квадрат.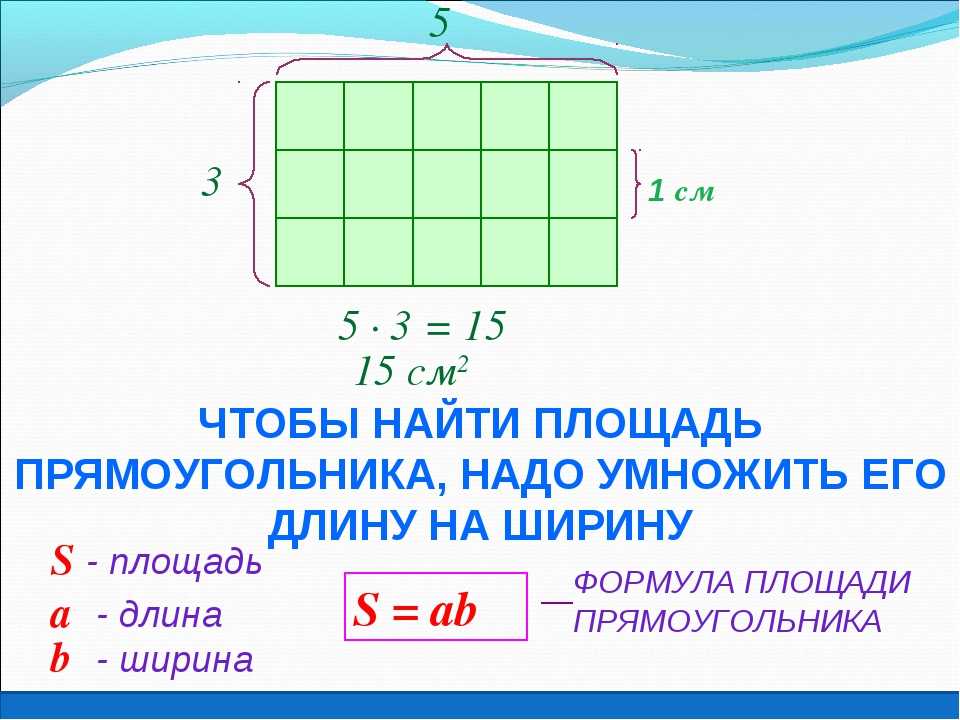 Формулы и свойства квадрата Прямоугольник. Формулы и свойства прямоугольника Параллелограмм. Формулы и свойства параллелограмма Ромб. Формулы и свойства ромба Трапеция. Формулы и свойства трапеции — Равнобедренная трапеция. Формулы и свойства равнобедренной трапеции — Прямоугольная трапеция. Формулы и свойства прямоугольной трапеции Формулы площади геометрических фигур Формулы периметра геометрических фигур Формулы объема геометрических фигур Формулы площади поверхности геометрических фигур

Все таблицы и формулы

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

дана формула для нахождения периметра p прямоугольника длины l и ширины w. какая формула показывает, как можно определить длину прямоугольника f

Алгебра 1

Бб Т.

спросил 28.12.15

Пожалуйста, помогите мне, я не понимаю. Возможные варианты:

A. L = p/2 — 2w

B. L = p — 2w/2

C. L = p/2 + w

D. L = p-2/2w

Подписаться І 3

Подробнее

Отчет

2 ответа от опытных наставников

Лучший Новейшие Самый старый

Автор: Лучшие новыеСамые старые

Артур Д. ответил 28.12.15

Репетитор

5,0 (148)

Сорокалетний педагог: Класс, Летняя школа, Заместитель, Репетитор

Об этом репетиторе ›

Об этом репетиторе ›

P=2l+2w

P-2w=2l

(P-2w)/2=l

B. это ответ, но он должен содержать скобки (  )

Голосовать за 0 голос против

Подробнее

Отчет

Джим Б. ответил 28.12.15

Репетитор

4,8 (111)

Опытный преподаватель и репетитор по математике и информатике

См. таких репетиторов

Смотрите таких репетиторов

Периметр прямоугольника равен сумме длин всех сторон  : p = L + L + w + w

 

Половина длины периметра равна p/2, что равно сумме L + ж.

 

, значит, p/2 = L + w 

 

Чтобы найти L, вычтите w из обеих частей, так что p/2 — w = L

 

, и если вы запишете уравнение с L в левой части, L = p/2 — w.

 

Вы будете часто сталкиваться с подобными задачами, используя любую формулу, которую вам придется решать для любой переменной.

 

По возможности нарисуйте рисунок. Для этого примера нарисуйте прямоугольник, затем посмотрите, как сумма длины и ширины будет равна половине периметра.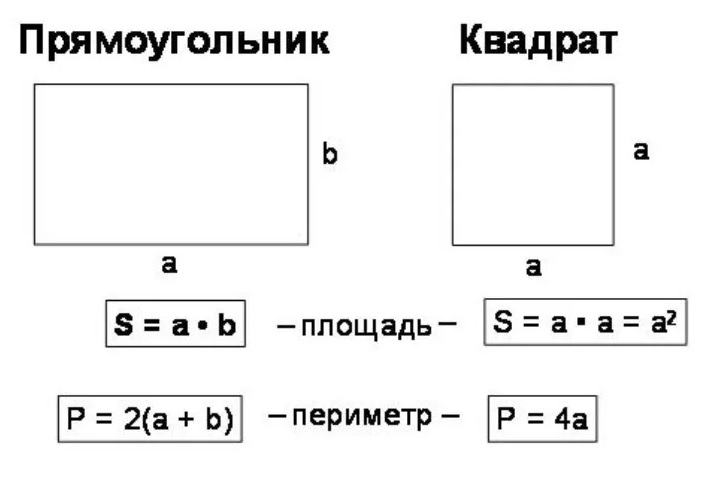

 

p = l + l + w + w

p = 2L + 2W после объединения, подобные условиям

2L = P — 2W

Теперь делят обе стороны на 2 — с обеих сторон

L = (p – 2w)/2    это может соответствовать варианту B, если в скобках указан вариант, не показанный выше.

 

Голосовать за 0 голос против

Еще

Отчет

Все еще ищете помощь? Получите правильный ответ, быстро.

Задайте вопрос бесплатно

Получите бесплатный ответ на быстрый вопрос.
Ответы на большинство вопросов в течение 4 часов.

ИЛИ

Найдите онлайн-репетитора сейчас

Выберите эксперта и встретьтесь онлайн. Никаких пакетов или подписок, платите только за то время, которое вам нужно.

Как рассчитать периметр прямоугольника

Чему равен периметр прямоугольника?

В математике вы встретите много разных форм и размеров, таких как квадраты, круги, многоугольники… и вам будет предложено вычислить их периметр или даже объем. Прямоугольник – это четырехугольник. Это форма, с которой вы будете часто сталкиваться, поэтому важно, чтобы вы знали, как рассчитать ее периметр и площадь.

Прямоугольник — это многоугольник с четырьмя сторонами. Все его углы прямые (90°), а противоположные параллельные стороны всегда имеют одинаковую длину. Периметр прямоугольника — это общая длина его фигуры, известная как сумма длин всех сторон прямоугольника. Это означает, что вам нужно сложить длины его сторон, чтобы найти его периметр.

Какова формула периметра?

Чтобы вычислить периметр, вам просто нужно сложить длины сторон прямоугольника. Поскольку параллельные стороны прямоугольника всегда равны, вам нужно только найти длину двух сторон, чтобы найти периметр прямоугольника.

Если мы предположим, что длина прямоугольника равна a, а ширина равна b. Формула для периметра P:

P = a+a+b+b

P = 2a+2b

P = 2(a+b)

Следовательно, формула для периметр прямоугольника умножен на 2 (сумма смежных сторон).

Как вычислить периметр прямоугольника?

Вот несколько примеров вычисления периметра прямоугольника:

• Пример 1

Длина и ширина прямоугольника 7 см и 3 см соответственно.

Периметр этого прямоугольника равен P = 7+7+3+3 = 2x(7+3)= 20 см

• Пример 2 

Одна сторона прямоугольника 12 см, а другая 5 см.

Мы знаем, что периметр прямоугольника равен P = 2x(сумма смежных сторон)

Следовательно, периметр этого прямоугольника равен P = 2x(12+5)= 34 см

• Пример 3 

Поле прямоугольной формы имеет длину 20 м и ширину 13 м.

Периметр этого поля равен P = 2x(20+13) = 66 м

В чем разница между площадью и периметром?

Периметр — это расстояние вокруг двумерной фигуры, тогда как площадь — это измерение пространства внутри фигуры. Площадь — это двухмерное понятие, которое измеряется квадратными метрами ². Это количество двухмерного пространства, которое занимает фигура.

Например, площадь прямоугольника — это площадь поверхности, ограниченная сторонами прямоугольника. Чтобы найти площадь прямоугольника, нужно длину прямоугольника умножить на ширину.

Если мы предположим, что длина прямоугольника равна а, а ширина равна b. Формула площади A:

A = a x b

Нужна помощь в математике?

Математика может быть действительно сложным предметом для многих учащихся, будь то начальная школа, начальная или даже средняя школа. Если вы когда-нибудь сталкивались с трудностями при выполнении уроков математики и выполнении домашних заданий, решения Tutorax для репетиторства помогут вам.