Парабола 2 x: Найдите,при каком значении а график функции y=x^2-ax+3 имеет единственную точку с прямой y=2x-1

2+6x-7\). Рассчитаем вершины : \(x_1=\frac{-2}{2*1}=-1\)  и \(x_2=\frac{-6}{-2*1}=3.\) Свободный член \(3\) и \(-7\) означает пересечение с осью \(y\), то есть сдвиг графика по оси  \(OY.\)

 

Коэфиицент \(b\)  означает симметричность  относительно оси \(OY.\)  Если \(b=0\), то веришна лежит оси \(OY.\)

 

 

Парабола  с греческого относится к конкретной плоской Кривой. Слово parabolh означает «сравнение», буквально » бросание рядом. 

Применение параболы 

Радиоволны часто должна быть сконцентрирована в одной точке например, радиотелескопы, платные телевизионные тарелки, солнечные коллекторы.

Излучение должно передаваться из одной точки в широкий параллельный луч (например, отражатели фар).

Параллельные радиоволны собираются параболической антенной. Параллельные лучи отражаются от антенны и встречаются в точке F, называемой фокусом.

 

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа».

Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Оксана Николаевна Хаустова

Репетитор по математике

Стаж (лет)

Образование:

Саратовский государственный университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Амаяк Варданович Варданян

Репетитор по математике

Стаж (лет)

Образование:

Российский университет дружбы народов

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Антон Евгеньевич Кукьян

Репетитор по математике

Стаж (лет)

Образование:

Белорусский государственный университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Предметы

• Математика
• Репетитор по физике
• Репетитор по химии
• Репетитор по русскому языку
• Репетитор по английскому языку
• Репетитор по обществознанию
• Репетитор по истории России
• Репетитор по биологии
• Репетитор по географии
• Репетитор по информатике

Специализации

• Репетитор по геометрии
• Репетитор по алгебре
• Подготовка к олимпиадам по химии
• Репетитор по русскому языку для подготовки к ЕГЭ
• Репетитор по английскому языку для подготовки к ОГЭ
• Репетитор по грамматике английского языка
• ВПР по математике
• Репетитор для подготовки к ОГЭ по обществознанию
• Репетитор по биологии для подготовки к ОГЭ
• Репетитор по географии для подготовки к ЕГЭ

Похожие статьи

• Жизни математиков (часть 2)
• Площадь параллелограмма
• Свойства логарифма
• Движение в одном направлении
• Выпускной-2021: актуальные образы для 9-классников
• Разрешать ли ребенку красить волосы
• Как перестать программировать детей на бедность?
• Как обустроить комнату для школьника?

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Текст с ошибкой:

Расскажите, что не так

01Математика — Профиль — Пересечение прямая/корень и парабола/парабола

По условию задачи рафики функций \(\displaystyle f\left(x\right)=a\sqrt{x} \) и \(\displaystyle g\left(x\right)=kx+b\) пересекаются в точке \(\displaystyle A{\small . }\) Самой точки \(\displaystyle A\) на рисунке не видно.

1. Найдем коэффициент \(\displaystyle a\) из уравнения функции \(\displaystyle f\left(x\right)=a\sqrt{x}{ \small .}\)

Заметим, что на графике функции \(\displaystyle f\left(x\right)=a\sqrt{x}\) отмечена точка с координатами \(\displaystyle (\color{blue}{4};\color{green}{5}){ \small .}\)

Значит, при подстановке её  координат \(\displaystyle x=\color{blue}4\) и \(\displaystyle y=\color{green}5\) в уравнение \(\displaystyle y=a \sqrt{x}\) получим верное равенство.

Подставляя, получаем уравнение:

\(\displaystyle \color{green}5=a\cdot \sqrt{\color{blue}4}{ \small ,} \)

\(\displaystyle 5=a \cdot 2{ \small ,} \)

откуда

\(\displaystyle a=2{,}5{ \small .}\)

Таким образом, исходная функция имеет вид:

\(\displaystyle f\left(x\right)=2{,}5\sqrt{x} \small.\)

2. Найдем коэффициенты \(\displaystyle k\) и \(\displaystyle b\) из уравнения прямой \(\displaystyle g\left(x\right)=kx+b{ \small . }\)

По рисунку видим, что точки \(\displaystyle С\) c координатами \(\displaystyle (2;-2)\) и \(\displaystyle D\) c координатами \(\displaystyle (4;-1)\) принадлежат графику функции \(\displaystyle g\left(x\right)=kx+b{ \small .}\)

 

Подставим координаты точек \(\displaystyle C(2;\,-2)\) и \(\displaystyle D(4;-1)\) в уравнение прямой \(\displaystyle y=kx+b\,{\small . } \)

Точка \(\displaystyle C(\color{blue}{ 2};\color{green}{-2}) \) имеет координаты \(\displaystyle x=\color{blue}{ 2}\) и \(\displaystyle y=\color{green}{ -2}{\small , }\) поэтому

\(\displaystyle \color{green}{-2}=k\cdot \color{blue}{ 2}+b \)
или, что то же самое,
\(\displaystyle 2k+b=-2{\small . }\)

Точка \(\displaystyle D(\color{blue}{ 4};\color{green}{ -1}) \) имеет координаты \(\displaystyle x=\color{blue}{ 4}\) и \(\displaystyle y=\color{green}{ -1}{\small , }\) поэтому

\(\displaystyle \color{green}{ -1}=k\cdot \color{blue}{ 4}+b {\small , }\)
или, что то же самое,
\(\displaystyle 4 k+b=-1{\small . } \)

Мы получили два уравнения для коэффициентов \(\displaystyle k \) и \(\displaystyle b {\small . }\) Запишем систему уравнений:

\(\displaystyle \left\{\begin{aligned}2k+b&=-2{\small , }\\4k+b&=-1{\small . }\end{aligned}\right.\)

Решим эту систему.

Решение системы

Таким образом, \(\displaystyle k=0{,}5 \) и \(\displaystyle b=-3{\small . } \)

Подставляя найденные значения для \(\displaystyle k \) и \(\displaystyle b \) в уравнение прямой \(\displaystyle y=kx+b{\small , } \) получаем:

\(\displaystyle y=0{,}5x-3{\small . } \)

3. Найдем абсциссу точки \(\displaystyle A{ \small .}\)

Точка \(\displaystyle A\) – это точка пересечения графиков функций \(\displaystyle f\left(x\right)=2{,}5\sqrt{x}\) и \(\displaystyle g\left(x\right)=0{,}5x-3{\small . }\) Значит, её координаты удовлетворяют уравнениям обеих функций:

\(\displaystyle \left\{\begin{aligned}y&=2{,}5\sqrt{x}{ \small ,}\\y&=0{,}5x-3{ \small . 2-37x+36=0{\small.}\)

Корень \(\displaystyle x=1\) не удовлетворяет неравенству \(\displaystyle x\ge6{ \small .}\)

Корень \(\displaystyle x=36\) удовлетворяет неравенству \(\displaystyle x\ge6{ \small .}\)

Значит, решением иррационального уравнения \(\displaystyle 5\sqrt{x}=x-6\) является  \(\displaystyle x=36{ \small .}\)

Таким образом, абсцисса точки \(\displaystyle A\) равна \(\displaystyle 36{\small.}\)

Ответ: \(\displaystyle 36{\small.}\)

2-20*x-(-49)=0

Пошаговое решение :

Шаг 1 :

Уравнение в конце шага 1 :

 (2x  2  - 20x) - -49 = 0
 

Шаг 2 :

Попытка разложения путем разделения среднего члена

Средний член равен -20x, его коэффициент равен -20.
Последний член, «константа», равен +49.

Шаг-1: Умножьте коэффициент первого члена на константу   2 • 49 = 98 

Шаг-2: Найдите два множителя 98, сумма которых равна коэффициенту среднего члена, который равен -20.

. 0041

	-98	+	-1	=	-99
	-49	+	-2	=	-51
	-14	+	-7	=	-21
	-7	+	-14	=	-21
	-2	+	-49	=	-51
	-1	+	-98	=	-99
	1	+	98	=	99
	2	+	49	=	51
	7	+	14	=	21
	14	+	7	=	+	7	=	+	7	=	+	7	=	+	7	=	21
	49	+	2	=	51
	98	+	1	=	99

Наблюдение: Невозможно найти два таких фактора!!
Вывод: Трехчлен нельзя разложить на множители

Уравнение в конце шага 2 :

 2x  2  - 20x + 49= 0
 

Шаг 3 :

Парабола, поиск вершины :

 3.1      Найдите вершину   y = 2x ² -20x+49

Параболы имеют наивысшую или низшую точку, называемую вершиной. Наша парабола раскрывается и, соответственно, имеет низшую точку (абсолютный минимум). Мы знаем это еще до того, как начертили «у», потому что коэффициент первого члена, 2 , положителен (больше нуля).

 Каждая парабола имеет вертикальную линию симметрии, проходящую через ее вершину. Из-за этой симметрии линия симметрии, например, будет проходить через середину двух точек пересечения x (корней или решений) параболы. То есть, если парабола действительно имеет два действительных решения.

 Параболы могут моделировать многие реальные жизненные ситуации, такие как высота над землей объекта, брошенного вверх через некоторый период времени. Вершина параболы может предоставить нам такую ​​информацию, как максимальная высота, на которую может подняться объект, брошенный вверх. По этой причине мы хотим иметь возможность найти координаты вершины.

 Для любой параболы, Ax ² +Bx+C, x-координата вершины определяется как -B/(2A) . В нашем случае координата x равна   5,0000  

Подключение к формуле параболы 5.0000 Для x Мы можем рассчитать y -координату:
y = 2,0 * 5,00 * 5,00 -20,0 * 5,00 + 49,0
или y = -1000

Парабола, график вершины и x -Intercepts:

Корневой график для:  y = 2x ² -20x+49
Ось симметрии (штриховая)  {x}={ 5,00} 
Вершина в  {x,y} = {5,00,-1,00} 
 x -Перехваты (корни ) :
Корень 1 в точке {x,y} = {4,29, 0,00}
Корень 2 в точке {x,y} = {5,71, 0,00} 

Решить квадратное уравнение, заполнив квадрат

 3. 2     Решение   2x ² -20x+49 = 0, заполнив квадрат .

 Поделите обе части уравнения на 2, чтобы получить 1 в качестве коэффициента при первом члене:
   x ² -10x+(49/2) = 0

Вычтите 49/2 из обеих частей уравнения:
   x ² -10x = -49/2

Теперь немного хитрости: возьмем коэффициент при x, равный 10, разделим на два, получим 5, и, наконец, возведем его в квадрат, получим 25

Добавьте  25 к обеим частям уравнения:
  В правой части мы имеем :
   -49/2  +  25    или,  (-49/2)+(25/1) 
  Общий знаменатель двух дробей равен 2   Прибавление (-49/2)+(50/2) дает 1/2 
  Таким образом, прибавив к обеим частям, мы окончательно получим:
   x ² -10x+25 = 1/2

Добавление 25 завершило левую руку стороны в полный квадрат:
   x ² -10x+25  =
   (x-5) • (x-5)  =
  (x-5) ²
Вещи, равные одной и той же вещи, также равны друг другу. Поскольку
   x ² -10x+25 = 1/2 и
   x ² -10x+25 = (x-5) ²
, то по закону транзитивности
   (x-5) 2 = 1/2

Мы будем называть это уравнение уравнением #3. 2.1  

Принцип квадратного корня гласит, что когда две вещи равны, их квадратные корни равны.

Обратите внимание, что квадратный корень из
   (x-5) ²   равен
   (x-5) ^2/2  =
  (x-5) ¹  =
   x-5

Теперь, применяя принцип квадратного корня к уравнению #3.2.1  получаем:
   x-5 = √ 1/2

Добавьте  5 к обеим частям, чтобы получить:
   x = 5 + √ 1/2

Так как квадратный корень имеет два значения, одно положительное, а другое отрицательное число
   x ² — 10x + (49/2) = 0
   имеет два решения:
  x = 5 + √ 1/2
   или
  x = 5 — √ 1/2

1/√2 can. быть записано как
  √ 1 / √ 2   что равно 1/√ 2 

Принято упрощать до тех пор, пока знаменатель не станет свободным от радикалов.

Здесь этого можно добиться, умножив числитель и знаменатель на √ 2 

После этого умножения числовое значение   1 /√ 2 остается неизменным, поскольку оно умножается на √ 2  / √ 2 , что равно   1 

Хорошо, давайте сделаем это:

 1 • √ 2  1 • √ 2  
 ————————————— = ——————————— 
 √ 2  • √ 2  2 
 

Решение квадратного уравнения с помощью квадратной формулы

 3. 3     Решение    2x ² -20x+49 = 0 с помощью квадратной формулы .

Согласно квадратичной формуле, x, решение для AX ² +BX +C = 0, где A, B и C являются числами, часто называемыми коэффициентами, определяются как:

-B ± √ B ² -4AC
  x =   ————————
                     2A

В нашем случае A = 2
B = -20
C = 49

Соответственно, B ² -4AC =
400-392 =
8

. x  =    —————
                    4

Можно ли упростить √ 8 ?

Да! Разложение числа 8 на простые множители – это
   2•2•2 
. Чтобы можно было удалить что-то из-под радикала, должно быть  2 этих экземпляра (потому что мы берем квадрат, т.е. второй корень).

√ 8 = √ 2 • 2 • 2 =
± 2 • √ 2

√ 2, округление до 4 десятичных цифр, составляет 1,4142
, так что теперь мы смотрим на:
x = (20 ± 2 • 1,414)// 4

Два действительных решения:

 x =(20+√8)/4=5+1/2√ 2 = 5,707

или:

 x =(20-√8)/4=5-1/ 2√ 2 = 4,293

Были найдены два решения:

1. x =(20-√8)/4=5-1/2√ 2 = 4,293
2. x =(20+√8)/4=5+ 1/2√ 2 = 5,707

SAT Математические вопросы по параболе

Вопрос 1 :

График параболы в плоскости xy имеет точки пересечения по оси x -1/5 и 3/2. Какое из следующих уравнений может быть уравнением параболы?

A) y = (5x — 1)((2x + 3)

B) y = (5x + 1)(2x — 3)

C) y = (5x — 3)(2x + 1)

D) y = (5x + 3)(2x — 1)

Ответ:

Чтобы найти точки пересечения x любой кривой, мы должны подставить y = 0 в ее уравнение и найти значения x.

В каждом из вариантов ответа плагин y = 0 и найти x-перехваты.

A) y = (5x — 1)((2x + 3) :

(5x — 1)((2x + 3) = 0

5x — 1 = 0 или 2x + 3 = 0

x = 1/5 или x = -3/2

точки пересечения x равны 1/5 и -3/2.

B) y = (5x + 1)((2x — 3) :

(5x + 1) ((2x — 3) = 0

5x + 1 = 0 или 2x — 3 = 0

x = -1/5 или x = 3/2

точки пересечения x равны -1/5 и 3/2.

С) у = (5х — 3)(2х + 1) :

(5x — 3)((2x + 1) = 0

5x — 3 = 0 или 2x + 1 = 0

x = 3/5 или x = -1/2

точки пересечения x равны 3/5 и -1/2.

D) y = (5x + 3)(2x — 1) :

(5x + 3)((2x — 1) = 0

5x + 3 = 0 или 2x — 1 = 0

x = -3/5  или  x = 1/2

точки пересечения x равны -3/5 и 1/2

Правильный вариант ответа (B)

Вопрос 2 :

y = x ²  — 2x — 3

Парабола в плоскости xy задается приведенным выше уравнением.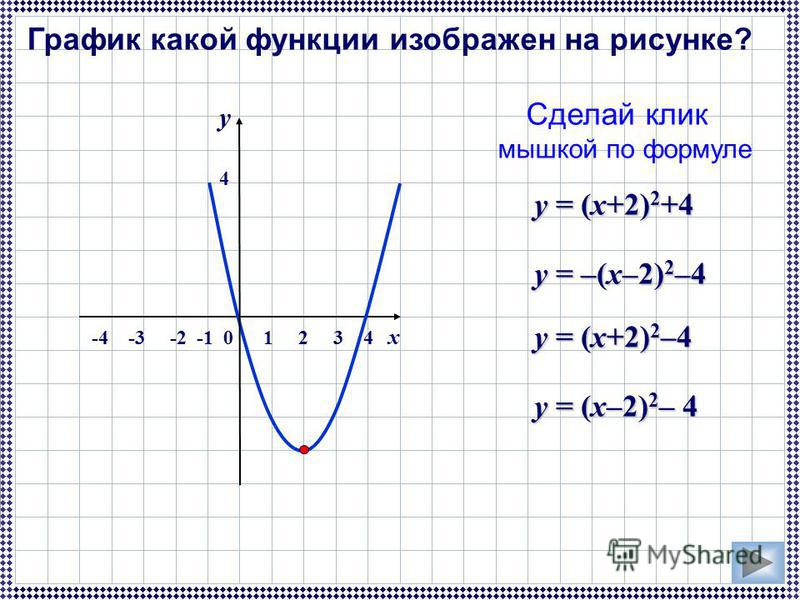 Какая из следующих эквивалентных форм уравнения отображает координаты вершины параболы в виде констант или коэффициентов?

A) y = (x — 1) ²  — 4

B) y = (x — 1) ²  — 2

C) y = (x — 3)(x + 1)

D) y + 3 = x(x + 2)

Ответ:

Уравнение формы вершины параболы y = a(x — h) ²  + k отображает координаты вершины (h, k ) как константы или коэффициенты.

Запишите данное уравнение параболы в вершинной форме, используя метод квадратов.

у = х ²  — 2х — 3

y = x ²  — 2(x)(1) — 3

y = x ²  — 2(x)(1) + 1 ²  — 1 ²  — 3

Используя алгебру тождество, (a + b) ²  = a ²  + 2ab + b ² ,

y = (x — 1) ²  — 1

2 x  — 3 9000 ) ²  — 1 — 3

y = (x — 1) ²  — 4

Вариант правильного ответа открыт (A).

Вопрос 3 :

у = х ²  + 10х + 16

Приведенное выше уравнение представляет собой параболу в плоскости xy. Какая из следующих эквивалентных форм уравнения отображает минимальные значения y в виде константы или коэффициента?

A) y = (x + 8)(x + 2)

B) y — 16 = x(x + 10)

C) y = (x + 5) ² — 9

D) y = (x — 5) ²  + 9

Ответ:

Минимальное или максимальное значение y в параболе — это координата y в вершине.

Если парабола раскрывается вверх, у нас есть минимальное значение y, а если парабола раскрывается вниз, у нас есть максимальное значение y.

Когда дано уравнение параболы и если вы хотите найти минимальное значение y, то запишите данное уравнение параболы в вершинной форме.

Уравнение формы вершины параболы: y = a(x — h) ²  + k, где (h, k) — вершина. Когда a > 0, парабола раскрывается вниз и минимальное значение y равно k.

y = x ²  + 10x + 16

y = x ²  + 2(x)(5) + 160015 2 — 5 ² + 16

с использованием алгебраической идентичности, (A + B) ² = A ² + 2AB + B ² ,

Y = (x + 5) ^{2 2 ,}

Y = (x + 5) ² 2 ,

Y = (x + 5) ² — 5 ²  + 16

y = (x + 5) ²  — 25 + 16

y = (x + 5) ²  — 9

Выбор правильного ответа открыт (C).

Вопрос 4 :

y = x ²  — 10x + k

В приведенном выше уравнении k является константой. Если уравнение представляет собой параболу в плоскости xy, которая касается оси x, каково значение k?

Ответ:

Если парабола касается оси x, ее уравнение имеет только одно решение при y = 0.

x ²  — 10x + k = 0 решения значение дискриминанта b ² — 4ac должно быть равно нулю.

Сравнение ax ²  + bx + c = 0 и x ²  — 10x + k = 0,

a = 1, b = -10 и c = k

b ^{2 9004ac = 0 — 5}

(-10) ² — 4(1)k = 0

100 — 4k = 0

-4k = -100

k = 25

Вопрос 5 :

Парабола показана в плоскости xy выше. Какое из следующих уравнений правильно представляет параболу, отображая пересечения параболы по оси x в виде констант или коэффициентов?

А) у = (х + 1,5) ² — 20,25

В) у = (х — 1,5) ² — 20,25

В) у = (х + 6 )(900 — 05) D) y = (x — 6)(x + 3)

Ответ :

Судя по графику, два отрезка x равны -6 и 3.