Парабола функция ее свойства и график: Свойства квадратичной функции y = ax² — урок. Алгебра, 8 класс.

Квадратичная функция, ее график и свойства

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Квадратичная функция. Её свойства и график.

Определение квадратичной
функции
Квадратичной функцией называется
функция , которую можно задать формулой
вида:
y=
2
ax +bx
+c
где: a, b, c –
числа
Х – независимая переменная
а 0
График квадратичной функции – парабола.

3.

Алгоритм построения параболы у = ах2 + bх + с :1. Найти координаты вершины параболы, построить
на координатной плоскости соответствующую точку,
провести ось симметрии.
2.
Определить направление ветвей параболы.
3. Найти координаты еще нескольких точек,
принадлежащих искомому графику ( в частности,
координаты точки пересечения параболы с осью у и
нули функции, если они существуют).
4. Отметить на координатной плоскости
найденные точки и соединить их плавной линией.
—
.
Графиком квадратичной функции
у = ах2 + bх + с является парабола, которая получается из
параболы
у = ах2 параллельным переносом.
Вершина параболы — ( х0; уо) ,
b
где : хо = 2a
у0 =
4ac b 2
4a
Осью параболы будет прямая
b
х=2a

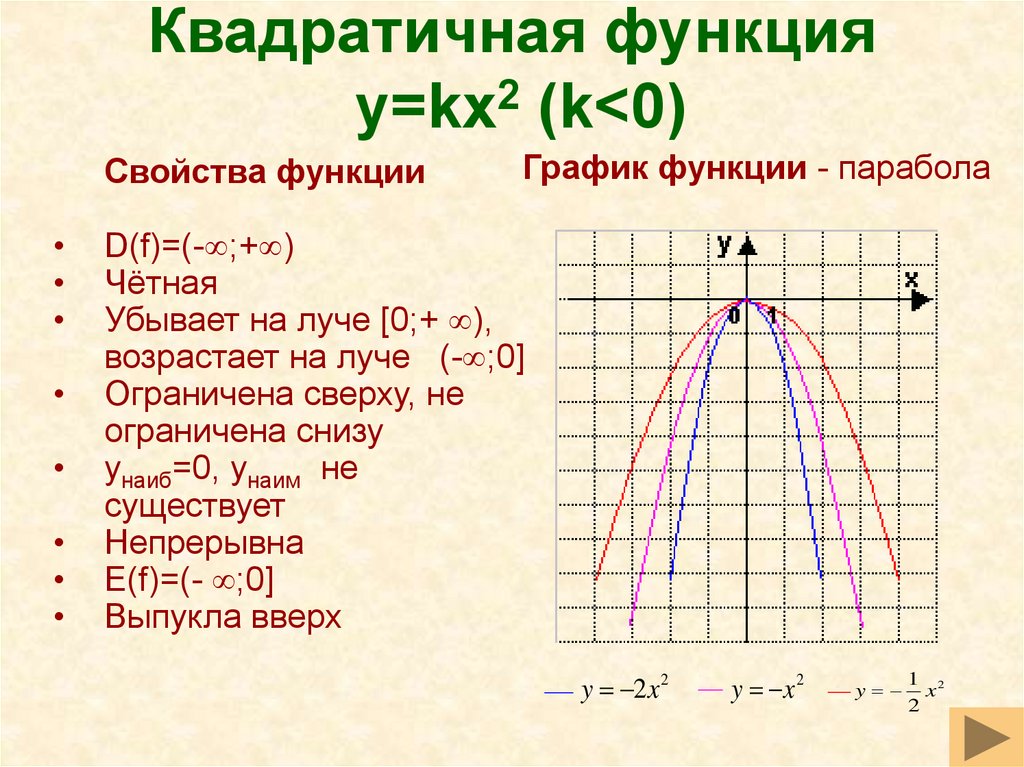
5. Свойства квадратичной функции

Функция непрерывна
Множество значений при a>0 —
Множество значений при a<0 10
8
6
4
2
0
-3
-2
-1
0
-2
1
2
3
4
5
Многие свойства
квадратичной функции
зависят от значения
дискриминанта.
Дискриминантом квадратного уравнения
ах2 + bх + с = 0 называется выражение
D =b2 – 4ac
Возможны три случая:
D 0
D 0
D 0
если дискриминант больше нуля, то парабола
пересекает ось абсцисс в двух точках,
если дискриминант равен нулю, то парабола
касается оси абсцисс,
если дискриминант меньше нуля, то парабола не
пересекает ось абсцисс,
абсцисса вершины параболы равна
—
ветви параболы
направлены вверх,
При
у
b
2a
При
ветви параболы
направлены
вниз
у
f(x0)
х
х
b
2a

9. Область значений функции – Е (f) = [ -1 ; + )

Функция возрастает в
промежутке [ +3; +
)
Функция убывает в
промежутке ( ;+3]
Наименьшее значение
функции равно -1
Наибольшего значения
функции не существует
f(x) > 0 при х < 2, или
х>4
f(x) < 0 при 2 < х < 4
Ось симметрии
Область значений функции –

10. Постройте график функции у=2х²+4х-6, опишите его свойства

Проверь себя:
1. 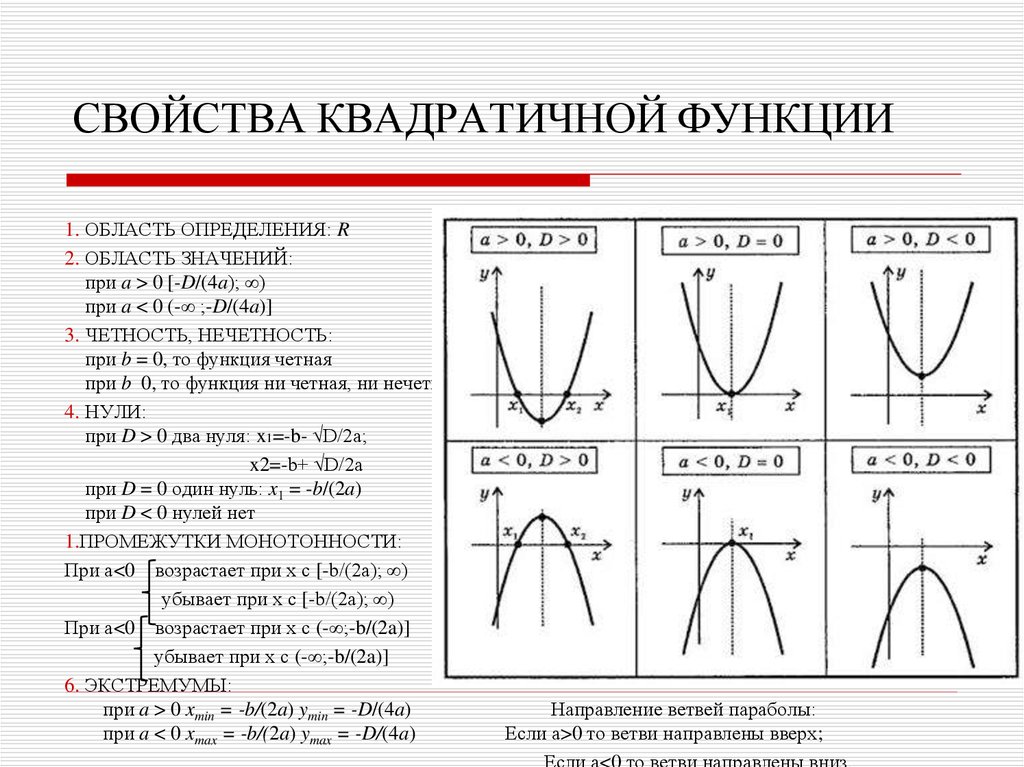D(y)=
;
У
2. у=0, при х=1; -3
3. у>0, при х ; 3 1;
у<0, при х 3;1
4. у↓, если х ; 1
у↑, если х 1;
5. унаим= -8, если х= -1
унаиб – не существует.
6. Е(y): 8 ;
1
-1
-2
1 2 3
Х
Задание
1. Построить график функции и
описать ее свойства у=2х²+4х-1
2. Построить график функции и
описать ее свойства у= -7х²-х+3

English     Русский Правила

Внеклассный урок — Квадратичная функция. Функция y = ax2, ее график и свойства

Квадратичная функция. Функция y = ax², ее график и свойства

 

Квадратичная функция – это функция, которую можно задать формулой вида

                                                 y  =  ax²  +  bx  +  c,

где x – независимая переменная, a, b и c – некоторые числа, причем а ≠ 0.

Областью определения квадратичной функции является множество всех чисел. (Напомним: областью определения функции называется совокупность значений независимой переменной, см.раздел «Функции и их графики»)

 

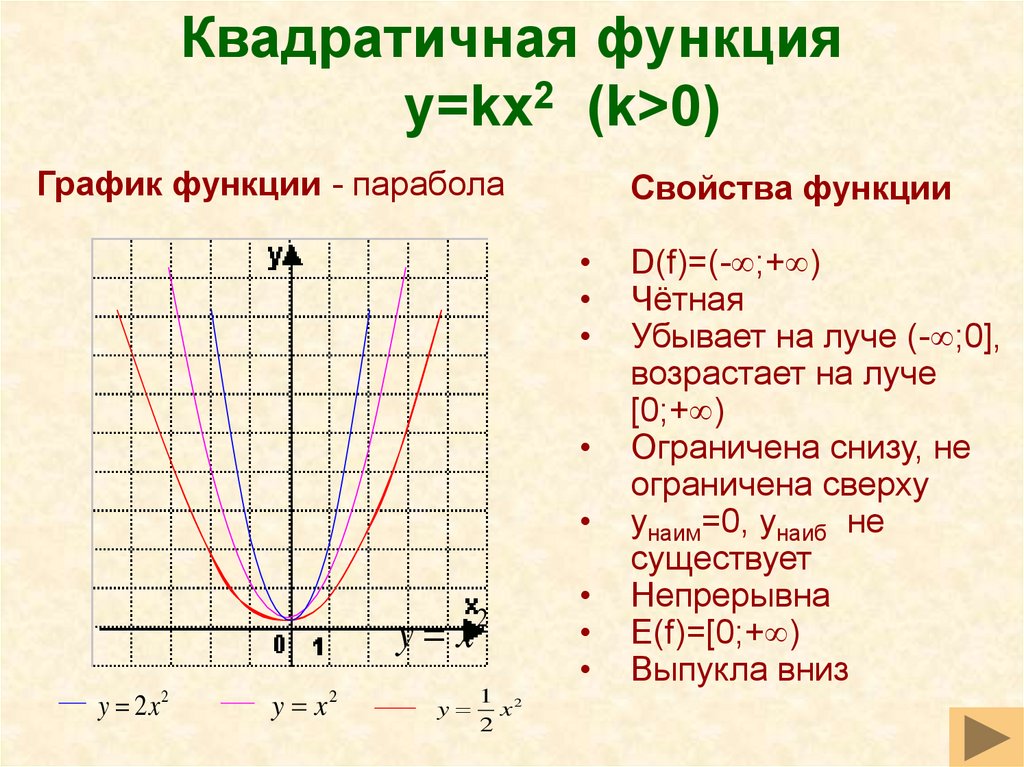
Функция  y = ax².

Функция y = ax² – это частный случай квадратичной функции.

Графиком функции y = ax² является парабола.

 

 

 

Свойства функции  y = ax² при a > 0:

1. Если x = 0, то y = 0. График функции проходит через начало координат.   2. Если x ≠ 0, то y > 0. График функции расположен в верхней полуплоскости.   3. Противоположным значениям аргумента соответствуют равные значения функции. Пояснение: допустим, x = –2, y = 8. При x = 2 значение y не меняется и составляет 8.   4. В промежутке (–∞; 0] функция убывает, а в промежутке [0; +∞) — возрастает.   5. Наименьшее значение функции равно нулю. Это значение она принимает при x = 0 (см.пункт 1). Наибольшего значения функция не имеет. Т.е. областью значений функции является промежуток [0; +∞).

 

Свойства функции  y = ax² при a < 0:

1. Если x = 0, то y = 0. График функции проходит через начало координат.   2. Если x ≠ 0, то y < 0. График функции расположен в нижней полуплоскости.   3. Противоположным значениям аргумента соответствуют равные значения функции. График функции представляет собой симметричную фигуру относительно оси y. Пояснение: допустим, x = –4, y = –8. При x = 4 значение y не меняется и составляет –8.   4. В промежутке (–∞; 0] функция возрастает, а в промежутке [0; +∞) — убывает.   5. Наибольшее значение функции равно нулю. Это значение она принимает при x = 0 (см.пункт 1). Наименьшего значения функция не имеет. Т.е. областью значений функции является промежуток (–∞; 0].

 

 

Параболическая функция — определение, формула, график, свойства, примеры, часто задаваемые вопросы

LearnPracticeDownload

Параболическая функция — это функция формы форма, она имеет форму параболы. Уравнение, представляющее параболическую функцию, является квадратным уравнением со второй степенью по x.

Давайте узнаем больше о параболической функции, графике параболической функции, свойствах параболической функции с помощью примеров, часто задаваемых вопросов.

1.	Что такое параболическая функция?
2.	График параболической функции
3.	Свойства параболической функции
4.	Примеры параболической функции
5.	Практические вопросы
6.	Часто задаваемые вопросы о параболической функции

Что такое параболическая функция?

Параболическая функция представляет собой функцию вида f(x) = ax ² + bx + c. Это квадратное выражение во второй степени по х. Параболическая функция имеет график, аналогичный параболе, поэтому функция называется параболической функцией.

Параболическая функция имеет одно и то же значение диапазона для двух разных значений домена. Общий вид параболической функции f(x) = ax ² + bx + c имеет одно значение f(x) или значение y для двух значений x, которые равны x ₁ , x ₂ . Две возможные точки на графике параболической функции: (x ₁ , y), (x ₂ , y). Следовательно, параболическую функцию также можно назвать функцией «многие к одному».

График параболической функции

График параболической функции похож на параболу. График параболы следует основному определению параболы. Парабола — это геометрическое место точки, равноудаленной от фиксированной точки, называемой фокусом, и неподвижной линии, называемой директрисой.

График параболической функции симметричен прямой линии, и эта линия называется осью параболы. Ось параболы может быть линией, параллельной любой оси координат, или линией, наклоненной под углом к ​​оси координат.

Свойства параболической функции

Ниже приведены некоторые важные свойства параболической функции, которые помогут лучше понять эту функцию.

• Параболическая функция имеет один и тот же кодовый домен для двух разных значений домена.
• Набор из двух точек, удовлетворяющих уравнению параболической функции, имеет разные абсциссы и одинаковые ординаты.
• Область определения параболической функции может быть положительной или отрицательной, но диапазон параболической функции является положительным значением.
• Параболическую функцию также можно назвать множеством единиц.
• График параболической функции симметричен относительно прямой, и эта линия называется осью параболы.
• Уравнение, представляющее параболическую функцию, удовлетворяет всем свойствам геометрической параболы.

Связанные темы

Следующие темы помогут понять концепцию параболической функции.

• Обратная функция
• Сюръективная функция
• Биективная функция
• Инъекционная функция
• Периодическая функция

 

Примеры параболической функции

1. Пример 1: Найдите параболическую функцию, представляющую параболу с фокусом (4, 0), осью x в качестве оси параболы и началом координат в качестве вершины параболы.

   Решение:

   Фокус параболы равен (a, 0) = (4, 0) и a = 4.

   Для параболы, имеющей ось x в качестве оси и начало координат в виде вершина, уравнение параболы y ² = 4 оси.

   Отсюда уравнение параболы: y ² = 4(4)x или y ² = 16x.

   Параболическая функция равна y = \(4\sqrt x\)

   Следовательно, уравнение, представляющее параболическую функцию, имеет вид y = \(4\sqrt x\).

2. Пример 2: Найти вершину параболической функции y = 0,5x ² + 3x + 4.

   Решение:

   Сравнение данного уравнения с y = ax ² + bx + c, имеем a = 0,5, b = 3 и c = 4.

   Координата x вершины: h = -b/2a = -3/2(0,5) = — 3/1 = -3.

   Y-координата вершины k = 0,5(-3) ²

   + 3(-3) + 4 = -0,5.

   Вершина данной параболы есть, (h, k) = (-3, -0,5)

   Ответ: Вершина параболы = (-3, -0,5).

перейти к слайдуперейти к слайду

Разложите сложные концепции с помощью простых визуальных средств.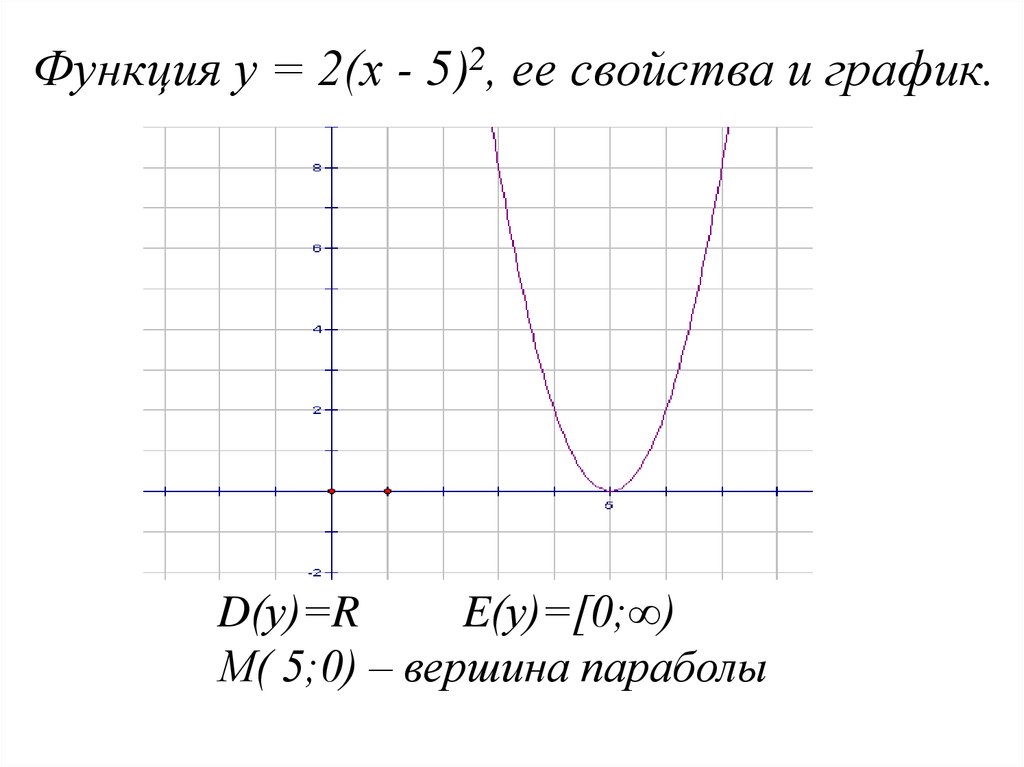

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Забронировать бесплатный пробный урок

Практические вопросы по параболической функции

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о параболической функции

Что такое параболическая функция?

Параболическая функция представляет собой функцию вида f(x) = ax ² + bx + c. Это квадратное выражение во второй степени по х. Параболическая функция имеет график, аналогичный параболе, поэтому функция называется параболической функцией.

Как решить параболическую функцию?

Выражение параболической функции имеет вид f(x) = ax ² + bx + c, и его можно решить относительно x. Параболическая функция также решается аналогично квадратичной функции. Это выражение можно приравнять к нулю и либо разложить на множители, либо решить методом формул.

Каков диапазон параболической функции?

Диапазон параболической функции — все положительные действительные числа.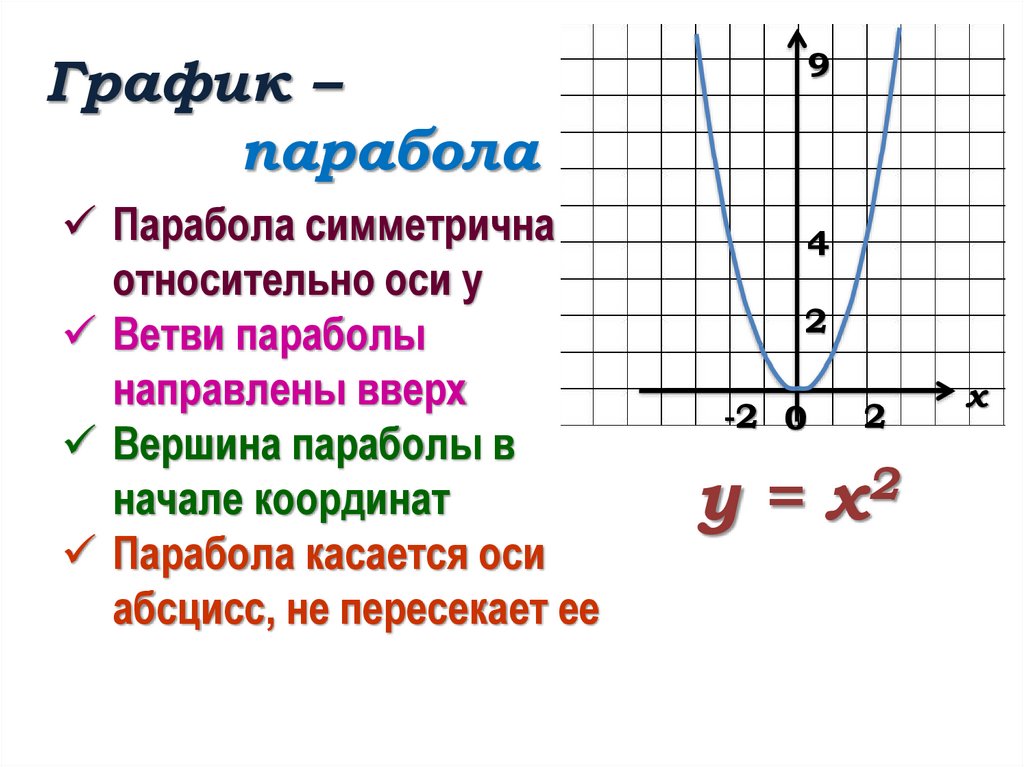 Диапазон параболической функции представлен на оси Y.

Что такое область определения параболической функции?

Область определения параболической функции включает все действительные числа. Областью определения параболической функции обычно являются значения x функции, представленные как на положительной, так и на отрицательной оси x.

Какой тип функции является параболической функцией?

Параболическая функция является разновидностью многих функций. Для параболической функции у нас есть два значения домена и одно значение диапазона. Возможный набор точек на графике параболической функции равен (x ₁ , у) и (х ₂ , у).

В чем разница между параболической функцией и квадратичной функцией?

Параболическую функцию также можно рассматривать как квадратичную функцию. Общее выражение параболической функции имеет вид f(x) = = ax ² + bx + c, что аналогично квадратному выражению. Квадратное выражение является второй степенью как по x, так и по y, поэтому каждое квадратное выражение нельзя назвать параболической функцией.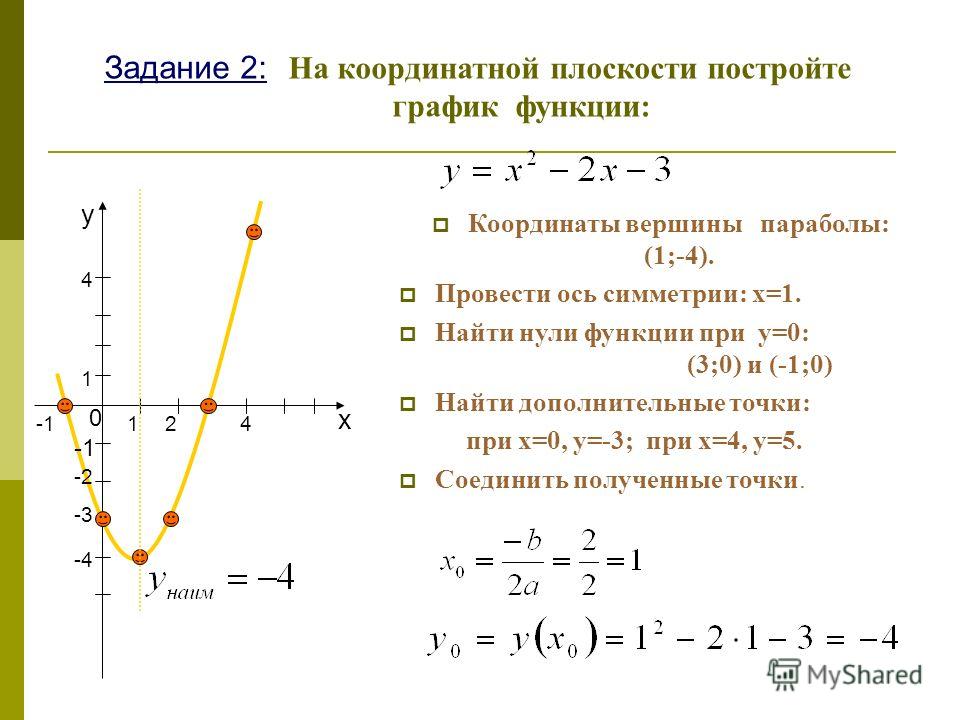

Рабочие листы по математике и
наглядный учебный план

Характеристики парабол | Колледж Алгебра

Результаты обучения

• Определите вершину, ось симметрии, [латекс]y[/латекс]-пересечение, а также минимальное или максимальное значение параболы на ее графике.
• Определите квадратичную функцию, записанную в общей и вершинной формах.
• Для заданной квадратичной функции в общем виде найдите вершину.
• Определите область определения и диапазон квадратичной функции, указав вершину как максимум или минимум.

График квадратичной функции представляет собой U-образную кривую, называемую параболой . Одной из важных особенностей графа является то, что он имеет крайнюю точку, называемую вершиной . Если парабола раскрывается, вершина представляет собой самую низкую точку на графике или минимальное значение квадратичной функции. Если парабола открывается вниз, вершина представляет собой наивысшую точку на графике или максимальное значение .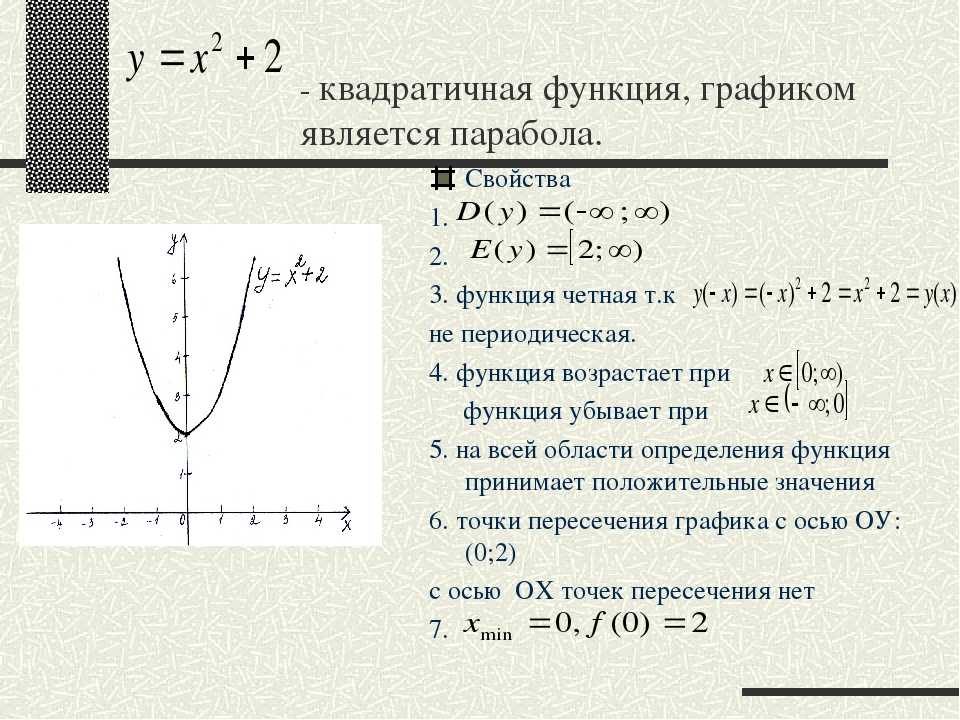 В любом случае вершина является поворотной точкой на графе. График также симметричен, а вертикальная линия проходит через вершину, называемую 9.0103 ось симметрии .

Точка пересечения [latex]y[/latex] — это точка пересечения параболы с осью [latex]y[/latex]. Точки пересечения [latex]x[/latex] — это точки, в которых парабола пересекает ось [latex]x[/latex]. Если они существуют, то пересечения [latex]x[/latex] представляют собой 90 103 нулей 90 104 или 90 103 корней 90 104 квадратичной функции, значения [latex]x[/latex] при которых [latex]y=0 [/латекс].

Пример: определение характеристик параболы 9{2}+4x+3[/латекс]. В этой форме [латекс]а=1,\текст{ }b=4[/латекс] и [латекс]с=3[/латекс]. Поскольку [latex]a>0[/latex], парабола открывается вверх. Ось симметрии: [латекс]x=-\dfrac{4}{2\left(1\right)}=-2[/latex]. Это также имеет смысл, поскольку на графике видно, что вертикальная линия [latex]x=-2[/latex] делит график пополам. Вершина всегда находится вдоль оси симметрии.

Для параболы, которая открывается вверх, вершина находится в самой нижней точке графика, в данном случае [латекс]\влево(-2,-1\вправо)[/латекс]. [latex]x[/latex]-перехваты, те точки, где парабола пересекает [latex]x[/latex]-ось, находятся в [latex]\left(-3,0\right)[/latex] и [латекс]\влево(-1,0\вправо)[/латекс]. 9{2}+k[/latex]

, где [latex]\left(h,\text{ }k\right)[/latex] — вершина. Поскольку вершина появляется в стандартной форме квадратичной функции, эта форма также известна как вершинная форма квадратичной функции .

Для заданной квадратичной функции в общем виде найдите вершину параболы.

Одна из причин, по которой мы можем захотеть идентифицировать вершину параболы, заключается в том, что эта точка сообщит нам, где происходит максимальное или минимальное значение вывода, [latex]k[/latex], и где оно происходит, [latex]h [/латекс]. Если нам дан общий вид квадратичной функции: 92+bx+c[/latex]

Мы можем определить вершину [latex](h,k)[/latex], выполнив следующие действия:

• Идентифицировать [latex]a[/latex], [latex] ]b[/латекс] и [латекс]с[/латекс].
• Найдите [latex]h[/latex], координату [latex]x[/latex] вершины, подставив [latex]a[/latex] и [latex]b[/latex] в [latex]h =-\dfrac{b}{2a}[/latex].
• Найдите [latex]k[/latex], [latex]y[/latex]-координату вершины, оценивая [latex]k=f\left(h\right)=f\left(-\dfrac{ б}{2а}\справа)[/латекс] 9{2}-6x[/latex], напишите уравнение в общем виде, а затем в стандартном виде.

  Показать решение

  Нахождение области определения и диапазона квадратичной функции

  Любое число может быть входным значением квадратичной функции. Следовательно, областью определения любой квадратичной функции являются все действительные числа. Поскольку параболы имеют максимум или минимум в вершине, диапазон ограничен. Так как вершина параболы будет либо максимальной, либо минимальной, диапазон будет состоять из всех [latex]y[/latex]-значений, больших или равных [latex]y[/latex]-координате вершины или меньше или равно [latex]y[/latex]-координате в точке поворота, в зависимости от того, открывается ли парабола вверх или вниз.

  No related posts.