Парабола | это… Что такое Парабола?
У этого термина существуют и другие значения, см. Парабола (значения).
| Парабола, её фокус и директриса | |
| Коническое сечение: | |
| Эксцентриситет: | |
| Уравнение: | |
| гипербола · парабола · эллипс · окружность | |
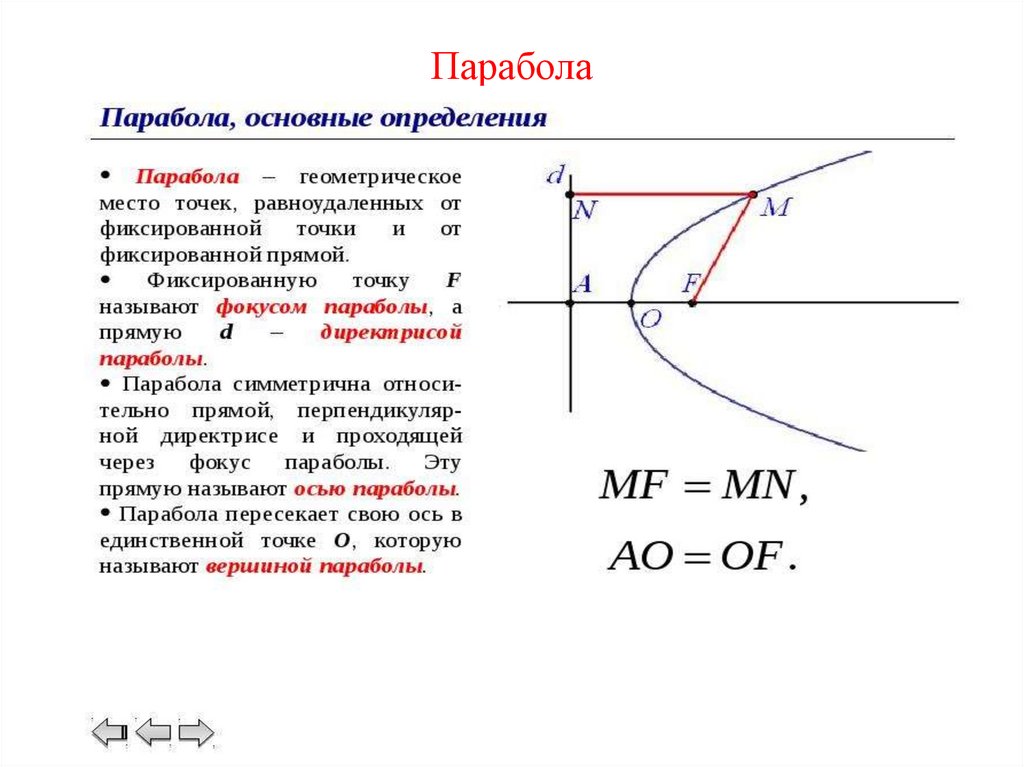
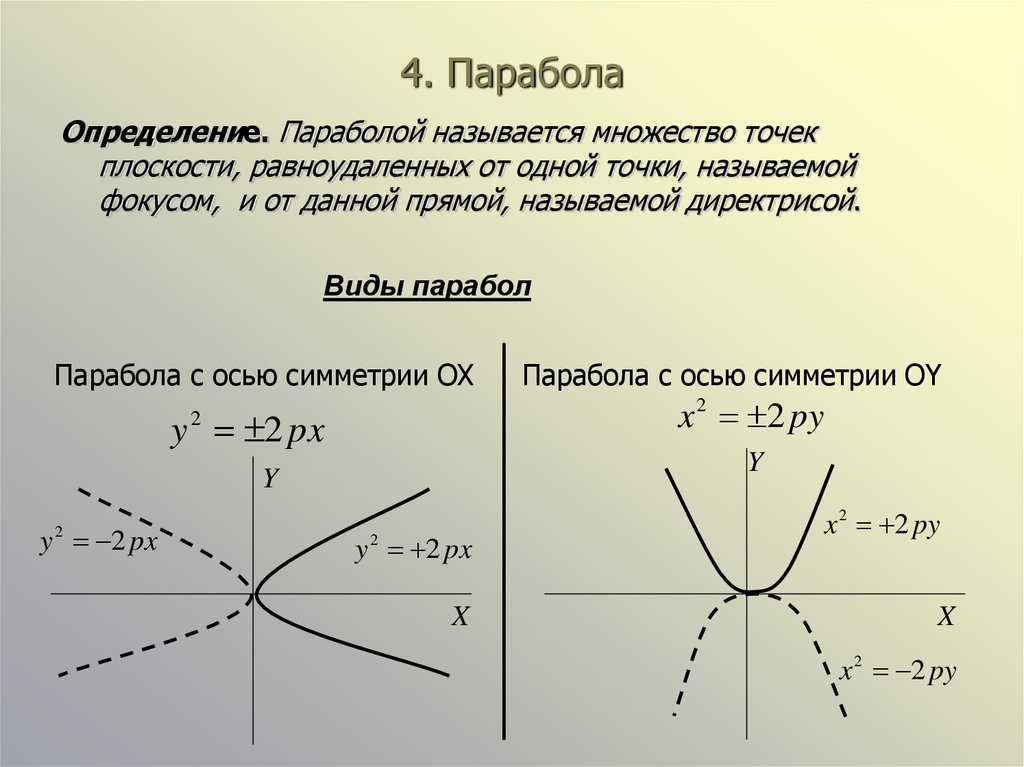
Пара́бола (греч. παραβολή — приложение) — геометрическое место точек, равноудалённых от данной прямой (называемой директрисой параболы) и данной точки (называемой фокусом параболы).
Наряду с эллипсом и гиперболой, парабола является коническим сечением. Она может быть определена как коническое сечение с единичным эксцентриситетом.
Изображение конического сечения, являющегося параболой
Построение параболы как конического сечения
Содержание
|
Уравнения
Каноническое уравнение параболы в прямоугольной системе координат:
- (или , если поменять местами оси).
Число p называется фокальным параметром, оно равно расстоянию от фокуса до директрисы[1]. Поскольку каждая точка параболы равноудалена от фокуса и директрисы, то и вершина — тоже, поэтому она лежит между фокусом и директрисой на расстоянии от обоих.
| Вывод |
|---|
Уравнение директрисы : , фокус — , таким образом начало координат — середина отрезка .
После возведения в квадрат и некоторых преобразований получается равносильное уравнение . |
Квадратное уравнение при также представляет собой параболу и графически изображается той же параболой, что и , но в отличие от последней имеет вершину не в начале координат, а в некоторой точке , координаты которой вычисляются по формулам:
- где — дискриминант
Ось её симметрии проходит через вершину параллельно оси ординат, при a>0 (a<0) фокус лежит на этой оси над (под) вершиной на расстоянии a/4, а директриса — под (над) вершиной на таком же расстоянии и параллельна оси абсцисс. Уравнение может быть представлено в виде , а в случае переноса начала координат в точку каноническим уравнением. Таким образом для каждого квадратного уравнения можно найти систему координат такую, что в этой системе оно представляется каноническим.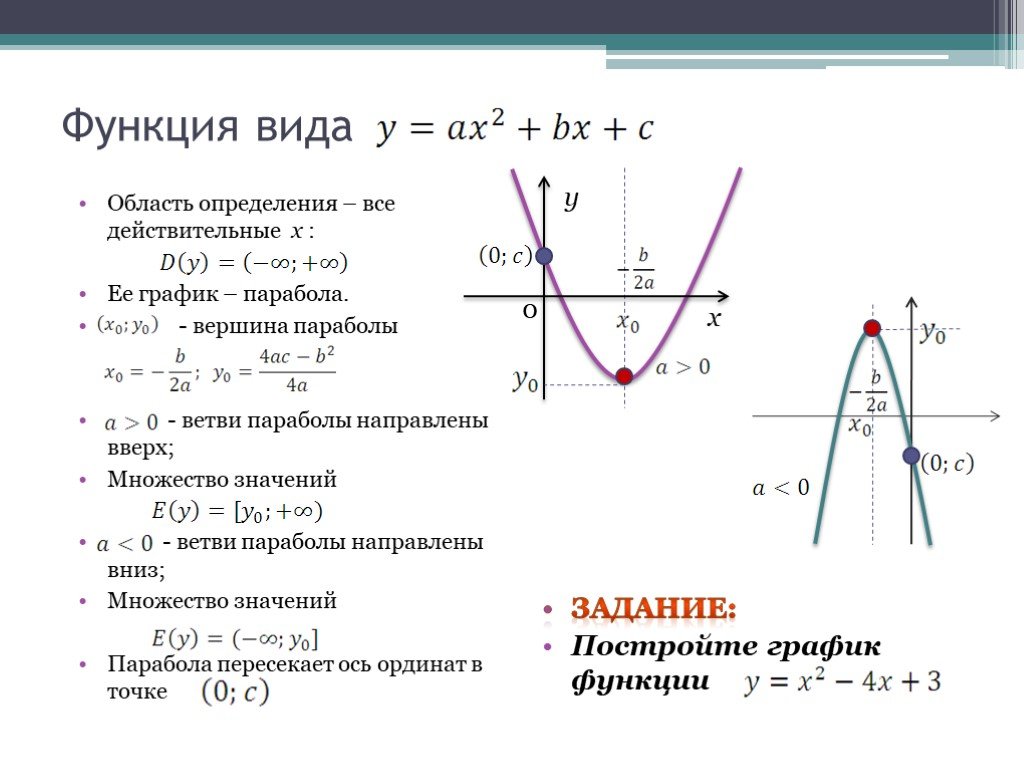
Расчёт коэффициентов квадратного уравнения
Если для уравнения известны координаты 3-х различных точек его графика , , , то его коэффициенты могут быть найдены так:
Свойства
Расстояние от Pn до фокуса F такое же, как и от Pn до Qn (на директрисе L)
Длина линий F-Pn-Qn одинакова. Можно сказать, что, в отличие от эллипса, второй фокус у параболы — в бесконечности (см. также Шары Данделена)
- Парабола — кривая второго порядка.
- Она имеет ось симметрии, называемой осью параболы. Ось проходит через фокус и вершину перпендикулярно директрисе.
- Оптическое свойство. Пучок лучей, параллельных оси параболы, отражаясь в параболе, собирается в её фокусе. И наоборот, свет от источника, находящегося в фокусе, отражается параболой в пучок параллельных её оси лучей.
- Если фокус параболы отразить относительно касательной, то его образ будет лежать на директрисе.

- Парабола является антиподерой прямой.
- Все параболы подобны. Расстояние между фокусом и директрисой определяет масштаб.
Связанные определения
- При вращении параболы вокруг оси симметрии получается эллиптический параболоид.
Параболы в физическом пространстве
Параболический компас Леонардо да Винчи
Траектории некоторых космических тел (комет, астероидов и других), проходящих вблизи звезды или другого массивного объекта (звезды или планеты) на достаточно большой скорости имеют форму параболы (или гиперболы). Эти тела вследствие своей большой скорости не захватываются гравитационным полем звезды и продолжают свободный полёт. Это явление используется для гравитационных манёвров космических кораблей (в частности аппаратов Вояджер).
При отсутствии сопротивления воздуха траектория полёта тела в приближении однородного гравитационного поля представляет собой параболу.
Также параболические зеркала используются в любительских переносных телескопах систем Кассергена, Шмидта — Кассергена, Ньютона, а в фокусе параболы устанавливают вспомогательные зеркала, подающие изображение на окуляр.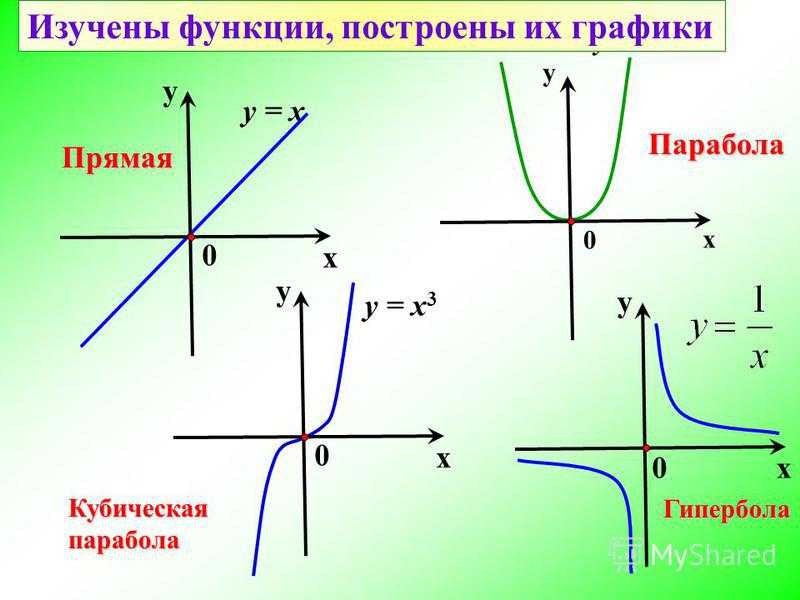
При вращении сосуда с жидкостью вокруг вертикальной оси поверхность жидкости в сосуде и вертикальная плоскость пересекаются по параболе.
Свойство параболы фокусировать пучок лучей, параллельных оси параболы, используется в конструкциях прожекторов, фонарей, фар, а также телескопов-рефлекторов (оптических, инфракрасных, радио…), в конструкции узконаправленных (спутниковых и других) антенн, необходимых для передачи данных на большие расстояния, солнечных электростанций и в других областях.
Форма параболы иногда используется в архитектуре для строительства крыш и куполов.
См. также
- Кубическая парабола
- Конические сечения:
- Эллипс
- Гипербола
- Окружность
- Шары Данделена
- Цепная линия
- Каустика
- Телескоп
Примечания
- ↑ Александров П.С. Парабола // Курс аналитической геометрии и линейной алгебры. — М.: Наука, 1979. — С. 69—72. — 512 с.
Литература
- Бронштейн И.
 , Парабола, Квант, № 4, 1975.
, Парабола, Квант, № 4, 1975. - Математическая энциклопедия (в 5-и томах), Москва, «Советская Энциклопедия», 1982 г.
- Маркушевич А. И. Замечательные кривые, Популярные лекции по математике, выпуск 4, Гостехиздат 1952 г., 32 стр.
- А. А. Акопян, А. В. Заславский Геометрические свойства кривых второго порядка. Москва, Издательство МЦНМО, 2007 год.
Ссылки
- Статья в справочнике «Прикладная математика».
- Анимированные рисунки, иллюстрирующие некоторые свойства параболы.
- Информация (англ.) о связи параболы с физикой.
- Учебный фильм о параболе
Парабола | это… Что такое Парабола?
У этого термина существуют и другие значения, см. Парабола (значения).
| Парабола, её фокус и директриса | |
| Коническое сечение: | |
| Эксцентриситет: | |
| Уравнение: | |
| гипербола · парабола · эллипс · окружность | |
Пара́бола (греч.
Наряду с эллипсом и гиперболой, парабола является коническим сечением. Она может быть определена как коническое сечение с единичным эксцентриситетом.
Изображение конического сечения, являющегося параболой
Построение параболы как конического сечения
Содержание
|
Уравнения
Каноническое уравнение параболы в прямоугольной системе координат:
- (или , если поменять местами оси).
Число p называется фокальным параметром, оно равно расстоянию от фокуса до директрисы[1]. Поскольку каждая точка параболы равноудалена от фокуса и директрисы, то и вершина — тоже, поэтому она лежит между фокусом и директрисой на расстоянии от обоих.
Поскольку каждая точка параболы равноудалена от фокуса и директрисы, то и вершина — тоже, поэтому она лежит между фокусом и директрисой на расстоянии от обоих.
| Вывод |
|---|
Уравнение директрисы : , фокус — , таким образом начало координат — середина отрезка . По определению параболы для любой точки , лежащей на ней выполняется равенство . и , тогда равенство приобретает вид:
После возведения в квадрат и некоторых преобразований получается равносильное уравнение . |
Квадратное уравнение при также представляет собой параболу и графически изображается той же параболой, что и , но в отличие от последней имеет вершину не в начале координат, а в некоторой точке , координаты которой вычисляются по формулам:
- где — дискриминант
Ось её симметрии проходит через вершину параллельно оси ординат, при a>0 (a<0) фокус лежит на этой оси над (под) вершиной на расстоянии a/4, а директриса — под (над) вершиной на таком же расстоянии и параллельна оси абсцисс. Уравнение может быть представлено в виде , а в случае переноса начала координат в точку каноническим уравнением. Таким образом для каждого квадратного уравнения можно найти систему координат такую, что в этой системе оно представляется каноническим. При этом .
Уравнение может быть представлено в виде , а в случае переноса начала координат в точку каноническим уравнением. Таким образом для каждого квадратного уравнения можно найти систему координат такую, что в этой системе оно представляется каноническим. При этом .
Расчёт коэффициентов квадратного уравнения
Если для уравнения известны координаты 3-х различных точек его графика , , , то его коэффициенты могут быть найдены так:
Свойства
Расстояние от Pn до фокуса F такое же, как и от Pn до Qn (на директрисе L)
Длина линий F-Pn-Qn одинакова. Можно сказать, что, в отличие от эллипса, второй фокус у параболы — в бесконечности (см. также Шары Данделена)
- Парабола — кривая второго порядка.
- Она имеет ось симметрии, называемой осью параболы. Ось проходит через фокус и вершину перпендикулярно директрисе.
- Оптическое свойство. Пучок лучей, параллельных оси параболы, отражаясь в параболе, собирается в её фокусе.
 И наоборот, свет от источника, находящегося в фокусе, отражается параболой в пучок параллельных её оси лучей.
И наоборот, свет от источника, находящегося в фокусе, отражается параболой в пучок параллельных её оси лучей. - Если фокус параболы отразить относительно касательной, то его образ будет лежать на директрисе.
- Парабола является антиподерой прямой.
- Все параболы подобны. Расстояние между фокусом и директрисой определяет масштаб.
Связанные определения
- При вращении параболы вокруг оси симметрии получается эллиптический параболоид.
Параболы в физическом пространстве
Параболический компас Леонардо да Винчи
Траектории некоторых космических тел (комет, астероидов и других), проходящих вблизи звезды или другого массивного объекта (звезды или планеты) на достаточно большой скорости имеют форму параболы (или гиперболы). Эти тела вследствие своей большой скорости не захватываются гравитационным полем звезды и продолжают свободный полёт. Это явление используется для гравитационных манёвров космических кораблей (в частности аппаратов Вояджер).
При отсутствии сопротивления воздуха траектория полёта тела в приближении однородного гравитационного поля представляет собой параболу.
Также параболические зеркала используются в любительских переносных телескопах систем Кассергена, Шмидта — Кассергена, Ньютона, а в фокусе параболы устанавливают вспомогательные зеркала, подающие изображение на окуляр.
При вращении сосуда с жидкостью вокруг вертикальной оси поверхность жидкости в сосуде и вертикальная плоскость пересекаются по параболе.
Свойство параболы фокусировать пучок лучей, параллельных оси параболы, используется в конструкциях прожекторов, фонарей, фар, а также телескопов-рефлекторов (оптических, инфракрасных, радио…), в конструкции узконаправленных (спутниковых и других) антенн, необходимых для передачи данных на большие расстояния, солнечных электростанций и в других областях.
Форма параболы иногда используется в архитектуре для строительства крыш и куполов.
См. также
- Кубическая парабола
- Конические сечения:
- Эллипс
- Гипербола
- Окружность
- Шары Данделена
- Цепная линия
- Каустика
- Телескоп
Примечания
- ↑ Александров П.
 С. Парабола // Курс аналитической геометрии и линейной алгебры. — М.: Наука, 1979. — С. 69—72. — 512 с.
С. Парабола // Курс аналитической геометрии и линейной алгебры. — М.: Наука, 1979. — С. 69—72. — 512 с.
Литература
- Бронштейн И., Парабола, Квант, № 4, 1975.
- Математическая энциклопедия (в 5-и томах), Москва, «Советская Энциклопедия», 1982 г.
- Маркушевич А. И. Замечательные кривые, Популярные лекции по математике, выпуск 4, Гостехиздат 1952 г., 32 стр.
- А. А. Акопян, А. В. Заславский Геометрические свойства кривых второго порядка. Москва, Издательство МЦНМО, 2007 год.
Ссылки
- Статья в справочнике «Прикладная математика».
- Анимированные рисунки, иллюстрирующие некоторые свойства параболы.
- Информация (англ.) о связи параболы с физикой.
- Учебный фильм о параболе
12.3: Парабола — Математика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 3289
- OpenStax
- OpenStax
Цели обучения
- Параболы графа с вершинами в начале координат.

- Запишите уравнения парабол в стандартной форме.
- Параболы графа с вершинами не в начале координат.
- Решение прикладных задач на параболах.
А вы знали, что олимпийский огонь зажигают за несколько месяцев до начала игр? Церемониальный метод зажжения пламени такой же, как и в древние времена. Церемония проходит в храме Геры в Олимпии, Греция, и уходит своими корнями в греческую мифологию, отдавая дань уважения Прометею, который украл огонь у Зевса, чтобы раздать его всем людям. Одна из одиннадцати действующих жриц помещает факел в фокус параболического зеркала (рис. \(\PageIndex{1}\)), которое фокусирует солнечные лучи и зажигает пламя.
Рисунок \(\PageIndex{1}\): Олимпийский факел завершает свое кругосветное путешествие, когда от него зажигают олимпийский котел во время церемонии открытия. (Источник: Кен Хэкман, ВВС США) Параболические зеркала (или отражатели) способны улавливать энергию и фокусировать ее в одной точке. О преимуществах этого свойства свидетельствует обширный список параболических объектов, которые мы используем каждый день: спутниковые тарелки, подвесные мосты, телескопы, микрофоны, прожекторы и автомобильные фары, и это лишь некоторые из них. Параболические отражатели также используются в устройствах альтернативной энергии, таких как солнечные плиты и водонагреватели, потому что они недороги в производстве и не требуют особого обслуживания. В этом разделе мы рассмотрим параболу и ее использование, в том числе недорогие и энергоэффективные солнечные конструкции.
О преимуществах этого свойства свидетельствует обширный список параболических объектов, которые мы используем каждый день: спутниковые тарелки, подвесные мосты, телескопы, микрофоны, прожекторы и автомобильные фары, и это лишь некоторые из них. Параболические отражатели также используются в устройствах альтернативной энергии, таких как солнечные плиты и водонагреватели, потому что они недороги в производстве и не требуют особого обслуживания. В этом разделе мы рассмотрим параболу и ее использование, в том числе недорогие и энергоэффективные солнечные конструкции.
Графики парабол с вершинами в начале координат
Ранее мы видели, что эллипс образуется, когда плоскость пересекает прямой круговой конус. Если плоскость параллельна ребру конуса, образуется неограниченная кривая. Эта кривая представляет собой параболу (рис. \(\PageIndex{2}\)).
Рисунок \(\PageIndex{2}\): Парабола Подобно эллипсу и гиперболе, парабола также может быть определена набором точек на координатной плоскости.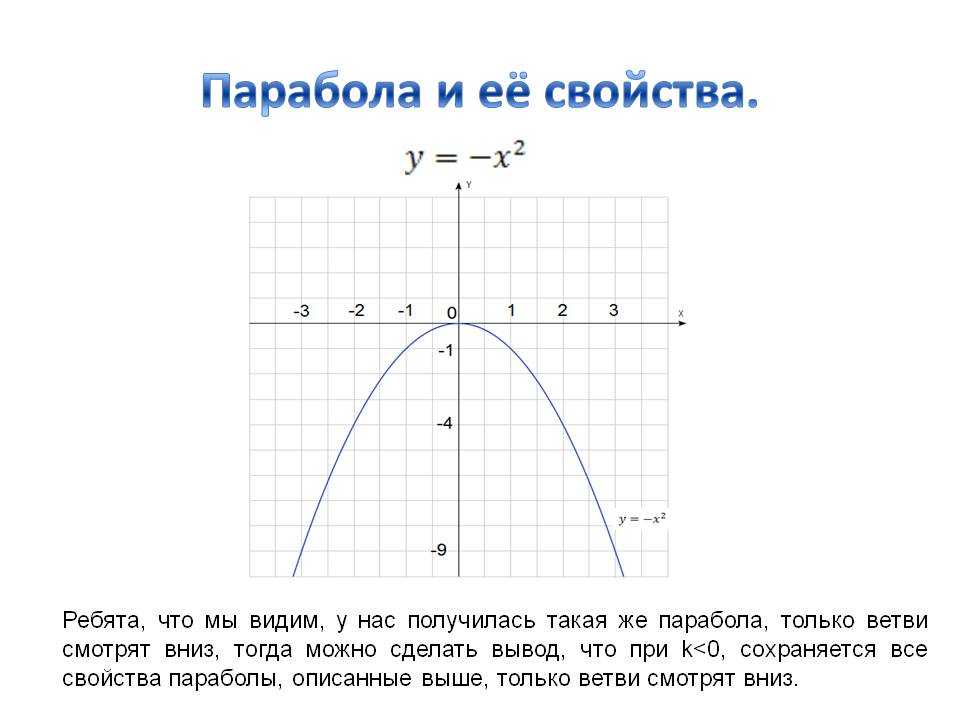 Парабола — это множество всех точек \((x,y)\) на плоскости, которые находятся на одинаковом расстоянии от фиксированной линии, называемой директриса , а фиксированная точка ( фокус ) не на директрисе.
Парабола — это множество всех точек \((x,y)\) на плоскости, которые находятся на одинаковом расстоянии от фиксированной линии, называемой директриса , а фиксированная точка ( фокус ) не на директрисе.
Ранее мы узнали о вершине параболы и оси симметрии. Теперь мы расширим обсуждение, включив в него другие ключевые свойства параболы (рис. \(\PageIndex{3}\)). Обратите внимание, что ось симметрии проходит через фокус и вершину и перпендикулярна директрисе. Вершина — это середина между директрисой и фокусом. Отрезок, проходящий через фокус и параллельный директрисе, называется 9-м.0050 широкая прямая кишка . Концы широкой прямой кишки лежат на кривой. По определению расстояние d от фокуса до любой точки \(P\) на параболе равно расстоянию от \(P\) до директрисы.
Рисунок \(\PageIndex{3}\): Основные характеристики параболы Для работы с параболами в координатной плоскости мы рассмотрим два случая: с вершиной в начале координат и с вершиной в точке .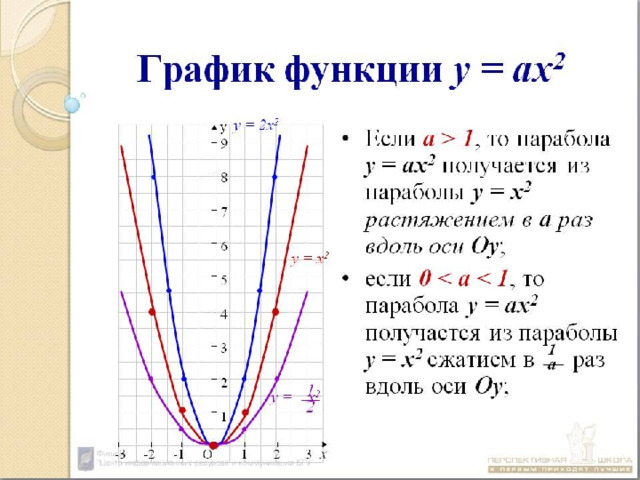 точку, отличную от исходной. Начнем с первого.
точку, отличную от исходной. Начнем с первого.
СТАНДАРТНЫЕ ФОРМЫ ПАРАБОЛ С ВЕРШИНОЙ \((0,0)\)
Таблица \(\PageIndex{1}\) и рисунок \(\PageIndex{5}\) суммируют стандартные характеристики парабол с вершиной в Происхождение.
| Ось симметрии | 92=4py\)\((0, р)\) | \(у=-р\) | \((\pm 2p, p)\) |
|---|
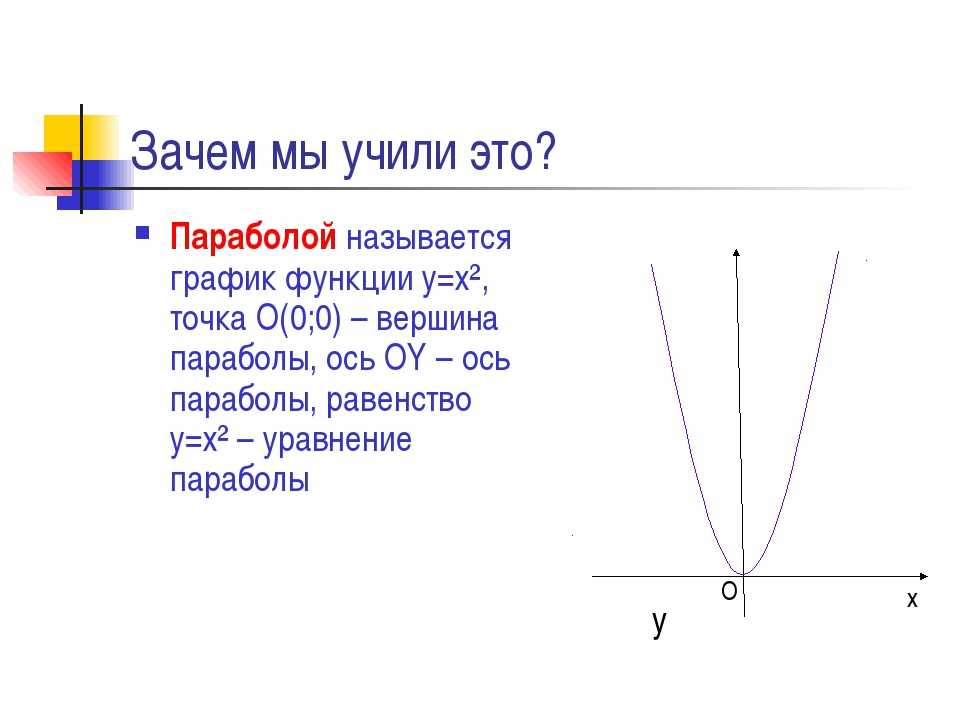 (c) Когда \(p<0\) и осью симметрии является ось y, парабола раскрывается. (d) Когда \(p<0\) и осью симметрии является ось y, парабола открывается вниз.
(c) Когда \(p<0\) и осью симметрии является ось y, парабола раскрывается. (d) Когда \(p<0\) и осью симметрии является ось y, парабола открывается вниз.Ключевыми характеристиками параболы являются ее вершина, ось симметрии, фокус, директриса и широкая прямая кишка (рис. \(\PageIndex{5}\)). Получив стандартное уравнение для параболы с центром в начале координат, мы можем легко определить ключевые особенности для построения графика параболы. Прямая называется касательной к кривой, если она пересекает кривую ровно в одной точке. Если мы нарисуем линии, касающиеся параболы в конечных точках прямой кишки , эти линии пересекутся на оси симметрии, как показано на рисунке \(\PageIndex{6}\). 92=4px\), тогда
- осью симметрии является ось \(x\), \(y=0\)
- набор \(4p\) равный коэффициенту \(x\) в данном уравнении для решения \(p\). Если \(p>0\), парабола открывается вправо. Если \(p<0\), парабола открывается влево.
- используйте \(p\) для нахождения координат фокуса, \((p,0)\)
- используйте \(p\) для нахождения уравнения направляющей, \(x=−p\)
- используйте \(p\) для нахождения концов широкой прямой кишки, \((p,\pm 2p)\).
 В качестве альтернативы подставьте \(x=p\) в исходное уравнение. 92=4py\), тогда
В качестве альтернативы подставьте \(x=p\) в исходное уравнение. 92=4py\), тогда- осью симметрии является ось \(y\), \(x=0\)
- набор \(4p\) равный коэффициенту \(y\) в данном уравнении, которое нужно решить для \(p\). Если \(p>0\), парабола раскрывается. Если \(p<0\), парабола раскрывается вниз.
- используйте \(p\) для нахождения координат фокуса, \((0,p)\)
- используйте \(p\) для нахождения уравнения направляющей, \(y=−p\)
- используйте \(p\) для нахождения концов широкой прямой кишки, \((\pm 2p,p)\) 92=4px\). Таким образом, осью симметрии является ось x . Отсюда следует, что:
- \(24=4p\), значит \(p=6\). Так как \(p>0\), парабола выходит вправо на
- координаты фокуса \((p,0)=(6,0)\)
- уравнение направляющей \(x=−p=−6\)
- конечные точки широкой прямой кишки имеют одинаковую координату x в фокусе.
 Чтобы найти конечные точки, подставьте \(x=6\) в исходное уравнение: \((6,\pm 12)\)
Чтобы найти конечные точки, подставьте \(x=6\) в исходное уравнение: \((6,\pm 12)\)
- \(−6=4p\), поэтому \(p=−\dfrac{3}{2}\). Так как \(p<0\), парабола направлена вниз.
- координаты фокуса \((0,p)=(0,−\dfrac{3}{2})\)
- уравнение направляющей \(y=−p=\dfrac{3}{2}\)
- конечные точки широкой прямой кишки можно найти, подставив \(y=\dfrac{3}{2}\) в исходное уравнение, \((\pm 3,−\dfrac{3}{2})\)
Далее наносим фокус, директрису и 92=8у\). Определите и обозначьте фокус, направляющую и конечные точки прямой кишки latus .
- Ответить
- Фокус: \((0,2)\)
- Директриса: \(y=−2\)
- Конечные точки широкой прямой кишки: \((\pm 4,2)\).
Запись уравнений параболы в стандартной форме
В предыдущих примерах мы использовали уравнение стандартной формы параболы для расчета расположения ее ключевых элементов.
 2=4p(y−k)\) для парабол, у которых ось симметрии параллельна \( у\)-ось. Эти стандартные формы приведены ниже вместе с их общими графиками и ключевыми характеристиками.
2=4p(y−k)\) для парабол, у которых ось симметрии параллельна \( у\)-ось. Эти стандартные формы приведены ниже вместе с их общими графиками и ключевыми характеристиками.СТАНДАРТНЫЕ ФОРМЫ ПАРАБОЛ С ВЕРШИНОЙ \((H, K)\)
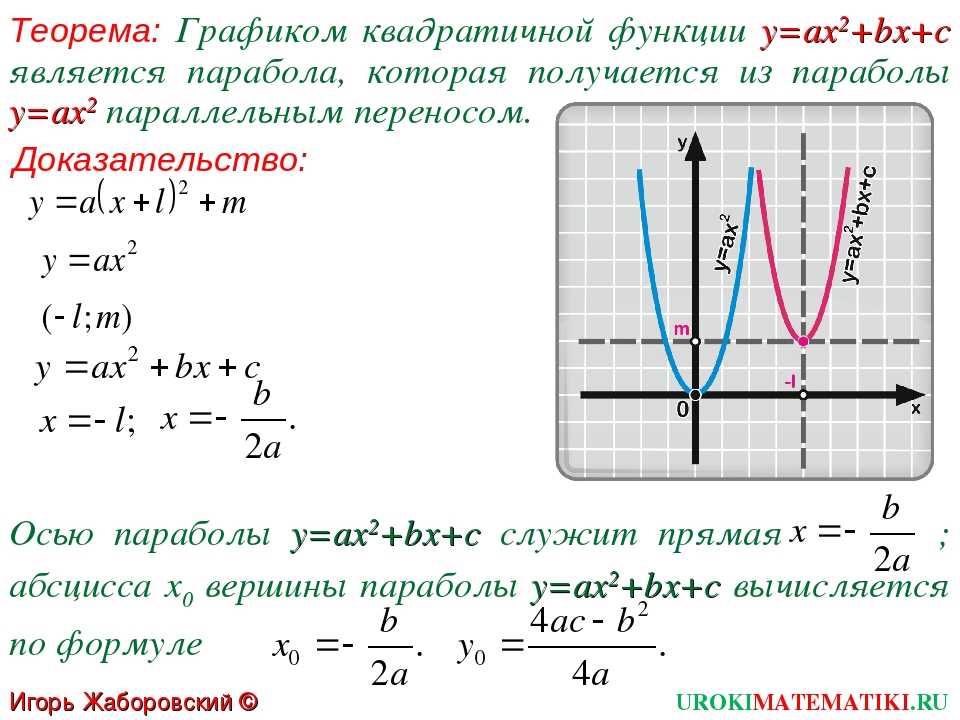
Таблица \(\PageIndex{2}\) и рисунок \(\PageIndex{11}\) суммируют стандартные характеристики парабол с вершиной в точка \((h,k)\).
Рисунок \(\PageIndex{11}\): (a) Когда \(p>0\), парабола открывается вправо.Таблица \(\PageIndex{2}\) Ось симметрии Уравнение Фокус Директриса Конечные точки широкой прямой кишки 92=4р(у-к)\) \((ч, к+р)\) \(у=к-р\) \((ч\пм 2р, к+р)\)  2=4p(y−k)\). 92=4p(x−h)\), тогда:
2=4p(y−k)\). 92=4p(x−h)\), тогда:- использовать данное уравнение для определения \(h\) и \(k\) для вершины, \((h,k)\)
- использовать значение \(k\) для определения оси симметрии, \(y=k\)
- набор \(4p\) равный коэффициенту \((x−h)\) в данном уравнении для решения \(p\). Если \(p>0\), парабола выходит вправо. Если \(p<0\), парабола открывается влево.
- используйте \(h\), \(k\) и \(p\) , чтобы найти координаты фокуса, \((h+p, k)\) 92=4p(y−k)\), тогда:
- использовать данное уравнение для определения \(h\) и \(k\) для вершины, \((h,k)\)
- использовать значение \(h\) для определения оси симметрии, \(x=h\)
- набор \(4p\) равный коэффициенту \((y−k)\) в данном уравнении для решения \(p\). Если \(p>0\), парабола раскрывается. Если \(p<0\), парабола раскрывается вниз.
- используйте \(h\), \(k\) и \(p\) , чтобы найти координаты фокуса, \((h, k+p)\)
- используйте \(k\) и \(p\) для нахождения уравнения направляющей, \(y=k−p\)
- используйте \(h\), \(k\) и \(p\) , чтобы найти концы широкой прямой кишки, \((h\pm 2p, k+p)\)
- Постройте вершину, ось симметрии, фокус, директрису и прямую кишку, а затем нарисуйте плавную кривую, чтобы сформировать параболу.

- вершина равна \((h,k)=(−3,1)\)
- ось симметрии \(y=k=1\)
- \(−16=4p\), поэтому \(p=−4\). Так как \(p<0\), парабола открывается влево.
- координаты фокуса равны \((h+p,k)=(−3+(−4),1)=(−7,1)\)
- уравнение направляющей \(x=h−p=−3−(−4)=1\)
- концы широкой прямой кишки равны \((h+p,k\pm 2p)=(−3+(−4),1\pm 2(−4))\), или \((−7,− 7)\) и \((−7,92=4(х-8)\). Определите и обозначьте вершину, ось симметрии, фокус, направляющую и конечные точки прямой кишки latus .
- Ответить
- Вершина: \((8,−1)\)
- Ось симметрии: \(y=−1\)
- Фокус: \((9,−1)\)
- Директриса: \(x=7\)
- Концы широкой прямой кишки : \((9,−3)\) и \((9,1)\).

92&= 4⋅7⋅(y+8) \end{align*}\]- вершина равна \((h,k)=(4,−8)\)
- ось симметрии \(x=h=4\)
- так как \(p=7\), \(p>0\) и таким образом парабола раскрывается
- координаты фокуса равны \((h,k+p)=(4,−8+7)=(4,−1)\)
- уравнение направляющей равно \(y=k−p=−8−7=−15\)
- концы широкой прямой кишки равны \((h\pm 2p,k+p)=(4\pm 2(7),−8+7)\) или \((−10,−1)\) и \((18,−1)\) 92=−20(y−3)\). Определите и обозначьте вершину, ось симметрии, фокус, направляющую и конечные точки прямой кишки latus .
- Ответить
- Вершина: \((−2,3)\)
- Ось симметрии: \(x=−2\)
- Фокус: \((−2,−2)\)
- Директриса: \(y=8\)
- Конечные точки широкой прямой кишки : \((−12,−2)\) и \((8,−2)\).
Решение прикладных задач, связанных с параболами
Как мы упоминали в начале раздела, параболы используются для проектирования многих объектов, которые мы используем каждый день, таких как телескопы, подвесные мосты, микрофоны и радиолокационное оборудование.
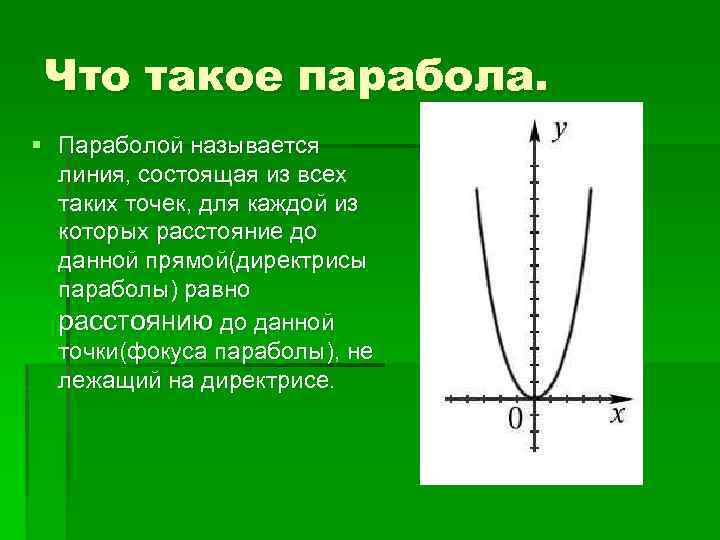
Рисунок \(\PageIndex{16}\): отражающее свойство парабол Параболические зеркала, такие как то, которое использовалось для зажигания олимпийского огня, обладают уникальными отражающими свойствами. Когда лучи света, параллельные оси симметрии параболы, направляются на любую поверхность зеркала, свет отражается прямо в фокус (рис. \(\PageIndex{16}\)). Вот почему олимпийский факел зажигается, когда его держат в фокусе параболического зеркала.
Параболические зеркала, такие как то, которое использовалось для зажигания олимпийского огня, обладают уникальными отражающими свойствами. Когда лучи света, параллельные оси симметрии параболы, направляются на любую поверхность зеркала, свет отражается прямо в фокус (рис. \(\PageIndex{16}\)). Вот почему олимпийский факел зажигается, когда его держат в фокусе параболического зеркала.Параболические зеркала способны фокусировать солнечную энергию в одной точке, повышая температуру на сотни градусов за считанные секунды. Таким образом, параболические зеркала используются во многих недорогих, энергоэффективных солнечных продуктах, таких как солнечные плиты, солнечные обогреватели и даже дорожные разжигатели огня.
Пример \(\PageIndex{6}\): решение прикладных задач, связанных с параболами
На рисунке \(\PageIndex{17}\) показано поперечное сечение конструкции переносного солнечного пожарного пускателя. Солнечные лучи отражаются от параболического зеркала к объекту, прикрепленному к воспламенителю.
 2=4py\), где \(p>0\). Воспламенитель, который является фокусом, находится на \(1,7\) дюймах выше вершины тарелки. Таким образом, мы имеем \(p=1,7\). 92&=6.8y\qquad \text{Подставить } 2.25 \text{ вместо } x\\ y&\ приблизительно 0.74\qquad \text{Решить для } y \end{выравнивание*}\]
2=4py\), где \(p>0\). Воспламенитель, который является фокусом, находится на \(1,7\) дюймах выше вершины тарелки. Таким образом, мы имеем \(p=1,7\). 92&=6.8y\qquad \text{Подставить } 2.25 \text{ вместо } x\\ y&\ приблизительно 0.74\qquad \text{Решить для } y \end{выравнивание*}\]Блюдо примерно \(0.74 \) дюймов глубиной.
Упражнение \(\PageIndex{6}\)
Солнечные плиты размером с балкон были разработаны для семей, живущих в Индии. Верх блюда имеет диаметр \(1600\) мм. Солнечные лучи отражаются от параболического зеркала в сторону «варки», расположенной \(320\) мм от основания.
- Найдите уравнение, моделирующее поперечное сечение солнечной плиты. Предположим, что вершина параболического зеркала является началом координатной плоскости и что парабола выходит вправо (т. е. имеет 92=4р(у-к)\)
Ключевые понятия
- Парабола — это множество всех точек \((x,y)\) на плоскости, находящихся на одинаковом расстоянии от фиксированной прямой, называемой фокус) не на директрисе.

- Стандартная форма параболы с вершиной \((0,0)\) и осью x в качестве оси симметрии может быть использована для построения графика параболы. Если \(p>0\), парабола открывается вправо. Если \(p<0\), парабола открывается влево. См. пример \(\PageIndex{1}\).
- Стандартная форма параболы с вершиной \((0,0)\) и осью y в качестве оси симметрии может быть использована для построения графика параболы. Если \(p>0\), парабола раскрывается. Если \(p<0\), парабола раскрывается вниз. См. пример \(\PageIndex{2}\).
- Зная фокус и направляющую параболы, мы можем записать ее уравнение в стандартной форме. См. пример \(\PageIndex{3}\).
- Стандартная форма параболы с вершиной \((h,k)\) и осью симметрии, параллельной оси \(x\) может быть использована для построения параболы. Если \(p>0\), парабола открывается вправо. Если \(p<0\), парабола открывается влево. См. пример \(\PageIndex{4}\).
- Стандартная форма параболы с вершиной \((h,k)\) и осью симметрии, параллельной оси \(y\) может быть использована для построения параболы.
 Если \(p>0\), парабола раскрывается. Если \(p<0\), парабола раскрывается вниз. См. пример \(\PageIndex{5}\).
Если \(p>0\), парабола раскрывается. Если \(p<0\), парабола раскрывается вниз. См. пример \(\PageIndex{5}\). - Реальные ситуации можно моделировать с помощью стандартных уравнений парабол. Например, зная диаметр и фокус поперечного сечения параболического отражателя, мы можем найти уравнение, моделирующее его стороны. См. пример \(\PageIndex{6}\).
Эта страница под названием 12.3: The Parabola распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать страницу TOC
- нет
- Теги
- парабола
- Парабола с горизонтальной осью
- Парабола с вертикальной осью
- источник@https://openstax.
 org/details/books/precalculus
org/details/books/precalculus - стандартная форма параболы
Парабола | Определение, уравнение и факты
- Развлечения и поп-культура
- География и путешествия
- Здоровье и медицина
- Образ жизни и социальные вопросы
- Литература
- Философия и религия
- Политика, право и правительство
- Наука
- Спорт и отдых
- Технология
- Изобразительное искусство
- Всемирная история
- В этот день в истории
- Викторины
- Подкасты
- Словарь
- Биографии
- Резюме
- Популярные вопросы
- Инфографика
- Демистификация
- Списки
- #WTFact
- Товарищи
- Галереи изображений
- Прожектор
- Форум
- Один хороший факт
- Развлечения и поп-культура
- География и путешествия
- Здоровье и медицина
- Образ жизни и социальные вопросы
- Литература
- Философия и религия
- Политика, право и правительство
- Наука
- Спорт и отдых
- Технология
- Изобразительное искусство
- Всемирная история
- Britannica объясняет
В этих видеороликах Britannica объясняет различные темы и отвечает на часто задаваемые вопросы.
- Britannica Classics
Посмотрите эти ретро-видео из архивов Encyclopedia Britannica. - Demystified Videos
В Demystified у Britannica есть все ответы на ваши животрепещущие вопросы. - #WTFact Videos
В #WTFact Britannica делится некоторыми из самых странных фактов, которые мы можем найти. - На этот раз в истории
В этих видеороликах узнайте, что произошло в этом месяце (или любом другом месяце!) в истории.
- Студенческий портал
Britannica — лучший ресурс для учащихся по ключевым школьным предметам, таким как история, государственное управление, литература и т. д. - Портал COVID-19
Хотя этот глобальный кризис в области здравоохранения продолжает развиваться, может быть полезно обратиться к прошлым пандемиям, чтобы лучше понять, как реагировать сегодня. - 100 женщин
Britannica празднует столетие Девятнадцатой поправки, выделяя суфражисток и политиков, творящих историю.
- Парабола — это множество всех точек \((x,y)\) на плоскости, находящихся на одинаковом расстоянии от фиксированной прямой, называемой фокус) не на директрисе.
Отсюда следует, что:
Пример \(\PageIndex{4}\): построение параболы с вершиной \((h, k)\) и осью симметрии, параллельной оси \(x\) 92=4p(x−h)\). Таким образом, ось симметрии параллельна оси \(х\). Отсюда следует, что:


 , Парабола, Квант, № 4, 1975.
, Парабола, Квант, № 4, 1975.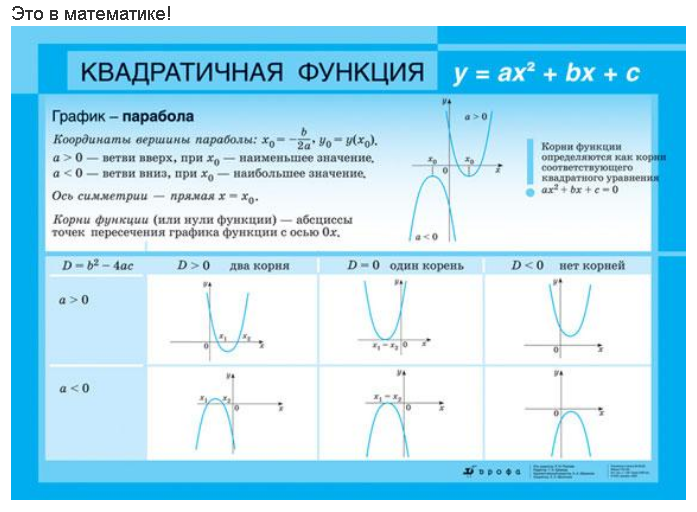 И наоборот, свет от источника, находящегося в фокусе, отражается параболой в пучок параллельных её оси лучей.
И наоборот, свет от источника, находящегося в фокусе, отражается параболой в пучок параллельных её оси лучей. С. Парабола // Курс аналитической геометрии и линейной алгебры. — М.: Наука, 1979. — С. 69—72. — 512 с.
С. Парабола // Курс аналитической геометрии и линейной алгебры. — М.: Наука, 1979. — С. 69—72. — 512 с.
 В качестве альтернативы подставьте \(x=p\) в исходное уравнение. 92=4py\), тогда
В качестве альтернативы подставьте \(x=p\) в исходное уравнение. 92=4py\), тогда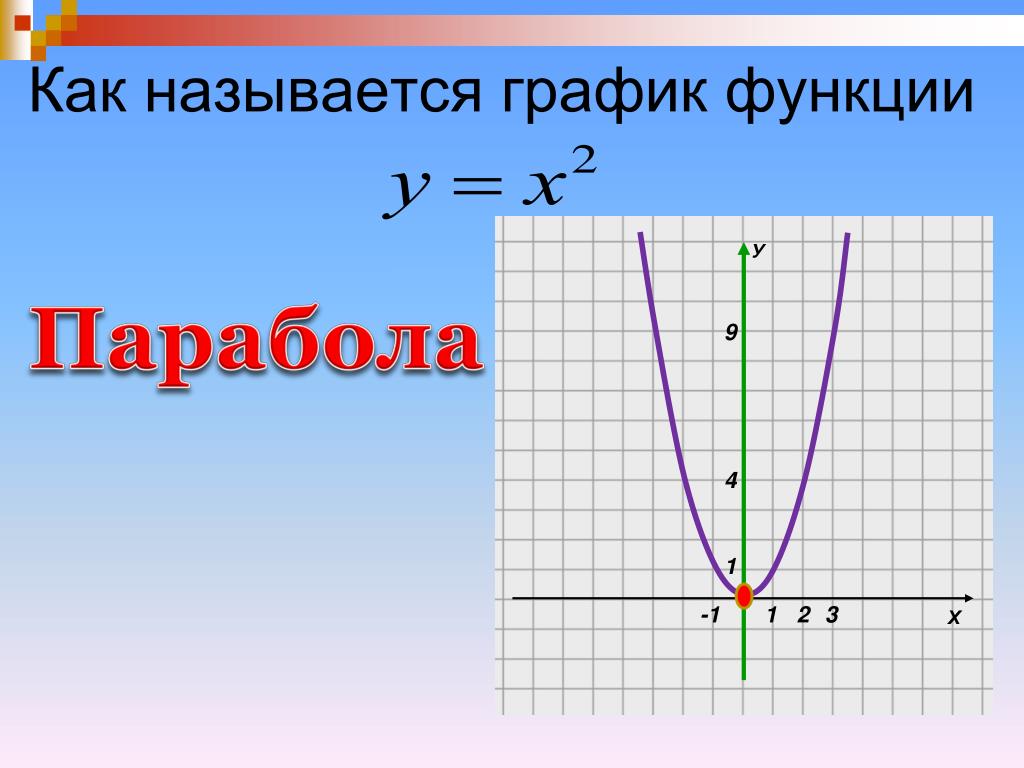 Чтобы найти конечные точки, подставьте \(x=6\) в исходное уравнение: \((6,\pm 12)\)
Чтобы найти конечные точки, подставьте \(x=6\) в исходное уравнение: \((6,\pm 12)\) 2=4p(y−k)\) для парабол, у которых ось симметрии параллельна \( у\)-ось. Эти стандартные формы приведены ниже вместе с их общими графиками и ключевыми характеристиками.
2=4p(y−k)\) для парабол, у которых ось симметрии параллельна \( у\)-ось. Эти стандартные формы приведены ниже вместе с их общими графиками и ключевыми характеристиками. 2=4p(y−k)\). 92=4p(x−h)\), тогда:
2=4p(y−k)\). 92=4p(x−h)\), тогда:
 Параболические зеркала, такие как то, которое использовалось для зажигания олимпийского огня, обладают уникальными отражающими свойствами. Когда лучи света, параллельные оси симметрии параболы, направляются на любую поверхность зеркала, свет отражается прямо в фокус (рис. \(\PageIndex{16}\)). Вот почему олимпийский факел зажигается, когда его держат в фокусе параболического зеркала.
Параболические зеркала, такие как то, которое использовалось для зажигания олимпийского огня, обладают уникальными отражающими свойствами. Когда лучи света, параллельные оси симметрии параболы, направляются на любую поверхность зеркала, свет отражается прямо в фокус (рис. \(\PageIndex{16}\)). Вот почему олимпийский факел зажигается, когда его держат в фокусе параболического зеркала. 2=4py\), где \(p>0\). Воспламенитель, который является фокусом, находится на \(1,7\) дюймах выше вершины тарелки. Таким образом, мы имеем \(p=1,7\). 92&=6.8y\qquad \text{Подставить } 2.25 \text{ вместо } x\\ y&\ приблизительно 0.74\qquad \text{Решить для } y \end{выравнивание*}\]
2=4py\), где \(p>0\). Воспламенитель, который является фокусом, находится на \(1,7\) дюймах выше вершины тарелки. Таким образом, мы имеем \(p=1,7\). 92&=6.8y\qquad \text{Подставить } 2.25 \text{ вместо } x\\ y&\ приблизительно 0.74\qquad \text{Решить для } y \end{выравнивание*}\]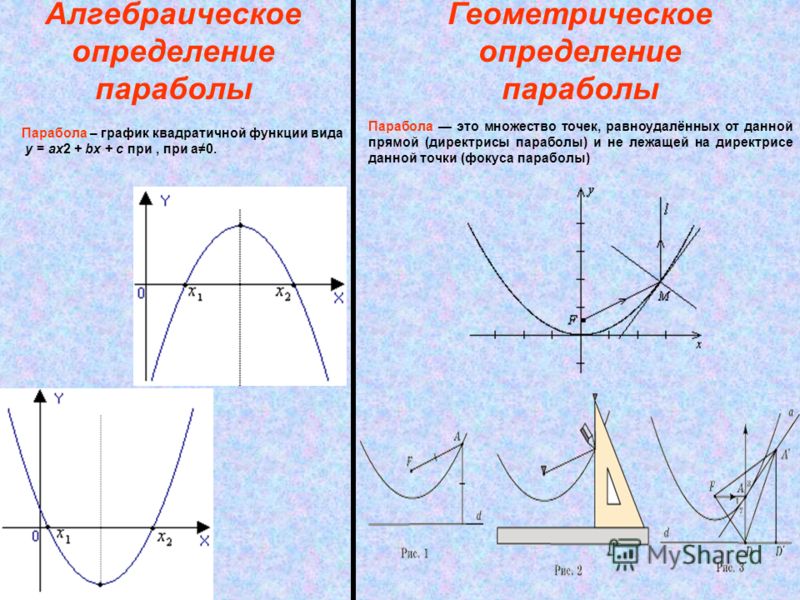
 Если \(p>0\), парабола раскрывается. Если \(p<0\), парабола раскрывается вниз. См. пример \(\PageIndex{5}\).
Если \(p>0\), парабола раскрывается. Если \(p<0\), парабола раскрывается вниз. См. пример \(\PageIndex{5}\). org/details/books/precalculus
org/details/books/precalculus