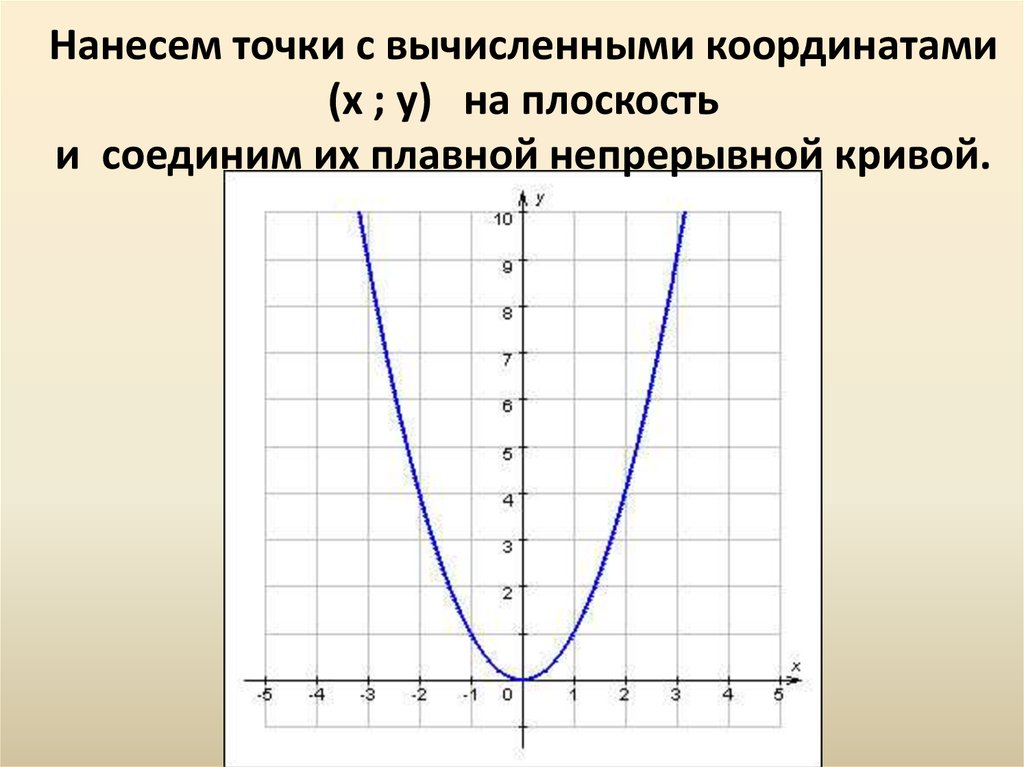
Квадратичная функция, ее график.
1º. Функция, заданная формулой , гдеx, y– переменные,a, b, c– действительные числа, причема ≠ 0, называетсяквадратичной.
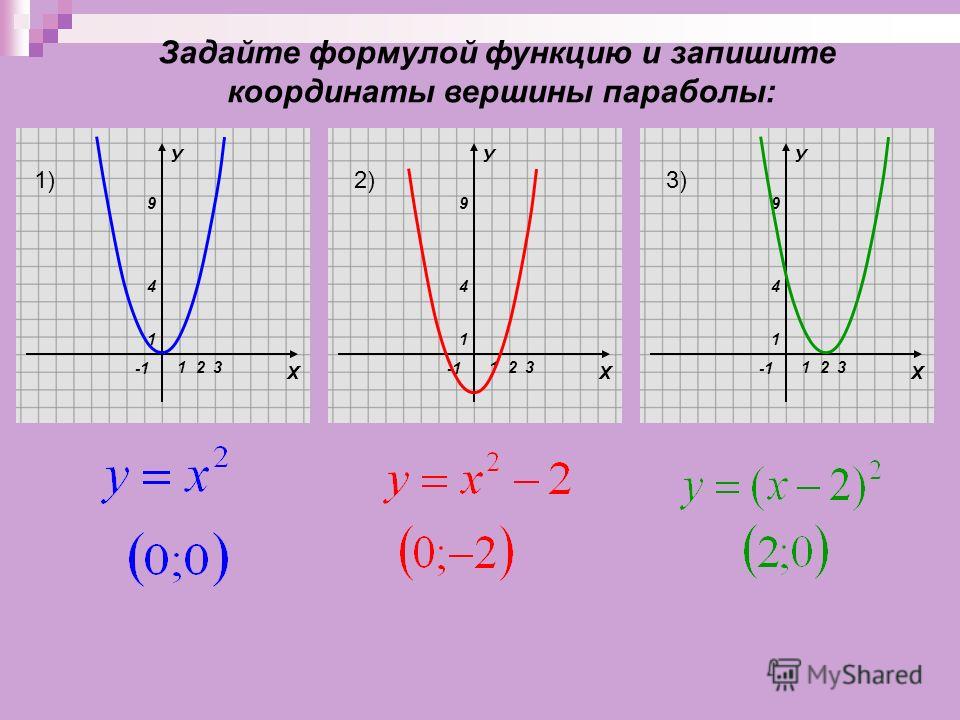
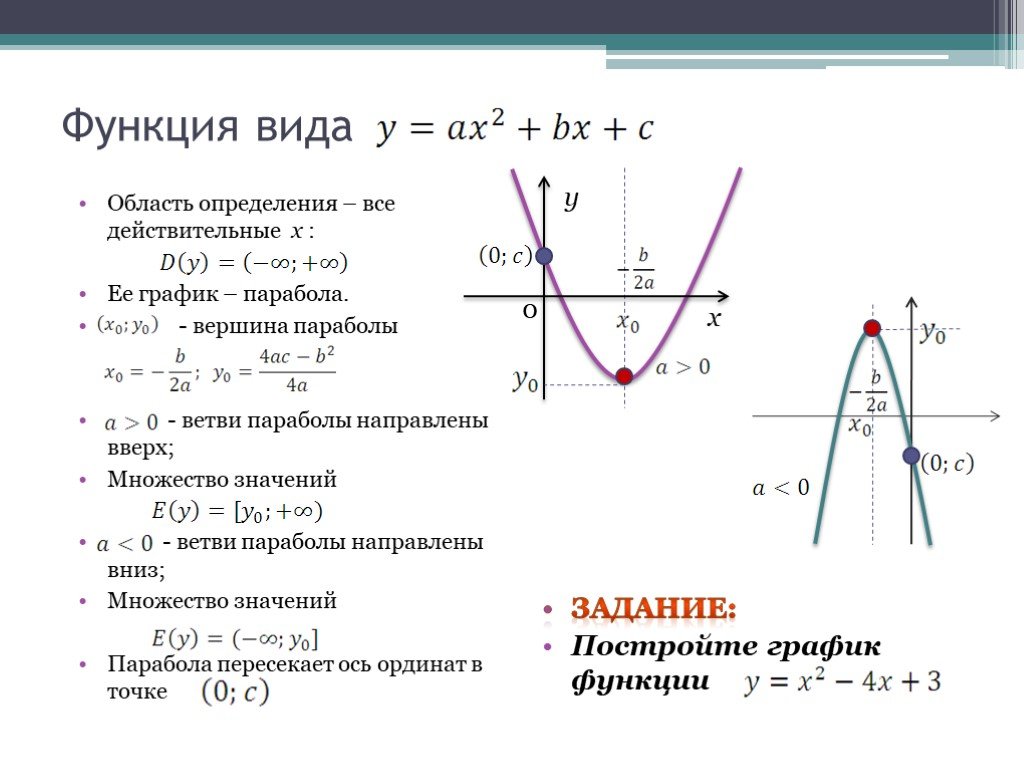
2º. Графиком функции является парабола – кривая, симметричная относительно прямой, проходящей через вершину параболы.
Координаты вершины параболы определяются по формулам:
.
Если квадратичную функцию путем выделения полного квадрата привести к виду, то точка (x0;y0) – вершина параболы.
График квадратичной функции получается из графика функциис помощью параллельного переноса.
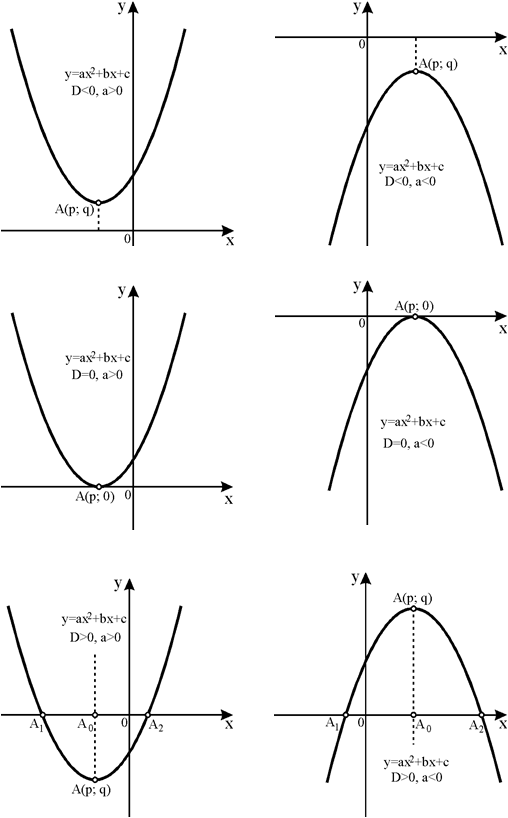
3º. Если коэффициент a > 0, ветви параболы направлены вверх, еслиa < 0– вниз.
При
парабола пересекает ось абсцисс в двух
точках, приD=0– в одной (т.
Пример 3. Построим график функции .
Выполним следующие преобразования (называемые «выделением полного квадрата»):
График функции получается из графика функциипараллельным переносом на 2 единицы влево и на две единицы вниз.
Уравнения, содержащие переменную под знаком модуля.
1º. Модуль (абсолютная величина)числааопределяется следующим образом:
.
Геометрический смысл модуля: |a| есть расстояние от точки числовой оси, изображающей данное числоа, до начала отсчета — точки О, а |x—a| есть расстояние между точками числовой оси, соответствующими числамхиа.
2º. Уравнения вида можно решать геометрически.
Рассмотрим аналитические способы решения уравнений, содержащих переменную под знаком модуля, на примерах.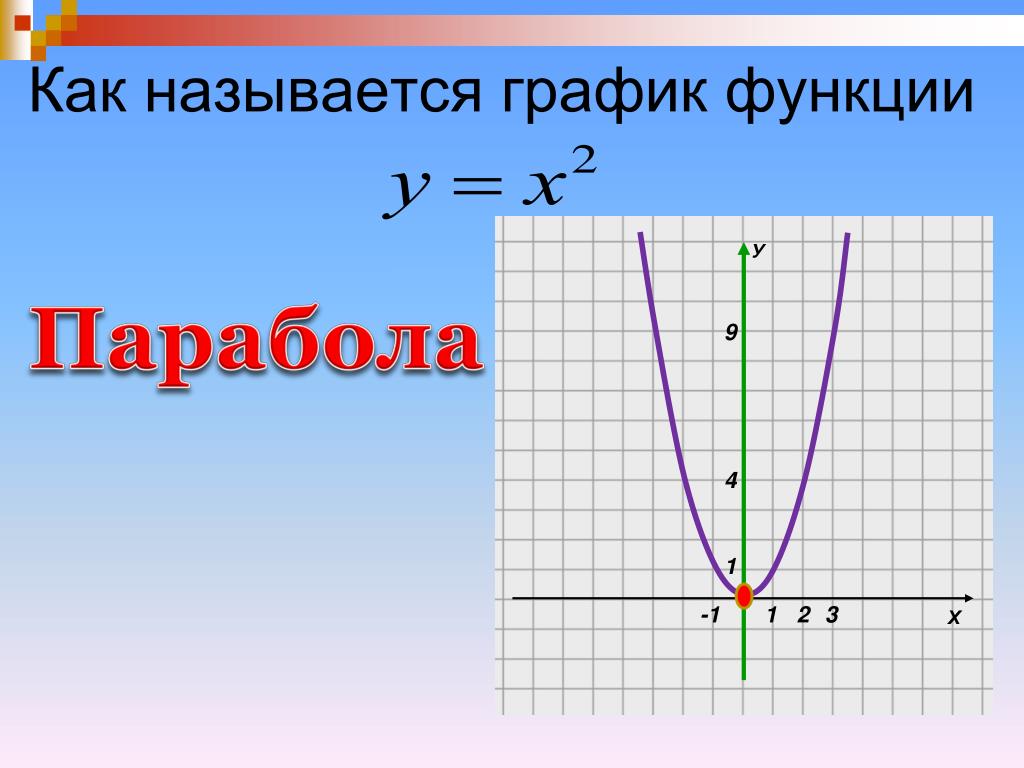
При решении уравнений важно уметь в соответствии с определением модуля освободиться от вертикальных скобок.
Например, , еслиa≥ 5;
, еслиa< 5.
Пример 4. Решим уравнение , используя определение модуля числа.
Решение: Уравнение имеет решение, если x+1≥0, т.е.x≥-1.
.
Условие x≥-1 выполняется в обоих случаях.
Ответ: 4; 2/3.
Пример 5. Решим уравнение , используя свойство модулей («модули противоположных чисел равны»).
Решение:
.
|2x+1|=7=>2x+1=7или2x+1=-7=>
|2x+1|-3=-4 => |2x+1|=-1 – нет решений.
Ответ: 3; -4.
Пример 6.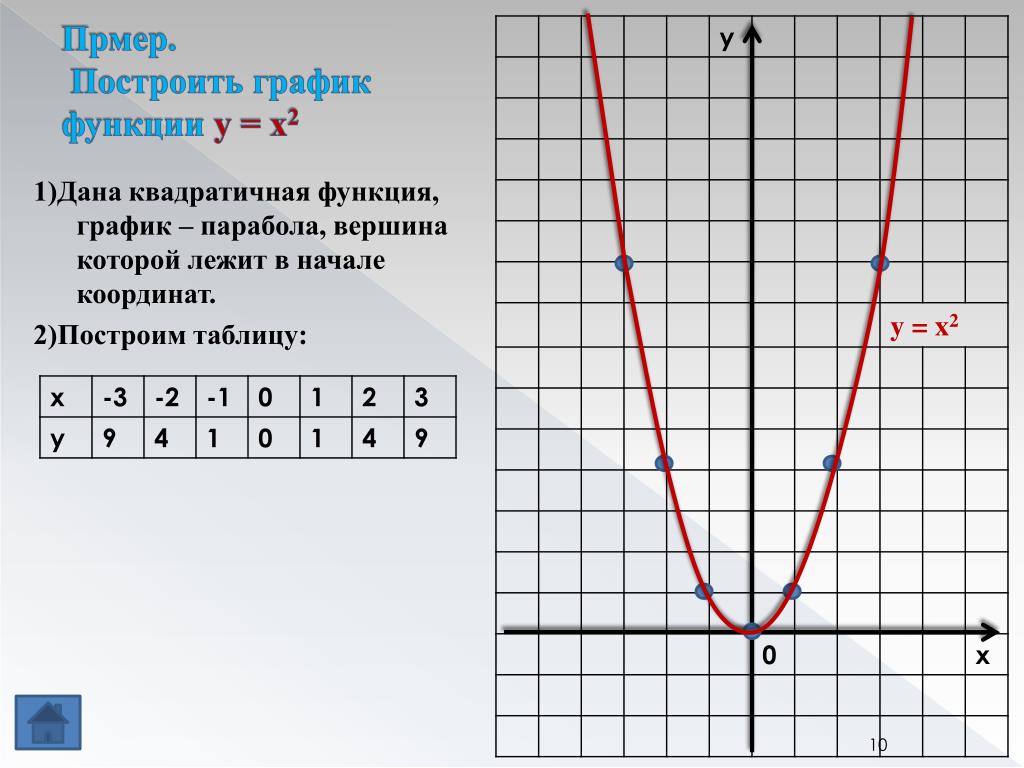 Решим уравнение
,
рассматривая решения на интервалах.
Решим уравнение
,
рассматривая решения на интервалах.
Решение: Найдем нули модулей, т.е. такие значения x, при которыхи: .
Рассмотрим уравнение на интервалах (-∞; -2), [-2; -1), [-1; +∞).
а) Для уравнение примет вид:
-(x+1)-(x+2)=2; —x-1-x-2=2; -2x=5; x=-2,5;=>x=-2,5– корень уравнения.
б) Для уравнение примет вид:
-(x+1)+(x+2)=2; —x-1+x+2=2; 0·x=1- нет корней.
в) Для уравнение примет вид:
x+1+x+2=2; 2x=-1; x=-0,5;=>x=-0,5– корень уравнения.
Ответ: -2,5; -0,5.
Дидактический материал.
Решите уравнения, сводящиеся к линейным:
1. ; 2.; 3.;
4. ; 5.;
6. ; 7.;
8. ; 9.;
10. ; 11..
Решите квадратные уравнения:
12. ; 13.;
14. ; 15.;
16. .
Разложите на линейные множители:
17. ; 18.; 19.;
; 18.; 19.;
20. ; 21..
Сократите дроби:
22. ; 23.; 24.;
25. ; 26.; 27..
Упростите выражение:
28. ; 29..
Найдите среднее арифметическое всех действительных корней уравнения:
30. ; 31.;
32. ; 33.;
34. ; 35.;
36. .
Найдите расстояние от вершины параболы до точки М:
37. ; 38.;
39. ; 39..
Постройте график функции:
40. ; 41.; 42.;
43. ; 44.; 45.;
46. ; 47.; 48.;
49. ; 50.; 51..
52. По графику квадратичной функции определить знаки ее коэффициентов и их суммы:
Найдите рациональные корни уравнения:
53. ; 54.; 55.;
56. ; 57.; 58.;
59. ; 60.; 61..
Решите уравнения:
62. ; 63.; 64.;
65. ; 66.; 67.;
68. ; 69.;
70. ; 71.; 72..
Эллипс и парабола — Техническая графика
Вопрос 6 — Эллипсы и параболы
Основные части эллипса
|
Ключевые понятия
|
|
Как нарисовать эллипс методом окружности
1 — Нарисуйте круг диаметром, равным большой оси , и круг диаметром, равным малой оси используя один и тот же центр 2 – Разделите круги на 12 частей, используя угольник с углом 30 градусов. 4 — Используйте эти точки, чтобы нарисовать эллипс от руки |
Как провести касательную к эллипсу в точке, стр.
1 — Найдите 2 точки фокусировки, F1 и F2 3 — Разделите пополам угол между линиями фокусных точек, как показано синим цветом 4 — Касательная — это линия, которая делит пополам угол в точке P |
Проблема эллипса — p230 Q6
| youtube.com/embed/eY6iZNoBwhU?wmode=opaque» frameborder=»0″ allowfullscreen=»»> |
Парабола
Как нарисовать параболу (метод прямоугольника)
|
График параболы — JavaTpoint
следующий → ← предыдущая Графики квадратичных функций известны в математике как параболы. Параболы — это плоские кривые с зеркальной симметрией, которые обычно имеют U-образную форму. В этой главе будет изложена история стандартной формулы параболы, показаны примеры нескольких стандартных форм и описаны характеристики параболы. ВведениеУравнение параболы имеет точку на кривой, равноотстоящую от фиксированной точки и фиксированной линии. Фокус параболы — это неподвижная точка, а направляющая параболы — это неподвижная линия. Критические кривые в координатной геометрии являются параболическими кривыми. Также важно помнить, что фиксированная точка не находится на фиксированной линии. Расположение точек, известных как параболы, равноудалено от точки фокусировки и определенной линии (директрисы). Формула ПараболыПарабола обычно определяется как y = an (x-h)2 + k или x = a(y-k)2 + h, где (h,k) обозначает вершину. Формула y2 = 4ax определяет правильную параболу. Чтобы понять компоненты и характеристики параболы, вы должны быть знакомы с приведенными ниже словами. Точка служит фокусом параболы (a, 0). Директриса: Директриса — это гипотетическая линия, проведенная перпендикулярно оси Y и проходящая через (-a, 0). Параболы с перпендикулярными осями встречаются в параболах. Фокусная хорда: Хорда, проходящая через центр параболы, называется фокальной хордой. В двух местах эта хорда пересекает параболу. Фокусное расстояние: Фокусное расстояние — это расстояние между фокусом и точкой на параболе с координатами (x1, y1). В результате фокус находится на том же расстоянии и перпендикулярно директрисе. Lacus Rectum: хорда, проходящая через центр параболы и перпендикулярная ее оси. Эксцентриситет: (e = 1). Это отношение расстояния точки от фокуса к расстоянию от директрисы. При рассмотрении параболы она равна 1, Стандартные уравнения параболыДля параболы существует четыре общих уравнения. Четыре общие формы зависят от оси и ориентации параболы. Эти параболы имеют различные поперечные и сопряженные оси. Четыре общих уравнения и формы параболы можно увидеть на следующем изображении. Из уравнений в их стандартной форме можно сделать следующие выводы:
Формула параболыФормула параболы представляет общую форму параболического пути на плоскости. Формулы, используемые для определения параметров параболы, перечислены ниже.
График параболыВот график следующего квадратного уравнения в форме параболы. Примите во внимание формулу y = 32 — 6x + 5. A, B и C в этой параболе равны трем. При положительном значении парабола расширяется. Вершина: (ч,к) (ч,к) ч = -b/2а = 6/(2 × 3) = 1 к = f(ч) (ч) = f(1) = 3(1)2 — 6 (1) + 5 = 2 , поэтому вершина (1,2) Широкая прямая кишка = (4a) = (4 + 3) = (12) Фокус: (1,25/12) = (ч, к+ 1/4а) Ось симметрии x = 1. Y = k-1/4a в директрисе у = 2 — 1/12 ⇒ у — 23/12 = 0 Характеристики Параболы Здесь мы попытаемся понять некоторые ключевые характеристики и словарный запас параболы. Касательная: Линия, касающаяся параболы, называется касательной. Уравнение yy1=2a(x+x1) выполняется в точке касания (x1,y1)(x1,y1) касательной к параболе y2 = 4ax. Обычный: Эта линия проходит через точку касания и фокус параболы и перпендикулярна к ней. Нормальное уравнение (yy1)=y12a(xx1)(yy1)(xx1), проходит через точку (x1,y1)(x1,y1) и имеет наклон m = -y1/2a для параболы с уравнение y2 = 4ax. Хорда контакта: Хорда контакта проведена в точке, где соприкасаются две касательные к параболе. Уравнение хорды контакта yy1=2x(x+x1)yy1=2x(x+x1) в точке (x1,y1)(x1,y1) вне параболы. Полюс и поляра: Нарисуйте внешнюю точку параболы — расположение точек пересечения касательных — на концах хорд. Полюс определяется как поляра, проведенная из этой точки. В результате, когда используется термин «полярный», он относится к полюсу. Для полюса с координатами (x1,y1)(x1,y1) уравнение поляры имеет вид yy1=2x(x+x1)yy1, где y2 = 4ax для параболы. |

 меньший круг. Отметьте точки пересечения горизонтальных и вертикальных линий.
меньший круг. Отметьте точки пересечения горизонтальных и вертикальных линий.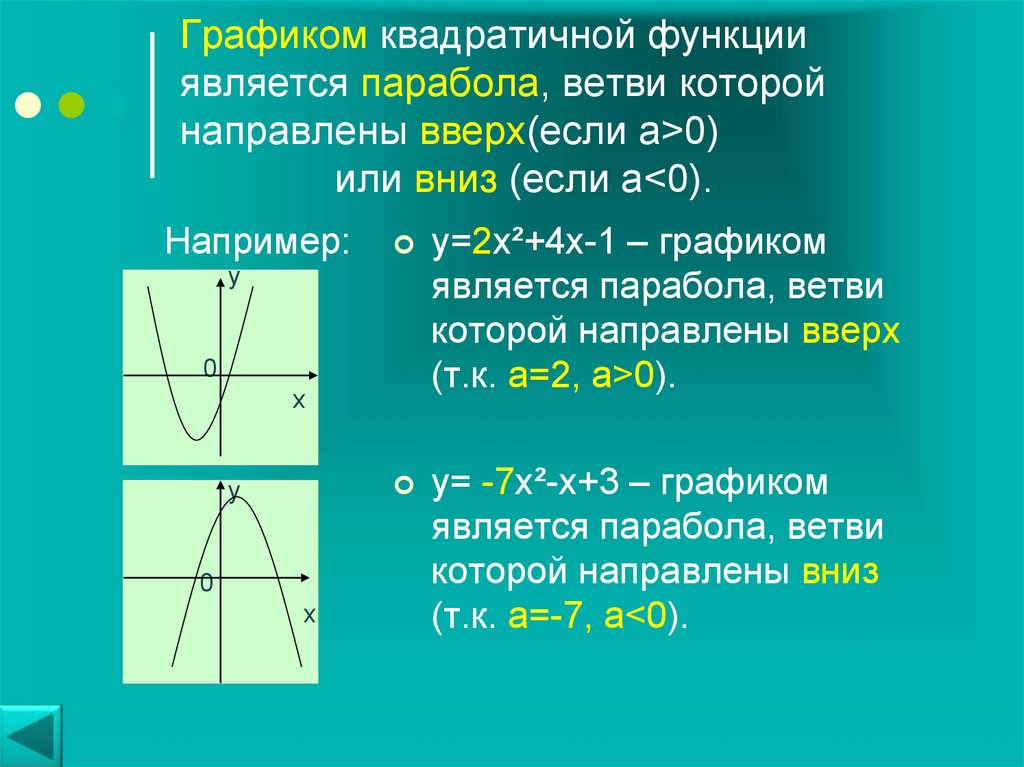 Паскаль определил параболу как проективную кривую окружности. Большую часть времени физические движения тела совершают криволинейный маршрут в форме параболы. Снаряды, падающие с равномерной гравитацией, следуют по траектории, которую Галилей назвал параболической траекторией.
Паскаль определил параболу как проективную кривую окружности. Большую часть времени физические движения тела совершают криволинейный маршрут в форме параболы. Снаряды, падающие с равномерной гравитацией, следуют по траектории, которую Галилей назвал параболической траекторией.
 По формуле LL’ = 4а, длина широкой прямой кишки. Концы широкой прямой кишки: (а, -2а), (а, -2а) и (а, а).
По формуле LL’ = 4а, длина широкой прямой кишки. Концы широкой прямой кишки: (а, -2а), (а, -2а) и (а, а).