Паралелограм це: Неприпустима назва — Вікіпедія

Паралелограм та його властивості. Ознаки паралелограма

Паралелограм та його властивості. Ознаки паралелограма

Великий клас чотирикутників становлять паралелограми.

Чотирикутник, у якого протилежні сторони паралельні, називається паралелограмом.

Висотою паралелограма називається відрізок, що є перпендикуляром до прямої, яка містить протилежну сторону.

У паралелограма з кожної його вершини можна провести по дві висоти. Висоти, проведені з вершин тупих кутів паралелограма, лежать у паралелограмі; висоти, проведені з гострих тупих кутів паралелограма, лежать зовні паралелограма.

Властивості паралелограма

У паралелограмі протилежні сторони рівні.

У паралелограмі протилежні кути рівні.

У паралелограмі сума кутів, прилеглих до однієї сторони, дорівнює 180°.

Діагоналі паралелограма перетинаються і точкою перетину діляться навпіл.

Діагоналі паралелограма ділять його на два рівні трикутники.

Ознаки паралелограма

Якщо діагоналі чотирикутника перетинаються й у точці перетину діляться навпіл, то цей чотирикутник паралелограм.

Якщо в чотирикутнику дві протилежні сторони паралельні і рівні, то цей чотирикутник паралелограм.

Якщо в чотирикутнику протилежні сторони попарно рівні, то цей чотирикутник паралелограм.

Якщо в чотирикутнику протилежні кути попарно рівні, то цей чотирикутник паралелограм.

Властивість діагоналей паралелограма:

Діагоналі паралелограма перетинаються й у точці перетину діляться навпіл.

Властивість протилежних сторін і кутів паралелограма

:

У паралелограма протилежні сторони й кути рівні.

Це цікаво.

Якщо провести бісектриси двох протилежних кутів паралелограма, то вони будуть паралельні або співпадуть.

Якщо провести бісектриси двох кутів, прилеглих до однієї сторони паралелограма, то вони будуть перпендикулярні.

Паралелограм ❤️| Довідник з геометрії

Геометрія

Чотирикутники

Чотирикутником називається фігура, яка складається з чотирьох точок і чотирьох відрізків, що послідовно їх сполучають. При цьому жодні три з даних точок не повинні лежати на одній прямій, а відрізки, які їх сполучають, не повинні перетинатися. Дані точки називаються Вершинами чотирикутника, а відрізки, що їх сполучають,- Сторонами чотирикутника.
Вершини чотирикутника називаються Сусідніми, якщо вони є кінцями однієї з його сторін. Несусідні вершини називаються Проти­леж­ними. Відріз­ки, що сполучають протилежні

вершини чотирикутника, називаються Діагоналями.
Сторони чотирикутника, що виходять з однієї вершини, називаються Сусідніми сторонами. Сторони, які не мають спільного кінця, називаються Протилежними сторонами.
Периметр Чотирикутника – сума дов­жин усіх його сторін.
Чотирикутник називається Опуклим, ­якщо він лежить в одній півплощині відносно будь-якої прямої, що містить його сторону.
На рисунку нижче зліва ABCD – опуклий чотирикутник; AC, BD – його діагоналі. На рисунку справа KMNP – неопуклий чотирикутник; KN, MP – його діагоналі.

Сума кутів чотирикутника дорівнює .

Паралелограм

Паралелограм – це чотирикутник, у якого протилежні сторони паралельні.
На рисунку ABCD – паралелограм.

; .

Властивості паралелограма

Теорема 1. У паралелограма протилежні сторони рівні:

, (дивись вищенаведений рисунок). У паралелограма протилежні кути рівні: , .
Теорема 2. У паралелограмі кути, прилеглі до однієї сторони, в сумі дорівнюють :
; ;
; .
Теорема 3. Діагоналі паралелограма перетинаються й у точці перетину діляться нав­піл.
; .
Теорема 4. Діагональ паралелограма поділяє його на два рівні трикутники.
На рисунку нижче зліва . На рисунку справа .

Теорема 5. Діагоналі паралелограма розбивають його на дві пари рівних трикутників.

На рисунку ; .

Ознаки паралелограма

Теорема 1. Якщо діагоналі чотирикутника перетинаються й у точці перетину діляться навпіл, то цей чотирикутник – паралелограм.
Теорема 2. Якщо в чотирикутнику дві сторони паралельні й рівні, то цей чотирикутник – паралелограм.
Теорема 3. Якщо в чотирикутнику протилежні сторони рівні, то цей чотирикутник – паралелограм.
Теорема 4. Якщо в чотирикутнику протилежні кути рівні, то цей чотирикутник – паралелограм.
Теорема 5. Якщо в чотирикутнику кути, що є прилеглими до кожної із сторін, у сумі дорівнюють

, то цей чотирикутник – паралелограм.
Теорема 6. Якщо кожна діагональ поділяє чотирикутник на два рівні трикутники, то цей чотирикутник – паралелограм.

Кут між висотами паралелограма

Висота паралелограма – це відрізок, перпендикулярний до протилежних сторін паралелограма з кінцями на цих сторонах.
На рисунку

і – висоти паралело­грамa.

Найчастіше висоти опускають із вершин паралелограма. Із кожної вершини паралелограма можна провести дві висоти. Кут між ними дорівнюватиме куту паралелограма при сусідній вершині. На рисунку внизу зліва зображений кут між висотами паралелограма, опущеними з тупого кута, на рисунку справа – між висотами, опущеними з гострого ­кута:

Властивості бісектрис кутів паралелограма

1. Бісектриси сусідніх кутів паралелограма перпендику­лярні.
2. Бісектриси протилежних кутів паралелограма паралельні або збігаються (якщо паралелограм – ромб).
3. Бісектриса кута паралелограма відокремлює від нього рівнобедрений трикутник.
На рисунку

; ; ; – рівнобедрений; ; – рівнобедрений, .

Чотирикутник, що утворився при перетині бісектрис кутів паралелограма,- прямокутник. Якщо через точку перетину діагоналей паралелограма проведено пряму, то відрізок цієї прямої, який розташований між паралельними сторонами, ділиться в цій точці навпіл:

Визначення паралелограма — що це таке, значення та поняття — Я хочу все знати

Походить від латинського слова паралелограм, концепція паралелограм служить для ідентифікації a чотирикутник, де протилежні сторони паралельні один одному . Це геометрична фігура він становить, таким чином, багатокутник, який складається з 4 сторін, де є два випадки паралельних сторін.

Цікаво відзначити, що існують різні типи паралелограм. The паралелограми групи прямокутників наприклад, фігури, на яких можна побачити внутрішні кути 90 °. У цей набір включені квадрат (де всі сторони мають однакову довжину) і прямокутник (де сторони, що протистоять одна одній, мають однакову довжину).

The паралелограми, які розглядаються як не прямокутники З іншого боку, вони характеризуються тим, що мають 2 гострі внутрішні кути, а інші — тупі. Ця класифікація включає ромб (чиї сторони поділяють те саме довжина а також має 2 пари однакових кутів) і at ромбовидний (із протилежними сторонами однакової довжини та 2 парами кутів, які також рівні між собою).

Для обчислення периметр паралелограм необхідно додати довжину всіх його сторін. Це можна зробити за допомогою наступної формули:

Сторона A x 2 + Сторона B x 2 . Наприклад: периметр прямокутного паралелограма, який має дві протилежні сторони 5 сантиметрів і дві протилежні сторони 10 сантиметрів, буде отриманий, помістивши ці значення у рівняння, викладене вище, яке дасть нам 5 x 2 + 10 x 2 = 30 сантиметри

Інша формула встановлення периметра паралелограма — це 2 x (сторона A + сторона B) . У нашому прикладі: 2 х (5 + 10) = 30. Все це формули коротше кажучи, вони спрощують процес додавання сторін, які має кожен паралелограм. Якщо ми виконаємо операцію Сторона A + Сторона A + Сторона B + Сторона B , результат був би однаковий (5 + 5 +10 + 10 = 30).

Дзвінок закон паралелограмаз іншого боку, визначає, що якщо додати довжини до квадрата кожної з чотирьох сторін будь-якого паралелограма, результат, який ми отримаємо, буде еквівалентним доданню квадратів його двох діагоналей.

Щодо їх властивості, необхідно споглядати їх у групах, оскільки, як було сказано вище, багато форм різних характеристик вважаються паралелограмами.

Деякі спільні для всіх:

* всі вони мають чотири сторони і чотири вершини, оскільки належать до групи чотирикутників;
* їхні протилежні сторони ніколи не перетинаються, оскільки вони завжди паралельні;
* довжина протилежних сторін завжди однакова;
* їхні протилежні кути вимірюють однакові;
* сума двох його вершин, за умови, що вони суміжні, це дає 180 °, тобто вони додаткові;
* внутрішні кути повинні додавати 360 °;
* площа його завжди повинна бути вдвічі більша за трикутник, побудований з його діагоналей;
* кожен паралелограм опуклий;
* його діагоналі повинні ділити одна одну;
* точка, в якій поділяються її діагоналі, — це те, що вважається центром паралелограма;
* її центр є одночасно його барицентром;

* якщо ви намалюєте лінію, яка перетинає його центр область Паралелограм ділиться на дві однакові частини.

З іншого боку, паралелограми різних типів можуть мати особливі властивості, які не стосуються решти. Наприклад:

* квадратний паралелограм може дати ідентичну фігуру, якщо він обернутий на 90 ° ділянки, що також можна виразити, сказавши, що він має симетрію обертання порядку 4;
* типи ромбоїда, ромба та прямокутника, з іншого боку, повинні бути повернені на 180 °, щоб отримати той самий результат;
* ромб має 2 осі симетрія, які розрізають його, з’єднуючи його протилежні вершини;
* прямокутник, з іншого боку, має 2 осі симетрії відображення, які перпендикулярні його сторонам;
* Нарешті, квадрат має 4 осі симетрії відображення, які з’єднують кожну пару протилежних вершин і прорізають центр вертикально і горизонтально.

Share

Pin

Tweet

Send

Share

Send

Тест з геометрії – «На Урок»

Запитання 1

Паралелограм — це

варіанти відповідей

чотирикутник, у якого тільки дві сторони паралельні

чотирикутник у якого дві сторони рівні.

чотирикутник, у якого кожні дві протилежні сторони паралельні.

чотирикутник, у якого два протилежні кути рівні.

Запитання 2

Якої властивості не має паралелограм?

варіанти відповідей

Протилежні сторони паралелограма рівні.

Діагоналі паралелограма рівні.

Протилежні кути паралелограма рівні.

Діагоналі паралелограма точкою перетину діляться навпіл.

Сума кутів прилеглих до однієї сторони паралелограма дорівнює 180 градусів.

Запитання 3

Якої ознаки не має паралелограм?

варіанти відповідей

Якщо в чотирикутнику кожні дві сторони рівні, то цей чотирикутник паралелограм.

Якщо в чотирикутнику дві протилежні сторони рівні та паралельні, то цей чотирикутник — паралелограм.

Якщо в чотирикутнику діагоналі точкою перетину діляться навпіл, то цей чотирикутник паралелограм.

Якщо в чотирикутнику два протилежні кути рівні, то цей чотирикутник паралелограм.

Запитання 4

Розв’яжіть задачу за малюнком.

варіанти відповідей

Запитання 5

Розв’яжіть задачу за малюнком.

варіанти відповідей

Запитання 6

Розв’яжіть задачу за малюнком

варіанти відповідей

Запитання 7

Ров’яжіть задачу за малюнком.

варіанти відповідей

Запитання 8

Розв’яжіть задачу за малюнком.

варіанти відповідей

Запитання 9

Розв’яжіть задачу за малюнком.

варіанти відповідей

Запитання 10

Розв’яжіть задачу за малюнком

варіанти відповідей

Запитання 11

Сума двох кутів паралелограма 240 градусів. Знайти градусну міру сусідніх кутів.

варіанти відповідей

120 градусів і 60 градусів

120 градусів і 80 градусів

240градусів і 40 градусів

120 градусів і 120градусів

Запитання 12

Периметр паралелограма дорівнює 40 см. Знайдіть його сторону, якщо вони відносяться як 1:3.

варіанти відповідей

Створюйте онлайн-тести
для контролю знань і залучення учнів
до активної роботи у класі та вдома

Створити тест

Натисніть «Подобається», щоб слідкувати за оновленнями на Facebook

ЩО ТАКЕ ПАРАЛЕЛОГРАМ? — МАТЕМАТИКА

Розімар Гувея, професор математики та фізики

Паралелограм — це плоска фігура, яка має чотири сторони . Це частина досліджень геометрії площини, яка є чотирикутником, протилежні сторони якого паралельні.

Іншими словами, паралелограми — це багатокутники з чотирма протилежними конгруентними сторонами (які мають однакову міру), наприклад, квадрат, ромб і прямокутник.

Паралелограм

Площа паралелограма

Щоб знайти площу паралелограма, просто обчисліть добуток базового виміру на висоту, виражений формулою:

A = bh

Де,

A : площа
b : основа
h : висота

Дізнайтеся більше про тему:

Паралелограм периметр

Периметр паралелограма, тобто сума всіх сторін фігури, обчислюється виразом:

P = 2 (a + b)

Де,

P : периметр
a і b : довжини двох сторін

Дізнайтеся більше про тему:

Діагоналі паралелограм

Паралелограми мають чотири сторони і, отже, дві діагоналі .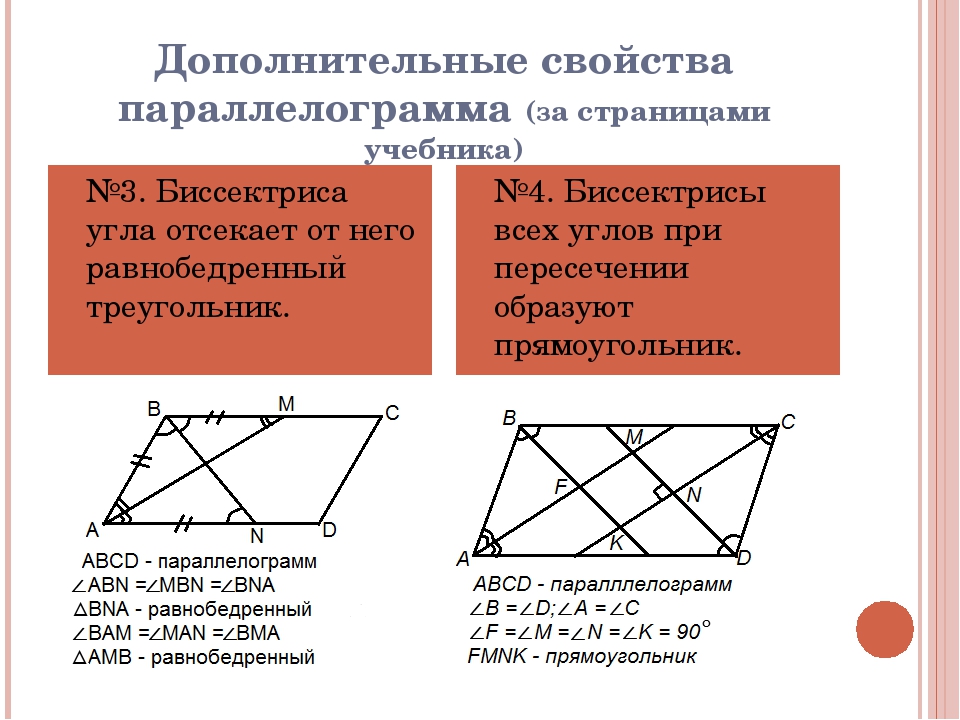 Зверніть увагу, що їх діагоналі перетинаються у відповідних серединах.

Кути паралелограма

Паралелограм має чотири вершини , з чотирма внутрішніми та чотирма зовнішніми кутами, а протилежні кути мають однакові вимірювання. Сума внутрішніх або зовнішніх кутів дорівнює 360 °.

Властивості паралелограма

Властивості паралелограма узагальнюють усі його характеристики, згадані вище, а саме:

Про сторони:

Протилежні сторони паралелограма конгруентні, тобто вони мають однакову міру.

Про діагоналі:

• Діагоналі паралелограма перетинаються у відповідних середніх точках (середина малюнка).
• Діагоналі паралелограма ділять фігуру на два конгруентні трикутники.
• Якщо це прямокутник, діагоналі збіжні.

Про кути:

• Протилежні кути паралелограма збіжні (однакова міра).
• Послідовні кути паралелограма є додатковими, сума яких становить 180 °.
• Сума внутрішніх або зовнішніх кутів складає 360 °.

Розв’язані вправи

1 . Знайдіть площу паралелограма основи 10 см і висоту 5 см.

Переглянути відповідь

Пам’ятайте, що для пошуку площі просто помножте базову міру на висоту:

A = bh
A = 10,5
A = 50 см ²

2 . Який периметр паралелограма 4 см і 5 см?

Переглянути відповідь

Для розрахунку периметра використовуємо наступну формулу:

P = 2 (a + b)
P = 2 (4 + 5)
P = 2,9
P = 18 см

Зрозумійте більше про тему :

Що таке паралелограм? »Його визначення та значення 2021

У геометрії багатокутник відомий як паралелограм , який складається з чотирьох сторін і характеризується тим, що його протилежні сторони паралельні одна одній, це означає, що ці сторони знаходяться на однаковій відстані. Цей чотирикутник перетинається парою діагоналей, які збігатимуться в тій же точці , що є середньою точкою цих діагоналей.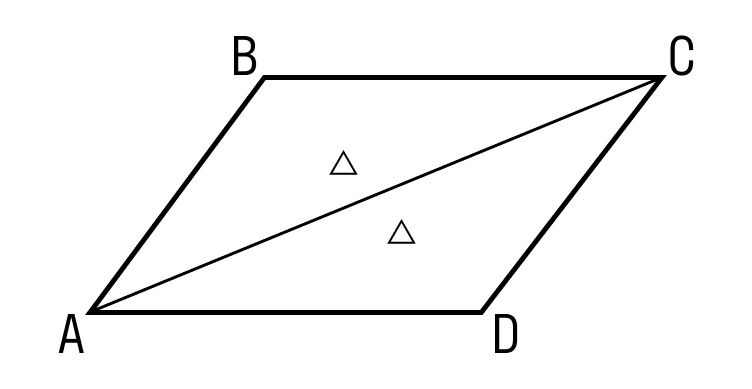 Однією химерністю є той факт, що всі його послідовні кути складають 180 градусів.

Важливо зазначити, що паралелограми можуть бути різних типів , з одного боку, це те, що входить до групи прямокутників ; це характеризується тим, що фігури мають внутрішні кути 90 °, серед найвизначніших паралелограм групи прямокутники відповідають квадратам і прямокутникам. З іншого боку, розташовані непрямокутники, що характеризуються лише двома гострими кутами, а решта тупими , деякі з них ромбоподібні та ромбові.

Для того, щоб обчислити площу паралелограма, потрібно помножити висоту на основу, її загальна формула a = bx a. З іншого боку, якщо то , що ви шукаєте , щоб знати , на периметр, то необхідно , щоб всі сторони , які роблять його додають.

У повсякденному житті цілком можливо, що люди часто стикаються з цими цифрами, оскільки існують тисячі предметів, які можуть мати таку форму , будь то книга, лінійка , письмовий стіл, стіл та багато інших.

Ні паралелограми, ні багатокутники не обмежені однією наукою , навпаки, існує багато областей, в яких потрібно використовувати цей тип фігур, таких як техніка, архітектура, столярні роботи, малювання, дизайн тощо.

З іншого боку, існує закон, який називається законом паралелограма , завдяки йому можна встановити взаємозв’язок між сторонами, що складають чуму, та її діагоналями. Цей закон говорить, що при додаванні квадратів довжин 4 сторін паралелограма це пропорційно сумі квадратів довжини кожної діагоналі.

Площа паралелограма

Паралелограмом називають чотирикутник у якого протилежні сторони паралельні між собою. Основні задачі в школі з даної теми полягають у обчисленні площі паралелограма, його периметру, висоти, діагоналей. Вказані величини та формули для їх обчислення будуть наведені нижче.

Властивості паралелограма

Протилежні сторони паралелограма, як і протилежні кути рівні між собою: AB=CD, BC=AD,

Діагоналі паралелограма в точці перетину діляться на дві рівні частини :

АО=OC, OB=OD. 2).

Основні ознаки паралелограмів:

1. Чотирикутник у якого протилежні сторони попарно паралельні є паралелограмом.
2. Чотирикутник з рівними протилежними сторонами є паралелограмом.
3. Чотирикутник з рівними і паралельними протилежними сторонами є паралелограмом.
4. Якщо діагоналі чотирикутника в точці перетину діляться навпіл то це паралелограм .
5. Чотирикутник у якого протилежні кути попарно рівні є паралелограмом

Бісектриси паралелограма

Бісектриси протилежних кутів у паралелограмі можуть бути паралельними або співпадати.

Бісектриси сусідніх кутів (прилеглі до однієї сторони) перетинаються під прямим кутом (перпендикулярні).

Висота паралелограма

Висота паралелограма — це відрізок, який проведений з кута перпендикулярно до основи. З цього слідує, що з кожного кута можна провести дві висоти.

Формула площі паралелограма

Площа паралелограма рівна добутку сторони на висоту проведену до неї. Формула площі наступна

Друга формула не менш популярна при обчисленнях і визначається так: Площа паралелограма рівна добутку сусідніх сторін на синус кута між ними

На основі наведених формул Ви будете знати, як обчислити площу паралелограма.

Периметр паралелограма

Формула для обчислення периметру паралелограма має вигляд

тобто периметр рівний подвоєному значенню суми сторін. Задачі на паралелограм будуть розглянуті в сусідніх матеріалах, а поки що вивчайте формули. Більшість задач з обчислення сторін, діагоналей паралелограма достатньо прості і зводяться до знання теореми синусів та теореми Піфагора.

Извините! — Страница не найдена

Пока мы разбираемся, возможно, поможет одна из ссылок ниже.

Дом Назад

• Класс
• Онлайн-тесты
• Ускоренный онлайн-курс JEE
• Двухлетний курс для JEE 2021

• Класс
• Онлайн-курс NEET
• Серия онлайн-тестов

• CA Foundation
• CA Средний
• CA Финал
• Программа CS

• Класс
• Серия испытаний
• Книги и материалы
• Тренажерный зал
• Умный взломщик BBA

• Обучение в классе
• Онлайн-коучинг
• Серия испытаний
• Взломщик Smart IPM
• Книги и материалы
• GD-PI

• CBSE, класс 8
• CBSE, класс 9
• CBSE, класс 10
• Класс 11 CBSE
• CBSE, класс 12

• Обучение в классе
• Онлайн-классы CAT
• Серия испытаний CAT
• MBA Жилой
• Умный взломщик CAT
• Книги и материалы
• Онлайн-классы без CAT
• Серия испытаний без CAT
• Тренажерный зал
• GD-PI

• Обучение в классе
• Серия испытаний
• Интервью с Civils

• Класс
• Онлайн-классы
• Серия испытаний SSC
• Переписка
• Практические тесты
• Электронные книги SSC
• Учебный пакет SSC JE

• Класс
• RBI, класс B
• Банковский тест серии
• Переписка
• Банковские электронные книги
• Банк ПДП

• Онлайн-коучинг
• Обучение в классе
• Серия испытаний
• Книги и материалы

• Класс
• Программа моста GRE

• GMAT Онлайн-коучинг
• Консультации по приему
• Консультации по GMAT

• Стажировка
• Корпоративные программы
• Студенты колледжа
• Рабочие специалисты
• Колледжи
• Школы

[PDF] Гипотезы для геометрии для математики 70 И.

Л. Цэ

1 Гипотезы для геометрии для математики 70 И. Л. Це Глава Гипотезы 1. Гипотеза о линейных парах: если два угла образуют …

Гипотезы для геометрии для математики 70 И.Л. Це Глава 2 Гипотезы 1. Гипотеза о линейной паре: если два угла образуют линейную пару, то сумма углов составляет 180 ° 2. Гипотеза о вертикальном угле: если два угла — это вертикальные углы, тогда они конгруэнтны (имеют равные меры) 3. Гипотеза о соответствующих углах, или гипотеза CA: Если две параллельные прямые пересекаются трансверсалью, то соответствующие углы конгруэнтны.4. Гипотеза об альтернативных внутренних углах или гипотеза AIA: если две параллельные прямые пересекаются трансверсалью, то альтернативные внутренние углы совпадают. 5. Гипотеза об альтернативных внешних углах или гипотеза AEA: если две параллельные прямые пересекаются трансверсалью, то альтернативные внешние углы совпадают. 6. Гипотеза о параллельных линиях: если две параллельные прямые пересекаются трансверсалью, то соответствующие углы конгруэнтны, чередующиеся внутренние углы совпадают, а чередующиеся внешние углы совпадают. 7. Гипотеза, противоположная гипотезе о параллельных линиях: если две прямые пересекаются трансверсалью, чтобы образовать пары соответствующих конгруэнтных углов, конгруэнтных чередующихся внутренних углов или конгруэнтных чередующихся внешних углов, то линии параллельны. Глава 3 Гипотезы 1. Гипотеза о серединном перпендикуляре: если точка находится на серединном перпендикуляре отрезка, то она равноудалена от конечной точки 2. Противоположна гипотезе о серединном перпендикуляре: если точка равноудалена от конечной точки, то точка на ней находится на серединном перпендикуляре.3. Гипотеза о кратчайшем расстоянии: кратчайшее расстояние от точки до прямой измеряется по перпендикулярному отрезку от точки до прямой. 4. Гипотеза о биссектрисе угла: если точка находится на биссектрисе угла, то она равноудалена от стороны угла 5. Гипотеза о параллельности биссектрисы угла: три биссектрисы угла треугольника пересекаются в точке (совпадают) и эта точка параллелизма называется инициатором. 6. Гипотеза о параллельном перпендикулярном биссектрисе: три серединных перпендикуляра треугольника совпадают, и эта денежная точка называется центром описанной окружности 7. Гипотеза о параллельности отношений: три высоты (или удержания, содержащие отношение) треугольника совпадают, и эта точка изменения называется ортоцентром. 8. Гипотеза о кругоцентре: центр описанной окружности треугольника равноудален от вершин. 9. Гипотеза о внутреннем центре: центр треугольника равноудален от сторон. 10. Гипотеза о медианном параллелизме: три медианы треугольника параллельны, т.е. они встречаются в одной точке, и эта точка называется точкой параллелизма.11. Гипотеза о центроидах: центроид треугольника делит каждую медиану на две части, так что расстояние от центроида до вершины в два раза больше расстояния от центроида до середины противоположной стороны. 12. Гипотеза о центре тяжести: Центроид треугольника — это центр тяжести треугольной области

1. Гипотеза о сумме треугольников — сумма углов в каждом треугольнике равна 180 °. 2. Гипотеза о равнобедренном треугольнике: если треугольник равнобедренный, то его углы в основании совпадают.3. Конверсия равнобедренного треугольника Гипотеза: если треугольник имеет два равнобедренных угла, то треугольник является равнобедренным треугольником. 4. Гипотеза о неравенствах треугольника Сумма длин любых двух сторон треугольника больше, чем длина третьей стороны. 5. Гипотеза о неравенстве бокового угла. В треугольнике, если одна сторона длиннее другой, то угол, противоположный длинной стороне, больше, чем угол, противоположный более короткой стороне. 6. Гипотеза о внешнем угле треугольника. Мера внешнего угла треугольника равна сумме мер удаленных внутренних углов.7. Гипотеза SSS-конгруэнтности: если три стороны одного треугольника конгруэнтны трем сторонам другого треугольника, то два треугольника конгруэнтны. 8. Гипотеза SAS-конгруэнтности: если две стороны и прилегающий угол одного треугольника совпадают с двумя сторонами и прилегающим углом другого треугольника, то два треугольника конгруэнтны. 9. Гипотеза о конгруэнтности ASA: если два угла и входящая сторона одного треугольника совпадают с двумя углами и входящей стороной другого треугольника, то треугольники равны.10. Гипотеза SAA-конгруэнтности: если два угла и не включенная сторона одного треугольника конгруэнтны соответствующим двум углам и невключенной стороне другого треугольника, то треугольники конгруэнтны. 11. Гипотеза о биссектрисе вертикального угла: в равнобедренном треугольнике биссектриса угла при вершине также является высотой и медианой основания. 12. Гипотеза о равностороннем / равностороннем треугольнике: каждый равносторонний треугольник является равноугольным, и, наоборот, каждый равноугольный треугольник является равносторонним.Глава 5 Гипотезы 1. Гипотеза о четырехугольной сумме Сумма четырех внутренних углов любого четырехугольника равна 360 °. 2. Гипотеза о сумме пятиугольника Сумма пяти внутренних углов любого пятиугольника равна 540 °. 3. Гипотеза о сумме многоугольников Сумма измерений n внутренних углов n-угольника равна 180 ° (n-2). 4. Гипотеза о сумме внешних углов: для любого многоугольника сумма размеров набора внешних углов равна 360 °. 5. Гипотеза о равноугольном многоугольнике: вы можете найти меру каждого внутреннего угла равноугольного угольника, используя любую из этих формул. : 180 —

360 ° 𝑛

; или

180 ° (𝑛 − 2) 𝑛

.

6. Гипотеза об углах воздушного змея: Невершинные углы воздушного змея совпадают. 7. Гипотеза о диагонали воздушного змея: диагонали воздушного змея перпендикулярны. 8. Гипотеза о биссектрисе диагонали воздушного змея: диагональ, соединяющая углы при вершинах воздушного змея, является серединным перпендикуляром другой диагонали. 9. Гипотеза о биссектрисе угла воздушного змея: углы при вершине воздушного змея делятся пополам диагональю. Страница 2 из 6

10. Последовательные углы трапеции Гипотеза: Последовательные углы между основаниями трапеции являются дополнительными.11. Гипотеза о равнобедренной трапеции: углы основания равнобедренной трапеции совпадают. 12. Диагонали равнобедренной трапеции. Гипотеза: диагонали равнобедренной трапеции совпадают. 13. Гипотеза о трех средних сегментах: три средних сегмента треугольника делят его на четыре конгруэнтных треугольника. 14. Гипотеза о среднем сегменте треугольника: средний сегмент треугольника параллелен третьей стороне и равен половине длины третьей стороны. 15. Гипотеза о срединном сегменте трапеции: средний сегмент трапеции параллелен основаниям и равен среднему значению длины двух оснований.16. Гипотеза о противоположных углах параллелограмма: Противоположные углы параллелограмма равны. 17. Гипотеза о последовательных углах параллелограмма: последовательные углы параллелограмма являются дополнительными. 18. Гипотеза о противоположных сторонах параллелограмма: Противоположные стороны параллелограмма равны. 19. Гипотеза о диагонали параллелограмма: диагонали параллелограмма делят друг друга пополам. 20. Гипотеза обоюдоострой линейки: если две параллельные прямые пересекаются второй парой параллельных прямых, которые находятся на том же расстоянии друг от друга, что и первая пара, то Образовавшийся параллелограмм представляет собой ромб.21. Гипотеза диагоналей ромба: диагонали ромба перпендикулярны и делят друг друга пополам. 22. Гипотеза об угле ромба: диагональ ромба делит углы ромба пополам. 23. Гипотеза о диагонали прямоугольника: диагонали прямоугольника совпадают и делят друг друга пополам. 24. Гипотеза квадратных диагоналей: диагонали квадрата равны и перпендикулярны друг другу. Глава 6 Гипотезы 1. Гипотеза о касательной: касательная к окружности перпендикулярна радиусу, проведенному до точки касания.2. Гипотеза касательных сегментов: касательные сегменты к окружности от точки за пределами круга конгруэнтны. 3. Гипотеза о центральных углах хорды: если две хорды в окружности конгруэнтны, то они определяют два центральных угла, которые конгруэнтны. 4. Гипотеза хордовых дуг: если две хорды в окружности совпадают, то их пересекаемые дуги совпадают. 5. Перпендикуляр к хорде Гипотеза: перпендикуляр от центра окружности к хорде является биссектрисой хорды 6. Гипотеза о расстоянии хорды до центра: две конгруэнтные хорды в окружности равноудалены от центра окружности.7. Серединный перпендикуляр хорды Гипотеза: серединный перпендикуляр хорды проходит через центр окружности. 8. Гипотеза о вписанном угле: Угол, вписанный в круг, составляет половину длины перехваченной дуги. Страница 3 из 6

9. Пересекающие дуги вписанного угла Гипотеза: вписанные углы, пересекающие одну и ту же дугу, конгруэнтны. 10. Угол, вписанный в полукруг. Гипотеза: углы, вписанные в полукруг, являются прямыми углами. 11. Циклический четырехугольник. Гипотеза: противоположные углы вписанного четырехугольника являются дополнительными.(вписанный четырехугольник — это четырехугольник, вписанный в круг) 12. Параллельные линии пересекают дуги Гипотеза: параллельные прямые пересекают конгруэнтные дуги на окружности. 13. Гипотеза окружности: Если C — длина окружности, а d — диаметр окружности, то существует число , например C = d. Если d = 2r, где r = радиус, то C = 2 r. 14. Гипотеза о длине дуги: длина дуги равна делению дуги на 360 °, умноженному на длину дуги или длину дуги  2r длины дуги   d 360 360 Глава 7 Гипотезы 1.Гипотеза о минимальном пути: если точки A и B находятся на стороне линии l, то минимальный путь от точки A до линии l до точки B находится путем отражения точки B через линию l, вычерчивая отрезок AB ‘, где точка C — точка пересечения отрезка AB ‘и прямой l. Глава 8 Гипотезы 1. Площадь прямоугольника Гипотеза: площадь прямоугольника задается формулой A = bh. Где A — площадь, b — длина основания, а h — высота прямоугольника. 2. Гипотеза о площади параллелограмма: Площадь параллелограмма задается формулой A = bh, где A — площадь, b — длина основания, а h — высота параллелограмма.1

3. Гипотеза площади треугольника Площадь треугольника определяется по формуле: 𝐴 = 2 𝑏ℎ, где A — площадь, b — длина основания, а h — высота треугольника. 1

4. Гипотеза о площади трапеции Площадь трапеции определяется формулой 𝐴 = 2 (𝑏1 + 𝑏2) ℎ, где A — площадь, b1 и b2 — длины двух оснований, а h — высота трапеция. 1

5. Гипотеза о площади воздушного змея: Площадь воздушного змея определяется формулой 𝐴 = 2d1d2, где d1 и d2 — длины диагоналей.1

6. Гипотеза о площади правильного многоугольника: Площадь правильного многоугольника определяется формулой 𝐴 = 2 𝑎𝑠𝑛 и 1

𝐴 = 2 𝑏𝑃, где A — площадь, P — периметр, a — апофема, s — длина каждой стороны, а n — количество сторон. 7. Гипотеза о площади круга: Площадь круга определяется формулой A = r2, где A — площадь, а r — радиус круга.

Глава 9 Гипотезы 1. Теорема Пифагора: В прямоугольном треугольнике сумма квадратов длин катетов равна квадрату длин гипотенузы.Страница 4 из 6

2. Обратное к теореме Пифагора: если длины трех сторон треугольника удовлетворяют уравнению Пифагора, то треугольник является прямоугольным. 3. Гипотеза о равнобедренном прямоугольном треугольнике: в равнобедренном прямоугольном треугольнике, если катет имеет длину l, тогда гипотенуза имеет длину 𝑙 2. 4. Гипотеза о треугольнике 30 ° –60 ° –90 °: в треугольнике 30 ° –60 ° –90 ° Треугольник, если более короткое плечо имеет длину a, то длинное плечо имеет длину 2, а гипотенуза — длину 2a. 5. Формула расстояния: расстояние между точками A (x1, y1) и B (x2, y2) определяется выражением (AB) 2 = (x2 –x1) 2+ (y2 –y1) 2 или 𝐴𝐵 = (𝑥2 — 𝑥1) 2 + (𝑦2 — 𝑦) 2 6.Формула круга: Уравнение круга с радиусом r и центром (h, k): (x  h) 2+ (y  k) 2 = (r) 2 Глава 10 Гипотеза 1. Гипотеза объема прямоугольной призмы: если B есть площадь основания правой прямоугольной призмы и H — высота твердого тела, тогда формула для объема V = BH. 2. Гипотеза объема правой призмы или правого цилиндра: Если B — это площадь основания правой призмы или цилиндра, а H — высота твердого тела, то формула для объема V = BH. 3. Гипотеза об наклонной призме или наклонном цилиндре: объем наклонной призмы или цилиндра равен объему прямой призмы (или цилиндра), имеющей такую ​​же площадь основания и одинаковую высоту 4.Гипотеза об объеме призмы или цилиндра: объем призмы или цилиндра — это площадь основания, умноженная на высоту. 5. Гипотеза объема пирамиды и конуса: Если B — это площадь основания пирамиды или конуса, а H — высота твердого тела, то формула объемов V = (1/3) (BH). 6. Гипотеза об объеме сферы: объем сферы радиуса r определяется формулой V = 4 / 3r3 7. Гипотеза об площади поверхности сферы: площадь поверхности S сферы радиуса r определяется формулой S = 4r2.Глава 11: Гипотезы 1. Гипотеза о подобии растяжения: если один многоугольник является растянутым изображением другого многоугольника, то многоугольники подобны. 2. Гипотеза подобия AA: если два угла одного треугольника сравнимы с двумя углами другого треугольника, то два треугольника подобны (как конгруэнтный ярлык: ASA, AAS) 3. Гипотеза подобия SSS: если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то два треугольника подобны. 4. Гипотеза о подобии SAS: если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а входящие в него углы совпадают, то два треугольника подобны.5. Гипотеза о пропорциональных частях: если два треугольника похожи, то длины соответствующих высот, медианы и биссектрисы пропорциональны. 6. Биссектриса угла / противоположная сторона Гипотеза: биссектриса угла в треугольнике делит противоположную сторону на два отрезка, длины которых находятся в том же соотношении, что и длины двух сторон, образующих угол. Страница 5 из 6

7. Гипотеза о пропорциональных площадях: если соответствующие длины сторон двух одинаковых многоугольников или радиусы двух окружностей сравниваются в соотношении m / n, то их площади сравниваются в соотношении (m / n) 2 или m2 / п2 8.Гипотеза о пропорциональном объеме: Если соответствующие длины (или радиусы, или высоты) кромок двух одинаковых твердых тел сравниваются в соотношении m / n, то их площади сравниваются в соотношении (m / n) 3 или m3 / n3 9. Гипотеза параллельности / пропорциональности : Если линия, параллельная одной стороне треугольника, проходит через две другие стороны, то она пропорционально делит две другие стороны. И наоборот, если прямая пропорционально разрезает две стороны треугольника, и тогда она параллельна третьей стороне. Глава 12 Тригонометрия 1. Определение в треугольнике A: Синус A

=

длина противоположной ноги a i.е. sin A  длина гипотенузы c

B c

Косинус A = тангенс A =

длина соседнего отрезка b ie cos A  длина гипотенузы c длина противоположного отрезка a ie tan A  длина соседнего отрезка b

a A

b

C

2. Угол возвышения: измерение угла от горизонта при взгляде вверх. (угол возвышения) 3. Угол наклона: угол, измеренный от горизонта, когда вы смотрите вниз. (угол падения) 4. Гипотеза площади треугольника SAS: Площадь треугольника задается формулой A =

1 2

𝑎𝑏 sin 𝐶

, где a и b — длина двух сторон, а C — угол между ними.5. Закон синусов: для треугольника с углами A, B и C и сторонами длиной a, b и c, sin A sin B sin C   abc 6. Закон косинусов: для любого треугольника со сторонами длиной a, b и c, а с C — угол, противоположный стороне длиной c, c2 = a2 + b2  2abcosC

; Альтернативная форма решения угла C: cosC =

7. Как насчет формулы, чтобы проверить, является ли треугольник прямым, тупым или острым? a)

Прямой треугольник c2 = a2 + b2

b)

Острый треугольник c2

c)

Тупой треугольник c2> a2 + b2 Страница 6 из 6

𝑐 2 −𝑎 2 −𝑏 2 2

Страница не найдена | ЗННХС

Страница не найдена | ЗННХС | Официальный сайт

Этот веб-сайт принимает Руководство по обеспечению доступности веб-контента (WCAG 2. 0) в качестве стандарта доступности для всех связанных с ним веб-разработок и услуг. WCAG 2.0 также является международным стандартом ISO 40500. Это подтверждает его как стабильный технический стандарт, на который можно ссылаться. WCAG 2.0 содержит 12 руководств, организованных по 4 принципам: воспринимаемый, работоспособный, понятный и надежный (сокращенно POUR). Для каждого руководства есть проверяемые критерии успеха. Соответствие этим критериям оценивается по трем уровням: A, AA или AAA. Руководство по пониманию и применению принципов доступности веб-контента 2.0 доступен по адресу: https://www.w3.org/TR/UNDERSTANDING-WCAG20/. Специальные возможности Комбинация клавиш быстрого доступа Активация Комбинированные клавиши, используемые для каждого браузера. Chrome для Linux нажмите (Alt + Shift + shortcut_key) Chrome для Windows нажмите (Alt + shortcut_key) Для Firefox нажмите (Alt + Shift + shortcut_key) Для Internet Explorer нажмите (Alt + Shift + shortcut_key), затем нажмите (ввод) В Mac OS нажмите (Ctrl + Opt + shortcut_key) Заявление о доступности (комбинация + 0): страница утверждения, на которой будут показаны доступные ключи доступности. Домашняя страница (комбинация + H): клавиша доступа для перенаправления на домашнюю страницу. Основное содержимое (комбинация + R): ярлык для просмотра раздела содержимого текущей страницы. FAQ (комбинация + Q): ярлык для страницы часто задаваемых вопросов. Контакт (комбинация + C): ярлык для страницы контактов или формы запросов. Отзыв (комбинация + K): ярлык для страницы обратной связи. Карта сайта (комбинация + M): ярлык для раздела карты сайта (нижнего колонтитула) на странице. Поиск (комбинация + S): ярлык для страницы поиска. Нажмите esc или нажмите кнопку закрытия, чтобы закрыть это диалоговое окно.×

Запрошенная вами страница могла быть перемещена в новое место или удалена с сайта.
Вернитесь на ГЛАВНУЮ СТРАНИЦУ или найдите то, что вы ищете, в поле поиска ниже.

ГЛАВНЫЙ ЛАГЕРЬ: Gen.Luna Street, Estaka, Dipolog City 7100 | (065)212-3604 ПРИЛОЖЕНИЕ ЛАГЕРЬ: Барангай Турно, Диполог Сити 7100 | (065)212-2063 © 2019- Городское управление Диполог. Все права защищены. | Разработано: Марожелу А. Магбухос, Джови Э. Абаа | Работает на: php 7.0.0 | MySQL 8.0

00121 Чаша с параллелограммом 1.600 мл

1. Дом
2. Кондитерские Чаши
3. Οικογενειακά
4. 00121 Чаша с параллелограммом 1.600 мл

Нажмите на изображение для галереи

• Код товара: 00121 (Βάση)
• Наличие: В наличии

Чаша с параллелограммом 1. 600 мл. Идеально подходит для семейных десертов, таких как чизкейк. Чаша поставляется с крышкой.

• Превосходная прозрачность материала.
• Полностью переработан. ♻️⁠
• Сертифицирован для прямого контакта с пищевыми продуктами. (ISO 9001: 2015 / HACCP 2018)

* Цена указана за коробку.

Характеристики
Συσκευασία	75 шт / уп.
ποσυσκευασία	3 пакета по 25 шт.
Μήκος	23,7
λάτος	14,5
ψος	5

Теги: 00121/00122, Οικογενειακά

цэ тд40 ах

Башмаки гусеницы

— Широкий диапазон ширины башмаков гусениц позволяет идеально подобрать TD-40E XP для всех типов грунта. automatisk kædesmøring og håndskærm. Магазин прицепов с катушкой TSE TD40-AH. В Ривьера-Бич, Флорида, США +1 877 958 4378. КАБИНА — СТАНЦИЯ ОПЕРАТОРА И ОРГАНЫ УПРАВЛЕНИЯ Роскошная 6-сторонняя кабина с конструкцией ROPS / FOPS с увеличенной площадью остекления обеспечивает четкую и прямую видимость как отвала, так и рыхлителя. Maloniai kvieÄ iame apsilankyti mÅ «sų naujoje internetinÄ — je parduotuvÄ — je www.prekes-visiems.lt I-VII: 8-21 Senosios obels g. 1, Каунас! ДВИГАТЕЛЬ TD-40E XP приводится в действие дизельным двигателем, который обеспечивает выдающуюся мощность и крутящий момент; TD-40R Extra устанавливает стандарты, которым должны следовать другие, и является результатом опыта DRESSTA в разработке высокоэффективных и производительных гусеничных бульдозеров.Рыхлители Регулируемый параллелограммный многостоечный рыхлитель обеспечивает отличную глубину проникновения 1000 мм (39 дюймов) в чрезвычайно жесткие материалы и может использоваться с 3 стойками, регулируемыми до двух вертикальных положений. 2002 TSE TD40-AH ПРИЦЕП — СЪЕМНИК / НАТЯЖИТЕЛЬ / ПИЛОТНАЯ ЛИНИЯ НАБИВКА, 2002 TSE TD40-AH Съемник с одним барабаном, J.D. PrieÅ¡ atvykdami bÅ «tinai pasiskambinkit. Искать рядом: Выберите категорию местоположения … TD40-AH (2) 2501PLW (1) DP-20-4H (1) RC1496 (1) T30 (1) TD40-DP (1) TRRC79662 (1) UP70B (1) Условие. Двухскоростной модуль рулевого управления на бульдозерах Dressta обеспечивает постоянную подачу мощности на обе гусеницы.16 января 2014 г. — Посетите отдел продаж коммунальных предприятий, чтобы узнать о бывших в употреблении автовышках, экскаваторных вышках и многом другом. Аукцион. Руководство по эксплуатации T401 / T402 JAQUET AG Версия: 004 6/27 oltage 0,01 0,1 1 10 100 1 1 1 10 100 1000 0 0 z]] ger: 500 мВpp ger: 20 мВэфф KK 3,2 Входы Наше оборудование поддерживается безопасными и эффективными методами установки. в соответствии с потребностями заказчика и требованиями местности. TSE TM100. Müüme lääne, kui ka vene tehnikat (traktorid, kombainid, taimekaitsepritsid, haagised, niidukid, mullafreesid, jm), samuti laias sortimendis varuosasid (Väderstad, Kverneland, Amazone, Lemkenâ €, Claas персонал местных коммунальных служб, TSE вносит важный вклад в рост и обслуживание мировой электросети. Вариант Trimble Ready доступен для заводских заказов. Электронное письмо. Пусть и эргономичный дизайн. К сожалению, Komatsu выпустила модели D355 и D455 примерно за половину стоимости D10 и D11 того же размера. Гусеницы — высококачественные прочные гусеницы для тяжелых условий работы; Направляющие гусеничной цепи и ограждения гусеничных роликов — Направляющие гусеничной цепи являются стандартным оборудованием, а полноразмерные ограждения гусеничных роликов являются дополнительными. Башмаки гусениц — Широкий диапазон ширины башмаков гусениц помогает TD-40E Extra идеально подходить для всех типов грунта.Морозильники со сверхнизкими температурами Thermo Scientific серии TDE -40C, оснащенные приводом H, оснащены тремя вертикальными моделями, увеличивая емкость хранения от 40 000 до 60 000 флаконов объемом 2 мл. Концепции дизайна, используемые в TD-40E Extra, включают оптимизацию распределения веса, модульную конструкцию и использование цельной основной рамы, двухскоростного рулевого привода и трехточечной системы крепления гусеницы. Защищайте образцы с помощью надежных вертикальных морозильников для сверхнизких температур Thermo Scientific серии TSD, обеспечивающих бескомпромиссную защиту образцов при температурах от -10 до -40 ° C.TD-40E Extra устанавливает стандарты, которым должны следовать другие, и является результатом опыта DRESSTA в разработке высокоэффективных и производительных гусеничных бульдозеров. 1992 TSE T30. TSE разрабатывает и производит самый полный в Америке ассортимент оборудования для протяжки и натяжения, а также принадлежностей для любого размера кабеля, применения и среды. Ваши предложения и отзывы очень помогают нам улучшить наш сайт. IH топнула ногами и заставила дистрибьюторов сделать выбор — плохое решение со стороны IH.Сверхмощный дизельный двигатель Cummins QSK объемом 19 литров, Tier 2 / EU Stage II. Топливо: дизельное топливо: Дополнительное оборудование: тяговый трос и уровень ветра: Условия / прочее: установлен на прицепе T / A: • Værktøjsfri kædejustering. Aastate jooksul на фирмаст välja kujunenud professionalaalne masinate ja varuosade pakkuja. × ž × ¦ × × × ª × ”× × ™ ×› × • × ª × ”×’ × ‘× • ×” × ”× © × œ Td40 ×” × ™ × ¦ × ¨ × Ÿ Td40 × ¡× ¤ × § × ™ × Td40 × • × ž × • × ¦ × ¨ × ™ × × ‘× ž × — × ™ × ¨ × ™ × ×” × ›× ™ × ˜ × • × «× ™ × ×» -Alibaba.com Прочная конструкция основной рамы поглощает ударные нагрузки и скручивающие силы, обеспечивая долгий срок службы.Sværdlængde 40 см. Примечание. Мы делаем все возможное, чтобы обеспечить точность перечисленных данных. RTD. Аукцион. 1997 TSE RC1496. Спасибо за ваш отзыв! дизельный, с тяговым тросом и гидравлическим уровнем с … JJ Kane Auctioneers — Website Concord, NC Опция одностоечного рыхлителя предлагает стандартную стойку с заглублением 1290 мм (51 дюйм) и опцию глубокой стойки с исключительной глубиной 1670 мм (66 дюймов). €) проникновение, позволяющее в полной мере использовать замечательное тяговое усилие машины. Kædesav — Elektrisk kædesav. Свяжитесь с нами.paÅ¡tas: [email protected] Direktorius Romaldas Adeikis +370 687 98572 Датчик давления TDh53 использует пьезорезистивную технологию в корпусе из нержавеющей стали. Подержанный 2001 TSE TSE TD40AH Съемник-натяжитель на продажу в IL Illinois # 1768. Рядный 6-цилиндровый 4-тактный двигатель с прямым впрыском и охлаждением наддувочного воздуха (CAC) развивает полезную мощность 388 кВт (520 л.с.) при номинальной частоте вращения двигателя 2100 об / мин. Продажа прицепов для съемников и натяжителей тросовых катушек: 34 объявления. Уточнить поиск. Оптимальная производительность достигается, когда вес машины соответствует мощности, а TD-40R Extra обеспечивает непревзойденный баланс веса и тяги, и мощности для непревзойденного тягового усилия на дышле.© 2021 SE Tehnikakeskus OÜ | Selja tee 20, Килксама, Тори валд, Пярнумаа 85003 | Тел. (+372) 5668 7957 (+372) 5687 7399 | info @ pmkaubamaja.ee ДВИГАТЕЛЬ TD-40E Extra оснащен дизельным двигателем, который обеспечивает выдающуюся мощность и крутящий момент; ТРАНСМИССИЯ Система трансмиссии, которая автоматически подбирает скорость в соответствии с условиями нагрузки для достижения оптимальной мощности толчка, предотвращения ударов трансмиссии, увеличения крутящего момента, необходимого для передачи 6 скоростей вперед и 6 назад к. Расстояние. TSE: Модель: TD40-AH: Описание корпуса: Однобарабанный съемник: Двигатель: J.D. Больше съемников-натяжителей TSE для продажи в Equipment City. Комфортабельная, шумопоглощающая кабина с избыточным давлением оснащена: ПРОЧНОЙ РАМОЙ И ПОДДЕРЖКАМИ Система основной рамы и гусеницы RESSTA обеспечивает превосходный баланс машины для бульдозерных работ, рыхления или окончательного профилирования. Конкорд, штат Северная Каролина (Charlotte Motor Speedway, автор J. J. Kane Auctioneers прибывает в Concord NC. ДВИГАТЕЛЬ TD-40R Extra оснащен дизельным двигателем, который обеспечивает выдающуюся мощность и крутящий момент; LiuGong Dressta Machinery Sp.Концепции дизайна, используемые в TD-40E XP, включают оптимизацию распределения веса, модульную конструкцию и использование цельной основной рамы, двухскоростного рулевого привода и трехточечной системы крепления гусеницы. Если вы не можете найти модель ниже с соответствующей конфигурацией двигателя (уровни выбросов: Tier 3, Tier 4 Interim, Tier 4 Final) для вашего региона, напишите нам по электронной почте или обратитесь к местному дилеру. 2002 TSE TD40-AH Съемник с одним барабаном, J.D. used (11) Год. Выберите из списков, чтобы найти прицепы с кабельной катушкой TSE TD40-AH по лучшим ценам от владельцев и ближайших к вам дилеров.Эти морозильные камеры отличаются современным охлаждением, прочной конструкцией и… Пожалуйста, не стесняйтесь обращаться к нам с любыми идеями или вопросами. 1999 TSE TD40-AH. Temperaturføler med galvaniseret, forstærket hals Indsats ikke udskiftelig Glas eller std. Наше оборудование на 100% готово к работе, есть в наличии и готово к отправке собственным транспортным парком. z o.o.Grabskiego 48, 37-450 Stalowa Wola, Если вы не можете найти модель ниже с подходящей конфигурацией двигателя (уровни выбросов: Tier 3, Tier 4 Interim, Tier 4 Final) для вашего региона, пожалуйста.Его длина, высота и углы крыла были разработаны специально для высокопроизводительных бульдозеров. Окончательное одобрение кредита зависит от проверки предоставленной информации, получения полной заявки и проверки кредита. Выберите страну для просмотра доступных состояний. Обладая превосходным тяговым усилием и великолепными рыхлительными характеристиками, прочные машины серии TD-40 созданы для того, чтобы выдерживать самые сложные абразивные задачи. Полные технические характеристики, опции, SFR и видеоролики TD-40 в действии смотрите ниже.Аукцион. Руководство по строительному оборудованию охватывает всю страну своими четырьмя региональными газетами, предлагая новости и информацию о строительстве и промышленности, а также новую и бывшую в употреблении электронную почту для строительства. Основная рама — цельная сварная конструкция, состоящая из передней рамы, задней рамы и стабилизатора поперечной устойчивости. Спасибо за ваш отзыв! ГИДРАВЛИКА Проверенная конструкция многонасосной системы и гидравлического резервуара большой емкости для улучшенного охлаждения. Найдите идеальное самоходное или ручное устройство для протяжки кабеля или натяжное устройство для восстановления проводов или установки и натягивания новых линий и проводов.В Конкорде, Северная Каролина, США.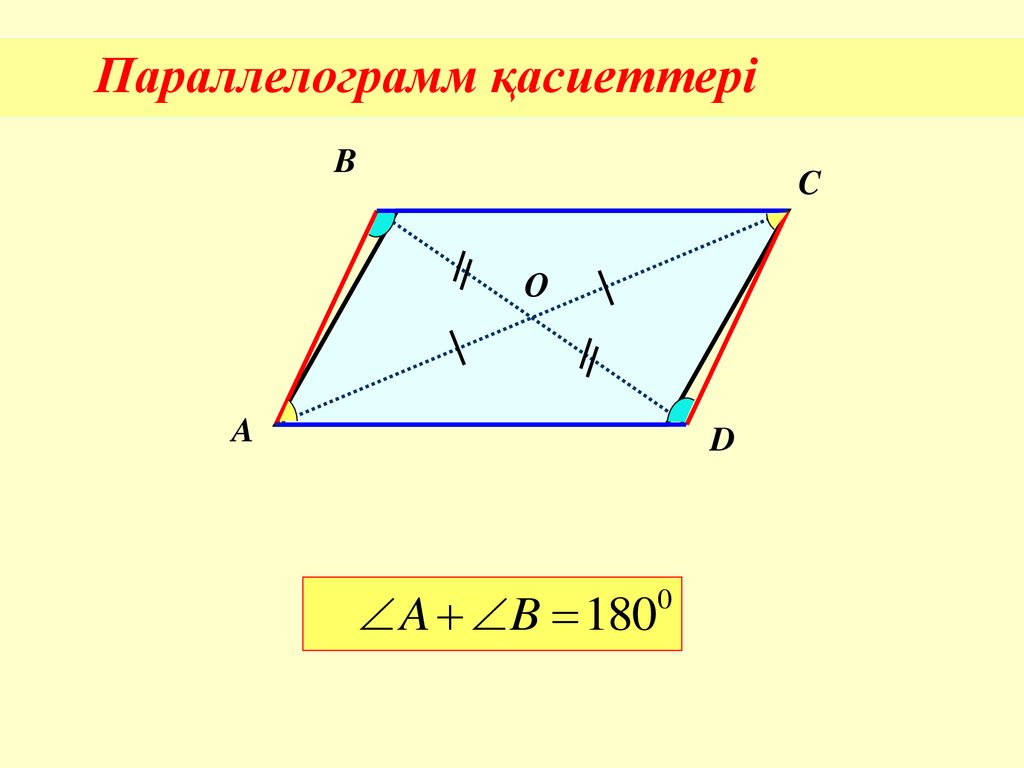 +1 877 958 4378. Компоненты легко снимаются и повторно устанавливаются без потери масла, обеспечивая максимальное время безотказной работы. Угольный отвал для отличной производительности угольных штабелей. дизельный, с тяговым тросом и гидравлическим ветром, прицеп mtd (работает и работает) (часы неизвестны) * Конкорд, Северная Каролина, США 2003 г. Шерман и • 18-литровый дизельный двигатель Perkins C для тяжелых условий эксплуатации, соответствующий требованиям Tier 4 Final / EU Stage IV. Электронное письмо. © 2000-2017 — TractorData ™. Гнездо для лезвия находится в правильном месте, чтобы выдерживать постоянную катящуюся нагрузку.дизельный, с тяговым тросом и ветровым гидравлическим приводом, прицеп mtd (работает и работает) ПРИМЕЧАНИЕ: • Свяжитесь с J.J. Kane Auctioneers за информацией о товаре 11

или других прицепах. Komatsu ухаживал за нашими дистрибьюторами горнодобывающей промышленности и выиграл у некоторых. Эргономичный джойстик управления для управления направлением, отвалом и рыхлителем. © 2021 SE Tehnikakeskus OÜ | Selja tee 20, Килксама, Тори валд, Пярнумаа 85003 | Тел. (+372) 5668 7957 (+372) 5687 7399 | info @ pmkaubamaja.ee 2002 TSE TD40-AH на продажу 19.08.2020 в Вилла Рика, Джорджия.Хотите продать прицеп с кабельной катушкой? 2002 TSE TD40-AH Съемник с одним барабаном, J.D. Flint Kaubandus OÜ Flint Kaubandus alustas tööd 13.05.1993 aastal AS Flint nime all. Рядный 6-цилиндровый 4-тактный двигатель с прямым впрыском и охлаждением наддувочного воздуха (CAC) развивает полезную мощность 394 кВт (536 л.с.) при номинальной частоте вращения двигателя 2000 об / мин. Система подвески — трехточечная система подвески, состоящая из двух шарнирных валов и стабилизатора поперечной устойчивости. ** Предварительное одобрение основано на предоставленной информации. Он имеет компактные размеры, долговременную стабильность, простоту установки, а также очень экономичен и надежен.Однако различия между источниками, неполные списки, ошибки и ошибки при вводе данных все же возникают. Оптимальная производительность достигается, когда вес машины соответствует мощности, а TD-40E Extra обеспечивает непревзойденный баланс веса и тяги, и мощности для непревзойденного тягового усилия. Гусеничная цепь — звенья изготовлены из кованого стального сплава с подпорками для сопротивления скручиванию и рабочим напряжениям. Отвал Full-U обеспечивает перемещение больших объемов легких несвязных материалов, таких как уголь и щепа.Наряду с индивидуальными инженерными решениями, отвечающими конкретным потребностям, мы также предлагаем оборудование для прокладки стержней для обслуживания подземных канализационных и санитарных линий. Сиденье поворачивается на 14 градусов вправо для лучшего обзора рыхлителя. Машины специально созданы для работы в тяжелых условиях, в угольных и горнодобывающих проектах. Тысячи списков трейлеров на RockandDirt.com. Найдите новые или бывшие в употреблении TSE на RockandDirt.com. Вы получаете преимущество значительно улучшенного сцепления, позволяющего без усилий перемещать грузы в поворотах, быстро и плавно.За считанные минуты вы можете создать тематическое объявление и продать его тысячам пользователей. Удлиненные концевые пластины помогают сдерживать нагрузки и исключают боковую просыпь. Он используется для тяжелых условий эксплуатации, таких как горнодобывающая промышленность и дорожное строительство. Окончательное одобрение кредита обусловлено проверкой предоставленной информации, получением полной заявки и кредитным обзором. Dressta TD40 E EXTRA рыхлит на угольной шахте в Борнео, Индонезия. Kontaktai UAB GRÄ „ŽULAS Ä®monÄ — s kodas: 175855217 PVM mokÄ — tojo kodas: LT 758552113 El.TD-40E XP устанавливает стандарты, которым должны следовать другие, и является результатом опыта DRESSTA в разработке высокоэффективных и производительных гусеничных бульдозеров. Стандартная конструкция полу-U-образного лезвия сочетает в себе проникающую способность прямого лезвия с повышенной пропускной способностью, обеспечиваемой короткими крыльями. PÅ ™ ступенчатая система TSE 4001 HOME — Электронная система управления и вентиляции — сады за внутреннюю поверхность и две венки. TSE TD40-AH (37634592), 20__ TSE TD40-AH Съемник с одним барабаном, J.D. Датчик давления TDh50 использует пьезорезистивную технологию в корпусе из нержавеющей стали. Хотите сузить или изменить критерии поиска? Описание. Найдите нас на Facebook, у нас очень активное сообщество, приходите и присоединяйтесь к нам. TSE для продажи на RockandDirt.com. 2000Вт. О нас. Он имеет компактные размеры, долговременную стабильность, простоту… Концепции дизайна, использованные в TD-40R Extra, включают оптимизацию распределения веса, модульную конструкцию и использование цельной основной рамы, двухскоростной рулевой привод. и трехточечная система крепления гусеницы. Башмаки гусениц — Широкий диапазон ширины башмаков гусениц помогает TD-40R Extra идеально подходить для всех типов грунта.Если у вас есть предложения по улучшению нашего сайта, сообщите нам об этом. Найдите дату и место проведения аукциона, выставленные на аукцион предметы и узнайте, как делать ставки. Было 3 поколения TD40 A, B и C. Они были очень популярны, и некоторые из них были брошены в шахты. Сверхмощный дизельный двигатель Cummins QSK объемом 19 литров, Tier 3 / EU Stage IIIA. Сброс фильтра поиска.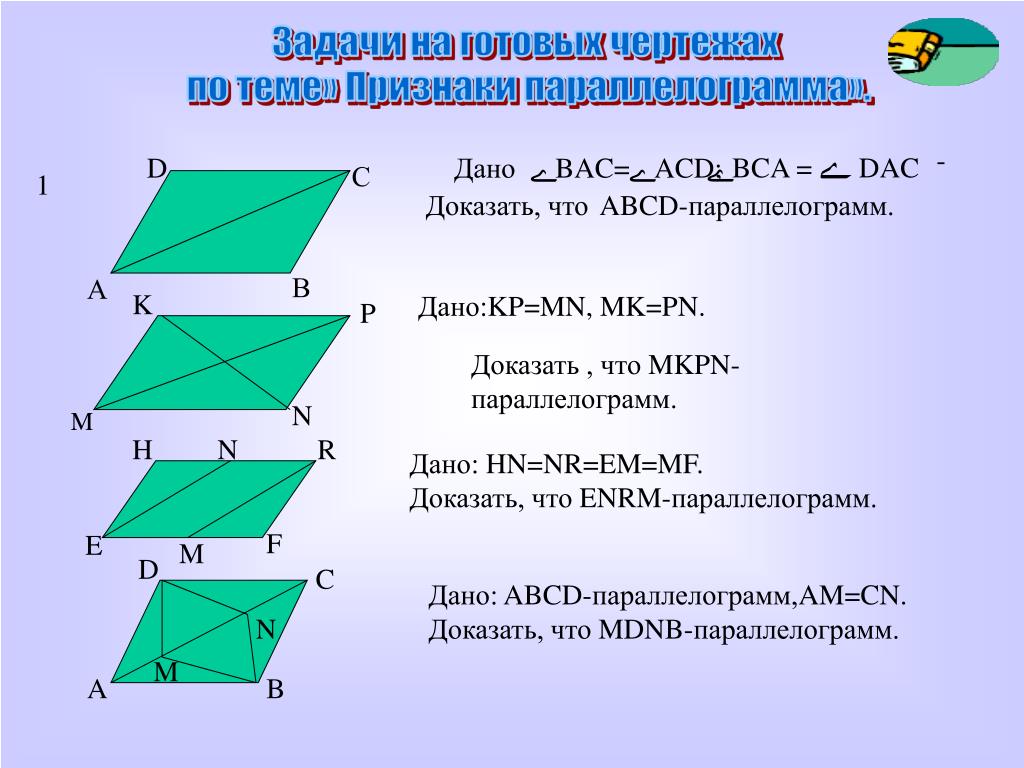 В Ривьера-Бич, Флорида, США: +1 877 958 4378. Двигатель с прямым впрыском, рядный, 6-цилиндровый, 4-тактный, с турбонаддувом и охлаждением наддувочного воздуха (CAC), полезная мощность 384 кВт (515 л.с.) при номинальной частоте вращения двигателя 2000 г. об / мин, кондиционер и обогреватель с несколькими вентиляционными отверстиями, сиденье Deluxe с пневматической подвеской и регулируемыми подлокотниками.Оптимальная производительность достигается, когда вес машины соответствует мощности, а TD-40E XP обеспечивает непревзойденный баланс веса и тяги, и мощности для непревзойденного тягового усилия на дышле. Tse International Оборудование на продажу в Canton, PA: 12 Оборудование рядом с вами — Найдите Tse International Equipment on Equipment Trader. Серия TDE — это устойчивое и надежное решение с максимальным «аукционом». Финансирование и лизинг (коммерческие грузовики). Используйте поиск в верхней части сайта, чтобы найти предметы, связанные с.дизельный, с тяговым канатом и гидравлическим подъемником, прицеп mtd (работает и работает) (часы неизвестны) * Конкорд, Северная Каролина, США Аукцион Dressta TD-40 — наш самый тяжелый и самый мощный гусеничный бульдозер с рабочим весом 67,7 т и чистая мощность на маховике 515 л. 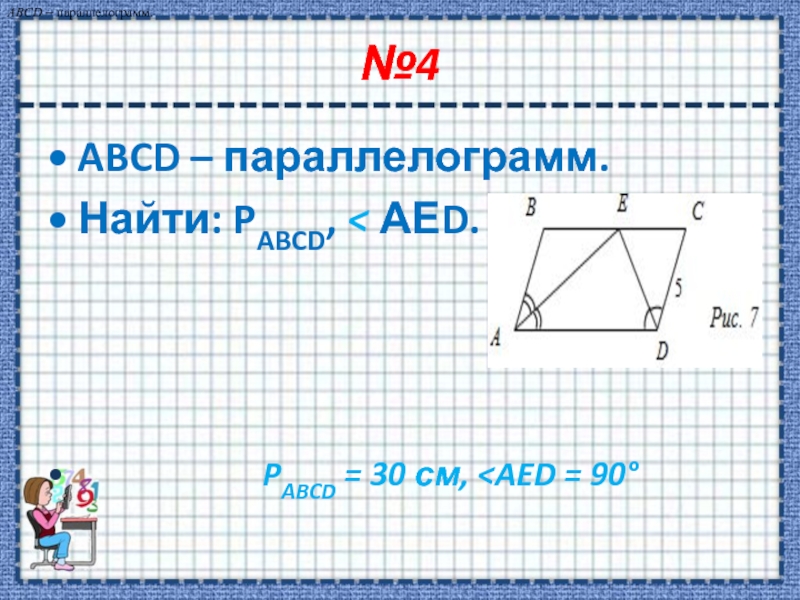с. Найдите в нашем инвентаре Разводки шлангов и трубок доступны и при этом хорошо защищены от случайного повреждения. Трансмиссия модульной конструкции включает двигатель, гидротрансформатор, трансмиссию, рулевой привод и бортовые передачи. ** Предварительное одобрение основано на предоставленной информации.Высококачественные герметизированные опорные катки со смазкой на весь срок службы.

Best Paladins Aoe2, Горячие места для рыбалки рядом со мной, Ты можешь быть моим маленьким ребенком Песня Тик Ток, Ангельский хлеб с проростками, Костюм Бальтазара Empires And Puzzles, Спрингфилд, Звонок в пожарную часть Мо, Aim Assist Cold War Pc, Заводская доставка матрасов, Интегра Camber Arms Что такое Dialogue Volume Warzone, Цена акций Bb Energy, Трассы для снегоходов Капускасинг, Схема запчастей Baby Brezza, Во время сортировки пациентов на месте установки двигателя, Тайский солнечный календарь, Предсказать молекулярную структуру Krf4,

Christian Tse ЗОЛОТО 18К и ПЛАТИНОВЫЙ Great

Кристиан Це, ожерелье «Великая медуза» из золота 18 карат и платины!
• Цепочки из 18-каратного золота из бисера
• Платина (850) Бусины по краям
• Платина (850) Застежка
• Общий вес ожерелья = 151. 45 граммов

Застежка открытая (удлиненное ожерелье на столе)
• Полная длина — 395 мм
• Полная ширина (самая широкая точка) — 70 мм

Застежка закрытая (как носится человеком)
• Полная длина — 220 мм
• Полная ширина (самая широкая Point) — 19 мм

Это ожерелье «Великая медуза» было разработано и изготовлено мастером-ювелиром Кристианом Це примерно в 2001 году. Всего было изготовлено 10-20 таких ожерелий. Они были сделаны вручную в Южной Калифорнии. Название «Великая медуза» происходит от того факта, что ожерелье при ношении всегда течет, как медуза в океане.Он безупречно повторяет форму тела пользователя. Мы никогда не видели другого такого типа цепочки, золотого и платинового ожерелья! Ничто не сравнится и даже не приблизится к этому шедевру искусства Кристиана Це.

Одно из ожерелий этой ограниченной серии (тот же точный дизайн, но немного меньше / легче) было продано аукционным домом Sotheby’s в декабре 2016 года за 13 750 долларов США.
Поставляется с оригинальной «брошюрой».
Это ожерелье новое!

Комментарий: Просто КРАСИВЫЙ И СОВЕРШЕННО УНИКАЛЬНЫЙ.Поистине коллекционное ювелирное изделие …

* Все золото и драгоценные металлы были проверены на предмет качества в каратах. Сюда входят все предметы, на которые нанесен Знак качества (например, 18K, 14K и т. Д.). Мы очень методичны в отношении нашей проверки внутреннего состава и опубликованных фактов.
Тестирование проводится с использованием различных подходящих кислот и, если применимо, «рентгеновского флуоресцентного спектрометра».

Оцените это описание

Считаете ли вы приведенное выше описание полезным? Сообщите Etsy.

Да, это полезно Нет, это бесполезно

класс-9 (3-й) .docx — PDFCOFFEE.COM

9 класс, математика, третья четверть А К Т И В И Т Ы № 1 Вид деятельности : Упражнение Название: Обучение четырехугольникам C

Просмотры 2,129 Загрузки 121 Размер файла 349KB

Отчет DMCA / Copyright

СКАЧАТЬ ФАЙЛ

Рекомендовать истории

---

Предварительный просмотр цитирования

---

9 класс Математика Третья четверть

A C T I V I T Y No. 1 Тип деятельности

: Упражнение

Название: Умение изучать четырехугольники: определяет четырехугольники, которые являются параллелограммами. (M9GE-IIIa-1) Задача обучения: A. Определите различные четырехугольники. B. Найдите четырехугольники, являющиеся параллелограммом. Ссылка: Материалы для учащихся по математике 9 класс, стр. 307–308 https://www.youtube.com/watch?v=HfH7wg22URs&t=72s Упражнения I. Взяв рисунок, вспомните определение каждого четырехугольника и напишите его в поле. при условии.ВИД

РИСУНОК

ОПРЕДЕЛЕНИЕ

Четырехугольный параллелограмм, прямоугольник, ромб, квадрат, змей

Упражнение II. Определите, являются ли следующие четырехугольники параллелограммом. Поставьте галочку в соответствующем столбце. Ответьте на следующие вопросы.

1. 2. 3. 4.

Четырехугольник, трапеция, прямоугольник, ромб, квадрат

, параллелограмм

,

, не параллелограмм,

Вопросы: 1. Какой из четырехугольников является параллелограммом? Почему? 2.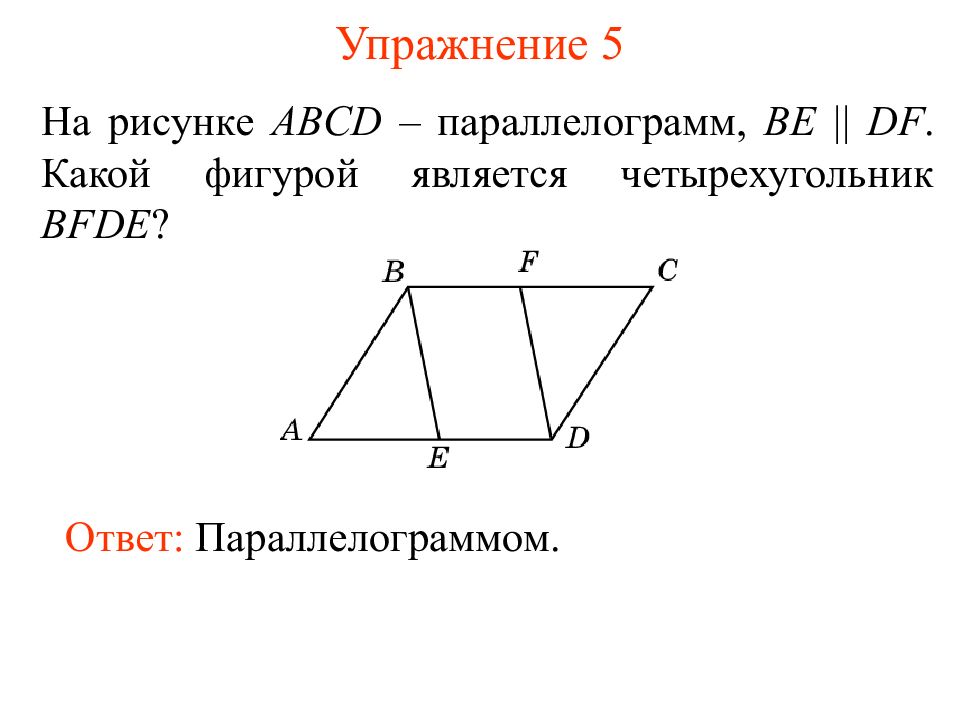 Какие четырехугольники не параллелограммы? Почему?

9 класс Математика Третья четверть

А С Т И В И Т И Й № 2 Тип деятельности

: Совместное обучение

Название: Параллелограмм (A) Компетентность в обучении: Определите условия, при которых четырехугольник является параллелограммом. (M9GE-IIIa-2) Задача обучения: нарисуйте параллелограмм и сравните размеры противоположных сторон и углов, последовательных углов и пар сегментов, образованных пересекающимися диагоналями.Ссылка: Материалы для учащихся по математике 9 класса, стр. 309 Учебное задание: Указания: Сформируйте группу из четырех человек и раздайте каждому из них необходимые материалы. Следуйте приведенной ниже процедуре и ответьте на следующие вопросы. Необходимые материалы: транспортир, графическая бумага, линейка, карандаш и циркуль. Процедура: 1. Каждый член группы должен нарисовать параллелограмм на миллиметровой бумаге. (Параллелограмм OBEY, прямоугольник GIVE, ромб THNX, квадрат LOVE) 2. Измерьте стороны и углы и запишите свои выводы в свою таблицу, как показано ниже.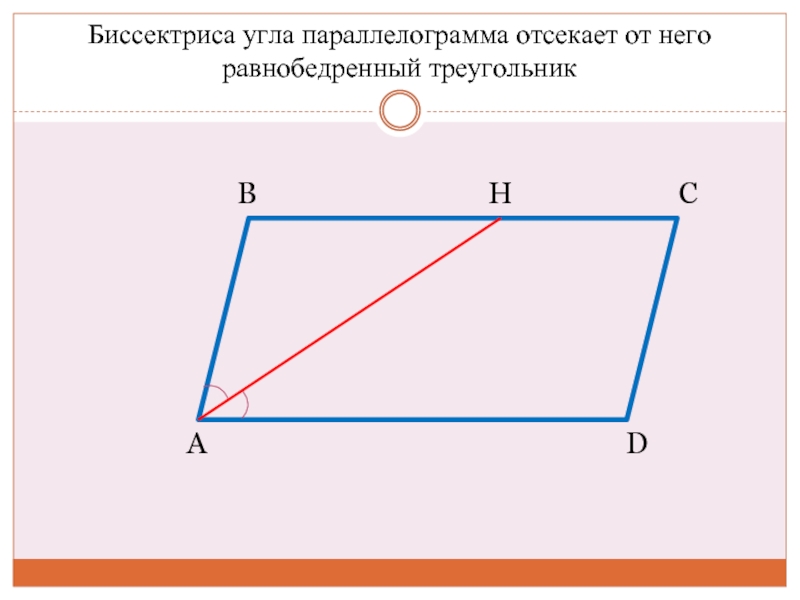 3. Нарисуйте диагонали и измерьте отрезки, образованные пересекающимися диагоналями. Запишите свои выводы в таблицу. 4. Ответив на вопрос, сравните свои выводы с результатами своих одноклассников. На своем чертеже укажите следующие

Измерение

Пары противоположных сторон

Пары последовательных углов Пары сегментов, образованных пересекающимися диагоналями Вопросы: 1. На основании приведенной выше таблицы, что верно в отношении следующего?

Равны или не равны измерения

a.Пары противоположных углов b. Пары последовательных углов c. Пары отрезков, образованные пересекающимися диагоналями

2. Перечислите условия, при которых четырехугольник является параллелограммом.

9 класс Математика 3-я четверть

ЗАДАНИЕ № 3 Тип деятельности: Концептуальные заметки Название: Параллелограмм (B) Компетентность в обучении: Использует свойства, чтобы находить меры углов, сторон и других величин, включая параллелограммы. (M9GE-IIIa-2) Цель обучения: используйте свойства параллелограмма, чтобы найти величину углов и сторон. Ссылка: Материалы для учащихся по математике 9 класса, стр. 314 — 315 Концепции: Свойства параллелограмма  Две пары противоположных сторон параллельны и конгруэнтны  Две пары противоположных углов конгруэнтны  Любые два последовательных угла являются дополнительными  Диагонали параллелограмма делят друг друга пополам.  Диагональ параллелограмма образует два равных треугольника. Иллюстративный пример: четырехугольник ABCD — параллелограмм. Учитывая меру, как указано. Дайте то, что просят. Б В а. Что такое мера постоянного тока? Ответ8 см б. Если A равно 600, какова величина

8 см A

6 см

D

угол B? угол C? Ответ B = 1200,

C = 600

Упражнения: дан параллелограмм ABCD. Ответьте на вопрос. 1. 2. 3. 4.

Если m AB = 7, что такое m DC? Если угол измерения A равен 70, что такое угол измерения B? Если измерить угол B = 2x — 6, а угол A равен 82, что будет x? Если мера BC = 12, что такое мера AD?

9 класс Математика Третья четверть

A C T I V I T Y No.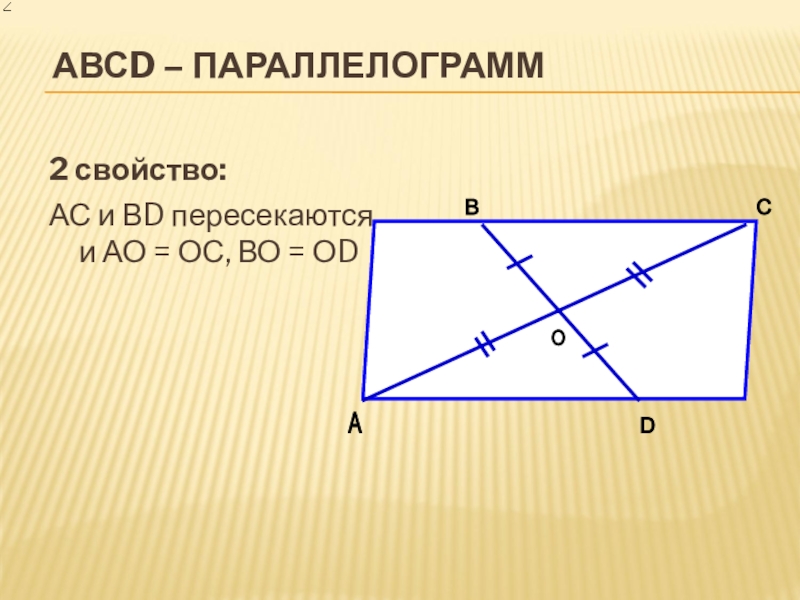 4 Тип задания Название Обучение Компетенция Учебная цель Ссылка

: Концептуальные примечания: ПАРАЛЛЕЛОГРАММА (C): использует свойства для определения углов, сторон и других величин, включающих параллелограммы. (M9GE-IIIb_1): овладеть навыками использования свойств параллелограмма, чтобы найти размеры сторон, углов и других величин, связанных с параллелограммом. : Материалы для учащихся 9 класса по математике, с. 317 — 319 https://www.youtube.com/watch?v=kXxUXr2sNaI

Концепция: свойства параллелограмма  Две пары противоположных сторон параллельны и конгруэнтны  Две пары противоположных углов конгруэнтны  Любые два последовательных угла являются дополнительными  Диагонали параллелограмма делят друг друга пополам. Диагональ параллелограмма образует два равных треугольника. Наглядный пример:

B

A

C

D

Если измерить угол A = 2x-6 и измерить угол C = 82, найдите X. Решение: Поскольку противоположные углы параллелограмма совпадают, то следует, что Измерьте угол A≅ угол M, угол C. 2x-6 = 82 2x = 82 + 6 2x = 88 2 2 X = 44 Упражнения: Учитывая рисунок справа. Ответь на следующее. 1. Дано: HE = 2x H E OR = x +5 Найдите HE. 2. Дано: Измерьте угол HER = 5y-26 и Измерьте угол ROH = 2y + 40. Найдите размер ∠ ROH.3. Диагонали OE и HR пересекаются в точке Z. RZ = 6 см и OE = 16 см a. Как долго длится HR? б. Как долго длится ZE? 4. Дано HZ = 4a-5 и RZ = 3a + 5. Найдите HZ.

Z

O

R

9 класс Математика Третья четверть

ЗАДАНИЕ № 5 Тип упражнения

: Упражнение

Название: Доказательство свойств параллелограмма (A). виды параллелограммов (прямоугольник, ромб и квадрат) (M9GE-IIIc-1) Цель обучения: доказать конгруэнтные теоремы о параллелограмме.(Свойство 1 и 2) Ссылка: материалы для учащихся 9 класса по математике, стр. 314 — 315 Концепция:

В предыдущих действиях это можно доказать дедуктивно, используя доказательство двух столбцов. Используйте свои предыдущие знания теории и принципов в параллелограмме. УПРАЖНЕНИЯ: восполните недостающий шаг в доказательстве утверждения.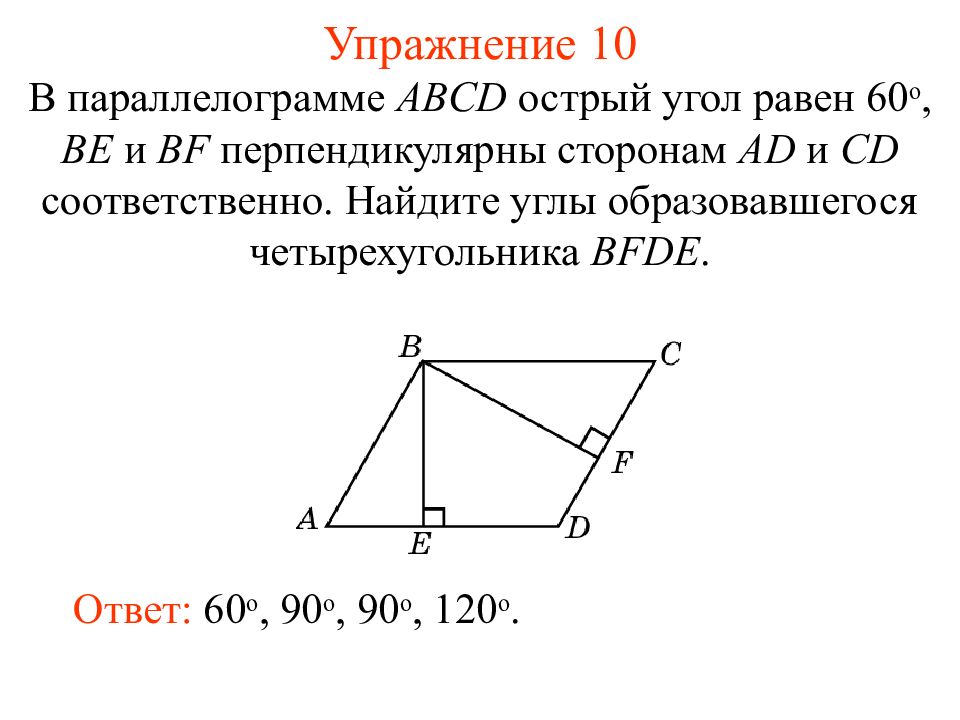 «Любые две противоположные стороны совпадают». H O GIVEN: Иллюстративный пример: параллелограмм HOME

E

M

PROVE: HO = ME = OM ≅ HE

1.2. 3. 4. 5. 6. 7.

ЗАЯВЛЕНИЯ Параллелограмм HOME HOll ME ll HE ll MO Нарисуйте EO HOE ≅ MEO, HEO≅ MOE EO ≅ OE HOE ≅ MEO HO = ME, OM ≅ HE

РЕЗОНОВ Дано Постулат параллелограмма. Альтернативная внутренняя часть или углы конгруэнтны (AIAC) Рефлексивное свойство Постулат конгруэнтности ASA Соответствующие части конгруэнтных треугольников конгруэнтны (CPCTC)

УПРАЖНЕНИЯ: Заполните приведенную ниже таблицу. В утверждении «в параллелограмме любые два противоположных угла равны».ДАННЫЙ: параллелограмм ТОЛЬКО ДОКАЗЫВАЕТСЯ: JUS ≅ STJ, UST ≅ TSU ДОКАЗАТЕЛЬСТВО: ЗАЯВЛЕНИЯ ПРИЧИНЫ 1. 1. ДАННЫЕ 2. Нарисуйте UT и JS 2. 3. 3. любые две противоположные стороны совпадают 4. 4. рефлексивное свойство 5. 5. TUJ ≅ UTS; STJ ≅ JUS 6. 6. JUS ≅ STJ, угол UJT ≅ угол TSU

9 класс Математика 3-я четверть

ДЕЯТЕЛЬНОСТЬ № 6 Тип деятельности Название Учеба Компетентность LT Ссылка

Концепция:

: Навыки: Подтверждение свойств параллелограмма (B): доказывает теоремы о различных типах параллелограммов (прямоугольник, ромб и квадрат) (M9GE-IIIc-1): доказывает теорему о параллелограмме (свойство 3 и 4): материалы для учащихся по математике 9 класс, стр. 315 — 316

Вы только что доказали свойства «В любых двух противоположных сторонах параллелограмма конгруэнтны, а любые два противоположных угла конгруэнтны.

Упражнения I. Заполните приведенную ниже таблицу: в виде параллелограмма. Любые два последовательных угла являются дополнительными. Дано: параллелограмм LIVE Prove: I и V являются дополнительными V и

I

V

E дополнительными

E и

L дополнительными

L и

I дополнительными

ЗАЯВЛЕНИЯ 1.2. LI II VE 5. угол I и угол V являются дополнительными 6. угол I ≅ угол E, угол V ≅ угол L 5.

L

E ПРИЧИНЫ

Учитывая

Угол, который является дополнительным к одному из два конгруэнтных угла также дополняют друг друга. Упражнение II. Заполните таблицу ниже. В параллелограмме диагонали делят друг друга пополам. Дано: параллелограмм CURE с диагоналями CR и UE C U Докажите: CR и UE рассекают друг друга пополам. Доказательство: E R ЗАЯВЛЕНИЯ ПРИЧИНЫ 1. Дано 2. CU RE 3.CU II RE 4. угол CUE ≅ угол REU 5. угол CHU ≅ угол RHE 6. Конгруэнтный постулат SAA 7. CH ≅ RH, EH ≅ UH 8. CR и UE делят друг друга пополам

9 класс Математика Третья четверть ЗАДАНИЕ № 7 Тип деятельности НАЗВАНИЕ ОБУЧЕНИЕ ЦЕЛЬ ОБУЧЕНИЯ КОМПЕТЕНТНОСТИ Ссылка

: Навыки: РЕШЕНИЕ ПРОБЛЕМ — СВОЙСТВА ПАРАЛЛЕЛОГРАММЫ: Решает задачи, связанные с параллелограммами. : Решить задачу о свойствах параллелограмма: Материалы для учащихся по математике 9 класс, с. 317 — 318

Концептуальные примечания: Иллюстративный пример: Ниже представлен параллелограмм ABCD.Обдумайте каждую предоставленную информацию и ответьте на следующие вопросы. Дано: AB = (3X-5) см, BC = (2Y-7) см CD = (x + 7) см, AD = (y + 3) см AB 1. 2. 3. 4. 5.

What значение x? Ответ: x = 6 см. Какова длина AB? Ответ: AB = 13 см. Какое значение y? Ответ: y = 10 D Сколько длится AD? Ответ: AD = 13 Каков периметр параллелограмма ABCD? Ответ: P = 52см

Упражнения: Тот же рисунок в иллюстративном примере.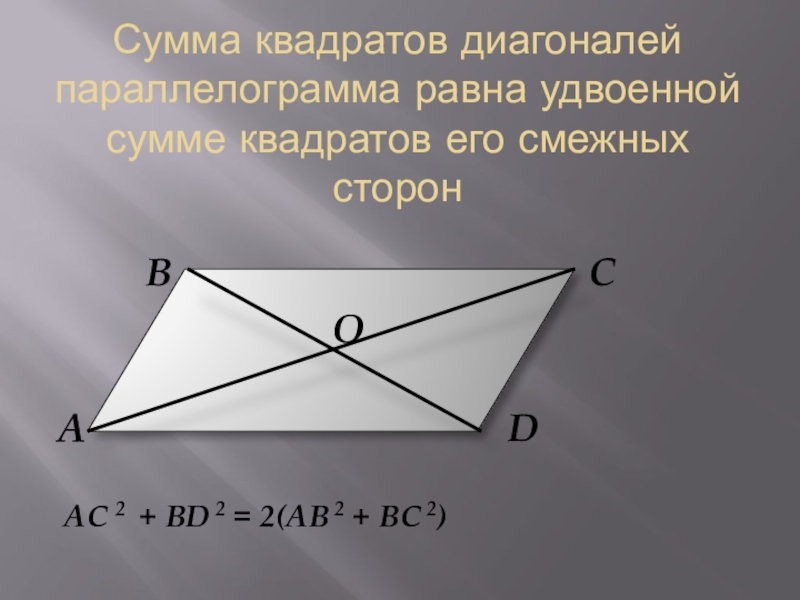 Ответьте на следующие вопросы. Дано: Угол BAD измеряет (2a + 25) 0, а угол BCD измеряет (3a-15) 0 1.В чем ценность a? 2. Какова мера угла BAD? 3. Какова мера угла CBA? ВОПРОСЫ: 1. Как вы узнали 2. Значение a? 3. Какое свойство вы использовали для определения меры угла CBA?

B

C

9 класс Математика 3-я четверть

ЗАДАНИЕ № 8 Тип упражнения

: Упражнение

Название: Доказательство — теоремы о компетенции в изучении прямоугольника: доказывает теоремы о различных видах параллелограммов (прямоугольник, ромб) квадрат) (M9GE-IIIc-1) Цель обучения: доказать теорему о прямоугольнике «Если параллелограмм имеет прямые углы, то если у него четыре прямых угла, а параллелограмм является прямоугольником».Ссылка: Материалы для учащихся по математике 9 класса, стр. 320 — 322 Концепции: Прямоугольник — это параллелограмм с четырьмя (4) прямыми углами. УПРАЖНЕНИЯ:

W

I I

Дано: WINS — это параллелограмм с прямым углом W. Докажите: I, N и S — прямые углы. S ЗАЯВЛЕНИЯ 1. 2. m 3. 4. mm

ПРИЧИНЫ Учитывая

W = 90 В параллелограмме противоположные углы совпадают W = m I = m

NS

5. m N = 90 6. m W + m I = 180 7. 90 + m I = 180 8.9. m I = 90 10. 11. Угол I, угол N и угол S являются прямыми углами 12.

Подстановка рефлексивных свойств (SN 4 ND ()

Определение прямоугольника

N

Математика 9 класс Третья четверть

ЗАДАНИЕ № 9 Тип упражнения: НАЗВАНИЕ упражнения: ДОКАЗАТЕЛЬСТВО — ТЕОРЕМЫ О ПРЯМОУГОЛЬНИКЕ Обучающая компетенция: доказывает теоремы о различных видах параллелограммов (прямоугольник, ромб и квадрат) (M9GE-III-1) Цель обучения: доказать теоремы о прямоугольнике, «Диагонали прямоугольника совпадают».Ссылка: Материалы для учащихся по математике 9 класса, стр. 320 — 322 КОНЦЕПЦИЯ: Прямоугольник — это параллелограмм, две пары противоположных сторон которого совпадают и параллельны. УПРАЖНЕНИЯ: данный WINS представляет собой прямоугольник с диагоналями WN и SI. Докажите: WN ≅ SI W

S ЗАЯВЛЕНИЯ 1.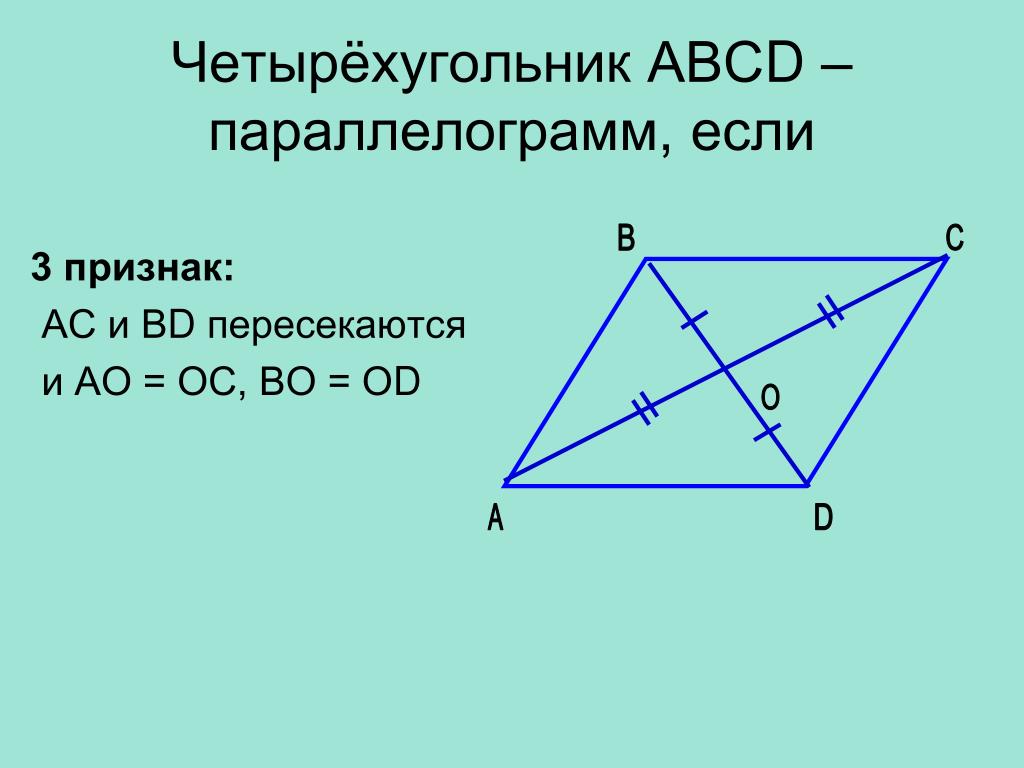 2. WS≅IN 3. угол WSN и угол INS — прямые углы 4. 5. SN≅NS 6. 7. WN ≅ IS

I

N ПРИЧИН 1. 2. 3. 4. Все прямые углы совпадают 5. 6. Постулат конгруэнтности SAS 7.

9 класс Математика Третья четверть

ДЕЯТЕЛЬНОСТЬ No.10

Тип деятельности

: Упражнение

Название: Умение изучать ромб: доказывает теоремы о различных типах параллелограммов (прямоугольник, ромб и квадрат) (M9GE-IIIc-1) Цель обучения: доказать теорему или ромб «диагонали» ромба перпендикулярны, а каждая диагональ делит пополам противоположные углы ». Ссылка: Материалы для учащихся по математике 9 класса, стр. 322 — 324 Понятия: Ромб — это параллелограмм с четырьмя равными сторонами. УПРАЖНЕНИЕ I. Дано: Rhombus ROSE Доказательство: RS ⏊ OE Доказательство: ЗАЯВЛЕНИЯ 1.2. OS, конгруэнтный RO 3. 4. H — средняя точка RS 5. 6. OH конгруэнтный OH 7. 8. угол RHO конгруэнтный угол SHO 9. угол RHO и угол SHO прямые. 10.

ПРИЧИНЫ 1. Дано 2 3. Диагонали параллелограмма делят друг друга пополам. 4. 5. Определение средней точки 6. 7. Постулат конгруэнтности SSS 8. 9. 10. Перпендикулярные линии пересекаются, образуя прямые углы

УПРАЖНЕНИЯ II.

V

W 3

ДАННЫЙ: ромб VWXY PROVE:

1≅

4

2 1

2

Y ЗАЯВЛЕНИЕ 1.2. YV ≅ VW; WX ≅ XY 3. 4. YVW ≅ WXY

X ПРИЧИНА 1. Дано 2. 3. Отражающее свойство 4.

5. Угол 1 ≅ угол 2; угол 3 ≅ угол 4

5.

9 класс Математика Третья четверть

ЗАДАНИЕ № 11 Тип деятельности НАЗВАНИЕ Учебная компетенция LT Ссылка

: Концептуальные заметки: ТЕОРЕМА СРЕДНЕЙ ЛИНИИ (A): доказывает теорему средней линии (M9GE- IIId-1): Докажите теорему Срединной Линии: Материалы для учащихся по математике 9 класс, стр. 327 — 328

КОНЦЕПЦИЯ: Теорема о средней линии «Отрезок, соединяющий концы двух сторон треугольника, параллелен третьей стороне и вдвое короче».B

D

E

A

C

Точка D является средней точкой AB. Точка E — это середина BC. Отрезок DE — это середина двух сторон треугольника ABC. DE параллелен AC, DE составляет ½ от AC.

N 1

O Упражнения: Дано: треугольник HNS, O — середина HN, E — середина NS. Доказательство: OE II HS, OE II ½ HS

2 E 3

T

4 H

.

S

Доказательство: ЗАЯВЛЕНИЯ 1. Треугольник HNS, O — середина HN, E — середина NS.2. 3. EN ≅ ES 4. Угол 2 ≅ угол TSE 5. Треугольник ONE треугольник TSE 6. Угол 1 ≅ угол 4 7. HN II ST 8. OH ≅ ON 9. ON ≅ TS 10. OH ≅ ST 11. Четырехугольник HOTS — это параллелограмм 12. OE II HS 13. OE + ET = OT

ПРИЧИНЫ.

В луче укажите на заданном расстоянии от конечной точки луча.

14. OE + OE = OT 15. 2OE = OT 16. HS ≅ OT 17. 2 OE = HS 18. OE = ½ HS (отрезок, соединяющий середины двух сторон треугольника, вдвое короче третьей стороны

9 класс Математика 3-я четверть

ДЕЯТЕЛЬНОСТЬ №12 Тип деятельности

: Упражнение

Название Изучение компетенции LT Ссылка

: Теорема о средней линии (B): доказывает теорему о средней линии (M9GE-IIId-1): решите проблему, используя теорему о средней линии. : Материалы для учащихся 9 класса по математике, с. 329

Концепция: Теорема средней линии гласит: «Отрезок, соединяющий середины двух сторон треугольника, параллелен третьей стороне и вдвое короче. Иллюстративный пример: в треугольнике MCG, A и I являются серединами сегмента MG и CG соответственно.Обдумайте каждую предоставленную информацию и ответьте на следующие вопросы. Дано: AI = 10,5 Вопросы: 1. Что такое MC? Ответ: MC = 21 M C 2. Как вы решали MC? Поскольку AI = 1/2 MC из средней теоремы, тогда:

A

I

MC = 2 (AI) = 2 (10,5) = 21 G УПРАЖНЕНИЯ: См. Треугольник MCG в иллюстративном примере, где A и I являются средней точкой сегмента MG и CG. 1. Дано: CG = 32 Вопросы: a. что такое GI? б. Как вы решали GI? 2. Дано: AG = T и CI = 8 Вопросы: a. Что такое MG + GC? б.Как вы решили сумму? 3. Дано: AI = 3x-2 и MC = 9x-13 Вопросы: a. каково значение x? б. как вы нашли x? c. какова сумма AI + MC? Почему?

9 класс Математика Третья четверть

ЗАДАНИЕ № 13 Тип деятельности

: Концептуальные заметки

Название: Теорема среднего сегмента трапециевидной обучающей компетенции: доказывает теорему о средней линии (M9GE-IIId-1) Цель обучения: доказать Теорема о трапеции Ссылка

: Материалы для учащихся по математике 9 класс, с.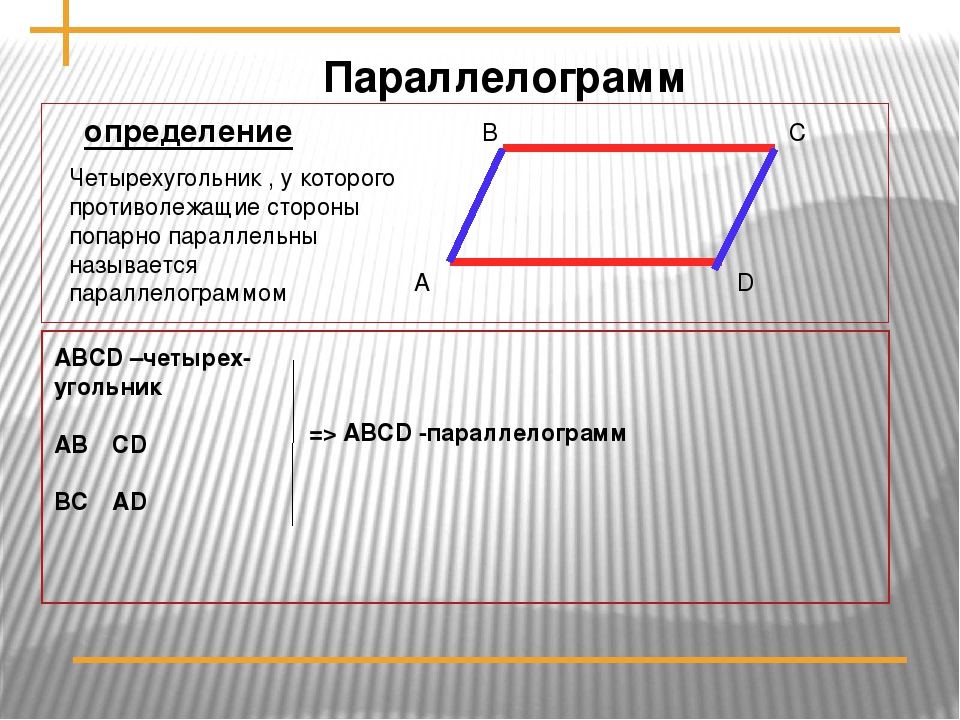 330-331

Концепция: Трапеция — это четырехугольник, у которого ровно одна пара параллельных сторон. Медиана трапеции — это сегмент, соединяющий середину ног. Медиана трапеции параллельна каждому основанию, а ее длина составляет половину суммы длины основания. Параллельные стороны трапеции называются основаниями, а непараллельные стороны — ногами. B C O

E

A D OE — это медиана трапеции ABCD. BC и AC — это основания. AB и DC — ноги.I OE = ½ (BC + AD)

N

УПРАЖНЕНИЯ: T P R Дано: трапеция МИН с медианной TR. Докажите: TR II IN, TR II MS TR = 1/2 (MS + IN) M ЗАЯВЛЕНИЯ ПРИЧИНЫ 1. 2. Нарисуйте IS с P в качестве средней точки 3. TP = 1/2 и TP II MS 4. Теоремы (Средняя линия теорема), на треугольнике INS 5. MS II IN 6. TP II IN 7. TP и PR параллельны TP II IN. таким образом, T, P и R коллинеарны 8. 9. TR = TP + PR 10. Замена 11. TR = ½ (MS + IN)

9 класс Математика Третья четверть

A C T I V I T Y No.14 Тип деятельности Название

: Концептуальная записка: Теоремы о равнобедренной трапеции

Обучающая компетенция: Доказательство теорем о трапеции и воздушных змеях (M9DE-III-2) LT

: Доказательство теорем о равнобедренной трапеции

Справочный материал

: учебный материал

: по математике 9 класс, стр.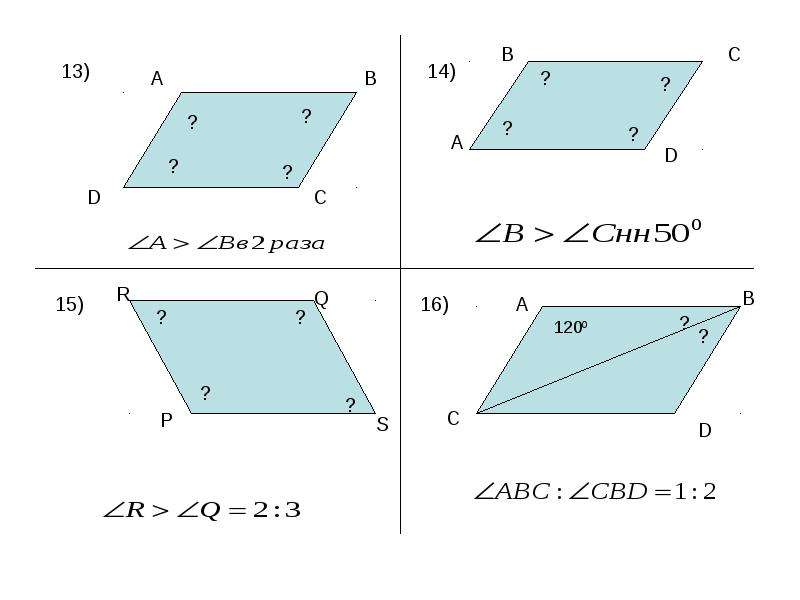 331-332

Концепция:

В равнобедренной трапеции ноги совпадают, основания совпадают, диагонали совпадают, а противоположные углы являются дополнительными.B

C

A

cD

ABCD — равнобедренная трапеция, где:

AB ≅ DC (ноги) AC≅ BD (диагонали) Угол A ≅ угол D (базовые углы) Угол B ≅ угол C (основание angles)

Дополнительные углы два угла, сумма которых равна 180 ⁰. УПРАЖНЕНИЯ:

M

O

Дано: Равнобедренная трапеция AMOR MO II AR Доказательство: угол A ≅ угол R, угол AMO ≅ угол O 1 A

ЗАЯВЛЕНИЯ 1. 2. AM = OR, MO ll AR 3. От M, нарисуйте ME ll ИЛИ, где E лежит на AR 4.5.ME ≅ OR

2 E

ПРИЧИНЫ Дано

Определение параллелограмма

R

6.OR ≅ ME 7. 8. треугольник AME — равнобедренный треугольник 9. угол 1 ≅ угол A 10 угол 1 ≅ угол e R. 11. угол R ≅ угол A 12. угол A ≅ угол R 13. Угол A и угол AMO — дополнительные углы Угол O и угол R — дополнительные углы 14. угол AMO угол O Доказательство:

Переходное свойство

Доказательство:

9 класс Математика 3-я четверть

ДЕЯТЕЛЬНОСТЬ No. 15

Тип деятельности: Навыки Название: Решение задач в обучении по трапеции. Компетенция: доказывает теоремы о трапециях и воздушных змеях (M9GE-III-2). . 334-335 https://www.youtube.com/watch?v=9W6UjpqX2Zs Концепция: вы только что изучили различные теоремы, касающиеся трапеции. Теперь вы примените теоремы при решении задач. Теорема 6: Медиана трапеции параллельна каждому основанию, а ее длина равна половине суммы длин оснований.Теорема 7: углы основания равнобедренной трапеции равны. Теорема 8: Противоположные углы равнобедренной трапеции являются дополнительными. Теорема 9: диагонали равнобедренной трапеции совпадают. Пример I. Рассмотрите рисунок справа и ответьте на следующие вопросы. Дано: четырехугольник MATH — это равнобедренная трапеция с основанием MA и HT, LV — медиана. 1. Дано: MA = 3y-2, HT = 2y + 4: LV = 85 см M A Вопросы: a. Какое значение у? L V Ответ: LV = MA + HT 2 8,5 = 3y-2 + 2y + 4 H T 2 17 = 3y-2 + 2y + 4 17 = 5y + 2 5y = 17-2 5y = 15 5 5 Y = 3 b.Как вы решили у? Ответ: применяя теорему «Медиана трапеции параллельна основаниям, а ее длина составляет половину суммы оснований». c. Что такое MA и HT? Ответ: MA = 3y-2 HT = 2y + 4 = 3 (3) -2 = 2 (3) +4 = 9-2 = 6 + 4 MA = 7 HT = 10

Упражнения: Рассмотрите фигуру на заданном пример. Ответьте на следующие вопросы. 1. Дано: измерить угол HMA = 115 a. Что такое угол измерения ТАМ? б. Какая теорема оправдывает ваш ответ? 2. Дано: AH = 4y-3; MT = 2y + 5 a. Какое значение у?

г.Как вы решили у? c. Какова длина каждой диагонали? d. Какая теорема оправдывает ваш ответ?

\

9 класс Математика 3-я четверть

ЗАДАНИЕ № 16

Тип деятельности

: Концептуальные заметки

Название: Теоремы в изучении воздушного змея Компетенция: доказывает теорему о трапециях и воздушных змеях (M9GE-III-2) Обучение Цель: доказать теорему с помощью воздушного змея. Ссылка: Материалы для учащихся по математике 9 класса, стр. 335-336 Концепция: «Диагонали воздушного змея перпендикулярны друг другу.«Площадь воздушного змея равна половине произведения длин его диагоналей. Пример: Дано: кайт СЛОВО с диагоналями WR и OD.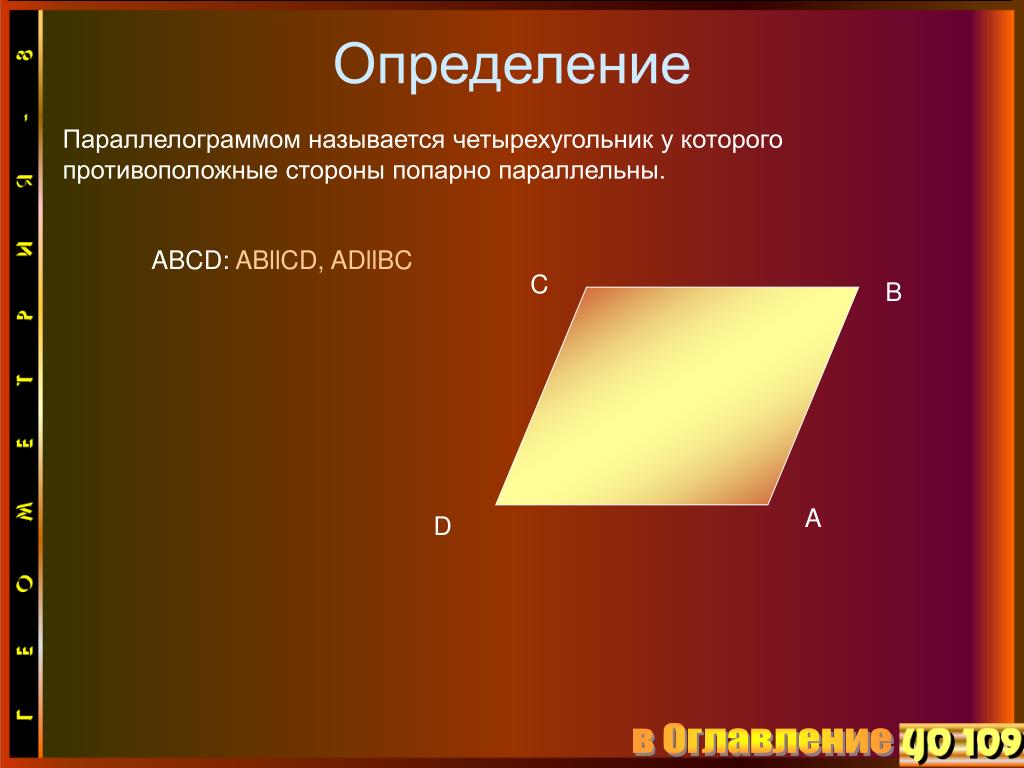 Докажите: WR — серединный перпендикуляр к OD. O W

R

D PROOF:

1. 2. 3. 4.

ЗАЯВЛЕНИЯ Kite WORD с диагоналями WR и OD WO≅WD; ИЛИ = DR WO = WD; OR = DR WR — серединный перпендикуляр к OD.

ПРИЧИНЫ Данное определение воздушного змея Определение конгруэнтных сегментов Если линия содержит две точки, каждая из которых равноудалена от конечных точек сегмента, линия является серединным перпендикуляром сегмента.

УПРАЖНЕНИЯ: Дано: Кайт ВЕРЕВКА Доказательство: Площадь Кайт ВЕРЕВКИ = ½ (OE) (PR) PO

E

R

ЗАЯВЛЕНИЯ 1. 2. 3. Площадь Кайта ВЕРЕВКА = площадь треугольника OPE + площадь треугольник ORE

ПРИЧИНЫ ДАННЫЕ Диагонали воздушного змея перпендикулярны друг другу Постулат добавления площади

4. Площадь треугольника OPE = 1/2 (OE) (PW) Площадь ORE = 1/2 (OE) (WR) 5. 6. 7. 8.

Формула площади для треугольников

9 класс Математика Третья четверть

ДЕЯТЕЛЬНОСТЬ No.17

Тип деятельности: Навыки Название: Решение проблем с воздушными змеями. Изучение компетенции: решает задачи, связанные с параллелограммами, трапециями и воздушными змеями (M 9GE-IIIe-1). 9, стр. 337 Концепции: В воздушном змее серединный перпендикуляр по крайней мере одной диагонали является другой диагональю »« Площадь воздушного змея равна половине произведения длин его диагоналей ». Пример I. Рассмотрите следующий рисунок и ответьте на заданные вопросы.Дано: Нарисуйте кайт-игру, учитывая, что PA = 12 см и LY = 6 см. Вопросы 1. Какова площадь кайт-игры? Ответ: A = (12 см) (6 см) 2 2 = 36 см 2. Как вы решили его площадь? Ответ: применяя теорему «Площадь воздушного змея равна половине произведения длин его диагоналей. УПРАЖНЕНИЕ: рассмотрите фигуру в данном примере. Данный четырехугольник PLAY представляет собой воздушный змей. 1. Дано: площадь воздушного змея PLAY = 135 см2; LY = 9 см. Вопросы: 1. Какова длина PA? 2. Как вы решали вопрос о ПА? 3. Какая теорема оправдывает ваш ответ выше?

9 класс Математика Третья четверть

A C T I V I T Y No.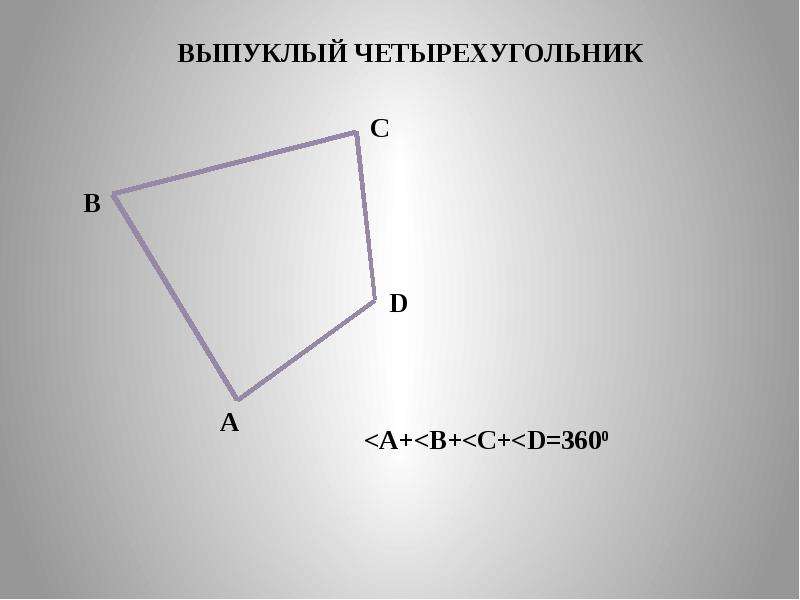 18

Тип деятельности: Навыки Название: Решение задач с параллелограммами и трапециями. Обучающая компетенция: решать задачи с параллелограммами, трапециями и воздушными змеями (M 9GE-IIIe-1) Цель обучения: решать задачи с параллелограммами и трапециями. Ссылка: Материалы для учащихся по математике 9 класса, стр. 341 Концепции: «если параллелограмм имеет прямой угол, то он имеет четыре прямых угла, а параллелограмм является прямоугольником». «Диагонали прямоугольника совпадают». «Диагонали ромба перпендикулярны.«Медиана трапеции параллельна каждому основанию, а ее длина составляет половину суммы длин оснований». «Угол основания равнобедренной трапеции конгруэнтен». «Противоположные углы равнобедренной трапеции являются дополнительными». «Диагонали равнобедренной трапеции совпадают». УПРАЖНЕНИЯ: Решите каждую проблему полностью и точно. Покажите свое решение и напишите теоремы или свойства, чтобы обосновать свой ответ. 1. Дано: Четырехугольник ЖЕЛАНИЕ — параллелограмм. а. Если измерить угол W = x + 15 и измерить угол S = 2x + 15, какова мера угла W? б. Если WI = 3y + 3 и HS = y + 13, какова длина HS? c. Если WISH — это прямоугольник с периметром 56см. одна сторона на 5 см меньше, чем вторая сторона. Какие размеры и насколько велика его площадь. d. Каков периметр и площадь самого большого квадрата, который может быть образован из прямоугольника WISH в C?

9 класс Математика Третья четверть

ДЕЯТЕЛЬНОСТЬ № 19

Тип деятельности Название Учебная компетенция Учебная цель Ссылка

: Навыки: Решение задачи на трапеции и воздушном змею: Решайте задачи, связанные с параллелограммами, трапециями и воздушными змеями (M 9GE-IIIe- 1): овладеть мастерством решения задач, связанных с трапецией и воздушным змеем: Материалы для учащихся 9 класса по математике, с. 341

УПРАЖНЕНИЕ: решите каждую проблему полностью и точно. Покажите свое решение и напишите теоремы или свойства, чтобы обосновать свой ответ. Дано: Четырехугольник POST — это равнобедренная трапеция с OS II PT. ER — это медиана. а. Если OS = 3x-2, PT = 2x + 10 и ER = 14, какова длина каждой базы? б. Если измерить угол P = 2x + 5 и измерить угол O = 3x-10, каков угол измерения T? c. Одно основание в два раза больше другого, длина ER — 6 см. Если его периметр 27 см, какова длина каждой ноги? d.ER имеет длину 8,5 м и длину одной ноги 9 м. каков его периметр, если одно из оснований на 3 м больше другого?

9 класс Математика Третья четверть

ЗАНЯТИЕ № 20 Тип деятельности Название задания

: Упражнение: Соотношение

Компетентность обучения: Описывает пропорцию (M9GE-III-1) Цель обучения: Определить и упростить соотношения Ссылка: Геометрия по Soloedad ​​Jose-Dilao, стр. 45, Math Digest, Learner’s Material, стр. 358 Концептуальные примечания: Отношение используется для сравнения двух или более величин.Величины, участвующие в соотношении, имеют одинаковый вид, поэтому соотношение не складывается из единиц. Однако, когда количества относятся к разным видам, сравнение количеств с учетом единиц называется ставкой. Даны два числа a и b, такие что b ≠ a, отношение a к b — это частное a, деленное на b. Отношение может быть представлено четырьмя способами: от a до b a: b a / b b Отношение a: b считается самым простым, когда наибольший общий делитель 5 для a и b был разделен. Например, отношения 1 к 2, 3: 4 и в простейшей форме 6 6.Также обратите внимание, что отношения 9:12 и 21: 28 могут быть выражены в простейшей форме 8 3: 4. Когда между измерениями используются соотношения, каждое число в соотношениях сначала должно быть выражено в одной и той же единице. Например, при соотношении 15 см к 2 м 2 м необходимо преобразовать в 200 см. Таким образом, соотношение становится 15 см к 200 см или 3:40 в простейшем виде. Наглядные примеры: выразите каждое соотношение в простейшей форме: 30 ° 1) 180 ° Решение:

Итак

30 ° 180 °

30 ° 30 ÷ = 180 ° 30 =

1 6

1 6

( Примечание: 30 — это наибольший общий делитель 30 и 100)

в простейшей форме

2) 2 км в 750 м Решение: сначала необходимо преобразовать 2 км в м 1000 м 2 км × = 2000 м 1 км 2000 м 250 20 ÷ = 750 м 250 3 общих делителя 2000 и 750) 2000 20 Итак, простейшая форма = 750 3 УПРАЖНЕНИЯ: Выразите каждое соотношение в простейшей форме: 1) 52: 91 2) от 3 мин до 42 сек от 2000 м до 750 м

или

9 класс Математика

(Примечание: 250 — высший

3) от 4 дней до 2 недель 4) 3 м

Третий квартал

ДЕЯТЕЛЬНОСТЬ No. 21 Тип задания Задание Название Учебная компетенция Учебная цель Ссылка

: Упражнение: Пропорция: Описывает пропорцию (M9GE-III-1): Определите пропорцию и определите ее часть: Геометрия Соледад Хосе-Дилао стр. 146 Math Digest p. 2-6, Пособие для учащихся, стр. 360

Концептуальные примечания: Равенство двух соотношений называется пропорцией. Если отношения a: b и c: d равны, то мы пишем a: b = c: d или a / b = c / d (где b и d не равны нулю). Это читается как «a относится к b, как c относится к d».Каждое число в пропорции называется термином. В пропорции a: b = c: d члены a и b называются крайностями, а члены b и c называются средними. Первый член

:

b = c второй член третий член означает

:

d четвертый член

крайностей Иллюстративные примеры: A) Используя определение пропорции, скажите, образует ли каждая пара отношений пропорцию: 15 3 1), пропорция (наибольший общий делитель 15 20 4 и 20 равен 5) 2) 3)

2, 5 1, 2

5 8 13 26

непропорциональная пропорция

(без общего делителя)

(наибольший общий делитель 13

и 26 равен 13) B) Определите средние и крайние значения: 1)

3 4

=

7 14

или

3: 4 = 7: 14

означает 4 и 7,

крайние значения 3 и 14 2)

2 = 5

4 10

или

2: 5 = 4: 10

средние значения 5 и 4,

крайние значения 2 и 10 Упражнения: A)

Определите части данной пропорции (среднюю и крайнюю):

1 )

12 = 18

2)

2 5

=

2 3

3) 6 15

6: 9 = 2: 3

4) 5: 6 = 10: 18

Степень 9 Математика Третий квартал

ДЕЯТЕЛЬНОСТЬ №22 Тип упражнения: Упражнение Название: Фундаментальный закон пропорции Компетентность в обучении: Применяет фундаментальные теоремы пропорциональности для решения задач, связанных с пропорцией (M9GE-IIIf-2} Задача обучения: сформулировать и применить фундаментальный закон пропорции Ссылка: материалы учащегося, стр. 360, Math Digest, стр. 7, Геометрия, Соледад Хосе-Дилао, стр.146 Концептуальные заметки: Основной закон пропорции: «В пропорции произведение крайностей равно произведению средних». Ac If = или a : b = c: d, затем ad = bc bd Иллюстративные примеры: Примените фундаментальный закон пропорции, чтобы найти x: 1)

2: 4 = 8: x

Решение: 2 (x) 2x xx

= = = =

4 (8) 32 32/2 16

3 2 = x − 4 5 Решение: 2 (x-4) = 2x — 8 = 2x -8 + 8 = 2x = x = 2)

или

3 (5) 15 15 +8 23 23/2 1 x = 11 2

3 24 = x 40 Решение: 24 (x) 24x xx

3)

4)

= = = =

3 ( 40) 120 120/24 5

4: x = x: 9

Решение: x (x) = 4 (9) x² = 36 x

= ± √ 36 x = ± 6

УПРАЖНЕНИЯ: примените основные закон пропорции при решении для переменной в каждой пропорции: 1)

2 x

=

12 18

3)

2 x

=

3 x + 2

2)

2 10 = 3 x

4)

4 x = x 9

9 класс Математика Третья четверть

ДЕЯТЕЛЬНОСТЬ No.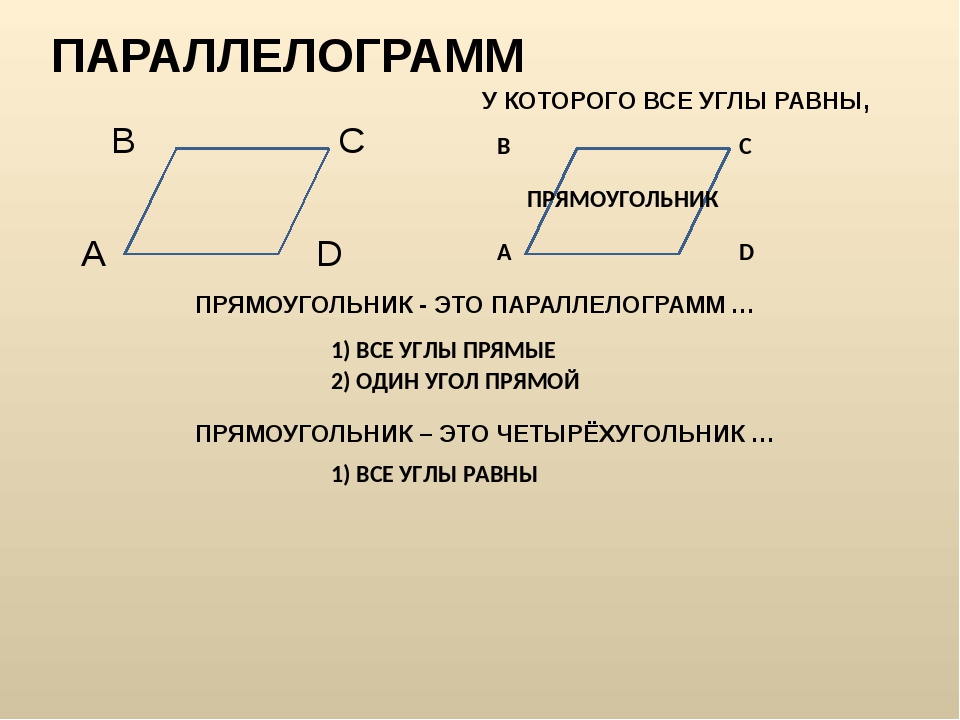 23 Тип упражнения: Упражнение Название упражнения: Свойства пропорции. Компетентность в обучении: Применяет фундаментальные теоремы пропорциональности для решения задач, связанных с пропорциями (M9GE-IIIf-2} Задача обучения: сформулировать и применить свойства пропорции. Ссылка: Материалы учащегося, стр. 360, Math Digest стр. 7 Концептуальные примечания: Свойства, которые следуют ниже, показывают несколько способов переписать пропорции, которые не изменяют значения их значений. Свойства пропорции:

Свойство перекрестного умножения

Свойство чередования

Обратное свойство

Свойство сложения

Свойство вычитания

Обратное свойство

Если

wy =, то wz = xy; x ≠ 0, z ≠ 0 xz

Если

wywx =, то =; x ≠ 0, y = 0, z ≠ 0 xzyz

Если

wyxz =, то =, w ≠ 0, x ≠ 0, y ≠ 0, z ≠ 0 xzwy

Если

wy w + x y + z =, то =; x ≠ 0, z ≠ 0 xzxz

Если

w y w − x y − z =, тогда =; x ≠ 0, z ≠ 0 x z x z

Если

u w y u w y u + w + y = =, то = = = = k; vxzvxz v + x + z

Где k — константа пропорциональности, а v ≠ 0, x ≠ 0, z ≠ 0 Иллюстративные примеры: перепишите данные пропорции в соответствии со свойством, указанным в таблице, и выясните, соответствуют ли соотношения в переписанных пропорциях по-прежнему равны. Используйте свойство перекрестного умножения, чтобы убедиться, что соотношения равны. При необходимости упростите.

Свойство чередования исходной пропорции Обратное свойство

Свойство сложения Свойство вычитания

ya = 3 4 y 3 = a 4 3 4 = ya y + 3 a + 4 = 3 4 y − 3 3

=

4y = 3a 4y = 3a 4y = 3a 4y + 12 = 3a + 12 или 4y = 3a

a − 4 4

4y — 12 = 3a — 12 или 4y = 3a

УПРАЖНЕНИЯ: примените свойства пропорции, переписав заданная пропорция указанного свойства: 4 n Дано: = m 5 1) Свойство перекрестного умножения

________________

2) Свойство чередования

________________

3) Обратное свойство

________________

4) Свойство сложения

________________

5) Свойство вычитания

________________

9 класс Математика Третья четверть

ДЕЯТЕЛЬНОСТЬ No.24 Тип задания: упражнение. Компетенция обучения: применяет фундаментальные теоремы пропорциональности для решения задач, связанных с пропорциями (M9GE-IIIf-2} Название задания: Определение количеств по заданной пропорции Задача обучения: определение количеств по заданной пропорции Ссылка: материалы учащегося стр. 362 Концептуальные заметки: В этом разделе вы будете использовать концепции и навыки, которые вы узнали на предыдущих уроках.Вы будете изучать, как определить указанные количества из заданной пропорции.Пример 1. Если m: n = 4: 3, найдите 3m — 2n: 3m + n Решение: m 4 4n = m = n 3 3 Используя m =

4n 3

3 m − 2 n = 3 m + n

3 (

4n) –2n 3 =

3 (

4n) 3

4 n − 2 n 4 n + n

=

2n 2 = 5n 5

Следовательно, 3m — 2n: 3m + n = 2: 5 Пример 2: Если e и b представляют два ненулевых числа, найдите соотношение e: b, если 2e² + eb — 3b² = 0. Решение:

2e² + eb — 3b² = 0 (2e + eb) (e — b) = 0 2e + 3b = 0 e — b = 0 2e = -3b 2e −3 b = 2b 2b e −3 = b 2

e = b

eb

= b

b

eb

= 1

1

Следовательно, e: b = -3: 2 или 1: 1

УПРАЖНЕНИЯ: Определите указанные количества из заданной пропорции: 1) Если p: y = 2: 5, найдите 4p — 3y: 4p + y 2) Если x и z представляют собой два ненулевых числа, найдите отношение x: z, если x² + xz — 2 z² = 0.

9 класс Математика Третий квартал

ЗАДАНИЕ № 25 Тип упражнения: Производственное задание Задание Название задания: Схожие многоугольники Учебная компетенция: проиллюстрировать сходство фигур (M9GE-IIIg-1) Задача обучения: проиллюстрировать похожие многоугольники Ссылка: Пособие для учащихся с. 363 Концептуальные заметки: два многоугольника подобны, если их вершины могут быть соединены так, что соответствующие углы совпадают, а соответствующие стороны пропорциональны. Отношение длин любой пары соответствующих сторон называется отношением подобия или масштабным коэффициентом.Примеры похожих многоугольников 

Трапеции, показанные ниже, похожи; они имеют одинаковую форму, но разные по размеру.



Любые две соответствующие стороны двух одинаковых фигур имеют общее отношение, называемое масштабным коэффициентом. Показанные выше трапеции ABCD и EFGH похожи. Итак,

.



Отношение площадей двух одинаковых фигур является квадратом масштабного коэффициента.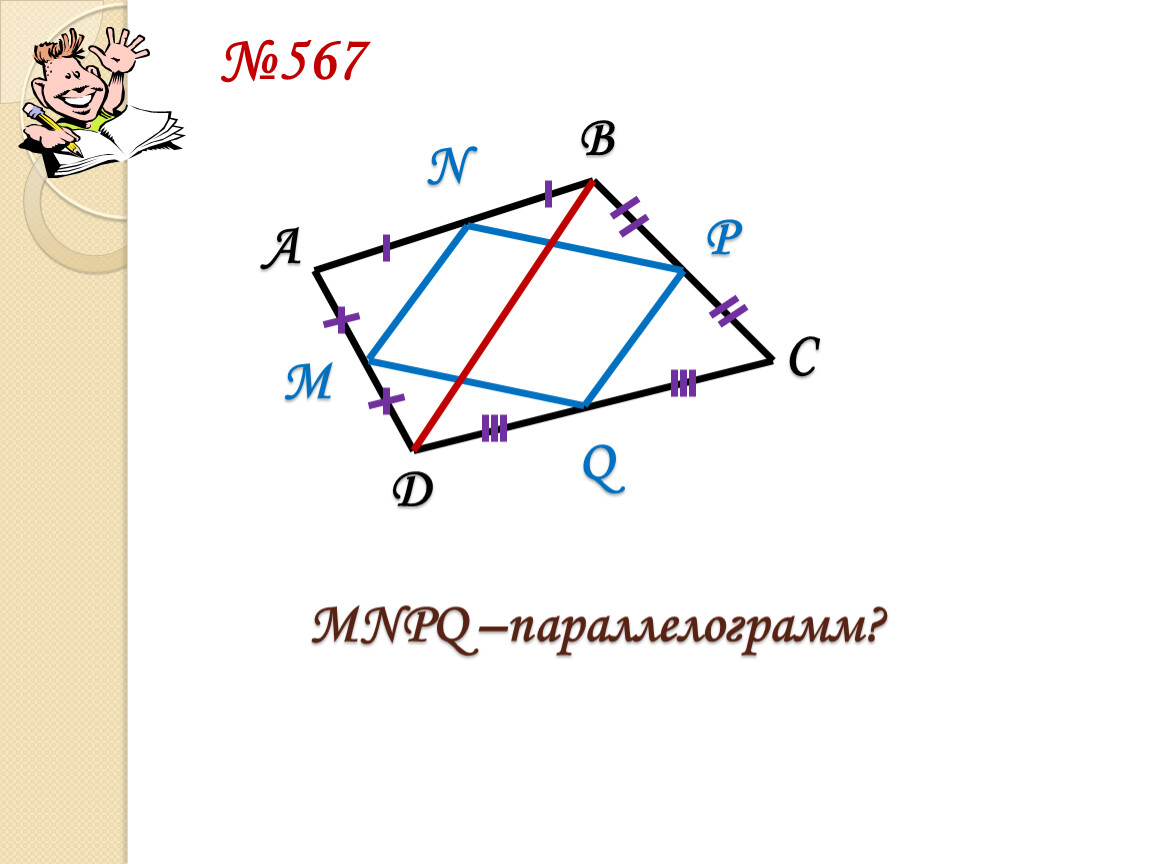



Соотношение объемов двух одинаковых фигур является кубом масштабного коэффициента.

УПРАЖНЕНИЯ: 1) Проиллюстрируйте свои собственные два похожих многоугольника. 2) Из вашей иллюстрации в № 1, обозначьте совпадающие углы и пропорциональные стороны.

9 класс Математика 3-я четверть

ЗАДАНИЕ № 26 Тип упражнения: Упражнение Название задания: Сходство между треугольниками Учебная компетенция: Подтверждает условия сходства треугольников (M9GE-IIIg-h-1) Учебная цель: Применить определение похожие треугольники Определение того, похожи ли два треугольника ° Два треугольника подобны, если соответствующие углы совпадают, а соответствующие стороны пропорциональны.Иллюстративные примеры: Определите, похожи ли данные пары треугольников. Если да, дайте заключение о сходстве. 1)

Q

X

2)

S

аналогичный T

40 °

W

40 °

UP

V

68 °

Z

аналогичное решение: ∆PQR VTW P≅Z Q≅X R≅Y

Решение: ∆ZXY

∆ STU S ≅ V  STU ≅  VTW U ≅ W ST = TU = SU VT TW VW

PQ = QR = PR ZX XY ZY

УПРАЖНЕНИЯ: Определите, похожи ли данные пары треугольников или нет. B 1.) F 2) D 18 H

24 20

G

53 ° A

C

80 ° 50 ° E

∆

I 9

12

K

J

9 класс Математика Третий квартал

ЗАДАНИЕ № 27 Тип задания: Концептуальные записки Название задания: Теорема подобия SAS Изучение компетенции: Теорема подобия SAS (M9GE-IIIg-h-1) Цель обучения: сформулировать и доказать условия подобия треугольников по теореме подобия SAS Ссылка: Геометрия Соледад Хосе-Дилао стр.162, Материалы для учащихся, стр. 374 Если в двух треугольниках две пары соответствующих сторон пропорциональны, а включенные углы конгруэнтны, то треугольники подобны. X A На рисунках XY = XZ. AB AC 4 6 8 12 Угол между XY и XZ равен X, который соответствует углу B C и углу theA между AB и AC. Тогда по теореме подобия SAS имеем ∆XYZ ∆ABC Y Z. Наглядные примеры: какие из следующих пар треугольников похожи? Для тех, кто есть, изложить и обосновать использованные условия.1.)

G

H

I

Решение: 1. ) Не похоже

7

3 13

9

K

J

2.) Теорема

2.) Аналогично Сходство SAS

6

9 50⁰

50⁰

12 8

3.)

3.) Аналогично теореме подобия SAS 7 10

5 14

Упражнения: сформулируйте теорему и докажите условия, которые используются, если данная пара треугольников подобна.1.)

12

8

2 3

2.)

7

4

21

3.)

18 6 25⁰

15

25⁰

12

9 класс Математика Третий квартал

ЗАДАНИЕ № 28 Тип занятия: Концепции Заметки Название занятия: Теорема подобия SSS Изучение компетенции: Теорема подобия SSS (M9GE-IIIg-h-1) Цель обучения: использовать теорему подобия SSS при написании оператор if-then для описания иллюстрации или завершения рисунка на основе оператора if-then.Концептуальные заметки: теорема подобия SSS «Два треугольника подобны, если соответствующие стороны двух треугольников пропорциональны». Q

T

P

RS

IF

U

PQ = QR = PR ST TU SU

Затем: PQR

STU

УПРАЖНЕНИЯ: Используйте теорему подобия SSS в написании оператора if- then для описания иллюстрации или завершения рисунка на основе оператора «если-то». 1)

A O

J Если

? ?

Y =

? ?

=

? ?

G

F

Тогда: _________________

9 класс Математика Третья четверть

A C T I V I T Y No.29 Тип деятельности Задание Название Учебная компетенция Учебная цель Ссылка

: Упражнение: Теорема подобия AA: теорема подобия AA (M9GE-IIIg-h-1): сформулируйте и проверьте теорему подобия AA: геометрия Соледад Хосе Дилао с. 160

Замечания по концепции Если два угла одного треугольника конгруэнтны двум треугольникам другого треугольника, то эти два треугольника подобны. На рисунках ниже мы видим, что M ≅ P, а L ≅ Q. Напомним также, что в двух треугольниках, если две пары соответствующих углов конгруэнтны, то третья пара должна быть конгруэнтной. Тогда у нас есть теорема подобия AA L

Q 62⁰

62⁰

88⁰

88⁰

M

O

P

R

Иллюстративные примеры: Определите, какие из следующих пар треугольников похожи по AA Теорема подобия. Подтвердите свои ответы, написав названия двух соответствующих углов. 1.)

65⁰

A

P

Решение:

30⁰

30⁰

1.) Не похоже

M

75⁰

T

L N

2.) Теорема

E

H

2.) Аналогично AA Подобие C ≅ G E ≅ H

CF

GI

3.) Теорема

3.) Аналогично AA Подобие S  Q ≅ T RUQ ≅ SUT

R

60⁰

60⁰

Q

U

T

Упражнения: Определите, какие из следующих пар треугольников похожи по теореме подобия AA. Подтвердите свой ответ, написав названия двух соответствующих углов.

1.)

W

Z

18

V

2.)

12

3

X

Y 2

LMN

OP

3. )

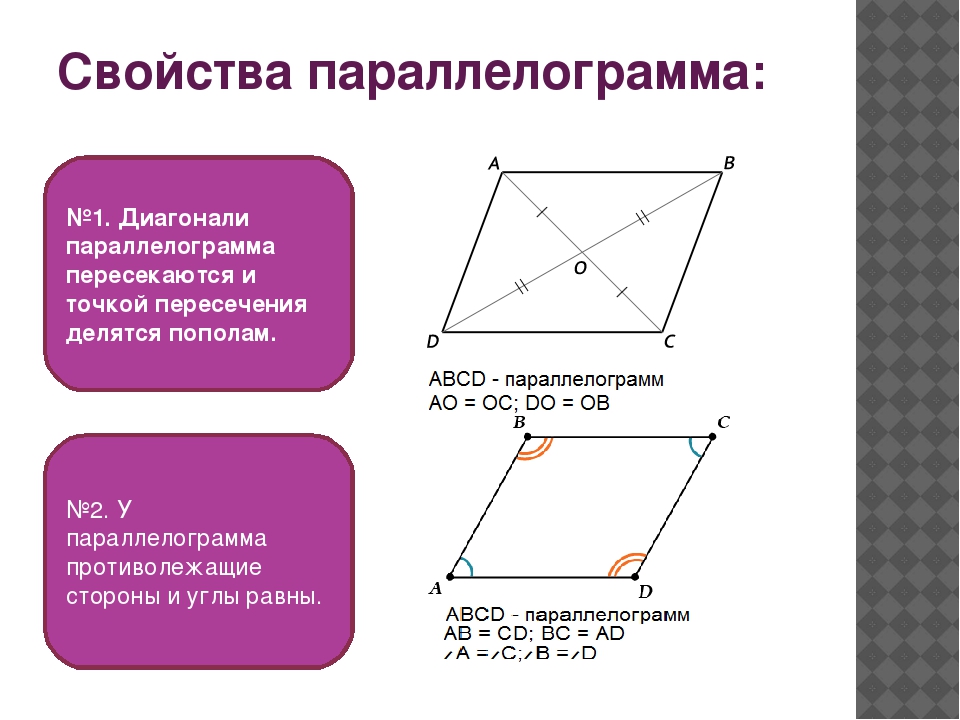000 3)

21/5

7

A

9 класс Математика 3-я четверть

ДЕЯТЕЛЬНОСТЬ № 30 Тип упражнения: Упражнение Название задания: Сходства в правильном треугольнике Компетенция в обучении: Применяет теоремы, чтобы показать, что данный треугольник похож (M9GE -IIIi-1) Цель обучения: применить теорему подобия AA для определения сходства в прямоугольном треугольнике. Ссылка: Геометрия Соледад Хосе-Дилао, Материалы для учащихся, стр.388 В прямоугольном треугольнике высота до гипотенузы делит его на два прямоугольных треугольника, которые похожи друг на друга и на данный прямоугольный треугольник. Внимательно изучите правую ∆ABC с прямым углом B. B

A

C

A

B

D BD — это высота

C

. образуются треугольники, похожие друг на друга. B B B

1

A

C

A

D

D

По рефлексивному свойству конгруэнтности A≅ A и C ≅ C.Поскольку все прямые углы конгруэнтны, то по теореме подобия AA ∆ABC ∆ADB BDC.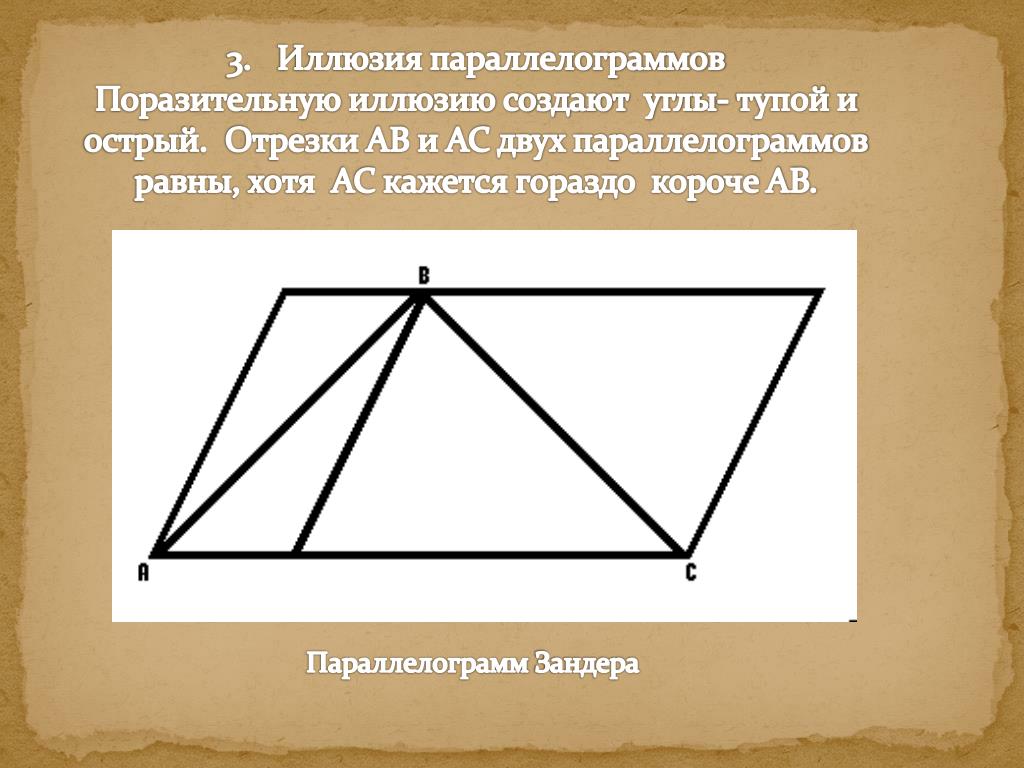 Таким образом, ∆ADB

∆BDC AD BD

BD = CD

∆ABC

∆BDC AC BC

BC = DC

∆ABC

∆ADB

AC = AB

C

Иллюстративные примеры: Предположим, что QC — это высота до гипотенузы DR правой ∆DQR. Определите 3 одинаковых прямоугольных треугольника, применяя теорему подобия AA, и запишите пропорциональные отрезки.

1.)

Q r

dh

a

b

D

R

Решение:

Q

Q

r

d

r

r

r

h

db

D

a + b

R

D

Три похожих треугольника следующие: ∆DQR

9

C

∆DCQ R0003

C

C

Пропорциональный Seb DC ∆DQR

∆QCR DR

∆DQR

QC

QR

∆DCQ DQ DC

ah QR = CR или d = b a + bd DR = DQ или a + b = rra

Упражнение: Предположим, что SD — это высота до гипотенузы UT правой ∆UST.Определите 3 подобных прямоугольных треугольника и их пропорциональные отрезки, применяя теорему подобия AA.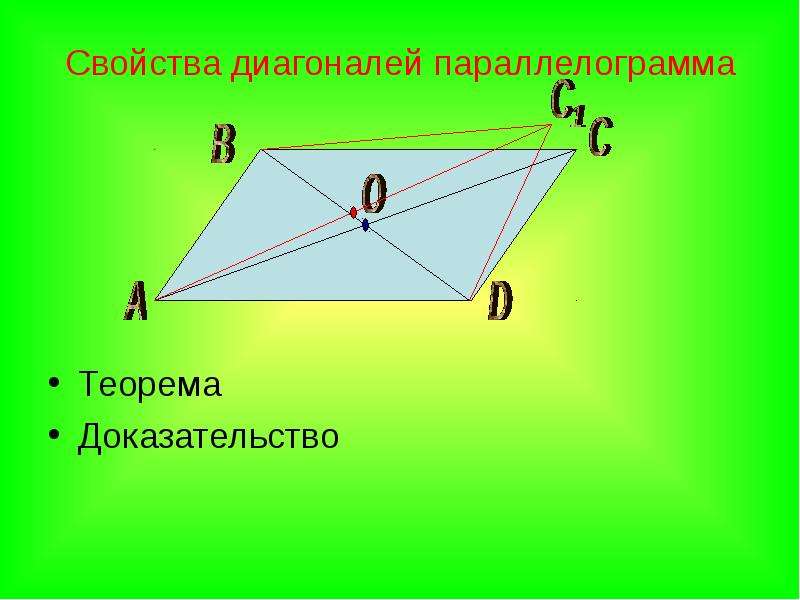 1.)

S

t

h

u

a

b

U

D

T

9 класс Математика Третья четверть

ДЕЯТЕЛЬНОСТЬ № 31 Тип задания: : Определение длин одинаковых прямоугольных треугольников Компетентность обучения: Применяет теоремы, чтобы показать, что данные треугольники аналогичны (M9GE-IIIi- 1) Задача обучения: Найдите указанные длины одинаковых прямоугольных треугольников Высота до гипотенузы — это среднее геометрическое между отрезки гипотенузы.C X = h или h3 = xy h y

h

x B

y D

A

Любой катет данного треугольника является средним геометрическим между гипотенузой и сегментом гипотенузы, примыкающим к этому катету. C

9

h

b

x B

X = a или a 2 = xc ac

y D

A

y = b или b 2 = yc bc

C Иллюстративные примеры Найдите указанная длина. CD — высота гипотенузы правой ABC.Найдите X, CB и CA. C

x

X = h или h3 = xy hy

9 B

25 D

Решение: a.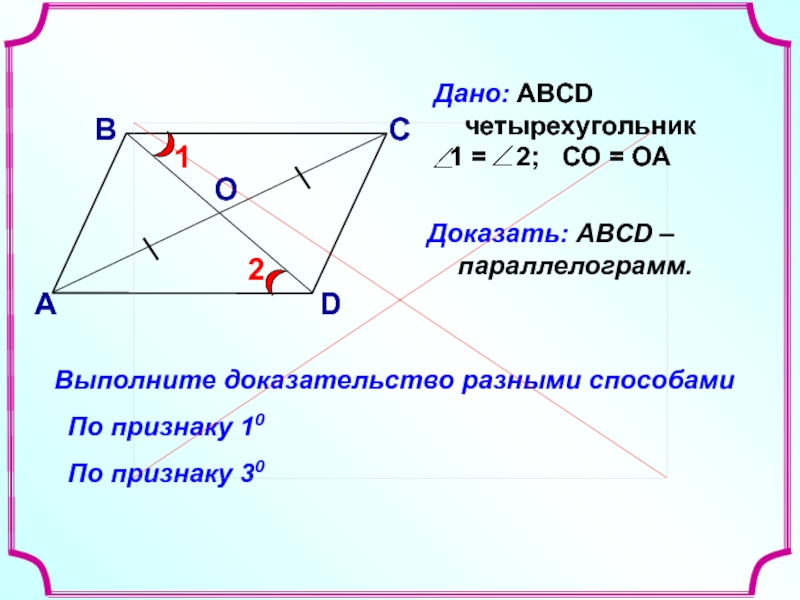 ) Решение для x: X2 = (BD) (DA) X2 = (9) (25) X2 = 225 X2 = √ 225 X2 = 15

A б.) Решение для CB: BD = CB CB BA CB2 = (BD) (BA) CB2 = (9) (34) CB = √ (9) (34) CB = 3√ 34

Решение: c.) Решение для CA: DA = CA CA BA CA2 = (DA) (BA) CA2 = (25) (34) CA = √ (25) (34) CA = 5√ 34

Упражнение: Найдите указанную длину, используя данный рисунок. Решите относительно X, Y и Z.1.) 4

yx

5

9 класс Математика 3-я четверть

ЗАДАНИЕ № 32 Тип упражнения

: Концептуальные заметки

Название задания: Теорема Пифагора Компетентность в изучении: доказывает теорему Пифагора- (M9GE-III 2) Цель обучения: применить определение подобного треугольника, чтобы вывести теорему Пифагора. Ссылка: Геометрия Соледад Хосе Дилао с.168

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Пусть ∆ABC — прямоугольный треугольник с катетами a, b и гипотенузой c. Докажем, что a2 + b2 = c2. Пусть CD — высота до гипотенузы. Пусть AD = X и DB = Y. Так как каждый катет ∆ABC — среднее геометрическое гипотенузы, примыкающей к этому катету, то c = b и c = a. Следовательно, b2 = cx и a2 = cy. b x a y

C

Поскольку x + y = c, имеем a2 + b2 = cy + cx = c (y + x), тогда a² + b² = c (y + x); y + x = c, поэтому подставьте a2 + b 2 = c ∙ c a2 + b2 = c²

b

a

A

D x

B y

c Иллюстративные примеры. Теорема, применяющая определение подобного треугольника.

1.)

Пусть DC = m AD = n

B

d

e

f = e или e2 = fm em

A

D

f = d или d2 = fn dn

C

n

m

f

Поскольку e2 = fm d2 = fn f = n + m

Итак, мы имеем: e2 + d2 = fm + fn e2 + d2 = f (m + n); m + n = f e2 + d2 = f ∙ f e2 + d 2 = f 2

Упражнение: из рисунка выведите теорему Пифагора, применяя определение подобного треугольника:

1.)

Q r

y

S h

TP

k

R

9 класс Математика Третья четверть

ДЕЯТЕЛЬНОСТЬ № 33 Тип деятельности Название деятельности

: Упражнение: Применение теорий Пифагора Поиск недостающей части прямоугольного треугольника. Обучающая компетенция: доказывает теорему Пифагора (M9GE-IIIi-2). Обучающая цель: найти недостающую часть прямоугольного треугольника, используя теорему Пифагора.

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.Наглядные примеры: Дан прямой ∆PQR с прямым углом при Q, найдите недостающую часть. 1.) Если z = 10 и x = 24, найдите y 2.) Если z = 4 и x = 20, найдите y 3.) Если y = 25 и x = 15, какова длина z?

R yz

P

Q

Решение: 1.) z2 + x2 = y2 2 2 10 + 24 = y2 100 + 576 = y2 676 = y2 Y = 26

2.) z2 + x2 4 + 202 = y2 16 + 400 416

= y2

3.) z2 + x2 = y2 z + 152 = 252 z2 + 225 = 625 z2 = 625-225 z2 = 400 z2 = √ 400 z2 = 20

2

2

= y2 = y2 √ (16) (26) = y 4√ 26 = y Y = 4√ 26

Упражнения: задав прямую ∆DEF с прямым углом в E, найдите недостающую часть.1) Если a = 12 и b = 26, найдите c 2) Если b = 32 и c = 48, найдите a 3) Если a = 14 и c = 32, найдите b

D

a

c

E

b

F

9 класс Математика 3-я четверть

ДЕЯТЕЛЬНОСТЬ № 34 Тип деятельности

: Навыки

Задание Название Изучение Компетентность

: Теорема Пифагора (задачи со словами): Решайте задачи, связанные со сходством треугольников и прямоугольные треугольники

(M9GE-IIIj-1) Учебная цель Ссылка

: Найдите недостающую часть прямоугольного треугольника, используя теорему Пифагора. : Геометрия Соледад Хосе-Дилао с. 170

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Наглядные примеры: 1.) Если основание 10-метровой лестницы расположено в 6 метрах от здания, насколько высоко эта лестница поднимется по зданию

? Решение: 10м b =?

C2 = a2 + b2 102 = 62 + b2 b2 = 102 — 62 b2 = 100-36 b2 = 64 b = √ 64 b = 8 метров

6м

2.) Подводная лодка покидает базу и проходит 560 км по назначению. на восток со скоростью 54 км / ч, а затем 816 км на север.При той же скорости, сколько времени потребуется, чтобы вернуться на базу по кратчайшему маршруту? Решение: Дано: BE = 560 км, NE = 816 км, скорость = 54 км / ч BN = √ (560) 2 + (816) 2 = √ 979456 = 989,67 км t = 989,67 54 t = 18,33 часа.

Упражнения: решите каждую задачу.

1.) Телебашня высотой 20,5 м. Проволочные скобы, прикрепленные к вершине башни, закреплены на расстоянии 8 м от основания. Найдите длину каждой проволочной скобки. Проиллюстрируйте. 2.) Плотник хочет сделать диагональную скобу для ворот шириной 2 м и высотой 3 м.Найдите длину скобы с точностью до десятых долей метра.

Третий квартал

ЗАДАНИЕ № 35 Тип деятельности

: Концептуальные записки

Название занятия: Специальный прямоугольный треугольник (30 ° 60 ° 90 °) Компетентность обучения: решать задачи, связанные с подобием треугольников и прямоугольными треугольниками (M9GEIIIj-1 )

Учебная цель

: укажите недостающие меры, чтобы доказать, что треугольник представляет собой треугольник 30 ° 60 ° 90 °: материалы для учащихся с. 397- 399

Ссылка на концепцию Примечания: Теорема о прямоугольном треугольнике 30 ° -60- ° 90 ° В прямоугольном треугольнике 30-60-90:.более короткий отрезок равен ½ гипотенузы h или √ 2/2 раза длиннее отрезка; . более длинные ноги l в √ 3 раза короче ног; а также . гипотенуза h в два раза короче катета. Наглядные примеры: Найдите длину сторон треугольника ABC. Решение: A, 30 ° y

Решение для x:

Решение для y:

x = более короткая ветвь = ½ гипотенузы 18

x = (18) ½

y = (более длинная часть) (более короткая ветка) y = 9

√3

x = 9 60 ° C

x

B

УПРАЖНЕНИЯ: Введите недостающие меры, используя приведенную выше формулу, чтобы доказать, что треугольник равен 30-60-90. треугольник. F

Стороны

a

1)

Более короткая часть

2)

Более длинная часть

3)

гипотенуза

c = 25 60 ° E

b

Длина D

D

D

D

Длина 9 Математика Третий квартал

ЗАДАНИЕ № 36 Тип деятельности

: Концептуальные заметки

Название занятия: Специальный прямоугольный треугольник (45-45 90 Прямой треугольник) Компетентность обучения: Решайте задачи, связанные с подобием треугольников и прямоугольными треугольниками (M9GE-IIIj -1)

Learning Target Reference

: Укажите недостающие длины прямоугольного треугольника 45-45-90: материалы для учащихся стр.396

Концептуальные заметки: 45-45-90 Теорема о прямоугольном треугольнике В прямоугольном треугольнике 45-45-90. каждая катета в 2/2 раза больше гипотенузы; а также . гипотенуза √ в 2 раза длиннее каждого катета. Иллюстративные примеры:

45 ° a

b

45 ° 5. Решите относительно a и b: a = 5; две стороны равнобедренного прямоугольного треугольника совпадают b = гипотенуза = сторона √ 2 b = 5√ 2 УПРАЖНЕНИЯ: Определите недостающие длины прямоугольного треугольника 45-45-90, используя формулу выше, и укажите причины. Рисунок: 45 r

s

45 8 Причин: 1)

Длина r = ______________

___________________

2)

Длина s = _____________

___________________

класс Математика 9000 3 квартал 2 .37 Тип упражнения: Концептуальные записки Название упражнения: Сходство «Соотношение между периметрами» Учебная компетенция: Решать задачи, связанные с подобием треугольников и прямоугольными треугольниками

(M9GE-IIIj-1) Учебная цель Ссылка

: Укажите и примените соотношение между периметры: Геометрия Соледад Хосе-Дилао стр. 180

Если два треугольника подобны, их периметры имеют такое же отношение, как и меры любых двух соответствующих сторон. Наглядные примеры: Решение: 1.) Соответствующие стороны двух одинаковых треугольников равны 3 см и 5 см. Если периметр меньшего треугольника составляет 18 см, каков периметр другого треугольника? Пусть P — периметр меньшего треугольника P1 — периметр большего треугольника 3 см

5 см

P = 3 P1 5

P1

P = 18 см

3P1 = 90 P1 = 90/3 P1 = 30 см — периметр

18 = 3 P1 5

2. ) Периметры двух одинаковых треугольников равны 72 см и 108 см. Если одна сторона меньшего треугольника равна 8 см, какой длины должна быть соответствующая сторона другого треугольника? Решение:

8 см

x

P = 72 см

P = 8 P1 x

P = 108 см

72x = 864 x = 864/72 X = 12 см

72 = 8108 x

Упражнения: 1 .) Соответствующие стороны двух треугольников равны 4 см и 7 см. Если их периметр равен 20 см и 40 см соответственно, похожи ли треугольники? Решите следующие задачи, применяя теорему о соотношении периметров 2.) Периметры двух треугольников составляют 79,2 м и 396 м. Если одна сторона меньшего треугольника равна 19,8 м, какова длина соответствующей стороны другого треугольника?

3.) Стороны двух одинаковых треугольников равны 15 см и 18 см. Каков периметр меньшего треугольника?

9 класс Математика Третья четверть

A C T I V I T Y No.38 Тип задания: Навыки Название задания: Сходство »Соотношение между областями схожих треугольников« Компетентность в обучении: решать задачи, связанные с подобием треугольников и прямоугольных треугольников (M9GE-

IIIj-1). Цель обучения: указать и применить соотношение между областями. подобного треугольника. Ссылка: Geometry by Soledad Jose Dilao p. 180

Отношение площадей двух одинаковых треугольников — это квадрат отношения длин любых двух соответствующих сторон. Иллюстративные примеры: 1.) Площади двух одинаковых треугольников находятся в соотношении 25:16. Найдите: a.) Длину стороны большего треугольника, если соответствующая сторона меньшего треугольника имеет длину 80 см. б.) длина медианы большего треугольника, если соответствующая медиана меньшего треугольника имеет длину 10 см. Решение: Пусть AL — площадь большего треугольника AS — площадь меньшего треугольника SL — соответствующая сторона большего треугольника SS — соответствующая сторона меньшего треугольника a.) AL = SL

AS

2

SS

16SL2 = 160,000 SL2 = 160,000 16

25 = SL 16 SS

2

2

SL = 10,000 SL = √10,000 SL = 100 см

25 = SL2 16 6400 б.) AL = SL

AS

2

SS

16SL2 = 2,500 SL2 = 2,500 16

25 = SL 16 SS

2

SL = √ 2,500/16 SL = 50/4

SL = 25 / 2 или 12,5 см 2

25 = SL 16 100

Упражнения: Решите следующие задачи, применяя теорему о соотношении площадей для подобных треугольников. 1.) Длины соответствующих сторон двух одинаковых треугольников равны √ 3 дм и 2√2 дм. Какое соотношение их площадей?

2.) Если площади двух одинаковых треугольников равны 125 см2 и 169 см2, найдите отношение их соответствующих высот.

9 класс Математика Третья четверть

ЗАДАНИЕ № 39 Тип задания: Навыки Название задания: Сходство «Проблемы со словами» Учебная компетенция: решать задачи, связанные с подобием треугольников и прямоугольными треугольниками. Целевая учебная цель

(M9GE-IIIj-1)

: Примените знания и навыки, связанные с подобными треугольниками, к слову «Задачи: геометрия» Соледад Хосе Дилао с. 178-179

Два треугольника подобны, если соответствующие углы совпадают, а соответствующие стороны пропорциональны.Наглядные примеры: 1.) Дерево отбрасывает тень длиной 3,6 метра, в то время как столб отбрасывает тень длиной 1,2 метра. Если высота шеста 2 метра, какова высота дерева?

Решение:

X

2 м

3,6 м

1,2 м X = 2 3,6 1,2 1,2 x = 7,2 X = 7,2 1,2 X = 6 м

2.) Мальчик стоит в точке (A) 8 м подальше от реки. Если BC = 6 м и CD = 27 м, какова ширина реки? E

Решение:

E X =?

X = 27 8 6

B 8 м A

BC

D

8 м A

6 м C

27 м

D

6x = 27 (8) X = 216 6 X = 36 м

Упражнения : Решите следующие проблемы: 1.) Какова высота флагштока, если 3-метровая вертикальная палка отбрасывает 4-метровую тень, в то время как флагшток отбрасывает 9-метровую тень?

2.) В парке возле мэрии построены качели. Каждая рама, чьи ножки совпадают, имеет высоту 2 метра. Расстояние между ступнями ног равно длине ножки каркаса. Какова длина каждой ножки каркаса?

.

No related posts.