Геометрия Лобачевского. Можно ли ее применить в реальной жизни
Свежий номер
РГ-Неделя
Родина
Тематические приложения
Союз
Свежий номер
07.02.2014 08:38
Общество
Текст:
Майя Керн
7 февраля 1832 года Николай Лобачевский представил на суд коллег свой первый труд по неевклидовой геометрии. Этот день стал началом переворота в математике, а работа Лобачевского — первым шагом к теории относительности Эйнштейна. Мы собрали пятерку самых распространенных заблуждений о теории Лобачевского.
Николай Лобачевский.
Миф первый. Геометрия Лобачевского не имеет ничего общего с Евклидовой
На самом деле геометрия Лобачевского не сильно отличается от привычной нам Евклидовой. Дело в том, что из пяти постулатов Евклида четыре первых Лобачевский оставил без изменения. То есть он согласен с Евклидом в том, что между двумя любыми точками можно провести прямую, что ее всегда можно продолжить до бесконечности, что из любого центра можно провести окружность с любым радиусом, и что все прямые углы равны между собой. Не согласился Лобачевский только с пятым, наиболее сомнительным с его точки зрения постулатом Евклида. Звучит его формулировка чрезвычайно мудрено, но если переводить ее на понятный простому человеку язык, то получается, что, по мнению Евклида, две непараллельные прямые обязательно пересекутся. Лобачевский сумел доказать ложность этого посыла.
Не согласился Лобачевский только с пятым, наиболее сомнительным с его точки зрения постулатом Евклида. Звучит его формулировка чрезвычайно мудрено, но если переводить ее на понятный простому человеку язык, то получается, что, по мнению Евклида, две непараллельные прямые обязательно пересекутся. Лобачевский сумел доказать ложность этого посыла.
Миф второй. В теории Лобачевского параллельные прямые пересекаются
Это не так. На самом деле пятый постулат Лобачевского звучит так: «На плоскости через точку, не лежащую на данной прямой, проходит более чем одна прямая, не пересекающая данную». Иными словами, для одной прямой можно провести как минимум две прямые через одну точку, которые не будут ее пересекать. То есть в этом постулате Лобачевского речи о параллельных прямых вообще не идет! Говорится лишь о существовании нескольких непересекающихся прямых на одной плоскости. Таким образом, предположение о пересечении параллельных прямых родилось из-за банального незнания сути теории великого российского математика.
Миф третий. Геометрия Лобачевского — единственная неевклидова геометрия
Неевклидовы геометрии — это целый пласт теорий в математике, где основой является отличный от Евклидова пятый постулат. Лобачевский, в отличие от Евклида, к примеру, описывает гиперболическое пространство. Существует еще теория, описывающая сферическое пространство — это геометрия Римана. Вот в ней-то как раз параллельные прямые пересекаются. Классический тому пример из школьной программы — меридианы на глобусе. Если посмотреть на лекало глобуса, то окажется, что все меридианы параллельны. Меж тем, стоит нанести лекало на сферу, как мы видим, что все ранее параллельные меридианы сходятся в двух точках — у полюсов. Вместе теории Евклида, Лобачевского и Римана называют «три великих геометрии».
Миф четвертый. Геометрия Лобачевского не применима в реальной жизни
Напротив, современная наука приходит к пониманию, что Евклидова геометрия — лишь частный случай геометрии Лобачевского, и что реальный мир точнее описывается именно формулами русского ученого. Сильнейшим толчком к дальнейшему развитию геометрии Лобачевского стала теория относительности Альберта Эйнштейна, которая показала, что само пространство нашей Вселенной не является линейным, а представляет собой гиперболическую сферу. Между тем, сам Лобачевский, несмотря на то, что всю жизнь работал над развитием своей теории, называл ее «воображаемой геометрией».
Сильнейшим толчком к дальнейшему развитию геометрии Лобачевского стала теория относительности Альберта Эйнштейна, которая показала, что само пространство нашей Вселенной не является линейным, а представляет собой гиперболическую сферу. Между тем, сам Лобачевский, несмотря на то, что всю жизнь работал над развитием своей теории, называл ее «воображаемой геометрией».
Миф пятый. Лобачевский первым создал неевклидову геометрию
Это не совсем так. Параллельно с ним и независимо от него к подобным выводам пришли венгерский математик Янош Бойяи и знаменитый немецкий ученый Карл Фридрих Гаусс. Однако труды Яноша не были замечены широкой публикой, а Карл Гаусс и вовсе предпочел не издаваться. Поэтому именно наш ученый считается первопроходцем в этой теории. Однако существует несколько парадоксальная точка зрения, что первым неевклидову геометрию придумал сам Евклид. Дело в том, что он самокритично считал свой пятый постулат не очевидным, поэтому большую часть из своих теорем он доказал, не прибегая к нему.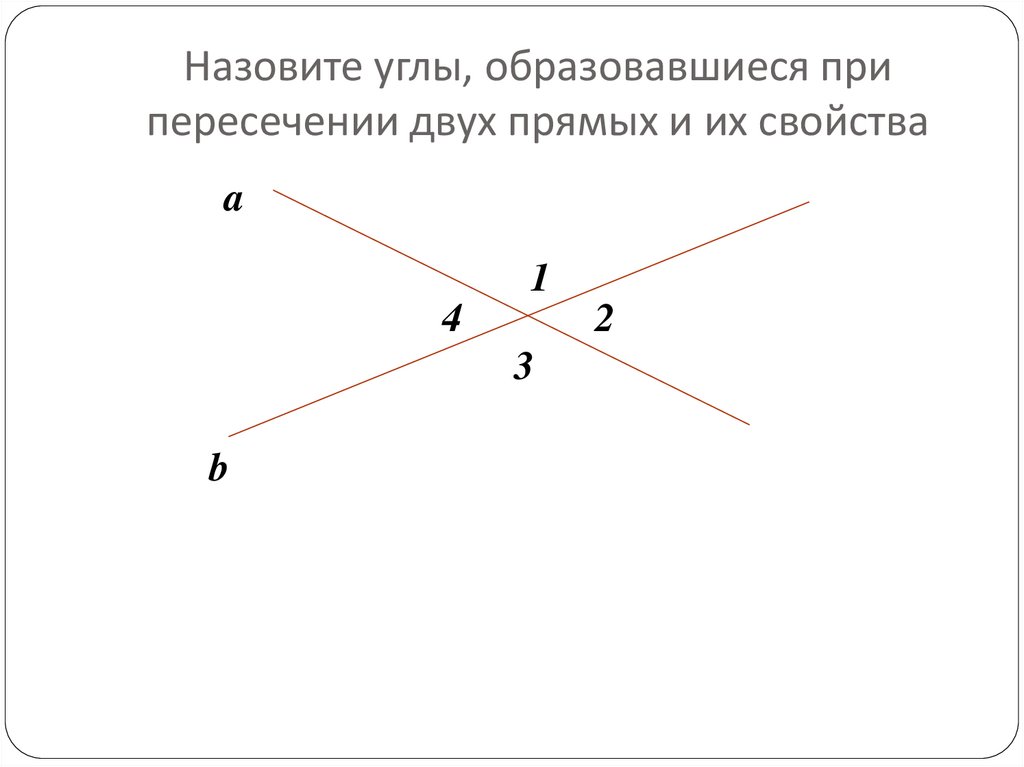
Темы дня:
«Своя Великая Отечественная». На Non/fictioN представили специальный выпуск журнала «Родина»
Почему 86-летняя ленинградская блокадница никогда не уедет из Донецка
Честное имя Виктора Третьякевича. Его вернул комиссару «Молодой гвардии» журналист-фронтовик Ким Костенко
Руководитель союза поисковиков Украины Дмитрий Заборин — о святых находках на поле последнего боя донбассовцев
22-летняя летчица Лидия Литвяк героически воевала и погибла в небе Донбасса
Все параллельно. Как Лобачевский открывал свою геометрию
Все мы слышали про параллельные прямые. Сначала нас учат, что они никогда не пересекаются, а потом где-то на факультативах в районе старших классов и седьмых уроков тихо добавляют, что из этого правила бывают исключения в геометрии, придуманной нашим соотечественником Николаем Лобачевским еще в XIX веке. Так ли это на самом деле, как вообще это возможно и при чем здесь Эйнштейн — читайте в нашем материале.
Год 1819-й, знаменитый французский математики Лаплас мечтает для контакта с инопланетянами установить посреди Сибири огромную светящуюся фигуру, символизирующую теорему Пифагора, а в Казанский университет прибывает новый попечитель — Михаил Магницкий. Он уличает профессоров и преподавателей в вольнодумстве и безбожии и предлагает Александру I торжественно снести здание, приютившее порок.
Император отказывается, университет перезапускают, и новым ректором становится Григорий Никольский — 35-летний, карьеристкого склада математик, любивший обращаться к студентам словами «государики» и повторявший им, что «гипотенуза в прямоугольном треугольнике есть символ сретения правды и мира, правосудия и любви через ходатая бога и человека…» Примерно тогда же в голове 28-летнего Лобачевского, всю жизнь проработавшего в Казанском университете, крутилась и вращалась одна смутная мысль: с пятым постулатом Евклида что-то не так. Но — все по порядку.
В начале были постулаты
Примерно в двух тысячах лет назад по прямой от Лобачевского жил великий древнегреческий математик Евклид, который собрал все имевшиеся до него знания о геометрии в одну большую книгу — «Начала». Начиналась эта книга с семи определений и пяти постулатов — недоказуемых, интуитивно принимаемых на веру утверждений, на фундаменте которых возводились все дальнейшие рассуждения и теоремы.
Начиналась эта книга с семи определений и пяти постулатов — недоказуемых, интуитивно принимаемых на веру утверждений, на фундаменте которых возводились все дальнейшие рассуждения и теоремы.
Первые четыре постулата были лаконичны и стройны:
- От всякой точки до всякой точки можно провести прямую.
- Ограниченную прямую можно непрерывно продолжать по прямой.
- Из всякого центра всяким радиусом может быть описан круг.
- Все прямые углы равны между собой.
В их истинности, наверное, никто не сомневался за всю историю мира, но пятый постулат звучал гораздо более запутанно и мало напоминал неоспоримую истину:
- Если прямая, пересекающая две прямые, образует внутренние односторонние углы, меньшие двух прямых, то, продолженные неограниченно, эти две прямые встретятся с той стороны, где углы меньше двух прямых.
Позже это утверждение в разных формулировках (самая распространенная из них гласит, что в плоскости через точку, не лежащую на данной прямой, можно провести одну и только одну прямую, параллельную данной) пытались доказать десятки математиков, но все они втягивались в одну и ту же историю. Их доказательства как будто сами себя кусали за хвост — упирались в утверждения, доказать которые без самого пятого постулата было абсолютно невозможно. Они больше напоминали сюжеты картин Эшера, чем строгие математические построения.
Их доказательства как будто сами себя кусали за хвост — упирались в утверждения, доказать которые без самого пятого постулата было абсолютно невозможно. Они больше напоминали сюжеты картин Эшера, чем строгие математические построения.
Лобачевского пятый постулат смущал не столько своей неаккуратностью, сколько философской нагрузкой: он поселял материю в какое-то застывшее абсолютное пространство, в систему координат, независимую от самой материи и существующую отныне и вовеки для всей Вселенной. Лобачевскому это не нравилось: он считал, что геометрия и реальность переплетены между собой, и писал в своих дневниках: «В природе мы познаем, собственно, только движение, без которого чувственные впечатления невозможны. Итак, все прочие понятия, например Геометрические, произведены нашим умом искусственно, будучи взяты в свойствах движения; а потому пространство само собой, отдельно, для нас не существует. После чего в нашем уме не может быть никакого противоречия, когда мы допускаем, что некоторые силы в природе следуют одной, другие — своей особой Геометрии».
Твердый материалист, он не мог принимать исключительно на веру, что параллельные прямые не пересекаются где-нибудь в бесконечности космоса. Да, Лобачевский сам не раз проводил геодезические измерения на местности и видел, что сумма углов в треугольнике всегда равняется 180 (а это еще одна эквивалентная формулировка пятого начала Евклида), но не мог обещать, что так будет со всеми треугольниками в нашем бесконечном пространстве.
Работа на пересеченной местности
Часто в математике, да и вообще в науке, бывает очень сложно доказать, что что-нибудь неверно или не работает. Примерно так же было и с пятым постулатом Евклида: у людей не получалось доказать его верность, но опровергнуть его было еще сложнее, особенно учитывая, что вся махина теорем геометрии Евклида была стройна и непротиворечива.
Поэтому Лобачевский в своей битве с пятым постулатом обратился к доказательству от противного. Чтобы посмотреть, что будет после этого со всей системой геометрических теорем, он попробовал заменить пятый постулат на его зеркальное отражение («Через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие ее». ). Не появится ли в них внутренних противоречий, косвенно указывающих на то, что изначальная версия пятого постулата — такая неаккуратная и контринтуитивная — была все-таки неизбежно верна в нашем пространстве? Но такого не случилось — противоречий не нашлось.
). Не появится ли в них внутренних противоречий, косвенно указывающих на то, что изначальная версия пятого постулата — такая неаккуратная и контринтуитивная — была все-таки неизбежно верна в нашем пространстве? Но такого не случилось — противоречий не нашлось.
Поэтому Лобачевский взял первые четыре постулата Евклида, добавил к ним новый пятый и на этом стал строить новую непротиворечивую геометрию, описывающую реальный мир, как он надеялся, точней и глубже, чем геометрия евклидова.
Лобачевский даже хотел проверить свою геометрию в космосе — посчитать сумму углов в треугольнике, составленном из звезд, и посмотреть, будет ли она равняться 180 градусам, но все его эксперименты терпели неуспех. В них вкрадывались неточности и колоссальные ошибки, а самого Лобачевского рвали на части: в родном университете он теперь преподавал не только математику, но еще и физику с астрономией; ректор Никольский, мечтавший охладить его пыл, заставил Лобачевского наводить порядок в университетской библиотеке, а попечитель Магницкий сделал математика членом строительной комиссии при университете (судя по всему, проворовавшийся на строительстве Магницкий надеялся скинуть всю вину на нерадивого, витающего в небесах математика, но этот план не удался).
На чистую науку оставались жалкие крупицы времени, но Лобачевский все углублял свою геометрию — формулировал новые теоремы, строил утверждения и наконец 7 февраля (по старому стилю) 1826 года представил перед ученой комиссией Казанского университета свой труд — «Сжатое изложение начал геометрии со строгим доказательством теоремы о параллельных».
Геометрия новая — проблемы старые
Задним числом жизнь великих идей кажется проще, чем она была в реальности. Да, вокруг косные люди, да, везде недоверие и нежелание расшатывать лодку, но даже с учетом этих отягчающих поправок траектория великой идеи в худшем случае кажется упругой сжатой спиралью, раскручивающейся через вязкую повседневность к свету истины. В реальности это скорей ломаная кривая блужданий — доклад Лобачевского от 7 февраля провалился.
Мы не знаем, какой формы был стол в помещении, где шел доклад, — прямоугольный, круглый или, может быть, овальный; мы не знаем, какие там были окна, стены, двери, но точно понимаем одно: мысли всех присутствовавших тогда шли совершенно перпендикулярными с неевклидовой геометрией путями.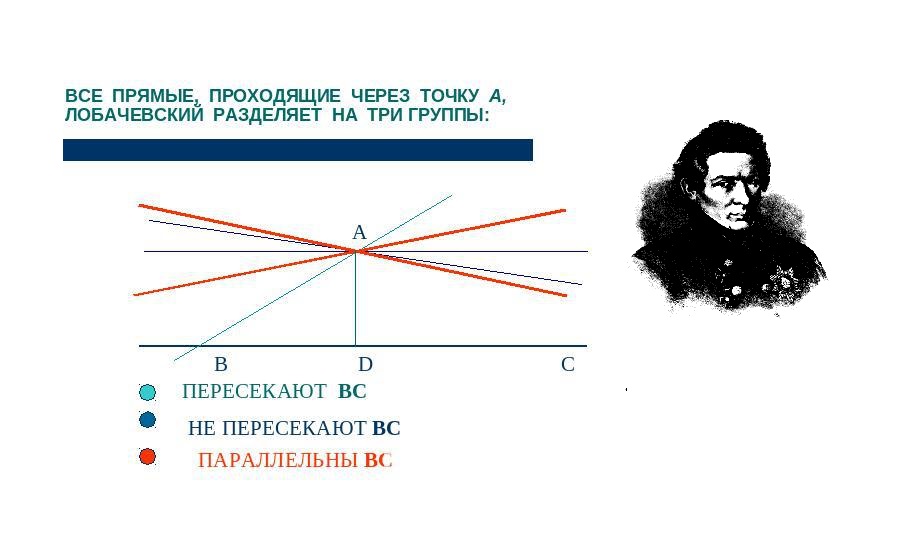 Незадолго до этого новый император Николай I сместил Магницкого с его должности, и все члены комиссии теперь думали, как это резкое движение извне поменяет их жизнь, и почти не обращали внимания на странноватого математика, рассказывавшего на французском о какой-то инопланетной геометрии.
Незадолго до этого новый император Николай I сместил Магницкого с его должности, и все члены комиссии теперь думали, как это резкое движение извне поменяет их жизнь, и почти не обращали внимания на странноватого математика, рассказывавшего на французском о какой-то инопланетной геометрии.
Броуновское движение наночастиц в воде
Дальше рукопись была отдана на рецензию некоторым членам комиссии, но они в суматохе мрачных дней, видимо, просто позабыли о ней, и сам доклад так и не был одобрен к публикации. Тогда вся геометрия Лобачевского могла навсегда остаться внутри его головы, если бы не одна неожиданность: новым ректором университета вскоре был избран именно он.
Вряд ли у Лобачевского стало после этого меньше работы и больше сил, но постепенно он оформил свои идеи в законченный труд «О началах геометрии», который сначала напечатали в журнале «Казанский вестник», а потом представили на отзыв в Академию наук, где рецензия досталась одному из самых сильных русских математиков того времени — Михаилу Остроградскому.
«Автор, по-видимому, задался целью написать таким образом, чтобы его нельзя было понять. Он достиг этой цели; большая часть книги осталась столь же неизвестной для меня, как если бы я никогда не видел ее…» — вот его ответ. Новая геометрия остается непонятной. Блуждание продолжается.
Круги по воде
Понимание Лобачевский находит несколькими годами позже. Он публикует свои труды в европейских журналах, где их замечает великий немец Гаусс, который сам не один год втайне ото всех занимался неевклидовой геометрией. Чтобы лучше понять казанского ученого, он оперативно учит русский и потом, впечатленный смелостью и ясностью мыслей Лобачевского, выдвигает того в члены-корреспонденты Геттингенского королевского научного общества.
Признание встречает своего гения, хотя на родине Остроградский и люди его окружения раз за разом отклоняют все работы по неевклидой геометрии вплоть до самой смерти Лобачевского в 1856 году.
Проходит 12—15 лет, и математики находят сразу несколько реальных моделей, в которых работает именно геометрия Лобачевского. В самой простой из них, проективной, за плоскость принимают внутренность круга, а за прямую — его хорду. В результате тот очевидный факт, что через одну точку P, лежащую внутри круга, можно провести сколько угодно хорд, не пересекающихся с одной фиксированной хордой а, автоматически становится в таких правилах игры иллюстрацией пятого начала геометрии Лобачевского.
В самой простой из них, проективной, за плоскость принимают внутренность круга, а за прямую — его хорду. В результате тот очевидный факт, что через одну точку P, лежащую внутри круга, можно провести сколько угодно хорд, не пересекающихся с одной фиксированной хордой а, автоматически становится в таких правилах игры иллюстрацией пятого начала геометрии Лобачевского.
В 1868 году выходит доклад Римана — другого первопроходца с другой неевклидовой геометрией, в которой через каждую точку в пространстве уже невозможно провести ни одной параллельной прямой, и математикам постепенно становится понятно, что геометрии Римана и Лобачевского — невероятно похожие шаги влево и вправо от привычной евклидовой геометрии. Первая работает на поверхностях с положительной кривизной — вроде шаров или геоидов (параллельные у экватора меридианы встречаются на полюсах), а вторая — на поверхностях с отрицательной кривизной — вроде гиперболоидов или седел.
И еще чуть позже, в начале XX века, новая геометрия наконец встретится с физикой. Эйнштейн сформулирует свою общую теорию относительности в терминах геометрии Римана, и мысли людей, привыкшие ходить по одним и тем же параллельным рельсам, откроют новые маршруты: пространство и время не абсолютны. Движение меняет геометрию. А тысячелетние аксиомы не всегда верны.
Михаил Петров
Теги
МатематикаИсторияРоссийская наука
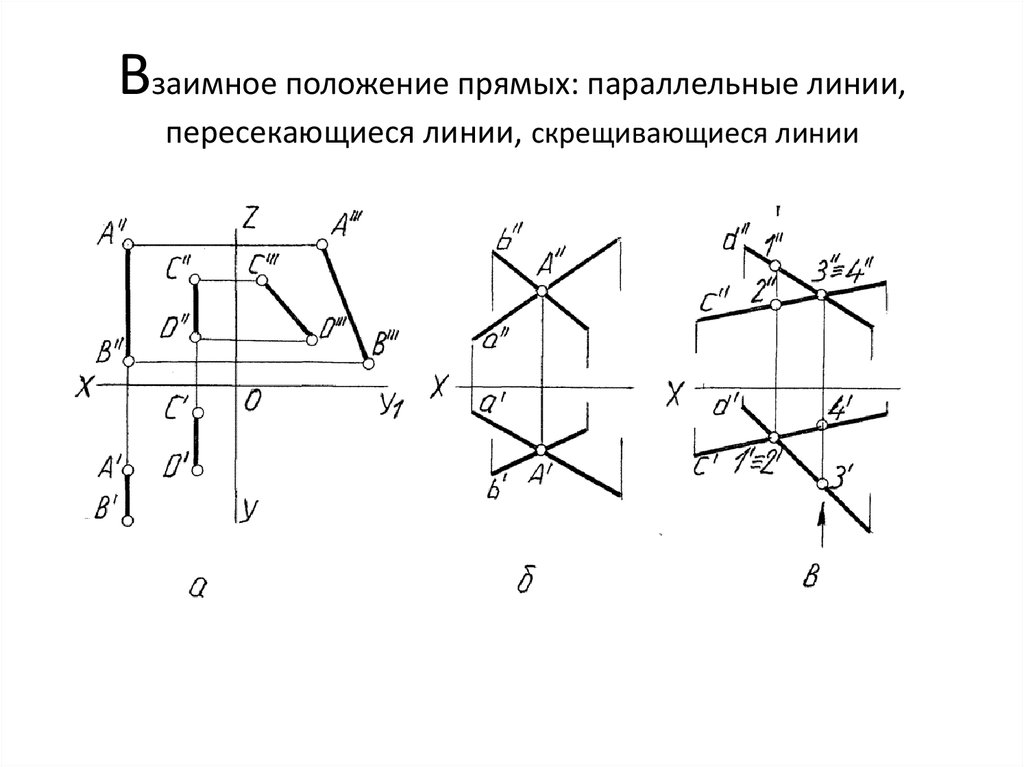
Что такое параллельные и перпендикулярные линии? Определение, примеры
Что такое параллельные и перпендикулярные линии?
Параллельные и перпендикулярные линии — два важных понятия в геометрии. Параллельные прямые — это прямые, которые никогда не пересекаются друг с другом. Таким образом, две параллельные прямые всегда сохраняют между собой постоянное расстояние. Перпендикулярные прямые — это две прямые, пересекающиеся под прямым углом.
Мы сталкиваемся с примерами параллельных и перпендикулярных линий в повседневной жизни. Обратите внимание на белые линии или полосы на отмеченном пешеходном переходе. Они представляют собой параллельные линии. Когда аналоговые часы показывают 03:00, минутная и часовая стрелки часов представляют собой перпендикулярные линии, поскольку они образуют прямой угол (9угол 0°).
Обратите внимание на белые линии или полосы на отмеченном пешеходном переходе. Они представляют собой параллельные линии. Когда аналоговые часы показывают 03:00, минутная и часовая стрелки часов представляют собой перпендикулярные линии, поскольку они образуют прямой угол (9угол 0°).
Родственные игры
Определение параллельных и перпендикулярных линий
Параллельные и перпендикулярные линии играют жизненно важную роль в геометрии. Оба они имеют различные свойства и области применения.
Определение параллельных прямых
Две прямые называются параллельными, если они лежат в одной плоскости и расстояние между ними одинаково. Параллельные линии никогда не пересекаются. Мы используем символ || для параллельных линий.
Если прямые AB и CD параллельны, мы представляем их как $AB\; || \;CD$.
Определение перпендикулярных прямых
Две прямые называются перпендикулярными, если они пересекаются и всегда встречаются под углом 90°. Мы используем символ $\bot$ для обозначения перпендикулярных линий.
Мы используем символ $\bot$ для обозначения перпендикулярных линий.
Если прямые PQ и RS перпендикулярны, мы пишем $PQ\; \bot \;$$.
Давайте посмотрим на наглядные примеры перпендикулярных линий и параллельных линий!
Свойства параллельных и перпендикулярных линий
Давайте обсудим несколько важных свойств параллельных и перпендикулярных линий. 9{\circ}$.
Разница между параллельными и перпендикулярными линиями
| Параллельные линии | Перпендикулярные линии |
| Параллельные линии никогда не пересекаются друг с другом. Это непересекающиеся линии. | Перпендикулярные линии — это две пересекающиеся прямые.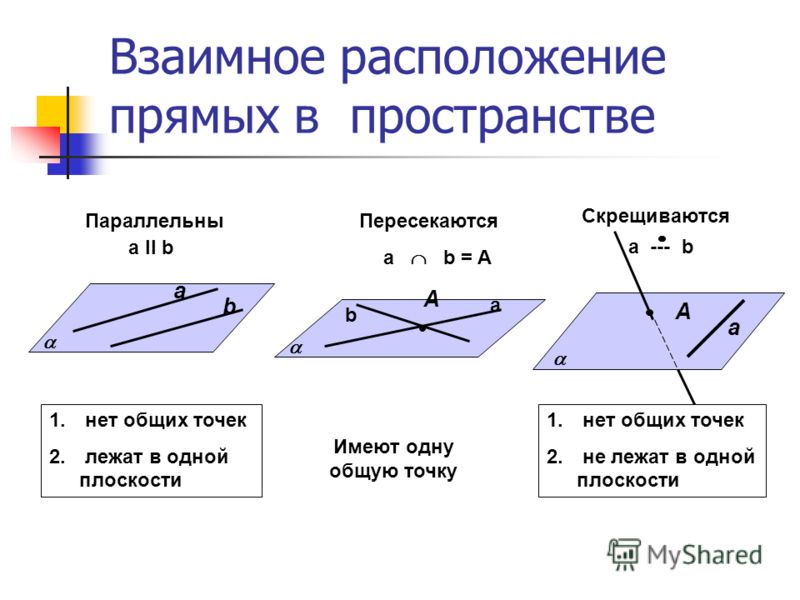 Они пересекаются друг с другом под прямым углом. Они пересекаются друг с другом под прямым углом. |
| Параллельные прямые обозначаются символом $||$. $AB\; || \;CD$ | Перпендикулярные прямые обозначим символом $\bot$. $AB \bot CD$ |
| Наклоны параллельных прямых равны. | Произведение наклонов двух перпендикулярных линий равно $-1$. |
| Примеры: Трамвайные пути, Вертикальные линии в букве H | Примеры: Горизонтальная и вертикальная линии в букве T, Стрелки часов, когда аналоговые часы показывают 09:00 |
Уравнения параллельных и перпендикулярных линий
Представляем прямую через уравнение $y = mx + c$, где «m» представляет собой наклон линии, а c — точку пересечения с осью y. Две параллельные прямые никогда не пересекаются и имеют одинаковую крутизну, поэтому их наклоны всегда равны.
Рассмотрим две строки $y = 2x\; – \;1$ и $y = 2x + 3$. Мы видим, что оба уравнения имеют один и тот же наклон, 2. В математических терминах мы можем выразить это как $m_1 = m_2 = 2$, где $m_1$ и $m_2$ — наклоны линий.
В математических терминах мы можем выразить это как $m_1 = m_2 = 2$, где $m_1$ и $m_2$ — наклоны линий.
Наклоны перпендикулярных линий неодинаковы. Наклон одной линии является обратной отрицательной величиной другой линии. Другими словами, их произведение равно $-1$. Математически это можно выразить как $m_1 \times m_2 = \;-1$, где $m_1$ и $m_2$ — наклоны двух перпендикулярных прямых.
Предположим, у нас есть две линии $y = 2x +3$ и $y = \;-\frac{1}{2}x \;-\; 1$.
Здесь $m_1 = 2$ и $m_2 = \;-\;\frac{1}{2}$.
Итак, $m_1 \times m_2 = \;-1$.
Нанесем эти перпендикулярные линии на график.
Итого:
- Если наклоны двух линий одинаковы, они параллельны.
- , если наклоны двух заданных прямых являются отрицательными обратными величинами друг к другу, они являются перпендикулярными прямыми.
Написание уравнений параллельных прямых
Предположим, у нас есть линия, уравнение которой $y = 4x \;-\;3$, а точка на другой прямой, параллельная ей, есть $(2,\;12)$. Здесь наклоны $m_1 = m_2 = 4$, так как прямые параллельны.
Здесь наклоны $m_1 = m_2 = 4$, так как прямые параллельны.
Мы знаем, что уравнение прямой с наклоном m имеет вид $y = m_2 x + c$.
Подставляя значения $(x,\;y)$ и m, получаем:
$12 = 8 + c$
$c = 12 \;-\; 8 = 4$
Итак, уравнение прямой, параллельной $y = 4x \;-\; 3$ равно $y = 4x +4$.
Написание уравнений перпендикулярных линий
Предположим, у нас есть линия, уравнение которой $y = 3x + 2$, а точка на другой прямой, параллельная ей, равна (0,1). Здесь наклон $m_1 \times m_2 = \;-\;1$, так как прямые перпендикулярны.
$m_2 = \frac{-1}{m_1} = \frac{-1}{3}$
Мы знаем, что уравнение прямой с наклоном m имеет вид $y = m_2 x + c$.
Подставляя значения $(x,\;y)$ и $m_2$, получаем:
$1 = \frac{-1}{3} \times 0 + c$
$c = 1$
Итак, уравнение прямой, перпендикулярной $y = 3x +2$, равно $y = \frac{-1}{3} x + 1$.
Решенные примеры на параллельных и перпендикулярных прямых
1 . В каком треугольнике прямые перпендикулярны?
В каком треугольнике прямые перпендикулярны?
Решение: В прямоугольном треугольнике прямые перпендикулярны.
2. Если наклон одной из двух параллельных прямых равен 5, то каков будет наклон другой параллельной прямой?
Решение: $m_1 = 5$
Мы знаем, что наклоны двух параллельных прямых равны, т. е. $m_1 = m_2$.
Итак, $m_2 = 5$.
3. Найдите наклоны прямых $5x + 2y\;-\;6 = 0$ и $-2x + 5y + 3 = 0$. Кроме того, какие это типы линий?
Решение: Преобразовав оба уравнения в форму пересечения наклона, мы получим:
$5x + 2y\;-\;6 = 0 \Rightarrow 2y = \;-\;5x + 6y = \frac{-5}{2} x + 3$. Итак, $m_1 = \frac{-5}{2}$.
$ – 2x + 5y + 3 = 0 \Стрелка вправо 5y = 2x\;-\;3 \Стрелка вправо y = \frac{2}{5}x\;-\;\frac{3}{5}$. Итак, $m_2 = \frac{2}{5}$.
$m_1 \times m_2 = \frac{\;-\;5}{2} \times \frac{2}{5} = \;-\;1$
Прямые перпендикулярны.
4. Укажите истину и ложь для следующих утверждений. Кроме того, аргументируйте.
а.) Буква V имеет набор параллельных линий. 9\circ$.
5. Если две прямые параллельны друг другу и уравнение одной прямой равно $y = \;-\;7x + 3$ и точка на другой прямой равна $(2,-5)$ , то каким будет уравнение другой линии?
Решение: Наклон $y = \;-\;7x + 3$ равен $m_1 = \;-7$.
Поскольку прямые параллельны, то $m_1 = m_2 = \;-7$.
Мы знаем, что уравнение прямой с наклоном $m$ имеет вид $y = m_2\; х + с$.
Подставляя значения $(x,\;y)$ и m, получаем:
$-5 = \;-7 \times 2 + c$
$c = \;-5 + 14 = 9$
Уравнение будет: $y = \;-7x + 9$.
Практические задачи на параллельных и перпендикулярных прямых
1
Что из следующего является примером параллельных прямых?
Смежные стороны прямоугольника
Стороны равностороннего треугольника
Знак плюс
Противоположные стороны параллелограмма
Правильный ответ: Противоположные стороны параллелограмма
Противоположные стороны параллелограмма параллельны друг другу.
2
Какая из следующих букв не является примером перпендикулярных линий?
L
T
N
H
Правильный ответ: N
L, T и H являются примерами перпендикулярных линий. N не имеет перпендикулярных прямых.
3
Если наклон одной перпендикулярной прямой равен $\frac{-3}{4}$, то каков будет наклон другой перпендикулярной прямой?
$\frac{-3}{4}$
$\frac{-4}{3}$
$\frac{3}{4}$
$\frac{4}{3}$
Правильный ответ: $\frac{4}{3}$
Наклон перпендикулярной прямой является отрицательной обратной величиной другой перпендикулярной прямой.
Итак, наклон другой линии $= \frac{4}{3}$.
4
Какое слово лучше всего описывает строки $3x + 4y \;-\; 6 = 0$ и $12x + 16y +9 = 0$.
Пересекающиеся
Перпендикулярные
Параллельные
Смежные
Правильный ответ: Параллельные
$3x + 4y \;-\; 6 = 0 \Стрелка вправо 4y = \;-\; 3x + 6 \Rightarrow y = \frac{-3}{4} + \frac{6}{4}$. Итак, $m_1 = \frac{-3}{4}$.
Итак, $m_1 = \frac{-3}{4}$.
$12x + 16y + 9 = 0 \Стрелка вправо 16y = \;-\;12x\;-\;9 \Стрелка вправо y = \frac{-12}{16}\;-\;\frac{9}{16 }$. Итак, $m_2 = \frac{-12}{16} = \frac{-3}{4}$.
$m_1 = m_2$.
Следовательно, прямые параллельны.
5
Если две прямые перпендикулярны, то что из следующего верно?
Они никогда не пересекаются друг с другом.
Их наклоны являются отрицательными обратными величинами.
Их наклоны равны.
Ничего из этого.
Правильный ответ: их наклоны являются отрицательными обратными величинами.
Если две прямые перпендикулярны, их наклоны являются отрицательными обратными величинами.
Часто задаваемые вопросы о параллельных и перпендикулярных линиях
В чем разница между параллельными и пересекающимися линиями?
Параллельные линии — это линии, которые никогда не пересекаются друг с другом, даже если мы продлим их бесконечно, тогда как пересекающиеся линии встречаются в одной точке.
Все ли пересекающиеся прямые перпендикулярны?
Нет. Пересекающиеся линии могут пересекаться под любым углом. Но все перпендикулярные прямые являются пересекающимися прямыми.
Какие общие характеристики имеют параллельные и перпендикулярные линии?
Общим признаком является то, что оба имеют прямые линии.
Может ли фигура иметь как параллельные, так и перпендикулярные линии?
Да. Фигура может иметь как параллельные, так и перпендикулярные линии. Некоторые примеры: буква H, буква E, квадрат, прямоугольник и т. д.
Сколько пар параллельных и перпендикулярных прямых в прямоугольнике?
В прямоугольнике 2 пары параллельных прямых и 4 пары перпендикулярных прямых.
Параллельные прямые — определение, свойства, уравнение, примеры и ответы на часто задаваемые вопросы
Параллельные прямые определяются как те прямые, которые лежат в одной плоскости и всегда равноудалены друг от друга и, следовательно, никогда не пересекаются друг с другом, называются параллельными прямыми. Параллельные прямые не пересекаются и пересекаются в бесконечности. В общих чертах линии можно разделить на параллельные линии, пересекающиеся линии и перпендикулярные линии. Давайте подробно узнаем о параллельных линиях, их свойствах, аксиомах, теоремах и примерах.
Параллельные прямые не пересекаются и пересекаются в бесконечности. В общих чертах линии можно разделить на параллельные линии, пересекающиеся линии и перпендикулярные линии. Давайте подробно узнаем о параллельных линиях, их свойствах, аксиомах, теоремах и примерах.
Что такое параллельные линии?
Параллельные линии — это две или более линий, которые всегда параллельны друг другу и лежат в одной плоскости. Как бы ни были длинны параллельные линии, они никогда не пересекутся. Параллельные прямые и пересекающиеся прямые противоположны друг другу. Параллельные линии — это линии, которые ни в коем случае не пересекаются и не имеют шансов встретиться. На приведенной ниже диаграмме параллельные прямые показаны двумя способами: прямая a параллельна прямой b, а прямая x параллельна прямой y.
Параллельные прямые и поперечные
Когда прямая пересекает две параллельные или непараллельные прямые, она называется поперечной. Из-за поперечной линии создается множество отношений между парой углов. Они могут быть дополнительными или конгруэнтными углами. Предположим, что данная диаграмма образует углы a, b, c, d и p, q, r, s за счет трансверсали. Эти восемь отдельных углов, образованных параллельными прямыми и поперечными, отражают некоторые свойства.
Они могут быть дополнительными или конгруэнтными углами. Предположим, что данная диаграмма образует углы a, b, c, d и p, q, r, s за счет трансверсали. Эти восемь отдельных углов, образованных параллельными прямыми и поперечными, отражают некоторые свойства.
Углы в параллельных прямых
Углы образованы поперечными и параллельными прямыми 1 и 2. Рассмотрим свойства, которыми обладают эти углы:
- Альтернативные внутренние углы: на параллельных линиях, и они равны по своей природе. Например, здесь ∠c = ∠p и ∠d = ∠q. Лучший способ определить альтернативные внутренние углы — создать в уме букву «Z». Углы, образованные Z, являются альтернативными внутренними углами и равны друг другу.
- Альтернативные внешние углы: Альтернативные внешние углы также равны по своей природе. На диаграмме выше альтернативные внешние углы равны ∠a = ∠r и ∠b = ∠s.
- Смежные внутренние углы: Смежные внутренние углы также известны как совмещенные внутренние углы.
 Это углы, образованные поперечными внутри параллельных прямых, и они дополняют друг друга. На приведенной выше диаграмме ∠d + ∠p = 180° и ∠c + ∠q = 180°.
Это углы, образованные поперечными внутри параллельных прямых, и они дополняют друг друга. На приведенной выше диаграмме ∠d + ∠p = 180° и ∠c + ∠q = 180°. - Вертикально противоположные углы: Вертикально противоположные углы образуются при пересечении двух прямых. Противоположные углы называются вертикально противоположными углами и параллельны друг другу. На приведенной выше диаграмме ∠a = ∠c, ∠b = ∠d, ∠p = ∠r, ∠q = ∠s.
- Соответствующие углы: Соответственные углы параллельных прямых равны друг другу. На приведенной выше диаграмме ∠a = ∠p, ∠d = ∠s, ∠b = ∠q и ∠c = ∠r.
Свойства параллельных линий
Ниже приведены некоторые важные свойства параллельных линий:
- Две или более линий могут считаться параллельными, если даже при продолжении линий нет шансов, что линии встретятся или пересекутся (пересекутся).
- Параллельные линии имеют особое свойство сохранять одинаковый наклон.
- Расстояние между параллельными линиями всегда остается одинаковым.
 Примечание. Здесь линии, которые считаются параллельными, не обязательно должны быть равны по своей длине, но обязательным условием для того, чтобы линии считались параллельными, является то, что расстояние между линиями остается одинаковым, даже на продолжении линий.
Примечание. Здесь линии, которые считаются параллельными, не обязательно должны быть равны по своей длине, но обязательным условием для того, чтобы линии считались параллельными, является то, что расстояние между линиями остается одинаковым, даже на продолжении линий. - Параллельные линии обозначаются символом трубы (||). Например: если две прямые А и В параллельны друг другу. Их можно представить параллельными друг другу через A || B.
Как узнать, параллельны ли прямые?
Когда две или более параллельных прямых пересекаются секущей, тогда угол, образуемый секущей с параллельными прямыми, проявляет некоторые отличительные свойства:
- Параллельные линии, пересекаемые секущей, имеют равные внутренние углы.
- Параллельные прямые при пересечении секущей имеют равные внешние углы.
- Параллельные прямые при пересечении секущей имеют равные соответствующие углы.
- Параллельные прямые при пересечении секущей имеют последовательные внутренние углы на той же стороне, что и дополнительные.

Нарушение любого из вышеуказанных свойств приведет к тому, что линии не будут считаться параллельными линиями.
Уравнение параллельных прямых
В уравнении параллельных прямых наклон линий всегда одинаков. Уравнение прямой линии имеет форму пересечения наклона, то есть y = mx + c, где m — наклон. Для параллельных прямых m будет одинаковым; однако перехват не то же самое. Например, y = 3x + 8 и y = 3x + 2 параллельны друг другу. Следовательно, в уравнении параллельной линии точка пересечения различна и не имеет общих точек, но наклон одинаков, чтобы линии были параллельны друг другу.
Аксиомы и теоремы о параллельных прямых
Ниже приведены аксиомы и теоремы о параллельных прямых:
Аксиома о соответствующем угле: Соответствующие углы равны друг другу. В аксиомах соответствующих углов говорится, что если истинно обратное свойство, то есть если причина свойства истинна, утверждение также должно быть истинным. Аксиома соответствующих углов гласит, что если соответствующие углы равны, то это означает, что прямые, на которых проведена секущая, параллельны друг другу.
Теорема 1: Если провести секущую на двух параллельных прямых, то вертикально противоположные углы будут равны. Из приведенного ниже рисунка:
Доказать ∠3 = ∠5, ∠4 = ∠6
Доказательство: ∠1 = ∠3 и ∠5 = ∠7 (вертикально противоположные углы)
∠9001 = ∠5 (соответствующие углы)
Следовательно, ∠3 = ∠5.
Аналогично, ∠4 = ∠6.
Обратное утверждение теоремы также верно; то есть, если вертикально противоположные углы равны друг другу, линии параллельны по своей природе.
Теорема 2. Если две прямые параллельны друг другу и пересекаются секущей, то пары внутренних углов дополняют друг друга.
Чтобы доказать: ∠4 + ∠5 = 180° и ∠3 + ∠6 = 180°.
Доказательство: ∠4 = ∠6 (чередующиеся внутренние углы)
∠6 + ∠5 = 180° (линейная пара)
Следовательно, ∠4 + ∠5 = 180°
Аналогично, ∠3 + ∠6 = 180°.
Обратное утверждение теоремы также верно; то есть, если внутренние углы дополняют друг друга, линии параллельны по своей природе.
Символ параллельных линий
Символ параллельных линий обозначается как || поскольку они никогда не встречаются и не пересекаются, независимо от того, как долго они продлеваются. Итак, для обозначения параллельных прямых используется символ ||. Например, если AB параллелен XY, мы запишем это как AB || XY.
Применение параллельных линий в реальной жизни
Параллельные линии можно легко наблюдать в реальной жизни. Одним из лучших примеров параллельных линий являются железнодорожные пути. Эти пути в реальной жизни буквально параллельны линиям, так как они должны быть всегда параллельны друг другу, чтобы любой ценой зацепить колеса поезда. Некоторыми другими примерами параллельных линий из реальной жизни являются края альмиры, шкалы (линейки) и т. д.
Решенные примеры на параллельных прямых
Пример 1: На данном рисунке угол CMQ равен 45. Найдите остальные углы.
Решение:
∠CMQ = 45°.
Из вертикально противоположных углов,
∠PMD = 45°.
Из линейной пары:
∠PMD + ∠PMC = 180°.
∠PMC = 135°.
Из линейной пары:
∠CMQ + ∠DMQ = 180°
∠DMQ = 135°.
Из линейной пары:
∠DMQ + ∠DMP = 180°.
∠DMP = 135°.
Из линейной пары:
∠CMP + ∠CMQ = 180°.
∠ТТМ = 135°
∠АНД = ∠ТТМ = 135°. (соответствующие углы)
∠BNP = ∠DMQ = 135°. (Соответствующие углы)
Пример 2: Проверьте, параллельны ли следующие линии.
Решение:
Поскольку расстояние между двумя прямыми постоянно уменьшается, их нельзя назвать параллельными прямыми.
Пример 3: Проверьте, параллельны ли следующие линии.
Решение:
Поскольку при удлинении две линии не пересекаются, а расстояние между двумя линиями остается прежним.
Итак, да, линии можно назвать параллельными линиями.
Пример 4: Найдите значения x и y на данном рисунке, где AB параллельна CD.
Решение:
На рисунке выше:
2x + 5y + 3x = 180 (Линейная пара)
5x + 5y = 180
x + y = 36
x + y = 3x (соответствующие углы)\ 900 3x
x = 12
x + y = 36
12 + y = 36
y = 24
Часто задаваемые вопросы о параллельных линиях
Вопрос 1 Что такое параллельные линии?
Ответ:
Параллельные прямые — это прямые, которые всегда находятся на одинаковом расстоянии друг от друга и пересекаются на бесконечности. То есть они не встречаются при вытягивании. Символ параллельных прямых ||. АБ || CD означает, что прямая AB параллельна прямой CD.
Вопрос 2: Каково расстояние между параллельными прямыми?
Ответ:
Расстояние между двумя параллельными линиями может быть любым, но они остаются одинаковыми на всем протяжении.
Параллельные линии всегда имеют одинаковое расстояние между собой.
Вопрос 3: Каков наклон параллельных линий?
Ответ:
Если две прямые параллельны, то они будут иметь одинаковый наклон. Например, наклон 1 линии равен y = 3x + 8. Теперь наклон этой линии равен 3; если есть другая линия, имеющая наклон 3, эта линия будет параллельна данной линии.
Вопрос 4: Где пересекаются две параллельные прямые?
Ответ:
Две параллельные прямые пересекаются на бесконечности. Параллельные прямые никогда не пересекаются друг с другом, независимо от того, насколько они удлинены. Поэтому говорят, что параллельные прямые пересекаются в бесконечности.
Вопрос 5: Какие бывают типы углов в параллельных прямых?
Ответ:
При пересечении пары параллельных прямых секущей образуется много пар углов.

 Это углы, образованные поперечными внутри параллельных прямых, и они дополняют друг друга. На приведенной выше диаграмме ∠d + ∠p = 180° и ∠c + ∠q = 180°.
Это углы, образованные поперечными внутри параллельных прямых, и они дополняют друг друга. На приведенной выше диаграмме ∠d + ∠p = 180° и ∠c + ∠q = 180°. Примечание. Здесь линии, которые считаются параллельными, не обязательно должны быть равны по своей длине, но обязательным условием для того, чтобы линии считались параллельными, является то, что расстояние между линиями остается одинаковым, даже на продолжении линий.
Примечание. Здесь линии, которые считаются параллельными, не обязательно должны быть равны по своей длине, но обязательным условием для того, чтобы линии считались параллельными, является то, что расстояние между линиями остается одинаковым, даже на продолжении линий.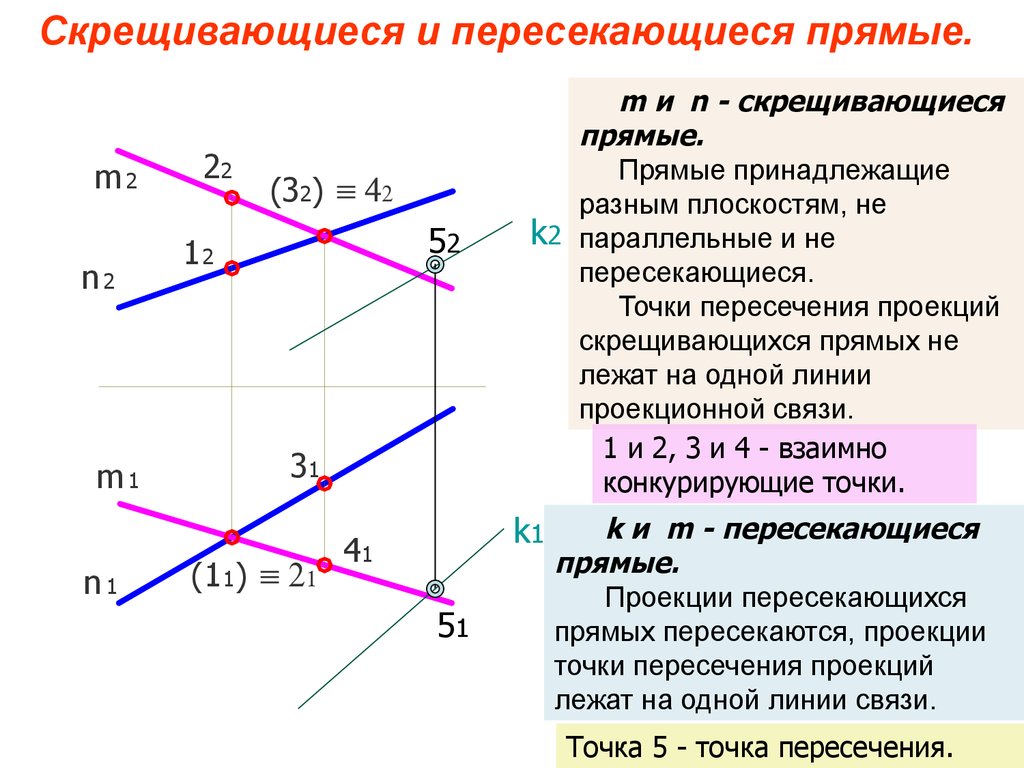

 Итак, да, линии можно назвать параллельными линиями.
Итак, да, линии можно назвать параллельными линиями. Параллельные линии всегда имеют одинаковое расстояние между собой.
Параллельные линии всегда имеют одинаковое расстояние между собой.