Параллелограмм что это: Параллелограмм — урок. Геометрия, 8 класс.

Параллелограм | это… Что такое Параллелограм?

ТолкованиеПеревод

Параллелограм

Параллелограмм

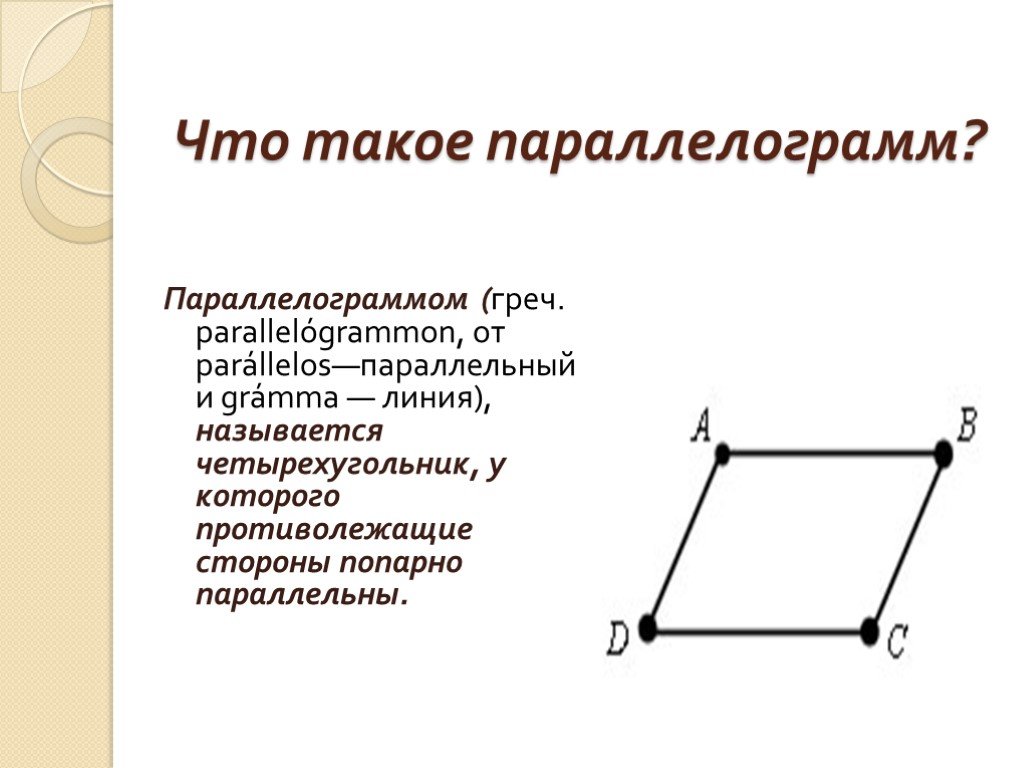
Параллелогра́мм (от греч. parallelos — параллельный и gramme — линия) — это четырёхугольник, у которого противолежащие стороны попарно параллельны, т. е. лежат на параллельных прямых. Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.

Содержание 1 Свойства 2 Признаки параллелограмма 3 Площадь 4 См. также

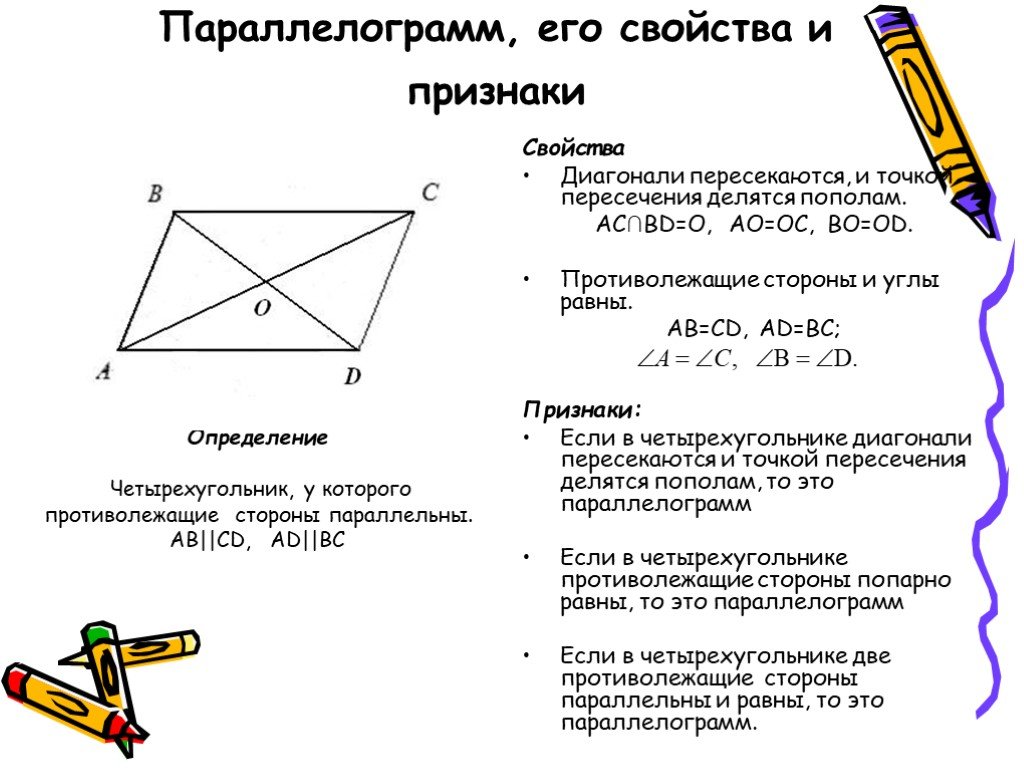
Свойства

• Противоположные стороны параллелограмма равны

  | AB | = | CD | , | AD | = | BC | .

• Противоположные углы параллелограмма равны

• Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам

  | AO | = | OC | , | BO | = | OD | .

• Сумма углов, прилежащих к одной стороне, равна 180°.
• Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его сторон:

пусть а — длина стороны AB, b — длина стороны BC, d₁ и d₂ — длины диагоналей; тогда

Доказательства  

Проведя диагональ BD, мы получим два треугольника ABD и BCD, которые равны, т.к. одна сторона у них общая, а соответственные углы при стороне BD равны как накрест лежащие при параллельных прямых AB

• Аффинное преобразование всегда переводит параллелограмм в параллелограмм. Для любого параллелограмма существует аффинное преобразование, которое отображает его в квадрат.

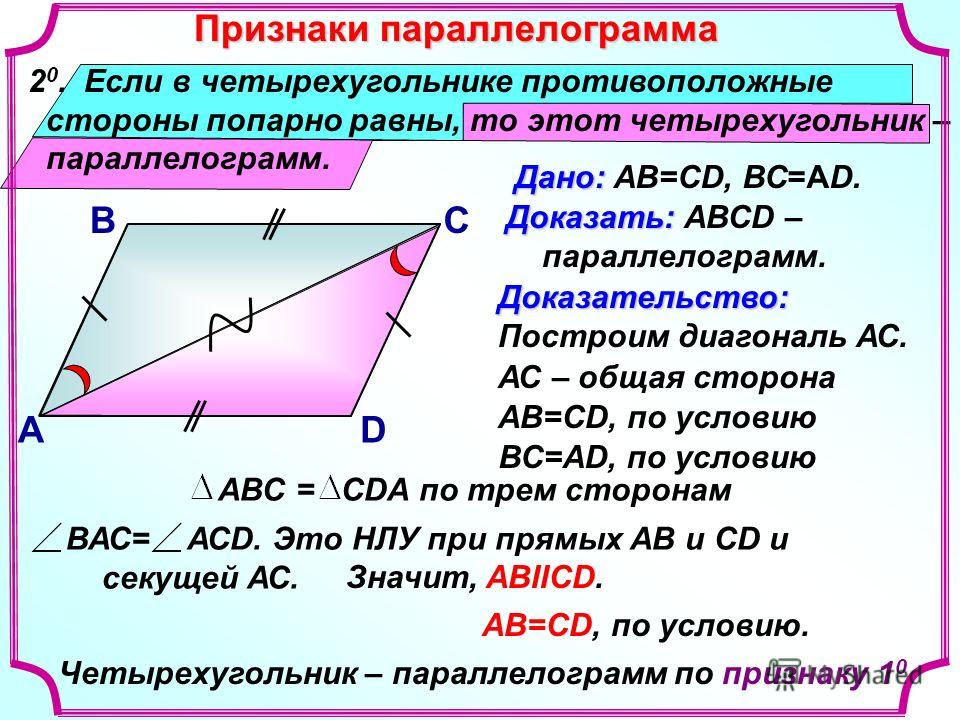
Признаки параллелограмма

Четырёхугольник ABCD является параллелограммом, если выполняется одно из следующих условий:

1. Противоположные стороны попарно равны (|AB| = |CD|, |AD| = |BC|).
2. Противоположные углы попарно равны (∠A = ∠C, ∠B = ∠D).
3. Две противоположные стороны равны и параллельны (|AB| = |CD|, AB || CD).
4. Диагонали делятся в точке их пересечения пополам (|AO| = |OC|, |BO| = |OD|).

Площадь

Площадь параллелограмма S_ABCD можно найти по следующим формулам:

где h_AD — высота опущенная на сторону AD, , β — угол между диагоналями.

См. также

• Трапеция
• Прямоугольник
• Ромб
• Дельтоид
• Параллелепипед
• Параллелограмм Вариньона

Wikimedia Foundation. 2010.

Игры ⚽ Поможем написать курсовую

• Параллакс (фотография)
• Параллелоэдры

Полезное

Параллелограмм / Этюды // Математические этюды

Параллелограмм / Этюды // Математические этюды

Математические этюды

К списку

Парал­ле­лограмм — это четырёх­уголь­ник, у кото­рого про­ти­вопо­лож­ные сто­роны попарно парал­лельны. Одно из немногих школь­ных опре­де­ле­ний, кото­рые пом­ним всю жизнь… И, ока­зы­ва­ется, не зря — многие окружающие пред­меты рабо­тают при­вычно для нас именно благо­даря свойствам парал­ле­лограмма.

Равен­ство про­ти­вопо­лож­ных сто­рон парал­ле­лограмма явля­ется уже след­ствием при­ве­дён­ного опре­де­ле­ния, т.е. парал­лель­но­сти сто­рон. И даже если сде­лать парал­ле­лограмм шар­нир­ным, напри­мер, из дет­ского кон­струк­тора, то при изги­ба­ниях сто­роны все­гда остаются парал­лель­ными. Такая про­стая модель, кстати, пока­зы­вает, что в отли­чие от прямо­уголь­ника, площадь парал­ле­лограмма не опре­де­ля­ется только дли­нами сто­рон: при изги­ба­ниях их длины не меняются, а площадь изме­ня­ется.

В настоль­ной лампе мас­сив­ное осно­ва­ние и абажур соеди­нены иногда одним, но чаще двумя парал­ле­лограммами. Такая кон­струкция поз­во­ляет менять положе­ние лампы, не изме­няя при этом угол её наклона по отноше­нию к столу.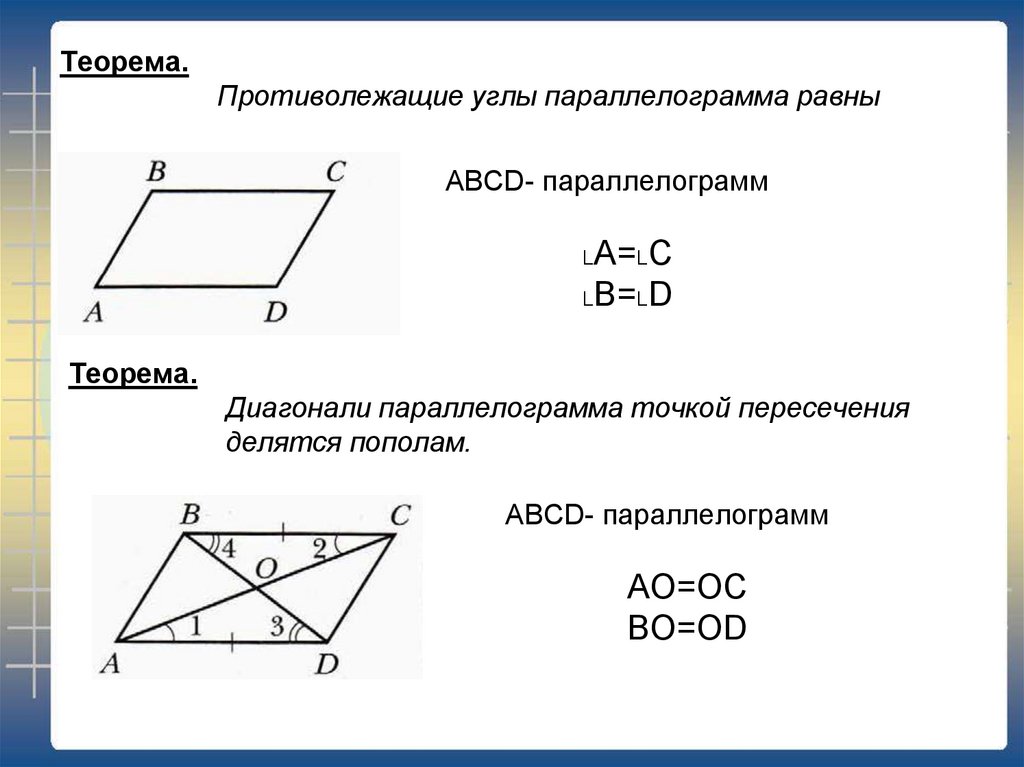 Таким же функци­о­на­лом обла­дают и, напри­мер, стойки-пан­тографы для сту­дий­ных мик­ро­фо­нов.

Шар­нир­ный парал­ле­лограмм поз­во­ляет изме­нять положе­ние лампы с сохра­не­нием угла наклона: сто­рона парал­ле­лограмма, к кото­рой крепится абажур, все­гда оста­ётся парал­лель­ной про­ти­вопо­лож­ной, не меняющей своё направ­ле­ние, сто­роне. Но если стойка сде­лана в виде одного парал­ле­лограмма, то перемеще­ние лампы пред­опре­де­лено — она может двигаться только по окруж­но­сти. Двой­ной (шар­нир­ный) парал­ле­лограмм — два парал­ле­лограмма с общей сто­ро­ной, или же соеди­нён­ные через деталь, не меняющую свою геомет­рию, — поз­во­ляет и сохра­нить угол наклона лампы, и при этом поме­стить её в про­из­воль­ную точку довольно большой обла­сти про­стран­ства.

В 1669 году в Париж­ской ака­демии наук Жиль Робер­валь про­де­мон­стри­ро­вал весы, пока­за­ния кото­рых не зави­сели от положе­ния груза на чаш­ках. Кстати, это тот самый Робер­валь, кото­рый вычис­лил площадь под аркой ⁠⁠цик­ло­иды, сведя эту площадь к площади под сину­со­и­дой (так назы­ва­емые «лепестки Робер­валя», см.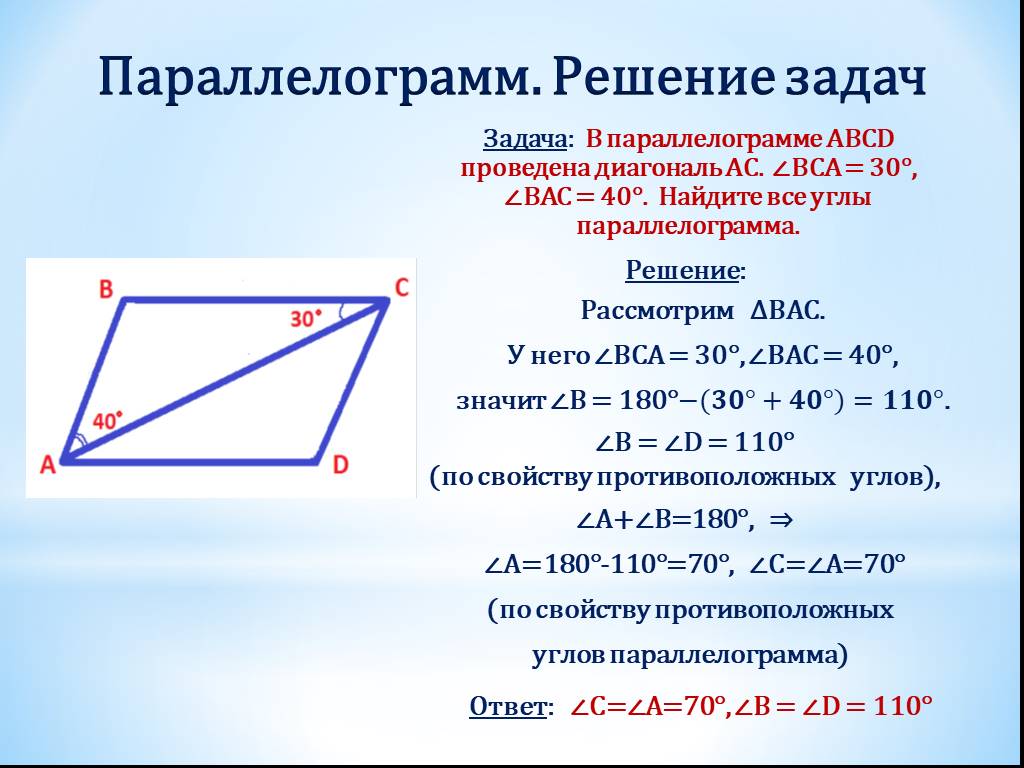  брошюру Берман Г. Н. «Цик­ло­ида»).

И осно­вой весов Робер­валя снова явля­ется шар­нир­ный парал­ле­лограмм! Его сто­роны, на кото­рых уста­нав­ли­ваются чашки весов, все­гда остаются вер­ти­каль­ными. Именно благо­даря исполь­зо­ва­нию парал­ле­лограмма, пока­за­ния весов не зави­сят от положе­ния груза. Сам Робер­валь, будучи и матема­ти­ком, и меха­ни­ком, уста­но­вил это экс­пе­римен­тально, а строгое кинема­ти­че­ское дока­за­тельство появи­лось лишь в начале XIX века. Весы, как важ­ный инструмент в жизни обще­ства, много раз усо­вершен­ство­вали, и сей­час суще­ствует множе­ство схем раз­ной слож­но­сти. Но большин­ство из них и по сей день так или иначе исполь­зуют свойства парал­ле­лограмма.

С начала XX века и до появ­ле­ния компью­те­ров глав­ным чер­тёж­ным инструмен­том инже­не­ров во всём мире был кульман. Это устройство, уна­сле­до­вавшее имя немец­кого предпри­нима­теля и изоб­ре­та­теля Франца Кульмана, состоит из чер­тёж­ной доски и рычаж­ного меха­низма.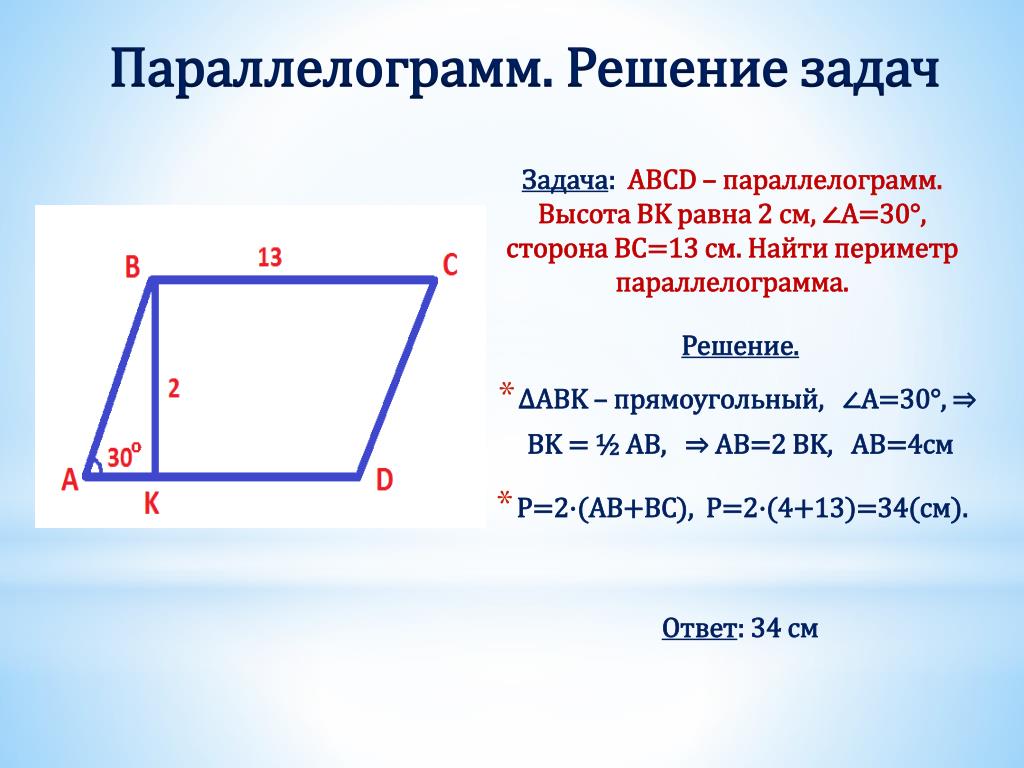

И осно­вой рычаж­ного меха­низма кульмана снова явля­ется… двой­ной парал­ле­лограмм. Жёстко при­креп­лён­ный к чер­тёж­ной доске одной сто­ро­ной и оснащён­ный пово­рот­ной шай­бой с линей­ками, двой­ной парал­ле­лограмм поз­во­ляет про­во­дить прямые линии под любыми углами. В част­но­сти, вычер­чи­вать парал­лель­ные. Из кото­рых и состоит сам парал­ле­лограмм.

Другие этюды раздела «Шарнирные механизмы»

  Шарнирные механизмы  Прямило Липкина  Сдвиг и поворот  Трисекция угла  Степени свободы

Математические этюды

Параллелограммы (ключевой этап 2)

Урок

Параллеграмм – это четырехсторонняя фигура, у которой противоположные стороны параллельны и равны по длине.

Оксфордский словарь английского языка определяет параллелограмм как «четырехстороннюю плоскую прямолинейную фигуру, противоположные стороны которой параллельны, особенно ту, стороны которой не пересекаются под прямым углом».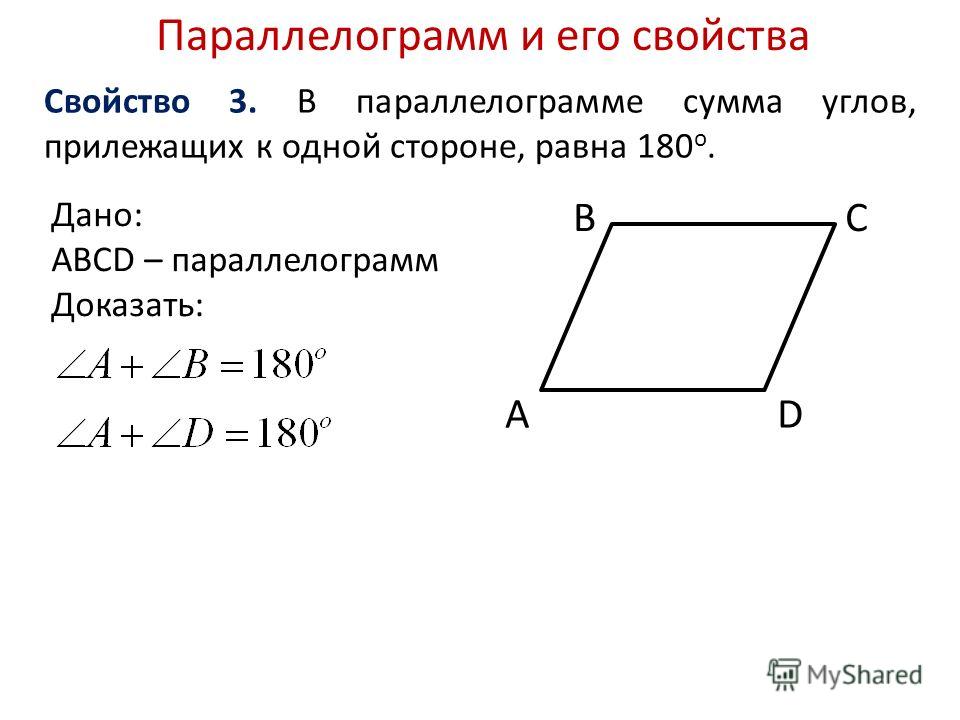

Свойства параллелограммов

• Противоположные стороны параллелограмма параллельны.

• Противоположные стороны параллелограмма имеют одинаковую длину.

• Противолежащие углы параллелограмма равны.

• Смежные углы параллелограмма в сумме дают 180°. Это дополнительные углы.

• Сумма всех углов параллелограмма равна 360°.

• Диагонали параллелограмма делят друг друга пополам. Диагонали пересекаются на половине своей длины.

Периметр параллелограмма

Периметр параллелограмма находится по формуле:

В этой формуле b — длина основания, а s — длина стороны параллелограмма.

Площадь параллелограмма

Площадь параллелограмма находится по формуле:

В этой формуле b — длина основания и ч — высота параллелограмма.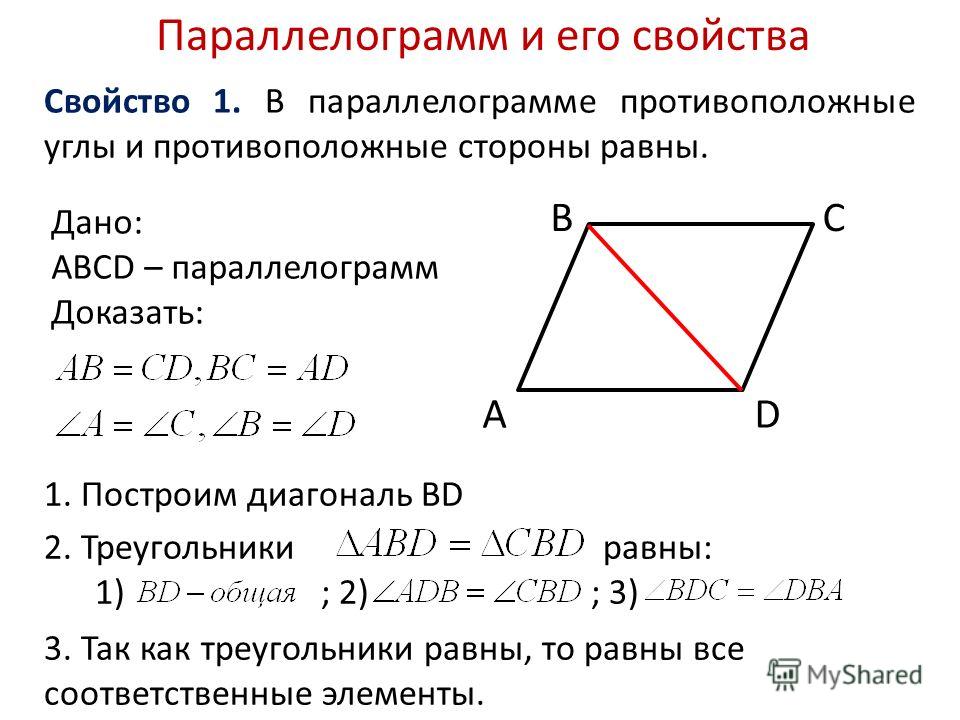
Подробнее о том, как найти площадь параллелограмма

Интерактивный виджет

Вот интерактивный виджет, который поможет вам узнать о параллелограммах.

Что в имени?

Параллелограмм происходит от греческого слова «parallelogrammon», что означает «параллельные стороны».

Параллелограмм является многоугольником

Параллелограмм является разновидностью многоугольника. Многоугольник — это двумерная фигура с прямыми сторонами. Параллелограмм – это неправильный многоугольник. Неправильные многоугольники имеют разную длину сторон и разные углы.

Параллелограмм является четырехугольником

Параллелограмм – это четырехугольник. Четырехугольник – это четырехугольник. Квадраты, прямоугольники и трапеции также являются четырехугольниками.

Внутренние углы параллелограмма

Параллелограмм – это четырехугольник. Сумма внутренних углов n-стороннего многоугольника равна:

(п — 2) × 180°

Это означает, что внутренние углы четырехугольника (где n = 4) составляют в сумме:

(4 − 2) × 180° = 360°

Это относится ко всем четырехугольникам, таким как квадраты, прямоугольники и трапеции.

Площади параллограммов и прямоугольников

Формула площади параллелограмма та же, что и для площади прямоугольника. Можете ли вы понять, почему на изображении ниже?

Рабочий лист

(печатная и отправляемая)

Как доказать, что четырехугольник-параллелограмм

от: Марк Райан и

Обновлен: 07-12-2021

с Книгой: 07-12-2021

от книги: 07-12-2021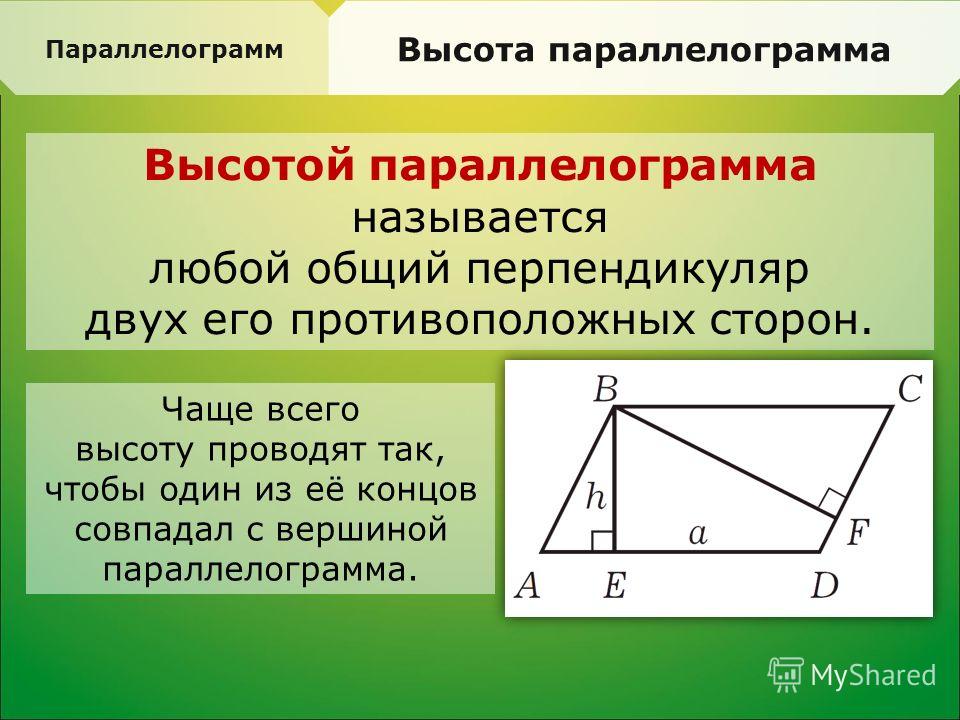

. Для чайников

Геометрия Для чайников

Посмотреть книгу Купить на Amazon

Существует пять способов доказать, что четырехугольник является параллелограммом. Первые четыре являются обратными свойствами параллелограмма (включая определение параллелограмма). Убедитесь, что вы помните необычное пятое свойство, которое не является обратным свойством, потому что оно часто бывает полезным:

• Если обе пары противоположных сторон четырехугольника параллельны, то это параллелограмм (обратное определение).

• Если обе пары противоположных сторон четырехугольника равны, то это параллелограмм (обратное свойство).

  Подсказка: Чтобы понять, почему этот метод проверки работает, возьмите две зубочистки и две ручки или карандаша одинаковой длины и соедините их все вместе кончик к кончику; создайте замкнутую фигуру, с зубочистками друг напротив друга. Единственная фигура, которую вы можете сделать, это параллелограмм.

• Если обе пары противоположных углов четырехугольника равны, то это параллелограмм (обратное свойство).

• Если диагонали четырехугольника делят друг друга пополам, то это параллелограмм (обратное свойство).

  Совет: Возьмите, скажем, карандаш и зубочистку (или две ручки или карандаша разной длины) и скрестите их посередине. Как бы вы ни меняли угол, который они образуют, их кончики образуют параллелограмм.

• Если одна пара противоположных сторон четырехугольника параллельна и конгруэнтна, то это параллелограмм (ни обратное определение, ни обратное свойство).

  Совет: Возьмите две ручки или карандаша одинаковой длины, по одной в каждую руку. Если вы будете держать их параллельно, как бы вы их ни двигали, вы увидите, что их четыре конца образуют параллелограмм.

Предыдущий список содержит обратные свойства четырех из пяти свойств параллелограмма.

No related posts.