| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | ||
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | загар((5pi)/3) | ||
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Тоан 11 — Бай тэп лам тхем
bạn đang xem 20 trang mẫu của tài liệu «toán 11 — bài tập làm thêm» , ể tải tài liệu gốc về máy bạn click vào nút . PHƯƠNG TRÌNH LƯỢNG GIÁC
A. CÔNG THỨC LƯỢNG GIÁC CẦN NHỚ
I. Một số công thức lượng giác cần nhớ
.
Конг Тхок Конг:
Công thức nhân đôi: sin2x = 2sinxcosx
cos2x = cos2x – sin2x = 2 cos2x – 1 = 1 — 2 sin2x
Конг Тхок Хо Бок:
Конг Тхок Нхан Ба:
Sin3x = 3sinx – 4sin3x; cos3x = 4cos3x – 3cosx.
Công thức biểu diễn theo tanx:
.
Công thức biến đổi tích thành tổng:
Công thức biến đổi tổng thành tích:
B. MỘT SỐ DẠNG BÀI TẬP VÊ PHƯƠNG TRÌNH LƯỢNG GIÁC
Dạng 1. Phương trình bậc hai.
Бай 1. Giải cac phương trình sau:
1) 2cosx — = 0 2) tanx — 3 = 0
3) 3cot2x + = 0 4) sin3x – 1 = 0
5) cosx + sin2x = 0
Бай 2. Giải cac phươn trình sau:
1) 2cos2x – 3cosx + 1 = 0 2) cos2x + sinx + 1 = 0
3) 2cos2x + cosx – 2 = 0 4) cos2x – 5sinx + 6 = 0
5) cos2x + 3cosx + 4 = 0 6) 4cos2x — 4cosx + 3 = 0
7) 2sin2x – cosx + = 0 8) 2sin2x – 7sinx + 3 = 0
9) 2sin2x + 5cosx = 5.
Бай 3. Giải cac phương trình:
2sin2x — cos2x — 4sinx + 2 = 0 3) 9cos2x — 5sin2x — 5cosx + 4 = 0
3) 5sinx(sinx — 1) — cos2x = 3 4) cos2x + sin2x + 2cosx + 1 = 0
5) 3cos2x + 2(1 + + sinx)sinx – (3 + ) = 0
6) tan2x + (- 1)tanx – = 0 7)
8)
9) .
PHƯƠNG TRÌNH LƯỢNG GIÁC
A. CÔNG THỨC LƯỢNG GIÁC CẦN NHỚ
I. Một số công thức lượng giác cần nhớ
.
Конг Тхок Конг:
Công thức nhân đôi: sin2x = 2sinxcosx
cos2x = cos2x – sin2x = 2 cos2x – 1 = 1 — 2 sin2x
Конг Тхок Хо Бок:
Конг Тхок Нхан Ба:
Sin3x = 3sinx – 4sin3x; cos3x = 4cos3x – 3cosx.
Công thức biểu diễn theo tanx:
.
Công thức biến đổi tích thành tổng:
Công thức biến đổi tổng thành tích:
B. MỘT SỐ DẠNG BÀI TẬP VÊ PHƯƠNG TRÌNH LƯỢNG GIÁC
Dạng 1. Phương trình bậc hai.
Бай 1. Giải cac phương trình sau:
1) 2cosx — = 0 2) tanx — 3 = 0
3) 3cot2x + = 0 4) sin3x – 1 = 0
5) cosx + sin2x = 0
Бай 2. Giải cac phươn trình sau:
1) 2cos2x – 3cosx + 1 = 0 2) cos2x + sinx + 1 = 0
3) 2cos2x + cosx – 2 = 0 4) cos2x – 5sinx + 6 = 0
5) cos2x + 3cosx + 4 = 0 6) 4cos2x — 4cosx + 3 = 0
7) 2sin2x – cosx + = 0 8) 2sin2x – 7sinx + 3 = 0
9) 2sin2x + 5cosx = 5.
Бай 3. Giải cac phương trình:
2sin2x — cos2x — 4sinx + 2 = 0 3) 9cos2x — 5sin2x — 5cosx + 4 = 0
3) 5sinx(sinx — 1) — cos2x = 3 4) cos2x + sin2x + 2cosx + 1 = 0
5) 3cos2x + 2(1 + + sinx)sinx – (3 + ) = 0
6) tan2x + (- 1)tanx – = 0 7)
8)
9) . Dạng 2. Phương trình bậc nhất đối với sinx và cosx
Бай 1. Giải cac phương trình sau:
1) 4sinx – 3cosx = 2 2) sinx – cosx = 1
3) sin3x + cos3x = 1 4) sin4x + cos4x =
5) 5cos2x – 12cos2x = 13 6) 3sinx + 4cosx = 5
Бай 2. Giải cac phương trình:
1) 2)
3) 4)
5)
Dạng 3. Phương trình đẳng cấp bậc hai đối với sin và cosin.
1) sin2x + 2sinxcosx + 3cos2x — 3 = 0 2) sin2x — 3sinxcosx + 1 = 0.
3) 4sinxcosx + 4cos2x = 2sin2x + .
4) .
5) а) ; б) .
6) cos2x – 3sinxcosx – 2sin2x – 1 = 0 7) 6sin2x + sinxcosx – cos2x = 2.
8) sin2x + 2sinxcosx — 2cos2x = 0 9) 4sin2x + sinxcosx + 3cos2x — 3 = 0.
10) .
Dạng 4. Phương trình đối xứng đối với sinx và cosx:
Бай 1. Giải cac phương trình sau:
1) (sinx + cosx) – 2sinxcosx = 2 + 1
2) 6(sinx – cosx) – sinxcosx = 6
3) 3(sinx + cosx) + 2sinxcosx + 3 = 0
4) sinx – cosx + 4sinxcosx + 1 = 0
5) sin2x – 12(sinx – cosx) + 12 = 0
Бай 2. Giải cac phương trình:
1) (sinx+cosx) — sinxcosx=1.
2) (1 – sinxcosx)(sinx+cosx) = .
3) .
4) sin3x + cos3x = .
5) sinx – cosx + 7sin2x = 1.
Dạng 2. Phương trình bậc nhất đối với sinx và cosx
Бай 1. Giải cac phương trình sau:
1) 4sinx – 3cosx = 2 2) sinx – cosx = 1
3) sin3x + cos3x = 1 4) sin4x + cos4x =
5) 5cos2x – 12cos2x = 13 6) 3sinx + 4cosx = 5
Бай 2. Giải cac phương trình:
1) 2)
3) 4)
5)
Dạng 3. Phương trình đẳng cấp bậc hai đối với sin và cosin.
1) sin2x + 2sinxcosx + 3cos2x — 3 = 0 2) sin2x — 3sinxcosx + 1 = 0.
3) 4sinxcosx + 4cos2x = 2sin2x + .
4) .
5) а) ; б) .
6) cos2x – 3sinxcosx – 2sin2x – 1 = 0 7) 6sin2x + sinxcosx – cos2x = 2.
8) sin2x + 2sinxcosx — 2cos2x = 0 9) 4sin2x + sinxcosx + 3cos2x — 3 = 0.
10) .
Dạng 4. Phương trình đối xứng đối với sinx và cosx:
Бай 1. Giải cac phương trình sau:
1) (sinx + cosx) – 2sinxcosx = 2 + 1
2) 6(sinx – cosx) – sinxcosx = 6
3) 3(sinx + cosx) + 2sinxcosx + 3 = 0
4) sinx – cosx + 4sinxcosx + 1 = 0
5) sin2x – 12(sinx – cosx) + 12 = 0
Бай 2. Giải cac phương trình:
1) (sinx+cosx) — sinxcosx=1.
2) (1 – sinxcosx)(sinx+cosx) = .
3) .
4) sin3x + cos3x = .
5) sinx – cosx + 7sin2x = 1.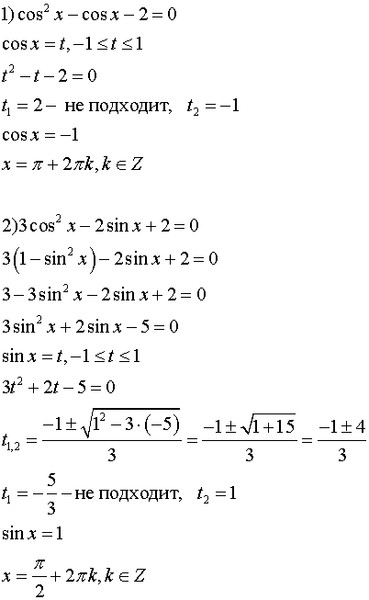 6) .
7) .
8) .
9) 1 + tgx = 2sinx.
10) sinxcosx + 2sinx + 2cosx = 2.
11) 2sin2x – 2(sinx + cosx) +1 = 0.
C. BÀI TẬP TỰ LUYỆN
Бай 1. Giải cac phương trình sau:
1) sin3x = 11) sin(2x — 3) = sin(x + 1)
2) cos2x = — 12) tan(3x + 2) + cot2x = 0
3) tan(x + 60o) = — 13) sin3x = cos4x
4) раскладушка = 14) tan3x.tanx = 1
5) sin2x = sin 15) sin(2x + 50o) = cos(x + 120o)
6) загар = загар 16) — 2sin2x = 0
7) cos(3x + 20o) = sin(40o — x) 17) 2cos — = 0
8) загар = — кроватка 18) 3загар + = 0
9) sin(2x — 10o) = với -120o < x < 90o 19) 2sinx - sin2x = 0
10) cos(2x + 1) = với - p < x < p 20) 8cos3x - 1 = 0
Бай 2. Giải cac phương trình:
1) sin2x = 11) sin2x + sin22x = sin23x
2) cos23x = 1 12) sintan2x = 0
3) sin4x + cos4x = 13) (2sinx + 1)2 - (2sinx + 1)(sinx - ) = 0
4) sinx + cosx = 1 14) sinx + sin2x + sin3x = 0
5) cosx.cos3x = cos5x.cos7x 15) cosx + cos2x + cos3x + cos4x = 0
6) cos2x.cos5x = cos7x 16) 1 + sinx + cos3x = cosx + sin2x + cos2x
7) sin3x.cos7x = sin13x.cos17x 17) cos7x + sin22x = cos22x - cosx
8) sin4x.
6) .
7) .
8) .
9) 1 + tgx = 2sinx.
10) sinxcosx + 2sinx + 2cosx = 2.
11) 2sin2x – 2(sinx + cosx) +1 = 0.
C. BÀI TẬP TỰ LUYỆN
Бай 1. Giải cac phương trình sau:
1) sin3x = 11) sin(2x — 3) = sin(x + 1)
2) cos2x = — 12) tan(3x + 2) + cot2x = 0
3) tan(x + 60o) = — 13) sin3x = cos4x
4) раскладушка = 14) tan3x.tanx = 1
5) sin2x = sin 15) sin(2x + 50o) = cos(x + 120o)
6) загар = загар 16) — 2sin2x = 0
7) cos(3x + 20o) = sin(40o — x) 17) 2cos — = 0
8) загар = — кроватка 18) 3загар + = 0
9) sin(2x — 10o) = với -120o < x < 90o 19) 2sinx - sin2x = 0
10) cos(2x + 1) = với - p < x < p 20) 8cos3x - 1 = 0
Бай 2. Giải cac phương trình:
1) sin2x = 11) sin2x + sin22x = sin23x
2) cos23x = 1 12) sintan2x = 0
3) sin4x + cos4x = 13) (2sinx + 1)2 - (2sinx + 1)(sinx - ) = 0
4) sinx + cosx = 1 14) sinx + sin2x + sin3x = 0
5) cosx.cos3x = cos5x.cos7x 15) cosx + cos2x + cos3x + cos4x = 0
6) cos2x.cos5x = cos7x 16) 1 + sinx + cos3x = cosx + sin2x + cos2x
7) sin3x.cos7x = sin13x.cos17x 17) cos7x + sin22x = cos22x - cosx
8) sin4x. sin3x = cosx 18) sinx + sin2x + sin3x = 1 + cosx + cos2x
9) 1 + 2cosx + cos2x = 0 19) sin3x.sin5x = sin11x.sin13x
10) cosx + cos2x + cos3x = 0 20) cosx — cos2x + cos3x =
Бай 3. Giải cac phương trình:
1) 2sin2x — 3sinx + 1 = 0 2) 4sin2x + 4cosx — 1 = 0
3) загар + 2кот — 3 = 0 4)
5) cot2x — 4cotx + 3 = 0 6) cos22x + sin2x + 1 = 0
7) sin22x — 2cos2x + = 0 8) 4cos2x — 2( — 1)cosx + = 0
9) tan4x + 4tan2x + 3 = 0 10) cos2x + 9cosx + 5 = 0
11) + 3кот2х = 5
Бай 5. Giải cac phương trình sau:
1) 3sinx + 4cosx = 5 2) 2sin2x — 2cos2x =
3) 2грех + грех =
4)
5) 2sin17x + cos5x + sin5x = 0
6) cos7x — sin5x = (cos5x — sin7x)
7) 4sinx + 2 cosx = 2 + 3tanx
Бай 6. Giải cac phương trình:
1) 2(sinx + cosx) — 4sinxcosx — 1 = 0 2) sin2x — 12(sinx + cosx) + 12 = 0
3) sinx — cosx + 4sinxcosx + 1 = 0 4) cos3x + sin3x = 1
5) 3(sinx + cosx) + 2sin2x + 2 = 0 6) sin2x — 3(sinx + cosx) + 5 = 0
7) 2(sinx — cosx) + sin2x + 5 = 0 8) sin2x + sin(x — 45o) = 1
9) 2sin2x + |sinx + cosx| + 8 = 0
10) (sinx — cosx)2 + ( + 1)(sinx — cosx) + = 0
Бай 7.
sin3x = cosx 18) sinx + sin2x + sin3x = 1 + cosx + cos2x
9) 1 + 2cosx + cos2x = 0 19) sin3x.sin5x = sin11x.sin13x
10) cosx + cos2x + cos3x = 0 20) cosx — cos2x + cos3x =
Бай 3. Giải cac phương trình:
1) 2sin2x — 3sinx + 1 = 0 2) 4sin2x + 4cosx — 1 = 0
3) загар + 2кот — 3 = 0 4)
5) cot2x — 4cotx + 3 = 0 6) cos22x + sin2x + 1 = 0
7) sin22x — 2cos2x + = 0 8) 4cos2x — 2( — 1)cosx + = 0
9) tan4x + 4tan2x + 3 = 0 10) cos2x + 9cosx + 5 = 0
11) + 3кот2х = 5
Бай 5. Giải cac phương trình sau:
1) 3sinx + 4cosx = 5 2) 2sin2x — 2cos2x =
3) 2грех + грех =
4)
5) 2sin17x + cos5x + sin5x = 0
6) cos7x — sin5x = (cos5x — sin7x)
7) 4sinx + 2 cosx = 2 + 3tanx
Бай 6. Giải cac phương trình:
1) 2(sinx + cosx) — 4sinxcosx — 1 = 0 2) sin2x — 12(sinx + cosx) + 12 = 0
3) sinx — cosx + 4sinxcosx + 1 = 0 4) cos3x + sin3x = 1
5) 3(sinx + cosx) + 2sin2x + 2 = 0 6) sin2x — 3(sinx + cosx) + 5 = 0
7) 2(sinx — cosx) + sin2x + 5 = 0 8) sin2x + sin(x — 45o) = 1
9) 2sin2x + |sinx + cosx| + 8 = 0
10) (sinx — cosx)2 + ( + 1)(sinx — cosx) + = 0
Бай 7. Giải cac Phương trình
1) sin2x — 10sinxcosx + 21cos2x = 0 2) cos2x — 3sinxcosx + 1 = 0
3) cos2x — sin2x — sin2x = 1
4) 3sin2x + 8sinxcosx + (8 — 9)cos2x = 0
5) 4sin2x + 3sin2x — 2cos2x = 4
6) 2sin2x + (3 + )sinxcosx + ( — 1)cos2x = 1
7) 2sin2x — 3sinxcosx + cos2x = 0 8) cos22x — 7sin4x + 3sin22x = 3
Бай 8. Giải cac Phương trình
1) 4cos2x — 2( + 1)cosx + = 0 2) tan2x + (1 — )tanx — 3 = 0
3) cos2x + 9cosx + 5 = 0 4) sin22x — 2cos2x + = 0
5) 2cos6x + tan3x = 1 6) + 3cot2x = 5
Бай 9. Giải cac Phương trình
1) sin2x + sin2xsin4x + sin3xsin9x = 1
2) cos2x — sin2xsin4x — cos3xcos9x = 1
3) cos2x + 2sinxsin2x = 2cosx
4) cos5xcosx = cos4xcos2x + 3cos2x + 1
5) cos4x + sin3xcosx = sinxcos3x
6) грех (4x + ) sin6x = грех (10x + )
7) (1 + tan2)(1 + sin2x) = 1
8) тангенс(-х) + тангенс(-х) + тангенс2х = 0
Бай 10. Giải cac Phương trình
1) (1 — cos2x)sin2x = sin2x
2) sin4x — cos4x = cosx
3)
4) 1 — (2 + )sinx =
5) загар2x =
6) 2(sin3x + cos3x) + sin2x(sinx + cosx) =
7) cosx(1 — tanx)(sinx + cosx) = sinx
8) (1 + tanx)(1 + sin2x) = 1 + tanx
9) (2sinx — cosx)(1 + cosx) = sin2x
Бай 10.
Giải cac Phương trình
1) sin2x — 10sinxcosx + 21cos2x = 0 2) cos2x — 3sinxcosx + 1 = 0
3) cos2x — sin2x — sin2x = 1
4) 3sin2x + 8sinxcosx + (8 — 9)cos2x = 0
5) 4sin2x + 3sin2x — 2cos2x = 4
6) 2sin2x + (3 + )sinxcosx + ( — 1)cos2x = 1
7) 2sin2x — 3sinxcosx + cos2x = 0 8) cos22x — 7sin4x + 3sin22x = 3
Бай 8. Giải cac Phương trình
1) 4cos2x — 2( + 1)cosx + = 0 2) tan2x + (1 — )tanx — 3 = 0
3) cos2x + 9cosx + 5 = 0 4) sin22x — 2cos2x + = 0
5) 2cos6x + tan3x = 1 6) + 3cot2x = 5
Бай 9. Giải cac Phương trình
1) sin2x + sin2xsin4x + sin3xsin9x = 1
2) cos2x — sin2xsin4x — cos3xcos9x = 1
3) cos2x + 2sinxsin2x = 2cosx
4) cos5xcosx = cos4xcos2x + 3cos2x + 1
5) cos4x + sin3xcosx = sinxcos3x
6) грех (4x + ) sin6x = грех (10x + )
7) (1 + tan2)(1 + sin2x) = 1
8) тангенс(-х) + тангенс(-х) + тангенс2х = 0
Бай 10. Giải cac Phương trình
1) (1 — cos2x)sin2x = sin2x
2) sin4x — cos4x = cosx
3)
4) 1 — (2 + )sinx =
5) загар2x =
6) 2(sin3x + cos3x) + sin2x(sinx + cosx) =
7) cosx(1 — tanx)(sinx + cosx) = sinx
8) (1 + tanx)(1 + sin2x) = 1 + tanx
9) (2sinx — cosx)(1 + cosx) = sin2x
Бай 10. Giải cac Phương trình
1) sinx + cosx — — 1 = 0
2) (1 + )(sinx + cosx) — sin2x — ( 1 + ) = 0
3) tanx + tan2x = tan3x
4)
D. MỘT SỐ BÀI THI ĐẠI HỌC VÊ PHƯƠNG TRÌNH LƯỢNG GIÁC
Бай 1. Giải cac phương trình
1) (1 + tanx)cos3x + (1 + cotx)sin3x =
2) tan2x — tanxtan3x = 2
3) = 1 — 2cosx
4) cos3xtan5x = sin7x
5) танкс + коткс = 4
6) + 2cosx = 0
7) 2танкс+коткс=
8) tanx + cotx = 2 (sin2x + cos2x)
9) 2sin3x(1 — 4sin2x) = 1
10)
11) cosx.cos2x.cos4x.cos8x =
12) cos10x + cos24x + 6cos3xcosx = cosx + 8cosxcos23x
13) sin2xcosx = + cos3xsinx
14) sin6x + cos6x = cos4x
15) sin4x + cos4x = раскладушка(х + )раскладушка( — х)
16)
17) sin3xcos3x + cos3xsin3x = sin34x
18) 2sin3x — = 2cos3x +
19) cos3xcos3x + sin3xsin3x =
20) (танкс+коткс)
21) 1 + танкс = 2синкс
22) cosx — sinx = cos3x
23)
24) sin3x + cos3x + sin3xcotx + cos3xtanx =
25) (2cosx — 1)(sinx + cosx) = 1
26) 2sin(3x + ) =
Бай 2. Giải cac Phương trình
1) sin4 + cos4 =
2) 4sin3x + 3cos3x — 3sinx — sin2xcosx = 0
3) cos3x — sin3x — 3cosxsin2x + sinx = 0
4)
5) sin2x(tanx + 1) = 3sinx(cosx — sinx) + 3
6) cos6x + sin6x =
Бай 3.
Giải cac Phương trình
1) sinx + cosx — — 1 = 0
2) (1 + )(sinx + cosx) — sin2x — ( 1 + ) = 0
3) tanx + tan2x = tan3x
4)
D. MỘT SỐ BÀI THI ĐẠI HỌC VÊ PHƯƠNG TRÌNH LƯỢNG GIÁC
Бай 1. Giải cac phương trình
1) (1 + tanx)cos3x + (1 + cotx)sin3x =
2) tan2x — tanxtan3x = 2
3) = 1 — 2cosx
4) cos3xtan5x = sin7x
5) танкс + коткс = 4
6) + 2cosx = 0
7) 2танкс+коткс=
8) tanx + cotx = 2 (sin2x + cos2x)
9) 2sin3x(1 — 4sin2x) = 1
10)
11) cosx.cos2x.cos4x.cos8x =
12) cos10x + cos24x + 6cos3xcosx = cosx + 8cosxcos23x
13) sin2xcosx = + cos3xsinx
14) sin6x + cos6x = cos4x
15) sin4x + cos4x = раскладушка(х + )раскладушка( — х)
16)
17) sin3xcos3x + cos3xsin3x = sin34x
18) 2sin3x — = 2cos3x +
19) cos3xcos3x + sin3xsin3x =
20) (танкс+коткс)
21) 1 + танкс = 2синкс
22) cosx — sinx = cos3x
23)
24) sin3x + cos3x + sin3xcotx + cos3xtanx =
25) (2cosx — 1)(sinx + cosx) = 1
26) 2sin(3x + ) =
Бай 2. Giải cac Phương trình
1) sin4 + cos4 =
2) 4sin3x + 3cos3x — 3sinx — sin2xcosx = 0
3) cos3x — sin3x — 3cosxsin2x + sinx = 0
4)
5) sin2x(tanx + 1) = 3sinx(cosx — sinx) + 3
6) cos6x + sin6x =
Бай 3.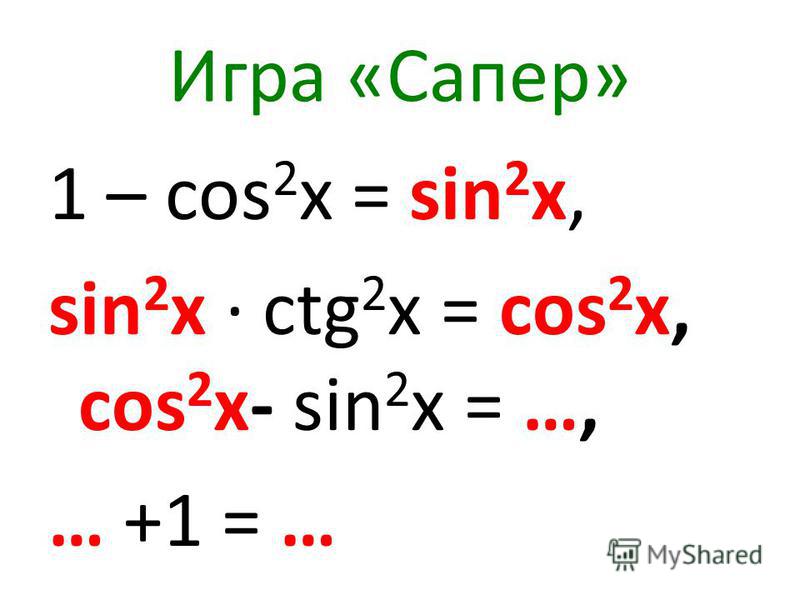 Giải cac phương trình
1) 2)
3) 4) sin4x = tanx
5) cos2x + sin2x 2cosx + 1 = 0 6) sin3x + 2cos2x — 2 = 0
7) cos2x + cos22x + cos23x + cos24x = 8) 2 + cos2x + 5sinx = 0
9) 3(tanx + cotx) = 2(2 + sin2x) 10) 4cos3x + 3sin2x = 8cosx
Бай 4. Giải phương trình lượng giác
1) cosx + sinx = 3 — 2) 3sin3x — cos9x = 1 + 4sin33x
3) cos7xcos5x — sin2x = 1 — sin7xsin5x 4) 4sin2x — 3cos2x = 3(4sĩnx — 1)
5) 4(sin4x + cos4x) + sin4x = 2 6) 4sin3x — 1 = 3sinx — cos3x
7) sin2x + cos2x = 8) 2(sinx + cosx)cosx = 3 + cos2x
9) cos2x — sin2x = 1 + sin2x
Бай 5. Giải cac phương trình (biến đổi đưa về dạng tích)
1) sin3x — sin2x = 2sinxcos2x
2) sin22x + cos28x = cos10x
3) (2sinx + 1)(2sin2x — 1) = 3 — 4cos2x
4) cosxcoscos — sinxsinsin =
5) tanx + tan2x — tan3x = 0
6) cos3x + sin3x = sinx — cosx
7) (cosx — sinx)cosxsinx = cosxcos2x
8) (2sinx — 1)(2cos2x + 2sinx + 1) = 3 — 4cos2x
9) 2cos3x + cos2x + sinx = 0
10) sin3x — sinx = sin2x
11)
12) sinx + sin2x + sin3x + sin4x + sin5x + sin6x = 0
13) cos4 — sin4 = sin2x
14) 3 — 4cos2x = sinx(2sinx + 1)
15) 2sin3x + cos2x = sinx
16) sin2x + sin22x + sin23x =
17) cos3x + sin3x = sinx — cosx
18) sin3x + cos3x = 2(sin5x + cos5x)
19) sin2x = cos22x + cos23x
20) sin23x — sin22x — sin2x = 0
21) 1 + sinx + cosx = sin2x + cos2x = 0
22) 2sin3x — sinx = 2cos3x — cosx + cos2x
23) 2sin3x — cos2x + cosx = 0
24) cosx + cos2x + cos3x + cos4x = 0
25) 2cos2x = (cosx — sinx)
26) 4cos3x + 3sin2x = 8cosx
27) sin3x + sin2x = 5sinx
Бай 6.
Giải cac phương trình
1) 2)
3) 4) sin4x = tanx
5) cos2x + sin2x 2cosx + 1 = 0 6) sin3x + 2cos2x — 2 = 0
7) cos2x + cos22x + cos23x + cos24x = 8) 2 + cos2x + 5sinx = 0
9) 3(tanx + cotx) = 2(2 + sin2x) 10) 4cos3x + 3sin2x = 8cosx
Бай 4. Giải phương trình lượng giác
1) cosx + sinx = 3 — 2) 3sin3x — cos9x = 1 + 4sin33x
3) cos7xcos5x — sin2x = 1 — sin7xsin5x 4) 4sin2x — 3cos2x = 3(4sĩnx — 1)
5) 4(sin4x + cos4x) + sin4x = 2 6) 4sin3x — 1 = 3sinx — cos3x
7) sin2x + cos2x = 8) 2(sinx + cosx)cosx = 3 + cos2x
9) cos2x — sin2x = 1 + sin2x
Бай 5. Giải cac phương trình (biến đổi đưa về dạng tích)
1) sin3x — sin2x = 2sinxcos2x
2) sin22x + cos28x = cos10x
3) (2sinx + 1)(2sin2x — 1) = 3 — 4cos2x
4) cosxcoscos — sinxsinsin =
5) tanx + tan2x — tan3x = 0
6) cos3x + sin3x = sinx — cosx
7) (cosx — sinx)cosxsinx = cosxcos2x
8) (2sinx — 1)(2cos2x + 2sinx + 1) = 3 — 4cos2x
9) 2cos3x + cos2x + sinx = 0
10) sin3x — sinx = sin2x
11)
12) sinx + sin2x + sin3x + sin4x + sin5x + sin6x = 0
13) cos4 — sin4 = sin2x
14) 3 — 4cos2x = sinx(2sinx + 1)
15) 2sin3x + cos2x = sinx
16) sin2x + sin22x + sin23x =
17) cos3x + sin3x = sinx — cosx
18) sin3x + cos3x = 2(sin5x + cos5x)
19) sin2x = cos22x + cos23x
20) sin23x — sin22x — sin2x = 0
21) 1 + sinx + cosx = sin2x + cos2x = 0
22) 2sin3x — sinx = 2cos3x — cosx + cos2x
23) 2sin3x — cos2x + cosx = 0
24) cosx + cos2x + cos3x + cos4x = 0
25) 2cos2x = (cosx — sinx)
26) 4cos3x + 3sin2x = 8cosx
27) sin3x + sin2x = 5sinx
Бай 6. Giải cac Phương trình
1) = cos2x + sin2x với 0 < x < 2p
2) sin(2x + ) - 3cos(x - ) = 1 + 2sinx với < x < 3p
3) cos7x - sin7x = - với
Bài 7. Tìm giả trị lớn nhất, giá trị nhỏ nhất của:
1) у = 2sin2x + 3sinxcosx + 5cos2x
2) y = trong khảng (-p; p)
3) у = 4sin2x +
4) у = sinx - cos2x +
Бай 8 (Cac đề thi ĐH, CĐ mới).
1) А_02. Giải phương trình: 5 = cos2x + 3
2) Д_02. Тим как Нгхим Тхук [0; 14] của phương trình:
cos3x - 4cos2x + 3cosx - 4 = 0
3) А_03. Giải phương trình: cotx - 1 = + sin2x - sin2x
4) Д_03. Giải phương trình: sin2(-)tan2x - cos2 = 0
5) Д_04. Giải phương trình: (2cosx - 1)(sinx + cosx) = sin2x - sinx
6) А_05. Giải phương trình: cos23xcos2x - cos2x = 0
7) Д_05. Giải phương trình: cos4x + sin4x + cos(x -) sin(3x -) - = 0
8) A_05_dự bị1. Тим нгим трен кханг (0; p) của phương trình:
4sin2 - cos2x = 1 + 2cos2(x - )
9) A_05_dự bị 2. Giải pt: 2cos3( x - ) - 3cosx - sinx = 0
10) D_05_dự bị 1. Giải pt: tan(- x) + = 2
11) D_05_dự bị 2. Giải pt: sin2x + cos2x - 3sinx - cosx - 2 = 0
12) A_06_dự bị 1.
Giải cac Phương trình
1) = cos2x + sin2x với 0 < x < 2p
2) sin(2x + ) - 3cos(x - ) = 1 + 2sinx với < x < 3p
3) cos7x - sin7x = - với
Bài 7. Tìm giả trị lớn nhất, giá trị nhỏ nhất của:
1) у = 2sin2x + 3sinxcosx + 5cos2x
2) y = trong khảng (-p; p)
3) у = 4sin2x +
4) у = sinx - cos2x +
Бай 8 (Cac đề thi ĐH, CĐ mới).
1) А_02. Giải phương trình: 5 = cos2x + 3
2) Д_02. Тим как Нгхим Тхук [0; 14] của phương trình:
cos3x - 4cos2x + 3cosx - 4 = 0
3) А_03. Giải phương trình: cotx - 1 = + sin2x - sin2x
4) Д_03. Giải phương trình: sin2(-)tan2x - cos2 = 0
5) Д_04. Giải phương trình: (2cosx - 1)(sinx + cosx) = sin2x - sinx
6) А_05. Giải phương trình: cos23xcos2x - cos2x = 0
7) Д_05. Giải phương trình: cos4x + sin4x + cos(x -) sin(3x -) - = 0
8) A_05_dự bị1. Тим нгим трен кханг (0; p) của phương trình:
4sin2 - cos2x = 1 + 2cos2(x - )
9) A_05_dự bị 2. Giải pt: 2cos3( x - ) - 3cosx - sinx = 0
10) D_05_dự bị 1. Giải pt: tan(- x) + = 2
11) D_05_dự bị 2. Giải pt: sin2x + cos2x - 3sinx - cosx - 2 = 0
12) A_06_dự bị 1.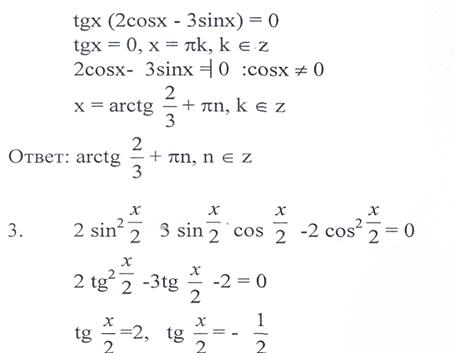 Giải pt: cos3xcos3x — sin3xsin3x =
13) A_06_dự bị 2. Giải pt: 4sin3x + 4sin2x + 3sin2x + 6cosx = 0
14) B_06_dự bị 1. Giải pt: (2sin2x — 1)tan22x + 3(2cos2x — 1) = 0
15) B_06_dự bị 2. Giải pt: cos2x + (1 + 2cosx)(sinx — cosx) = 0
16) D_06_dự bị 1. Giải pt: cos3x + sin3x + 2sin2x = 1
17) Д_06. Giải pt: cos3x + cos2x — cosx — 1 = 0
18) А_07. Giải phương trình: (1 + sin2x)cosx + (1 + cos2x)sinx = 1 + sin2x
19) В_07. Giải phương trình: 2sin22x + sin7x — 1 = sinx
21) Д_07. Giải phương trình: (sin2 + cos2)2 + cosx = 2
22) CĐ_07. Giải phương trình: 2sin2(- 2x) + cos4x = 4cos2x — 1
23) А_08. Giải phương trình:
24) Б_08. Giải phương trình: sin3x — cos3x = sinxcos2x — sin2xcosx
25) Д_08. Giải phương trình: 2sinx(1 + cos2x) + sin2x = 1 + 2cosx
26) CĐ_08. Общая часть: sin3x — cos3x = 2sin2x
ЧУЕН № 2
ĐẠI SỐ TỔ HỢP
A. MỘT SỐ DẠNG TOÁN THƯỜNG GẶP
I) QUY TẮC CỘNG VÀ QUY TẮC NHÂN:
Бай 1: Với cac chữ số 1, 2, 3, 4, 5 có thể lập được bao nhiêu:
1) Số lẻ gồm 4 chữ số khác nhau?
2) Số chẵn gồm 4 chữ số bất kỳ?
Bài 2: Có 4 con ường nối liền điểm a và điểm b, có 3 con ường nối liền điểm b và điểm c.
Giải pt: cos3xcos3x — sin3xsin3x =
13) A_06_dự bị 2. Giải pt: 4sin3x + 4sin2x + 3sin2x + 6cosx = 0
14) B_06_dự bị 1. Giải pt: (2sin2x — 1)tan22x + 3(2cos2x — 1) = 0
15) B_06_dự bị 2. Giải pt: cos2x + (1 + 2cosx)(sinx — cosx) = 0
16) D_06_dự bị 1. Giải pt: cos3x + sin3x + 2sin2x = 1
17) Д_06. Giải pt: cos3x + cos2x — cosx — 1 = 0
18) А_07. Giải phương trình: (1 + sin2x)cosx + (1 + cos2x)sinx = 1 + sin2x
19) В_07. Giải phương trình: 2sin22x + sin7x — 1 = sinx
21) Д_07. Giải phương trình: (sin2 + cos2)2 + cosx = 2
22) CĐ_07. Giải phương trình: 2sin2(- 2x) + cos4x = 4cos2x — 1
23) А_08. Giải phương trình:
24) Б_08. Giải phương trình: sin3x — cos3x = sinxcos2x — sin2xcosx
25) Д_08. Giải phương trình: 2sinx(1 + cos2x) + sin2x = 1 + 2cosx
26) CĐ_08. Общая часть: sin3x — cos3x = 2sin2x
ЧУЕН № 2
ĐẠI SỐ TỔ HỢP
A. MỘT SỐ DẠNG TOÁN THƯỜNG GẶP
I) QUY TẮC CỘNG VÀ QUY TẮC NHÂN:
Бай 1: Với cac chữ số 1, 2, 3, 4, 5 có thể lập được bao nhiêu:
1) Số lẻ gồm 4 chữ số khác nhau?
2) Số chẵn gồm 4 chữ số bất kỳ?
Bài 2: Có 4 con ường nối liền điểm a và điểm b, có 3 con ường nối liền điểm b và điểm c. ta muốn đi từ a ến c qua b, rồi từ c trở về o cũng bao nhiêu cách chọn lộ trình đi và về nếu ta không muốn dùng đường đi làm đường về trên cả hai chặng AB và BC?
Bài 3: Có 5 miếng bìa, trên mỗi miếng ghi một trong 5 chữ Số 0, 1, 2, 3, 4. lấy 3 miếng bìa này ặt lần lượt cạnh nhau từ từ trái sang phải ể ược cá ghm nhau từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ ố ượ ượ ượ ố gồ gồ nhau từ ể ặ ượ ượ ượ ượ ượ ố gồ gồ gồ Hỏi có thể lập được bao nhiêu số có nghia gồm 3 chữ số và trong đó có bao nhiêu số chẵn?
Bài 4: CHO 8 CHữ Số 0, 1, 2, 3, 4, 5, 6, 7. Từ 8 CHữ Số TRên Có Thể lập ược bao nhiêu số, mỗi số gồm 4 chữ sốô một khác nhau và khy chia hết чо 10.
Бай 5: Một người có 6 cái áo, trong đó có 3 áo sọc và 3 áo trắng; có 5 quần, trong đó có 2 quần đen; và có 3 đôi giày, trong đó có 2 đôi giầy đen. Hỏi người đó có bao nhiêu … trong khai triển của biểu thức sau thành đa thức:
е (х) =
Bài 8: Trong khai triển của thành đa thức:
P (x) = Hãy tìm hệ số ak lớn nhất (0 £ k £ 10)
Бай 9: Тим Со Нгуен Дон Сан Сан Чо: .
ta muốn đi từ a ến c qua b, rồi từ c trở về o cũng bao nhiêu cách chọn lộ trình đi và về nếu ta không muốn dùng đường đi làm đường về trên cả hai chặng AB và BC?
Bài 3: Có 5 miếng bìa, trên mỗi miếng ghi một trong 5 chữ Số 0, 1, 2, 3, 4. lấy 3 miếng bìa này ặt lần lượt cạnh nhau từ từ trái sang phải ể ược cá ghm nhau từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ từ ố ượ ượ ượ ố gồ gồ nhau từ ể ặ ượ ượ ượ ượ ượ ố gồ gồ gồ Hỏi có thể lập được bao nhiêu số có nghia gồm 3 chữ số và trong đó có bao nhiêu số chẵn?
Bài 4: CHO 8 CHữ Số 0, 1, 2, 3, 4, 5, 6, 7. Từ 8 CHữ Số TRên Có Thể lập ược bao nhiêu số, mỗi số gồm 4 chữ sốô một khác nhau và khy chia hết чо 10.
Бай 5: Một người có 6 cái áo, trong đó có 3 áo sọc và 3 áo trắng; có 5 quần, trong đó có 2 quần đen; và có 3 đôi giày, trong đó có 2 đôi giầy đen. Hỏi người đó có bao nhiêu … trong khai triển của biểu thức sau thành đa thức:
е (х) =
Bài 8: Trong khai triển của thành đa thức:
P (x) = Hãy tìm hệ số ak lớn nhất (0 £ k £ 10)
Бай 9: Тим Со Нгуен Дон Сан Сан Чо: . Бай 10: CMR:
Бай 11: Với mỗi n la số tự nhiên, hay tính tổng:
1)
2)
Bài 12: Cho đa thức P(x) = (3x — 2)10
1) Tìm hệ số của x2 trong khai triển trên của P(x)
2) Tính tổng của cac hệ số trong khai triển trên của P(x)
Bài 13: Biết tổng tất cả cá hệ số của khai triển nhị thức: bằng 1024 hãm tìm hệ số a (a là số tự nhiên) của số hạng a.x12 trong khai triển đ đ.
Bài 14: Trong khai triển nhị thức: hay tìm số hạng không phụ thuộc vào x biết rằng:
Bài15: Чонг Минь:
Bài 16: Tìm số hạng khong chứa x trong khai triển của biểu thức: x ¹ 0
Бай 17: Khai triển nhị thức:
Biết rằng trong khai triển đó và số hạng thứ tư bằng 20n, tìm n và x
Bài 18: Trong khai triển: Tìm số hạng chứa a, b có số mũ bằng nhau.
B. BÀI TẬP TỰ LUYỆN
Bài 1. Với cac chữ số 0,1,2,3,4,5, có thể lập được bào nhiêu số có 5 chữ số khac nhau?
Bài 2. Dùng 5 chữ số 2,3,4,6,8 để viết thành số gồm 5 chữ số khac nhau. Хай:
а. Bắt dầu bởi chữ số 2.
б. Bắt đầu bởi chữ số 36
в. Bắt đầu bởi chữ số 482
Bài 3. Dùng 6 chữ số 1,2,3,4,5,6 để viết thành số tự nhiên gồm 4 chữ số khac nhau.
Бай 10: CMR:
Бай 11: Với mỗi n la số tự nhiên, hay tính tổng:
1)
2)
Bài 12: Cho đa thức P(x) = (3x — 2)10
1) Tìm hệ số của x2 trong khai triển trên của P(x)
2) Tính tổng của cac hệ số trong khai triển trên của P(x)
Bài 13: Biết tổng tất cả cá hệ số của khai triển nhị thức: bằng 1024 hãm tìm hệ số a (a là số tự nhiên) của số hạng a.x12 trong khai triển đ đ.
Bài 14: Trong khai triển nhị thức: hay tìm số hạng không phụ thuộc vào x biết rằng:
Bài15: Чонг Минь:
Bài 16: Tìm số hạng khong chứa x trong khai triển của biểu thức: x ¹ 0
Бай 17: Khai triển nhị thức:
Biết rằng trong khai triển đó và số hạng thứ tư bằng 20n, tìm n và x
Bài 18: Trong khai triển: Tìm số hạng chứa a, b có số mũ bằng nhau.
B. BÀI TẬP TỰ LUYỆN
Bài 1. Với cac chữ số 0,1,2,3,4,5, có thể lập được bào nhiêu số có 5 chữ số khac nhau?
Bài 2. Dùng 5 chữ số 2,3,4,6,8 để viết thành số gồm 5 chữ số khac nhau. Хай:
а. Bắt dầu bởi chữ số 2.
б. Bắt đầu bởi chữ số 36
в. Bắt đầu bởi chữ số 482
Bài 3. Dùng 6 chữ số 1,2,3,4,5,6 để viết thành số tự nhiên gồm 4 chữ số khac nhau. Хай:
а. Có bao nhiêu số như vậy
б. Có bao nhiêu số bắt đầu bởi chữ số 1
Бай 4. Чо 8 чу со 0,1,2,3,4,5,6,7. Hỏi có thể lập được bao nhiêu số có 6 chữ số khac nhau trong đó nhất thiết phai có mặt chữ số 4.
Bài 5. Với cac chữ số 0,1,2,3,4,5,6 có thể lập được bao nhiêu số có 5 chữ số khac nhau trong đó nhất thiếs 5.ải cóố
Бай 6. Từ cac chữ số 1,2,3,4,5,6,7,8,9thiết lập tất cả cac số có 9 chữ số khac nhau. Hỏi trong cac số thiết lập được có bao nhiêu số mà chữ số 9 ng chính giữa.
Бай 7. Чо A = {0,1,2,3,4,5} có thể lập được bao nhiêu số chẵn, mỗi số có 4 chữ số khac nhau.
Бай 8.
а. Từ cac chữ số 4,5,6,7 có thể lập được bao nhiêu số có cac chữ số phân biệt.
б. Từ cac chữ số 0,1,2,3,4,5 có thể lập được bao nhiêu số chẵn gồm 5 chữ số đôi một khac nhau?
Бай 9. Чо тэп E = {0,1,2,3,4,5,6,7,8,9}
Hỏi có bao nhiêu số tự nhiên gồm 5 chữ số khac nhau chia hết cho 5?
Бай 10. Một tập thể gồm 14 người gồm 6 nam và 8 nữ, người ta muốn chọn 1 tổ cong tác gồm 6 người. Тим số cách chọn sao cho trong tổ phai có cả nam và nữ?
Bài 11.
Хай:
а. Có bao nhiêu số như vậy
б. Có bao nhiêu số bắt đầu bởi chữ số 1
Бай 4. Чо 8 чу со 0,1,2,3,4,5,6,7. Hỏi có thể lập được bao nhiêu số có 6 chữ số khac nhau trong đó nhất thiết phai có mặt chữ số 4.
Bài 5. Với cac chữ số 0,1,2,3,4,5,6 có thể lập được bao nhiêu số có 5 chữ số khac nhau trong đó nhất thiếs 5.ải cóố
Бай 6. Từ cac chữ số 1,2,3,4,5,6,7,8,9thiết lập tất cả cac số có 9 chữ số khac nhau. Hỏi trong cac số thiết lập được có bao nhiêu số mà chữ số 9 ng chính giữa.
Бай 7. Чо A = {0,1,2,3,4,5} có thể lập được bao nhiêu số chẵn, mỗi số có 4 chữ số khac nhau.
Бай 8.
а. Từ cac chữ số 4,5,6,7 có thể lập được bao nhiêu số có cac chữ số phân biệt.
б. Từ cac chữ số 0,1,2,3,4,5 có thể lập được bao nhiêu số chẵn gồm 5 chữ số đôi một khac nhau?
Бай 9. Чо тэп E = {0,1,2,3,4,5,6,7,8,9}
Hỏi có bao nhiêu số tự nhiên gồm 5 chữ số khac nhau chia hết cho 5?
Бай 10. Một tập thể gồm 14 người gồm 6 nam và 8 nữ, người ta muốn chọn 1 tổ cong tác gồm 6 người. Тим số cách chọn sao cho trong tổ phai có cả nam và nữ?
Bài 11. Một nhóm học sinh gồm 10 người, trong đó có 7 nam và 3 nữ. Hỏi có bao nhiêu cách xếp 10 hoc sinh trên thành 1 hàng dọc sao cho 7 học sinh nam phai đứng liền nhau?
Bài 12. Có một hộp đựng 2 viên bi đỏ, 3 vien bi trắng, 5 viên bi vàng. Chon ngẫu nhiên 4 viên bi lấy từ hộp đó.
Hỏi có bao nhiêu cách chọn để trong số viên bi lấy ra không đủ 3 màu?
Bài 13. Một lớp có 20 học sinh trong đó có 2 can bộ lớp. Hỏi có bao nhiêu cách cử 3 người đi dự hội nghị sinh viên của trường sao cho trong 3 người có it nhất một can bộ lớp?
Bài 14. Một đội văn Nghệ có 20 người trong đó có 10 nam và 10 nữ. Hỏi có bao nhiêu cách chọn ra 5 người sao cho:
1. Có đúng 2 người nam trong 5 người đó
2. Có ít nhất 2 nam và ít nhất 1 nữ trong 5 người đó
Bài 15. Có 5 nhà Toán học nam, 3 nhà Toán học nữ và 4 nhà Vật lý nam. Lập một oàn công tác cần có cả nam và nữ, cần có cả nhà Toán học và nhà Vật lý. Hỏi có bao nhiêu cách?
Bài 16. Một lớp học có 30 học sinh nam và 15 học sinh nữ. Có 6 học sinh được chọ ra để lập một tốp ок.
Một nhóm học sinh gồm 10 người, trong đó có 7 nam và 3 nữ. Hỏi có bao nhiêu cách xếp 10 hoc sinh trên thành 1 hàng dọc sao cho 7 học sinh nam phai đứng liền nhau?
Bài 12. Có một hộp đựng 2 viên bi đỏ, 3 vien bi trắng, 5 viên bi vàng. Chon ngẫu nhiên 4 viên bi lấy từ hộp đó.
Hỏi có bao nhiêu cách chọn để trong số viên bi lấy ra không đủ 3 màu?
Bài 13. Một lớp có 20 học sinh trong đó có 2 can bộ lớp. Hỏi có bao nhiêu cách cử 3 người đi dự hội nghị sinh viên của trường sao cho trong 3 người có it nhất một can bộ lớp?
Bài 14. Một đội văn Nghệ có 20 người trong đó có 10 nam và 10 nữ. Hỏi có bao nhiêu cách chọn ra 5 người sao cho:
1. Có đúng 2 người nam trong 5 người đó
2. Có ít nhất 2 nam và ít nhất 1 nữ trong 5 người đó
Bài 15. Có 5 nhà Toán học nam, 3 nhà Toán học nữ và 4 nhà Vật lý nam. Lập một oàn công tác cần có cả nam và nữ, cần có cả nhà Toán học và nhà Vật lý. Hỏi có bao nhiêu cách?
Bài 16. Một lớp học có 30 học sinh nam và 15 học sinh nữ. Có 6 học sinh được chọ ra để lập một tốp ок.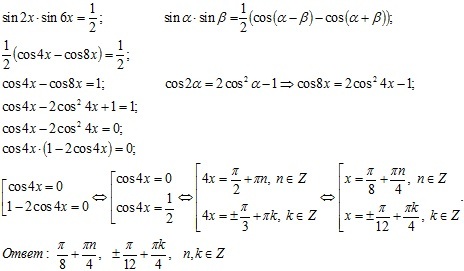 Hỏi có bao nhiêu cách chọn khac nhau.
1. Nếu phải có ít nhất 2 nữ.
2. Nếu phải chọn tuỳ ý.
Bài 17. Một tổ học sinh gồm 7 nam và 4 nữ. Giáo viên muốn chọn 3 học sinh xếp vào bàn ghế của lớp, trong đó có it nhất 1 nam. Hỏi có bao nhiêu cách chọn?
Бай 18. Чонг Минь Ронг:
.
Бай 19. Чон Минь Ронг:
Бай 20. Với n la số nguyên dương, chứng minh hệ thức sau:
Бай 21. Чон Минь Ронг:
Бай 22. Тинь Тонг:
Бай 23. Тинь Тонг:
Бай 24. Чон Минь Ронг:
Bài 25. Cho n la một số nguyên dương:
а. Тинь: я =
б. Тинь Тонг:
Bài 26. Тим Со Нгуен Дуонг Н Сао Чо:
Бай 27. Тим Со Нгуен Донг Н Сао Чо:
Бай 28. Тим Со Ту Нхиен н Тхао Ман Донг Тхок Сау:
Бай 29. Тинь Тонг:
,
бит ронг, вой н ла со нгуен дунг:
Bài 30. Тим Со Нгуен Дуонг Н Сао Чо:
Бай 31. Тим Хо Со Куа x8 trong khai triển thành đa thức của:
Бай 32. Gọi a3n — 3 là hệ số của x3n — 3 trong khai triển thanh đa thức của: (x2 + 1) n (x + 2) n.
Тим н để a3n — 3 = 26n
Бай 33. Тим Хо Со Куа Со Хунг Чуа x26 Чонг Кхай Триен Нхо Тхок Ньютон Куа
Биет ринг:
Bài 34.
Hỏi có bao nhiêu cách chọn khac nhau.
1. Nếu phải có ít nhất 2 nữ.
2. Nếu phải chọn tuỳ ý.
Bài 17. Một tổ học sinh gồm 7 nam và 4 nữ. Giáo viên muốn chọn 3 học sinh xếp vào bàn ghế của lớp, trong đó có it nhất 1 nam. Hỏi có bao nhiêu cách chọn?
Бай 18. Чонг Минь Ронг:
.
Бай 19. Чон Минь Ронг:
Бай 20. Với n la số nguyên dương, chứng minh hệ thức sau:
Бай 21. Чон Минь Ронг:
Бай 22. Тинь Тонг:
Бай 23. Тинь Тонг:
Бай 24. Чон Минь Ронг:
Bài 25. Cho n la một số nguyên dương:
а. Тинь: я =
б. Тинь Тонг:
Bài 26. Тим Со Нгуен Дуонг Н Сао Чо:
Бай 27. Тим Со Нгуен Донг Н Сао Чо:
Бай 28. Тим Со Ту Нхиен н Тхао Ман Донг Тхок Сау:
Бай 29. Тинь Тонг:
,
бит ронг, вой н ла со нгуен дунг:
Bài 30. Тим Со Нгуен Дуонг Н Сао Чо:
Бай 31. Тим Хо Со Куа x8 trong khai triển thành đa thức của:
Бай 32. Gọi a3n — 3 là hệ số của x3n — 3 trong khai triển thanh đa thức của: (x2 + 1) n (x + 2) n.
Тим н để a3n — 3 = 26n
Бай 33. Тим Хо Со Куа Со Хунг Чуа x26 Чонг Кхай Триен Нхо Тхок Ньютон Куа
Биет ринг:
Bài 34. Тим cac số hạng khong chứa x trong khai triển nhị thức Newton của:
với х > 0
Бай 35. Тим Сон Хонг Тхо 7 Чонг Кхай Трюн Нхо Тхок:
;
Бай 36. Чо:
Sau khi khai triên và rút gọn thì biểu thức A sẽ gồm bao nhiêu số hạng?
Бай 37. Тим Хо Со Куа Со Хонг Чуа x8 Чонг Кхай Триен Нхо Тхок Ньютон Куа
, бит ринг:
Bài 38. khai triển biểu thức (1–2x)n ta được đa thức có dạng:
.
Tỡm hệ số của, biet ao+a1+a2 = 71
Бай 39. Тим Хо Со Куа x5 Чонг Кхай Триен Да Тхок:
Бай 40. Тим Сой Хонг Кхонг Чоа х Чонг Кхай Трюн Нхо Тхок
Биет ринг:
Бай 41. Giải cac phương trình:
Бай 42. Giải cac hệ phương trình:
Бай 43. Giải cac bất phương trình:
CHUYÊN 3. PHƯƠNG PHÁP QUY NẠP TOÁN HỌC
Бай 1. Чонг Минь Ронг
а) 1,2 + 2,5 + 3,8 + … + n(3n — 1) = n2(n + 1) với n Î N*
б) 3 + 9 + 27 + … + 3n = (3n + 1 — 3) với n Î N*
в) 12 + 32 + 52 + … + (2n — 1)2 = với n Î N*
г) 13 + 23 + 33 + … + n3 = với n Î N*
д) 12 + 22 + 32 + … + n2 = với n Î N*
е) với n Î N*
ж) với n Î N*
h) với n Î N*
и) với n ³ 2
k) với n Î N*
Бай 2.
Тим cac số hạng khong chứa x trong khai triển nhị thức Newton của:
với х > 0
Бай 35. Тим Сон Хонг Тхо 7 Чонг Кхай Трюн Нхо Тхок:
;
Бай 36. Чо:
Sau khi khai triên và rút gọn thì biểu thức A sẽ gồm bao nhiêu số hạng?
Бай 37. Тим Хо Со Куа Со Хонг Чуа x8 Чонг Кхай Триен Нхо Тхок Ньютон Куа
, бит ринг:
Bài 38. khai triển biểu thức (1–2x)n ta được đa thức có dạng:
.
Tỡm hệ số của, biet ao+a1+a2 = 71
Бай 39. Тим Хо Со Куа x5 Чонг Кхай Триен Да Тхок:
Бай 40. Тим Сой Хонг Кхонг Чоа х Чонг Кхай Трюн Нхо Тхок
Биет ринг:
Бай 41. Giải cac phương trình:
Бай 42. Giải cac hệ phương trình:
Бай 43. Giải cac bất phương trình:
CHUYÊN 3. PHƯƠNG PHÁP QUY NẠP TOÁN HỌC
Бай 1. Чонг Минь Ронг
а) 1,2 + 2,5 + 3,8 + … + n(3n — 1) = n2(n + 1) với n Î N*
б) 3 + 9 + 27 + … + 3n = (3n + 1 — 3) với n Î N*
в) 12 + 32 + 52 + … + (2n — 1)2 = với n Î N*
г) 13 + 23 + 33 + … + n3 = với n Î N*
д) 12 + 22 + 32 + … + n2 = với n Î N*
е) với n Î N*
ж) với n Î N*
h) với n Î N*
и) với n ³ 2
k) với n Î N*
Бай 2. Chứng minh rằng với mọi n Î N * ta có:
а) n3 + 2n чиа хот чо 3
б) n3 + (n + 1)3 + (n + 2)3 чиа хэт чо 9c) n3 + 11n чиа хот чо 6
г) 2н3 — 3н2 + н чиа хэт чо 6
д) 4н + 15н — 1 чиа хэт чо 9
е) 32н + 1 + 2н + 2 чиа хот чо 7
g) n7 — n chia hết cho 7
з) н3 + 3н2 + 5н чиа хот чо 3
Бай 3. Chứng minh cac bất đẳng thức sau
а) 2n + 2 > 2n + 5 với n Î N*
б) 2n > 2n + 1 với n Î N*, n ³ 3
в) 3n > n2 + 4n + 5 với n Î N*, n ³ 3
г) 2н — 3 > 3н — 1 với н ³ 8
д) 3n — 1 > n(n + 2) với n ³ 4
ЧУЕН № 4: ДАЙ СЫ
Dạng 1. Xac định một số số hạng của dãy số. Xac định số hạng tổng quat
Bài 1. Viết 5 số hạng đầu của dãy số sau:
а) ун = б) ун =
б) (n > 2) в) ип =
г) (với k ³ 1) д) u1 = 2; не + 1 = (не + 1)
g) un = cos h) nsin + n2cos
Bài 2. Tìm số hạng tổng quat của dãy số
а) (и): 1; 2; 4; 8; 16;
б) (не): ;
c) (un): (với n ³ 1)
г) (не): ;
Bài 3. Cho dãy số (un): u1 = , un+ 1 = 4un + 7 với n ³ 1
а) Тинь и2, и3, и4, и5, и6
б) Chứng minh rằng: un = với n ³ 1
Bài 4. Cho dãy số (un): u1 = 1; ип + 1 = ип + 7 với ³ 1
а) Тинь и2, и3, и4, и5, и6
б) Chứng minh rằng: un = 7n – 6
Бай 5.
Chứng minh rằng với mọi n Î N * ta có:
а) n3 + 2n чиа хот чо 3
б) n3 + (n + 1)3 + (n + 2)3 чиа хэт чо 9c) n3 + 11n чиа хот чо 6
г) 2н3 — 3н2 + н чиа хэт чо 6
д) 4н + 15н — 1 чиа хэт чо 9
е) 32н + 1 + 2н + 2 чиа хот чо 7
g) n7 — n chia hết cho 7
з) н3 + 3н2 + 5н чиа хот чо 3
Бай 3. Chứng minh cac bất đẳng thức sau
а) 2n + 2 > 2n + 5 với n Î N*
б) 2n > 2n + 1 với n Î N*, n ³ 3
в) 3n > n2 + 4n + 5 với n Î N*, n ³ 3
г) 2н — 3 > 3н — 1 với н ³ 8
д) 3n — 1 > n(n + 2) với n ³ 4
ЧУЕН № 4: ДАЙ СЫ
Dạng 1. Xac định một số số hạng của dãy số. Xac định số hạng tổng quat
Bài 1. Viết 5 số hạng đầu của dãy số sau:
а) ун = б) ун =
б) (n > 2) в) ип =
г) (với k ³ 1) д) u1 = 2; не + 1 = (не + 1)
g) un = cos h) nsin + n2cos
Bài 2. Tìm số hạng tổng quat của dãy số
а) (и): 1; 2; 4; 8; 16;
б) (не): ;
c) (un): (với n ³ 1)
г) (не): ;
Bài 3. Cho dãy số (un): u1 = , un+ 1 = 4un + 7 với n ³ 1
а) Тинь и2, и3, и4, и5, и6
б) Chứng minh rằng: un = với n ³ 1
Bài 4. Cho dãy số (un): u1 = 1; ип + 1 = ип + 7 với ³ 1
а) Тинь и2, и3, и4, и5, и6
б) Chứng minh rằng: un = 7n – 6
Бай 5. Чо (ун): и1 = 2; ип + 1 = 3ун + 2н – 1
Чонг Минь Ронг: un = 3n — n
Dạng 2. Xét tính đơn điệu của một dãy số
Бай 6. Xét tính đơn điệu của cac dãy số sau
а) ип = ; б) ип = в) ип =
г) ип = д) ип = е) ип =
г) ип = з) ип =
Dạng 4. Xét tính bị chặn của dãy số
Бай 7. Xét tính bị chặn của cac dãy số
а) ип = 2п – 1 б) ип = в) ип = 3,22п – 1
г) ип = д) ип = е) ип =
BÀI TẬP TỰ LUYỆN
Bài 1. Тим cac giới hạn sau:
Bài 2. Тим cac giới hạn sau:
Bài 3. Тим cac giới hạn sau:
Bài 4. Тим cac giới hạn sau:
Bài 5. Тим cac giới hạn sau:
1. 2.
5. лим
Bài 6 Tim các giới hạn sau:
2.
3. 4.
6. 6.
ЧУИН № 5 . GIỚI HẠN CỦA HAM SỐ
Бай 1: Тим cac giới hạn sau (dạng):
1) 2)
3) 4)
5) 6)
7) 8)
Бай 2. Тим cac giới hạn sau (dạng):
1) 2)
3) 4)
5) 6)
7) 8)
9) 10)
11) 12)
13) 14)
15)
Бай 3. Тим cac giới hạn (dạng):
1) 2)
3) 4)
5) 6)
7) 8)
Bài 4. Тим cac giới hạn (dạng):
1) 2)
3) 4)
5) 6)
Bài 5. Tìm các giới hạn (¥ — ¥):
1) 2)
3) 4)
5) 6)
7) 8)
ЧУЕН ĐỀ 6. ĐẠO HAM
I. Тинь До Хам Бонг Дон Нгхиа
Bài 1.
Чо (ун): и1 = 2; ип + 1 = 3ун + 2н – 1
Чонг Минь Ронг: un = 3n — n
Dạng 2. Xét tính đơn điệu của một dãy số
Бай 6. Xét tính đơn điệu của cac dãy số sau
а) ип = ; б) ип = в) ип =
г) ип = д) ип = е) ип =
г) ип = з) ип =
Dạng 4. Xét tính bị chặn của dãy số
Бай 7. Xét tính bị chặn của cac dãy số
а) ип = 2п – 1 б) ип = в) ип = 3,22п – 1
г) ип = д) ип = е) ип =
BÀI TẬP TỰ LUYỆN
Bài 1. Тим cac giới hạn sau:
Bài 2. Тим cac giới hạn sau:
Bài 3. Тим cac giới hạn sau:
Bài 4. Тим cac giới hạn sau:
Bài 5. Тим cac giới hạn sau:
1. 2.
5. лим
Bài 6 Tim các giới hạn sau:
2.
3. 4.
6. 6.
ЧУИН № 5 . GIỚI HẠN CỦA HAM SỐ
Бай 1: Тим cac giới hạn sau (dạng):
1) 2)
3) 4)
5) 6)
7) 8)
Бай 2. Тим cac giới hạn sau (dạng):
1) 2)
3) 4)
5) 6)
7) 8)
9) 10)
11) 12)
13) 14)
15)
Бай 3. Тим cac giới hạn (dạng):
1) 2)
3) 4)
5) 6)
7) 8)
Bài 4. Тим cac giới hạn (dạng):
1) 2)
3) 4)
5) 6)
Bài 5. Tìm các giới hạn (¥ — ¥):
1) 2)
3) 4)
5) 6)
7) 8)
ЧУЕН ĐỀ 6. ĐẠO HAM
I. Тинь До Хам Бонг Дон Нгхиа
Bài 1. Dùng định nghĩa tính đạo ham của cac ham số sau tại cac điểm:
1) f(x) = 2×2 + 3x + 1, т.е. x = 1
2) f(x) = sinx tại x =
3) f(x) = tại x = 1
4) f(x) = tại x = 0
5) f(x) = tại x = 2
6) f(x) = tại x = 0
7) f(x) = tại x = 0
8) f(x) = tại x = 0
Bài 2. Dùng định nghĩa tính đạo ham của cac ham số sau:
1) у = 5х – 7 2) у = 3х2 – 4х + 93) у = 4) у =
5) у = х3 + 3х – 5 6) у = + х
II. Quan hệ giữa tính liên tục và sự có đạo ham
Бай 3. Чо хам со f (x) =
Chứng minh rằng ham số liên tục trên R nhưng không có đạo ham tại x = 0.
Bài 4. Cho ham số f(x) =
1) Chứng minh rằng ham số liên tục trên R
2) Hàm số có đạo ham tại x = 0 không? Tại sao?.
Бай 5. Чо хам со f (x) =
Tìm a, b để хам số có đạo хам tại x = 1
Бай 6. Чо хам со f (x) =
Tìm a, b để хам số có đạo хам tại x = 0
Бай 7. Чо хам со f (x) =
Tìm a để ham số không có đạo ham tại x = 3.
III. Тинь До Хам Бонг Конг Тхок:
Bài 8. Tính đạo ham của cac ham số sau:
1) у = х3 – 2х2 + 3х 2) у = — х4 + 2х2 + 3
3) у = (х2 + 1)(3 – 2х2) 4) у = (х – 1)(х – 2)(х – 3)
5) у = (х2 + 3)5 6) у = х(х + 2)4
7) у = 2х3 – 9х2 + 12х – 4 8) у = (х2 + 1)(х3 + 1)2(х4 + 1)3
Bài 9.
Dùng định nghĩa tính đạo ham của cac ham số sau tại cac điểm:
1) f(x) = 2×2 + 3x + 1, т.е. x = 1
2) f(x) = sinx tại x =
3) f(x) = tại x = 1
4) f(x) = tại x = 0
5) f(x) = tại x = 2
6) f(x) = tại x = 0
7) f(x) = tại x = 0
8) f(x) = tại x = 0
Bài 2. Dùng định nghĩa tính đạo ham của cac ham số sau:
1) у = 5х – 7 2) у = 3х2 – 4х + 93) у = 4) у =
5) у = х3 + 3х – 5 6) у = + х
II. Quan hệ giữa tính liên tục và sự có đạo ham
Бай 3. Чо хам со f (x) =
Chứng minh rằng ham số liên tục trên R nhưng không có đạo ham tại x = 0.
Bài 4. Cho ham số f(x) =
1) Chứng minh rằng ham số liên tục trên R
2) Hàm số có đạo ham tại x = 0 không? Tại sao?.
Бай 5. Чо хам со f (x) =
Tìm a, b để хам số có đạo хам tại x = 1
Бай 6. Чо хам со f (x) =
Tìm a, b để хам số có đạo хам tại x = 0
Бай 7. Чо хам со f (x) =
Tìm a để ham số không có đạo ham tại x = 3.
III. Тинь До Хам Бонг Конг Тхок:
Bài 8. Tính đạo ham của cac ham số sau:
1) у = х3 – 2х2 + 3х 2) у = — х4 + 2х2 + 3
3) у = (х2 + 1)(3 – 2х2) 4) у = (х – 1)(х – 2)(х – 3)
5) у = (х2 + 3)5 6) у = х(х + 2)4
7) у = 2х3 – 9х2 + 12х – 4 8) у = (х2 + 1)(х3 + 1)2(х4 + 1)3
Bài 9. Tính đạo ham của các ham số sau :
1) у = 2) у =
3) у = 4) у =
5) у = 6) у =
7) у = 8) у =
Bài 10. Tính đạo ham của cac ham số sau:
1) у = 2) у =
3) у = (х – 2) 4) у =
5) у = 6) у = х +
7) у = 8) у = +
III. Viết phương trình tiep tuyến của dồ thị tại một điểm
Бай 11. Чо хам су y = x3 — 2×2 + 3x (C)
1) Viết phương trình tiếp tuyến D với đồ thị (C) tại điểm có hoành độ là x = 2.
2) Chứng minh rằng D la tiếp tuyến có hệ số góc nhỏ nhất
Бай 12. Чо хам су у = -x3 + 3x + 1 (C)
1) Viết phương trình tiếp tuyến D của (C) tại điểm có hành độ là x = 0
2) Chứng minh rằng tiếp tuyến D là tiếp tuyến của (C) có hệ số góc lớn nhất.
Бай 13.
1) Viết phương trình tiếp tuyến với đồ thị của hs: y = x3 – 3×2 + 2 tại điểm (-1; -2)
2) Viết phương trình tiếp tuyến với đồ thị của ham số y = tại điểm có hoành độ x = 0
IV. Viết phương trình tiep tuyến của đồ thị (C) khi biết hệ số góc k.
Бай 14.
1) Viết phương trình tiep tuyến với đồ thị của ham số y = biết hệ số góc của tiếp tuyến là.
2) Viết phương trình tiếp tuyến với đồ thị của ham số y = x2 – 2x = 3 бит:
а) Tiếp tuyến song với đường thẳng 4x – 2y + 5 = 0
б) Tiếp tuyến vuông góc với đường thẳng x + 4y = 0
Бай 15.
Tính đạo ham của các ham số sau :
1) у = 2) у =
3) у = 4) у =
5) у = 6) у =
7) у = 8) у =
Bài 10. Tính đạo ham của cac ham số sau:
1) у = 2) у =
3) у = (х – 2) 4) у =
5) у = 6) у = х +
7) у = 8) у = +
III. Viết phương trình tiep tuyến của dồ thị tại một điểm
Бай 11. Чо хам су y = x3 — 2×2 + 3x (C)
1) Viết phương trình tiếp tuyến D với đồ thị (C) tại điểm có hoành độ là x = 2.
2) Chứng minh rằng D la tiếp tuyến có hệ số góc nhỏ nhất
Бай 12. Чо хам су у = -x3 + 3x + 1 (C)
1) Viết phương trình tiếp tuyến D của (C) tại điểm có hành độ là x = 0
2) Chứng minh rằng tiếp tuyến D là tiếp tuyến của (C) có hệ số góc lớn nhất.
Бай 13.
1) Viết phương trình tiếp tuyến với đồ thị của hs: y = x3 – 3×2 + 2 tại điểm (-1; -2)
2) Viết phương trình tiếp tuyến với đồ thị của ham số y = tại điểm có hoành độ x = 0
IV. Viết phương trình tiep tuyến của đồ thị (C) khi biết hệ số góc k.
Бай 14.
1) Viết phương trình tiep tuyến với đồ thị của ham số y = biết hệ số góc của tiếp tuyến là.
2) Viết phương trình tiếp tuyến với đồ thị của ham số y = x2 – 2x = 3 бит:
а) Tiếp tuyến song với đường thẳng 4x – 2y + 5 = 0
б) Tiếp tuyến vuông góc với đường thẳng x + 4y = 0
Бай 15.
