Тест Площадь параллелограмма (8 класс) по теме геометрии
Последний раз тест пройден 24 часа назад.
Для учителя
Вопрос 1 из 10
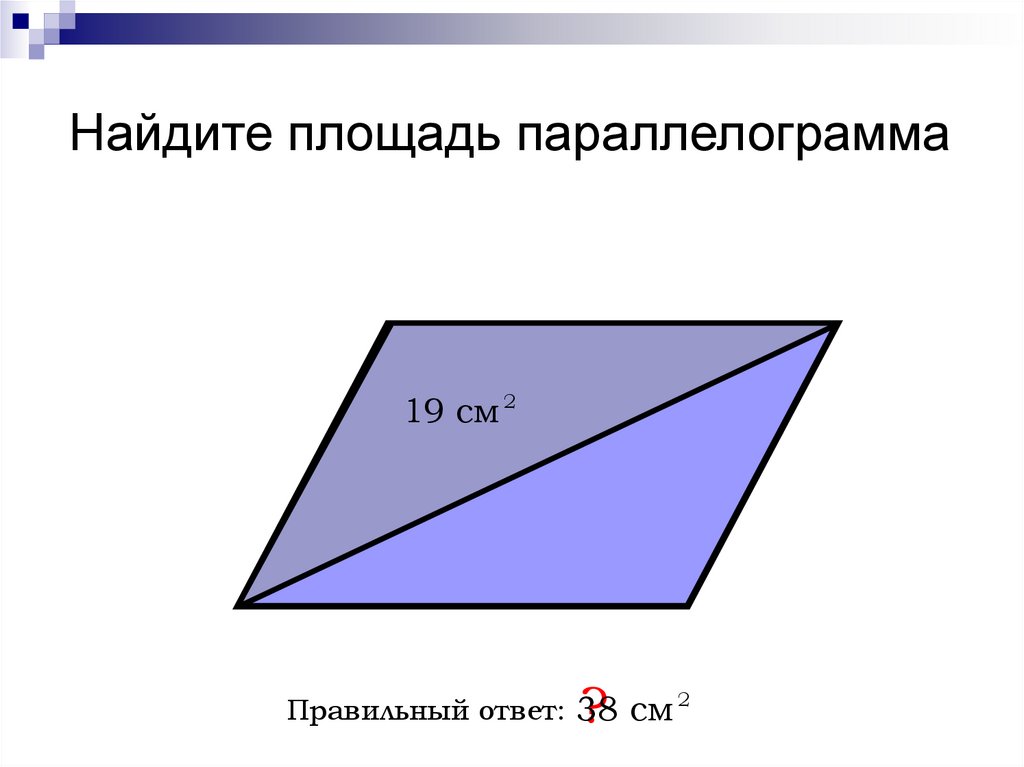
Стороны параллелограмма равны 10 см и 6 см, а угол между этими сторонами равен 150°. Чему равна площадь этого параллелограмма?
60 см2
30 см2
35 см2
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 2 из 10
Найдите площадь ромба, если его диагонали равны 4 и 12
12 см2
30 см2
24 см2
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 3 из 10
Площадь параллелограмма ABCD равна 189 см
2. Точка Е середина стороны AD. Найдите площадь трапеции AECB
Точка Е середина стороны AD. Найдите площадь трапеции AECB141,75 см2
110, 5 см2
118,2 см2
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 4 из 10
Найдите площадь ромба, если его стороны равны 1 см, а один из углов равен 150°
0,5 см2
1,5 см2
2 см2
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 5 из 10
Площадь параллелограмма ABCD равна 153 см
2. Найдите площадь параллелограмма A′B′C′D′, вершинами которого являются середины сторон данного параллелограмма80,5 см2
76,5 см2
63,2 см2
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 6 из 10
Найдите площадь параллелограмма, если две его стороны равны 8 и 10, а угол между ними равен 30°
30 см2
-
40 см2
60 см2
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 7 из 10
Параллелограмм и прямоугольник имеют одинаковые стороны.
 Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника
Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника60°
30°
50°
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 8 из 10
Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма
8
12
6
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 9 из 10
Высоты, проведенные из вершины тупого угла параллелограмма, составляют угол, равный 45°. Одна из высот делит сторону, на которую она опущена, на отрезки 3 см и 7 см, считая от вершины острого угла. Найдите площадь параллелограмма.
40 см2
20 см2
30 см2
Неправильный ответ
В вопросе ошибка?
Вопрос 10 из 10
Найдите площадь ромба, если его высота равна 2, а острый угол 30°
12
8
20
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Доска почёта
Чтобы попасть сюда — пройдите тест.
Иван Петров
8/10
Павел Аверьянов
10/10
Тест по теме «Площадь параллелограмма» соответствует министерской программе. Он предназначен для учеников среднего звена, которым нужно быстро оценить и закрепить выученный материал. Большинство вопросов подборки – задач разного уровня сложности. Для их решения нужно знать формулы, теоремы, законы этого и некоторых предыдущих разделов, уметь использовать теорию. Для удобства к вопросам открыт онлайн доступ, просматривать их можно с любого устройства.
Тест «Площадь параллелограмма» (8 класс) целесообразно использовать в процессе подготовки к текущим и проверочным занятиям, так как это один из лучших способов разложить материал «по полочкам».
Рейтинг теста
4.1
Средняя оценка: 4.1
Всего получено оценок: 285.
А какую оценку получите вы? Чтобы узнать — пройдите тест.
Четырехсторонняя геометрия Трапециевидный многоугольник Внутренний угол, неправильные линии, угол, текст, прямоугольник png
Четырехсторонняя геометрия Трапециевидный многоугольник Внутренний угол, неправильные линии, угол, текст, прямоугольник pngтеги
- угол,
- текст,
- прямоугольник,
- треугольник,
- многоугольник,
- число,
- форма,
- религия,
- ромб,
- неправильные линии,
- квадрат,
- трапеция,
- четырехугольник,
- параллелограмм,
- бумага,
- площадь,
- бренд,
- диаграмма,
- край,
- геометрия,
- внутренний угол,
- змей,
- линия,
- математика,
- вершина,
- png,
- прозрачный,
- бесплатная загрузка
Об этом PNG
- Размер изображения
- 1600x774px
- Размер файла
- 120.
 52KB
52KB - MIME тип
- Image/png
изменить размер PNG
ширина(px)
высота(px)
Лицензия
Некоммерческое использование, DMCA Contact Us
- прямоугольная зеленая иллюстрация, четырехугольная форма параллелограмма ромб, форма, угол, текст, прямоугольник png 2000x750px 31.22KB
- Четырехугольник Правильный многоугольник Квадратный параллелограмм, прямоугольник, угол, белый, прямоугольник png 1024x1024px 3.38KB
- Прямоугольник, параллелограмм, ромб, форма, змей, угол, черный, линия png 512x512px 1.25KB org/ImageObject»> Четырехугольник Правильный многоугольник Геометрия Параллелограмм, квадрат, разное, угол, белый png 1200x1200px 7.58KB
- Равнобедренная трапеция Угол Геометрическая форма, Фигуры, синий, прямоугольник, форма png 600x600px 7.12KB
- Форма линии геометрии параллелограмма, форма прямоугольника, угол, прямоугольник, треугольник png 1024x1024px 6.27KB
- Диаграммная бумага Изометрическая проекция Треугольник деления пополам, креативная пунктирная линия, угол, белый, текст png 1462x1096px 38.35KB
- шестиугольник, шестиугольник формы компьютерные иконки символ, шестиугольник, угол, прямоугольник, геометрическая форма png
512x512px
44.
 63KB
63KB - Перевод формы словаря шестиугольника многоугольника, шестиугольник, угол, белый, английский png 512x512px 3.77KB
- Геометрическая форма Ромб Геометрия Квадрат периметра, пустой значок дорожного знака, разное, угол, прямоугольник png 600x600px 404.97KB
- черная квадратная рамка, прямоугольник, ромб, прямоугольник, треугольник, геометрические фигуры, угол, симметрия, цвет png 512x512px 1.4KB
- Форма Ромб Геометрия Параллелограмм Полигон, Ромб, угол, лицо, прямоугольник png 600x600px 4.92KB
- Квадрат прямоугольник Wiktionary четырехугольник, угол, угол, белый, текст png
800x800px
3.
 79KB
79KB - Правильный многоугольник Shape Hexagon, форма, угол, белый, прямоугольник png 521x600px 9.71KB
- Форма ромба, Ромб, угол, белый, прямоугольник png 512x512px 3.82KB
- Геометрия Евклидова икона, нерегулярный геометрический фон, разноцветные геометрические изображения, фиолетовый, угол, треугольник png 2800x3664px 781.45KB
- Прямоугольный край, квадратная форма, многоугольник, край, прямоугольник, многоугольник, черный png 512x512px 4.19KB
- Треугольник Графический дизайн Логотип, triangulo, угол, текст, геометрическая форма png
948x814px
34.
 29KB
29KB - Геометрия круга света, наука и техника, синий механический, синий, угол, электроника png 800x800px 299.43KB
- Трапеция Геометрическая форма Геометрия Четырехугольник, штрихи, угол, прямоугольник, треугольник png 512x512px 2.33KB
- Треугольник, прямоугольник, четырехугольник, трапеция, ромб, угол, симметрия, геометрическая форма png 1024x652px 15.13KB
- Ромб ромб, ромб, разное, угол, текст png 1024x1024px 22.12KB
- Трапециевидный график функции Shape Line Четырехугольник, Трапеция, угол, белый, текст png 800x400px 3.13KB org/ImageObject»> Четырехсторонний правильный многоугольник, параллелограмм, геометрия, квадрат, угол, белый, прямоугольник png 768x768px 2.19KB
- Шестиугольник Многоугольник Двумерное пространство Геометрия, граница многоугольника, угол, белый, прямоугольник png 768x768px 11.63KB
- Трапециевидный график функции Shape Line Математика, форма, угол, белый, текст png 1024x512px 4.6KB
- иллюстрация треугольника, равносторонний треугольник, равнобедренный треугольник, геометрия формы, треугольник, угол, прямоугольник, треугольник png
600x600px
10.
 64KB
64KB - Четырехугольник Трапециевидная форма Прямоугольник Геометрия, четырехугольник, угол, прямоугольник, треугольник png 1024x768px 12.96KB
- Трапециевидный четырехугольник Трапециевидный параллелограмм Полигон, треугольник, угол, белый, прямоугольник png 600x600px 13.04KB
- Четырехугольная форма Трапециевидная геометрия Параллелограмм, геометрические фигуры, угол, белый, текст png 1200x581px 51.57KB
- Перевод словаря формы шестиугольника многоугольника, шестиугольник, угол, белый, английский png 512x512px 13.33KB
- Правильный многоугольник Шестиугольник Внутренний угол Гептагон, шестигранник, угол, белый, прямоугольник png
1024x1024px
16.
 14KB
14KB - Правильный многоугольник Hexagon Shape Geometry, шестиугольный, угол, белый, прямоугольник png 2000x2000px 36.48KB
- Евклидова геометрия, красочные абстрактные геометрические радиальные перспективы, зеленый, синий и желтый иллюстрации, синий, угол, цвет Всплеск png 568x569px 36.3KB
- несколько квадратных иллюстраций разных цветов, ромб евклидова цвета, красочные квадраты, цветной всплеск, текст, прямоугольник png 1200x1474px 894.06KB
- Равносторонний треугольник Прямой треугольник Геометрия Математика, круглый треугольник, угол, прямоугольник, треугольник png 512x512px 7.09KB org/ImageObject»> Число Десятичная Математика Прямоугольник Квадрат, черно-белая сетка, разное, угол, белый png 1024x1024px 8.29KB
- Четырехсторонняя форма Трапециевидная параллелограммная геометрия, четырехугольная, угол, текст, прямоугольник png 2000x968px 94.4KB
- Равнобедренная трапеция график функции форма математика, форма, угол, белый, текст png 1280x640px 6.3KB
- Шестигранник Правильная форма многоугольника, Шестиугольник, синий, угол, прямоугольник png 600x520px 7.58KB
- Правильный многоугольник Октагон Внутренний угол Равноугольный многоугольник, форма, угол, белый, прямоугольник png 800x800px 5.65KB org/ImageObject»> синий фон Геометрия, заголовок логотипа иллюстрации, синий, угол, текст png 847x994px 193.53KB
- Четырехсторонняя равнобедренная трапеция Параллелограмм, Математика, угол, прямоугольник, треугольник png 1200x764px 19.31KB
- Геометрическая форма Математика Геометрия, формы с, текст, треугольник, логотип png 7787x2653px 543.74KB
- белая треугольная призма, квадратная пирамида, форма, край, треугольник, пирамида, угол, лицо, симметрия png 1073x1024px 73.17KB
- Угол Геометрическая форма Пентагон Лайн, геоматрическая, фиолетовый, прямоугольник, треугольник png 800x800px 21.6KB org/ImageObject»> Правильный многоугольник Пентагон Правильный многогранник Геометрия, геометрические неправильные фигуры, угол, белый, прямоугольник png 1200x1200px 29.77KB
- иллюстрация иллюзии зеленого цвета, геометрический многоугольник, неправильный геометрический фон, текстура, синий, угол png 1300x1300px 1.77MB
- белый и синий фон, синий геометрический прямоугольник геометрии формы, коробка геометрии, разное, угол, треугольник png 1057x1057px 77.2KB
Неправильные многоугольники
Обзор
[Вернитесь к началу страницы]
Если вы просматривали страницу под названием «Правильные многоугольники», то, возможно, помните, что многоугольник — это замкнутая двухмерная фигура с несколькими (т. е. тремя или более) прямыми сторонами.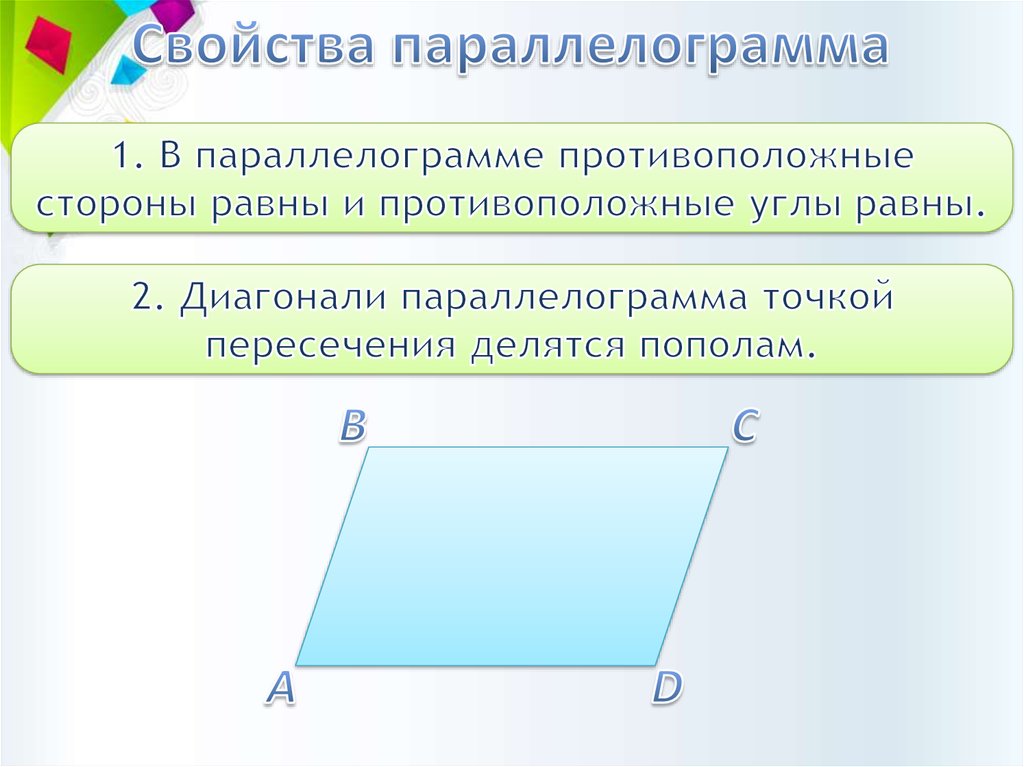 Так как правильный многоугольник — это такой многоугольник, в котором все стороны имеют одинаковую длину и все внутренние углы имеют одинаковую величину, отсюда следует, что неправильный многоугольник не соответствует этим критериям (т. е. он не является ни равносторонним , ни равноугольным ). Как и правильные многоугольники, неправильные многоугольники могут быть простыми (т.е. выпуклой или вогнутой фигурой, в которой стороны образуют границу вокруг одного замкнутого пространства, и ни один внутренний угол не превышает сто восемьдесят градусов) или сложными (два или более стороны будут пересекаться). Ниже мы приводим несколько примеров неправильных многоугольников.
Так как правильный многоугольник — это такой многоугольник, в котором все стороны имеют одинаковую длину и все внутренние углы имеют одинаковую величину, отсюда следует, что неправильный многоугольник не соответствует этим критериям (т. е. он не является ни равносторонним , ни равноугольным ). Как и правильные многоугольники, неправильные многоугольники могут быть простыми (т.е. выпуклой или вогнутой фигурой, в которой стороны образуют границу вокруг одного замкнутого пространства, и ни один внутренний угол не превышает сто восемьдесят градусов) или сложными (два или более стороны будут пересекаться). Ниже мы приводим несколько примеров неправильных многоугольников.
Примеры неправильных многоугольников
Здесь следует обратить внимание на то, что набор неправильных многоугольников, помимо того, что он бесконечно велик, включает в себя ряд форм, с которыми вы, возможно, уже знакомы.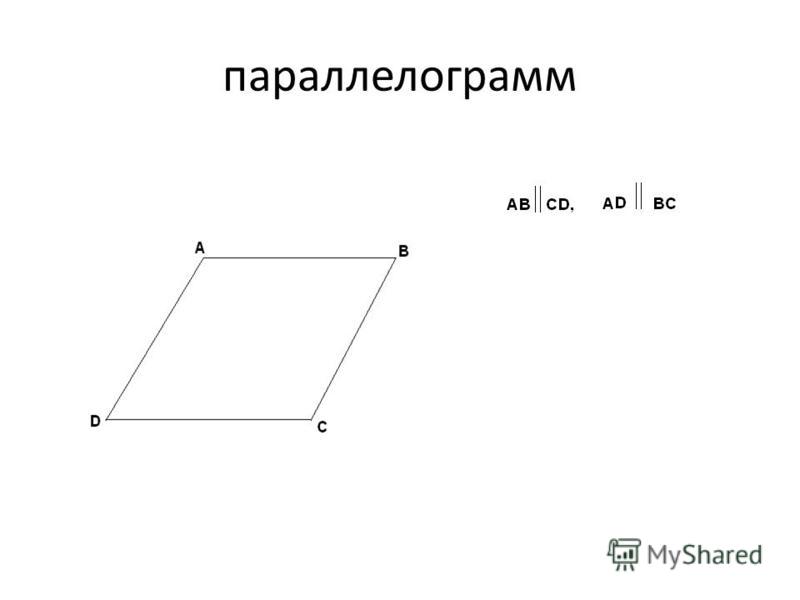 Форма (а), например, представляет собой прямоугольник (и, следовательно, по определению также параллелограмм и четырехугольник ). Он неправильный в силу того факта, что, хотя противоположные стороны равны по длине, соседние стороны — нет. Форма (b) — равнобедренный треугольник и неправильный, потому что равны только две стороны и равны только два угла. Фигура (c) является одновременно параллелограммом и четырехугольником . Он неправильный, потому что смежные стороны не равны, а смежные углы не равны. Форма (d) представляет собой трапецию и четырехугольник . У него две равные стороны и две пары равных углов, но он явно неправильный.
Форма (а), например, представляет собой прямоугольник (и, следовательно, по определению также параллелограмм и четырехугольник ). Он неправильный в силу того факта, что, хотя противоположные стороны равны по длине, соседние стороны — нет. Форма (b) — равнобедренный треугольник и неправильный, потому что равны только две стороны и равны только два угла. Фигура (c) является одновременно параллелограммом и четырехугольником . Он неправильный, потому что смежные стороны не равны, а смежные углы не равны. Форма (d) представляет собой трапецию и четырехугольник . У него две равные стороны и две пары равных углов, но он явно неправильный.
Остальные формы на самом деле не имеют конкретных имен. Форма (е) — сложный четырехугольник , у которого нет двух равных сторон и нет двух равных углов. Форма (f) технически представляет собой шестиугольник (потому что у него шесть сторон). Однако он одновременно неправильный, потому что имеет стороны разной длины и углы разной величины, и вогнутый, потому что один из его внутренних углов больше ста восьмидесяти градусов (> 180°). Точно так же фигура (g) технически является пятиугольником , поскольку у него пять сторон, но нет двух сторон одинаковой длины и только два из пяти внутренних углов одинаковы. Как и форма (f), форма (h) также является вогнутым шестиугольником, но в этом случае ни одна из сторон не равна, ни один из углов не равен, и никакие две стороны не параллельны.
Однако он одновременно неправильный, потому что имеет стороны разной длины и углы разной величины, и вогнутый, потому что один из его внутренних углов больше ста восьмидесяти градусов (> 180°). Точно так же фигура (g) технически является пятиугольником , поскольку у него пять сторон, но нет двух сторон одинаковой длины и только два из пяти внутренних углов одинаковы. Как и форма (f), форма (h) также является вогнутым шестиугольником, но в этом случае ни одна из сторон не равна, ни один из углов не равен, и никакие две стороны не параллельны.
Нахождение площади неправильного многоугольника
[Вернитесь к началу страницы]
Как и в случае с любым многоугольником, нахождение периметра — относительно тривиальное упражнение. Если вы знаете длину каждой стороны, вы можете просто сложить длины вместе, чтобы найти периметр. Если длины некоторых или всех сторон неизвестны, вам сначала нужно найти длину каждой стороны, измерив ее.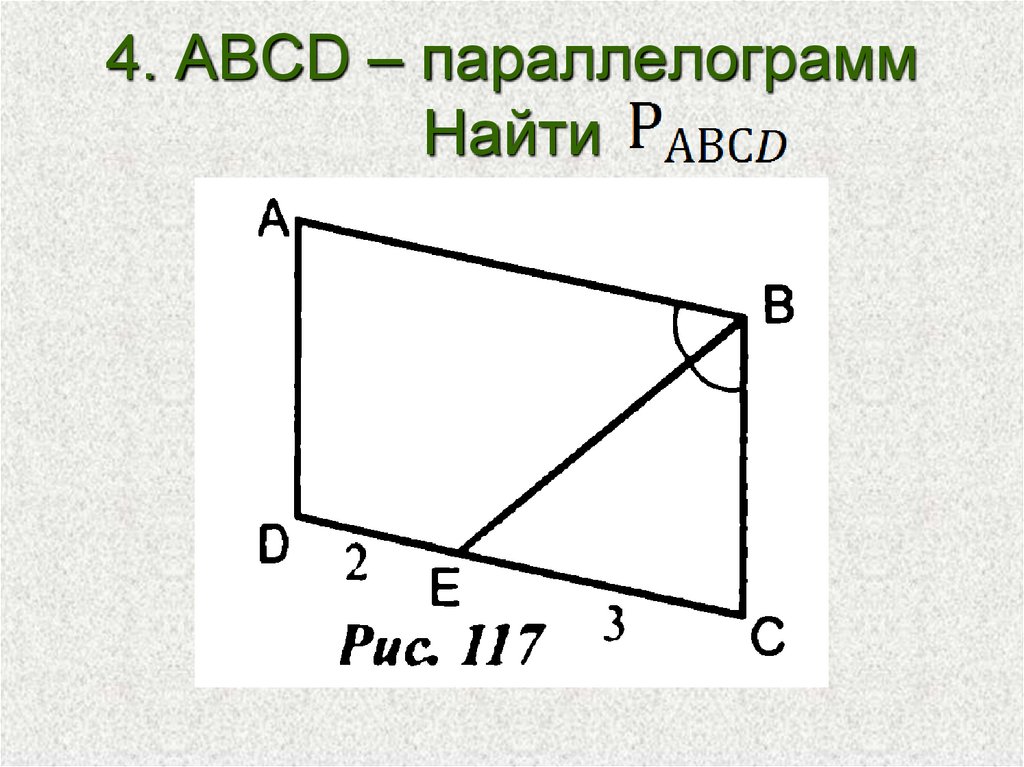 Найти площадь сложнее. В случае неправильных многоугольников, которые являются треугольниками или четырехугольниками, методы, которые можно использовать, описаны на соответствующих страницах. Для неправильных многоугольников, имеющих более четырех сторон, необходимо использовать другие методы. Точный метод, используемый в каждом конкретном случае, будет зависеть от типа неправильного многоугольника, с которым мы имеем дело. Рассмотрим, например, неправильный шестиугольник, показанный ниже.
Найти площадь сложнее. В случае неправильных многоугольников, которые являются треугольниками или четырехугольниками, методы, которые можно использовать, описаны на соответствующих страницах. Для неправильных многоугольников, имеющих более четырех сторон, необходимо использовать другие методы. Точный метод, используемый в каждом конкретном случае, будет зависеть от типа неправильного многоугольника, с которым мы имеем дело. Рассмотрим, например, неправильный шестиугольник, показанный ниже.
Неправильный шестиугольник
В этом случае мы знаем, что отрезки AB и DE равны по длине, как и отрезки BC , CD , EF и FA . Мы также знаем, что отрезки AB и DE параллельны. Из этой информации мы можем сделать вывод, что углы ABC и CDE равны, и что углы DEF и FAB идентичны. Мы также можем сделать вывод, что углы ABC и FAB являются дополнительными (в сумме дают сто восемьдесят градусов), как и углы CDE и DEF . Можно также показать, что отрезки BC и FA параллельны, как и отрезки CD и EF . Из этой информации вы должны увидеть, что если мы возьмем треугольную часть фигуры, определяемую точками B, C и D, и переместим ее так, чтобы она покрывала треугольную область, определяемую точками A, E и F, мы останется прямоугольник, как показано ниже.
Можно также показать, что отрезки BC и FA параллельны, как и отрезки CD и EF . Из этой информации вы должны увидеть, что если мы возьмем треугольную часть фигуры, определяемую точками B, C и D, и переместим ее так, чтобы она покрывала треугольную область, определяемую точками A, E и F, мы останется прямоугольник, как показано ниже.
Неправильный шестиугольник становится прямоугольником
Мы видим, что площадь неправильного шестиугольника ABCDEF эквивалентна прямоугольнику ABCD, поэтому площадь ABCDEF можно найти, взяв произведение длин отрезков AB и BD . Если эти длины известны, это простой расчет. Если нет, то их нужно сначала найти путем измерения. В случаях, подобных приведенным выше, часто можно преобразовать неправильный многоугольник в форму, для которой у нас уже есть метод вычисления площади и которая имеет ту же площадь, что и исходная форма. В других случаях это либо сложно, либо невозможно. В качестве альтернативы мы могли бы нарисовать отрезок FC , как показано ниже, эффективно разбивая фигуру на два параллелограмма равной площади. Затем мы могли бы найти площадь одного из параллелограммов и умножить результат на два, чтобы найти общую площадь фигуры.
В других случаях это либо сложно, либо невозможно. В качестве альтернативы мы могли бы нарисовать отрезок FC , как показано ниже, эффективно разбивая фигуру на два параллелограмма равной площади. Затем мы могли бы найти площадь одного из параллелограммов и умножить результат на два, чтобы найти общую площадь фигуры.
Неправильный шестиугольник можно разбить на два параллелограмма равной площади.
Один из методов, который работает для нахождения площади любого неправильного многоугольника (или любого правильного многоугольника , если на то пошло), включает в себя разбиение многоугольника на треугольники, определение площади каждого треугольника с использованием стандартных методов и сложение площадей отдельных треугольников вместе. (обратите внимание, что в некоторых случаях фигуру можно разбить на комбинацию треугольников и прямоугольников, но все многоугольники можно разбить на треугольники). Принцип проиллюстрирован ниже.
Принцип проиллюстрирован ниже.
Любой многоугольник можно разбить на несколько треугольных областей.
Площадь многоугольника равна сумме площадей треугольников T1, T2, T3, T4, T5 и T6. Основным недостатком этого метода является то, что он будет включать в себя выбор одной стороны каждого треугольника в качестве основания, построение перпендикулярного отрезка от основания к вершине треугольника (т.е. угол, противоположный основанию) и измерение размеров треугольника. каждый. Как только вы узнаете длину l основания и высота h для каждого треугольника, чтобы найти площадь, достаточно просто вычислить:
| Площадь = | л × ч | |
| 2 |
| Площадь = | ( x 1 Y 2 — Y 1 x 9000 2 978 9000 978978 9000 978 9000 9000 2 9000 9000 9000 2 9000 9000 2 2 2 9000 2 9000 9000 2 9000 2 9000 9000 2 9000 2 ) — г 2 x 3 ). . . + ( x N Y 1 — Y N x 1 ) . . + ( x N Y 1 — Y N x 1 ) |
Применив формулу к нашему шестистороннему неправильному многоугольнику, получим:
| Площадь = | ( x A Y B — Y A x . . . . . . . . ) . ) . ) ) ) ) . . ). . ) . . . . . . . ). — y B x C ) + ( x C y D — y C x D ) + ( x D y E — y D x E ) + ( x E Y F — Y E x F ) + ( x F Y A 8- 8 8 8 A 8 —8 8 A — 88 A — 8 A 8 A Y Y 188 8). |
| 2 |
| Площадь = | (2.5 — 3.4) + (4.5 — 5.7) + (7.1 — 5.9) + (9.2 — 1.6) + ( 6·1 — 2·3) + (3·3 — 1·2) |
| 2 |
| Площадь = | (10 — 12) + (20 — 12) 3 + (20 — 12) 3 45) + (18 — 6) + (6 — 6) + (9 — 2) |
| 2 |
| Площадь = 7 | 90 + 138 -3 — 11 -3 — 15 — 3 — 15
| 2 |
| Площадь = | -36 | = -18 |
| 2 |
Не переживайте, если результат окажется отрицательным. Просто измените знак минус на знак плюс. В качестве быстрой проверки результата можно вычислить площадь ограничивающего прямоугольника, так как полученный ответ всегда должен быть меньше этой цифры. В этом случае площадь ограничивающего прямоугольника будет произведением 9 — 2 (т.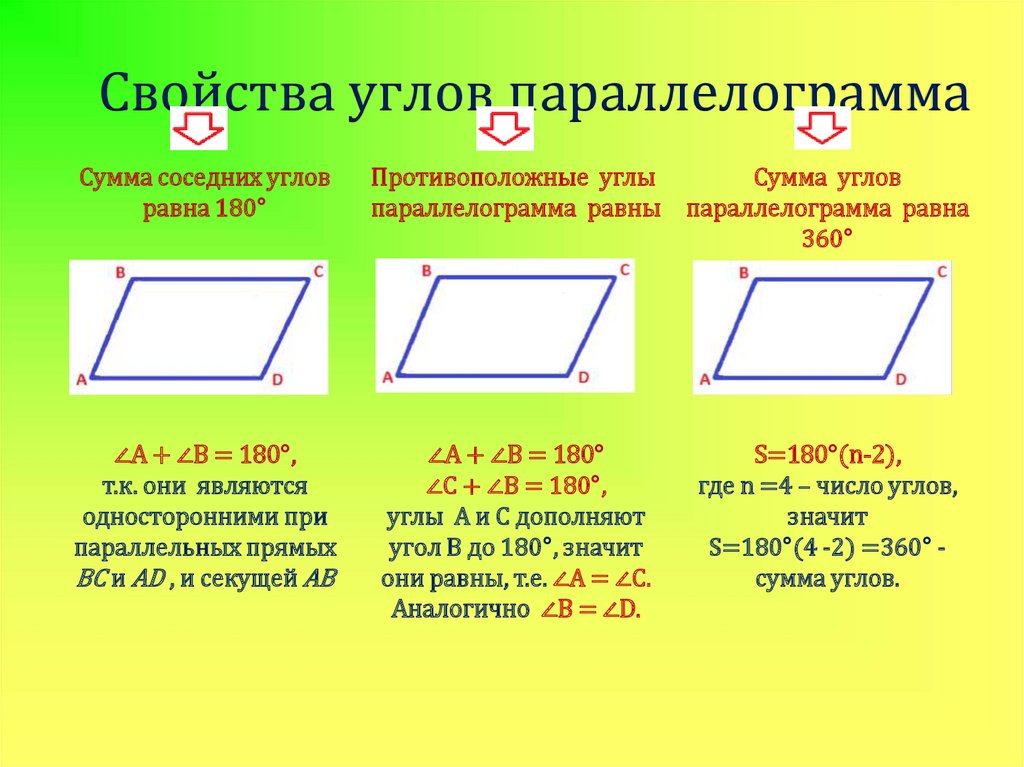 е. разницы между максимальным и минимальным x координат) и 5 - 1 (т.е. разница между максимальной и минимальной y координатами), что дает нам 7 × 4 = 28.
е. разницы между максимальным и минимальным x координат) и 5 - 1 (т.е. разница между максимальной и минимальной y координатами), что дает нам 7 × 4 = 28.
В качестве дополнительной проверки можно вычислить площади треугольников, образованных между периметром ограничивающего прямоугольника и периметром многоугольника, как в данном случае. Три из треугольников, образованных таким образом в приведенном нами примере, являются прямоугольными. Для этих треугольников мы знаем длины сторон, прилегающих к прямому углу, что по существу дает нам длину основания и высоту. Мы также знаем длину основания и высоту оставшегося треугольника (треугольник DEF ), хотя в этом треугольнике нет прямого угла.
Неправильный вогнутый шестиугольник с ограничивающим прямоугольником.
В результате расчет будет выглядеть примерно так:
| Площадь = (7 × 4)- | (2 × 2) + (2 × 4) + (6 × 1) + (1 × 2) |
| 2 | 2 |

| Область = 28 — 10 = |

 Точка Е середина стороны AD. Найдите площадь трапеции AECB
Точка Е середина стороны AD. Найдите площадь трапеции AECB Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника
Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника 52KB
52KB 63KB
63KB 79KB
79KB 29KB
29KB 64KB
64KB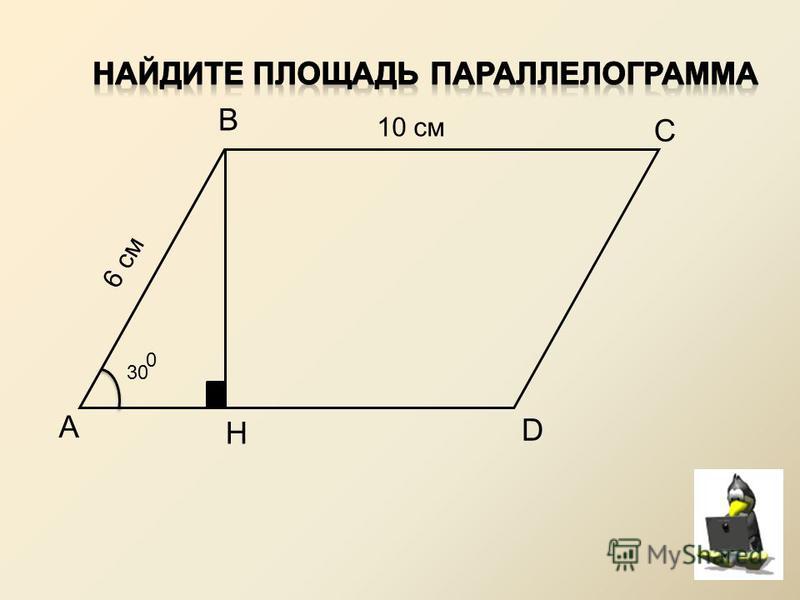 14KB
14KB Однако формулу можно использовать только если вы знаете координаты каждой из вершин. У него также есть недостаток, заключающийся в том, что его нельзя использовать для сложных многоугольников (т.е. многоугольников, в которых две или более сторон пересекаются друг с другом). Рассмотрим следующий вогнутый неправильный многоугольник:
Однако формулу можно использовать только если вы знаете координаты каждой из вершин. У него также есть недостаток, заключающийся в том, что его нельзя использовать для сложных многоугольников (т.е. многоугольников, в которых две или более сторон пересекаются друг с другом). Рассмотрим следующий вогнутый неправильный многоугольник: 
 Например: Круг
Например: Круг 
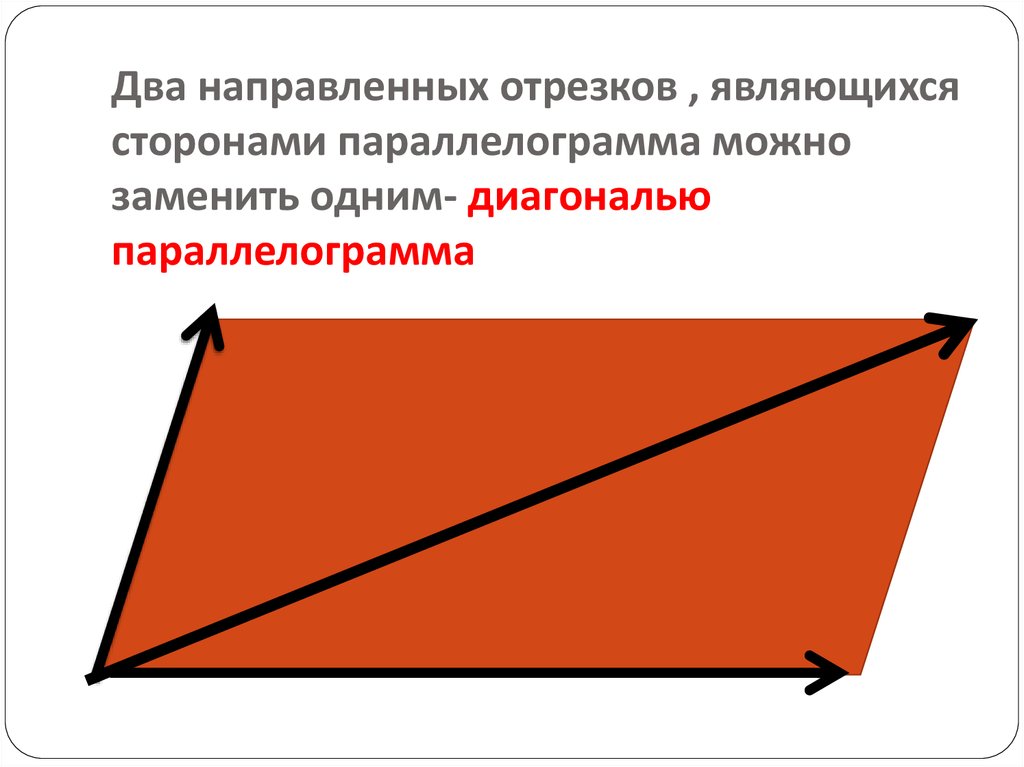
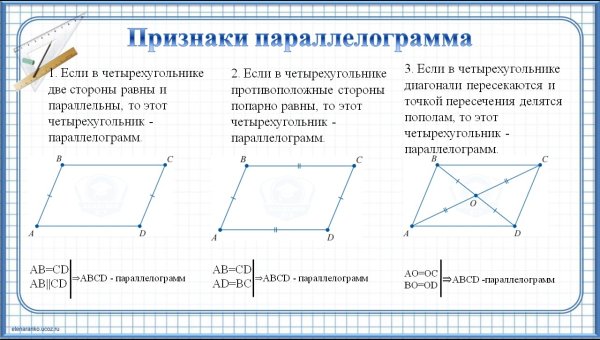 Следовательно, три угла не могут быть равны. Значит, это неправильный многоугольник. На следующем изображении показан пример одного из таких прямоугольных треугольников.
Следовательно, три угла не могут быть равны. Значит, это неправильный многоугольник. На следующем изображении показан пример одного из таких прямоугольных треугольников. Итак, мы можем разделить его на правильные многоугольники, для которых можно рассчитать площадь, а затем мы можем сложить их, чтобы получить площадь неправильного многоугольника.
Итак, мы можем разделить его на правильные многоугольники, для которых можно рассчитать площадь, а затем мы можем сложить их, чтобы получить площадь неправильного многоугольника.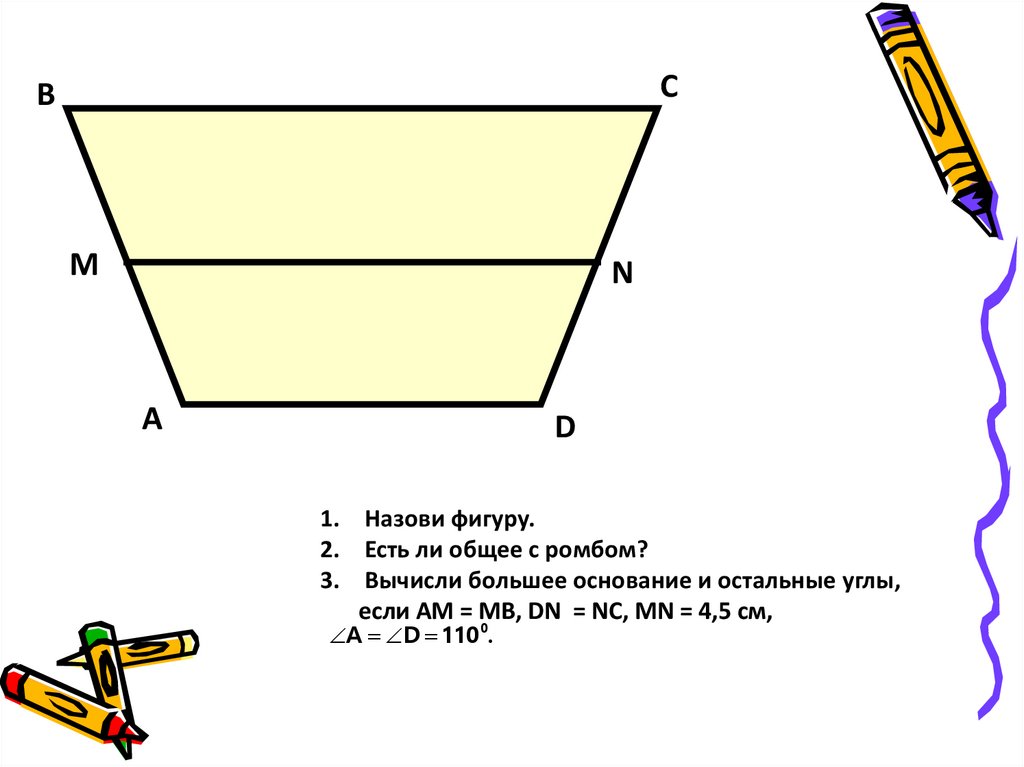 С другой стороны, внутренние углы — это углы между двумя соседними сторонами многоугольника. 9{\circ}$.
С другой стороны, внутренние углы — это углы между двумя соседними сторонами многоугольника. 9{\circ}$.
 {\circ}$. 9{\circ}$.
{\circ}$. 9{\circ}$. Значит, это правильный многоугольник.
Значит, это правильный многоугольник.