Параметрически заданной функции: Производная параметрически заданной функции

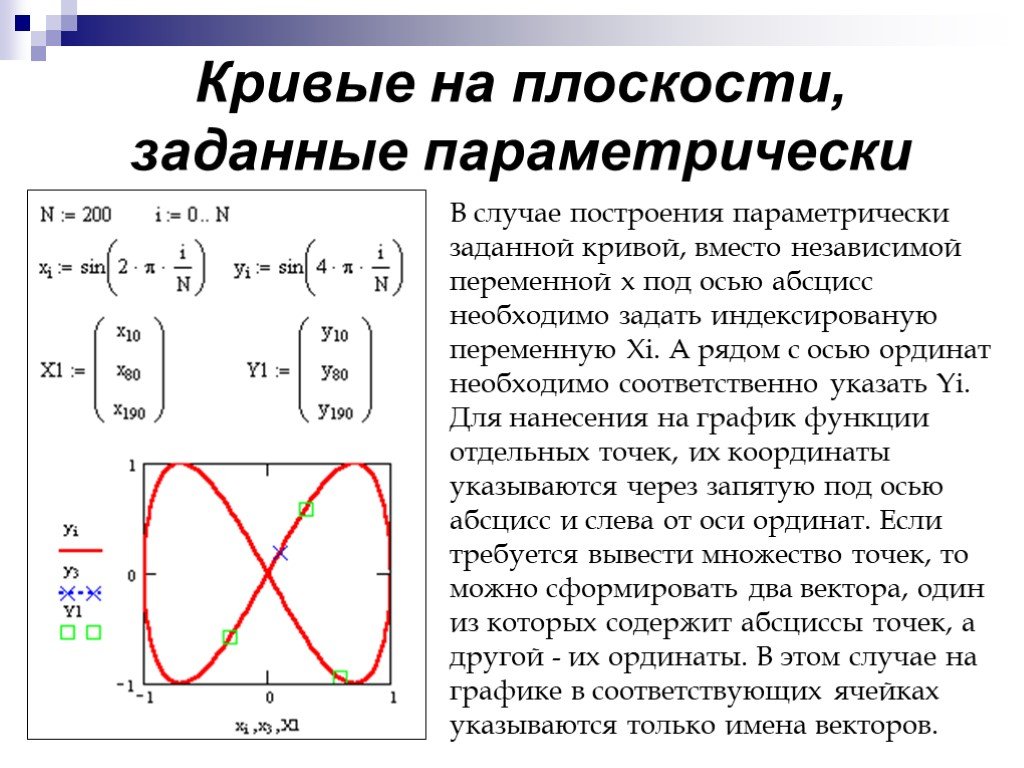
Краткий курс высшей математики

Краткий курс высшей математики

Шнейдер В. Е. и др. Краткий курс высшей математики. Учеб. пособие для втузов. М., «Высш. школа», 1972. 640 с. Данное учебное пособие предназначено для студентов вечерних факультетов втузов и заводов-втузов. Оно в основном охватывает весь материал, предусмотренный обязательной программой. Достаточное количество решенных примеров и задач способствует лучшему усвоению теоретического материала. Оглавление ПРЕДИСЛОВИЕ ГЛАВА I. МЕТОД КООРДИНАТ. ПОНЯТИЕ ФУНКЦИИ § 1. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА. КООРДИНАТЫ ТОЧКИ НА ПРЯМОЙ 2. Геометрическое изображение действительных чисел. Координаты точки на прямой 3. Абсолютная величина действительного числа 4. Расстояние между двумя точками на прямой § 2. КООРДИНАТЫ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ 2. Расстояние между двумя точками на плоскости 3. Деление отрезка в данном отношении 4. Координаты точки в пространстве 5. Расстояние между двумя точками в пространстве § 3. УГОЛ МЕЖДУ ДВУМЯ ОСЯМИ. ПОЛЯРНЫЕ КООРДИНАТЫ 2. Полярные координаты 3. Зависимость между декартовыми и полярными координатами § 4. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ 2. Понятие функции 3. График функции 4. Способы задания функций 5. Основные элементарные функции и их графики 6. Сложные функции. Элементарные функции 7. Целые и дробно-рациональные функции 8. Функции четные и нечетные. Периодические функции § 5. УРАВНЕНИЕ ЛИНИИ 2. Нахождение уравнения линии по ее геометрическим свойствам § 6 ПРЕОБРАЗОВАНИЕ КООРДИНАТ 2. Поворот осей координат ГЛАВА II. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ § 1. ПРЯМАЯ 2. Уравнение прямой с угловым коэффициентом 3. Уравнение прямой, параллельной оси ординат 4. Общее уравнение прямой и его частные случаи 5. Точка пересечения прямых. Построение прямой по ее уравнению 6. Вычисление угла между двумя прямыми. Условия параллельности и перпендикулярности двух прямых 7. Уравнение прямой, проходящей через данную точку в заданном направлении 8. Пучок прямых 9. Уравнение прямой, проходящей через две данные точки 10. Расстояние от точки до прямой § 2. КРИВЫЕ ВТОРОГО ПОРЯДКА 2. Окружность 3. Эллипс 4. Гипербола 5. Парабола 6. Окружность, эллипс, гипербола и парабола как конические сечения 7. Упрощение уравнения кривой второго порядка. График квадратного трехчлена 8. Уравнение равносторонней гиперболы, асимптоты которой приняты за оси координат 9. График дробно-линейной функции 10. Преобразование уравнения кривой второго порядка, не содержащего члена с произведением координат ГЛАВА III. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ И ВЕКТОРНОЙ АЛГЕБРЫ § 1. ЭЛЕМЕНТЫ ТЕОРИИ ОПРЕДЕЛИТЕЛЕЙ 2. Определитель третьего порядка 3. Понятие об определителях высших порядков § 2. СИСТЕМЫ УРАВНЕНИЙ ПЕРВОЙ СТЕПЕНИ 2. Однородная система двух уравнений первой степени с тремя неизвестными 3. Система трех уравнений первой степени с тремя неизвестными 4. Однородная система трех уравнений первой степени с тремя неизвестными § 3. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ 2. Линейные операции над векторами 4. Проекция вектора на ось и составляются вектора по оси 5. Разложение вектора на составляющие по осям координат 6. Направляющие косинусы вектора 7. Условие коллинеарности двух векторов 8. Скалярное произведение 9. Выражение скалярного произведения через проекции перемножаемых векторов 10. Косинус угла между двумя векторами 11. Векторное произведение 12. Выражение векторного произведения через проекции перемножаемых векторов 13. Смешанное произведение трех векторов 14. Геометрический смысл смешанного произведения 15. Условие компланарности трех векторов § 4. МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ 2. Равенство матриц. Действия над матрицами 3. Обратная матрица 4. Матричная запись и матричное решение системы уравнений первой степени § 5. ЛИНЕЙНЫЕ ОТОБРАЖЕНИЯ 2. Преобразование координат 3. Приведение квадратичной формы к каноническому виду 4. Упрощение общего уравнения кривой второго порядка ГЛАВА IV. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ § 1. ПЛОСКОСТЬ 2. Нормальный вектор плоскости. Уравнение плоскости, проходящей через данную точку 3. Общее уравнение плоскости и его частные случаи 4. Построение плоскости по ее уравнению 5. Угол между плоскостями. Условия параллельности и перпендикулярности двух плоскостей 6. Точка пересечения трех плоскостей § 2. ПРЯМАЯ В ПРОСТРАНСТВЕ 2. Общие уравнения прямой 3. Векторное уравнение прямой. Параметрические уравнения прямой 4. Канонические уравнения прямой 5. Уравнения прямой, проходящей через две точки 6. Угол между двумя прямыми. Условия параллельности и перпендикулярности прямых § 3. Прямая и плоскость в пространстве 2. Точка пересечения прямой с плоскостью 3. Расстояние от точки до плоскости 4. Пучок плоскостей § 4. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА 2. Цилиндрические поверхности 3. Конические поверхности 4. Поверхность вращения 6. Гиперболоиды 7. Параболоиды ГЛАВА V. ТЕОРИЯ ПРЕДЕЛОВ § 1. ПРЕДЕЛ ФУНКЦИИ 2. Предел функции при х -> -оо 3. Предел функции при х->х0 4. Бесконечно малые функции. Ограниченные функции 5. Бесконечно большие функции и их связь с бесконечно малыми функциями 6. Основные теоремы о пределах 7. Предел функции при x -> 0 8. Последовательность. Число e 9. Натуральные логарифмы 10. Сравнение бесконечно малых функций § 2. НЕПРЕРЫВНЫЕ ФУНКЦИИ 2. Операции над непрерывными функциями. Непрерывность элементарных функций 3. Свойства функций, непрерывных на сегменте 4. Понятие об обратной функции 5. Обратные тригонометрические функции 6. Показательная и логарифмическая функции 7. Понятие о гиперболических функциях ГЛАВА VI. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ 1. Приращение аргумента и приращение функции 2. Определение непрерывности функции с помощью понятии приращения аргумента и приращения функции 3. Задачи, приводящие к понятию производной 4. Определение производной и ее механический смысл 5. Дифференцируемость функции 6. Геометрический смысл производной 7. Производные некоторых основных элементарных функций 8. Основные правила дифференцирования 9. Производная обратной функции 10. Производные обратных тригонометрических функций 11. Производная сложной функции § 12. Производные гиперболических функций 13. Производная степенной функции с любым показателем 14. Сводная таблица формул дифференцирования 15. Неявные функции и их дифференцирование 16. Уравнения касательной а нормали к кривой 17. Графическое дифференцирование § 2. ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ 1. Нахождение производных высших порядков 2. Механический смысл второй производной § 3. ДИФФЕРЕНЦИАЛ ФУНКЦИИ 2. Производная как отношение дифференциалов 3. Дифференциал суммы, произведения и частного функций 4. Дифференциал сложной функции. Инвариантность формы дифференциала 5. Применение дифференциала к приближенным вычислениям 6. Дифференциалы высших порядков § 4. ФУНКЦИИ, ЗАДАННЫЕ ПАРАМЕТРИЧЕСКИ, И ИХ ДИФФЕРЕНЦИРОВАНИЕ 2. Дифференцирование функций, заданных параметрически § 5. ВЕКТОРНАЯ ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА 2. Векторная функция скалярного аргумента и ее производная 3. Уравнения касательной прямой и нормальной плоскости к пространственной кривой 4. Механический смысл первой и второй производных векторной функции скалярного аргумента § 6. НЕКОТОРЫЕ ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ 2. Теорема Ролля 3. Теорема Лагранжа 4. Правило Лопиталя § 7. ПРИЛОЖЕНИЕ ПРОИЗВОДНОЙ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ПОСТРОЕНИЮ ГРАФИКОВ 2. Максимум и минимум функции 3. Достаточный признак существования экстремума, основанный на знаке второй производной 4. Отыскание наибольшего и наименьшего значений функции 5. Применение теории максимума и минимума к решению задач 6. Выпуклость и вогнутость графика функции. Точки перегиба 7. Асимптоты графика функции 8. Общая схема исследования функции и построение ее графика § 8. ПРИБЛИЖЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ 2. Уточнение найденных значений корней методом хорд и касательных § 9. ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА ЛАГРАНЖА ГЛАВА VII. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО СВОЙСТВА 2. Геометрический смысл неопределенного интеграла 3. Таблица основных интегралов 4. Основные свойства неопределенного интеграла § 2. ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ 2. Интегрирование методом замены переменной 3. Интегрирование по частям § 3. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ФУНКЦИЙ 2. Рациональные дроби. Выделение правильной рациональной дроби 3. Интегрирование простейших рациональных дробей 4. Разложение правильной рациональной дроби на простейшие дроби 5. Метод неопределенных коэффициентов 6. Интегрирование рациональных дробей § 4. Интегрирование тригонометрических функций 2. Рациональные функции двух переменных 3. Интегралы вида § 5. ИНТЕГРИРОВАНИЕ НЕКОТОРЫХ ИРРАЦИОНАЛЬНЫХ ФУНКЦИЙ 2. Интеграл вида 3. Интегралы видов 4. Интегралы вида § 6. ОБЩИЕ ЗАМЕЧАНИЯ О МЕТОДАХ ИНТЕГРИРОВАНИЯ. ИНТЕГРАЛЫ, НЕ БЕРУЩИЕСЯ В ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ 2. Понятие об интегралах, не берущихся в элементарных функциях ГЛАВА VIII. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. ЗАДАЧИ, ПРИВОДЯЩИЕ К ОПРЕДЕЛЕННОМУ ИНТЕГРАЛУ 2. Задача о работе переменной силы § 2. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 2. Свойства определенного интеграла 3. Производная интеграла по переменной верхней границе 4. Формула Ньютона—Лейбница 5. Замена переменной в определенном интеграле 6. Интегрирование по частям в определенном интеграле § 3. ГЕОМЕТРИЧЕСКИЕ И ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА 2. Вычисление площади в полярных координатах 3. Вычисление объема тела по известным поперечным сечениям 4. Объем тела вращения 5. Длина дуги кривой 6. Дифференциал дуги 7. Площадь поверхности вращения 8. Общие замечания о решении задач методом интегральных сумм § 4. КРИВИЗНА ПЛОСКОЙ КРИВОЙ 2. Вычисление кривизны 3. Радиус кривизны. Круг кривизны. Центр кривизны 4. Эволюта и эвольвента § 5. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ 2. Интегралы от разрывных функций 3. Признаки сходимости несобственных интегралов § 6. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ 2. Метод трапеций 3. Метод параболических трапеций (метод Симпсона) ГЛАВА IX. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ § 1. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 2. График функции двух переменных 3. Функции трех и большего числа переменных § 2. Предел функции нескольких переменных. Непрерывность функции. Точки разрыва 2. Непрерывность функции нескольких переменных 3. Понятие области 4. Точки разрыва 5. Свойства функций, непрерывных в ограниченной замкнутой области § 3. ЧАСТНЫЕ ПРОИЗВОДНЫЕ 2. Геометрический смысл частных производных функции двух переменных 3. Частные производные высших порядков § 4. ПОЛНЫЙ ДИФФЕРЕНЦИАЛ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 2. Полный дифференциал функции 3. Приложение полного дифференциала к приближенным вычислениям § 5. Дифференцирование сложных и неявных функций 2. Инвариантность формы полного дифференциала 3. Дифференцирование неявных функций § 6. СКАЛЯРНОЕ ПОЛЕ 2. Производная по направлению 3. Градиент 4. Касательная плоскость а нормаль к поверхности 5. Геометрический смысл полного дифференциала функции двух переменных § 7. ЭКСТРЕМУМ ФУНКЦИЙ ДВУХ ПЕРЕМЕННЫХ 2. Наибольшее и наименьшее значения функции двух переменных ГЛАВА X. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ § 1. ДВОЙНОЙ ИНТЕГРАЛ 2. Двойной интеграл. Теорема существования 3. Свойства двойного интеграла 4. Вычисление двойного интеграла в декартовых координатах 5. Вычисление двойного интеграла в полярных координатах 6. Приложения двойного интеграла § 2. ТРОЙНОЙ ИНТЕГРАЛ 2. Тройной интеграл и его свойства 3. Вычисление тройного интеграла в декартовых координатах 4. Вычисление тройного интеграла в цилиндрических координатах 5. Приложения тройного интеграла § 3. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ 2. Задача о работе. Криволинейный интеграл 3. Вычисление криволинейного интеграла 4. Формула Остроградского — Грина 5. Независимость криволинейного интеграла от пути интегрирования 6. Отыскание первообразной по полному дифференциалу 7. Криволинейный интеграл по длине дуги ГЛАВА XI. РЯДЫ § 1. ЧИСЛОВЫЕ РЯДЫ 2. Геометрическая прогрессия 3. Простейшие свойства числовых рядов 4. Необходимый признак сходимости ряда 5. Достаточные признаки сходимости знакоположительных рядов 6. Знакопеременные ряды 7. Остаток ряда и его оценка § 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ 2. Правильно сходящиеся функциональные ряды и их свойства § 3. СТЕПЕННЫЕ РЯДЫ 2. Свойства степенных рядов 3. Ряды по степеням разности х-а 4. Разложение функций в степенные ряды. Ряд Тейлора 5. Разложение некоторых элементарных функций в ряды Тейлора и Маклорена § 4. ПРИЛОЖЕНИЕ РЯДОВ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ 2. Приближенное вычисление интегралов § 5. ПОНЯТИЕ О ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ. СТЕПЕННЫЕ РЯДЫ В КОМПЛЕКСНОЙ ОБЛАСТИ 2. Числовые ряды с комплексными членами 3. Степенные ряды в комплексной области § 6. РЯДЫ ФУРЬЕ 2. Ряд Фурье 3. Сходимость ряда Фурье 4. Ряды Фурье для четных и нечетных функций 5. Разложение в ряд Фурье функций с периодом 2l ГЛАВА XII. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ § 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА 2. Дифференциальные уравнения первого порядка 3. Уравнения с разделяющимися переменными 4. Однородные уравнения 5. Линейные уравнения 6. Уравнение в полных дифференциалах 7. Особые решения 8. Приближенное решение дифференциальных уравнений первого порядка методом Эйлера § 2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА 2. Простейшие уравнения второго порядка, допускающие понижение порядка 3. Понятие о дифференциальных уравнениях высших порядков § 3. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА 2. Линейные однородные дифференциальные уравнения второго порядка 3. Линейные неоднородные дифференциальные уравнения второго порядка 4. Метод вариации произвольных постоянных § 4. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ 2. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами 3. Приложение линейных дифференциальных уравнений второго порядка к изучению механических и электрических колебаний § 5. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ 2. Линейные дифференциальные уравнения n-го порядка с постоянными коэффициентами § 6. ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОМОЩЬЮ РЯДОВ § 7. ПОНЯТИЕ О СИСТЕМАХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 2. Системы линейных дифференциальных уравнений с постоянными коэффициентами ПРИЛОЖЕНИЕ 1. ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА НЬЮТОНА ПРИЛОЖЕНИЕ 2. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ

Дифференциальное и интегральное исчисления для втузов, т.1

Пискунов Н. С. Дифференциальное и интегральное исчисления для втузов, т.1: Учебное пособие для втузов.— 13-е изд.— М.: Наука. Главная редакция физико-математической литературы, 1985. — 432 с. Хорошо известное учебное пособие по математике для втузов с достаточно широкой математической подготовкой. Первый том включает разделы: введение в анализ, дифференциальное исчисление (функций одной и нескольких переменных), неопределенный и определенный интегралы. Настоящее издание не отличается от предыдущего (1978 г.). Для студентов высших технических учебных заведений. Оглавление ПРЕДИСЛОВИЕ К ДЕВЯТОМУ ИЗДАНИЮ ПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ ГЛАВА I. ЧИСЛО. ПЕРЕМЕННАЯ. ФУНКЦИЯ § 1. Действительные числа. § 2. Абсолютная величина действительного числа § 3. Переменные и постоянные величины § 4. Область изменения переменной величины § 5. Упорядоченная переменная величина. Возрастающая и убывающая переменные величины Ограниченная переменная величина § 6. Функция § 7. Способы задания функции § 8. Основные элементарные функции. Элементарные функции § 9. Алгебраические функции § 10. Полярная система координат Упражнения к главе I ГЛАВА II. ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ ФУНКЦИЙ § 1. Предел переменной величины. Бесконечно большая переменная величина § 2. Предел функции § 3. Функция, стремящаяся к бесконечности. n при n целом и положительном § 6. Производные от функций y = sinx; y = cosx § 7. Производные постоянной, произведения постоянной на функцию, суммы, произведения, частного § 8. Производная логарифмической функции § 9. Производная от сложной функции § 10. Производные функций y = tgx, y = ctgx, y = ln|x| § 11. Неявная функция и ее дифференцирование § 12. Производные степенной функции при любом действительном показателе, показательной функции, сложной показательной функции § 13. Обратная функция и ее дифференцирование § 14. Обратные тригонометрические функции и их дифференцирование § 15. Таблица основных формул дифференцирования § 16. Параметрическое задание функции § 17. Уравнения некоторых кривых в параметрической форме § 18. Производная функции, заданной параметрически § 19. Гиперболические функции § 20. Дифференциал § 21. Геометрическое значение дифференциала Рассмотрим функцию § 22. Производные различных порядков § 23. x, sin x, cos x Упражнения к главе IV ГЛАВА V. ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИЙ § 2. Возрастание и убывание функции § 3. Максимум и минимум функций § 4. Схема исследования дифференцируемой функции на максимум и минимум с помощью первой производной § 5. Исследование функции на максимум и минимум с помощью второй производной § 6. Наибольшее и наименьшее значения функции на отрезке § 7. Применение теории максимума и минимума функций к решению задач § 8. Исследование функции на максимум и минимум с помощью формулы Тейлора § 9. Выпуклость и вогнутость кривой. Точки перегиба § 10. Асимптоты § 11. Общий план исследования функций и построения графиков § 12. Исследование кривых, заданных параметрически Упражнения к главе V ГЛАВА VI. КРИВИЗНА КРИВОЙ § 1. Длина дуги и ее производная § 2. Кривизна § 3. Вычисление кривизны § 4. Вычисление кривизны линии, заданной параметрически § 5. Вычисление кривизны линии, заданной уравнением в полярных координатах § 6. Радиус и круг кривизны. Центр кривизны. Эволюта и эвольвента § 7. Свойства эволюты § 8. Приближенное вычисление действительных корней уравнения Упражнения к главе VI ГЛАВА VII. КОМПЛЕКСНЫЕ ЧИСЛА, МНОГОЧЛЕНЫ § 1. Комплексные числа. Исходные определения § 2. Основные действия над комплексными числами § 3. Возведение комплексного числа в степень и извлечение корня из комплексного числа § 4. Показательная функция с комплексным показателем и ее свойства § 5. Формула Эйлера. Показательная форма комплексного числа § 6. Разложение многочлена на множители § 7. О кратных корнях многочлена § 8. Разложение многочлена на множители в случае комплексных корней § 9. Интерполирование. Интерполяционная формула Лагранжа § 10. Интерполяционная формула Ньютона § 11. Численное дифференцирование § 12. О наилучшем приближении функций многочленами. Теория Чебышева Упражнения к главе VII ГЛАВА VIII. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ § 1. Определение функции нескольких переменных § 2. Геометрическое изображение функции двух переменных § 3. Частное и полное приращение функции § 4. Непрерывность функции нескольких переменных § 5. Частные производные функции нескольких переменных § 6. Геометрическая интерпретация частных производных функции двух переменных § 7. Полное приращение и полный дифференциал § 8. Применение полного дифференциала в приближенных вычислениях § 9. Приложение дифференциала к оценке погрешности при вычислениях § 10. Производная сложной функции. Полная производная. Полный дифференциал сложной функции § 11. Производная от функции, заданной неявно § 12. Частные производные различных порядков § 13. Поверхности уровня § 14. Производная по направлению § 15. Градиент § 16. Формула Тейлора для функции двух переменных § 17. Максимум и минимум функции нескольких переменных § 18. Максимум и минимум функции нескольких переменных, связанных данными уравнениями (условные максимумы и минимумы) § 19. Получение функции на основании экспериментальных данных по методу наименьших квадратов § 20. Особые точки кривой Упражнения к главе VIII ГЛАВА IX. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ К ГЕОМЕТРИИ В ПРОСТРАНСТВЕ § 1. Уравнения кривой в пространстве § 2. Предел и производная векторной функции скалярного аргумента. Уравнение касательной к кривой. Уравнение нормальной плоскости § 3. Правила дифференцирования векторов (векторных функций) § 4. Первая и вторая производные вектора по длине дуги. Кривизна кривой. Главная нормаль. Скорость и ускорение точки в криволинейном движении § 5. Соприкасающаяся плоскость. Бинормаль. Кручение. § 6. Касательная плоскость и нормаль к поверхности Упражнения к главе IX ГЛАВА X. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. Первообразная и неопределенный интеграл § 2. Таблица интегралов § 3. Некоторые свойства неопределенного интеграла § 4. Интегрирование методом замены переменной или способом подстановки § 5. Интегралы от некоторых функций, содержащих квадратный трехчлен § 6. Интегрирование по частям § 7. Рациональные дроби. Простейшие рациональные дроби и их интегрирование § 8. Разложение рациональной дроби на простейшие § 9. Интегрирование рациональных дробей § 10. Интегралы от иррациональных функций § 11. Интегралы вида … § 12. Интегрирование некоторых классов тригонометрических функций § 13. Интегрирование некоторых иррациональных функций с помощью тригонометрических подстановок § 14. О функциях, интегралы от которых не выражаются через элементарные функции Упражнения к главе X ГЛАВА XI. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. Постановка задачи. Нижняя и верхняя интегральные суммы § 2. Определенный интеграл. Теорема о существовании определенного интеграла § 3. Основные свойства определенного интеграла § 4. Вычисление определенного интеграла. Формула Ньютона — Лейбница § 5. Замена переменной в определенном интеграле § 6. Интегрирование по частям § 7. Несобственные интегралы § 8. Приближенное вычисление определенных интегралов § 9. Формула Чебышева § 10. Интегралы, зависящие от параметра. Гамма-функция § 11. Интегрирование комплексной функции действительной переменной Упражнения кглаве XI ГЛАВА XII. ГЕОМЕТРИЧЕСКИЕ И МЕХАНИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА § 1. Вычисление площадей в прямоугольных координатах § 2. Площадь криволинейного сектора в полярных координатах § 3. Длина дуги кривой § 4. Вычисление объема тела по площадям параллельных сечений § 5. Объем тела вращения § 6. Площадь поверхности тела вращения § 7. Вычисление работы с помощью определенного интеграла § 8. Координаты центра масс § 9. Вычисление момента инерции линии, круга и цилиндра с помощью определенного интеграла Упражнения к главе XII

Параметрическая функция/уравнение: определение, примеры

Типы функций >

Содержание :

1. Что такое параметрические функции?
   • Параметризация и имплицитизация
   • Использование параметрических функций
   • Из параметрических в прямоугольные формы
2. Параметрические производные

Параметрическая функция на самом деле просто другой способ записи функций , точно так же, как явные и неявные формы:

• Явные функции имеют форму y = f(x) для a < x < b. Это включает:
  • Рациональные функции (например, f(x) = (x ² − 1) / (x + 19)),
  • Экспоненциальные функции (например, f(x) = 2 ^x )
  • Полиномиальные функции (например, f(x) = x ² 5 + 12).
• Неявные функции , которые описывают формы, такие как круги, гиперболы и параболы. Они принимают вид: f(x, y) = 0 при a < x < b и c < y < d.
• Параметрическая функция принимает вид: p(t) = (f(t), g(t)) для a < t < b.

Более конкретно, параметрическая функция выражает определенные величины в терминах одной или нескольких независимых переменных, называемых «параметрами». Несколько зависимых переменных x и y обрабатываются как один объект, который зависит от явной независимой переменной (например, t ). Диапазон функции параметра представляет собой набор упорядоченных пар (x, y).

Формула

Параметрическая функция — это любая функция, следующая формуле:
p(t) = (f(t), g(t))
для a < t < b.

Изменение времени (t) дает разные значения координат (x, y).

В приведенной выше формуле f(t) и g(t) относятся к x и y соответственно. Некоторые авторы предпочитают использовать x(t) и y(t), но это может вызвать путаницу. Это потому, что если вы используете x(t) для описания значения функции в момент времени t, x также может описывать ввод по горизонтальной оси.

Пример

Неявная форма для окружности: x ² + y ² = r ² . Параметрическое уравнение для окружности:

Предположим, мы хотим переписать уравнение для параболы y = x ² в виде параболической функции. Самый простой способ сделать это — ввести новый свободный параметр — мы можем назвать его t. Тогда мы можем сказать:

Мы только что параметризовали нашу функцию.

Имплицитизация противоположно параметризации. Это означает взять параметрическую функцию и преобразовать ее обратно в единую формулу с неявной связью между x и y.

Для параболы это очень просто: поскольку x = t, замените t ² на x ² , и вы вернетесь к своей неявной формуле.

Давайте рассмотрим кое-что посложнее. Параметрическая формула для круга радиуса a:

. Мы можем разделить обе стороны на a и переписать это как 9.0003

Тождество треугольника Пифагора дает нам

Подставив сюда наши параметрические функции, мы получим

Итак, наконец,

Что для (стандартного круга) является неявным уравнением; так что мы успешно подразумевали это.

На вводных занятиях по математическому анализу параметрические функции обычно преподаются как представления графиков кривых, но их можно использовать для моделирования гораздо более широкого круга ситуаций. Например:

• Они полезны для моделирования путей движущихся объектов,
• Они необходимы для оптимизации многомерных функций.
• В целом, они позволяют свести сложные задачи с несколькими входными данными к более простой функции (Stalvey, (2014).
).

Что такое прямоугольная форма и параметрическая форма?

Прямоугольная форма (также называемая декартовой формой) относится к прямоугольным координатам — знакомым координатам (x, y). Функция, записанная в прямоугольной форме, есть y = f(x).

Параметрическая форма — это просто другой способ записи того же уравнения. Например, уравнение y = x ² , имеющее прямоугольную форму, можно переписать как пару уравнений в параметрической форме: x = t и y = t ² . Преобразование в параметрическую форму называется параметризацией.

Параметрические формы в прямоугольные

Общие шаги для преобразования параметрических форм в прямоугольные:

1. Решите одно уравнение для t или x,
2. Подставьте решение к другому уравнению,
3. Приведите в порядок свой ответ.

Решение какой переменной зависит от формата уравнений, которые вам даны. Найдите переменную, которая появляется в правой части обоих уравнений . Этот первый пример показывает вам одну задачу, решение которой для «t» является лучшим подходом; во втором примере показано решение для x.

Пример #1 :Преобразование следующего из параметрического в прямоугольный формат:
x = t + 1, y = t – 2.

Шаг 1: Решите одно из уравнений для t. Неважно, что вы выберете, но для этого примера я решу x = t + 1 для t:

• x = t + 1
• Переключить стороны : t + 1 = x
• Вычесть 1 с обеих сторон: t + 1 (-1) = x (-1)
• Упрощение: t = x – 1

Шаг 2: Замените t во втором уравнении (которое вы не выбрали на шаге 1) на результат, полученный на шаге 1:

• у = т – 2
• Замените t на результат шага 1 : y = (x – 1) – 2
• Упростить : y = x – 3

Пример #2 :Преобразуйте следующее из параметрической формы в прямоугольную:
y = 4x + 5, t = x + 1

Шаг 1: Решите одно из уравнений относительно x. Для этого примера я решу t = x + 1 для t:

• t = x + 1
• Переключить стороны : x + 1 = t
• Вычесть 1 с обеих сторон: х + 1 (-1) = т (-1)
• Упрощение: x = t – 1

Шаг 2: Замените x во втором уравнении (которое вы не выбрали в шаге 1) на результат, полученный в шаге 1:

• y = 4x + 5
• Замените x на результат шага 1 : y = 4(t – 1) + 5
• Упростить :
  • у = 4t – 4 + 5
  • у = 4т + 1

Из параметрических в прямоугольные формы: ссылки

Пилкингтон, А. Кривые, определяемые параметрическими уравнениями. Получено 11 июля 2021 г. с: https://www3.nd.edu/~apilking/Math20560/Lectures/Lecture%2034.pdf

Что такое параметрическая производная?

Если φ = (x(u), y(u)) — параметрическое уравнение для кривой, то параметрическая производная кривой в точке ₀ — это вектор:
Φ′ ( ₀ ) = [′ ( ₀ ), ′ ( ₀ )]

Параметрическая производная представляет собой касательную линию с длиной.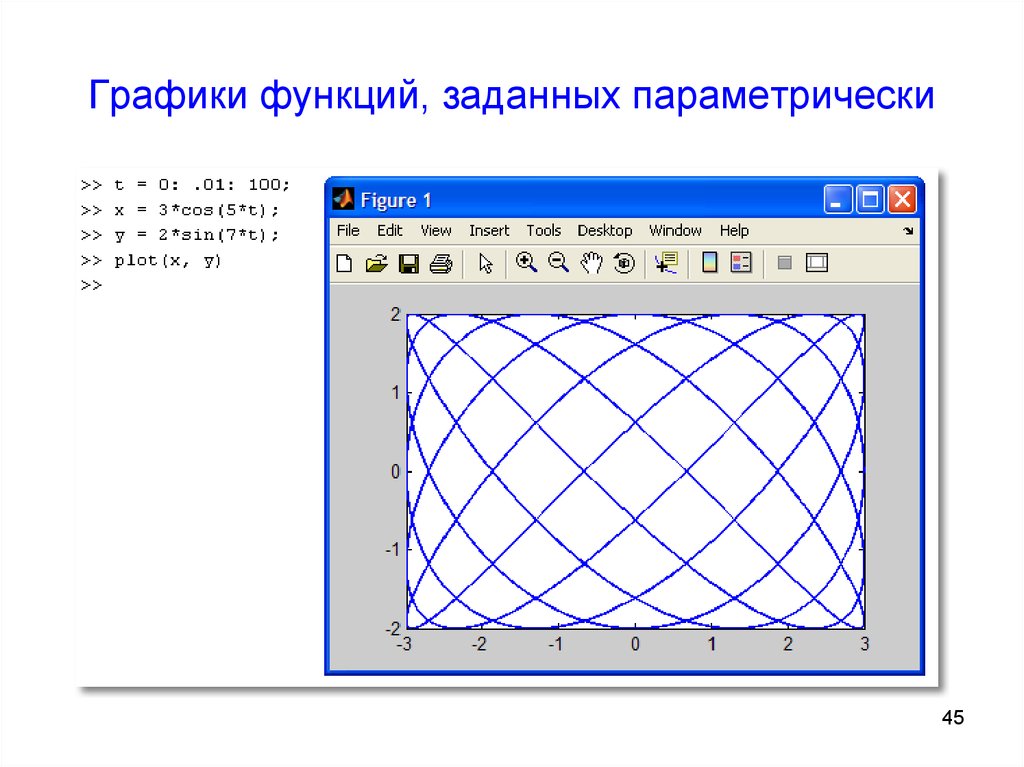 Направление вектора, касающегося кривой, зависит от пути кривой. Его величина определяется скоростью трассировки [1].

Как найти параметрическую производную?

Формула для нахождения параметрической первой производной:

Я использовал здесь θ в качестве примера, но вы также можете дифференцировать по t или другой переменной.

Пример вопроса : Найдите параметрическую производную кривой, определяемой соотношением x = cos(θ), y = 2sin(θ), когда θ = (5π)/6.

Шаг 1: Вычислите производную для обеих функций:

• x = cos(θ): dx/dθ = -sin (θ)
• y = 2sin(θ): dy/dθ = 2cos (θ)

Шаг 2: Подставьте производные из шага 1 в формулу вместе с заданным значением:

Вот и все!

Формула второй производной немного отличается от «обычной» второй производной. Нельзя просто взять производную от первой производной. Вместо этого возьмите производную первой производной, деленную на производную исходного члена x [2]:

Параметрическая производная: ссылки

Графика: Desmos. com
[1] Каждан М. Параметрические кривые. Получено 8 июля 2021 г. с: http://www.cs.jhu.edu/~misha/Fall20/20.pdf
[2] Math 231E, лекция 33. Параметрическое исчисление. Получено 8 июля 2021 г. с: https://faculty.math.illinois.edu/~rdeville/teaching/231-16/lectures/Lecture33.pdf

Другие ссылки

McQuarrie, B. Precalculus: Parametric Representations. Получено 20 мая 2019 г. с: http://cda.mrs.umn.edu/~mcquarrb/teachingarchive/Precalculus/Lectures/ParametricRepresentations.pdf
Сталви, Х. (2014). Преподавание и изучение параметрических функций: базовое исследование. Получено 20 мая 2019 г. по адресу: https://scholarworks.gsu.edu/math_diss/18/
Wilson, M. Задание десятое: исследование параметрических функций. Получено 20 мая 2019 г. с: http://jwilson.coe.uga.edu/EMAT6680Fa11/Wilson/MGW_10/mgw_10.html

ЦИФРОВАТЬ ЭТО КАК:
Стефани Глен . «Параметрическая функция/уравнение: определение, примеры» из StatisticsHowTo. com : Элементарная статистика для всех нас! https://www.statisticshowto.com/parametric-function/

Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на ваши вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!

10.5 Расчет с помощью параметрических уравнений

Мы уже видели, как вычислять наклоны кривых, заданных формулой параметрические уравнения — так мы рассчитывали наклоны в полярных координаты.

Пример 10.5.1. Найти наклон циклоиды $x=t-\sin t$, $y=1-\cos t$. Мы вычисляем $x’=1-\cos t$, $y’=\sin t$, поэтому $${dy\over dx} ={\sin t\over 1-\cos t}.$$ Обратите внимание, что когда $t$ кратно $\pi$, например, $\pi$ или $3\pi$, это $(0/2)=0$, так что есть горизонтальная касательная, по соглашению с рис. 10.4.1. При четных кратных $\pi$ дробь равна $0/0$, что не определено. На рисунке показано, что касательная в таких точках отсутствует. $\квадрат$ 9{2\pi} (1-\cos t)(1-\cos t)\;dt=3\pi.$$ Обратите внимание, что нам нужно преобразовать исходные лимиты $x$ в лимиты $t$. используя $x=t-\sin t$. Когда $x=0$, $t=\sin t$, что происходит только при $t=0$. Аналогично, когда $x=2\pi$, $t-2\pi=\sin t$ и $т=2\пи$. С другой стороны, потому что мы понимаем, как циклоида произведено, мы можем непосредственно видеть, что одна дуга генерируется $0\le t\le 2\pi$. В целом, конечно, лимиты $t$ будут отличается от лимита $x$. $\квадрат$

Этот метод позволит нам вычислить некоторые довольно интересные области, как показано на упражнениях. 9{2\pi} 2\sin(t/2)\;dt = 8.$$ $\квадрат$

Пример 10.5.1 Рассмотрим кривую упражнение 6 в раздел 10.4. Найдите все значения $t$, для которого кривая имеет горизонтальную касательную. (отвечать)

Пример 10.5.2 Рассмотрим кривую упражнение 6 в раздел 10.4. Найдите площадь под одна арка кривой. (отвечать)

Пример 10.5.3 Рассмотрим кривую упражнение 6 в раздел 10. 4. Установите интеграл на длину одной дуги кривой. (отвечать)

Пример 10.5.4 Рассмотрим гиперциклоиду упражнение 7 в раздел 10.4. Найдите все точки в что кривая имеет горизонтальную касательную. (отвечать)

Пример 10.5.5 Рассмотрим гиперциклоиду упражнение 7 в раздел 10.4. Найдите площадь между большой круг и одна арка кривой. (отвечать)

Пример 10.5.6 Рассмотрим гиперциклоиду упражнение 7 в разделе 10.4. Найдите длину одной дуги кривой. (отвечать)

Пример 10.5.7 Рассмотрим гипоциклоиду упражнение 8 в раздел 10.4. Найдите площадь внутри кривой. (отвечать)

Пример 10.5.8 Рассмотрим гипоциклоиду упражнение 8 в разделе 10.4. Найдите длину одной дуги кривой. (отвечать)

Пример 10.5.9 Вспомним эвольвенту окружности из упражнение 9 в раздел 10.4. Найдите точку в первом квадрант на рисунке 10.4.4 при котором касательная вертикальна. (отвечать)

Пример 10.5.10 903:50 Вспомним эвольвенту окружности из упражнение 9 в раздел 10.

No related posts.