«Как решать дробные уравнения?» — Яндекс Кью
Математика и математики
Популярное
Сообщества
Я пытался понять решения в MathEasy и других сервисов, но там объяснение не понятное. По типу: найдите общий знаменатель. А если там знаменатели x-5(2x+6), (x-6)*3. Как? В интернете информацию найти не могу. Кто добр, скиньте способ пропорциями.
ОбразованиеМатематика+3
Иван Абдуллаев
Математика и математики·
412
Ответить1УточнитьАлександр
Математика
174
Закончил физфак Новосибирского университета. Занимался теор. физикой и преподаванием… · 12 окт
Дайте точные координаты источника задач, я не знаком с такой терминологией.
Леонид Коганов
13 октября
А.И.! Поддерживаю! Считаю, надо поддержать действительно неглупого парня, копающего определённый класс пусть и… Читать дальше
Комментировать ответ…Комментировать…
Достоверно
Леонид Коганов
170
Член ММО — Московского математического Общества. Кстати, старейшего в мире. Л.М. Коганов. · 15 окт
Несмотря на то обстоятельство (немаловажное! — Л.К.), что Спрашивающий господин Иван Абдуллаев ныне ученик 7 класса, можно забежать немножко вперёд и воспользоваться пособием:
Соминский Илья Самуилович
Элементарная алгебра. Дополнительный курс.
Глава I. Элементарные методы решения алгебраических уравнений с одним неизвестным.
Параграф 9. Решение дробно-рациональных..
2 эксперта согласны
Александр
подтверждает
15 октября
Очень полезный и конструктивный ответ. Следование этому совету позволит освоить математическую терминологию и… Читать дальше
Комментировать ответ…Комментировать…
Вячеслав Че
41
Программист · 13 окт
В общем(конкретного уравнения нет?), дробные уравнения решаются путем избавления от дробей. Типа a(x)/b(x)=c(x)/d(x) <=> a(x)*d(x)=b(x)*c(x) <=> a(x)*d(x) -b(x)*c(x)=0. Общим знаменателем двух дробей будет произведение двух знаменателей. Пример. Для удобства f,g,h,j,i,k — это f(x),g(x),h(x),j(x),i(x),k(x) f/g+h/j=i/k <=> (f*j+g*h)/(g*j)=i/k <=>(f*j+g*h)*k=(g*j)*i <=>… Читать далее
Леонид Коганов
13 октября
Что значит «дробные уравнения»? Это — общепринятый термин? В каких источниках он употребляется, и в каких из этих.
2-x-2}$$
$$ {\left\{ \begin{array}{c} (a+3-5+3a)x-2(a+3)-(5-3a) = ax+3 \\ x \neq -1, x \neq 2 \end{array} \right.} $$
$$ (4a-2)x+a-11 = ax+3 $$
$$ (3a-2)x = 14-a \Rightarrow \left[ \begin{array}{cc} {\left\{ \begin{array}{c} a = \frac{2}{3} \\ 0 \cdot x = 5-\frac{2}{3}, x \in \varnothing \end{array} \right.} \\ {\left\{ \begin{array}{c} a \neq \frac{2}{3} \\ x = \frac{14-a}{3a-2} \end{array} \right.} \end{array} \right. \Rightarrow {\left\{ \begin{array}{c} a \neq \frac{2}{3} \\ x = \frac{14-a}{3a-2} \end{array} \right.} $$
Проверяем условия $x \neq -1, x \neq 2$.
$$ \frac{14-a}{3a-2} \neq -1 \Rightarrow 14-a \neq 2-3a \Rightarrow 2a \neq -12 \Rightarrow a \neq -6 $$
$$ \frac{14-a}{3a-2} \neq 2 \Rightarrow 14-a \neq 6a-4 \Rightarrow 7a \neq 18 \Rightarrow a \neq \frac{18}{7} $$
Ответ:
При a = $\{-6; \frac{2}{3}; \frac{18}{7}\}$ решений нет; при $a \neq \{-6; \frac{2}{3}; \frac{18}{7}\}$ один корень $x = \frac{14-a}{3a-2}$
Пример 2.
2}}{2} = \frac{a(1 \pm \sqrt{5})}{2} $$
2) Накладываем условия $z \neq 0, z \neq \pm a$ на полученные решения.
$$ z = — \frac{a}{4} \neq 0 \Rightarrow a \neq 0, z = -\frac{a}{4} \neq \pm a \Rightarrow a \neq 0 $$
$$ z = \frac{a(1 \pm \sqrt{5})}{2} \neq 0 \Rightarrow a \neq 0 $$
$$ z = \frac{a(1 \pm \sqrt{5})}{2} \neq \pm a \Rightarrow a(1 \pm \sqrt{5}) \neq \pm 2a \Rightarrow a \neq 0 $$
3) Особая точка a = 0.
При a = 0 исходное уравнение является ложным: 0 = 8, решений нет.
4) Возвращаемся к исходной переменной: x = z-2a
$$ x_1 = -\frac{a}{4}-2a = -\frac{9}{4} a $$
$$ x_2 = \frac{a(1-\sqrt{5})}{2}-2a = \frac{a(1-\sqrt{5}-4)}{2} = \frac{a(-\sqrt{5}-3)}{2} $$
$$ x_2 = \frac{a(1+\sqrt{5})}{2}-2a = \frac{a(1+\sqrt{5}-4)}{2} = \frac{a(\sqrt{5}-3)}{2} $$
Ответ:
При a = 0 корней нет
При $a \neq 0$ три корня $x_1 = -\frac{9}{4} a; x_{2,3} = \frac{a(\pm\sqrt{5}-3)}{2}$
РЕШЕНИЕ УРАВНЕНИЙ С ДРОБЯМИ
РЕШЕНИЕ УРАВНЕНИЙ С ДРОБЯМИПримечание:
- Рациональное уравнение – это уравнение, в котором хотя бы один знаменатель
содержит переменную.
- Когда знаменатель содержит переменную, существует ограничение на домен. Переменная не может принимать любое число, которое вызвало бы знаменатель равен нулю.
- Первым шагом решения рационального уравнения является преобразование уравнение к уравнению без знаменателей. Это новое уравнение может быть эквивалентны (те же решения, что и исходное уравнение) или могут не совпадать эквивалентные (посторонние решения).
- Следующим шагом является установка уравнения равным нулю и решение.
- Помните, что вы пытаетесь изолировать переменную.
- В зависимости от проблемы существует несколько способов помочь вы решаете проблему.
Если вы хотите получить более подробный обзор дробей, нажмите «Дроби».
Найдите x в следующем уравнении.
Пример 2:
Напомним, что на ноль делить нельзя. Поэтому мы должны устранить любые
значений x, которые приведут к тому, что знаменатель будет иметь нулевое значение.
Мы
определить эти значения, приравняв знаменатель к нулю и решив
для х.
Произведение равно нулю только в том случае, если хотя бы один из множителей равен
нуль.
Если какое-либо из решений окажется либо 8, либо 3, мы отбросим их как посторонние решения.
Упростите исходное уравнение, вычтя 2 x с обеих сторон уравнение.
Упростите уравнение, умножив обе части уравнения на x 2 -5 x -24 и упрощение результатов.
Произведение может быть равно нулю только в том случае, если хотя бы один из множителей
равен нулю.
Поскольку это не действительное число, единственными реальными решениями являются x = 10.
Проверьте решение x =10 в исходном уравнении для x. Если левая сторона
уравнения равен правой части уравнения после
замена, вы нашли правильный ответ.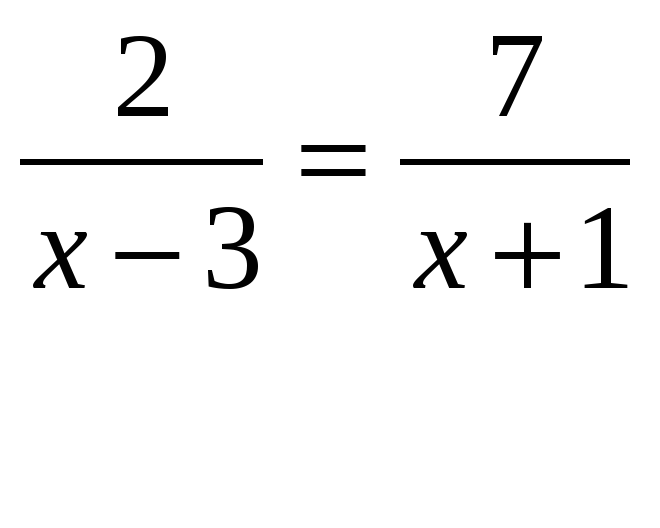
- Левая сторона:
- Правая сторона:
Так как левая часть исходного уравнения равна правой части исходное уравнение после того, как мы подставим значение 10 вместо x, тогда x = 10является решением.
Вы также можете проверить свой ответ, построив график
.
(образуется вычитанием правой части исходного уравнения из левой части). Посмотрите, где график пересекает ось x; это будет настоящим решением. Обратите внимание, что график пересекает ось x в одном месте, 10.
Это означает, что существует одно действительное решение, и решение равно x = 10.
Если вы хотите работать с другим примером, нажмите «Пример».
Если вы хотите проверить себя, решив некоторые задачи, подобные этой
например, нажмите Проблема
Если вы хотите вернуться к содержанию уравнения, нажмите
Содержание
Домашняя страница S.
O.S MATHematics
Вам нужна дополнительная помощь? Пожалуйста, разместите свой вопрос на нашем S.O.S. Математика CyberBoard.
Свяжитесь с нами
Математика Медикс, ООО. — П.О. Box 12395 — Эль-Пасо, Техас 79913 — США
пользователей онлайн за последний час
MathOnWeb — Электронная книга по алгебре — Дробные выражения и уравнения
В этой главе мы рассмотрим дроби в четвертый и последний раз. Давайте просмотрите наши предыдущие три встречи:
- Обыкновенные дроби. В разделе 1.2 мы представили
обозначение дроби, а / б ,
где a и b были целыми числами для
описать часть или часть целого объекта.
Например, ¾ означало, что мы разбили объект на 4 равные части. части и у нас было 3 из тех частей. Обратите внимание, что a / b было числом;
обозначения а / б не имели ничего общего с делением.
В разделе 1.2 мы также узнали, как преобразовать дробь в
самые низкие условия,
как складывать и вычитать дроби,
умножить дроби,
разделить дроби и как
преобразовать неправильную дробь
в смешанную дробь с помощью длинного деления.
- Разделение номеров. В разделе 2.4
мы определили деление двух чисел в терминах умножения.
Мы сказали, что деление a на b дает число c такое, что c умножить на b вернули
- Отдел выражений. В разделе 3.5
мы видели, что существует три различных способа разделения выражений в зависимости от
были ли числитель a и знаменатель b мономами, мультиномами или полиномами.
- Если бы они были мономами, затем деление a на b просто равносильно записи алгебраическая дробь, a / b , и уменьшив его до наименьших значений, как обыкновенную дробь.
- Если бы они были полиномами, то a можно разделить на b с использованием длинного деления, точно так же, как неправильная обыкновенная дробь может быть преобразована в смешанную дробь с помощью длинного деления.
- Если a было многочленом и b был одночленом, то мы поместили в каждый член а над б так, чтобы результатом деления была сумма
алгебраические дроби.
части и у нас было 3 из тех частей. Обратите внимание, что a / b было числом;
обозначения а / б не имели ничего общего с делением.
В разделе 1.2 мы также узнали, как преобразовать дробь в
самые низкие условия,
как складывать и вычитать дроби,
умножить дроби,
разделить дроби и как
преобразовать неправильную дробь
в смешанную дробь с помощью длинного деления.
В разделе 2.4 мы также узнали, что деление a на b может быть
заменяется умножением на на
обратная величина b .
Наконец, мы узнали правила деления с участием
знаки минус.
Осталось обсудить алгебраических дробей , то есть дробей, числитель и знаменатель являются алгебраическими выражениями. В этой главе обсуждаются алгебраические дроби и дробные уравнения. Он содержит следующие разделы:
- раздел 11.1 — В этом разделе мы говорим о упрощение алгебраических дробей. Главный новый результат состоит в том, что поскольку теперь мы знаем, как разложить выражение на множители, мы можем разложить числитель или знаменатель, и это открывает новый способ уменьшить алгебраическая дробь до младших членов.
- раздел 11.2 — В этом разделе мы Расскажите об умножении и делении алгебраических дробей.
- раздел 11.3 — В этом разделе мы Расскажите о сложении и вычитании алгебраических дробей.
- раздел 11.4 — В этом разделе мы покажем, как
решать уравнения, содержащие алгебраические дроби.
11.1 — Упрощение алгебраических дробей
Некоторые определения
- обыкновенная дробь – это число, которое записывается в форма или а / б , где a , числитель , и b , знаменатель , оба являются целыми числами. Обыкновенная дробь используется для описания части или доли целого объекта. Обозначение означает, что мы разбиваем объект на b равные части и у нас есть a тех частей. Часть или часть объекта, который у нас есть это а / б .
- Деление определяется с точки зрения умножения.
Деление числа a на число b дает число c такое, что c умножить на b дает обратно a .
Мы используем то же обозначение дроби, a / b , для обозначения деления a на b , потому что, когда a и b оба были целыми числами, тогда
деление на / b дает обыкновенную дробь a / b .
- Алгебраическая дробь — это дробь, у которой числитель или знаменатель являются алгебраическими
выражения.
Два примера алгебраических дробей:
и .
- A рациональная алгебраическая дробь — алгебраическая дробь, числитель и знаменатель являются полиномами. Первый пример выше — это рациональная алгебраическая дробь; второй нет.
- A правильная обыкновенная дробь обыкновенная дробь, числитель которой меньше ее знаменатель и неправильная обыкновенная дробь это тот, числитель которого больше или равен его знаменателю. Смешанная дробь — это сумма целого числа и правильной дроби. Длинное деление можно использовать для преобразования неправильную дробь в смешанную дробь.
- правильная алгебраическая дробь является рациональной алгебраической дробью
чей числитель имеет младшую степень чем его знаменатель, а неправильная алгебраическая дробь равна единице
числитель которого больше или равен знаменателю. Смешанное выражение представляет собой сумму многочлена и правильной алгебраической дроби. Длинное деление можно использовать для преобразования
неправильную алгебраическую дробь к смешанному выражению.
Смешанное выражение представляет собой сумму многочлена и правильной алгебраической дроби. Длинное деление можно использовать для преобразования
неправильную алгебраическую дробь к смешанному выражению.Деление на ноль
Эта операция не допускается в математике. Нажмите здесь, чтобы узнать, почему. Это означает, что в алгебраической дроби
,
x не может равняться 1 или −3, потому что эти значения x вызовут дробь, чтобы знаменатель был равен нулю.
Приведение алгебраической дроби к наименьшим членам
Посмотрите на алгебру, которую мы делаем здесь:
- Начнем с дроби a / b .
- Умножаем на 1. Это не изменит его значение.
- Запишем «1» как дробь d / d .
- Перемножаем две дроби. Числитель новой дроби равен ad и знаменатель bd .
- Последняя дробь равна , что эквивалентно первой дроби.
Если мы пойдем в обратном направлении, то мы скажем, что сводим дробь к ее простейшая эквивалентная дробь или низшая дробь . Для этого находим любой множитель, который содержится и в числителе, и в знаменателе. и отменить это или зачеркнуть , например:
Пример: Сократите обыкновенные дроби 10/6 и 10/5 до меньших значений.
| Разложите числитель и знаменатель на множители. Отмените общий делитель 2. | |
Разложите числитель и знаменатель на множители. Отмените общий делитель 5. Результат деления — целое число. Мы говорим, что знаменатель делится поровну в числитель. |
Если числитель и знаменатель алгебраической дроби являются мономами , то выполните все следующие шагов, чтобы сократить дробь до наименьшего члена :
- Получите знак, используя правила для знаков.
- Уменьшить коэффициент до минимума.
- Отменить идентичных множителей, которые появляются как в числителе, так и в знаменателе.
- Объедините экспоненты с одинаковым основанием, используя свойство деления экспонент.
Пример: Уменьшить алгебраическую дробь
на самые низкие условия.
Решение:
Знак − ставится перед результатом
или перед числителем; никогда не стоит перед знаменателем. Уменьшите коэффициент 6/9 до самые низкие условия. |
Пример: Уменьшить алгебраическую дробь
на самые низкие условия.
Решение:
| Два знака — заменены знаком +, который нам не нужно отображать.
Коэффициент снижается до ¼.
Числитель содержит другие множители, поэтому 1 в числителе можно опустить. Объедините экспоненты с основанием x , используя свойства экспонент. |
Пример: Уменьшить алгебраическую дробь
на самые низкие условия.
Решение:
Знак − ставится впереди. Коэффициент снижается до 1/3. одинаковых множителей из x 3 в числителе и знаменателе сокращаются. Числитель не содержит других множителей, поэтому на этот раз должна отображаться 1. |
Пример: Уменьшить алгебраическую дробь
на самые низкие условия.
Решение:
| После проведения всех упрощений знаменатель равен 1, поэтому нам не нужно его отображать. Таким образом, результатом является обычное выражение, не алгебраическая дробь. |
Если числитель и знаменатель алгебраической дроби равны многочленов , тогда в дополнение к шагам, перечисленным выше, попробуйте выполнить следующие шагов, чтобы сократить дробь до минимального значения :
- Фактор числителя или знаменателя или обоих. Иногда это вызывает новые появляются аннулирующие факторы.
- Множитель a − знак вне числителя или знаменателя. Иногда это приводит к появлению нового фактора отмены.
Иногда это приводит к появлению нового фактора отмены.В следующих примерах мы будем предполагать, что вы уже знаете как сделать факторинг поэтому мы просто покажем, как использовать множители для сведения алгебраических дробей к самые низкие условия.
Пример: Уменьшить алгебраическую дробь
на самые низкие условия.
Решение:
| Разложите числитель и знаменатель на множители. Отменить общий делитель x . |
Пример: Уменьшить алгебраическую дробь
на самые низкие условия.
Решение:
| Фактор числителя. Отменить общий делитель x − 2. |
Пример: Уменьшить алгебраическую дробь
на самые низкие условия.
Решение: Это та же алгебраическая дробь, что и в предыдущем примере, за исключением что знаменатель отличается знаком -.
| Разложить на множители числитель и фактор a − выйти
знаменателя. Отменить общий делитель x − 2. Поставить знак − в числителе и распространять его. |
11.2 — Умножение и деление алгебраических дробей
Умножение алгебраических дробей
Порядок умножения алгебраических дробей такой же, как и порядок умножения алгебраических дробей. умножение обыкновенных дробей.
| Умножение двух алгебраических дробей дает новую алгебраическую дробь. Умножьте два числителя, чтобы получить новый числитель, и умножьте два знаменателя, чтобы получить новый новый знаменатель: Затем упростите, сократив новую дробь до наименьших членов.  |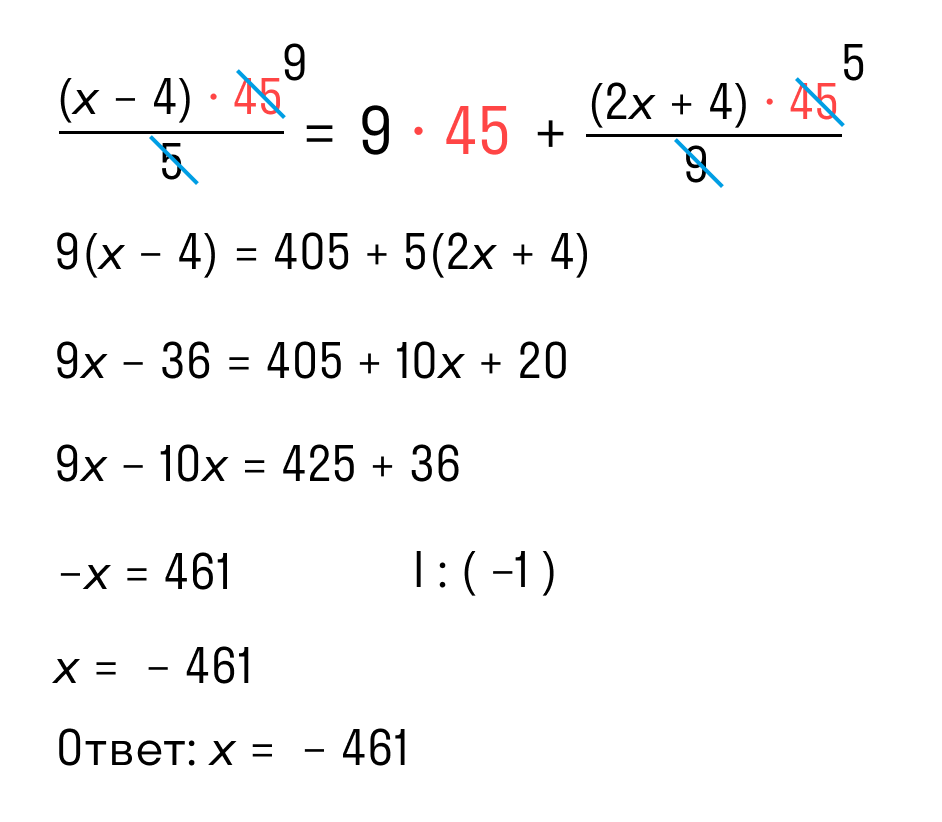
Примеры:
Деление алгебраических дробей
Порядок деления алгебраических дробей такой же, как и порядок деления алгебраических дробей. деления обыкновенных дробей.
| Замените деление на дробь на умножение на обратную дробь , например: Затем выполните умножение двух дробей как описано выше. |
Обратите внимание, что вы берете обратную дробь внизу!
| Вот почему эта процедура работает: Суть в том, что вместо того, чтобы видеть дробь, деленную на дробь, ищите одну дробь, числитель и знаменатель которой являются дробями.  На первом шаге мы умножили эту дробь на UFOO
числитель и знаменатель которого являются дробями. НЛО был
выбран так, чтобы дроби в знаменателе сокращались и давали 1. После другого
упрощение, оставившее только окончательное умножение дробей. |
Примеры: Найдите следующие три шага: (1) инвертируйте нижнюю дробь, (2) умножить дроби, (3) упростить.
11.3 — Сложение и вычитание алгебраических дробей
Процедура сложения или вычитания алгебраических дробей такая же, как и процедура сложение или вычитание обыкновенных дробей.
Сложение дробей с одинаковыми знаменателями
Фракции, имеющие равные знаменатели, также называются , как и дроби .
| Чтобы сложить или вычесть две одинаковые дроби, просто сложите или вычтите числители и поднесите результат к общему знаменателю, как это: |
Пример:
Сложение дробей с неравными знаменателями
| Чтобы сложить или вычесть дроби, у которых знаменатели не равны, их нужно сначала преобразовать равные дроби и имеют общий знаменатель.  Вот шаги:
|
Пример: . Чтобы вычесть эти дроби, выполните следующие действия:
- Найдите ЖК-дисплей, который равен 10.
- Поскольку в знаменателе первой дроби уже стоит LCD, нам нужно только умножьте вторую дробь на 5/5, чтобы преобразовать ее в эквивалентную дробь с знаменатель 10.
- Вычтите числители и поместите результат на ЖК-дисплей.
- Упростите, сократив дробь до наименьшего члена.
Пример: . Чтобы добавить эти дроби, выполните следующие действия:
- Найдите ЖК-дисплей, который имеет размер (4 x − 1)( x + 3).
- Умножить числитель и знаменатель первой дроби на ( x + 3) и числитель и знаменатель второй дроби на (4 x — 1):
- Обе дроби теперь имеют LCD в качестве знаменателя. Добавьте числители и поместите результат на ЖК-дисплей.
- Упростите, распределив числитель.
Сложение дробей с факторизуемыми знаменателями
| Вы должны всегда факторизовать знаменатели. 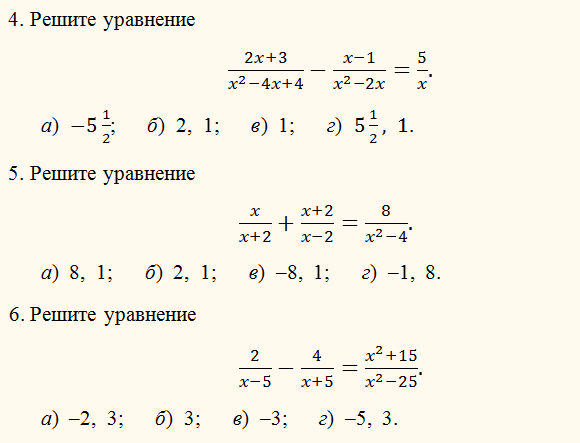 Это единственный способ определить, является ли фактор
появляется более чем в одном знаменателе. |
Пример: . Чтобы добавить эти дроби, выполните следующие действия:
- Разложите знаменатель первой дроби на множители. Тогда мы видим, что факторы x — 2 и x — 3 появляются более чем в одном знаменателе:
- Найдите ЖК-дисплей, который имеет размер ( x − 2)( x − 3).
- Умножьте числитель и знаменатель второй дроби на ( x − 3) и числитель и знаменатель третьей дроби на ( x — 2):
- Теперь обе дроби имеют LCD в качестве знаменателя. Добавьте числители и поместите результат на ЖК-дисплей.
- Упростите, распределив и добавив одинаковые члены в числителе.
Сложение дробей и не дробей (смешанные выражения)
| Чтобы сложить или вычесть дроби и не дроби, преобразуйте не дроби в дроби со знаменателем 1.  |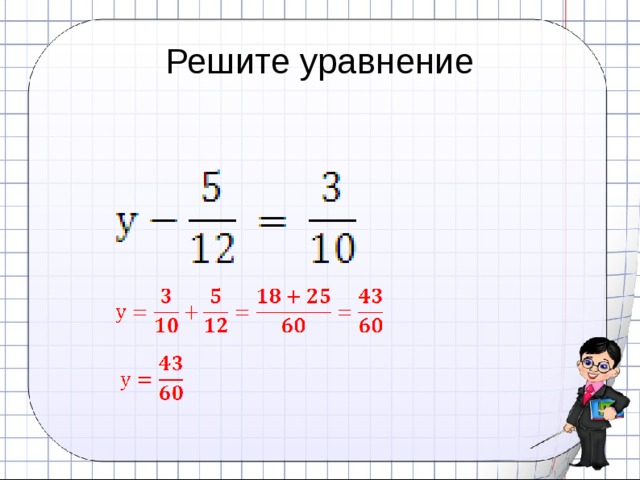
Пример: . Чтобы добавить эту дробь и не дробь, выполните следующие действия:
- Запишите не дробь в виде дроби со знаменателем 1:
- Найдите ЖК-дисплей, который, конечно же, ( x − 2).
- Умножить числитель и знаменатель первой дроби на ( х — 2):
- Обе дроби теперь имеют LCD в качестве знаменателя. Добавьте числители и поместите результат на ЖК-дисплей.
- Упростите, распределив и добавив одинаковые члены в числителе.
11.4 — Дробные уравнения
Прежде чем читать этот раздел, вы можете рассмотреть следующие темы:
- Основы решения уравнений.
- Техника очистки фракций для
решение линейных уравнений.
- Как найти наименьший общий знаменатель (ЖК) алгебраических дробей.
Дробное уравнение — это уравнение, содержащее дробные члены. В разделе 4.2 мы видели как решить линейное уравнение , содержащее дроби. Шаги для решения любого дробного уравнения точно такие же:
- Посмотрите на знаменателей всех дробей и найдите их наименьшее общее кратное (НОК) (это также называется наименьшим общим знаменателем (LCD) дробей).
- Умножьте обе части уравнения на LCM.
- Распределите LCM по обеим частям уравнения.
- Уравнение больше не содержит дробей, и вы можете продолжить его решение с помощью основных процедур решения уравнений.
- Проверьте решение. Это особенно важно для дробных уравнений. Там
две возможные проблемы:
- Если знаменатель любого члена дроби содержит x , то LCM будет
также содержит x , и умножение обеих частей уравнения на LCM даст
увеличьте степень x в уравнении. Это часто приводит к посторонним решениям.
- При подстановке решений обратно в исходное уравнение для их проверки, любое решение, в результате которого любой член дроби имеет нулевой знаменатель, должно быть отброшено. потому что деление на ноль запрещено в математике.
- Если знаменатель любого члена дроби содержит x , то LCM будет
также содержит x , и умножение обеих частей уравнения на LCM даст
увеличьте степень x в уравнении.
Это часто приводит к посторонним решениям.Пример 1: Решите это дробное уравнение для x :
Решение: Члены дробей имеют знаменатели 3, 2 и 6. НОК этих чисел равен 6. Умножьте обе части уравнения на 6. (Не забудьте заключить обе части уравнения в скобки.)
Распределите по обеим частям уравнения:
4 х — 3 = 6 x + 7.
Фракции теперь очищены, так что это больше не дробное уравнение.
Завершите решение уравнения, собрав линейные члены в левой части и
постоянные члены в правой части. Это дает:
−2 x = 10,
Разделите обе части на −2. Это дает решение:
х = -5.
Проверьте его, подставив обратно в исходное уравнение. Это дает -23/6 = -23/6, так что решение проверено.
Пример 2: Решите это дробное уравнение для x :
Решение: Члены дробей имеют знаменатели x 2 + x − 2, x +
2, и x – 1.
Может показаться, что LCM является продуктом всех трех, но поскольку x 2 + x − 2 можно разложить на множители
как ( x + 2)( x — 1), LCM на самом деле просто ( x + 2)( x — 1). Умножьте на него обе части уравнения.
(Не забудьте заключить обе части уравнения в скобки.)
Распределите по обеим частям уравнения:
9 = 3 ( х — 1) + 7 ( х + 2).
Теперь дроби очищены, так что это больше не дробное уравнение; это линейное уравнение. Решите ее, используя обычные методы. Распределите еще раз на правой стороне:
9 = 10 x + 11.
Соберите постоянные члены в левой части:
−2 = 10 х .
Разделите обе части на 10. Это дает решение:
х = −1/5.
Проверьте его, подставив обратно в исходное уравнение.
Это дает -25/6 = -25/6, так что решение проверено.
Пример 3: Цель этого примера — проиллюстрировать решение, которое должно быть отклонено, потому что это вызывает деление на ноль . Уравнение идентично один в предыдущем примере, за исключением того, что он отличается знаком одного термина. Решите это дробное уравнение для x :
Решение: Сравните каждый шаг здесь с соответствующим шагом в приведенном выше примере. Умножьте обе части уравнения на LCM, что снова равно ( х + 2)( х — 1):
Распределите по обеим частям уравнения:
9 = −3 ( x – 1) + 7 ( x + 2).
Распределите еще раз на правой стороне:
9 = 4 x + 17.
На этот раз решение х = -2.